1 Introduction

In the past decades, stability analysis of various classes of neural network models such as Hopfield neural networks, Cohen–Grossberg neural networks, cellular neural networks, and shunting inhibitory cellular neural networks (SICNNs) has been extensively investigated since the stable neural networks have been successfully applied to some practical engineering problems such as signal processing, pattern classification, associative memory design and control and optimization [1–9]. In particular, because of the complicated dynamic properties of the neural cells in the real world, the existing neural network models in many cases cannot characterize the properties of a neural reaction process precisely. Thus, it is natural and important that systems will contain some information about the derivative of the past state to further describe and model the dynamics for such complex neural reactions. Furthermore, the stability of SICNNs with neutral time-varying delays and continuously distributed delays has been the object of intensive analysis by numerous authors in recent years (see [10–13] and the references therein). Usually, time delays may lead to oscillation, divergence or instability which may be harmful to the system. Furthermore, the dynamic systems with proportional delays have many interesting applications in engineering and sciences such as biology, economy, control and electrodynamics [14–20]. Consequently, the stability of cellular neural networks (CNNs) with proportional delays has been extensively and intensively studied in [21, 22]. Most recently, there is a lively interest to analysis of finite-time stability (FTS) behavior for time-delay systems (see, e.g., [23–27] and the references therein). It is worth to mention here that FTS and Lyapunov asymptotic stability (LAS) are different concepts by mean a system may be FTS but not LAS and vice versa [1], and FTS is an useful concept to study in many practical systems in the vivid world [28–33]. However, to the best of our knowledge, no such work has been done on the SICNNs with neutral proportional delays. This motivates us to further study FTS of the following class of non-autonomous SICNNs with neutral proportional delays:

$$\begin{aligned} \left\{ \begin{array}{l} x '_{ij}(t)=-a_{ij}(t){x}_{ij}(t)-\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(t)f(x_{kl}(q_{kl} t) )x_{ij}(t)\\ \;\quad \qquad -\,\sum \limits _{C_{kl}\in N_{q}(i,j)}B_{ij}^{kl}(t)g\left( x_{kl}'(q_{kl} t) \right) x_{ij}(t)+L_{ij}(t), \quad t>0,\\ {x}_{ij}(0)={x}_{ij}^{0}, {x}_{ij}'(0)={x}_{ij}^{1},ij \in J:=\{11, \ldots , 1n, 21, \ldots , 2n, \ldots , m1, \ldots , mn \}, \end{array}\right. \end{aligned}$$
(1.1)

where \(C_{ij}\) denotes the cell at the (i, j) position of the lattice, the r-neighborhood \(N_{r}(i,j)\) of \(C_{ij}\) is

$$\begin{aligned} N_{r}(i,j)=\{C_{kl}:\max (|k-i|,|l-j|)\le r,1\le k\le m,1\le l\le n\}, \end{aligned}$$

\(N_{q}(i,j)\) is similarly specified, \(x_{ij}\) is the activity of the cell \(C_{ij}\), \(L_{ij}(t)\) is the external input to \(C_{ij}\), \(a_{ij}(t)\) represents the passive decay rate of the cell activity, \(C_{ij}^{kl}(t)\) and \(B_{ij}^{kl}(t)\) are the connection or coupling strength of postsynaptic activity of the cell transmitted to the cell \(C_{ij}\), and the activity function \(f(x_{kl})\) is a continuous function representing the output or firing rate of the cell \(C_{kl}\), \(q _{ij}, i j \in J,\) are proportional delay factors and satisfy \(0< q _{ij} < 1\), and \(x^{ 0 }=(x_{11}^{0}, \ldots ,x_{mn}^{0})^{T}, x^{ 1 }=(x_{11}^{1}, \ldots ,x_{mn}^{1})^{T}\in \mathbb {R}^{mn}\) are the initial value of \(x_{ij}(t)\) and \(x'_{ij}(t)\) at time \(t_{0}=0\), respectively.

For convenience, we denote by \(\mathbb {R}^{mn}\)(\(\mathbb {R}=\mathbb {R}^{1}\)) the set of all mn-dimensional real vectors (real numbers). For any \(x=\{x_{ij}\}=(x_{11}, \ x_{12}, \ldots , x_{ mn})^{T} \in \mathbb {R}^{ mn}\), we let |x| denote the absolute-value vector given by \(|x|=\{|x_{ij}|\}\), and define \(\Vert x \Vert =\max \nolimits _{ ij\in J} |x_{ij } |\). Throughout this paper, it will be assumed that \(a_{ij}, L_{ij}, \ C_{ij}^{kl}, \ B_{ij}^{kl} :[t_{0}, \ +\infty )\rightarrow \mathbb {R}\) are bounded and continuous functions, where \(ij \in J.\)

We also make the following assumptions which will be used later.

\((A_0)\) for \(ij \in J\), there exist a bounded continuous function \(a_{ij}^{*} :[t_{0}, \ +\infty )\rightarrow (0, \ +\infty )\) and a positive constant \(K_{ij}\) such that

$$\begin{aligned} e ^{ -\int _{s}^{t}a_{ij}(u)\mathrm{d}u}\le K_{ij} e ^{ -\int _{s}^{t}a^{*}_{ij}(u)\mathrm{d}u} \qquad \text{ for } \text{ all } t,s\in [t_{0}, \ +\infty ) \text{ and } t-s\ge 0. \end{aligned}$$

\((A_{1})\) there exist nonnegative constants \(\mu ^{f}\), \(\mu ^{g}\), \(M ^{f}\) and \(M ^{g}\) such that

$$\begin{aligned} \left| f(u )-f(v )\right| \le \mu ^{f} |u -v |, \ |f(u ) |\le M^{f}, |g(u )-g(v )|\le \mu ^{g} |u -v |, \ |g(u ) |\le M^{g}, \quad \text{ for } \text{ all } \ u , \ v \in \mathbb {R}. \end{aligned}$$

\((A_{2})\) for each \(ij\in J\), there exist positive constants \(\eta ^{1}_{ij}\), \(\eta ^{2}_{ij}\), \(\eta ^{3}_{ij}\) and \(\eta ^{4}_{ij}\) such that

$$\begin{aligned} -\eta ^{1}_{ij}= & {} \sup \limits _{t\ge 0}\left\{ - a_{ij}^{*}(t)+K _{ij} \left[ \sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(t)\right| M^{f}+ \sum \limits _{C_{kl}\in N_{q}(i,j)}\left| B_{ij}^{kl}(t)\right| M^{g} +\left| L_{ij} (t)\right| \right] \right\} <0, \end{aligned}$$
(1.2)
$$\begin{aligned} \eta ^{2}_{ij}= & {} \sup \limits _{t\ge 0}\left\{ \left| a_{ij}(t)\right| +\sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(t)\right| M^{f} +\sum \limits _{C_{kl}\in N_{q}(i,j)}\left| B_{ij}^{kl}(t)\right| M^{f}+\left| L _{ij}(t)\right| \right\} < 1, \end{aligned}$$
(1.3)
$$\begin{aligned} -\eta ^{3}_{ij}= & {} \sup \limits _{t\ge 0}\left\{ -a_{ij}^{*}(t)+K_{ij} \left[ \sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(t)\right| \left( M^{f} + \mu ^{f}\right) \right. \right. \nonumber \\&\left. \left. +\,\sum \limits _{C_{kl}\in N_{q}(i,j)}\left| B_{ij}^{kl}(t)\right| \left( M^{g} + \mu ^{g}\right) \right] \right\} <0, \end{aligned}$$
(1.4)

and

$$\begin{aligned} \eta ^{4}_{ij}=\sup \limits _{t\ge 0}\left\{ \left| a_{ij}(t)\right| +\sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(t)\right| \left( M^{f}+\mu ^{f}\right) + \sum \limits _{C_{kl}\in N_{q}(i,j)}\left| B_{ij}^{kl}(t)\right| \left( M^{g}+\mu ^{g}\right) \right\} <1. \end{aligned}$$
(1.5)

2 Main results

Definition 2.1

For a given time \(T > 0\) and positive numbers \(r_{1}< r_{2}\), a solution \(x^{*}(t)\) of (1.1) is said to be finite-time stable with respect to \((r_{1},r_{2},T )\) if for any solution x(t) of (1.1), \(\max \{\Vert x(0)-x^{*}(0)\Vert , \Vert x'(0)-x^{*} \ '(0)\Vert \}\le r_{1}\) implies that

$$\begin{aligned} \max \left\{ \left\| x(t)-x^{*}(t)\right\| , \left\| x'(t)-x^{*} \ '(t)\right\| \right\} \le r_{2} \end{aligned}$$

for all \(t \in [0,T]\). System (1.1) is said to be finite-time stable with respect to \((r_{1},r_{2},T )\) if any solution \(x^{*}(t)\) of (1.1) is FTS with respect to \((r_{1},r_{2},T )\).

Lemma 2.1

Let \((A_{0})\) \((A_{1})\) and \((A _{2})\) hold. Suppose that \(x(t)= \{x_{ij}(t)\}\) is a solution of system (1.1) with initial values

$$\begin{aligned} x_{ij}(0)= x_{ij}^{0}, \ x_{ij} '(0)= x_{ij}^{1}, \ \text{ and } \ \max \left\{ \left| x_{ij}^{0}\right| , \ \left| x_{ij}^{1}\right| \right\} <\frac{1}{M}, \quad \ ij \in J, \end{aligned}$$
(2.1)

where \(M\ge \max \{1, \ \max \nolimits _{ij\in J}K_{ij}\}\) is a constant. Then

$$\begin{aligned} \max \left\{ \left| x_{ij}(t)\right| , \ \left| x_{ij}'(t)\right| \right\} <1, \quad \text{ for } \text{ all } \ t\ge 0, \ ij \in J. \end{aligned}$$
(2.2)

Proof

From (2.1), we have

$$\begin{aligned} \max \left\{ \left\| x (0) \right\| , \ \left\| x '(0) \right\| \right\} <\frac{1}{M} \le 1. \end{aligned}$$

If the statement in (2.2) is false, there must exist \(ij \in J\) and \(\theta ^{*} >0\) such that

$$\begin{aligned} \max \left\{ \left| x_{ij}(\theta ^{*}) \right| , \ \left| x_{ij}'(\theta ^{*}) \right| \right\} =1, \end{aligned}$$
(2.3)

and

$$\begin{aligned} \max \left\{ \left| x_{kl}(t)\right| , \ \left| x_{kl}'(t)\right| \right\} <1 \quad \text{ for } \text{ all } t \in [0, \ \theta ^{*}), \ kl\in J. \end{aligned}$$
(2.4)

Note that

$$\begin{aligned}&x_{ij}'(s)+a_{ij}(s)x_{ij} (s ) \nonumber \\&\quad = -\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(s)f(x_{kl}(q_{kl} s ) )x_{ij}(s)\nonumber \\&\qquad -\sum \limits _{C_{kl}\in N_{q}(i,j)}B_{ij}^{kl}(s)g\left( x_{kl}'(q_{kl} s ) \right) x_{ij}(s)+L_{ij} (s),\ s\in [0, \ t], \ t\in [0, \ \theta ^{*}]. \end{aligned}$$
(2.5)

Multiplying both sides of (2.5) by \(e ^{ \int _{0}^{s}a_{ij}(u)\mathrm{d}u}\) and integrating it on \([0, \ t]\), we get

$$\begin{aligned} x_{ij} (t)\,&=\, x_{ij} (0) e ^{-\int _{0}^{t}a_{ij}(u)\mathrm{d}u}\\&\quad+\,\int _{0}^{t}e ^{ -\int _{s}^{t}a_{ij}(u)\mathrm{d}u}\left[ -\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(s)f(x_{kl}(q_{kl}s ))x_{ij}(s)\right. \\&\quad\left. -\,\sum \limits _{C_{kl}\in N_{q}(i,j)}B_{ij}^{kl}(s)g\left( x_{kl}'(q_{kl}s )\right) x_{ij}(s)+L_{ij} (s)\right] \mathrm{d}s, \ t\in [0, \ \theta ^{*}]. \end{aligned}$$

Thus, with the help of \((A_{0})\) \((A_{1})\), (1.2) and (2.4), we have

$$\begin{aligned} |x_{ij} (\theta ^{*})|=\, & {} \left| x_{ij} (0) e ^{-\int _{0}^{\theta ^{*}}a_{ij}(u)\mathrm{d}u} \right. \\&\left. +\,\int _{0}^{\theta ^{*}}e ^{ -\int _{s}^{\theta ^{*}}a_{ij}(u)\mathrm{d}u}\left[ -\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(s)f(x_{kl}(q_{kl}s) )x_{ij}(s)\right. \right. \\&\left. \left. -\,\sum \limits _{C_{kl}\in N_{q}(i,j)}B_{ij}^{kl}(s)g\left( x_{kl}'(q_{kl}s )\right) x_{ij}(s)+L_{ij} (s)\right] \mathrm{d}s \right| \\<&\frac{K_{ij}}{M} e ^{-\int _{0}^{\theta ^{*}}a^{*}_{ij}(u)\mathrm{d}u} + \int _{0}^{\theta ^{*}}e ^{ -\int _{s}^{\theta ^{*}}a^{*}_{ij}(u)\mathrm{d}u} K_{ij}\left[ \sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(s)\right| M^{f}\right. \\&\left. \sum \limits _{C_{kl}\in N_{q}(i,j)}\left| B_{ij}^{kl}(s)\right| M^{g}+|L_{ij} (s)| \right] \mathrm{d}s\\\le & {} \frac{K_{ij}}{M} e ^{-\int _{0}^{\theta ^{*}}a^{*}_{ij}(u)\mathrm{d}u} + \int _{0}^{\theta ^{*}}e ^{ -\int _{s}^{\theta ^{*}}a^{*}_{ij}(u)\mathrm{d}u} \left[ a^{*}_{ij}(s)- \eta ^{1}_{ij} \right] \mathrm{d}s\\< & {} \frac{K_{ij}}{M} e ^{-\int _{0}^{\theta ^{*}}a^{*}_{ij}(u)\mathrm{d}u} + \int _{0}^{\theta ^{*}}e ^{ -\int _{s}^{\theta ^{*}}a^{*}_{ij}(u)\mathrm{d}u} a^{*}_{ij}(s) \mathrm{d}s\\= & {} \left[ \left( \frac{K_{ij}}{M}-1\right) e ^{-\int _{0}^{\theta ^{*}} a^{*}_{ij}(u) \mathrm{d}u}+1 \right] \\\le & {} 1, \end{aligned}$$

which, together with (2.3), implies that

$$\begin{aligned} \max \left\{ \left| x_{ij}(\theta ^{*})\right| , \ \left| x_{ij}'(\theta ^{*}) \right| \right\} =\left| x'_{ij}(\theta ^{*})\right| = 1. \end{aligned}$$
(2.6)

From (1.3), (2.1), (2.3) and (2.5), we get

$$\begin{aligned} \left| x_{ij}'(\theta ^{*})\right|\le & {} \left| a_{ij}(\theta ^{*})\right| \left| x_{ij} (\theta ^{*} )\right| +\left| -\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(\theta ^{*})f(x_{kl}(q_{kl} \theta ^{*} ) )x_{ij}(\theta ^{*})\right. \\&\left. -\sum \limits _{C_{kl}\in N_{q}(i,j)}B_{ij}^{kl}(\theta ^{*})g\left( x_{kl}'(q_{kl} \theta ^{*})\right) x_{ij}(\theta ^{*}) +L _{ij}(\theta ^{*})\right| \\\le & {} \left| a_{ij}(\theta ^{*})\right| +\sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(\theta ^{*})\right| M^{f} +\sum \limits _{C_{kl}\in N_{q}(i,j)}\left| B_{ij}^{kl}(\theta ^{*})\right| M^{g}+\left| L _{ij}(\theta ^{*})\right| \\< & {} 1, \end{aligned}$$

which contradicts (2.6). This proves Lemma 2.1. \(\square\)

Theorem 2.1

Assume that the conditions in Lemma 2.1 hold. Let \(x^{*}(t)= \{x_{ij}^{*}(t)\}\) be a solution of (1.1) with the initial condition (2.1). Then, for given \(0< r_{1}< r_{2}\) and \(T > 0,\) \(x^{*}(t)\) is finite-time stable with respect to \((r_{1}, r_{2}, T)\) if

$$\begin{aligned} r_{2}>Mr_{1}. \end{aligned}$$

Proof

In view of Lemma 2.1, we obtain

$$\begin{aligned} \max \left\{ \left| x^{*}_{ij}(t)\right| , \ \left| x^{*'}_{ij}(t)\right| \right\} <1, \quad \text{ for } \text{ all } \ t\ge 0, \ ij \in J. \end{aligned}$$
(2.7)

Let \(x(t)= \{x_{ij}(t)\}\) be any solution of (1.1). We denote

$$\begin{aligned} \left\{ \begin{array}{l} z_{ij}(t)= x_{ij}(t)-x^{*}_{ij}(t),z_{ij}(0)= x_{ij}(0)-x^{*}_{ij}(0), z_{ij}'(0)= x'_{ij}(0)-x^{*'}_{ij}(0), \\ z^{0} = \{z_{ij}(0)\}, \ z^{1} = \left\{ z_{ij}'(0)\right\} , \Vert z \Vert _{\infty }=\max \left\{ \left\| z^{0}\right\| , \ \left\| z^{1}\right\| \right\} , \end{array}\right. \end{aligned}$$
(2.8)

where \(t\ge 0, \ ij\in J\). It follows from (1.1) that

$$\begin{aligned} z_{ij}'(t)= & {} -a_{ij}(t)z_{ij}(t)\nonumber \\&-\,\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(t)\left[ f\left( x_{kl}(q_{kl} t) \right) x_{ij}(t) -f\left( x_{kl}^{*}(q_{kl} t) \right) x_{ij}^{*}(t)\right] \nonumber \\&-\,\sum \limits _{C_{kl}\in N_{q}(i,j)}B_{ij}^{kl}(t)\left[ g\left( x_{kl}'(q_{kl} t) \right) x_{ij}(t) -g\left( x_{kl}^{*'}(q_{kl} t) \right) x_{ij}^{*}(t)\right] ,\quad t>0, \ ij\in J. \end{aligned}$$
(2.9)

For any \(\varepsilon >0\), we obtain

$$\begin{aligned} \max \left\{ \left| z_{ij}(0)\right| , \ \left| z_{ij}'(0)\right| \right\} < \left( \max \left\{ \left\| z^{0}\right\| , \ \left\| z^{1}\right\| \right\} +\varepsilon \right) \le M \left( \left\| z \right\| _{\infty }+\varepsilon \right) , \quad ij\in J. \end{aligned}$$
(2.10)

In the following, we will show

$$\begin{aligned} \max \left\{ \left| z_{ij}(t)\right| ,\ \left| z_{ij}'(t)\right| \right\} < M (\Vert z \Vert _{\infty }+\varepsilon ) \quad \text{ for } \text{ all } t \in (0, \ T], \ T>0 \ \text{ and } \ ij\in J. \end{aligned}$$
(2.11)

Otherwise, there must exist \(ij\in J\) and \(\theta \in (0, \ T)\) such that

$$\begin{aligned} \max \left\{ \left| z_{ij}(\theta ) \right| ,\ \left| z_{ij}'(\theta ) \right| \right\} = M (\Vert z \Vert _{\infty }+\varepsilon ), \end{aligned}$$
(2.12)

and

$$\begin{aligned} \max \left\{ \left| z_{kl}(t) \right| ,\ \left| z_{kl}'(t) \right| \right\} < M (\Vert z \Vert _{\infty }+\varepsilon ) \quad \text{ for } \text{ all } t \in [0, \ \theta ), \ kl \in J. \end{aligned}$$
(2.13)

In view of (2.9), we obtain

$$\begin{aligned}&z_{ij}'(s)+a_{ij}(s)z_{ij} (s ) \nonumber \\&\quad = -\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(s)\left[ f(x_{kl}(q_{kl} s) )x_{ij}(s) -f\left( x_{kl}^{*}(q_{kl} s) \right) x_{ij}^{*}(s)\right] \nonumber \\&\qquad -\,\sum \limits _{C_{kl}\in N_{q}(i,j)}B_{ij}^{kl}(s)\left[ g\left( x_{kl}'(q_{kl} s) \right) x_{ij}(s) -g\left( x_{kl}^{*'} (q_{kl} s) \right) x_{ij}^{*}(s)\right] ,\quad s\in [0, \ t], \ t\in [0, \ \theta ]. \end{aligned}$$
(2.14)

Multiplying both sides of (2.5) by \(e ^{ \int _{0}^{s}a_{ij}(u)\mathrm{d}u}\) and integrating it on \([0, \ t]\), we get

$$\begin{aligned} z_{ij} (t)=\, & {} z_{ij} (0) e ^{-\int _{0}^{t}a_{ij}(u)\mathrm{d}u}+ \int _{0}^{t}e ^{ -\int _{s}^{t}a_{ij}(u)\mathrm{d}u}\\&\times \left\{ -\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(s)\left[ f(x_{kl}(q_{kl} s) )x_{ij}(s) -f\left( x_{kl}^{*}(q_{kl} s) \right) x_{ij}^{*}(s)\right] \right. \\&\quad\left. -\,\sum \limits _{C_{kl}\in N_{q}(i,j)}B_{ij}^{kl}(s)\left[ g\left( x_{kl}'(q_{kl} s) \right) x_{ij}(s) -g\left( x_{kl}^{*'} (q_{kl} s) \right) x_{ij}^{*}(s)\right] \right\} \mathrm{d}s, \quad t\in [0, \ \theta ]. \end{aligned}$$

Thus, with the help of \((A_{0})\), \((A_{1})\), (1.4), (2.7) and (2.13), we have

$$\begin{aligned} |z_{ij} (\theta )|&= {} \left| z_{ij} (0) e ^{-\int _{0}^{\theta }a_{ij}(u)\mathrm{d}u}\right. \\&\quad\left. +\,\int _{0}^{\theta }e ^{ -\int _{s}^{\theta }a_{ij}(u)\mathrm{d}u}\left\{ -\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(s)\left[ f(x_{kl}(q_{kl} s) )x_{ij}(s) -f\left( x_{kl}^{*}(q_{kl} s) \right) x_{ij}^{*}(s)\right] \right. \right. \&\quad\left. \left. -\,\sum \limits _{C_{kl}\in N_{q}(i,j)}B_{ij}^{kl}(s)\left[ g\left( x_{kl}'(q_{kl} s) \right) x_{ij}(s) -g\left( x_{kl}^{*'} (q_{kl} s) \right) x_{ij}^{*}(s)\right] \right\} \mathrm{d}s \right| \\ &\quad\le {} | z_{ij} (0)| e ^{-\int _{0}^{\theta }a_{ij}(u)\mathrm{d}u}\\&\quad+\,\int _{0}^{\theta }e ^{ -\int _{s}^{\theta }a_{ij}(u)\mathrm{d}u} \left\{ \sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(s)\right| \left( \left| f(x_{kl}(q_{kl} s) )\left| \left| x_{ij}(s) - x_{ij}^{*}(s)\right| \right. \right. \right. \right. \\&\quad\left. \left. +\,\left| f\left( x_{kl}(q_{kl} s) \right) -f\left( x_{kl}^{*}(q_{kl} s) \right) \right| \left| x_{ij}^{*}(s)\right| \right) \right. \\&\quad\left. \sum \limits _{C_{kl}\in N_{q}(i,j)}\left| B_{ij}^{kl}(s)\right| \left( \left| g\left( x_{kl}'(q_{kl} s) \right) \right| \left| x_{ij}(s) - x_{ij}^{*} (s)\right| \right. \right. \\&\quad\left. \left. +\,\left| g\left( x_{kl}'(q_{kl} s) \right) -g\left( x_{kl}^{*'}(q_{kl} s) \right) \right| \left| x_{ij}^{*}(s)\right| \right) \right\} \mathrm{d}s \\&\qquad<(\Vert z \Vert _{\infty }+\varepsilon ) K_{ij} e ^{ -\int _{0}^{\theta }a_{ij}^{*}(u)\mathrm{d}u} \\&\quad+\,\int _{0}^{\theta }e ^{ -\int _{s}^{\theta }a_{ij}^{*}(u)\mathrm{d}u}K_{ij} \left[ \sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(s)\right| \left( M^{f} |z_{ij}(s) | + \mu ^{f}|z_{kl}(q_{kl} s) | \right) \right. \\&\quad\left. +\,\sum \limits _{C_{kl}\in N_{q}(i,j)}\left| B_{ij}^{kl}(s)\right| \left( M^{g} |z_{ij}(s) | + \mu ^{g}\left| z_{kl}'(q_{kl} s) \right| \right) \right] \mathrm{d}s \\&\qquad\le {} (\Vert z \Vert _{\infty }+\varepsilon ) K_{ij} e ^{ -\int _{0}^{\theta }a_{ij}^{*}(u)\mathrm{d}u} \\&\quad+\,\int _{0}^{\theta }e ^{ -\int _{s}^{\theta }a_{ij}^{*}(u)\mathrm{d}u}K_{ij}\left[ \sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(s)\right| \left( M^{f} + \mu ^{f} \right) \right. \\&\quad\left. +\,\sum \limits _{C_{kl}\in N_{q}(i,j)}\left| B_{ij}^{kl}(s)\right| ( M^{g} + \mu ^{g} )\right] \mathrm{d}s M(\Vert z \Vert _{\infty }+\varepsilon )\\&\qquad< {} M(\Vert z \Vert _{\infty }+\varepsilon ) \left\{ \frac{K_{ij}}{M} e ^{ -\int _{0}^{\theta } a_{ij}^{*}(u) \mathrm{d}u} + \int _{0}^{\theta }e ^{ -\int _{s}^{\theta } a_{ij}^{*}(u) \mathrm{d}u}a_{ij}^{*}(s) \mathrm{d}s \right\} \\&\quad= \, {} M (\Vert z \Vert _{\infty }+\varepsilon ) \left[ 1- \left( 1-\frac{K_{ij}}{M} \right) e ^{-\int _{0}^{\theta } a_{ij}^{*}(u) \mathrm{d}u} \right] \\&\qquad\le {} M (\Vert z \Vert _{\infty }+\varepsilon ), \end{aligned}$$

which, together with (2.12), implies that

$$\begin{aligned} \max \left\{ |z_{ij}(\theta ) |, \left| z'_{ij}(\theta ) \right| \right\} =\left| z'_{ij}(\theta ) \right| = M (\Vert z \Vert _{\infty }+\varepsilon ). \end{aligned}$$
(2.15)

From (1.5), (2.7) and (2.14), we get

$$\begin{aligned} \left| z_{ij}'(\theta )\right|\le & {} |a_{ij}(\theta )||z_{ij} (\theta )|+\left\{ \sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(\theta )\right| \left( \left| f(x_{kl}(q_{kl} \theta ) )\right| \left| x_{ij}(\theta ) - x_{ij}^{*}(\theta )\right| \right. \right. \\&\left. \left. +\,\left| f(x_{kl}(q_{kl} \theta ) ) -f\left( x_{kl}^{*}(q_{kl} \theta ) \right) \right| \left| x_{ij}^{*}(\theta )\right| \right) \right. \\&\left. \sum \limits _{C_{kl}\in N_{q}(i,j)}\left| B_{ij}^{kl}(\theta )\right| \left( \left| g\left( x_{kl}'(q_{kl} s) \right) \right| \left| x_{ij}(\theta ) - x_{ij}^{*} (\theta )\right| \right. \right. \\&\left. \left. +\,\left| g\left( x_{kl}'(q_{kl} \theta ) \right) -g\left( x_{kl}^{*'} (q_{kl} \theta ) \right) \right| \left| x_{ij}^{*}(\theta )\right| \right) \right\} \\\le & {} \left\{ |a_{ij}(\theta ) | +\sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(\theta )\right| \left( M^{f}+\mu ^{f}\right) \right. \\&\left. +\,\sum \limits _{C_{kl}\in N_{q}(i,j)}\left| B_{ij}^{kl}(\theta )\right| \left( M^{g}+\mu ^{g}\right) \right\} M (\Vert z \Vert _{\infty }+\varepsilon ) \\< & {} M (\Vert z \Vert _{\infty }+\varepsilon ), \end{aligned}$$

which contradicts (2.15). Hence, (2.11) holds. Letting \(\varepsilon \longrightarrow 0^{+}\), we have from (2.10) that

$$\begin{aligned} \max \left\{ |z_{ij}(t) |,\ \left| z_{ij}'(t) \right| \right\} \le M \max \left\{ \left\| x(0)-x^{*}(0)\right\|, \left\| x'(0)-x^{*'} (0)\right\| \right\} , t\in [0, \ T], ij \in J. \end{aligned}$$
(2.16)

Let \(\max \{\Vert x(0)-x^{*}(0)\Vert , \ \Vert x'(0)-x^{*'} (0)\Vert \}\le r_{1},\) by (2.16) and \(M r_{1} < r_{2}\), we have

$$\begin{aligned}&\max \left\{ \left\| x(t)-x^{*}(t)\right\| , \left\| x'(t)-x^{*'} (t)\right\| \right\} \\&\quad \le M \max \left\{ \left\| x(0)-x^{*}(0)\right\| , \left\| x'(0)-x^{*'}(0)\right\| \right\} \le M r_{1} < r_{2}, \quad \forall t\in [0, \ T]. \end{aligned}$$

This shows that \(x^{*}(t)\) is finite-time stable with respect to \(( r_{1},r_{2}, T)\). The proof is completed. \(\square\)

We can show the conditions in Theorem 2.1 ensure the following generalized exponential synchronization of system (1.1).

Theorem 2.2

Under the assumptions of Theorem 2.1, system (1.1) is generalized exponential synchronization at infinity, i. e., there exist two positive constants \(\beta\) and \(\sigma\), such that for any two solutions \(x(t), \bar{x} (t)\) of (1.1), the following inequality holds

$$\begin{aligned} \Vert x(t)-\bar{x} (t)\Vert _{\infty }\le \beta \frac{\max \left\{ \left\| x(0)-\bar{x} (0)\right\| , \left\| x'(0)-\bar{x'}(0)\right\| \right\} }{(1+t)^{\sigma }} \quad \text{ for } \text{ all } \ t\ge 0, \end{aligned}$$

where \(\Vert x(t)-x^{*}(t)\Vert _{\infty }=\max \{\Vert x(t)-x^{*}(t)\Vert , \Vert x'(t)-x^{*'} (t)\Vert \}\)

Proof

For any two solutions \(x(t), \bar{x} (t)\) of (1.1), we set \(x^{*}(t)\) be a solution of (1.1) with the conditions (2.1) and

$$\begin{aligned} \max \left\{ \left\| x(0)-x^{*}(0)\right\| , \left\| x'(0)-x^{*'} (0)\right\| \right\}>0, \max \left\{ \left\| \bar{x}(0)-x^{*}(0)\right\| , \left\| \bar{x}'(0)-x^{*'} (0)\right\| \right\} >0. \end{aligned}$$

Define continuous functions \(\Gamma _{ij} (\omega )\) and \(\Pi _{ij} (\omega )\) by setting

$$\begin{aligned} \Gamma _{ij}(\omega )= & {} \sup \limits _{t\ge 0}\left\{ \omega -a_{ij}^{*}(t) + K _{ij} \left[ \sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(t)\right| \left( M^{f}+\mu ^{f} e^{\omega \ln \frac{1}{q_{kl}}} \right) \right. \right. \\&\left. \left. +\,\sum \limits _{C_{kl}\in N_{q}(i,j)}\left| B_{ij}^{kl}(t)\right| \left( M^{g}+\mu ^{g} e^{\omega \ln \frac{1}{q_{kl}}} \right) \right] \right\} , \end{aligned}$$

and

$$\begin{aligned} \Pi _{ij}(\omega )= & {} \sup \limits _{t\ge 0}\left\{ |a_{ij}(t) | +\sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(t)\right| \left( M^{f}+\mu ^{f}e^{ \omega \ln \frac{1 }{ q_{kl} } }\right) + \sum \limits _{C_{kl}\in N_{q}(i,j)}\left| B_{ij}^{kl}(t)\right| \left( M^{g}+\mu ^{g}e^{ \omega \ln \frac{1 }{ q_{kl} } }\right) \right\} , \end{aligned}$$

\(\text{ where } \ \omega \in [0, \ \min \nolimits _{ij\in J}\inf \limits _{t\ge 0}a_{ij} ^{*}(t)], ij\in J.\) Then, from (1.4) and (1.5), we have

$$\begin{aligned} \Gamma _{ij}(0)<0, \Pi _{ij}(0)<1, \quad \ ij\in J, \end{aligned}$$

we can choose a constant \(\sigma \in (0, \ \ \min \limits _{ij\in J}\inf \limits _{t\ge 0}a_{ij} ^{*}(t) )\) such that

$$\begin{aligned} \Gamma _{ij}(\sigma )<0, \ \ \Pi _{ij}(\sigma )<1, \quad ij\in J. \end{aligned}$$

This, together with the facts that

$$\begin{aligned} \frac{\sigma }{1+t}\le \sigma , \ \ln \left( \frac{1+t}{1+q_{kl}t}\right) \le \ln \frac{1}{q_{kl}} \quad \text{ for } \text{ all } \ t\ge 0, \ kl\in J, \end{aligned}$$

implies that

$$\begin{aligned}&\sup \limits _{t\ge 0}\left\{ \frac{\sigma }{1+t}-a_{ij}^{*}(t) + K _{ij} \left[ \sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(t)\right| \left( M^{f}+\mu ^{f} e^{\sigma \ln \left( \frac{1+t}{1+q_{kl}t}\right) }\right) \right. \right. \nonumber \\&\quad\left. \left. +\,\sum \limits _{C_{kl}\in N_{q}(i,j)}\left| B_{ij}^{kl}(t)\right| \left( M^{g}+\mu ^{g} e^{\sigma \ln \left( \frac{1+t}{1+q_{kl}t}\right) }\right) \right] \right\} \nonumber \\\le & {} \sup \limits _{t\ge 0}\left\{ \sigma -a_{ij}^{*}(t) + K _{ij} \left[ \sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(t)\right| \left( M^{f}+\mu ^{f} e^{\sigma \ln \frac{1}{q_{kl}}} \right) \right. \right. \nonumber \\&\quad\left. \left. +\,\sum \limits _{C_{kl}\in N_{q}(i,j)}\left| B_{ij}^{kl}(t)\right| \left( M^{g}+\mu ^{g} e^{\sigma \ln \frac{1}{q_{kl}}} \right) \right] \right\} \nonumber \\=\, & {} \Gamma _{ij}(\sigma ) < 0, \quad \ ij\in J. \end{aligned}$$
(2.17)

We still use the notation defined in (2.8). For any \(\varepsilon >0\), consider the functions \(V_{ij}(t),ij\in J,\) defined as follows

$$\begin{aligned} V_{ij}(t)=M\ (\Vert z \Vert _{\infty }+\varepsilon ) e^{-\sigma \ln (1+ t)}, \quad t\ge 0. \end{aligned}$$

Therefore,

$$\begin{aligned} V_{ij}(q_{kl}t)& {}= M (\Vert z \Vert _{\infty }+\varepsilon ) e^{-\sigma \ln (1+q_{kl} t)}\nonumber \\& {}= M (\Vert z \Vert _{\infty }+\varepsilon ) e^{-\sigma \ln (1+ t)} e^{ \sigma \ln \left( \frac{1+t}{1+q_{kl}t}\right) }\nonumber \\\le & {} V_{ij}(t) e^{ \sigma \ln \frac{1 }{ q_{kl} } } \quad \text{ for } \text{ all } \ t\ge 0, \ ij, \ kl \in J, \end{aligned}$$
(2.18)

and

$$\begin{aligned} \max \left\{ |z_{ij}(0) |, \ \left| z_{ij}'(0) \right| \right\} < (\Vert z \Vert _{\infty }+\varepsilon ) \le M (\Vert z \Vert _{\infty }+\varepsilon ) = V_{ij}(0), \quad ij\in J. \end{aligned}$$
(2.19)

We next claim that

$$\begin{aligned} \max \left\{ |z_{ij}(t) |, \ \left| z_{ij}'(t) \right| \right\} < V_{ij}(t) \text{ for } \text{ all } t >0, ij\in J. \end{aligned}$$
(2.20)

Otherwise, there must exist \(ij\in J\) and \(\theta _{1} \in (0, \ +\infty )\) such that

$$\begin{aligned} \max \left\{ |z_{ij}(\theta _{1}) |, \ \left| z_{ij}'(\theta _{1}) \right| \right\} = V_{ij}(\theta _{1})= M (\Vert z \Vert _{\infty }+\varepsilon ) e^{-\sigma \ln (1+ \theta _{1})}, \end{aligned}$$
(2.21)

and

$$\begin{aligned} \max \left\{ |z_{kl}(t) |, \ \left| z_{kl}'(t) \right| \right\} < V_{kl}(t) \ \text{ for } \text{ all } t \in [0, \ \theta _{1}), \ kl \in J. \end{aligned}$$
(2.22)

According to (2.2), (2.17), (2.18), (2.19) and (2.22) yield

$$\begin{aligned} &|z_{ij} (\theta _{1})| \le | z_{ij} (0)| e ^{-\int _{0}^{\theta _{1}}a_{ij}(u)\mathrm{d}u}\\&\qquad+ \int _{0}^{\theta _{1}}e ^{ -\int _{s}^{\theta _{1}}a_{ij}(u)\mathrm{d}u} \left[ \sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(s)\right| \left( \left| f(x_{kl}(q_{kl} s) )\right| \left| x_{ij}(s) - x_{ij}^{*}(s)\right| \right. \right. \\&\qquad\left. \left. +\,\left| f(x_{kl}(q_{kl} s) ) -f\left( x_{kl}^{*}(q_{kl} s) \right) \right| \left| x_{ij}^{*}(s)\right| \right) \right. \\&\qquad\left. +\,\sum \limits _{C_{kl}\in N_{q}(i,j)}\left| B_{ij}^{kl}(s)\right| \left( \left| g\left( x_{kl}'(q_{kl} s) \right) \right| \left| x_{ij}(s) - x_{ij}^{*}(s)\right| \right. \right. \\&\qquad\left. \left. +\,\left| g\left( x_{kl}'(q_{kl} s) \right) -g\left( x_{kl}^{*'} (q_{kl} s) \right) \right| \left| x_{ij}^{*}(s)\right| \right) \right] \mathrm{d}s \\& \quad< (\Vert z \Vert _{\infty }+\varepsilon ) K_{ij} e ^{ -\int _{0}^{\theta _{1}}a_{ij}^{*}(u)\mathrm{d}u} \\&\qquad+\, \int _{0}^{\theta _{1}}e ^{ -\int _{s}^{\theta _{1}}a_{ij}^{*}(u)\mathrm{d}u}K_{ij}\left[ \sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(s)\right| \left( M^{f} |z_{ij}(s) | + \mu ^{f}|z_{kl}(q_{kl} s) | \right) \right. \\&\qquad\left. +\,\sum \limits _{C_{kl}\in N_{q}(i,j)}\left| B_{ij}^{kl}(s)\right| \left( M^{g} |z_{ij}(s) | + \mu ^{g}\left| z_{kl}'(q_{kl} s) \right| \right) \right] \mathrm{d}s \\& \quad\le (\Vert z \Vert _{\infty }+\varepsilon ) K_{ij} e^{ -\int _{0}^{\theta _{1}}a_{ij}^{*}(u)\mathrm{d}u} + \int _{0}^{\theta _{1}}e ^{ -\int _{s}^{\theta _{1}}a_{ij}^{*}(u)\mathrm{d}u}K_{ij}\\&\qquad\times \left[ \sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(s)\right| \left( M^{f} + \mu ^{f} e^{\sigma \ln \left( \frac{1+s}{1+q_{kl}s}\right) } \right) \right. \\&\qquad\left. +\,\sum \limits _{C_{kl}\in N_{q}(i,j)}\left| B_{ij}^{kl}(s)\right| \left( M^{g} + \mu ^{g} e^{\sigma \ln \left( \frac{1+s}{1+q_{kl}s}\right) } \right) \right] M(\Vert z \Vert _{\infty }+\varepsilon ) e^{-\sigma \ln (1+s)} \mathrm{d}s \\&\quad\,=\,M (\Vert z^{0}\Vert _{\infty }+\varepsilon ) e^{-\sigma \ln (1+ \theta _{1})} \left\{ \frac{K_{ij}}{M} e ^{ -\int _{0}^{\theta _{1}}(a_{ij}^{*}(u)-\frac{ \sigma }{1+u})\mathrm{d}u}\right. \\&\qquad\left. +\,\int _{0}^{\theta _{1}}e ^{ -\int _{s}^{\theta _{1}}(a_{ij}^{*}(u)- \frac{ \sigma }{1+u})\mathrm{d}u} K_{ij} \left[ \sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(s)\right| \left( M^{f} + \mu ^{f} e^{\sigma \ln \left( \frac{1+s}{1+q_{kl}s}\right) }\right) \right. \right. \\&\qquad\left. \left. +\,\sum \limits _{C_{kl}\in N_{q}(i,j)}\left| B_{ij}^{kl}(s)\right| \left( M^{g} + \mu ^{g} e^{\sigma \ln \left( \frac{1+s}{1+q_{kl}s}\right) }\right) \right] \mathrm{d}s\right\} \\ & \quad < M (\Vert z^{0}\Vert _{\infty }+\varepsilon ) e^{-\sigma \ln (1+ \theta _{1})} \left\{ \frac{K_{ij}}{M} e ^{ -\int _{0}^{\theta _{1}}(a_{ij}^{*}(u)-\frac{ \sigma }{1+u})\mathrm{d}u}\right. \\&\qquad\left. +\,\int _{0}^{\theta _{1}}e ^{ -\int _{s}^{\theta _{1}}\left( a_{ij}^{*}(u)- \frac{ \sigma }{1+u}\right) \mathrm{d}u} \left( a_{ij}^{*}(s)- \frac{ \sigma }{1+s}\right) \mathrm{d}s\right\} \\& \quad\,=\,M (\Vert z \Vert _{\infty }+\varepsilon ) e^{-\sigma \ln (1+ \theta _{1})} \left[ 1- \left( 1-\frac{K_{ij}}{M} \right) e ^{ -\int _{0}^{\theta _{1}}\left( a_{ij}^{*}(u)-\frac{ \sigma }{1+u}\right) \mathrm{d}u} \right] \\ &\quad\le M (\Vert z \Vert _{\infty }+\varepsilon ) e^{-\sigma \ln (1+ \theta _{1})}, \end{aligned}$$

which, together with (2.21), implies that

$$\begin{aligned} \max \left\{ \left| z_{ij}(\theta _{1}) \right| , \ \left| z'_{ij}(\theta _{1}) \right| \right\} =|z'_{ij}(\theta _{1}) |= M (\Vert z \Vert _{\infty }+\varepsilon ) e^{-\sigma \ln (1+ \theta _{1})}. \end{aligned}$$
(2.23)

From (2.2), (2.22) and \(\Pi _{ij}(\sigma )<1\), we get

$$\begin{aligned} \left| z_{ij}'(\theta _{1})\right|\le & {} |a_{ij}(\theta _{1})||z_{ij} (\theta _{1} )|+\,\left\{ \sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(\theta _{1})\right| \left( \left| f(x_{kl}(q_{kl} \theta _{1}) )\right| \left| x_{ij}(\theta _{1}) - x_{ij}^{*}(\theta _{1})\right| \right. \right. \\&\left. \left. +\,\left| f(x_{kl}(q_{kl} \theta _{1}) ) -f\left( x_{kl}^{*}(q_{kl} \theta _{1}) \right) \right| \left| x_{ij}^{*}(\theta _{1})\right| \right) \right. \\&\left. \sum \limits _{C_{kl}\in N_{q}(i,j)}\left| B_{ij}^{kl}(\theta _{1})\right| \left( \left| g\left( x_{kl}'(q_{kl} s) \right) \right| \left| x_{ij}(\theta _{1}) - x_{ij}^{*} (\theta _{1})\right| \right. \right. \\&\left. \left. +\,\left| g\left( x_{kl}'(q_{kl} \theta ) \right) -g\left( x_{kl}^{*'}(q_{kl} \theta _{1}) \right) \right| \left| x_{ij}^{*}(\theta _{1})\right| \right) \right\} \\\le & {} \left\{ |a_{ij}(\theta _{1}) | +\sum \limits _{C_{kl}\in N_{r}(i,j)}\left| C_{ij}^{kl}(\theta _{1})\right| \left( M^{f}+\mu ^{f}e^{ \sigma \ln \frac{1 }{ q_{kl} } }\right) \right. \\&\left. +\,\sum \limits _{C_{kl}\in N_{q}(i,j)}\left| B_{ij}^{kl}(\theta _{1})\right| \left( M^{g}+\mu ^{g}e^{ \sigma \ln \frac{1 }{ q_{kl} } }\right) \right\} M (\Vert z\Vert _{\infty }+\varepsilon ) e^{-\sigma \ln (1+ \theta _{1})} \\< & {} M (\Vert z\Vert _{\infty }+\varepsilon ) e^{-\sigma \ln (1+ \theta _{1})}, \end{aligned}$$

which contradicts (2.23). Hence, (2.20) holds. Letting \(\varepsilon \longrightarrow 0^{+}\), we have from (2.20) that

$$\begin{aligned} \left\| x(t)-x^{*}(t)\right\| _{\infty }= & {} \max \limits _{ij \in J}\left\{ \max \left\{ |z_{ij}(t)|, \left| z_{ij}'(t)\right| \right\} \right\} \\\le & {} M \frac{\max \left\{ \left\| x(0)-x^{*}(0)\right\| , \left\| x'(0)-x^{*'}(0)\right\| \right\} }{(1+t)^{\sigma }} \quad \text{ for } \text{ all } \ t\ge 0. \end{aligned}$$

Moreover, similar arguments to those above show that

$$\begin{aligned} \left\| \bar{x}(t)-x^{*}(t)\right\| _{\infty } \le M \frac{\max \left\{ \left\| \bar{x}(0)-x^{*}(0)\right\| , \left\| \bar{x}'(0)-x^{*'}(0)\right\| \right\} }{(1+t)^{\sigma }} \quad \text{ for } \text{ all } \ t\ge 0. \end{aligned}$$

Thus,

$$\begin{aligned} \left\| x(t)-\bar{x} (t)\right\| _{\infty }\le & {} \Vert x(t)-x^{*}(t)\Vert _{\infty }+ \left\| \bar{x}(t)-x^{*}(t)\right\| _{\infty }\\ {}\le & {} \beta \frac{\max \left\{ \left\| x(0)-\bar{x} (0)\right\| , \left\| x'(0)-\bar{x}' ( 0)\right\| \right\} }{(1+t)^{\sigma }} \quad \text{ for } \text{ all } \ t\ge 0, \end{aligned}$$

where

$$\begin{aligned} \beta =2M \frac{\max \left\{ \max \left\{ \left\| x(0)-x^{*}(0)\right\| , \left\| x'(0)-x^{*'}(0)\right\| \right\} , \ \max \left\{ \left\| \bar{x}(0)-x^{*}(0)\right\| , \left\| \bar{x}'(0)-x^{*'}(0)\right\| \right\} \right\} }{\max \left\{ \left\| x(0)-\bar{x} (0)\right\| , \left\| x'(0)-\bar{x}' ( 0)\right\| \right\} }. \end{aligned}$$

This proves Theorem 2.2. \(\square\)

Fig. 1
figure 1

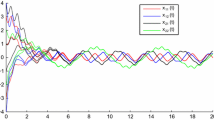
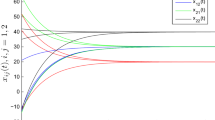
Numerical solutions to system (3.1) and its derivative with two groups of different initial values

Full size image
Fig. 2
figure 2

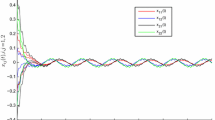
Synchronization errors \(x_{ij}(t)-x_{ij}^*(t)\) and its derivative for solutions of system (3.1) with two groups of different initial values

Full size image

3 Example and remark

Example 3.1

Consider the following SICNNs with neutral proportional delays:

$$\begin{aligned} \frac{\mathrm{d}x_{ij}}{\mathrm{d}t}= & {} -a_{ij}(t)x_{ij}(t )- \sum _{C_{kl}\in N_{1}(i,j)}C_{ij}^{kl} (t) \frac{1}{10}\sin \left( x_{kl}\left( \frac{1}{2}t \right) \right) x_{ij}(t)\nonumber \\&- \sum _{C_{kl}\in N_{1}(i,j)}B_{ij}^{kl} (t) \frac{1}{10}\cos \left( x_{kl}'\left( \frac{1}{2}t \right) \right) x_{ij}(t) +L_{ij}(t), \ \end{aligned}$$
(3.1)

where \(t> 0, {x}_{ij}(0)=x_{ij}^{0}, {x}_{ij}'(0)=x_{ij}^{1} \in \mathbb {R}, \ i,j=1,2,\)

$$\begin{aligned}&\left[ \begin{array}{ccc} a_{11}&{}a_{12} \\ a_{21}&{}a_{22} \end{array} \right] =\left[ \begin{array}{ccc} 0.1+0.2\sin 1000t &{}0.1+0.3\sin 1000t \\ 0.2+0.3\sin 1000t&{}0.2+0.4\sin 1000t \end{array} \right] , \end{aligned}$$
(3.2)
$$\begin{aligned}&\left[ \begin{array}{ccc} C_{11}&{}C_{12} \\ C_{21}&{}C_{22} \end{array} \right] =\left[ \begin{array}{ccc} B_{11}&{}B_{12} \\ B_{21}&{}B_{22} \end{array} \right] =\left[ \begin{array}{ccc} 0.01 |\cos t|&{}0.02 |\cos t| \\ 0.02 |\cos t|&{}0.01 |\cos t| \end{array} \right] , \end{aligned}$$
(3.3)
$$\begin{aligned}&\left[ \begin{array}{ccc} L_{11}&{}L_{12} \\ L_{21}&{}L_{22} \end{array} \right] =\left[ \begin{array}{ccc} 0.01\sin t&{} 0.01\sin t \\ 0.01\sin t&{} 0.01\sin t \end{array} \right] . \end{aligned}$$
(3.4)

Clearly,

$$\begin{aligned}&\left[ \begin{array}{ccc} a_{11}^{*}&{}a_{12}^{*} \\ a_{21}^{*}&{}a_{22}^{*} \end{array} \right] =\left[ \begin{array}{ccc} 0.1 &{}0.1 \\ 0.2&{}0.2 \end{array} \right] , K_{ij} \le e^{\frac{1}{1000}}=M,M ^{f}=\mu ^{f}=M ^{g}=\mu ^{g}=0.1, \\&\quad \sum _{C_{kl}\in N_{1}(i,j)}\left| {C_{ij}^{kl}}(t)\right| =\sum _{C_{kl}\in N_{1}(i,j)}\left| {B_{ij}^{kl}}(t)\right| \le 0.06, \left| L_{ij }(t)\right| \le 0.01, \quad i,j=1,2, \end{aligned}$$

which imply that system (3.1) satisfies \((A_{0})\), \((A_{1})\) and \((A_{2})\). Let us take \(r_{1}=1.5, r_{2}=10>r_{1}e^{\frac{1}{1000}}\) and \(M=e^{\frac{1}{1000}}\). By the consequence of Theorem 2.1, it follows that the solution \(x^{*}(t)=\{x_{ij}^{*}(t)\}\) of system (3.1) with \(\{|x_{ij}^{*}(0) |\}<\{e^{-\frac{1}{1000}}\}\) and \(\{|x_{ij}^{*} \ '(0) |\}<\{e^{-\frac{1}{1000}}\}\) is FTS with respect to \((r_{1}, r_{2}, T)\) for any \(T>0\). This fact is verified by the numerical simulation in Fig. 1, and there are two groups of different initial values which are \({x}_{11}(0)=1.1, {x}_{12}(0)=-1.3, {x}_{21}(0)=1.2, {x}_{22}(0)=1.5\), \({x}_{11}'(0)=1.1, {x}_{12}'(0)=-1.3, {x}_{21}'(0)=1.2, {x}_{22}'(0)=1.5,\) and \({x}_{11}^*(0)=0.2, {x}_{12}^*(0)=-0.1, {x}_{21}^*(0)=0.4, {x}_{22}^*(0)=0.6, {x}_{11}^{*'} (0)=0.2, {x}_{12}^{*'} (0)=-0.1, {x}_{21}^{*'} (0)=0.4,{x}_{22}^{*'} (0)=0.6\). Moreover, from (3.2) and (3.3), we can choose \(\sigma =0.01\) such that (2.17) holds. Then, Theorem 2.2 implies that (3.1) is generalized exponential synchronization at infinity, and for any two solutions \(x(t), x^{*} (t)\) of (3.1), the following inequality holds

$$\begin{aligned} \left\| x(t)-x^{*} (t)\right\| _{\infty }\le \beta \frac{\max \left\{ \left\| x(0)-x^{*} (0)\right\| , \left\| x'(0)-x^{*'} (0)\right\| \right\} }{(1+t)^{0.01}} \quad \text{ for } \text{ all } \ t\ge 0. \end{aligned}$$

The numerical simulation in Fig. 2 strongly supports the conclusion, and there are two different initial values which are

$$\begin{aligned} \left\{ x_{ij}^{0}\right\} = (1.1,-1.3,1.4,1.2), \left\{ x_{ij}^{1}\right\} = (1.5,1.3,-1.1,-1.2 ) \end{aligned}$$

and

$$\begin{aligned} \left\{ x^{*}_{ij} \ ^{0}\right\} =(1.2,-1.1,1.5,1.4), \left\{ x^{*}_{ij} \ ^{1}\right\} =(1.2,1.1,-1.3,-1.4). \end{aligned}$$

Remark 3.1

Since the finite-time stability of the non-autonomous SICNNs with neutral proportional delays has not been done before, all results in the references [10–13, 21–36] cannot be applicable to prove the finite-time stability and the generalized exponential synchronization of (3.1). Moreover, in this present paper, we employ a novel proof to establish some criteria to guarantee the finite-time stability and the generalized exponential synchronization for neural networks systems with neutral proportional delays.