1 Introduction

Various different methods have been used to forecast non-linear real-world time series in the literature [2]. These methods can be grouped as probabilistic methods, the methods based on fuzzy set theory and the methods based on artificial neural network. In recent years, there have been many studies which focus on ANN. Different approaches can be utilized when time series are forecasted with ANN. In these approaches, lagged variables of time series or more than one time series can be used as input values. The first one has been usually preferred in the literature. Multilayer perceptron neural networks are extensively used to forecast time series. The literature related to usage of this kind of neural network for time series forecasting was reviewed by Zhang et al. [22] and Zhang [21]. Crone and Kourentzes [7] and Crone et al. [8] discussed performance of artificial neural networks for forecasting. Multilayer perceptron uses McCuloch&Pitts neuron model which is based on an additive aggregation function. Thus, the output of the multilayer perceptron can be considered as non-linear transformation of sum of the inputs. Activation function provides non-linearity in here. In a multilayer perceptron which includes more than one neuron in the hidden layer, the output is a non-linear function of multiplication of weighted sum of the inputs. Especially, the number of neurons in hidden layer directly affects the performance of multilayer perceptron neural networks. Therefore, determination of the number of neurons in hidden layer is a vital issue. Egrioglu et al. [9], Aladag et al. [3], and Aladag [1] proposed some methods to determine the number of neurons in hidden layer and inputs of the model.

Yadav et al. [18] introduced multiplicative neuron model ANN (MNM-ANN) which has only one neuron in the hidden layer. This kind of neural network is different from multilayer perceptron neural network in aspect of the neuron model included. MNM-ANN is composed of multiplicative neuron model instead of McCuloch&Pitts neuron model. In multiplicative neuron model, aggregation function is not additive but multiplicative. Hence, the output of MNM-ANN is a non-linear function of multiplication of the inputs. This multiplicative structure strengthens non-linearity characteristic of the model. MNM-ANN uses less parameter than those employed by multilayer perceptron neural networks since it has only one neuron in the hidden layer. For time series forecasting, different ANN based on multiplicative neuron model such as linear and non-linear ANN (L&NL-ANN) and multiplicative seasonal artificial neural network (MS-ANN) were proposed by Yolcu et al. [19] and Aladag et al. [4], respectively.

In probabilistic models used for time series forecasting, inputs are lagged variables of time series (autoregressive terms) and lagged variables of error (moving average terms). Utilizing moving average (MA) terms in these models is as effective as using autoregressive (AR) terms. On the other hand, when ANN models are used for time series forecasting, AR terms are usually employed as inputs and MA terms are not taken into consideration. In addition to AR terms, if MA terms are also used, more accurate forecasts will be obtained. When MA terms are utilized, it is necessary to make important adjustments in ANN architectures and training algorithms of these architectures. Like using MA terms, Elman neural networks [11] have a mechanism in which neurons in context layer are fed from the hidden layer. However, Elman neural networks do not exactly including a MA term. To incorporate MA terms into ANN, the architecture should have a recurrent feedback structure from output layer. Jordan [14] suggested a recurrent architecture structure in which neurons in context layer are fed from the output layer. Jordan’s recurrent architecture structure is proper only for one step lag. However, it is a well-known fact capability of using more than one step lag cause an increase in forecasting performance of ANN. Recurrent neural networks were proposed in Giles et al. [12] and Lin et al. [17]. Zemouri and Patic [20] considered prediction error feedback as like MA term.

In some studies available in the literature such as Buhamra et al. [6], Egrioglu et al. [10], and Khashei and Bijari [16], hybrid methods were proposed and lagged variables of error were taken as inputs of ANN. On the other hand, in these studies, lagged variables of error were obtained from Box and Jenkins [5] models instead of ANN models. In the literature, a few artificial neural network models which uses lagged variables of its own error for feedback were proposed. In other words, an multiplicative neuron model artificial neural network model that has ARMA(\(p,q\)) structure does not exist in the literature. In this study, a novel artificial neural network model which has ARMA(\(p,q\)) structure and based on multiplicative neuron model is proposed for time series forecasting. The proposed model is an artificial neural network model which has ARMA structure. In the next section, the proposed model is introduced and the algorithm, which is based on particle swarm optimization (PSO), for training of this model is presented. In Sect. 3, the proposed model is applied to a real-world time series. Finally, the last section concludes the paper.

2 The Proposed Model

Forecasting is the process of making statements about events whose actual outcomes have not yet been observed. Forecasting methods can be classified into two classes as probabilistic and non-probabilistic methods. Artificial neural networks are non-probabilistic methods. Because artificial neural networks do not need strict assumptions such as normality, linearity, they have been commonly used in the literature in recent years. In the literature, many artificial neural network models have been proposed for forecasting. Yadav et al. [18] introduced multiplicative neuron model ANN (MNM-ANN) which has only one neuron in the hidden layer. Because MNM-ANN has one neuron, determining number of hidden layer neurons is not needed. This is very important, because determining number of hidden layer neurons is important problem for multilayer perceptron.

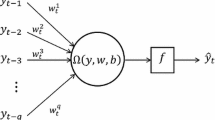
Although MNM-ANN has proved its success on forecasting problems in Yadav et al. [18], a major drawback of the method is that MNM-ANN does not have a recurrent feedback mechanism. In the time series literature, it is a well-known fact that using MA terms in forecasting models is as effective as using AR terms. In this study, a new recurrent ANN model based on multiplicative neuron model is proposed. The proposed model is called recurrent multiplicative neuron artificial neural network model (RMNM-ANN). In the proposed model, in addition to AR terms, MA terms are also incorporated into the model by feedbacking own error of the model. The architecture of the proposed ANN model is given in Fig. 1. In this figure, \(L\) and \(e_{t}\) are backshift operator and error for time \(t\) respectively, so \(Le_{t}=e_{t-1}.\, X_{t}\) represents observation value for time \(t\). \(f\) represents activation function which provides non-linear mapping. Sigmoid function is used as activation function in this study since this activation function is widely used in the literature. \(Output_{t}\) and \(Desired_{t}\) are the output value and target value of the model for time \(t\), respectively.

Fig. 1
figure 1

The architecture of the proposed RMNM-ANN model

Full size image

The algorithm of the calculation of the output values of the proposed method is given below.

Algorithm 1

Calculation of the output values of the proposed RMNM-ANN model.

Let \(n\) be the number of learning samples. First of all, the number of input of RMNM-ANN is determined, that is, values of \(p\) and \(q\) are decided. Then, according to these values of \(p\) and \(q\), the outputs of the proposed RMNM-ANN model can be computed as follows:

  • Step 1 Initialize the loop counter \(k\,(k = 0)\).

  • Step 2 Increase \(k\) by 1 (\(k=k + 1\)). Calculations for \(k{th}\) learning sample are performed. The inputs of RMNM-ANN are \(X_{t-1},X_{t-2}, \ldots ,X_{t-p} ,e_{t-1},e_{t-2},\ldots ,e_{t-q}\). As seen from Fig. 1, RMNM-ANN has one neuron in the hidden layer. Activation value of the neuron is represented by net and obtained from multiplication of inputs of RMNM-ANN by corresponding weights. When \(k=1,e_{t-1}, e_{t-2},\ldots ,e_{t-q} \) are taken as 0 since the output of RMNM-ANN has not been calculated yet. When \(k=2, e_{t-1}\) can be calculated. \(e_{t}\) equals to (\(Desired_{t} - Output_{t}\)) since the output of RMNM-ANN for the first learning sample was obtained. However, \(e_{t-1},\ldots ,e_{t-q} \) are taken as 0. In a similar way, last \(q - k\) terms of \(e_{t-1},e_{t-2},\ldots ,e_{t-q}\) will be taken as 0 for \(k\le q\). If \(k > q\) then, each \(e_{t-i} \left( {i=1,2,\ldots ,q}\right) \) can be calculated. Let \(WX_{i}\) and \(bX_i \left( {i=1,2,\ldots ,p}\right) \) be weights which connect \(X_{t-1},X_{t-2},\ldots ,X_{t-p}\) inputs to the neuron and the related bias values, respectively. Let \(WE_{i}\) and \(bE_i \left( {i=1,2,\ldots ,q}\right) \) be weights which connect \(e_{t-1},e_{t-2},\ldots ,e_{t-q}\) inputs to the neuron and the related bias values, respectively. Thus, for \(k{th}\) learning sample, activation value of the neuron \(net_{k}\) can be calculated using the formula (1).

    $$\begin{aligned} net_k =\mathop \prod \limits _{i=1}^p \left( {WX_i \times X_{t-i} +bX_i } \right) \times \mathop \prod \limits _{j=1}^q \left( {WE_j \times e_{t-j} +bE_j } \right) . \end{aligned}$$
    (1)

  • Step 3 Calculate the output value of RMNM-ANN by using \(net_{k}\) obtained in the previous step and the activation function \(f\) as follows:

    $$\begin{aligned} Output_t =f\left( {net_{\mathrm{k}}} \right) = \frac{1}{1+\hbox {exp}(-net_k ).} \end{aligned}$$
    (2)

  • Step 4 Calculate error \(e_{t}\) based on the difference between the obtained output value and desired value by using the formula given below.

    $$\begin{aligned} e_{t} =Desired_{t} -Output_{t} \end{aligned}$$
    (3)

    This \(e_{t}\) value will be used as an input of RMNM-ANN for the next learning sample.

  • Step 5 If \(k\le n\), then go to Step 2. Otherwise, terminate the algorithm.

PSO is utilized in order to train the proposed RMNM-ANN model. PSO introduced by Kennedy and Eberhart [15] is an intelligent optimization technique. In many applications, PSO method has produced better results than those produced by other methods such as gradient descent and Newton methods which require derivative. Especially, when it is very hard to calculate derivatives, good results can be obtained using PSO. Therefore, this optimization method has drawn a great amount of attention in recent years. For the architecture structure of the proposed RMNM-ANN model, it can be very hard to obtain derivatives so PSO is utilized to train the proposed model. In the PSO algorithm, positions of a particle are weights of proposed RMNM-ANN model. Hence, a particle has \(2(p+q) \) positions. Structure of a particle is illustrated in Fig. 2. The algorithm of the PSO method which is used to train the proposed model is given below.

Fig. 2
figure 2

Structure of a particle

Full size image

Algorihtm 2

PSO algorithm used to train the proposed RMNM-ANN model

  • Step 1 Positions of each \(m{\mathrm{th}}\left( \hbox {m}=1,2,\ldots ,pn \right) \) particles’ positions and velocities are randomly determined and kept in vectors \(X_{m}\) and \(V_{m}\) given as follows:

    $$\begin{aligned} X_m&= \left\{ {x_{m,1},x_{m,2},\ldots ,x_{m,d}}\right\} ,\quad m=1,2,\ldots ,pn \end{aligned}$$
    (4)
    $$\begin{aligned} V_m&= \left\{ {v_{m,1},v_{m,2},\ldots ,v_{m,d}} \right\} ,\quad m=1,2,\ldots ,pn \end{aligned}$$
    (5)

    where \(x_{m,j}(j=1,2,\ldots ,d)\) represents \(j\)th position of \(m\)th particle. \(pn\) and \(d\) represents the number of particles in a swarm and positions, respectively. The initial positions and velocities of each particle in a swarm are randomly generated from distribution (0,1) and \((-{vm,vm})\), respectively.

  • Step 2 The parameters of PSO are determined. In the first step, the parameters which direct the PSO algorithm are determined. These parameters are \(pn,vm,c_{1i} ,c_{1f},c_{2i},c_{2f},w_{1} \), and \(w_{2}\). Let \(c_{1}\) and \(c_{2}\) represents cognitive and social coefficients, respectively, and \(w\) is the inertia parameter. Let \(\left( {c_{1i},c_{1f}} \right) ,\left( {c_{2i},c_{2f}}\right) ,\) and (\(w_{1},w_{2}\)) be the intervals which includes possible values for \(c_{1},c_{2}\) and \(w\), respectively. At each iteration, these parameters are calculated by using the formulas given in (6)–(8).

    $$\begin{aligned} c_1&= \left( {c_{1f} -c_{1i} } \right) \frac{t}{\hbox {max}t}+c_{1i} \end{aligned}$$
    (6)
    $$\begin{aligned} c_2&= \left( {c_{2f} -c_{2i} } \right) \frac{t}{\hbox {max}t}+c_{2i}. \end{aligned}$$
    (7)
    $$\begin{aligned} w&= \left( {w_{2} -w_{1}} \right) \frac{\hbox {max}t-t}{\hbox {max}t}+w_{1}. \end{aligned}$$
    (8)

  • Step 3 Evaluation function values are computed. Evaluation function values for each particle are calculated. MSE given in below is used as evtion function.

    $$\begin{aligned} MSE=\frac{1}{n}\mathop \sum \limits _{t=1}^n \left( Desired_{t} -Output_{t} \right) ^{2}. \end{aligned}$$
    (9)

    where \(n\) represents the number of learning sample. The output value of the proposed model is calculated by Algorithm 1.

  • Step 4 \(Pbest_{m}(m = 1,2,\ldots ,pn)\) and Gbest are determined due to evaluation function values calculated in the previous step. \(Pbest_{m}\) is a vector stores the positions corresponding to the \(m{\mathrm{th}}\) particle’s best individual performance, and Gbest is the best particle, which has the best evaluation function value, found so far.

    $$\begin{aligned} Pbest_m&= \left( {p_{m,1},p_{m,2},\ldots ,p_{m,d}} \right) ,\quad m=1,2,\ldots ,pn \end{aligned}$$
    (10)
    $$\begin{aligned} Gbest&= \left( {p_{g,1}, p_{g,2},\ldots ,p_{g,d}} \right) \end{aligned}$$
    (11)

  • Step 5 The parameters are updated. The updated values of cognitive coefficient \(c_{1}\), social coefficient \(c_{2}\), and inertia parameter \(w\) are calculated using the formulas given in (6)–(8).

  • Step 6 New values of positions and velocities are calculated. New values of positions and velocities for each particle are computed by using the formulas given in (12) and (13). If maximum iteration number is reached, the algorithm goes to Step 3; otherwise, it goes to Step 7.

    $$\begin{aligned} v_{m,j}^{t+1}&= \left[ {w\times v_{m,j}^t +c_1 \times rand_1 \times \left( {p_{m,j} -x_{m,j}} \right) +c_2 \times rand_2 \times \left( {p_{g,j} -x_{m,j} } \right) } \right] . \end{aligned}$$
    (12)
    $$\begin{aligned} x_{m,j}^{t+1}&= x_{m,j}^{t} +v_{m,j}^{t+1},\quad \mathrm{where}\;m= 1,2,\ldots ,pn, j = 1,2,\ldots ,d \end{aligned}$$
    (13)

  • Step 7 The best solution is determined. The elements of Gbest re taken as the best weight values of the new ANN model.

3 The Application

The real-world time series used in the implementation is the amount of carbon dioxide measured monthly in Ankara capitol of Turkey (ANSO) between March 1995 and April 2006. The graph of time series data of the amount of \(\hbox {CO}_{2}\) in Ankara is given in Fig. 3. This time series has both trend and seasonal components and its period is 12. The first 124 observations are used for training and the last 10 observations are used for test set. In addition to the proposed approach, seasonal autoregressive integrated moving average (SARIMA), Winter’s multiplicative exponential smoothing (WMES), MLP-ANN, radial bases function ANN (RBF-ANN), E-ANN, MNM-ANN, MS-ANN and L&NL-ANN methods are also used to analyze ANSO data. For the test set, mean square error (MSE) and mean absolute percentage error (MAPE) values produced by all methods are summarized in Table 1. MAPE is calculated by formula (14).

$$\begin{aligned} MAPE=\frac{1}{n}\mathop \sum \limits _{t=1}^n \left| {\frac{Desired_{t} -Output_{t}}{Desired_{t}}} \right| \end{aligned}$$
(14)

In the training process of L&NL-ANN, MS-ANN and proposed RMNM-ANN model, the parameters of the PSO are determined as follows: \(\left( {c_{1i},c_{1f}}\right) =\left( {2,3} \right) \!,\left( {c_{2i},c_{2f}}\right) = \left( {2,3}\right) \!,\left( {w_{1},w_{2}} \right) = \left( {1,2}\right) \!, pn=30,\) and \(\mathrm{max}t=1000\). For the proposed RMNM-ANN model, the best result was obtained when \(p = 3\) and \(q = 13\). To determine the best values of \(p\) and \(q\), trial and error method was employed. According to Table 1, it is clearly seen that the best results in terms of both performance measures were obtained when the proposed RMNM-ANN model was used. The line graph of proposed method forecasts and test data is given in Fig. 4.

Fig. 3
figure 3

The time series data of the amount of \(\hbox {SO}_{2}\) in Ankara

Full size image
Table 1 The obtained forecasting results for ANSO data
Full size table
Fig. 4
figure 4

The line graph of proposed method forecasts and test data of ANSO

Full size image

Secondly, Australian beer consumption ([13], p. 84) between 1956 Q1 and 1994 Q1 is used to examine performance of proposed method. The last 16 observations of the time series were used for test set. Australian beer consumption was forecasted by using SARIMA, WMES, FFANN, RBF, L&NL-ANN, E-ANN, MS-ANN, MNM-ANN and proposed RMNM-ANN. All obtained forecasting results for Australian beer consumption are summarized in Table 2. The best result was obtained from proposed method when model orders are \(p=5\) and \(q=8\).

Table 2 The obtained forecasting results for Australian beer consumption
Full size table

The line graph of proposed method forecasts and test data is given in Fig. 5.

Fig. 5
figure 5

The line graph of proposed method forecasts and test data of Australian beer consumption

Full size image

Finally, the MLP-ANN, MNM-ANN and RMNM-ANN were compared by using statistical techniques. Three methods are applied 30 times for two real life time series by using random initial weights. The RMSE values for test data of ANSO and Australian beer consumption data were obtained. The obtained results were compared by using one way ANOVA method. The obtained results for ANSO data are summarized in Tables 3 and 4. In Table 3, it is given that the mean and standard deviation of RMSE values which are obtained from best architectures of MLP-ANN, MNM-ANN and RMNM-ANN methods. When Table 3 is examined, the proposed method has the smallest mean and standard deviation.

Table 3 Descriptive statistics for ANSO data
Full size table

In Table 4, one way ANOVA results are summarized. According to ANOVA results, there is statistically significant difference between RMSE values of LP-ANN, MNM-ANN and RNM-ANN methods. When multiple comparisons LSD tests are applied for data, it is concluded that RNM-ANN method has smaller mean than the other methods.

Table 4 ANOVA table for ANSO data
Full size table

Similar statistical methods were applied for Australian beer consumption data. The obtained results are summarized in Tables 5 and 6. Similar results are obtained from Australian beer consumption data. RMNM-ANN is better than MNM-ANN and MLP-ANN.

Table 5 Descriptive statistics for Australian beer consumption data
Full size table
Table 6 ANOVA table for Australian beer consumption data
Full size table

4 Conclusion

Although ANN models for non-linear time series use lagged variables of time series, they do not take lagged variables of error into account. Some hybrid approaches in the literature use lagged variables of error but these lagged variables are obtained from other approaches such as Box–Jenkins models. A new recurrent ANN model based on multiplicative neuron model is suggested in this study. The proposed RMNM-ANN model can produce lagged variables of error and use them as inputs because of the recurrent feedback structure it has. Also, unlike the most of the other ANN models, it does not the problem of determination of the number of neurons in hidden layer. Since it has only one neuron in hidden layer, it can reach results with less parameter. When the proposed RMNM-ANN model is applied, parameters needed to be determined are the number of lagged variables for time series and error. These parameters were determined using trial and error method in this study. The proposed model was applied to two real-world time series and the obtained results are compared to results produced by other methods available in the literature. It was observed that the proposed model produced the most accurate forecasts. In future studies, to determine the parameters of RMNM-ANN model, different systematic approaches can be utilized instead of trial and error method.