Introduction

Source rock reservoirs are rapidly growing into a major energy resource player as conventional hydrocarbon fields across the world continue to diminish. To determine accurately the potential of an unconventional shale reservoir requires in-depth knowledge of the distribution of the organic geochemical properties. Generally, the geochemical parameters provide an understanding of the organic matter content, type, and thermal distribution of the source rock (Cappuccio et al., 2020; Curiale & Curtis, 2016; Liu et al., 2020). The fundamental organic geochemical parameters include total organic carbon (TOC), which describes the amount of organic matter. S1 represents the amount of free hydrocarbon present in the rock sample before performing the pyrolysis process while S2 is the hydrocarbon formed during the pyrolysis of the sample. The S2 values give a general indication of the prevailing hydrocarbon generating potential. Rock–Eval pyrolysis is the most commonly used pyrolysis method for measuring the quantity of emitted carbon dioxide and hydrocarbons (Carvajal-Ortiz & Gentzis, 2015; Hakimi et al., 2020; Mani et al., 2017; Shalaby et al., 2019).

The most reliable method of quantifying the source rock is by performing organic geochemical analysis on core samples in the laboratory. However, coring is an expensive exercise to be conducted on all wells (Evenick, 2020; Mahmoud et al., 2017). In cases where there may not be enough core data, readily available drill cuttings are commonly used to compensate. The challenges of using drill cuttings are their difficulty for reconciling with depth and they can be contaminated (Bai & Tan, 2020). Concerning this, attempts have been made to generate TOC values from geophysical well logs based on the knowledge that well log parameters can detect the presence of organic matter. The two frequently employed conventional techniques are the Schmoker and ΔlogR models. The Schmoker model estimates TOC using the reciprocal of bulk density. However, the Schmoker approach is influenced heavily by the reservoir or geological characteristics (Schmoker, 1979; Mahmoud et al., 2019; Xiong et al., 2019). The widely adopted conventional method is the ΔlogR method proposed by Passey et al. (1990) using a porosity and resistivity log (Tenaglia et al., 2020). It is well documented that the shortcoming of the ΔlogR is the varying log-baseline in different wells, formations, and depositional environments (Charsky & Herron, 2013; Mahmoud et al., 2020). Zhu et al. (2019b) improved the classical ΔlogR method by incorporating shale mineralogy to develop the dual difference ΔlogR (DDΔlogR). The challenge with the implementation of the DDΔlogR is that it requires the mineral composition of shale rock samples.

The successful application of artificial intelligence in hydrocarbon exploration and production in recent years has seen the adoption of machine learning models in predicting TOC from well log data. The advantage of machine learning models is their ability to learn and adapt to the dynamics of reservoir conditions such as formation and depositional environment while making use of the entire suite of well logs for a better TOC prediction (Mahmoud et al., 2020; Tariq et al., 2020; Wang et al., 2019a, 2019b; Zhu et al., 2019a). Artificial neural network (ANN) has been the predominantly used machine learning method to predict geochemical data in studies such as (Amiri Bakhtiar et al., 2011; Mahmoud et al., 2020; Shalaby et al., 2020). From these researches, ANN outperformed conventional methods like ΔlogR due to its ability to map out patterns within the suite of input well logs and geochemical data. However, ANN suffers from intrinsic shortcomings such as overfitting and low convergence speed due to the constant manual tuning of model parameters like the number of hidden nodes, weights, and biases (Asante-Okyere et al., 2020; Bai & Tan, 2020; Zhu et al., 2018, 2019a). Several researches have proposed new concepts and improved machine learning algorithms as an alternative to the standard ANN. Gaussian process regression (GPR) has been implemented for the prediction of TOC by Yu et al. (2017) and Rui et al. (2020). However, GPR requires the user to specify the best kernel function to achieve the optimal prediction results. Support vector machine (SVM) and extreme learning machine (ELM) as an improved machine learning techniques have been proposed in determining TOC values in shale reservoirs (Shi et al., 2016; Tan et al., 2015; Wang et al., 2018). Similar to GPR, these machine learning models require an iterative tuning of training parameters to obtain the best performance. In addition to the aforementioned machine learning methods, deep learning techniques have been proposed to improve the evaluation of TOC (Wang et al., 2019a, 2019b; Zhu et al., 2019a, 2020).

Based on this, we examined for the first time the applicability of the group method of data handling (GMDH) as an improved neural network model in estimating TOC, S1, and S2 data from geophysical well logs. The GMDH neural network possesses a self-organizing nature to automatically tune model parameters and generate the optimal model structure during training. Unlike other machine learning models trained to predict TOC, the GMDH neural network does not require a manual adjustment of learning parameters to generate the best outcome as summarized in Table 1. A polynomial function of relevant input variables is also generated by GMDH neural network. To ascertain the performance of the proposed GMDH neural network in predicting TOC, S1, and S2, its results were fairly compared with ANN algorithms of backpropagation, radial basis function, and Passey’s conventional method of ΔlogR.

Table 1 Advantages and limitations of conventional and machine learning models previously used to estimate TOC
Full size table

Geological Setting and Data Descriptions

Geological Setting

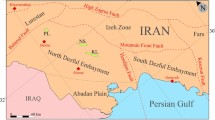
The Mandawa Basin is a rift basin situated within the coastal belt of Tanzania. It extends from the border of Kenya in the north to the border of Mozambique in the south. The basin occupies an area of 16,000 km2 bordered by the Indian ocean with offshore basins in the east and bounded by the basement of metamorphic terrain on the west side (Caracciolo et al., 2020; Hudson & Nicholas, 2014; Kagya, 1996). It circumscribes the Ruvuma Saddle to the south, which separates the Ruvuma basin from the Mandawa basin and by the Rufiji trough to the north (Fig. 1a). Karoo rifting (Permian–Triassic) was the major tectonic event that dominated the development of the Mandawa Basin. The depositional origin and the Mandawa Basin history are strongly influenced by the Gondwana break-up (Delvaux, 2001; Hou, 2015; Nerbråten, 2014).

Figure 1
figure 1

a Location of the Mandawa Basin. b Locations of exploration wells used in this study (Hudson, 2011)

Full size image

The Mandawa Basin is divided into the Kilwa, Mandawa, Pindiro, Mavuji and Songo Songo Groups (Fig. 2). During Early Cretaceous to Late Jurassic, the basin was subsiding at a higher rate in which clastic sediments were major deposits. The prograding of the Mavuji groups and Mandawa groups were then deposited in alluvial and river deposits (Emanuel et al., 2020; Fossum et al., 2020). The coastal Mandawa Basin, under the outer-mid shelf environment, subsided at a constant stage rate from Bajocia to Priabonian–Paleogene, which resulted in the deposition of the Kilwa Group. The Kilwa Group comprises the Kivinje, Nangurukuru, Masoko, and Pande Formations. The Mavuji Group consists of the Makonde, Kitiruka, and Kihuluhulu Formations, which are three time-equivalent formations (Emanuel et al., 2020; Hou, 2015; Hudson, 2011).

Figure 2
figure 2

The Mandawa Basin stratigraphical chart (from Fossum et al., 2019)

Full size image

The Nondwa Formation in an unconformable manner overlays the deltaic-fluvial from Upper Triassic to Lower Jurassic Mihambia and Mbuo Formations, which underlie the middle Jurassic Mtumbei Formation separated by the unconformity stage of the Aelenian-Bajocian. The basin was occupied with shoreface to offshore fine-grained, siltstones, mudstones and, sandstones of the Mbuo Formation (Einvik-Heitmann et al., 2015; Smelror et al., 2018). The study area consists of four exploration wells, which are Mbate-1, Mbuo-1, Mita Gamma-1, and East Lika-1 (Fig. 1b). It is important to remember that Mita Gamma-1 intersected both the Nondwa Formation and silicic limestones of the Mihambia Formation; Mbate-1 well is found in the Kivinje Formation while Mbuo-1 well intersected both the Nondwa and Mbuo Formations and, lastly, East Lika-1 intersected the Mbuo and Nondwa sequences.

Data Descriptions

Conventional well log suite of bulk density log (RHOB), sonic travel time (DT), deep lateral resistivity log (LLD), gamma-ray (GR), spontaneous potential log (SP), neutron porosity (NPHI), and measured geochemical results of TOC, S1 and S2 values obtained from Mandawa Basin were used in this study. Three wells namely Mbate-1, Mbuo-1, and Mita Gamma-1, which have a complete set of well log suites and core TOC, S1, and S2 data, were employed to develop the machine learning models. Mbate-1 and Mbuo-1 wells consisted of 33 sample data for TOC, and 25 sample data for both S1 and S2, which were used to train the models. The developed models were tested on the Mita Gamma-1 well, which consisted of 20 sample data of TOC, S1, and S2. The well log suite and geochemical results of Mbate-1, Mbuo-1, and Mita Gamma-1 wells are illustrated in Figures 3, 4 and 5. The input data of well logs and output data of TOC, S1, and S2 were normalized within the range of [0, 1] to avoid a case of bias treatment during the model development.

Figure 3
figure 3

Well log suite and measured TOC, S1 and, S2 for Mbuo-1 well used for training

Full size image
Figure 4
figure 4

Well log suite and measured TOC, S1 and, S2 for Mbate-1 well used for training

Full size image
Figure 5
figure 5

Well log suite and measured TOC, S1, and S2 for Mita gama-1 well used for testing

Full size image

Methods

ΔlogR Technique

Passey et al. (1990) introduced the method known as \(\Delta \log R\) for obtaining TOC from wireline data. The proper scaling of both the sonic transit time log and resistivity curve is a crucial initial step in the application of this technique, utilizing gamma-ray logs, fine-grained, organic-poor, non-source rock intervals to define baselines for the sonic and resistivity logs. Except in the case of an organic-rich source or a hydrocarbon reservoir interval, these two curves should be parallel and should be overlap (Passey et al., 1990, 2010). The curve of resistivity will react and respond to fluid formation and the sonic curve will react to the presence of kerogens of low velocity/density. At each depth, the corresponding separation of the two curves, i.e., \(\Delta \log R\) [Eq. (1)], can be estimated and used to evaluate organic-rich intervals. As long as the quantity of organic maturity (LOM) of an interval is defined or can be measured, the value of \(\Delta \log R\) at a specified depth can now be explicitly used in the TOC estimation [Eq. (2)]. The LOM is a typical numerical scale that reflects a whole petroleum generation thermal spectrum (Hood et al., 1975).

$$\Delta \log R = \log _{{10}} \left( {\frac{R}{{R_{{{\text{baseline}}}} }}} \right) + n*\left( {\Delta t + \Delta t_{{{\text{baseline}}}} } \right)$$
(1)
$$TOC = (\Delta \log R) * 10^{{(2.2970 - 0.1688 * LOM)}}$$
(2)

where the curve separation expressed in logarithmic cycles of resistivity is \(\Delta \log R\), R is the resistivity measured in Vm by the logging tool, Δt is the time taken during the transition, \(R_{{{\text{baseline}}}}\) is resistivity equivalent to the \(\Delta t_{{{\text{baseline}}}}\) value during non-source rocks reached the curved baseline, and n is created on the ratio of quantity of transition time cycle to one resistivity cycle usually given as 0.02. The baseline values are derived when 1 logarithmic deep resistivity value equivalent to 50 sonic overlaid with the DT log scaling on the deep resistivity log. An overlap between the high deep resistivity log and high sonic DT log in the lithology indicates the presence of a potential area in the zone in the crossover.

Artificial Neural Network (ANN)

An ANN is a computational model that mimics the human brain's role to learn from instances and discover solutions to complex problems in decision-making and classification challenges (Shanmuganathan, 2016). An ANN uses nonlinear and complex types of hypotheses \(h_{{w,b}} (x)\) to describe and interpret the predictions of new instances, provided the training dataset \(x_{i}\) with a vector of dimension m function feature, thus:

$$h_{{w,b}} (x) = f(w^{T} x + b) = \frac{1}{{1 + \exp ( - (w^{T} x + b))}}{\text{ }}$$
(3)

where \(x_{i}\) is the input,\(w\) is weight allocated to each input \(x_{i}\), b is the feature bias, and the output is \(h_{{w,b}} (x)\). The inputs used in this study were the well logs of DT, RHOB, LLD, GR, SP, and NPHI. To determine the output network values of TOC, S1, and S2, forward propagation is carried out based on:

$$z^{{l + 1}} = w^{l} \alpha ^{l} + b^{l}$$
(4)
$$\alpha ^{{l + 1}} = f(z^{{l + 1}} )$$
(5)

where l denotes the neural network layer, \(z_{i}^{l}\) denotes the cumulative weighted number of inputs in layer l for neuron i, and \(\alpha _{i}^{l}\) signifies the output after the activation function of \(z_{i}^{l}\). The sigmoid activation function for every neuron is represented by \(f(z)\). Depending on the activation functions and, model weights a hypothesis \(h_{{w,b}} (x)\) is determined after the forward propagation step. The error function \(J\left( {\omega ,b} \right) - \frac{1}{2}\left\| {h_{{\omega ,b}} \left( x \right) - y} \right\|^{2}\) is then determined with the purpose of decreasing the loss (error) function for the network training. The loss function is a technique of assessing how well the specific algorithm models the dataset given. Since the error function \(J(w,b)\) is given as a non-convex function, Adaptive Moment Estimation (Adam) or Stochastic Gradient Descent (SGD) as the optimization algorithms may be utilized to modify the weights from each neuron to minimize the local error (Zhang et al., 2019). The SGD updates weight (w) and bias (b), where \(\alpha\) is the learning rate, as seen in Eqs. (6) and (7).

$$w_{{ij}}^{l} = w_{{ij}}^{l} - \alpha \frac{\partial }{{\partial w_{{ij}}^{l} }}J(w,b)$$
(6)
$$b_{{ij}}^{l} = w_{{ij}}^{l} - \alpha \frac{\partial }{{\partial w_{{ij}}^{l} }}J(w,b)$$
(7)

The efficient method to calculate the partial derivatives to adjust the weights (w) can be given by the backpropagation algorithm [Eq. (8)]. The partial derivatives of the hidden layer can also be calculated and used to update weights \(j = l - 1;j > = 2;j - -\) thus:

$$\delta _{l} = \frac{\partial }{{\partial z_{i}^{l} }}\frac{1}{2}\left\| {h_{{w,b}} (x) - \left. y \right\|} \right.^{2} = - (y_{i} - \alpha _{i}^{l} )f'(z_{i}^{l} )$$
(8)
$$\delta ^{j} = ((w^{l} )^{T} \delta ^{{j + 1}} )f'(z^{j} )$$
(9)

The neurons throughout the previous layer are assigned a penalty \(\delta ^{j}\), for the weights, and the local error of each layer j is modified based on the penalty \(\delta ^{j}\). According to Qian (1999), the momentum coefficient is used to enhance the SGD mostly in the proper path to avoid becoming local minimum stuck during optimization; this is achieved by adding a fraction number of the updated layer of the past step time to the updated current layer. Proper weight adjustment results in lower error rates and hence, increasing its generalization, makes the model more efficient.

The present study employed the radial basis function neural network (RBFNN) and back-propagation neural network (BPNN). The optimal model structure for BPNN and RBFNN models was achieved based on the trial-and-error method by tuning the number of hidden neurons and the spread parameter, respectively, in order to achieve the least error margin. The gradient descent approach was adopted for RBFNN. The model learning process for BPNN was achieved for 1000 epochs with a learning rate of 0.03 and a momentum coefficient of 0.7. The ANN models were developed, coded, and implemented in MATLAB software R2019b.

Group Method of Data Handling (GMDH) Network

The objective of the GMDH model is to find a function, \(\hat{f}\), which is used as an approximation rather than a real function, f, to estimate the output, t, for a defined input vector U = (u1, u2, u3, …, un), close to its real output, p (TOC, S1, S2). Therefore, given single output with n multi-input data pair of observations, so that:

$$t_{i} = f\left( {u_{{i1}} ,u_{{i2}} ,u_{{i3}} , \ldots ,u_{{in}} } \right){\text{ }}\left( {i = 1,2,3, \ldots ,M} \right)$$
(10)

With any given input vector \(U = u_{{i1}} ,u_{{i2}} ,u_{{i3}} , \ldots ,u_{{in}}\), the GMDH network can then be trained to estimate the output values t, meaning:

$$t_{i} = \hat{f}\left( {u_{{i1}} ,u_{{i2}} ,u_{{i3}} , \ldots ,u_{{in}} } \right){\text{ }}\left( {i = 1,2,3, \ldots ,M} \right)$$
(11)

The GMDH builds the general relationship in the context of a mathematical description between output and input parameters called the reference to solve this problem. The problem here is to determine the GMDH network so that the square difference between the predicted and the actual output is minimized as:

$$\sum\limits_{{i = 1}}^{M} {\left[ {\hat{f}\left( {u_{{i1}} ,u_{{i2}} ,u_{{i3}} , \ldots ,u_{{in}} } \right) - p_{i} } \right]} ^{2} \to \min$$
(12)

The polynomial series known as the Kolmogorov–Gabor polynomial, which is the complex discrete form of the Volterra function (Anastasakis & Mort, 2001; Najafzadeh & Azamathulla, 2013), can express the general link between input parameters and output parameter in the mode of:

$$p = a_{o} + \sum\limits_{{i = 1}}^{N} {a_{i} u_{i} + } \sum\limits_{{i = 1}}^{N} {\sum\limits_{{j = 1}}^{N} {a_{{ij}} u_{i} u_{j} } + } \sum\limits_{{i = 1}}^{N} {\sum\limits_{{j = 1}}^{N} {\sum\limits_{{k = 1}}^{N} {a_{{ijk}} u_{i} u_{j} u_{k} + \cdots } } }$$
(13)

Equation (12) can be simplified using the simplified GMDH network's partial quadratic polynomial equation as (Shen et al., 2019):

$${\text{ }}t = W\left( {u_{i} ,u_{j} } \right) = a_{o} + a_{1} u_{i} + a_{2} u_{j} + a_{3} u_{i}^{2} + a_{4} u_{j}^{2} + a_{5} u_{i} u_{j}$$
(14)

The mathematical relationship between the variables of input–output specified in Eq. (13) is generated by this network of connected neurons. The coefficients of weighting (Eq. (14)) are computed using techniques of regression to minimize the variation between an actual (p) and predicted (t) output, as for each variable pair of ui and uj input is minimized (Armaghani et al., 2020). The schematic type of the GMDH network architecture is shown in Figure 6.

Figure 6
figure 6

Type of the GMDH network architecture

Full size image

Using the quadratic equation [Eq. (14)], a tree of polynomials is created in which the coefficients of weighting can be found by employing the least square approach technique. The quadratic function of weighting coefficients Wi is obtained to match the output optimally in the complete set of output–input data pairs as:

$$E = \frac{{\sum\nolimits_{{i = 1}}^{M} {(p_{i} - W_{i} ())^{2} } }}{M} \to \min$$
(15)

The possibilities for dual independent variables among the overall n input parameters are drawn to fit the general form of GMDH algorithms to build the regression polynomial defined in the form of Eq. (13), which suits better in the least-square sense of the dependent observations \((p_{i} ,i = 1,2,3 \ldots M)\). Consequently \(C_{n}^{2} = n\left( {n - 1} \right)/2\), quadratic polynomial neurons can be constructed from observations \(\left\{ {(p_{i} ;u_{{xi}} ,u_{{yi}} );{\text{ }}(i = 1,2,3 \ldots M)} \right\}\) for various \(x,{\text{ }}y \in \left\{ {1,{\text{ }}2,3, \ldots n} \right\}\) in the feed-forward network’s first layer. Triples of M data can now be built \(\left\{ {(p_{i} ;u_{{xi}} ,u_{{yi}} );{\text{ }}(i = 1,2,3 \ldots M)} \right\}\), using those \(x,{\text{ }}y \in \left\{ {1,{\text{ }}2,3, \ldots n} \right\}\) in the form of:

$$\left[ {\begin{array}{*{20}c} {u_{{1x}} } & {u_{{1y}} } & : & {p_{1} } \\ {u_{{2x}} } & {x_{{2y}} } & : & {p_{2} } \\ \ldots & \ldots & : & \ldots \\ {u_{{mx}} } & {u_{{my}} } & : & {p_{m} } \\ \end{array} } \right]$$
(16)

For every row of the m data triples, using the quadratic sub-expression shown in the form of Eq. (14), the following matrix expression can be found directly as:

$$Aa = P$$
(17)

where a represents an undefined vector of quadratic polynomial weighting coefficients in Eq. (14):

$$a = \left[ {a_{0} ,a,_{1} a_{2} ,a_{3} ,a_{4} ,a_{5} } \right]^{T}$$
(18)

where T indicates matrix transposition:

$$P = \left[ {p_{1} ,p_{2} ,p_{3} , \ldots p_{M} } \right]^{T}$$
(19)

Equation (16) represents a vector of outputs' observation written as:

$$A = \left[ {\begin{array}{*{20}c} 1 & {u_{{1x}} } & {u_{{1y}} } & {u_{{1x}} u_{{1y}} } & {u^{2} _{{1x}} } & {u^{2} _{{1y}} } \\ 1 & {u_{{2x}} } & {u_{{2y}} } & {u_{{2x}} u_{{2y}} } & {u^{2} _{{2x}} } & {u^{2} _{{2y}} } \\ \ldots & \ldots & \ldots & \ldots & \ldots & \ldots \\ 1 & {u_{{mx}} } & {u_{{my}} } & {u_{{mx}} u_{{my}} } & {u_{{mx}}^{2} } & {u_{{my}}^{2} } \\ \end{array} } \right]$$
(20)

The least-square approach derived from the technique of multiple-regression analysis results in normal equations being solved, which is in the form of:

$$a = \left( {A^{{TA}} } \right)^{{ - 1}} A^{T} P$$
(21)

For the whole set of triples of m data, Eq. (21) specifies the vector for the best quadratic weighting coefficients given in Eq. (10). The GMDH model was also coded and implemented in MATLAB software R2019b.

Results and Discussions

The GMDH and ANN models were developed using MATLAB R2019b. The results from the machine learning predictive models were compared fairly using mean square error (MSE) and mean absolute error (MAE) as statistical indices. The differences between the predictions and the measured TOC, S1, and S2 values were highlighted by MSE and MAE. For comparison of the models, MSE and MAE approaching zero proves that a model is an accepted predictor. The mathematical expressions for MSE and MAE are given, respectively, as:

$$MSE = \frac{1}{n}\sum\limits_{{i = 1}}^{n} {\left( {t_{i} - p_{i} } \right)^{2} }$$
(22)
$$MAE = \frac{1}{n}\sum\limits_{{i = 1}}^{n} {\left| {t_{i} - p_{i} } \right|}$$
(23)

where p is the predicted outcome, t is the measured value, and n is the total number of observations. During training, MSE and MAE approaching zero mean that a model trained well. However, more emphasis is placed on the ability of the trained model to perform well when tried on the withheld testing data. Therefore, testing results (MSE and MAE) approaching zero signify the best performing model with an improved generalization capacity.

TOC Prediction

The baseline for the resistivity and sonic well logs when estimating TOC using ΔlogR were observed at 335.83 µs/m and 0.866 Ωm for Mbuo-1, 52.30 µs/m and 42.47 Ωm for Mbate-1, 68.77 µs/m and 38.84 Ωm for Mita Gamma-1. The estimates from ΔlogR generated MSE and MAE of 8.795 and 1.66, respectively, for Mbate-1 and Mbuo-1; for Mita Gamma-1, the MSE and MAE were 1.418 and 0.890, respectively (Table 1). However, the ANN models of BPNN and RBFNN performed better than the conventional ΔlogR approach. The optimal BPNN model structure observed after training the TOC data was 6 inputs, a hidden layer with 12 neurons, while 6 inputs and a hidden layer with a spread parameter of 0.07 were identified for RBFNN. From Table 1, BPNN provided predictions having MSE and MAE of 0.606 and 0.56, respectively, for training; for testing, MSE and MAE were 1.269 and 0.819, respectively. It can be seen from Table 2 that RBFNN trained well with MSE and MAE of 0.0064 and 0.019 but failed to generate similar results when the model was tested on the Mita Gamma-1 well data as its predictions had MSE and MAE of 0.681 and 0.70, respectively. The best performing model was the GMDH, which trained well with its outcome having MSE and MAE of 0.018 and 0.098, respectively, while generalizing better than ΔlogR and ANN on Mita Gamma-1. The GMDH provided MSE and MAE of 0.4 and 0.455, respectively, for TOC during testing as expressed in Table 2. The performance of the TOC models is compared in Figure 7.

Table 2 Statistical parameters of TOC predictive models during training and testing
Full size table
Figure 7
figure 7

Plots of GMDH, ANN, and ΔlogR predictions and measured TOC

Full size image

S1 and S2 Prediction

For the hydrocarbon potential distribution parameters, S1 and S2, the results from RBFNN when training with Mbuo-1 and Mbate-1 data were excellent. RBFNN had MSE and MAE of 8 * 10–6 and 0.0008, respectively, for S1 while generating 0.0012 and 0.299, respectively, for S2 (Table 3). The optimal model structure of the S1 RBFNN model was 6 inputs, a hidden layer with a parameter spread of 0.03. The S2 RBFNN model that generated the best outcome had 6 inputs and a hidden layer with spread parameter of 0.01. Unsurprisingly, RBFNN was unable to generate similar results for the Mita Gamma 1 data during testing. During testing, RBFNN achieved relatively high MSE and MAE of 0.15 and 0.245, respectively, for S1, 1.14, and 0.87, respectively, for S2. On the other hand, the best BPNN model structure that produced the least error rate for S1 was 6 input, a hidden layer with 6 neurons. The S2 BPNN that had the optimal architecture was 6 inputs and a hidden layer with 2 neurons. From Table 3, the S1 BPNN model achieved MSE and MAE of 0.0102 0.056, respectively, for training. During testing, it generated predictions scoring 0.085 and 0.167 for MSE and MAE, respectively (Table 3). The BPNN for predicting S2 data produced comparatively the worst estimates with MSE and MAE of 5.52 and 1.33, respectively, and 1.96 and 0.9, respectively, for testing (Table 4). The BPNN outcome for the testing data of the Mita Gamma-1 well is illustrated in Figure 8.

Table 3 Statistical parameters of S1 predictive models during training and testing
Full size table
Table 4 Statistical parameters of S2 predictive models during training and testing
Full size table
Figure 8
figure 8

Plots of GMDH, BPNN, and RBFNN predictions and measured S1

Full size image

The prediction from the GMDH gave an error values of 0.0011 and 0.024 for S1, and 0.007 and 0.049 during training in the case of S2 (Tables 3 and 4). Looking at the generalization performance, the GMDH tested better than BPNN and RBFNN when it produced testing results with MSE and MAE of 0.04, 0.0702, respectively, for S1, and 1.16 and 0.07 for S2, respectively. This makes the GMDH the best performing model compared to ANN. Figure 9 describes the predictions of the GMDH, BPNN, and RBFNN.

Figure 9
figure 9

Plots of GMDH, BPNN, and RBFNN predictions and measured S2

Full size image

It was recognized that the performance of the GMDH in estimating S2 was generally low compared to the TOC and S1 results. This is due to the fact that the Mita Gamma-1 well, which was used as the testing data, had a high variation of S2 values. The high variation in S2 values of the testing data generated an imbalance distribution of the training and testing observations. However, the GMDH generalized better than ANN when handling the high variation of S2 values. Consequently, ANN models failed to account for the changes in S2 values of Mita-Gamma 1 well as observed in Figure 9.

Quality of Organic Matter and Hydrocarbon Generation Potential for East Lika 1

The constructed GMDH prediction model in this paper was further used to estimate the TOC, S2, and S1 for the East Lika-1 well, which had no core geochemical data. Figure 10 shows the well logs from East Lika-1 and the GMDH predicted values for TOC, S1, and S2. The TOC prediction showed a generally constant value across the entire depth of the well. According to the generated results from GMDH, we can confirm that East Lika-1 well has a low-quality source rock due to the near-constant TOC values across the entire depth of the well. Based on the relatively high S1 values compared to S2 from depths of 2060 m to 2140 m, it can be assumed that there exists evidence of hydrocarbon migration.

Figure 10
figure 10

Well logs from East Lika-1 and GMDH predicted values for TOC, S1, and S2

Full size image

Conclusions

The application of machine learning methods in evaluating geochemical data such as TOC from well log parameters has revealed the shortcomings of artificial neural networks (ANN). Therefore, this study proposed a group method of data handling (GMDH) neural network as a means of offering an improved performance when predicting TOC, S1, and S2. In line with this, Mbuo-1 and Mbate-1 wells were considered as training data, while the predictive capability of the models was judged on the Mita-Gamma-1 well.

When estimating TOC, the ANN models of radial basis function neural network (RBFNN) and backpropagation neural network (BPNN) trained well but failed to generate similar results when the developed models were tested on Mita-Gamma-1 well. The conventional ΔlogR model obtained the highest error rate from its estimates. However, the GMDH performed well during training and further produced the least error margin compared to ANN and ΔlogR during testing.

A similar scenario was observed when estimating the hydrocarbon potential parameters of S1 and S2. RBFNN and BPNN generated close to perfect training results for both S1 and S2 but failed to generate similar results when tested on the Mita-Gamma well data. The GMDH provided the least error margins despite its excellent training capabilities. Based on the outcomes, we suggest GMDH as an improved machine learning method as an alternative to the ANN algorithms for estimating geochemical results like TOC, S1, and S2. The proposed GMDH was further used to determine the TOC, S1 and S2 results for East Lika-1 well, which has no core geochemical data. The predictions revealed a low-quality source rock for East Lika-1 well and a possible hydrocarbon migration occurring between the depths of 2060 m and 2140 m.