Strength of Stacking Technique of Ensemble Learning in Rockburst Prediction with Imbalanced Data: Comparison of Eight Single and Ensemble Models

Abstract

Rockburst is a common dynamic geological hazard, severely restricting the development and utilization of underground space and resources. As the depth of excavation and mining increases, rockburst tends to occur frequently. Hence, it is necessary to carry out a study on rockburst prediction. Due to the nonlinear relationship between rockburst and its influencing factors, artificial intelligence was introduced. However, the collected data were typically imbalanced. Single algorithms trained by such data have low recognition for minority classes. In order to handle the problem, this paper employed stacking technique of ensemble learning to establish rockburst prediction models. In total, 246 sets of data were collected. In the preprocessing stage, three data mining techniques including principal component analysis, local outlier factor and expectation maximization algorithm were used for dimension reduction, outlier detection and outlier substitution, respectively. Then, the pre-processed data were split into a training set (75%) and a test set (25%) with stratified sampling. Based on the four classical single intelligent algorithms, namely k-nearest neighbors (KNN), support vector machine (SVM), deep neural network (DNN) and recurrent neural network (RNN), four ensemble models (KNN–RNN, SVM–RNN, DNN–RNN and KNN–SVM–DNN–RNN) were built by stacking technique of ensemble learning. The prediction performance of eight models was evaluated, and the differences between single models and ensemble models were analyzed. Additionally, a sensitivity analysis was conducted, revealing the importance of input variables on the models. Finally, the impact of class imbalance on the prediction accuracy and fitting effect of models was quantitatively discussed. The results showed that stacking technique of ensemble learning provides a new and promising way for rockburst prediction, which exhibits unique advantages especially when using imbalanced data.

Introduction

Rockburst is a common geological disaster and a dynamic instability phenomenon in deep engineering excavation and deep resource extraction; it is accompanied with rock loosening, peeling, ejection and even throwing (Adoko et al. 2013; Zhou et al. 2018; Zhang et al. 2020a). Its occurrence is controlled by multiple factors, both internal and external causes (Zhang et al. 2020b). External causes include mainly ground stress and excavation disturbance. Rockburst usually occurs in high ground stress zone. Due to disturbance, the stress state existing in rock mass is changed, leading to stress redistribution and stress concentration. Internal causes such as rock strength, brittleness and integrity determine energy storage capacity of rock mass. When the elastic strain energy stored in rock mass exceeds that consumed by deformation and fracture, the rest will be converted into kinetic energy. In this situation, rock pieces are ejected at a certain velocity, namely rockburst. From the aspect of internal causes, rockburst tends to occur in the intact and hard rock mass. Additionally, rockburst is extremely destructive, which directly threatens the safety of workers and equipment, affects construction progress and even destroys an entire project and induces earthquakes (Xu et al. 2018).

Since the first recorded rockburst at the Leipzig coal mine in the United Kingdom in 1738 (He et al. 2017), rockbursts have been reported in many countries around the world. In South Africa (Zhou et al. 2012), almost all gold mines have suffered rockburst. It occurred only seven times in 1908 while the number of rockbursts rose to 680 in 1975. During this period, gold mines gradually shifted from shallow mining to deep mining. In Germany (Baltz and Hucke 2008), the number of hazardous rockbursts reached 283 only at the Luer mining area between 1910 and 1978. In Canada (Pu et al. 2018), rockbursts have taken place in many copper–nickel mines from the mid-twentieth century and consequently several mines were closed. In China (Cai et al. 2018), rockbursts happened at the Shengli coal mine in Fushun in 1933 for the first time. According to statistics, there were more than 2000 rockbursts in mines from 1949 to 1997 (Shi et al. 2005). Besides mining industry, rockbursts also frequently occurred in hydropower, transportation and other fields. For example, on November 28, 2009, a highly strong rockburst occurred in the drainage tunnel of Jinping II Hydropower Station (Zhou et al. 2016b); support systems were destroyed, tunnel boring machines worth 120 million were permanently buried and seven people were killed. With the development of underground space, rockburst has become a major challenge for the safety of deep underground engineering (Pu et al. 2019a). It is urgent to carry out studies on rockburst prediction.

Early research mainly focused on rockburst prediction from a single influencing factor (Ouyang et al. 2015). Several empirical criteria from the perspective of strength theory, stiffness theory, energy theory, stability theory, fractal theory and catastrophe theory have been proposed, such as Russenes criterion (Russenes 1974), Barton criterion (Barton 2002) and Hoek criterion (Hoek and Brown 1980). As research continued, it was recognized that the occurrence of rockburst is affected by multiple factors, not just by a single factor (Ma et al. 2018). There is a significant nonlinear relationship between rockburst and these factors. In addition, these factors are interactive such that it is difficult to achieve high prediction accuracy using traditional empirical criteria. Artificial intelligence provides a powerful tool for solving such problems and it has been used widely in geotechnical engineering (Sun et al. 2019a, b, c, 2020a, b). Feng and Wang (1994) first used artificial neural network to predict rockburst, and later, some scholars (e.g., Jia et al. 2013; Sun et al. 2009) carried out related studies. Zhou et al. (2016a) utilized supervised learning to build ten rockburst prediction models and compared their performance. Pu et al. (2019b) employed support vector machine (SVM) to predict rockburst in kimberlite pipes at a diamond mine and achieved good results. Besides, many other intelligent models (Zhou et al. 2012; Adoko et al. 2013; Dong et al. 2013; Li et al. 2017a, b; Sousa et al. 2017; Li and Jimenez 2017; Pu et al. 2018; Roohollah and Abbas 2019; Wu et al. 2019; Xue et al. 2020, Zhou et al. 2020) have been applied for rockburst prediction (Table 1).

Table 1 Intelligent models used for rockburst prediction

With the improvement of data acquisition approaches, massive data have emerged. However, data is generally imbalanced in practice. If trained by such data, single algorithms have low recognition for minority classes (Ganganwar 2012). Some researches (Díez-Pastor et al. 2015; Salunkhe and Mali 2016) indicated that ensemble learning has better performance when using imbalanced data. As seen in Table 1, there is little research about ensemble learning for rockburst prediction. In this paper, stacking technique (Wolpert 1992) of ensemble learning was adopted to build rockburst prediction models. This fills the gap and demonstrates the superiority of ensemble learning when using imbalanced data to predict rockburst.

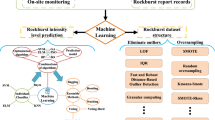
Stacking technique of ensemble learning can combine advantages of several single models to form a stronger one (Dietterich 2000). In this study, k-nearest neighbors (KNN), support vector machine (SVM), deep neural network (DNN) and recurrent neural network (RNN) were chosen as single models, which are also called base models. Based on them, four ensemble models (KNN–RNN, SVM–RNN, DNN–RNN and KNN–SVM–DNN–RNN) were set up by stacking technique. In total, 246 sets of data were collected. After dimension reduction with principal components analysis (PCA), outlier detection with local outlier factor (LOF) and outlier substitution with expectation maximization algorithm (EM), the data were divided into a training set (75%) and a test set (25%) by stratified sampling. The prediction performances of the eight models were evaluated based on the test set and the differences in performances between ensemble models and single models were analyzed. Moreover, a sensitivity analysis was conducted through permutation importance to reveal the contribution of input variables on the models. Finally, the impact of class imbalance on prediction accuracy and fitting effect was discussed quantitatively. Figure 1 shows the flowchart of this study.

Figure 1

Flowchart of this paper

Data Acquisition and Preprocessing

Data Acquisition

The database was compiled from Pu et al. (2019b) and Zhou et al. (2016a), which indicates it is reliable and valid. It consisted of 246 sets of rockburst data from more than 20 engineering projects, including Jinping II hydropower station, Chengchao iron mine, Dongguashan copper mine, Daxiangling tunnel, Tongyu tunnel, Qinling tunnel and others (Zhou et al. 2012). Each set of data was composed of seven variables and a corresponding level of rockburst intensity. In this study, rockburst intensity was classified into four levels: none rockburst, low rockburst, moderate rockburst and high rockburst. The employed classification criterion was in accordance with Zhou et al. (2016a), and it is reported in Table 2. In the database, there were 43 sets with none rockburst, 78 sets with low rockburst, 81 sets with moderate rockburst, and 44 sets with high rockburst. Figure 2 shows the proportion of rockburst at four levels. Because the number of rockburst cases at each level was different, the database was imbalanced.

Table 2 Classification criterion of rockburst intensity (Zhou et al. 2016a)

Figure 2

Proportion of rockburst at four levels

The seven variables were maximum tangential stress of surrounding rock ($\sigma_{\theta }$), uniaxial compressive strength of rock ($\sigma_{c}$), uniaxial tensile strength of rock ($\sigma_{t}$), stress concentration factor (SCF), rock brittleness indices ($B_{1}$, $B_{2}$) and elastic strain energy index ($W_{et}$). Among these variables,$\sigma_{c}$, $\sigma_{t}$, $B_{1}$ and $B_{2}$ represent rock mechanical properties,$\sigma_{\theta }$ reflects ground stress, $W_{et}$ is rock-energy storage capacity, and SCF stands for rock mechanical properties as well as ground stress. According to the mechanism of rockburst generation, the occurrence of rockburst depends not only on rock mechanical properties, but also on $W_{et}$ and $\sigma_{\theta }$ (Afraei et al. 2019). Values of SCF, $B_{1}$, $B_{2}$ and $W_{et}$ can be calculated, respectively, as:

$${{SCF}} = \frac{{\sigma_{\theta } }}{{\sigma_{c} }}$$

(1)

$$B_{1} = \frac{{\sigma_{c} }}{{\sigma_{t} }}$$

(2)

$$B_{2} = \frac{{\sigma_{c} - \sigma_{t} }}{{\sigma_{c} + \sigma_{t} }}$$

(3)

$$W_{et} = \frac{{\phi_{sp} }}{{\phi_{st} }}$$

(4)

where $\phi_{sp}$ and $\phi_{st}$ represent the stored elastic strain energy and the dissipated elastic strain energy, respectively, in a hysteresis looping test (Pu et al. 2019b).

Numerous empirical criteria for rockburst prediction have been raised based on one or several of the above seven variables. In this paper, $\sigma_{\theta }$, $\sigma_{c}$, $\sigma_{t}$, SCF, $B_{1}$, $B_{2}$ and $W_{et}$ were all considered as the input variables to quantitatively predict rockburst. The basic statistics of all the variables in the database are shown in Table 3.

Table 3 Basic statistics of variables in the database

Correlation Analysis and Dimension Reduction

Correlation Analysis with Pearson Correlation Coefficient

When there is a correlation between variables, the redundancy of information will increase, which will increase the time for model training and prediction. Hence, it is necessary to perform correlation analysis on the selected variables. Pearson correlation coefficient (Mu et al. 2018) is one of the most widely used methods to measure the correlation. Normally, it is defined as:

$$r_{xy} = \frac{{\sum {\left( {x_{i} - \bar{x}} \right)\sum {\left( {y_{i} - \bar{y}} \right)} } }}{{\sqrt {\sum {\left( {x_{i} - \bar{x}} \right)^{2} } \sqrt {\sum {\left( {y_{i} - \bar{y}} \right)^{2} } } } }}$$

(5)

where $r_{xy}$ is the Pearson correlation coefficient for two variables X and Y, and $\bar{x}$ and $\bar{y}$ are the means of X and Y, respectively. The range of $r_{xy}$ is [− 1, 1]. When X and Y are positively correlated, the sign of $r_{xy}$ is positive; otherwise, it is negative. The relationship between Pearson correlation coefficient and correlation strength is shown in Table 4 (Mohamed Salleh et al. 2015).

Table 4 Relationship between Pearson correlation coefficient and correlation strength

By analyzing 246 sets of data using Eq. 5, values of $r_{xy}$ for pairs of variables are obtained (Table 5). The absolute value of $r_{xy}$ is > 0.4 for variable pairs $\sigma_{\theta }$ and SCF, $\sigma_{\theta }$ and $W_{et}$, $\sigma_{c}$ and $\sigma_{t}$, $\sigma_{t}$ and $B_{1}$, $\sigma_{t}$ and $B_{2}$, $B_{1}$ and $B_{2}$, suggesting relatively strong correlations between these variables. Especially for $\sigma_{\theta }$ and SCF, the absolute value of $r_{xy}$ reaches 0.92, indicating that $\sigma_{\theta }$ is very strongly correlated with SCF.

Table 5 Pearson correlation matrix for the seven variables used in this study

Dimension Reduction with Principal Component Analysis

Principal Component Analysis (PCA) is a kind of feature extraction technique for multivariate data (Cai et al. 2016). Its basic idea is to map high-dimensional space into low-dimensional space via mathematical transformation. In the field of data mining, it is used to reduce dimension.

From the correlation analysis, relatively strong correlations exist between several variables. Dimension reduction is an effective way to eliminate correlations. The original data used are 7-dimensional. In such high-dimensional situation, dimension disasters are prone to occur, such as sparse data and complex distance calculation. Thus, PCA was implemented to avoid the above problems in this study. The detailed steps were as follows:

• 1. Build the original data matrix $X = \left( {x_{ij} } \right)_{m \times n}$, where m is number of samples, n is number of variables, and $x_{ij}$ denotes the value for variable j of sample i.

• 2. For eliminating dimension effects and making variables comparable, standardize the original data as:

  $$x_{ij}^{*} = \frac{{x_{ij} - \bar{x}_{j} }}{{s_{j} }}$$

  (6)

  where $\bar{x}_{j}$ and $s_{j}$ are the mean and standard deviation of the jth variable, respectively.

• 3. Calculate correlation coefficient matrix $R = \left( {r_{ij} } \right)_{n \times n}$ for the standardized data, where $r_{ij}$ is the Pearson correlation coefficient for variables i and j.

• 4. Calculate eigenvalues $\lambda_{1}$, $\lambda_{2}$ ,…, $\lambda_{n}$ and eigenvectors $v_{1}$, $v_{2}$ ,…, $v_{n}$ of the matrix R.

• 5. Select appropriate principal components as new variables instead of original variables to achieve dimension reduction. In general, the first few principal components, whose eigenvalues are more than 1 and cumulative contribution rate exceeds 80%, are elected. The cumulative contribution rate of the first k principal components can be computed as:

  $$\eta_{k} = \frac{{\lambda_{1} + \lambda_{2} + \cdots + \lambda_{k} }}{{\lambda_{1} + \lambda_{2} + \cdots + \lambda_{n} }} .$$

  (7)

In the results of PCA (Table 6), the eigenvalues of the first three principal components are greater than 1. Moreover, their cumulative contribution rate reaches 82.07% (> 80%), which indicates that they contain more than 80% of the original variable information. Therefore, the first three principal components can be used as new variables to replace the original variables, which are separately denoted as $X_{1}$, $X_{2}$ and $X_{3}$. Table 7 shows the data after dimension reduction.

Table 6 Principal component analysis results

Table 7 Data after dimension reduction with PCA

Outlier Detection and Substitution

Outlier Detection with Local Outlier Factor

Outliers are defined as data that seriously deviate from others in a group, which may result from random error, artificial error, variation and so on (Knorr and Ng 1998). They can interfere with the training of models. Thus, it is essential to conduct outlier detection in a database.

In recent years, outlier detection algorithms have received more and more attention in the field of data mining, and they can be divided into two categories: distance-based and density-based. Distance-based algorithms can only detect global outliers but not local outliers in comparison with density-based algorithms. Local outlier factor (LOF) (Breunig et al. 2000) is a classic density-based outlier detection algorithm. When using LOF to detect whether an object is an outlier, it is critical to calculate the LOF of the object and compare it with a threshold. If it exceeds the threshold, the object is determined as an outlier. Given a database D and an object O, the detailed steps for calculating the local outlier factor of O were as follows:

• 1. Find a set $N_{k} \left( O \right)$ including k nearest neighbors of O in the database D.

• 2. Calculate the k-distance of O as:

  $${\text{dist}}_{k} (O) = \hbox{max} \left\{ {{\text{dist}}(O,P)|P \in N_{k} (O)} \right\}$$

  (8)

  where ${\text{dist}}(O,P)$ denotes Euclidean distance between O and P.

• 3. Calculate the reachability distance between O and P as:

  $${\text{dist}}_{\text{reach}} (O,P) = \hbox{max} \left\{ {{\text{dist}}_{k} (O),{\text{dist}}(O,P)} \right\}$$

  (9)

• 4. Calculate the local reachability density of O as:

  $${\text{lrd}}(O) = \frac{k}{{\sum\nolimits_{{P \in N_{k} (O)}} {{\text{dist}}_{\text{reach}} (O,P)} }}$$

  (10)

• 5. Calculate the LOF of O as:

  $${\text{lof}}(O) = \frac{{\sum\nolimits_{{P \in N_{k} (O)}} {\frac{{{\text{lrd}}(P)}}{{{\text{lrd}}(O)}}} }}{k}$$

  (11)

In this paper, k was set to the default value of 6. It was found after analysis that the LOF was distributed in the range [0, 6.5] for about 99% of the data in the database. Only three (i.e., 1%) among the 246 sets of data had LOF of > 7, which evidently deviated from the others. Referring to the definition of outliers, these are a minority in the database compared to normal points. For this reason, the threshold was fixed at 6.5. Finally, three outliers were detected, namely (0.2114, − 1.1297, − 3.0158), (− 0.1164, 2.3938, − 4.3962) and (− 0.0638, − 1.8155, − 4.7533). The results are shown in Figure 3.

Figure 3

Data visualization after outlier detection with LOF

Outlier Substitution with Expectation Maximization Algorithm

To explore fully the value of data, outlier substitution was conducted instead of directly removing outliers from the database. However, for minimizing disturbance to the data, substitution variable should be first determined. With regard to the variables $X_{1}$, $X_{2}$ and $X_{3}$, they were separately analyzed by LOF. The calculation results of LOF indicated that the abnormality of three outliers was induced mainly by $X_{3}$ (Fig. 4). Then, the expectation maximization (EM) algorithm (Dempster et al. 1977) was used to substitute $X_{3}$ so that the outliers turn into normal points. Its basic idea is as follows.

• 1. Calculate the expectation $\eta^{\left( 0 \right)}$ of the variable $X_{3}$ for normal points in each class.

• 2. According to the class to which an outlier belongs, replace the outlier in variable $X_{3}$ with the expectation $\eta^{\left( 0 \right)}$ of the corresponding class.

• 3. Denote $\eta^{\left( 0 \right)}$ as the initial iteration value and $\eta^{\left( i \right)}$ as the ith iteration value.

• 4. Calculate $Q(\eta ,\eta^{(i - 1)} )$ in each iteration:

  $$Q(\eta ,\eta^{(i - 1)} ) = \log P\left( {Y,Z\left| \eta \right.} \right)P\left( {Z\left| {Y,\eta^{{\left( {i - 1} \right)}} } \right.} \right)$$

  (12)

  where Y and Z represent observable and latent variables, separately, in the database; $P\left( {Y,Z\left| \eta \right.} \right)$ indicates the joint probability distribution of Y and Z; $P\left( {Z\left| {Y,\eta^{{\left( {i - 1} \right)}} } \right.} \right)$ signifies the conditional probability distribution of Z given Y and $\eta^{{\left( {i - 1} \right)}}$.

• 5. Maximize $Q(\eta ,\eta^{(i - 1)} )$ and then determine $\eta^{\left( i \right)}$:

  $$\eta^{\left( i \right)} = \arg \;\mathop {\hbox{max} }\limits_{\eta } Q\left( {\eta ,\eta^{{\left( {i - 1} \right)}} } \right)$$

  (13)

• 6. Repeat steps (4) and (5) until the iteration converges.

Figure 4

Calculation results of LOF for $X_{1}$, $X_{2}$ and $X_{3}$

EM was implemented on SPSS23.0 software. The outliers (0.2114, − 1.1297, − 3.0158), (− 0.1164, 2.3938, − 4.3962) and (− 0.0638, − 1.8155, − 4.7533) were substituted by (0.2114, − 1.1297, 0.9177), (− 0.1164, 2.3938, 1.8912) and (− 0.0638, − 1.8155, 1.4495), respectively. The distribution of LOF after outlier substitution is illustrated in Figure 5. The outlier substitution was successful, as no LOF exceeded the afore-mentioned threshold.

Figure 5

Distribution of LOF after outlier substitution

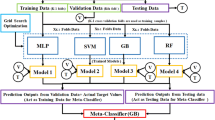
To ensure that data in the training set and test set were sufficiently representative, the database was divided into two parts by stratified sampling after outlier substitution: 75% (185 sets of data) for training and 25% (61 sets of data) for testing. Because stratified sampling does not change data structure, the ratio between the numbers of rockburst at different levels in the training set is consistent with that in the database. Namely, the training set was imbalanced, too. Analyzing the prediction performance of models trained by imbalanced data was the focus of this paper.

Construction of Classification Models

Eight classification models were built to carry out the prediction study of rockburst. The first four models were based on KNN, SVM, DNN and RNN; the rest—KNN–RNN, SVM–RNN, DNN–RNN and ALL (KNN–SVM–DNN–RNN)—were based on the stacking technique of ensemble learning. From analysis, RNN had the best performance among four single models. Thus, RNN was used as the base learner of four ensemble models simultaneously. A detailed introduction to the eight classification models is given below.

In view of the nature of hyper-parameters, it can be divided into continuous and discrete ones. As for continuous hyper-parameters, grid search method (GSM), particle swarm optimization (PSO), cat swarm optimization (CSO), genetic algorithm (GA) and so on are commonly used as optimization algorithms (Zhou et al. 2012; Xue et al. 2020). With respect to discrete hyper-parameters, hold-out method, ten-fold cross-validation, five-fold cross-validation and leave-one-out method are frequently adopted for tuning (Zhou et al. 2016a, 2020). In this study, considering that c and g in SVM belong to continuous hyper-parameters, GSM was used as optimization algorithm. Regarding the number of nearest neighbors in KNN, the number of neurons in the hidden layer in DNN and RNN, they belong to discrete hyper-parameters, and so leave-one-out method was chosen as optimization algorithm. Another reason for employing leave-one-out method was that it was more reasonable and effective for relatively small database while hold-out method, ten-fold cross-validation and five-fold cross-validation were more used commonly for big database. The hyper-parameters of base learners of ensemble models inherit the ones of corresponding single models.

KNN is a commonly used supervised learning algorithm. Its primary aim is to calculate the distance between an object and its neighbors with known labels using Eq. 14:

$$d\left( {x,y} \right) = \left( {\sum\limits_{i = 1}^{q} {\left| {x_{i} - y_{i} } \right|^{p} } } \right)^{1/p}$$

(14)

where x is the object, y is its neighbor with known label; when p is 1 and 2, the distance is Manhattan distance and Euclidean distance, respectively. Then, KNN proceeds to assign the label with the highest frequency among the selected k nearest neighbors to this object. Compared with other supervised learning algorithms, KNN has no explicit training process so that the execution time of training process is zero. When receiving the test sample, training samples are processed. The disadvantage is that training samples need to be reprocessed each time a new test sample is received. The number of nearest neighbors (k) has a significant impact on the classification results of the model. Figure 6 shows the relationship between k and the prediction performance of the model. It was found that the prediction performance of the model was optimal when k was set to 7.

Figure 6

Effect of the number of nearest neighbors k on KNN prediction performance

SVM is a statistical learning algorithm with superior performance in classification tasks. Its basic idea is to find a hyperplane in the sample space to separate samples with different labels. The hyperplane can be defined as:

$$w^{\text{T}} x + b = 0$$

(15)

where $w = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)$ is the normal vector, which determines the direction of hyperplane; and b is the displacement term, which determines the distance between hyperplane and the origin.

However, when the sample space is not linearly separable, no hyperplane can divide correctly the samples into different classes. Because there is a significant nonlinear relationship between rockburst and its influencing factors, rockburst prediction is a typical linear inseparable problem. To solve this problem, radial basis function (RBF) kernel was adopted to map the original sample space to a higher-dimensional space where samples are linearly separable. The form of RBF kernel is expressed as:

$$\kappa \left( {x_{i} ,x_{j} } \right) = \exp \left( { - \frac{{\left\| {x_{i} - x_{j} } \right\|^{2} }}{{2\sigma^{2} }}} \right)$$

(16)

where $\sigma$ is the kernel width.

Two parameters (c and g) play an important role in SVM: c is the penalty coefficient and represents the tolerance of errors; and g comes with RBF kernel and determines the number of support vectors. They are optimized by GSM and the optimization process is shown in Figure 7. The values of c and g were finally taken as 1.320 and 0.002, respectively.

Figure 7

Optimization process to search optimal c and g for SVM

DNN is a representative deep learning algorithm. It has more hidden layers in comparison with traditional artificial neural networks, such as standard BP neural network, RBF network. Theoretically, the higher the complexity of the model, the more complex learning tasks it can complete. In this work, DNN was designed as feedforward neural network with double hidden layers and it was trained with gradient descent using error back-propagation. During feedforward process, the output of neurons was calculated by Eq. 17.

$$y = f\left( {\sum\limits_{i = 1}^{n} {w_{i} x_{i} - \theta } } \right)$$

(17)

where $x = \left( {x_{1} ,x_{2} , \ldots ,x_{n} } \right)$ and y are the input and output of neurons, respectively; $w = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)$ and θ are the weights and bias of network, respectively; and $f\left( * \right)$ is the activation function. The weights and bias of network are updated through a back-propagation process, thus:

$$w_{i} = w_{i} - \eta \frac{\partial E}{{\partial w_{i} }}$$

(18)

where$w = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)$$\theta$ E is the error between output and the actual value; and $\eta \in \left( {0,1} \right)$ is the learning rate.

Referring to Figure 8a and b, the first hidden layer consisted of 12 neurons and the second was made up of eight neurons. At this time, the prediction performance of the model was the best. In addition, sigmoid tangent function was used as the activation function for the neurons.

Figure 8

Effect of the number of neurons in two hidden layers on DNN prediction performance

RNN is another representative deep learning algorithm. It is different from feedforward neural networks, in which loops are allowed to exist so that the output of some neurons can be fed back as input. The Elman network, one of the most widely used RNN frameworks, is composed of four layers: input layer, hidden layer, state layer and output layer. The state layer allows the hidden layer to see its own previous output. Consequently, the subsequent behavior is affected by both the current input and the previous output of the hidden layer. The nonlinear state space of the Elman network can be expressed as Eqs. 19, 20 and 21.

$$y\left( k \right) = g\left( {w^{3} x\left( k \right)} \right)$$

(19)

$$x\left( k \right) = f\left( {w^{1} x_{c} \left( k \right) + w^{2} u\left( {k - 1} \right)} \right)$$

(20)

$$x_{c} \left( k \right) = x\left( {k - 1} \right)$$

(21)

where u is input vector, y is output vector, x is vector of hidden layer, $x_{c}$ is vector of state layer; $w^{3}$ represents the weights between output layer and hidden layer; $w^{2}$ represents the weights between input layer and hidden layer; $w^{1}$ represents the weights between state layer and hidden layer; and $g\left( * \right)$ and $f\left( * \right)$ are the activation functions of the output and hidden layers, respectively.

The number of state layer units is equal to the number of output variables. As shown in Figure 9, the model achieves the best prediction performance when the number of hidden layer units was set to 20. Furthermore, the Levenberg–Marquardt algorithm was selected to the train Elman network, which is greatly useful for solving nonlinear problems.

Figure 9

Effect of the number of neurons in the hidden layer on RNN prediction performance

Ensemble learning is the first of the four research directions of machine learning. It can enhance notably the generalization performance of models. Its basic idea is to accomplish learning tasks by combining multiple learners. According to combination strategies, ensemble learning can be classified into stacking (Wolpert 1992), bagging (Breiman 1996) and boosting (Friedman 2001). Bagging and boosting directly put several weak learners together to form a strong learner. The output of a strong learner is determined by averaging or voting on the outputs of weak learners. However, there are differences between bagging and boosting. The weak learners of the former are independent and can be generated in parallel while the ones of the latter have strong dependencies and they must be generated serially. Random Forest and AdaBoost are representative algorithms for bagging and boosting, respectively. Unlike bagging and boosting, stacking utilizes a meta-learner to gather a group of base learners. The combination of prediction results of base learners on the training set is regarded as new training set to train the meta-learner and that on the test set is used as new test set. The final output of stacking model is determined by the prediction results of meta-learner on the new test set. Its process is demonstrated in Figure 10.

Figure 10

Process of stacking technique

In this research, stacking technique was adopted to establish four ensemble models (KNN–RNN, SVM–RNN, DNN–RNN and KNN–SVM–DNN–RNN). BP neural network using mind evolutionary algorithm served as the meta-learner, whose workflow is illustrated in Figure 11. Before training the BP neural network, its initial weights and bias were optimized via mind evolutionary algorithm, which avoids the randomness. In comparison with other evolutionary computations such as genetic algorithm and evolutionary programming, mind evolutionary algorithm overcomes the shortcomings of slow convergence and premature. To increase the diversity of base learners, output smearing (Breiman 2000) was applied, in which the initial classification output of base learners was transformed into the regression output and then input to the meta-learner.

Figure 11

Workflow of meta-learner of stacking technique

Model Evaluation Metrics

To measure the prediction performance of models, numerous evaluation metrics have been proposed (Hossin and Sulaiman 2015). Considering class imbalance of the data, accuracy (ACC), sensitivity (SNS), precision (PRC) and F₁-score (F₁) were picked as evaluation metrics in this study (Luque et al. 2019). ACC, which is characterized by intuition and simplicity, is the most widely used, indicating the ratio of correctly predicted samples to all predicted samples. SNS represents the proportion of correct predictions among all samples predicted as a certain class while PRC refers to the proportion of correct predictions among all samples belonging to a certain class. F₁ is a comprehensive index combining SNS and PRC, which eliminates their one-sidedness. In particular, F₁ is the harmonic average of SNS and PRC. These metrics can be calculated based on binary confusion matrix. With rockburst prediction being a 4-classification problem, it can be split into four binary classification problems according to one-versus-rest. Correspondingly, four binary confusion matrices were presented. The matrix consisted of four elements, which are named TP (true positive), FP (false positive), TN (true negative) and FN (false negative). Taking moderate rockburst as an example, moderate rockburst is regarded as one class while the rest (none rockburst, low rockburst and high rockburst) is classified as another class. Under the circumstances, the case with actual label being moderate rockburst is called positive; otherwise, it is called negative. The above four elements successively mean both the predicted label and the actual label are moderate rockburst, the prediction label is moderate rockburst but the actual label is not, neither the prediction label nor the actual label is moderate rockburst, the actual label is moderate rockburst but the prediction label is not. The explanation of binary confusion matrix is shown in Figure 12.

Figure 12

Binary confusion matrix (taking moderate rockburst as an example)

Based on the TP, FP, TN and FN, the four evaluation metrics can be as:

$${\text{ACC}} = \frac{{{\text{TP}} + {\text{TN}}}}{{{\text{TP}} + {\text{TN}} + {\text{FP}} + {\text{FN}}}}$$

(22)

$${\text{SNS}} = \frac{\text{TP}}{{{\text{TP}} + {\text{FN}}}}$$

(23)

$${\text{PRC}} = \frac{\text{TP}}{{{\text{TP}} + {\text{FP}}}}$$

(24)

$$F_{1} = 2\frac{{{\text{SNS}} \times {\text{PRC}}}}{{{\text{SNS}} + {\text{PRC}}}}$$

(25)

Because ACC is a global metric, which is applicable to binary classification problems as well as multi-classification problems, its expression can be generalized as:

$${\text{ACC}} = \frac{{{\text{correct}}\;{\text{prediction}}}}{{{\text{correct}}\;{\text{prediction}} + {\text{wrong}}\;{\text{prediction}}}} .$$

(26)

Engineering Validation

In total, 61 rockburst cases were used to test the applicability and practicability of models in engineering. The evaluation metrics introduced in the preceding section were calculated (Table 8). It was found that the maximum of four metrics appeared in ensemble models. Moreover, the metrics of ensemble models were generally larger than that of single models. The results signify that ensemble models achieved better prediction performance than the single models. In particular, ensemble model KNN–RNN had the best prediction performance, whose four metrics simultaneously reached the maximum among the eight classification models.

Table 8 Evaluation metrics for the eight classification models

Based on ACC, SVM had the worst performance with ACC of 47.54%, followed by KNN and DNN with 52.46%; KNN–RNN had the best performance with 91.80%. The ACC of the ensemble models was generally > 80% but those single models were < 55%. Thus, ensemble learning can greatly improve the prediction performance when using imbalanced data. In addition, RNN achieved the highest ACC among the single models. This is why RNN was used as the base learner of the four ensemble models simultaneously.

For detailed analysis of model performance, Figure 13 demonstrates the histograms of errors produced by the eight classification models. Because rockburst prediction is a multi-classification problem, unlike regression problems, its error values were discrete. The range of errors was {− 3, − 2, − 1, 0, 1, 2, 3}. The magnitude represents the degree of deviation from the actual rockburst level. The positive sign indicates that the predicted level is higher than the actual level. In contrast, the negative sign means that the predicted level is lower than the actual level.

Figure 13

Histograms of errors produced by the eight classification models

When the predicted level is higher, it will lead to a waste of resources. However, when the predicted level is lower, the existing engineering support measures are not enough to withstand rockburst, which will cause construction safety risks, and even yield huge property damage and casualties. From the perspective of engineering safety, positive errors are better than negative errors. Moreover, the smaller the magnitude of errors, the better the prediction performance.

Regarding the ensemble models, more than 90% of errors were non-negative and only a few test samples had errors of > 1. Especially for KNN–RNN, only one of the 61 test samples had a lower predicted level than the actual level and there were no errors > 1. However, as for single models, the proportion of non-negative errors was about 80% and more test samples had errors > 1. In particular, DNN and RNN had errors reaching − 3, which means that the actual level was high rockburst but was predicted as none rockburst. This result is not acceptable in engineering applications.

In general, classification models perform better on the classes with more training samples (Kautz et al. 2017). Because the data used in this study was imbalanced, it is necessary to analyze the prediction accuracy of the eight classification models on each class. Figure 14 shows the prediction results of the eight classification models on each class. For the same model, the prediction accuracy on none/low/high rockburst was lower than that on moderate rockburst. This is in accordance with the distribution of the data, in which none/low/high rockburst were minority classes and moderate rockburst was majority class. However, ensemble models had higher prediction accuracy on the minority classes in comparison with single models. Taking none rockburst as example, the average accuracy of single models was 27.27% while the average accuracy of ensemble models was 65.91%. This means that ensemble learning can enhance the recognition ability for minority classes.

Figure 14

Prediction results of the eight classification models on each class

Relative Importance of Input Variables

In this study, the contributions of input variables to eight classification models were evaluated quantitatively by means of permutation importance (Corteza and Embrechtsb 2013). Its basic idea is to shuffle an input variable in the test set and leave the others in place, then calculate the difference of prediction accuracy on no-shuffled and shuffled test set. Obviously, it was implemented after the model has been trained. The importance score of input variables can be as:

$$S_{j} { = }\frac{{V_{j} }}{{\sum\nolimits_{i = 1}^{n} {V_{i} } }} \times 100$$

(27)

where $S_{j}$ is the importance score of the j-th input variable,$V_{j}$ is the difference of prediction accuracy on no-shuffled and shuffled test set when shuffling the j-th input variable.

Figure 15 lists the importance scores of input variables on the eight classification models. It was found that the models were sensitive to input variables $X_{1}$, $X_{2}$ and $X_{3}$. $X_{1}$ was the most important, followed by $X_{2}$ and $X_{3}$. Furthermore, $X_{3}$ was more important than $X_{2}$. Although the importance score for the same input variable was not consistent on different models, the level of the relative importance was identical.

Figure 15

Importance score of input variables on the eight classification models

Discussion

Impact of Class Imbalance on Prediction Accuracy

In previous work (e.g., Daskalaki et al. 2006; Branco et al. 2017), it has been proved that class imbalance has a significant impact on the prediction accuracy of classification models. For quantitatively investigating the impact of class imbalance on the eight classification models established in this paper, it was necessary to conduct the sensitivity analysis of prediction accuracy to class imbalance. Herein, a balanced training set was created based on the original imbalanced training set. The classification models were separately trained by the two training sets and then their prediction accuracy was compared on the same test set.

Sampling technology is an effective means to eliminate class imbalance, which can be roughly divided into two categories: under-sampling and over-sampling. The former is to remove some samples from majority classes to achieve the balance between different classes. The advantage is that the size of training set becomes smaller and the consumed time of training process is reduced. The following disadvantage is that some important information may be lost. The latter achieves the rebalance of classes through adding some samples into minority classes. It should be noted that the same training samples cannot be sampled repeatedly; otherwise, this will result in serious over-fitting. Considering the limited amount of training samples, over-sampling was employed in this study to ensure information integrity. The synthetic minority over-sampling technique (SMOTE) is one of the representative algorithms for over-sampling (Chawla et al. 2011). The basic idea of SMOTE is to increase the minority class samples by interpolation. The procedure to implement SMOTE is shown below, whereby the number of nearest neighbors was fixed at the default value of 5 (Chawla et al. 2011).

Based on SMOTE, a balanced training set was built. For the original training set, no/low/high rockburst was minority class and moderate rockburst was majority class. After SMOTE, the number of no/low/high rockbursts became 61, which is the same as the number of moderate rockbursts.

Table 9 shows the prediction accuracy on the test set for the eight classification models separately trained by different training sets. After eliminating class imbalance, the accuracy of single models was improved and the average improvement was 19.93%. However, the accuracy improvement of ensemble models was small; an average of merely 3.27%. Thus, ensemble models are relatively stable against class imbalance while single models are sensitive. Although the accuracy of single models was improved after eliminating class imbalance, it was still less than that of the ensemble models.

Table 9 Comparison of prediction accuracy on the test set before and after eliminating class imbalance

Impact of Class Imbalance on Fitting Effect

In the training process, over-fitting frequently occurs. This causes the prediction accuracy on the training set to be much higher than that on the test set, which suggests that the generalization performance of models is poor. This situation needs to be avoided. The scatter plot, taking the prediction accuracy on the test set as x axis and the prediction accuracy on the training set as y axis, is a useful tool to examine the fitting effect of models. When a point falls above the line $y = x$, over-fitting tends to occur. Moreover, the larger the deviation from the line $y = x$, the more serious the over-fitting is; it is satisfactory if a point falls on or below the line.

Figure 16 shows the relationship between the prediction accuracy on the training set and test set for the eight classification models. Although all the points were above the line $y = x$, the points after eliminating class imbalance were closer to be line $y = x$. The results from the scatter plot intuitively indicate that eliminating class imbalance can improve fitting effect of models. Next, the impact of class imbalance on fitting effect was analyzed quantitatively.

Figure 16

Scatter plot between the prediction accuracy on the training set and test set

The difference between the prediction accuracy on the training set and test set was used as quantitative index to measure fitting effect, which geometrically represents the vertical distance from the points shown in Figure 16 to the line $y = x$. When the difference is larger, the deviation from the points to the line $y = x$ is bigger, which means that over-fitting is more serious. Table 10 shows the results of difference before and after eliminating class imbalance. After eliminating class imbalance, the difference for the eight classification models all decreased, which suggests that class imbalance had an impact on fitting effect. Specifically, eliminating class imbalance can improve fitting effect. Among the eight classification models, the change of difference for DNN after eliminating class imbalance was maximal, reaching 21.17%. This means that class imbalance had the greatest impact on DNN.

Table 10 Comparison of difference between prediction accuracy on the training set and test set before and after eliminating class imbalance

Conclusions

The database including 246 sets of data was analyzed in this paper. To eliminate correlation among the variables and avoid dimension disasters, principal components analysis was employed to transform the original data from seven dimensions to three dimensions. In addition, local outlier factor and expectation maximization algorithm were used to detect and substitute outliers, respectively, in the database. Then, the database was split into the training set (75%) and test set (25%) by stratified sampling.

Eight classification models were established for rockburst prediction, including four single models (KNN, SVM, DNN and RNN) and four ensemble models (KNN–RNN, SVM–RNN, DNN–RNN and KNN–SVM–DNN–RNN). The ensemble models were built based on stacking technique of ensemble learning. Considering class imbalance of the data, accuracy, sensitivity, precision and F₁ score were used as model evaluation metrics. The results indicate that, when using imbalanced data, the ensemble models performed better than the single models. Moreover, the prediction performance on minority classes was improved by stacking technique of ensemble learning. After that, a sensitivity analysis was conducted, which revealed the importance of input variables on the eight classification models.

Finally, the impact of class imbalance on prediction accuracy and fitting effect was analyzed quantitatively. The results showed that ensemble models were relatively stable against class imbalance while single models were sensitive to it. Furthermore, eliminating class imbalance can improve fitting effect of models. In conclusion, the use of stacking technique of ensemble learning serves as a new and promising way for rockburst prediction. Especially in the case of imbalanced data, it shows unique advantages.