Introduction

Self-potential (SP) is a passive geophysical technique that measures naturally occurring electric potentials, which are generated in the Earth’s surface due to different mechanisms (electrokinetic, electrochemical, thermoelectric and mineralization potential). The method was introduced to decipher the formation of mineralization potential principally linked to sulfide and graphite ore structure (Sato and Mooney 1960; Sundararajan et al. 1998; Mendonca 2008) within the subsurface and it was later used for oxide ore deposits as well (Biswas and Sharma 2014a, 2016). The method has varied applications apart from mineral exploration. It has been extensively applied in engineering problems, hydrogeological surveys, environmental contaminant monitoring, and tracing shear zones (Kulessa et al. 2003; Jardani et al. 2008; Mendonca 2008; Mehanee 2014, 2015; Gobashy et al. 2020). A review of different applications of SP data can be found in Biswas (2017).

Numerous quantitative interpretation techniques for SP data have been developed in the past considering two different categories (Mehanee et al. 2011; Mehanee 2015; Essa and El-Hussein 2017). The first category corresponds to 2D and/or 3D subsurface geologic structures with arbitrary shape and size. The second category is based on idealized buried structures, which can be understood assuming simple geometrical shapes such as a sphere, cylinder, fault, and thick sheet. The detail of these categories can be seen in few publications (e.g., Mehanee et al. 2011; Mehanee 2015; Essa and El-Hussein 2017; Abdelrahman et al. 2019). The concern of this present work is that, in some geological settings, there can be a single polarized body that can be interpreted individually (Asfahani and Tlas 2005). In such case, a technique of the second category, with high computational facilities, can be used to interpret the SP anomaly from a single polarized body that does not need a priori data nearby the subsurface geology of that area.

In the past, several approaches have been developed and applied to infer SP anomalies formed due to simple geometrical structures. For example, 2D inclined sheet-type structures have been interpreted by various workers (Paul 1965; Rao et al. 1982; Murthy and Haricharan 1985; Sundararajan et al. 1990, 1998; Jagannadha et al. 1993; Abdelrahman et al. 2003; Murthy et al. 2005; El-Kaliouby and Al-Garani 2009; Monteiro Santos 2010; Essa 2011; Roudsari and Beitollahi 2013; Sharma and Biswas 2013; Biswas and Sharma 2014a, b; Biswas 2016, 2019; Gobashy et al. 2020). Spherical- and cylindrical-type structures have also been interpreted (Paul et al. 1965; Rao et al. 1970; Roy and Mohan 1984; Murthy and Haricharan 1985; Abdelrahman and Sharafeldin 1997; Tlas and Asfahani 2007; Essa et al. 2008; Göktürkler and Balkaya 2012; Tlas and Asfahani 2013; Biswas and Sharma 2015; Mehanee 2015; Roudsari and Beitollahi 2015; Di Maio et al. 2016aa, b; Abdelrahman et al. 2019; Abdelazeem et al. 2019). Moreover, 2D inclined thick sheet-like bodies have been elucidated by Dmitriev (2012) and later by Biswas and Sharma (2017). A comprehensive review of different interpretation approaches developed for specific subsurface structures can be found in Murthy and Haricharan (1985), Sundararajan et al. 1998, and Biswas (2013). However, in the case of 2D inclined plate-type structures, very few works have been carried out in the past. Hafez (2005) developed a technique for interpreting SP anomaly using first-order moving filters specifically for a short profile. Mehanee et al. (2011) developed a second moving average method for interpreting SP anomalies, which can sufficiently eliminate the SP effect of deeper subsurface structure. Essa and El-Hussein (2017) developed a technique constructed on second horizontal gradient, which can eliminate undesirable anomaly from measured SP anomalies.

In the present work, we encompass the work of Hafez (2005) and Mehanee et al. (2011) as well as the interpretation method of Essa and El-Hussein (2017) for the delineation of 2D plate-type structure for SP anomaly using the forward formula of Lile (1994) and Abdelrahman et al. (1998). As mentioned by Mehanee et al. (2011), there is a need for an effective interpretation of current flow lines, depth, and width of the plate-type structure. Hence, the present work is focused on the interpretation of all parameters associated with plate-type structures. To interpret effectively the SP responses from subsurface mineralized bodies, we used the very fast simulated annealing (VFSA) algorithm intended for the delineation of SP anomaly. We choose this nonlinear global optimization inversion for this study because long SP anomalies are mostly nonlinear. The inversion algorithm does not require a priori information for the interpretation of SP data. The benefit of this inversion algorithm is that it can interpret effectively short and long profile data, single as well as multiple structures, and it can determine precisely parameters from shallow and deeper structures. The method is exemplified and analyzed on noise-free and noisy synthetic examples, and trialed to elucidate three field anomalies for exploration.

Methodology

Forward Formulation

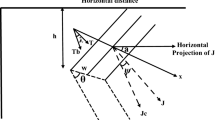
Self-potential for a 2D inclined plate (Fig. 1) is given by (Lile 1994; Abdelrahman et al. 1998):

$$V\left( x \right) = \frac{\pi }{2}\left( {I_{1} - I_{2} } \right) - I_{1} \tan^{ - 1} \left( {\frac{x + w}{z}} \right) + I_{2} \tan^{ - 1} \left( {\frac{x - w}{z}} \right)$$
(1)

where z is depth, w is half-width of the body, x is location of the body on the surface, I1 and I2 are line currents (Fig. 1). An inclined plate (I1 > I2) will show an asymmetrical anomaly, while a vertical plate (I1 = I2) produces a symmetrical anomaly curve.

Figure 1
figure 1

A 2D inclined plate-type structure within the subsurface (after Mehanee et al. 2011)

Full size image

Global Optimization

The present global optimization is a modified form of simulated annealing (SA), i.e., VFSA, which was derived from the analogy of heat bath algorithm (Sen and Stoffa 2013) and was applied extensively in interpreting various geophysical data. Details of the VFSA can be found in many publications (Rothman 1985, 1986; Sharma 2012; Sen and Stoffa 2013; Sharma and Biswas 2013) and are not briefed here for brevity. It was developed to overcome the limitations of linear inversion and, because of its stability and robustness, it can negate the problem of non-uniqueness and resolution. The other advantages of this inversion method are that it takes less time in computing a large set of data and in finding a global solution (Sen and Stoffa 2013). Moreover, it is quite efficient with minimum CPU time and it takes a lesser amount of memory and with high resolution (Ingber and Rosen 1992).

Every inversion method needs an error vector or objective function to be minimized and, in the present case, the error can be calculated from the equation given below to determine the variation between the observed and calculated anomalies (Kaikkonen and Sharma 1998), thus:

$$\varphi = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left( {\frac{{V_{i}^{0} - V_{i}^{c} }}{{|V_{i}^{0} | + \left( {V_{\hbox{max} }^{0} - V_{\hbox{min} }^{0} } \right)/2}}} \right)^{2}$$
(2)

where N refers to number of data, \(V_{i}^{0}\) and \(V_{i}^{c}\) are the ith observed and model responses, respectively, \(V_{\hbox{max} }^{0}\) and \(V_{\hbox{min} }^{0}\) are the maximum and minimum values, respectively, of synthetic/field data.

Moreover, to find a global solution, a single run is not sufficient, and hence in the present case, 10 runs were completed to find the mean model. Next, a Gaussian probability density function (PDF) was calculated to find the most appropriate model and to minimize the uncertainty in the final mean model, which is close to the global mean model. To achieve this, we followed the work of Mosegaard and Tarantola (1995) and Sen and Stoffa (1996). The particulars of the global model, besides uncertainty analysis, can be understood from several works of literature, viz. Biswas (2016, 2018) and Trivedi et al. (2020), who applied this for interpretation of various geophysical data. The code was implemented using MS FORTRAN Developer studio in Windows 10 platform. The computation of the entire process takes 30 s (not CPU time). The details of the optimization process are shown in Figure 2.

Figure 2
figure 2

Flowchart of the inversion process (after Biswas 2013)

Full size image

Results

Theoretical Examples

Model 1

A self-potential anomaly was generated, using Eq. (1), for a 2D inclined plate-type structure (Fig. 3a) with different parameters (Table 1). The inversion algorithm developed for such type of structure was applied to interpret the synthetic data. All five parameters for 2D inclined plate-type structures were delineated, and the results are shown in Table 1. Out of five parameters, as mentioned in the theoretical formulation, the important for mineral exploration is the zero-crossing (x0), half-width (w), and the depth (z). Hence, we tried to study whether inversion can delineate these parameters or not. Next, we tried to study the histogram of x0, w, and z. We found that x0 and z show peaks in true values; however, w shows a wide solution (Fig. 4a). This suggests that x0 and z can be well resolved but there is uncertainty in w. To confirm these observations, we again tried to see a 3D cross-plot analysis between x0, w, and z. It can be also be seen from the cross-plot that x0 and z are very close to their true values, but w shows a wide solution (Fig. 5a). However, the elucidated parameters are very close to their true values, which were taken for synthetic analysis, and the parameters (x0, w, and z) were inside the uncertainty boundaries and peak PDF range.

Figure 3
figure 3

Computed response for model 1

Full size image
Table 1 Computed parameters for model 1
Full size table
Figure 4
figure 4

Histogram analysis for model 1

Full size image
Figure 5
figure 5

3D cross-plot for model 1. Yellow points represent true values. Red fields represent uncertainty boundaries and peak PDF range

Full size image

Next, to see the influence of noisy synthetic data, 5% Gaussian noise (i.e., data multiplied by Gaussian random values with mean of 1 and standard deviation of 0.2) was added to the same data and the VFSA procedure was carried out again (Fig. 3b). The inversion algorithm successfully inverted all the parameters. It was found that x0 and z show peaks of their true values, but w shows a varied array of solutions according to a histogram analysis (Fig. 4b). To confirm this, we again studied the cross-plot and found the same as for the noise-free synthetic data. 5b shows the cross-plot for the noise-corrupted synthetic data. Figure 3a and b shows the responses from synthetic and calculated data. Table 1 shows the interpreted parameters for this model.

Model 2

The second model (Fig. 6a), a 2D inclined plate, was taken to see the variations of w and z. The inversion procedure was executed for this model and the parameters were interpreted. Again, it was found that w shows varied solutions; however, x0, and z can be determined precisely. Histograms and cross-plots were very similar as for model 1 and hence were not shown here for brevity. Moreover, to check the consistency in higher degree of noise-corrupted data, 10% Gaussian noise was added to this model (Fig. 6b). The inversion procedure was again executed for this model, and the results were the same as discussed for model 1. Table 2 shows the final interpreted parameters, and Figure 6a and b shows the calculated anomalies in case of noise-free and noisy data, respectively.

Figure 6
figure 6

Computed response for model 2

Full size image
Table 2 Computed parameters for model 2
Full size table

Model 3

The third model, a 2D vertical plate-type (I1 = I2) structure, was taken to see whether it can be interpreted as well by the inversion procedure as a different model (Fig. 7a). The inversion procedure was used to interpret the data and it yielded the same results as for Models 1 and 2. The histograms and cross-plots were found to agree with those of model 1. Moreover, to check whether noisy data for this model can be interpreted, 20% Gaussian noise was added to the data and the VFSA process was again applied (Fig. 7b). The results were the same as discussed earlier (Table 3). Figure 7 shows the computed responses for both types of data for model 3.

Figure 7
figure 7

Computed response for model 3

Full size image
Table 3 Computed parameters for model 3
Full size table

Field Examples

To confirm the usefulness and consistency of the present method, three field examples were used.

Polymetallic Sulfide Deposit

The first example was from a polymetallic vein-type deposit in the Caucasus (after Eppelbaum and Khesin 2012). The anomaly data were digitized at 2.57 m intervals. The data were interpreted by Essa and El-Hussein (2017) considering 2D plate and by Gobashy et al. (2020) considering a 2D inclined sheet-type structure. These field data were again interpreted here using the proposed inversion algorithm. It was found that the important parameters for 2D inclined plate-type structures were depth and half-width. The present results show that the depth of the body was 44 m and half-width 21 m. Figure 8 shows the responses from the field and calculated data, and Table 4 shows the interpreted parameters.

Figure 8
figure 8

Computed response for field data (polymetallic vein, Caucasus)

Full size image
Table 4 Computed parameters for field example (polymetallic vein, Caucasus)
Full size table

Surda Anomaly

The second field example was from copper sulfide deposits in the Surda area, India (Murthy and Haricharan 1984; Sundararajan et al. 1998). The data, taken from Sharma and Biswas (2013), have been used widely for interpretation considering 2D inclined sheet-type subsurface structures (Sundararajan et al. 1998; Sharma and Biswas 2013; Biswas and Sharma 2014b; Biswas 2017; Gobashy et al. 2020). However, the same SP anomaly data were also interpreted considering a 2D inclined plate-type structure (Mehanee et al. 2011; Essa and El-Hussein 2017). The SP data were re-interpreted here considering 2D inclined plate, and the depth and half-width interpreted were 16 m and 10 m, respectively. The interpreted data were consistent with the interpreted depth and half-width from Mehanee et al. (2011) and Essa and El-Hussein (2017). The responses from the field and calculated data are illustrated in Figure 9, and all the interpreted models are shown in Table 5.

Figure 9
figure 9

Computed response for field data (Surda anomaly)

Full size image
Table 5 Computed parameters for field example (Surda anomaly, India)
Full size table

Kalava Anomaly

The last field example (Fig. 10) was from a sulfide mineralized deposit in a fault zone in Cuddapah Basin, India (Rao et al. 1982). The data, taken from Biswas and Sharma (2015), were interpreted earlier considering a sheet-type structure (Sundararajan et al. 1990; Jagannadha et al. 1993; Murthy et al. 2005; El-Kaliouby and Al-Garani 2009; Gobashy et al. 2020), a horizontal cylinder-type structure (Biswas and Sharma 2015), a vertical cylinder (Mehanee 2014), and a 2D inclined plate-type structure (Mehanee et al. 2011). The data were re-interpreted here considering a 2D inclined plate-type structure. A histogram was also prepared for these field data to see whether the responses were the same as those found from the synthetic examples. It was found that w also shows a wide range; however, x0 and z were close to their near probable values (Fig. 11). Moreover, a 3D cross-plot also shows that x0 and z were very close to the probable values but w widely varies (Fig. 12). The interpreted z and w were 7 m and 3.8 m, respectively. The interpreted depth is consistent with Biswas and Sharma (2015) but somewhat different from Mehanee et al. (2011). Figure 10 shows the computed response, and Table 6 shows the interpreted parameters.

Figure 10
figure 10

Computed response for field data (Kalava anomaly)

Full size image
Figure 11
figure 11

Histogram analysis for Kalava anomaly

Full size image
Figure 12
figure 12

3D cross-plot for Kalava anomaly

Full size image
Table 6 Computed parameters for field example (Kalava anomaly, India)
Full size table

Conclusions

We have developed an inversion algorithm for the delineation, from self-potential data, of different parameters associated with a 2D plate-type structure. The method of VFSA was applied to determine the 2D plate viz. location of the body (x0), its half-width (w) and its depth (z). The solutions show that the technique can delineate all the three parameters; however, there some small uncertainty in determining w, which varies widely but within uncertainty limits. Analyses of histograms and cross-plots reveal the same. The technique was verified using noise-free and noisy synthetic data, and it can guess all the three parameters with good accuracy. Three field examples were also interpreted, and the results were consistent with results of other techniques published in the literature. The inversion method can interpret self-potential data considering a 2D inclined plate-type structure without a priori evidence of the subsurface structure and variation in resistivity data. However, the present method cannot be considered as a final interpretation for mineral exploration; rather, it should be integrated with other geophysical techniques for more reliable results. The method can be used as well for single and/or multiple structures associated with mineralization.