Magnetic Data Interpretation Using a New R-Parameter Imaging Method with Application to Mineral Exploration

Abstract

A new imaging method has been developed for elucidating the observed magnetic data gauged along profile. The method is based on the calculation of the correlation factor (the R-parameter) between the analytic signal of the measured magnetic anomaly and the analytic signal of the calculated response of some geometrically simple interpretive models in the confined category of sheets, cylinders, and spheres. The characteristic parameters (amplitude coefficient, depth, location, approximative shape of the buried structure, and effective angle of magnetization) of the interpretive model correspond to the maximum R-parameter value. The scheme has been verified on a number of noise-free synthetic examples and recovered the actual model parameters. Prior to applying the developed scheme to real-field examples, the accuracy of it has been carefully investigated on synthetic examples which are contaminated with realistic noise levels, interference effects, and regional field. Finally, the method has been successfully applied to three real-field data examples from the USA, Senegal, and Egypt for mineral exploration, and it is found that the obtained results are in good concordance with those obtained from drilling and/or the published literature.

Introduction

Magnetic methods are useful in geothermal exploration, environmental, and engineering applications, archaeological investigation, mapping of unexploded military ordnance (UXO), and tectonic studies (Hinze 1990; Munschy et al. 2007; Robinson et al. 2008; Domra Kana et al. 2016; Elkhadragy et al. 2018; Augusto et al. 2019; Linford et al. 2019). In addition, magnetic methods have a remarkable application in mapping economically significant targets, such as ores and hydrocarbons (Eventov 1997; Piskarev and Tchernyshev 1997; Abdelrahman et al. 2007a; Mandal et al. 2014; Archer and Reid 2016; Essa et al. 2017, 2018; Innocent et al. 2019).

Analysis and interpretation of the magnetic data anomaly gauged along profile by some geometrically simple idealized body (such as faulted structure, sphere, horizontal cylinder, and sheet) remains of interest in the field of exploration geophysics (Abdelrahman and Essa 2015; Essa and Elhussein 2019). In this context, the model parameters we seek to retrieve for the interpretive idealized body are the amplitude coefficient, depth, shape, and the location.

Several numerical and graphical techniques have been developed for interpreting the magnetic data using some simple geometrical body. These techniques include the characteristic curves method, nomograms, characteristic points and distances method, curve matching and standardized curves method (Gay 1963; McGrath and Hood 1970; Atchuta Rao and Ram Babu 1980; Prakasa Rao et al. 1986; Prakasa Rao and Subrahmanyam 1988; Dondurur and Pamuku 2003; Subrahmanyam and Prakasa Rao 2009), Werner and Euler deconvolution methods (Werner 1953; Thompson 1982; Reid et al. 1990; FitzGerald et al. 2004; Reid et al. 2014), linear and nonlinear least-squares methods (Abdelrahman and Essa 2005; Abo-Ezz and Essa 2016), spectral methods (Al-Garni 2011; Clifton 2017), Hilbert transforms (Mohan et al. 1982), parametric curves method (Abdelrahman et al. 2012), Walsh transform technique (Shaw and Agarwal 1990), local wave number method (Salem et al. 2005), window curves method (Abdelrahman et al. 2007b), derivatives-based method (Essa and Elhussein 2017), tilt-depth and contact-depth methods (Salem et al. 2007; Cooper 2016), moving average methods (Abdelrahman et al. 2003), semi-automatic method (Abdelrahman et al. 2002), and correlation techniques (Ma and Li 2013; Ma et al. 2017). However, the drawback of most of these methods includes the personal subjectivity in the interpretation, the use of a few data points and distances out of the measurement profile (rather than the entire data points of the profile), sensitivity to the noise embedded into the magnetic data, impact of the neighboring effect (which might deteriorate the accuracy of the results), and independence in the sense that these methods rely upon a priori information, which sometimes may not be available (Essa and Elhussein 2018).

Moreover, new metaheuristics algorithms were developed for interpreting the magnetic data, such as anti-colony optimization inversion (Liu et al. 2015; Kushwaha et al. 2018), differential evolution algorithm (Balkaya et al. 2013, 2017), genetic algorithm (Montesinos et al. 2016; Kaftan 2017), neural networks method (Hajian et al. 2012; Al-Garni 2015), particle swarm optimization (Xiong and Zhang 2015; Essa and Elhussein 2020), and simulated annealing (Biswas and Acharya 2016). However, these approaches require wide search ranges to recover the best-fitting model parameters, which could be time-consuming in some cases.

In this paper, we propose an imaging method (R-parameter imaging method) to interpret the magnetic data taken along profile by some simple geometrical bodies in the confined category of sheet, semi-infinite vertical cylinder, infinitely long horizontal cylinder- and sphere-shaped models. The primary goal in this case is to recover the characteristic model parameters (depth, effective angle, amplitude coefficient, origin point, and shape factor) of the underlying approximative model. The method calculates the R-parameter (a statistical parameter called the correlation coefficient) between the analytic signal of the measured magnetic field and the analytic signal of the synthetic response of an assumed interpretive model out of the aforementioned class. The best interpretive model is that with the characteristic source parameters (evolved from the developed imaging method) which correspond to the maximum R-parameter value. The proposed scheme has a number of benefits. First, it uses an exact formula for the direct problem (i.e., the forward modeling solution). Second, it uses the entire data points of the measurement magnetic profile in computing the depth and horizontal location of the buried source, which are considered substantial parameters in exploration geophysics. Third, it is not very sensitive to noise as will be seen in “Synthetic Examples” section.

The layout of the present paper is described as follows. “Forward Modeling Solution” section presents the direct problem. The formulation of the proposed imaging scheme is described in “Methodology” section. The developed scheme is then verified on synthetic models (including different levels of noise, studying the interference effects, and the embedded regional background) in “Synthetic Examples” section. The applicability of the scheme to real data examples is carefully investigated and discussed in “Field Examples” section. Finally, conclusions are drawn.

Forward Modeling Solution

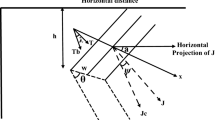
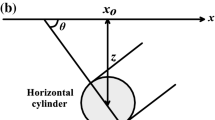
The magnetic forward modeling solution along profile of some geometrically simple bodies in the context of sheets, cylinders, and spheres (Fig. 1) (Gay 1963; Rao et al. 1977; Prakasa Rao et al. 1986; Prakasa Rao and Subrahmanyam 1988; Abdelrahman et al. 2012) is given by

$$\begin{aligned} T(x_j, x_o, z, z_o, \theta , q, K) =K\Big [\frac{A(z_o-z)^2+B(x_j-x_o)+C(x_j-x_o)^2}{\Big ((x_j-x_o)^2+(z_o-z)^2\Big )^q}\Big ], \quad j = 1, \, 2, \, 3, \ldots , \, n \end{aligned}$$

(1)

where $x_j$ and $x_o$ are the horizontal coordinates (m) of the observation point and the center of the buried source (Fig. 1), z and $z_o$ are the vertical coordinates (m) of the observation point and the buried source (Fig. 1), $\theta$ is the effective angle of magnetization ($^{\circ }$), q is the shape factor (dimensionless, where $q = 2.5$, 2 and 1 for sphere, infinitely long horizontal cylinder, and thin sheet models), K is the amplitude coefficient of the unit of which in this particular formulation is nT m$^{2q-2}$, n is the total number of the data points of the magnetic profile to be interpreted, and A, B, and C are some parameters defined in Table 1. In the case of sphere-shaped body, the parameters K and $\theta$ are the magnetic moment and effective angle of magnetization (Rao et al. 1973; Prakasa Rao and Subrahmanyam 1988). The detailed definition of these parameters for the thin sheet and horizontal cylinder bodies is given in Table 2.

Table 1 Definition of the parameters A, B, and C of Eq. 1 and their vertical derivatives (Gay 1963; Rao et al. 1977; Prakasa Rao et al. 1986; Prakasa Rao and Subrahmanyam 1988; Abdelrahman et al. 2012)

Table 2 Characteristic amplitude coefficient (K) and an effective angle of magnetization ($\theta$) for vertical, horizontal, and total magnetic field anomalies due to thin sheet and horizontal cylinder

Figure 1

Simple geometrical-shaped models configuration and its parameters: sphere (top), infinitely long horizontal cylinder (middle), and thin sheet (bottom)

Methodology

Analytic Signal Estimation

Nabighian (1972) demonstrated that the analytic signal AS can be expressed in terms of the horizontal ($\frac{\partial T}{\partial x_{j}}$) and vertical derivatives ($\frac{\partial T}{\partial z}$) of the magnetic anomaly T as

$$\begin{aligned} {\mathrm{AS}}(x_{j},z) = \frac{\partial T}{\partial x_{j}} - i \frac{\partial T}{\partial z}, \, \, \, \, i = \sqrt{-1}. \end{aligned}$$

(2)

Thereby, the amplitude of the analytic signal, $|\mathrm{AS}(x_j,z)|$, of magnetic anomaly is

$$\begin{aligned} \Big |\mathrm{AS}(x_{j},z)\Big |= \sqrt{\Big ( \frac{\partial T}{\partial x_{j}}\Big )^2+ \Big ( \frac{\partial T}{\partial z_{j}}\Big )^2}. \end{aligned}$$

(3)

By evaluating the horizontal and vertical derivatives of the magnetic anomaly analytically from forward modeling Eq. 1, and by substituting the corresponding results into Eq. 3, we get

$$\begin{aligned} {\big |{\mathrm{AS}}(x_{j},z)\big |= \big |K \big | \; \sqrt{ \frac{\big [\big (2C(x_j-x_o)+B\big )^2+(\mathrm{PPP})^2\big ]\big [(x_j-x_o)^2+(z_o-z)^2\big ]+4q(\mathrm{RRR})\big [q(\mathrm{RRR})-\big (B(x_j-x_o)+2C(x_j-x_o)^2+2A(z_o-z)^2+z(\mathrm{PPP})\big )\big ]}{\big [(x_j-x_o)^2+(z_o-z)^2\big ]^{2q+1}}}}. \end{aligned}$$

(4)

where the parameters A, B, and C are defined in Table 1, RRR = $A(z_o-z)^2 + B(x_j-x_o) + C(x_j-x_o)^2$ and PPP = $A^{*} (z_o-z)^2 + B^{*} (x_j-x_o) + C^{*} (x_j-x_o)^2$. The parameters $A^{*}$, $B^{*}$, and $C^{*}$, which are the vertical derivatives of the parameters A, B, and C ($A^{*} = \frac{\partial A}{\partial z}$, $B^{*} = \frac{\partial B}{\partial z}$, and $C^{*} = \frac{\partial C}{\partial z}$), are given in Table 1. Equation (4) represents the general formula of the two-dimensional (2D) amplitude analytic signal for some geometrically simple structures (sheets, cylinders, and spheres).

From Eq. 4, the amplitudes of the analytic signal of the thin sheet ($q = 1$) and 2D horizontal cylinder ($q = 2$) models are

$$\begin{aligned} \Big |\mathrm{AS}(x_{j},z)\Big |= & {} \big |K \big | \frac{1}{\Big [(x_j-x_o)^2+(z_o-z)^2\Big ]}, \, {\rm and } \end{aligned}$$

(5)

$$\begin{aligned} \Big |\mathrm{AS}(x_{j},z)\Big |= & {} \big |2K \big | \frac{1}{\Big [(x_j-x_o)^2+(z_o-z)^2\Big ]^{3/2}}. \end{aligned}$$

(6)

Finally, the amplitude analytic signal anomaly of the horizontal, vertical, and total magnetic components of a sphere model (q = 2.5) is

$$\begin{aligned} \big |\mathrm{AS}(x_{j},z)\big |= & {} \big |K \big | \frac{\sqrt{\big [(eee)\big ((x_j-x_o)^2+(z_o-z)^2\big )+5\big (2\cos (\theta )(x_j-x_o)^2-3(z_o-z)(x_j-x_o)\sin (\theta )-(z_o-z)^2\cos (\theta )\big )^2\big ]}}{\big [(x_j-x_o)^2+(z_o-z)^2\big ]^{3}},\, \end{aligned}$$

(7)

$$\begin{aligned} \big |\mathrm{AS}(x_{j},z)\big |= & {} \big |K \big | \frac{\sqrt{\big [(sss)\big ((x_j-x_o)^2+(z_o-z)^2\big )+5\big (2(z_o-z)^2\sin (\theta )-3(z_o-z)(x_j-x_o)\cos (\theta )-\sin (\theta )(x_j-x_o)^2\big )^2\big ]}}{\big [(x_j-x_o)^2+(z_o-z)^2\big ]^{3}}, \, {\rm and } \end{aligned}$$

(8)

$$\begin{aligned} \big |\mathrm{AS}(x_{j},z)\big |= & {} \big |K \big | \frac{\sqrt{\big [(fff)\big ((x_j-x_o)^2+(z_o-z)^2\big )+5\big ((z_o-z)^2(3\sin ^{2}(\theta )-1)-3(z_o-z)(x_j-x_o)\sin (\theta )+(x_j-x_o)^2(3\cos ^{2}(\theta )-1)\big )^2\big ]}}{\big [(x_j-x_o)^2+(z_o-z)^2\big ]^{3}}, \end{aligned}$$

(9)

where eee, $4 \cos ^{2}(\theta )(4(x_j-x_o)^2+(z_o-z)^2) - 12 (z_o-z) (x_j-x_o)\sin (\theta )\cos (\theta ) + 9 \sin ^{2}(\theta )((x_j-x_o)^2+(z_o-z)^2)$; sss, $4 \sin ^{2}(\theta )((x_j-x_o)^2+ 4 (z_o-z)^2) - 12 (z_o-z) (x_j-x_o)\sin (\theta )\cos (\theta ) + 9 \sin ^{2}(\theta )((x_j-x_o)^2+(z_o-z)^2)$; and fff, $4 (x_j-x_o)^2 (3\cos ^{2}(\theta )-1)^2 + 4 (z_o-z)^2(3\sin ^{2}(\theta )-1)^2 - 12 (z_o-z) (x_j-x_o)\sin (\theta ) + 9 \sin ^{2}(\theta )((x_j-x_o)^2+(z_o-z)^2)$.

Model Search

The main goal of the interpretation process, which requires an initial model, is to assess the model parameters of a subsurface buried structure from the observed magnetic data (Tarantola 2005). The initial model can be constructed from the available drilling, geological, and/or geophysical information (Mehanee and Essa 2015).

In this paper, an R-parameter imaging technique is used to estimate the model parameters. A 2D (X–Z) mosaic of the R-parameter (the correlation coefficient, dimensionless) is constructed from the analytic signal amplitudes $|\mathrm{AS}_{\mathrm{Obs}}|$ and $|\mathrm{AS}_{\mathrm{Cal}}|$ determined, respectively, from the measured magnetic data and the calculated magnetic anomaly generated by an assumed geometrical source $j\mathrm{{th}}$ and is given as:

$$\begin{aligned} R = \frac{\sum \nolimits _{j=1}^{n} {|\mathrm{AS}_{\mathrm{Obs}}|_{j} |\mathrm{AS}_{\mathrm{Cal}}|_{j}}}{\sqrt{\sum \nolimits _{j=1}^{n} {|\mathrm{AS}_{\mathrm{Obs}}|_j}^2 \sum \nolimits _{j=1}^{n}{|\mathrm{AS}_{\mathrm{Cal}}|_{j}}^2}}. \end{aligned}$$

(10)

It is noted that $|\mathrm{AS}_{\mathrm{Obs}}|$ is obtained numerically using Eq. 3, and that $|\mathrm{AS}_{\mathrm{Cal}}|$ of an assumed source is calculated analytically using Eqs. 5–9.

In order to image the R-parameter variation around the spatial location ($z_o$ and $x_{o}$) of an assumed source, a 2D discretization in the X- and Z-coordinates is performed. It is noted that the computation of the R-parameter does not need a prior knowledge about the amplitude coefficient (K) of the assumed source model as is seen in Eq. 10. In the case of sphere-shaped model the R-parameter approaches the extreme value (R-max) when the depth ($z_o$), the origin location (${x_{o}}$). and the effective angle of magnetization ($\theta$) of the observed magnetic profile match the real source for a given data set. The amplitude coefficient K is calculated from the observed magnetic response at $x_{j} = {x_{o}}$ by substituting $z_o$, ${x_{o}}$, ${x_{j}}$, $\theta$ and q into Eq. 1. In the case of thin sheet and horizontal cylinder models the parameter K is calculated from Eqs. 5 and 6 at $x_{j} = {x_{o}}$. The parameter $\theta$ is then calculated from the observed magnetic response at $x_{j} = {x_{o}}$ by substituting $z_o$, ${x_{o}}$, ${x_{j}}$, K and q into Eq. 1.

The estimated magnetic response can then be calculated from Eq. 1 along the measurement profile to evaluate the misfit between the observed and predicted responses. Figure 2 summarizes the workflow of the developed scheme.

Figure 2

Flowchart showing the workflow of the developed scheme

Synthetic Examples

To verify and demonstrate the constancy of the proposed scheme, three numerical models with various anomalous sources (thin sheet, horizontal cylinder, or sphere) have been investigated. In Model 1 (thin sheet), we first verify the scheme on noise-free magnetic data profile. Following that, the noise impact on the accuracy of the model parameters ($z_o, K, x_o \, {\rm and } \, \, \theta$) has been carefully assessed by contaminating the aforementioned magnetic data by various noise levels (3, 5, 7, and 10%) prior to interpreting these data. In some geological settings, the magnetic response of the main target (anomalous body) can be influenced by the minor (secondary) structures present in the vicinity of the target. Having known that, Model 2 (horizontal cylinder) examines and assesses influence of the neighboring structures on the accuracy of the parameters recovered for the main target. Finally, the effect of the embedded regional field has been studied in Model 3 to demonstrate further the developed method. It is noted that hereinafter the parameter z of Eq. 1 is set to 0 in order to simplify the calculations; that is the depth of the observation level is set to 0, which subsequently means that the parameter $z_{o}$ in this case refers to the source’s depth of burial.

Model 1

Figure 3a shows the magnetic anomaly profile generated, from Eq. 1, for a sheet model ($q =1$, Fig. 3b) with $K = 500$ nT m, $z_o$ = 8 m, $x_o$ = 60 m, and $\theta$ = $-35^{\circ }$. The profile length is 120 m. Figure 3c presents the horizontal and vertical derivatives (calculated from the data of the magnetic anomaly depicted in Fig. 3a), which are used to construct the amplitude profile of the analytic signal (Fig. 3d).

Figure 3

Model 1: noise-free theoretical example. (a) magnetic anomaly generated by the thin sheet model presented in (b), (c) horizontal and vertical derivatives of the magnetic anomaly shown in (a), (d) amplitude of analytic signal of the magnetic anomaly shown in (a), and (e) 2D surface of the estimated R-parameter (R), and the R-max value (black dot)

The 2D imaging surface S (over which the R-parameter values are calculated) expanded to 120 $\times$ 15 m in both the X- and Z-directions (which means $(x_o, z_o) \in S = (0, 120) \times (1, 15))$, was discretized into 1-m intervals in both directions (Fig. 3e). Figure 3e illustrates the R-parameter image constructed from Eq. 10 using a sheet source (this means that the parameter q was set to unity in Eq. 4). Figure 3e shows a maximum value for the R-parameter (“R-max”) of 1, at which the optimal model parameters ($K = 500$ nT m, $z_o$ = 8 m, $x_o$ = 60 m, and $\theta$ = $-35^{\circ }$) have been achieved, which precisely correspond to the actual model parameters (Table 3). In other words, this means that the imaging scheme has successfully retrieved the actual values of the model. To realize better the analysis, Eq. 10 has been used to determine the R-parameter values for two other sources, namely sphere and horizontal cylinder (Table 4). The table shows that the maximum value of the parameter “R-max” corresponds to the actual source, which is the thin sheet model.

Table 3 Model 1: recovered model parameters for the noise-free synthetic example presented in Figure 3

Table 4 Model 1: the R-parameter calculated for different shapes for the noise-free synthetic example presented in Figure 3

To analyze further the performance of the suggested method, subsequent white Gaussian noise levels of about 3, 5, 7, and 10% have been added into the magnetic data profile presented in Figure 3a. Each noise level was separately generated and added into the magnetic noise-free data using the MATLAB function “awgn” in order to produce the corresponding corrupted data set subject to interpretation (Mehanee and Essa 2015). The noise percentage was calculated as follows (Mehanee and Zhdanov 2002; Zhdanov 2002)

$$\begin{aligned} {\rm Noise}\, {\rm percentage } = \frac{\Vert T_{\mathrm{noisy}} - T \Vert }{\Vert T_{\mathrm{noisy}}\Vert } \times 100\%, {\rm where } \end{aligned}$$

$T_{\mathrm{noisy}}$ and T are the noisy and noise-free magnetic data vectors. It is noted that hereinafter all presented noisy data are calculated as described above. Figure 4 depicts the corresponding noisy magnetic data. By applying the aforementioned procedures for each noisy data set, the corresponding horizontal and vertical derivatives, estimated amplitudes, and estimated R-parameters are, respectively, shown in panels (c), panels (d), and panels (e) of Figure 4. Table 5 presents the corresponding results, which demonstrate that “R-max” decreases with increasing the noise level, and that the accuracy of the model parameters is not significantly influenced by the embedded noise levels. Thus, it can be concluded that the scheme proposed here is stable with respect to noise.

Figure 4

Model 1: noisy theoretical example for the thin sheet model (Fig. 3a) after adding 3% noise (I), 5% noise (II), 7% noise (III), and 10% noise (IV). The true shape factor (that is $q = 1$) is used in the calculations

Table 5 Model 1: results and R-max obtained from the proposed scheme using the actual shape factor (that is, q was set to 1 in the calculations) of different noise levels (Fig. 4)

In order to examine the developed method with respect to the shape factor, we have re-interpreted the aforementioned noisy data sets using a q value of 2 (that is, a horizontal cylinder model) and then using another q value of 2.5 (that is, a sphere-shaped model) (Figs. 5, 6). Tables 6 and 7, respectively, present the corresponding results, which suggest that inaccuracy in the parameter q does not notably influence the accuracy of the parameter $x_o$ when the true value of the parameter $\theta$ is used in the calculations. The tables also suggest that the parameters K and $z_o$ encountered some inaccuracy, which is not unexpected because of the difference in the units of the parameter K and that the depth in the case of horizontal cylinder and sphere models is measured to the center of the body, not to the top of the body as in the case of the sheet model (Fig. 1), which is the true model in this analysis.

Table 6 Model 1: as in Table 5, but using an incorrect shape factor of 2 (that is $q = 2$) (Fig. 5)

Table 7 Model 1: as in Table 5, but using an incorrect shape factor of 2.5 (that is $q = 2.5$) (Fig. 6)

Figure 5

As in Figure 3, but using an incorrect shape factor of 2 (that is $q = 2$)

Figure 6

As in Figure 3, but using an incorrect shape factor of 2.5 (that is $q = 2.5$)

Model 2

Figure 7a presents the composite magnetic anomaly due to two nearby geological bodies (Fig. 7b). The first (considered the main target) is a horizontal cylinder model ($q_1$ = 2) the parameters of which are: $K_1$ = 7000 nT m$^2$, $z_{o1}$ = 10 m, $x_{o1}$ = 30 m, and $\theta _{1}$ = $- 45^\circ$. The second (considered an interfering secondary body) is a thin sheet model ($q_2$ = 1) with $K_2$ = 400 nT m, $z_{o2}$ = 5 m, $x_{o2}$ = 100 m, and $\theta _{2}$ = $- 30^{\circ }$. The horizontal and vertical derivatives, analytic signal amplitude, and R-parameter image are displayed in Figure 7c, d, and e. Figure 7e depicts the “R-max” of the main target (R-$\mathrm{max}_1$ = 0.73) and the interfering structure (R-$\mathrm{max}_2$ = 0.68). The corresponding model parameters, respectively, are ($K_1$ = 7502 nT m$^2$, $z_{o1}$ = 10.7 m, $x_{o1}$ = 30 m, and $\theta _{1}$ =$- 44^{\circ }$) and ($K_2$ = 642.4 nT m, $z_{o2}$ = 7.4 m, $x_{o2}$ = 100 m, and $\theta _{2}$ = $- 32.7^{\circ }$) (Table 8). The results support that the scheme presented here is stable, and the retrieved model parameters exhibited some inaccuracy depending upon the extent of the neighboring effect, which is not unexpected.

Table 8 Model 2: obtained model parameters for the noise-free interfering structures

Figure 7

Model 2: influence of interfering structures: (a) magnetic anomaly generated by two different adjacent bodies of horizontal cylinder and thin sheet models (b), (c) horizontal and vertical derivatives of the magnetic anomaly shown in (a), (d) amplitude of the analytic signal of the magnetic anomaly shown in (a), and (e) 2D surface of the estimated R-parameter and the R-max value (black dots; R-max$_1$ = 0.73 at $q_1$ = 2 and R-max$_2$ = 0.68 at $q_2$ = 1.0)

To investigate the scheme further, the data presented in Figure 7a have been corrupted by 5% noise prior to interpretation (Fig. 8a, b, c, d, and e). The results of the main and interfering targets are (R-$\mathrm{max}_1$ = 0.73, $K_1$ = 8372.1 nT m$^2$, $z_{o1}$ = 11.5 m, $x_{o1}$ = 30 m, and $\theta _1$ = $- 47.77^{\circ }$) and (R-$\mathrm{max}_2$ = 0.67, $K_2$ = 794.1 nT m, $z_{o2}$ = 8 m, $x_{o2}$ = 100 m, and $\theta _2 = - 39.19^{\circ }$) (Table 9), which remain in good agreement with the actual ones.

Table 9 Model 2: obtained model parameters after adding 5% noise to the interfering structures

Figure 8

Model 2: (a) noisy magnetic anomaly generated by the data set shown in Figure 7a after adding 5% noise, (b) model sketch, (c) horizontal and vertical derivatives of the magnetic anomaly shown in (a), (d) amplitude of the analytic signal of the magnetic anomaly shown in (a), and (e) 2D surface of the estimated R-parameter and the R-max value (black dots; R-$\mathrm{max}_1$ = 0.73 at $q_1$ = 2 and R-$\mathrm{max}_2$ = 0.67 at $q_2$ = 1.0)

In order to further assess the neighboring effect on the accuracy of the scheme, we have reduced the distance that separates the two bodies presented in Figure 7b and corrupted the resulting forward modeling magnetic anomaly by 5% noise. The new locations of the two bodies are ${x}_{o1}$ = 30 and ${x}_{o2}$ = 45 m; the other model parameters remained unchanged (Fig. 9a, b, c, d, and e). Table 10 presents the corresponding results of the two bodies ($K_1$ = 45,792 nT m$^2$, $z_{o1}$ = 22 m, $x_{o1}$ = 34 m, and $\theta _1$ = $- 52.17^{\circ }$ with R-$\mathrm{max}_1$ = 0.94) and ($K_2$ = 3008.1 nT m, $z_{o2}$ = 22.7 m, $x_{o2}$ = 39 m, and $\theta _2$ = $- 68.51^{\circ }$ with R-$\mathrm{max}_2$ = 0.93), which suggests that the neighboring effect can be notable when the separation distance is small in the presence of noise.

Table 10 As in Table 9, but the distance between the two anomalous bodies is much smaller

Figure 9

Model 2: (a) the magnetic anomaly generated by the data set shown in Figure 7a after decreasing the distance between the two sources and adding 5% noise to the magnetic anomaly, (b) sources outlines of the two given models (horizontal cylinder and thin sheet model), (c) the horizontal and vertical derivatives the magnetic anomaly shown in (a), (d) the amplitude of the analytic signal of the magnetic anomaly shown in (a), and (e) 2D surface of the estimated R-parameter and the R-max value (black dots; R-max$_1$ = 0.94 at $q_1$ = 2 and R-max$_2$ = 0.93 at $q_2$ = 1.0)

Model 3

A 120-m magnetic anomaly profile (Fig. 10a) due to a total effect of sphere model (K = 150,000 nT m$^3$, $z_o$ = 7 m, $\theta$ = $25^{\circ }$, $x_o$ = 75 m, and q = 2.5) and a first-order regional (Fig. 10b) is introduced to assess the effect of the embedded regional background. Figure 10c and d renders the horizontal and vertical derivatives as well as the amplitude of the analytic signal. Figure 10e illustrates the mosaic of the R parameter on which an “R-$\mathrm{max}$” of 0.99 is shown.

Figure 10

Model 3: the effect of regional field: (a) magnetic anomaly generated by a sphere model (b) and a first-order regional, (c) horizontal and vertical derivative of the magnetic anomaly shown in (a), (d) amplitude of analytic signal of the magnetic anomaly in (a), and (e) 2D surface of the estimated R-parameter, and the R-max value (black dot)

By adapting the procedures reported above, the obtained model parameters of the total effect of the spherical shaped model (q = 2.5) after adding the regional background are found to be K = 158,590 nT m$^3$, $z_o$ = 7.6 m, $\theta$ = $26^{\circ }$, and $x_o$ = 76 m, which have a good coincidence with the actual parameters (Table 11).

Table 11 Model 3: recovered model parameters of a composite magnetic anomaly generated by both a sphere model and an embedded regional background

For realistic investigation, we added 10% noise into the magnetic anomaly depicted in Figure 10a. Figure 11a, b, c, and d demonstrates the magnetic anomaly profile to be analyzed, horizontal and vertical derivatives of this magnetic anomaly, and its analytic signal amplitude. The R-parameter image (Fig. 11e) yielded an “R-max” of 0.87 with model parameters of K = 141,280 nT m$^3$, $z_o$ = 7.8 m, $\theta$ = $22^{\circ }$ and $x_o$ = 76 m, which is well matched with the actual source model (Table 11). The obtained results in both cases confirm the constancy of this method in magnetic data interpretation.

Figure 11

Model 3: (a) noisy magnetic anomaly generated by the data set shown in Figure 10a after adding 10% noise, (b) model sketch, (c) horizontal and vertical derivative of the magnetic anomaly shown in (a), (d) amplitude of analytic signal of the magnetic anomaly in (a), and (e) 2D surface of the estimated R-parameter, and the R-max value (black dot).

Field Examples

The scheme is applied to three magnetic field examples for mineral exploration.

Case Study 1: the Pima Copper Mine, The USA

The Pima Province represents one of the most important real sources of copper in the USA. The Pima mining district is situated in the southern-west of Tucson city, on the eastern part of the Sierrita Mountains in Pima County, Arizona, USA. Figure 12a shows the vertical magnetic field profile acquired from the Pima copper mine (Gay 1963). The magnetic anomaly profile is 750 m long and was digitized at 10-m sampling intervals. The horizontal and the vertical derivatives and the amplitude of the analytic signal are rendered in Figure 12b and c. The 2D mosaic image shows an “R-max” of 0.99, as is illustrated by the black dot shown in Figure 12d. Table 12 shows the R-parameter computed for all possible shape factors (q = 1, 2, and 2.5), where R-max encountered its maximum value at q = 1, which suggests that the buried structure resembles a thin sheet. The corresponding approximative solution is K = 46,424.38 nT m, $z_o$ = 71 m, $x_o$ = 370 m, $\theta$ = $- 55.11^{\circ }$, and q = 1. The predicted response has been calculated from this solution and is found in good match with the observed magnetic data (Fig. 12a).

Table 12 Case study 1: the Pima copper mine, USA

Figure 12

The Pima copper mine anomaly, USA. (a) True (red) and calculated (black) anomalies, (b) horizontal and vertical derivatives of the magnetic anomaly shown in (a), (c) amplitude of the analytic signal of the magnetic anomaly shown in (a), and (d) 2D surface of the estimated R-parameter and the R-max value (black dot; R-max = 0.99 at q = 1.0, $K = 46{,}424.38$ nT m, $z_o$ = 71 m, $x_o$ = 370 m and $\theta$ = $-55.11^{\circ }$). The standard deviation between the true and calculated magnetic anomalies is 28.27 nT.

The magnetic profile analyzed here has been interpreted by several authors (Gay 1963; Asfahani and Tlas 2007). Table 13 compares the results obtained from the scheme developed here against those reported in the published literature. The table shows that the depth and interpretive idealized model determined using the present developed method are compatible and consistent with those confirmed from drilling and the published literature.

Table 13 Case study 1: the Pima copper mine, USA

Case Study 2: West Coast anomaly, Senegal

Figure 13a represents the observed magnetic anomaly (total field) measured in a region at the western coast of Senegal of West Africa continent (Nettleton 1976). The base line and the zero crossing of the profile are those given by Nettleton (1976) and Prakasa Rao and Subrahmanyam (1988). The magnetic anomaly profile is 40 km long and was digitized at 0.5-km intervals. Nettleton (1976) reported that the causative body is comprised of a basic intrusion within the basement rock.

Figure 13

The West Coast anomaly, Senegal. (a) True (red) and calculated (black) anomalies, (b) horizontal and vertical derivatives of the magnetic anomaly shown in (a), (c) amplitude of the analytic signal of the magnetic anomaly shown in (a), and (d) 2D surface of the estimated R-parameter and the R-max value (black dot; R-max = 0.99 at q = 2.5, K = 461,865.90 nT km$^3$, $z_o$ = 10 km, $x_o$ = 29 km and $\theta$ = $19^{\circ }$). The standard deviation between the true and calculated magnetic anomalies is 33.83 nT.

Figure 13b, c, and d shows the horizontal and vertical derivatives, analytic signal response, 2D surface for the R-parameter. Figure 13d reveals an R-max value of 0.99 using a sphere model the corresponding model parameters of which are K = 461,865.90 nT km$^3$, $z_o$ = 10 km, $x_o$ = 29 km and $\theta$ = $19^{\circ }$, and q = 2.5. Table 14 presents the R-parameters calculated for various shape factors (q = 1, 2, and 2.5), and the maximum of the R-parameter corresponds to a shape factor q of 2.5, which suggests that the buried structure can be reasonably described by a sphere body.

Table 14 Case study 2: the West Coast of Senegal anomaly, West Africa

Table 15 compares the results obtained here against those reported in the published literature (Nettleton 1976; Prakasa Rao and Subrahmanyam 1988; Abdelrahman et al. 2007a). The comparison supports that the depth and index angle recovered by the scheme developed in our paper are in good match with those reported in the published literature.

Table 15 Case study 2: the West Coast of Senegal anomaly, West Africa

Case Study 3: the Hamrawein anomaly, the Red Sea, Egypt

The total observed magnetic anomaly of the Hamrawein field example was measured by a highly definition airborne magnetic survey along the Hamrawein area, over the western margin of the Red Sea, Egypt (Salem et al. 1999). Generally, the Hamrawein area is covered by sedimentary and meta-volcanic rocks and the observed magnetic anomaly is represented by two main anomalies (Salem 2005; Salem et al. 2005). The profile of the magnetic anomaly has a length of 17,800 m digitized at 200-m intervals (Fig. 14a).

Figure 14

The Hamrawein anomaly, the Red Sea, Egypt. (a) True (red) and calculated (black) anomalies, (b) horizontal and vertical derivatives of the magnetic anomaly shown in (a), (c) amplitude of the analytic signal of the magnetic anomaly shown in (a), and (d) 2D surface of the estimated R-parameter and the R-max values; R-max$_1$ = 0.80 at ($q_1$ = 1.0, $K_1$ = 102,046 nT m, $z_{o1}$ = 480 m, $x_{o1}$ = 4550 m and $\theta _1$ = $70.49^{\circ }$) and R-max$_2$ = 0.59 at ($q_2$ = 1.0, $K_2$ = 56,549.52 nT m, $z_{o2}$ = 400 m, $x_{o2}$ = 15,200 m and $\theta _2 = 55.04^{\circ }$). The standard deviation between the true and calculated magnetic anomalies is 26.57 nT.

The horizontal and vertical derivatives as well as the amplitude of the analytic signal of the magnetic anomaly are shown in Figure 14b and c, respectively. The 2D mosaic surface of the R-parameter reveals two maxima: R-max$_1$ = 0.80 and R-max$_2$ = 0.59, as is shown by the black dot shown in Figure 14d. Table 16 shows the R-parameters calculated for all possible shapes, and that R-max approaches its maximum when the shape factor is 1 for the two main targets. The corresponding model parameters are ($K_1$ = 102,046 nT m, $z_{o1}$ = 480 m, $x_{o1}$ = 4550 m and $\theta _1$ = $70.49^{\circ }$, and $q_1$ = 1.0) and ($K_2$ = 56549.52 nT m, $z_{o2}$ = 400 m, $x_{o2}$ = 15,200 m and $\theta _2$ = $55.04^{\circ }$, and $q_2$ = 1.0), respectively. Figure 14a shows that the observed and modeled (predicted) responses are in good match.

Table 16 Case study 3: the Hamrawein anomaly, the Red Sea, Egypt

Table 17 demonstrates a comparison between the outcomes obtained by the present approach and the other published methods (Salem et al. 2005; Essa and Elhussein 2018). Salem et al. (2005) interpreted the Hamrawein anomaly as two sheet structures at a depth of $z_{o1}$ = 555.7 and $z_{o2}$ = 441.2 m. Salem (2005) reported a depth of $z_{o1}$ = 540 m and $z_{o2}$ = 447 m. Salem (2011) interpreted the Hamrawein anomaly using the local wave number (LW) method with depths of $z_{o1}$ = 432.6 m and $z_{o2}$ = 422.8 m and using the total gradient (TG) method with depths of $z_{o1}$ = 486.5 m and $z_{o2}$ = 440.4 m. Essa and Elhussein (2018) interpreted these anomalies using the particle swarm optimization (PSO) ($z_{o1}$ = 623.05 m and $z_{o2}$ = 494.14 m). It can be concluded that the depths obtained by the developed scheme ($z_{o1}$ = 480 m and $z_{o2}$ = 400 m) are in good agreement with those reported in the published literature.

Table 17 Case study 3: the Hamrawein anomaly, the Red Sea, Egypt

Conclusions

The R-parameter imaging technique is a fast (it takes about 2 s on a simple PC) and automatic imaging approach that can estimate the model parameters of a buried anomalous body (depth, location, effective angle of magnetization, amplitude coefficient, and shape). The developed method utilizes the amplitude of the analytic signal of the real data and the amplitude of the analytic signal of the calculated data caused by some assumed sources. It approaches the maximum (R-max) when the model parameters match the true ones. The three numerical examples investigated in this paper show that developed scheme is stable with respect to noise, and that the neighboring effect can impact the accuracy of the recovered model parameters. The method has been successfully applied to three real-field data examples from the USA, Senegal, and Egypt, and affirmed that the obtained results are reasonable and reliable with the background information that was obtained from drilling and other methods. The developed R-parameter imaging method is appropriate in ore and mineral exploration and reconnaissance studies intended to delineate the subsurface structures from magnetic data.