Predictive Geological Mapping Using Closed-Form Non-stationary Covariance Functions with Locally Varying Anisotropy: Case Study at El Teniente Mine (Chile)

Abstract

This paper is concerned with the problem of predicting the surface elevation of the Braden breccia pipe at the El Teniente mine in Chile. This mine is one of the world’s largest and most complex porphyry-copper ore systems. As the pipe surface constitutes the limit of the deposit and the mining operation, predicting it accurately is important. The problem is tackled by applying a geostatistical approach based on closed-form non-stationary covariance functions with locally varying anisotropy. This approach relies on the mild assumption of local stationarity and involves a kernel-based experimental local variogram a weighted local least-squares method for the inference of local covariance parameters and a kernel smoothing technique for knitting the local covariance parameters together for kriging purpose. According to the results, this non-stationary geostatistical method outperforms the traditional stationary geostatistical method in terms of prediction and prediction uncertainty accuracies.

Introduction

One of the most important goals in geostatistical applications is the prediction of a physical quantity of interest over the entire study domain from measurements in some locations. This problem is fundamentally based on modeling and estimation of the spatial dependence structure of data. Describing the spatial dependence structure of data is usually carried out using statistical tools such as the variogram or covariogram, which is calculated over the entire study domain under the stationarity assumption. However, this assumption that states that the spatial dependence structure of data remains constant over the entire study domain is driven more by mathematical convenience than by reality. In practice, it can be doubtful due to some local influences or localized effects, which can be reflected by computing local stationary variograms whose characteristics may vary spatially. The use of a stationary geostatistical approach in such cases is not suitable because it could produce less accurate predictions, including an incorrect assessment of the prediction error.

Various approaches have been proposed over the years to deal with non-stationarity of the spatial dependence structure of data (Guttorp and Schmidt 2013; Sampson et al. 2001; Guttorp and Sampson 1994). One of the most interesting is the classes of explicit non-stationary covariance functions with locally varying anisotropy developed by Paciorek and Schervish (2006) and Stein (2005). The covariance functions belonging to these classes are locally stationary and their parameters can vary spatially yielding local variances, ranges, geometric anisotropies, and other. The estimation of these spatially varying parameters is a challenging problem. Paciorek and Schervish (2006) suggest to estimate these parameters as in the moving windows non-stationary geostatistical approach based on the variogram (Haas 1990a, b; Harris et al. 2010; Magneron et al. 2010; Machuca-Mory and Deutsch 2013). Anderes and Stein (2011) propose a weighted local likelihood approach where the influence of faraway observations is smoothly down-weighted. Fouedjio et al. (2016) propose a distribution-free approach involving a local stationary variogram kernel estimator, a weighted local least-squares method in combination with a kernel smoothing method.

In this article, we address the problem of predicting the surface elevation of the breccia pipe called Braden at the El Teniente mine in Chile. As described by Skewes et al. (2002), Maksaev et al. (2004), and Spencer et al. (2015), the supergiant El Teniente deposit is one of the world’s largest and most complex porphyry-copper ore bodies, containing an estimated premining resource of approximately 95 million metric tons Cu and 2.5 million metric tons Mo. The mine is located approximately 70 km southeast of Santiago on the western margin of the Andean Cordillera and within the confines of the central Chilean porphyry Cu belt. The center of the deposit is composed of a late-stage diatreme known as the Braden pipe, which is 1200 m in diameter at the surface and close to 600 m at a depth of 1800 m. The pipe is poorly mineralized and surrounded by different kinds of mineralized geological units. Knowing the exact location of the pipe surface is important because it constitutes the internal limit of the deposit and the mining operation. To do this, a geostatistical approach based on closed-form non-stationary covariance functions with locally varying anisotropy proposed by Fouedjio et al. (2016) is used. Previously, Fouedjio (2015) applied a non-stationary geostatistical approach based on space deformation to address this problem. The purpose of this present contribution is to highlight the added value of a non-stationary geostatistical approach compared to a stationary one.

The remainder of paper is structured as follows. The geostatistical approach based on closed-form non-stationary covariance functions with locally varying anisotropy is described in “Closed-Form Non-stationary Covariances Based Approach” section. The application of this non-stationary geostatistical approach on the breccia pipe elevation dataset is presented in “Application to Breccia Pipe Elevation” section. Comparisons are made to the conventional stationary method. Concluding remarks are provided in “Concluding Remarks” section.

Closed-Form Non-stationary Covariances Based Approach

Modeling

Consider $Y(\cdot )=\{Y({\textbf{x}}): {\textbf{x}} \in G \subseteq {\mathbb{R}}^p, p\ge 1\}$ a random field defined on a fixed continuous study domain G and reflecting the studied phenomenon. We consider that $Y(\cdot )$ is governed by the following equation:

$$Y({\textbf{x}})=m({\textbf{x}})+ \sigma ({\textbf{x}})Z({\textbf{x}}), \quad \forall {\textbf{x}} \in G, $$

(1)

where $m(\cdot ): {{\mathbb{R}}}^p \rightarrow {\mathbb{R}}$ is an unknown fixed function, $\sigma(\cdot ){:}\,{\mathbb{R}}^p \rightarrow {\mathbb{R}}^{+}$ is an unknown positive fixed function, and $Z(\cdot )$ is a zero expectation, unit variance random field with correlation function defined by

$$ R^{NS}({\textbf{x}},{\textbf{y}})=\phi _{{\textbf{xy}}}R^{S}\left( \sqrt{ Q_{{\textbf{xy}}}({\textbf{x}}-{\textbf{y}})}\right) , \quad \forall ({\textbf{x}}, {\textbf{y}}) \in G \times G $$

(2)

with ${\phi _{{\textbf{xy}}}={\left| {\varvec{\Sigma}}_{{\textbf{x}}}\right| }^{\frac{1}{4}}{\left| {\varvec{\Sigma}}_{{\textbf{y}}}\right| }^{\frac{1}{4}}{\left| {\frac{{\varvec{\Sigma }}_{{\textbf{x}}}+ {\varvec{\Sigma}}_{{\textbf{y}}}}{2}}\right| }^{-\frac{1}{2}}},$ $\displaystyle {Q_{{\textbf{xy}}}({\textbf{h}})={{\textbf{h}}}^{T}{\left( \frac{\varvec{\Sigma }_{{\textbf{x}}}+{\varvec{\Sigma}}_{{\textbf{y}}}}{2}\right) }^{-1}{\textbf{h}}}, \ \forall {\textbf{h}} \in {\mathbb{R}}^p .$ ${\varvec{\Sigma}}(\cdot ): {\mathbb{R}}^p \rightarrow PD_{p}({\mathbb{R}}), {\textbf{x}} \mapsto {\varvec{\Sigma}}_{{\textbf{x}}}$ is a mapping from ${\mathbb{R}}^p$ to $PD_{p}({\mathbb{R}})$ the set of real-valued positive definite p-dimensional square matrices; $R^{S}(\cdot )$ is a continuous isotropic stationary correlation function, positive definite on ${\mathbb{R}}^p$, for all $p \in {\mathbb{N}}^\star$.

The class of closed-form non-stationary covariance functions depicted by Eq. (2) is that developed by Paciorek and Schervish (2006). Fouedjio et al. (2016) shows that this class is obtained by convolving an orthogonal random measure with a spatially varying random weighting function. The intuition behind this class is that at each location ${\textbf{x}}$ is assigned a matrix ${\varvec{\Sigma}}_{{\textbf{x}}}$ interpreted as a locally varying geometric anisotropy matrix. The correlation between two locations ${\textbf{x}}$ and ${\textbf{y}}$ is obtained by averaging the two matrices at ${\textbf{x}}$ and ${\textbf{y}}$. In this way, the local characteristics at both locations influence the correlation of the corresponding target values, allowing to account for the non-stationarity. One will note that this class provides non-stationary versions of some well-known stationary correlation functions, for a specific choice of the isotropic stationary correlation function $R^{S}(\cdot )$ (Gaussian, exponential, power exponential, and Matérn). However, this class does not enable the use of isotropic stationary correlation function with compact support like the spherical model (Paciorek and Schervish 2006; Fouedjio et al. 2016). Indeed, the correlation function $R^{S}(\cdot )$ specified in Eq. (2) must be positive definite in all dimensions.

From model defined in Eq. (1), the two first moments of the random field $Y(\cdot )$ are given by

$$ {\mathbb{E}}(Y({\textbf{x}}))= m({\textbf{x}}), \ \forall {\textbf{x}} \in G, $$

(3)

$$ {\mathbb{C}}\text{ov }(Y({\textbf{x}}),Y({\textbf{y}}))= \sigma ({\textbf{x}})\sigma ({\textbf{y}})R^{NS}({\textbf{x}},{\textbf{y}})\equiv C^{NS}({\textbf{x}},{\textbf{y}}), \ \forall ({\textbf{x}},{\textbf{y}}) \in G \times G. $$

(4)

Then, the non-stationarity of the random field $Y(\cdot )$ is characterized by the spatially varying parameters $m(\cdot )$, $\sigma (\cdot )$ , and ${\varvec{\Sigma}}(\cdot )$ defined at any location of the study domain. Under the local stationarity assumption (Matheron 1971), parameters are smooth functions varying slowly in space so that at any location ${\textbf{x}}_0 \in G$, we can define a neighborhood ${\mathcal{V}}_{{\textbf{x}}_0}= \{{\textbf{x}} \in G, \ \Vert {\textbf{x}}_0-{\textbf{x}}\Vert \le b\}$ wherein the mean $m(\cdot )$ and the covariance function $C^{NS}(\cdot ,\cdot )$ are approximately stationary. Thus, $\forall ({\textbf{x}},{\textbf{y}}) \in {\mathcal{V}}_{{\textbf{x}}_0} \times {\mathcal{V}}_{{\textbf{x}}_0}$ Eqs. (3) and (4) are reduced as follows:

$$ m({\textbf{x}})\approx m({\textbf{y}}) \approx m({\textbf{x}}_0), $$

(5)

$$ C^{NS}({\textbf{x}},{\textbf{y}})\approx {\sigma }^2({{\textbf{x}}_0})R^S\left( \sqrt{({{\textbf{x-y}}})^{T}{\varvec{\Sigma }}_{{\textbf{x}}_0}^{-1}({\textbf{x-y}})}\right) \equiv C^S({\textbf{x}}-{\textbf{y}};{\textbf{x}}_0). $$

(6)

Thus, locally, the mean $m(\cdot )$ is constant as shown in Eq. (5) and the non-stationary covariance function depicted by Eq. (4) is reduced to the anisotropic stationary covariance function given in Eq. (6). The anisotropy matrix ${\varvec{\Sigma }}_{{\textbf{x}}_0}$ at any location ${\textbf{x}}_0 \in G$ is parameterized through the spectral decomposition, thus ensuring its positive definiteness. Formally, we have ${\varvec{\Sigma }}_{{\textbf{x}}_0}={\varvec{\Psi }}_{{\textbf{x}}_0}{\varvec{\Lambda }}_{{\textbf{x}}_0}{\varvec{\Psi }}_{{\textbf{x}}_0}^T$, where ${\varvec{\Lambda }}_{{\textbf{x}}_0}$ is the diagonal matrix of eigenvalues and ${\varvec{\Psi }}_{{\textbf{x}}_0}$ is the eigenvector matrix formulated in 2d as follows:

$$ {\varvec{\Lambda }}_{{\textbf{x}}_0}= \left(\begin{array}{cc} \lambda _1^2({{\textbf{x}}_0})&{}0\\ 0&{}\lambda _2^2({{\textbf{x}}_0}) \end{array}\right) , \quad {\varvec{\Psi }}_{{\textbf{x}}_0}= \left(\begin{array}{cc} \cos \psi ({{\textbf{x}}_0})&{}\sin \psi ({{\textbf{x}}_0})\\ -\sin \psi ({{\textbf{x}}_0})&{}\cos \psi ({{\textbf{x}}_0}) \end{array}\right) , $$

where $\lambda _1({{\textbf{x}}_0}),\lambda _2({{\textbf{x}}_0})>0$ controls the local ranges and $\psi ({{\textbf{x}}_0}) \in [0,\pi )$ specifies the local azimuth.

Inference

Suppose that n data $Y({\textbf{s}}_1),\ldots ,Y({\textbf{s}}_n)$ are collected, at known spatial locations, ${\textbf{s}}_1,\ldots ,{\textbf{s}}_n \in G$. The goal is to estimate the mean function $m(\cdot )$, the standard deviation function $\sigma (\cdot )$ , and the anisotropy function ${\varvec{\Sigma}}(\cdot )$ characterized by $\lambda _1(\cdot ), \lambda _2(\cdot )$ and $\psi (\cdot )$. This is achieved by using a step-by-step estimation procedure developed by Fouedjio et al. (2016) and similar to one proposed by Machuca-Mory and Deutsch (2013). First, a local stationary variogram kernel estimator is defined at any location of interest. Then, this is used in a weighted local least-squares procedure to estimate parameters at a representative set of locations referred to as anchor locations. Finally, a kernel smoothing technique is used to make available the parameter values at any location of interest.

Step 1

A non-parametric kernel moment estimator of the local stationary variogram $\gamma ({\textbf{h}};{\textbf{x}}_0)={\sigma }^2({{\textbf{x}}_0})-C^S({\textbf{h}};{\textbf{x}}_0)$ at a fixed location ${\textbf{x}}_0 \in G$ and for a spatial lag ${\textbf{h}} \in {\mathbb{R}}^p, \ \Vert {\textbf{h}}\Vert \le b$ is defined as follows (Fouedjio et al. 2016):

$$ {\widehat{\gamma }}_{\epsilon }({\textbf{h}};{\textbf{x}}_0)=\frac{\sum _{V({\textbf{h}})}K^{\star }_{\epsilon }({\textbf{x}}_0,{\textbf{s}}_i)K^{\star }_{\epsilon }({\textbf{x}}_0,{\textbf{s}}_j){[Y({\textbf{s}}_i)-Y({\textbf{s}}_j)]}^2}{2\sum _{V({\textbf{h}})}K^{\star }_{\epsilon }({\textbf{x}}_0,{\textbf{s}}_i)K^{\star }_{\epsilon }({\textbf{x}}_0,{\textbf{s}}_j)}, $$

(7)

where $K^{\star }_\epsilon ({\textbf{x}}_0,{\textbf{s}}_i)=K_\epsilon ({\textbf{x}}_0,{\textbf{s}}_i)/\sum _{r=1}^nK_\epsilon ({\textbf{x}}_0,{\textbf{s}}_r)$ are standardized weights and $K_\epsilon (\cdot ,\cdot )$ is a non-negative, symmetric kernel on ${\mathbb{R}}^p \times {\mathbb{R}}^p$, with bandwidth parameter $\epsilon >0$. $V({\textbf{h}})=\{({\textbf{s}}_i,{\textbf{s}}_j) \in G \times G: {\textbf{s}}_i-{\textbf{s}}_j = {\textbf{h}} \}$ is the set of all pairs of locations separated by vector ${\textbf{h}}$. For irregularly spaced data where there are usually not enough observations separated by exactly ${\textbf{h}}$, $V({\textbf{h}})$ is commonly modified by $\{({\textbf{s}}_i,{\textbf{s}}_j)\in G \times G: {\textbf{s}}_i-{\textbf{s}}_j \in T({\textbf{h}}) \}$, where $T({\textbf{h}})$ is a tolerance region surrounding ${\textbf{h}}$.

The role of the kernel function in Eq. (7) is to smoothly down-weight the squared differences (for each spatial lag) according to the distance of these paired values from a target location. A pair of locations receives a weight that is proportional to the product of the individual weights. Geographically weighted estimators similar to one described by Eq. (7) have been proposed by Harris et al. (2010) and Machuca-Mory and Deutsch (2013) for the moving windows non-stationary geostatistical approach. Regarding the choice of the kernel function, Fouedjio et al. (2016) suggest a Gaussian kernel whose support is non-compact. Indeed, a kernel function with non-compact support includes all observations, then allows to avoid artifacts caused by using only observations close to the target location. It also reduces instability of the kernel estimator of the local stationary variogram at regions with low sampling density. Furthermore, the use of a Gaussian kernel provides a smooth parameter estimates and then it is compatible with the local stationarity assumption. The size of the local stationarity neighborhood b is set with respect to the bandwidth $\epsilon$: $b=\sqrt{3}\epsilon$ so that the standard deviation of the isotropic stationary Gaussian kernel matches the isotropic stationary uniform kernel, which has a compact support. Another possible choice for b is a quantile of the isotropic stationary Gaussian kernel (e.g., $b\approx 2\epsilon$).

Step 2

Let ${\mathcal{A}}$ be a set of representative locations referred to as anchor locations over the study domain G. Given the local stationary variogram kernel estimator defined in Eq. (7), the estimation of the parameters vector ${\varvec{\theta}}({\textbf{x}}_0)=\left( {\sigma }({\textbf{x}}_0),\lambda _1({\textbf{x}}_0),\lambda _2({\textbf{x}}_0),\psi ({\textbf{x}}_0)\right)$ at an anchor location ${\textbf{x}}_0 \in {\mathcal{A}}$ is given by following minimization problem (Fouedjio et al. 2016):

$$\widehat{\varvec{\theta}}({\textbf{x}}_0)= \mathop {{\arg\min}}\limits _{{\varvec{\theta}}_0 \in \Theta } \Vert {\textbf{w}}_{\epsilon }({\textbf{x}}_0)\odot ({\varvec{\gamma}}({\varvec{\theta}}_0)-\widehat{\varvec{\gamma}}_{\epsilon }({\textbf{x}}_0))\Vert, $$

(8)

where ${\varvec{\theta}}_0$ is the vector of unknown parameters and $\Theta$ is an open parameter space; ${\varvec{\gamma}}^T({\varvec{\theta}}_0)=[\gamma ({\textbf{h}}_l;{\varvec{\theta}}_0)]_{l=1\ldots L}$; ${\widehat{\varvec{\gamma }}^T}_{\epsilon }({\textbf{x}}_0)=[\widehat{\gamma }_{\epsilon }({\textbf{h}}_l;{\textbf{x}}_0)]_{l=1\ldots L}$; ${\textbf{w}}_{\epsilon }^{T}({\textbf{x}}_0)=[w_{\epsilon }({\textbf{h}}_l;{\textbf{x}}_0)]_{l=1\ldots L}$, with $w_{\epsilon }({{\textbf{h}}}_l;{\textbf{x}}_0)={\left[ \left( \sum _{V({{\textbf{h}}}_l;{\textbf{x}}_0)}K^{\star }_{\epsilon }({\textbf{x}}_0,{\textbf{s}}_i)K^{\star }_{\epsilon }({\textbf{x}}_0,{\textbf{s}}_j)\right) /\Vert {{\textbf{h}}}_l\Vert \right] }^{1/2}$; $\{{\textbf{h}}_{l} \in {\mathbb{R}}^p\}_{ l=1,\ldots ,L}$ is a collection of lag vectors; $\odot$ is the product term by term.

Given the parameter vector estimate $\widehat{\varvec{\theta }}({\textbf{x}}_0)$ at anchor location ${\textbf{x}}_0 \in {\mathcal{A}}$, which characterizes the local stationary spatial dependence structure of data, the mean $m({\textbf{x}}_0)$ is estimated explicitly by a local stationary kriging of the mean (Matheron 1971). As highlighted by Fouedjio et al. (2016), the estimation of parameters ${\sigma }(\cdot ),\lambda _1(\cdot ),\lambda _2(\cdot )$ and $\psi (\cdot )$ governing the non-stationary spatial dependence structure of data does not require the prior estimation of the mean $m(\cdot )$. Moreover, no model is specified for the latter. Indeed, the local stationary variogram kernel estimator given in Eq. (7) filters out the mean $m(\cdot )$ at short distances, because the mean is approximately equal to a constant in the quasi-stationarity neighborhood. For distances up to the radius of the quasi-stationarity neighborhood, the local stationary variogram kernel estimator thus estimates well the local stationary spatial dependence structure, whose parameters are estimated as shown in Eq. (8).

Step 3

For the kriging or simulation purpose, it is necessary to get the estimates of the spatially varying parameters at any location of interest, especially at unobserved and observed locations. In practice, it is unnecessary to solve the minimization problem depicted by Eq. (8) at each location of interest. Indeed, doing so is computationally intensive and redundant for close locations because their estimates are highly correlated. To reduce the computational burden, Fouedjio et al. (2016) propose to perform the parameter estimation as shown in step 2. Then, using the resulting parameter estimates at anchor locations, a kernel smoothing method is used to make them available at any location of interest. This idea was also proposed by Machuca-Mory and Deutsch (2013) for the moving windows non-stationary geostatistical approach. Fouedjio et al. (2016) suggest the Nadaraya-Watson kernel smoother (Wand and Jones 1995), which is suitable and relatively simple. However, other smoothers can be used as well (local polynomials, splines, etc.). The set of anchor locations may be chosen as a grid over the study domain. The number of anchor locations may depend on the complexity of the true underlying non-stationarity and especially it is a trade-off between the computing time and the accuracy of the estimation. Indeed, it is possible to choose the set of anchor locations as the large grid of locations to predict but it will be computationally demanding.

The estimation of the spatially varying parameters depends on the bandwidth parameter $\epsilon$ used in the computation of the local stationary variogram kernel estimator defined in Eq. (7). The estimation of the spatial dependence structure of data being rarely a goal per se but an intermediate step before kriging, the bandwidth parameter is selected by a data-driven method consisting for choosing the bandwidth value that gives the best cross-validation mean square prediction error (Fouedjio et al. 2016):

$$ {\text{MSPE}}(\epsilon ) = \frac{1}{n}\sum _{i=1}^{n}{\left( Z({\textbf{s}}_{i}) - \widehat{Z}_{-i}({\textbf{s}}_{i};\epsilon )\right) }^2, $$

(9)

where $\widehat{Z}_{-i}({\textbf{s}}_{i};\epsilon )$ is the kriging at location ${\textbf{s}}_{i}$ using all measured data excluding $\{Z({\textbf{s}}_{i})\}$. The prediction method is described in “Kriging” section.

Prediction

Kriging

Given measured data $Y({\textbf{s}}_1),\ldots ,Y({\textbf{s}}_n)$, the point predictor for the unknown value of the random field $Y(\cdot )$ at an unsampled location ${\textbf{s}}_0 \in G$ is given by the optimal linear predictor:

$$ \widehat{Y}({\textbf{s}}_{0})= m({\textbf{s}}_{0}) + \sum _{i=1}^{n}\eta _{i}({\textbf{s}}_{0})(Y({\textbf{s}}_{i})-m({\textbf{s}}_{i})), $$

(10)

where the kriging weight vector ${\varvec{\eta}}({\textbf{s}}_{0})=[\eta _i({\textbf{s}}_{0})]$ and the corresponding kriging variance $Q({\textbf{s}}_{0})$ are given by ${\varvec{\eta}}({\textbf{s}}_{0})={{\textbf{C}}}^{-1}{\textbf{C}}_0 \quad \text{ and } \quad Q({\textbf{s}}_{0})=\sigma ^2({\textbf{s}}_{0})- {{\textbf{C}}}_0^T{\textbf{C}}^{-1}{\textbf{C}}_0$, with ${\textbf{C}}_0=[C^{NS}({\textbf{s}}_{i},{\textbf{s}}_{0})]$; ${\textbf{C}}={[C^{NS}({\textbf{s}}_{i},{\textbf{s}}_{j})]}$.

Conditional Simulation

The unconditional simulation of the random field $Y(\cdot )= m(\cdot )+ \sigma (\cdot )Z(\cdot )$ involves the unconditional simulation of the random field $Z(\cdot )$ with zero expectation, unit variance and non-stationary correlation function $R^{NS}(\cdot ,\cdot )$. Since, we are in a non-stationary framework, conventional simulation methods such as spectral method or turning bands method (Lantuejoul 2002) are not adapted because they rely on the stationarity assumption. In the Gaussian framework, the unconditional simulation of the random field $Z(\cdot )$ can be carried out using a propagative version of the Gibbs sampler proposed by Lantuejoul and Desassis (2012). This algorithm allows to simulate a Gaussian vector at a large number of locations compared to existing classical algorithms such as Cholesky method or Gibbs sampler. This algorithm does not rely on a Markov assumption and requires neither the inversion nor the factorization of a covariance matrix. From an unconditional simulation of the random field $Y(\cdot )$, a conditional simulation of the latter can be obtained through the conditioning by kriging approach as in the stationary framework (Lantuejoul 2002).

Application to Breccia Pipe Elevation

Data Description

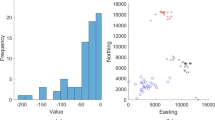
A visualization of the breccia pipe elevation data is given in Figure 1a. The geometric configuration of data is circular with high values located at margins of the mine, whereas the central part exhibits low values. There are more samples at the margin than at the center. The dataset comprises $n=816$ measurements partitioned into a training set ($n_1=616$ measurements) and a validation set ($n_2=200$ measurements) as shown in Figure 1b. The training data serve to estimate the model and the validation data serve to evaluate the prediction performances. A summary statistics of training, validation, and whole data are given in Table 1. The histogram and boxplot of data are slightly skewed with values ranging from 1429 to 2906 m, a mean of 2392 m and a median of 2401 m (Fig. 1c, d). The data present some outliers corresponding to the lowest values, which are located at the center of the study domain.

Figure 1

Elevation data, El Teniente mine, Chile

Table 1 Summary Statistics of Measured Elevation Data, El Teniente Mine, Chile

Exploring Evidence of Variogram Non-stationarity

An exploration of the non-stationarity of the spatial dependence structure of data is carried out through the local stationary variogram (Lloyd 2010). The latter is computed at some locations across the study domain as shown in Figure 2. There is clear evidence of variogram non-stationarity, as the variographic parameters (sill and range) vary spatially. Specifically, the East margin area (including the locations 1, 2, and 3) is an area of relatively low spatial correlation, while the West margin area (comprising the locations 4, 5, and 6) is an area of relatively high spatial correlation. Indeed, the former area has a short range (~300 m) and high variance (~60,000 m²) compared to the latter area, which has a long range (~400 m ) and low variance (~45,000 m²). This difference between the two sub-areas may be related to lithologic conditions. Moreover, the representation of data in Figure 2a shows a spatially varying azimuth, which follows circular geometric configuration of data.

Figure 2

The study domain: (a) measured data and (b–d) local stationary variograms at some specified locations

Model Estimation Results

Following the estimation procedure described in “Inference” section, raw estimates of spatially varying parameters $m(\cdot ),$ $\sigma ^2(\cdot )$ and ${\varvec{\Sigma}}(\cdot )$ at anchor locations are shown, respectively, in Figure 3b–d, thus demonstrating the non-stationarity in the data. One can observe for example in Figure 3c the locally varying geometric anisotropy. As mentioned in “Conditional Simulation” section, such directional effects are also quite visible in the data. Note that the stationary approach has not detected a global geometric anisotropy. Raw estimates of parameters are based on the non-stationary exponential covariance function with locally varying anisotropy. The geometric configuration of anchor locations is given in Figure 3a. Despite the fact that there is almost no data in the center of the domain, the use of a non-compact kernel function (Gaussian kernel) in the computing of the local stationary variogram kernel estimator defined in Eq. (7), makes possible the estimation because it considers all data.

Figure 3

The study domain: (a) data locations (dots) and anchor locations (cross), (b) estimated mean function $\widehat{\text{ m }}(\cdot )$ at anchor locations, (c) estimated anisotropy function $\widehat{\varvec{\Sigma }}(\cdot )$ at anchor locations (the ellipses were scaled to ease visualization) and (d) estimated variance function $\widehat{\sigma }^2(\cdot )$ at anchor locations

According to the bandwidth selection given by Eq. (9), Figure 4a, b shows, respectively, the mean square prediction error for cross-validation and external validation. The optimal value in cross-validation corresponds to $\epsilon =302$ m. This optimal value is consistent with those given by the external validation. Figure 5 shows the maps of smoothed parameters over the whole study domain for mean, variance, anisotropy ratio, and azimuth. The variance map portrays the difference between an area of relatively high variance (East margin region) and low variance (West margin region), thereby confirming the result obtained from the exploratory analysis of non-stationarity in “Exploring Evidence of Variogram Non-stationarity” section. Moreover, the variance map is consistent with results provided by the space deformation non-stationary geostatistical approach applied by Fouedjio (2015): areas of low variance are contracted, while those of high variance are stretched.

A visualization of the covariance function at certain locations (with all other locations) via the level contours under the estimated stationary and non-stationary models is given in Figure 6. The change of shape in the non-stationary spatial dependence structure of data from one location to another one is quite visible. The stationary model is a nested isotropic model (small nugget effect, exponential, and spherical), while the non-stationary model corresponds to the non-stationary exponential covariance function with locally varying anisotropy. This difference between the estimated stationary and non-stationary models is reflected by both the prediction accuracy and the prediction uncertainty accuracy (“Evaluation of Predictions” section).

Figure 4

Bandwidth parameter selection based on the mean square prediction error ${{MSPE}}(\epsilon )$ for (a) cross-validation and (b) external validation

Figure 5

The study domain: smoothed parameters for (a) mean, (b) variance, (c) anisotropy ratio, and (d) azimuth

Figure 6

Covariance level contours at few locations for (a) the estimated stationary model and (b) the estimated non-stationary model. Level contours correspond to 30,000 m² (black), 20,000 m² (red), and 10,000 m² (green)

Evaluation of Predictions

The evaluation of the predictive performance of the non-stationary method relative to the stationary method is carried out using some well-known statistics calculated in external validation, namely mean absolute error (MAE), root mean square error (RMSE), normalized mean square error (NMSE), logarithmic score (LogS), and continued ranked probability score (CRPS). These criteria are formulated as follows:

$$ {{{MAE}}=\frac{1}{n_2}\sum _{i=1}^{n_2}\left| \hat{Z}({\textbf{s}}_i)-Z({\textbf{s}}_i)\right| }, \quad {{{RMSE}} =\left[ {\frac{1}{n_2}\sum _{i=1}^{n_2}{\left( \hat{Z}({\textbf{s}}_i)-Z({\textbf{s}}_i)\right) }^2}\right] }^\frac{1}{2}, $$

$$ {{{NMSE}}=\frac{1}{n_2}\sum _{i=1}^{n_2}{\left( \frac{\hat{Z}({\textbf{s}}_i)-Z({\textbf{s}}_i)}{\hat{\sigma }({\textbf{s}}_i)}\right) }^2}, \quad {{{Log}}S=\frac{1}{n_2}\sum _{i=1}^{n_2}\left( \frac{1}{2}\log \left( 2\pi \hat{\sigma }^2({\textbf{s}}_i)\right) +\frac{1}{2}{\left( \frac{\hat{Z}({\textbf{s}}_i)-Z({\textbf{s}}_i)}{\hat{\sigma }({\textbf{s}}_i)}\right) }^2\right) }, $$

$$ {{{CRPS}}=\frac{1}{n_2}\sum _{i=1}^{n_2}\int\nolimits _{-\infty }^{+\infty }{\left( F_i(z)-{\mathbbm{1}}\{Z({\textbf{s}}_i)\le z\}\right) }^2dz},\ F_i(z)=P(Z({\textbf{s}}_i)\le z| \text{ training }\,\text{ data }), $$

where ${\widehat{Z}}({\textbf{s}}_{i})$ is the kriging at a validation data location ${\textbf{s}}_{i}$ computed from all training data and $\hat{\sigma }^2({\textbf{s}}_i)$ the corresponding kriging variance. $n_2$ is the number of validation data locations.

For MAE, RMSE, LogS and CRPS, the smaller, the better; for NMSE, the nearer to one the better. The prediction accuracy is measured by MAE and RMSE. The prediction uncertainty accuracy is assessed by NMSE, LogS, and CRPS, which combine the kriging and the kriging variance. The MAE, RMSE, and NMSE do not depend on the distribution of measured data. The LogS is equivalent to the pseudo-likelihood in the Gaussian framework. The CRPS corresponds to the distance between the distribution function of the predicted variable and the measured data (itself expressed as a distribution function). It is generally calculated in the Gaussian setting where it admits a closed-form expression. Although the LogS and CRPS scores are usually calculated in the Gaussian framework, they are quite robust. The probability Gaussian-type confidence interval is calculated also at each validation location (i.e., using $\hat{Z}({\textbf{s}}_i) \pm 1.96\hat{\sigma }({\textbf{s}}_i)$) and the proportion of validation locations where the $95\,\%$ confidence interval (PCI) actually includes the true value is computed. This proportion should be near $95\,\%$ for an accurate modeling of uncertainty. The correlation between true and predicted values (Rho) is computed also, the closer to one the better. A description of these criteria can be found in Chilès and Delfiner (2012), Zhang and Wang (2010), and Gneiting and Raftery (2007).

Scatter plots of kriged versus measured values for the stationary and non-stationary methods are presented in Figure 7. Globally, the non-stationary approach provides a more accurate prediction compared to the stationary approach. This is demonstrated by a reduced MAE and RMSE, and by an increased Rho (Table 2). For example, in terms of RMSE, the improvement is about $23\,\%$ with respect to the stationary approach. The reliability of the kriging variances by NMSE, LogS, CRPS, and PCI (Table 2) shows that the non-stationary approach is more accurate for modeling of uncertainty compared to the stationary approach. When considering the proportion of validation locations included in the $95\,\%$ confidence interval, the non-stationary approach shows 12 locations outside ($94\,\%$ of locations included in that interval), while the stationary approach shows 16 locations outside ($92\,\%$ of locations included in that interval) as shown in Figure 7 and reported in Table 2 (we expect about $200 \times 0.05=10$ locations outside). Specifically, the stationary approach has more difficulty in predicting the lowest values (located at the center) compared to the non-stationary approach. Furthermore, we note that this non-stationary approach gives slightly better results compared to the space deformation non-stationary geostatistical approach (Fouedjio 2015, Table 2).

Figure 7

Scatter plots of predicted versus measured values for (a) the stationary approach and (b) the non-stationary approach

Table 2 Validation Statistics of the Prediction Performance

The kriging results for the stationary and non-stationary methods are shown in Figure 8. The general appearance of the map of kriged values associated with each method differs significantly (Fig. 8a, c). The difference is particularly marked at the center of the domain where there are not enough data locations. The stationary and non-stationary methods differed notably in describing the uncertainty associated with the predictions (Fig. 8b, d). One can see that the non-stationary approach tends to provide a low prediction standard deviation in the area of low spatial variability (West margin area), while it tends to give a high prediction standard deviations in the area of high spatial variability (East margin area). Thus, prediction standard deviations reflect not only the samples configuration and availability around target locations, but also the local variability. On the other hand, kriging standard deviations map for the stationary approach shows slight differences over the margin areas of the mine, which were dependent on the sampling intensity. Such a pattern was expected for a stationary approach because it is based on identical global structural parameters throughout the study domain, while the non-stationary approach adapts to locally varying structure of data. Figure 9 shows some conditional simulations in the Gaussian framework, based on the estimated stationary and non-stationary models. Conditional simulations under the non-stationary model differ from one under the stationary model, especially in terms of the locally varying anisotropy.

Figure 8

Predictions and prediction standard deviations based on (a, b) the estimated stationary model and (c, d) the estimated non-stationary model

Figure 9

Two conditional simulations based on (a, b) the estimated stationary model and (c, d) the estimated non-stationary model

Concluding Remarks

This paper demonstrated the added value of using the geostatistical approach based on explicit non-stationary covariance functions with locally varying anisotropy, to predict the surface elevation of the Braden breccia pipe at the El Teniente mine, Chile. This non-stationary approach is capable of capturing some varying spatial features such as locally varying geometric anisotropy in the data that cannot be detected by a stationary method. Thus, the non-stationary approach outperforms the stationary one in terms of prediction and prediction uncertainty accuracies. Moreover, as an exploratory tool for the non-stationarity, it allows to identify areas of high and low spatial variability, and to detect the existence of relationship between the mean and the variance known as proportional effect.

The geostatistical approach based on explicit non-stationary covariance functions with locally varying anisotropy requires enough observations to be able to properly capture the non-stationarity as any non-stationary geostatistical approach. It is also based on local stationarity assumption, then it works well for smoothly varying non-stationarity. Thus, it can be difficult to apply on sparse data or data with abrupt spatial structure variations. In such cases, it may be advisable to proceed under a stationary framework or to divide the study domain if possible. Since this non-stationary method relies on the local stationary assumption, it should not be applied to intrinsically locally stationary spatial processes with unbounded local stationary variograms. Thus, it is important to check that the local stationary variogram kernel estimator used to describe local spatial variation has a sill, before deciding to use this non-stationary method. This is done by visualizing the local stationary variogram kernel estimator at anchor locations. This non-stationary approach is time-consuming compared to a stationary approach. For this case study, the computational time is 10 times more than that of the stationary method. However, if there are enough data to allow reliable inference, this non-stationary method will outperform a stationary method in terms of prediction and prediction uncertainty accuracies as in this case study.