Electrokinetic motion of a rectangular nanoparticle in a nanochannel

Abstract

This article presents a theoretical study of electrokinetic motion of a negatively charged cubic nanoparticle in a three-dimensional nanochannel with a circular cross-section. Effects of the electrophoretic and the hydrodynamic forces on the nanoparticle motion are examined. Because of the large applied electric field over the nanochannel, the impact of the Brownian force is negligible in comparison with the electrophoretic and the hydrodynamic forces. The conventional theories of electrokinetics such as the Poisson–Boltzmann equation and the Helmholtz–Smoluchowski slip velocity approach are no longer applicable in the small nanochannels. In this study, and at each time step, first, a set of highly coupled partial differential equations including the Poisson–Nernst–Plank equation, the Navier–Stokes equations, and the continuity equation was solved to find the electric potential, ionic concentration field, and the flow field around the nanoparticle. Then, the electrophoretic and hydrodynamic forces acting on the negatively charged nanoparticle were determined. Following that, the Newton second law was utilized to find the velocity of the nanoparticle. Using this model, effects of surface electric charge of the nanochannel, bulk ionic concentration, the size of the nanoparticle, and the radius of the nanochannel on the nanoparticle motion were investigated. Increasing the bulk ionic concentration or the surface charge of the nanochannel will increase the electroosmotic flow, and hence affect the particle’s motion. It was also shown that, unlike microchannels with thin EDL, the change in nanochannel size will change the EDL field and the ionic concentration field in the nanochannel, affecting the particle’s motion. If the nanochannel size is fixed, a larger particle will move faster than a smaller particle under the same conditions.

Introduction

With the advancement of nanofabrication technology, nanofluidic devices involving nanoparticles, such as for detecting aerosol nanoparticles and manipulating QDot and DNA, are highly desirable (Mijatovic et al. 2005; Huh et al. 2007; Bonthuis et al. 2008; Tegenfeldt et al. 2004; Reisner et al. 2010; Li et al. 2003; Yuan et al. 2007). Another important application of transporting nanoparticles in nanochannels is the electroporation where the nanoparticles (e.g., DNA and Qdots) are transported via nanopores of the cell membrane into the cell (Movahed et al. 2011; Fox et al. 2006; Lee et al. 2009). Particle motion in microchannels under applied electric field has been studied extensively (Ye and Li 2002, 2004a, b, 2005; Kang et al. 2009; Xuan et al. 2005; Li and Daghighi 2010; Wu and Li 2009; Wu et al. 2009). However, the electrokinetic motion of the nanoparticles in nanochannels has not been well studied.

New studies have been done on the electrokinetic effects and flow field in the nanoscale channels (Wang et al. 2008; Pennathur and Santiago 2005; Petsev and Lopez 2006; Fine et al. 2011; Liu et al. 2010; Kim and Zydney 2004; Movahed and Li 2012; Movahed and Li 2011a, b; Kim et al. 2011; Rafiei et al. 2012). By decreasing the size of the channels to the nanoscale, some conventional theories of electrokinetics lose their applicability. This is because of the relatively thick electric double layers (EDL) that may overlap in the small nanochannels. In the microscale channels, EDL is usually much smaller than the channel’s lateral dimension, and hence are not overlapped in the channel. Therefore, the electric potential of the EDL is equal to zero in the center region of the channel; consequently, the bulk ionic concentrations of positive and negative ions are equal in the center region of the channel (outside EDL). These two statements (zero electric potential and zero net electric charge outside of EDL or in the center of the channels) are the underlying assumptions for the conventional electrokinetic theories and the governing equations of the electrokinetics, such as the Boltzmann distribution of the ions, the Poisson–Boltzmann equation for the electric potential at the cross-section of microchannels, and the Helmholtz–Smoluchowski slip velocity for modeling the electroosmotic flow. In the small nanochannels (from a few nanometers to about 100 nm), EDL thickness becomes larger or at least comparable with the channel lateral dimensions. Hence, EDL from different channel walls may overlap, the electric potential is not zero at the center of the nanochannel, and the bulk ionic concentrations of co- and counter-ions are not equal in the nanochannels.

There are a few papers reporting studies of the electrokinetic motion of the nanoparticles in nanopores and nanochannels. Lee et al. (2010) studied diffusiophoretic motion of a charged spherical particle in a two-dimensional nanopore. In that article, walls of the nanopore are electrically neutral and the nanoparticle’s motion is determined by the ionic concentration gradient in the nanopore. Ai and Qian (2011) conducted a two-dimensional numerical study on the translocation of a DNA-shaped nanoparticle through nanopores. They showed how externally applied electric field, the EDL thickness, and the initial orientation of the nanoparticle affects the movement of the nanoparticle through the nanopore. Their results show that thick EDL can trap the particle at the entrance of nanopore. However, the nanoparticles will always pass the nanopore if externally applied electric field is sufficiently high. Qian et al. studied the axial symmetric electrophoretic motion of a heterogeneous nanoparticle in a nanochannel (Qian and Joo 2008; Qian et al. 2008). They examined the flow field and the ionic concentrations around the nanoparticle. However, they used an incorrect boundary condition $n \cdot \vec{N}_{i} = 0$ for the non-permeating surface of the nanoparticle. The correct boundary condition for the non-permeating surface of the particle moving at a velocity $\vec{V}$ should be $n \cdot \vec{N}_{i} = n \cdot \left( {c_{i} \vec{V}} \right)$ (Keh and Anderson 1985). The right-hand side of this equation describes the convective flux on the impermeable surface of the particle due to the particle movement. This difference in the boundary conditions can significantly influence the concentration field, the flow field, and the particle’s velocity in a nanochannel, and will be discussed in the later section of this article.

Furthermore, the previous studies (Qian and Joo 2008; Qian et al. 2008) considered effectively an infinite long nanochannel and did not consider the end effects. For any practical applications, the nanochannels have a finite length, comparable with the nanochannel diameter; and the two ends of the nanochannel must connect to reservoirs or microchannels. The ends of the nanochannels have major influences on the electrokinetic transport phenomena and processes. Because of the overlap of EDL in the small nanochannels, co-ions and counter-ions do not have the same concentration in the nanochannel. Concentration polarization occurs at the entrance and the exit of the nanochannel to the reservoirs (Zangle et al. 2010). These affect the electric potential, the flow field, and the ionic concentration in the nanochannels, and consequently the electrophoretic and hydrodynamic forces exerting on the nanoparticle. Thus, in order to have an accurate analysis of the electrokinetic effects in the nanochannels, the effects of the reservoirs at the two ends of the nanochannel (for example, the microchannels connecting the nanochannel) should be considered in the model and simulation.

The present research aims to investigate the three-dimensional electrokinetic motion of nanoparticles in nanochannels with the consideration of the end reservoir effect. The effects of channel dimension, nanoparticle dimension, bulk ionic concentration, and surface electric charge of the nanochannel walls on the particle motion will be examined. Because crystallized quantum dots usually have cubic shape (Chattopadhyay et al. 2011; Oron et al. 2009), and the nanopores in the cell membrane can be approximated as nanochannels with a circular cross-section, a three-dimensional rectangular nanoparticle in a circular nanochannel will be considered in this study. In the following sections, a physical description and a mathematical modeling of the system in this study will be provided first. After outlining the numerical method, the numerical simulation results are presented and discussed. Effects of the Brownian force, the surface electric charge of the nanochannel wall, and the cross-sectional area of the nanochannel on the nanoparticle motion are described.

Modeling

Physical modeling

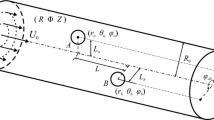
Figure 1 illustrates the nanochannel system of this study. The nanochannel has a circular cross-sectional area of radius R and length L and connects two reservoirs. The nanochannel and the reservoirs are filled with an aqueous solution (e.g., NaCl). A cubic nanoparticle (a × a × a) is considered at the center of the nanochannel. Application of electric potential at the two ends of the nanochannel causes liquid flow, ionic mass transfer, and motion of the nanoparticle through the nanochannel (electrokinetic effects). The dash lines in Fig. 1 outline the computational domain of this study. The effects of the two reservoirs at the ends of the nanochannel should be considered in the simulations; therefore, two sections ABKL and EFGH are included in the computational domain. CDIJ and MNPO represent the nanochannel and the nanoparticle in the computational domain, respectively. The details of the governing equations and the boundary conditions will be explained in the following sections.

Fig. 1

Schematic diagram of the nanochannel–nanoparticle system in this study. The dashed line encloses the computational domain. Two reservoirs are connected to the circular nanochannel of length L and radius R. Two electrodes located in the reservoirs apply electric potential to the ends of the nanochannel. The nanochannel wall is negatively charged. A negatively charged cubic particle is initially positioned at the center of the nanochannel

In the governing equations presented in the following sections, ϕ is the electric potential, $\vec{E}$ is the electric field, $\vec{D}$ is the electrical displacement, c _i , z _i , and $\vec{N}_{i}$ are the concentration, valance, and flux of ion species i, respectively. p, $\vec{u}$, and $\vec{V}_{\text{p}}$ are pressure, velocity vector, and translational velocity of the nanoparticle, correspondingly. m _p is the mass of the nanoparticle. t represents time. σ_w and σ_p are the surface electric charge densities on the nanochannel wall and on the surface of the nanoparticle, respectively. The constants includes permittivity (ε₀ε_r), medium density (ρ), Faraday number (F), fluid viscosity (η) and valance number (z _i ), diffusion coefficient (D _i ), and mobility (μ _i ) of ion species i. The values of these constants and parameters are listed in Table 1.

Table 1 The values for constants and parameters used in the simulations

Mathematical modeling

In order to model the electrokinetic motion of the nanoparticle in the nanochannel, it is necessary to find the forces exerted on the particle. The dominant forces acting on the nanoparticle are the electrophoretic and the hydrodynamic forces. Although the Brownian force can become important for such a nanoscale particle (Morgan and Green 2002), it will be shown later in this article that the influence of this force is negligible in comparison with the electrophoretic force. After finding the forces, the Newton’s second law can be utilized to determine the velocity of the nanoparticle.

The continuum approach will be used in developing the model. Existing experimental studies show that the continuum assumption for aqueous solutions is valid up to 4 nm (Zheng et al. 2003). The following set of highly coupled partial differential equations subjected to the proper boundary conditions are employed to describe the electric potential, the ionic concentration, and the flow field in the nanochannels (Movahed et al. 2011):

$$ - \nabla \left( {\varepsilon_{0} \varepsilon_{\text{r}} \nabla \phi } \right) = F\sum\limits_{i} {z_{i} c_{i} } $$

(1)

$$ \vec{E} = - \nabla \phi $$

(2)

$$ \frac{{\partial c_{i} }}{\partial t} + \nabla \cdot \vec{N}_{i} = 0 $$

(3)

$$ \vec{N}_{i} = \vec{u}c_{i} - D_{i} \vec{\nabla }c_{i} - z_{i} \mu_{i} c_{i} \nabla \phi $$

(4)

$$ \rho \frac{{\partial \vec{u}}}{\partial t} = - \nabla p + \mu \nabla^{2} \vec{u} - \left( {\sum\limits_{i} {z_{i} Fc_{i} } } \right)\nabla \phi $$

(5)

$$ \nabla \cdot \vec{u} = 0 $$

(6)

Equation (1) is the Poisson equation. This equation should be solved in order to obtain the electric potential distribution in the computational domain. The term $F\sum\nolimits_{i} {z_{i} c_{i} }$ on the right-hand side of this equation shows that how the difference of co- and counter-ions influence the electric potential inside the domain. The electric field is the gradient of the electric potential, as indicated by Eq. (2). Equation (3) is the Nernst–Plank equation, where the definition of ionic flux is given by Eq. (4). The first ($\vec{u}c_{i}$), second ($D_{i} \vec{\nabla }c_{i}$), and third (z _i μ _i c _i ∇ϕ) terms at the right-hand side of Eq. (4) represent how the flow field (electroosmosis effect), diffusion, and electric field (electrophoresis effect) contribute to the ionic mass transfer, respectively. The ionic concentration of each species can be found by solving these two equations. Equations (5) and (6) are the Navier–Stokes and the continuity equations, respectively, which describe the velocity field and the pressure gradient in the computational domain. Proper boundary conditions for these equations are described as follows:

Electric potential

Uniform surface electric charge is considered for the boundaries BC, CD, DE, JK, IJ, and HI that represent the walls of the channels (Eq. 8a), and the boundary MNPO that stands for the surface of the nanoparticle (Eq. 8b). Zero surface electric charge (Eq. 8c) is assumed at the boundaries AB, KL, EF, and GH. The applied electric potential at boundaries LA and FG are ϕ₁ (Eq. 9a) and ϕ₂ (Eq. 9b), respectively. In the following equations, $\vec{E}$ and $\vec{D}$ are the external electric field and electrical displacement, respectively. $\vec{n}$ is the normal vector directed from the surface to the fluid.

$$ \vec{D} = \varepsilon \varepsilon_{0} \vec{E} $$

(7)

$$ \vec{n} \cdot \vec{D}(r) = \sigma_{\text{w}} $$

(8a)

$$ \vec{n} \cdot \vec{D}(r) = \sigma_{\text{p}} $$

(8b)

$$ \vec{n} \cdot \vec{D}(r) = 0 $$

(8c)

$$ \phi_{\text{LA}} = \phi_{1} $$

(9a)

$$ \phi_{\text{FG}} = \phi_{2} $$

(9b)

Mass transfer

The walls of the solid nanochannels are impermeable for mass transfer (BC, CD, DE, JK, IJ, and HI). The symmetric boundary condition is assumed at the boundaries AB, KL, EF, and GH. Following mathematical equations represent these two kinds of boundary conditions (symmetric and impermeable). The following equations represent that the normal ionic concentration must be zero at these boundaries.

$$ \vec{n} \cdot \vec{N}_{i} = 0 $$

(10a)

$$ \vec{N}_{i} = - D_{i} \nabla c_{i} - z_{i} \mu_{i} c_{i} \nabla \phi + c_{i} \vec{u} $$

(10b)

Constant bulk ionic concentration (c ₀) is assumed at the boundaries LA and FG (two reservoirs):

$$ c_{i} = c_{0} .$$

(11)

The surface of the nanoparticle (boundary MNPO) is also impermeable for mass transfer. The mathematical condition representing the impermeable surface of the nanoparticle is given by (Keh and Anderson 1985):

$$ \vec{n} \cdot \vec{N} = \vec{n} \cdot \left( {c_{i} \vec{U}} \right), $$

(12)

where $\vec{n}$ is a unit vector normal to the surface of the nanoparticle. This equation means no molecule can penetrate into the particle. In this equation, $\vec{U}$ is the velocity of the liquid–particle interface. When the relative velocity of the ions and the surface is zero, ions do not enter to or exit from this boundary. In this study, for simplicity, the nanoparticle is considered to have a translational velocity $\vec{V}_{\text{p}}$ only and no rotation. Therefore, Eq. (12) can be re-written as:

$$ \vec{n} \cdot \vec{N} = \vec{n} \cdot \left( {c_{i} \vec{V}_{\text{p}} } \right) .$$

(13)

The open boundary condition is assumed for the surfaces LA and FG (Eq. 14); flow can both enter to and exit from the open boundary. For this type of boundary condition, it is assumed that there is no applied pressure gradient and viscous stress at these boundaries. This boundary condition is employed to model the connection of the nanochannel with the reservoirs. No slip velocity (Eq. 15) is applied at the walls of the nanochannel and the reservoirs, boundaries BC, CD, DE, JK, IJ, and HI. The computational domain boundaries AB, KL, EF, and GH are treated as the symmetric boundary condition (Eqs. 16, 17). In Eq. 17, I is the identity tensor matrix.

$$ \left( {\mu \left( {\nabla \vec{u} + (\nabla \vec{u})^{T} } \right)} \right)\vec{n} = 0,\quad p = 0 $$

(14)

$$ \vec{u} = 0 $$

(15)

$$ n \cdot \vec{u} = 0 $$

(16)

$$ \vec{t} \cdot \left[ { - pI + \mu \left( {\nabla \vec{u} + \left( {\nabla \vec{u}} \right)^{T} } \right)} \right] = 0 $$

(17)

No slip boundary condition is also assumed for the surface of the nanoparticle (boundary MNOP). At the solid–liquid interface of the nanoparticle translating at the velocity $\vec{V}_{\text{p}} .$, the no slip velocity is defined as (Keh, Keh and Anderson 1985):

$$ \vec{u} = \vec{V}_{\text{p}} $$

(18)

Equation (18) means that the relative velocity of the liquid to the solid particle must be zero.

Particle motion

As the surface of the nanoparticle is negatively charged, the externally applied electric field brings electrostatic force ($\vec{F}_{\text{ep}}$) on the nanoparticle (electrophoresis effect). Due to the particle motion and the electroosmotic flow of the liquid in the nanochannel, the frictional force (hydrodynamic force) is also exerted on the nanoparticle by the liquid flow ($\vec{F}_{\text{hd}}$). The total force acting on the particle is:

$$ \vec{F}_{\text{t}} = \vec{F}_{\text{ep}} + \vec{F}_{\text{hd}} .$$

(19)

The electrophoretic and the hydrodynamic forces can the calculated as follow:

$$ \vec{F}_{\text{ep}} = \mathop{\iint}\limits_{s} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} } \cdot {\text{d}}\vec{s} $$

(20a)

$$ T_{ij} = \varepsilon \varepsilon_{0} \left( {E_{i} E_{j} - \frac{1}{2}\delta_{ij} \left| E \right|^{2} } \right) $$

(20b)

$$ \vec{F}_{\text{hd}} = \mathop{\iint}\limits_{s} {\vec{n} \cdot \left( { - p\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {I} + \mu \left[ {\nabla \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} + \left( {\nabla \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} } \right)^{T} } \right]} \right){\text{d}}s} .$$

(21)

In the above equations, $\vec{I}$ is the identity tensor, and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T},$ is the Maxwell stress tensor, and $T_{ij}$ is the representation of this tensor with Einstein notation.

At each time steps, the Newton second law can be utilized to find the velocity of the nanoparticle ($\vec{V}_{\text{p}}$):

$$ \vec{F}_{\text{t}} = m_{\text{p}} \frac{{{\text{d}}\vec{V}_{\text{p}} }}{{{\text{d}}t}} .$$

(22)

Brownian force

It should be mentioned that the Brownian force is neglected in the above model. In the following, a simple two-dimensional analysis is presented to compare the effects of the electrophoretic and the Brownian forces on a cylindrical nanoparticle (radius a and a unit length) moving in the nanochannels. The Brownian force can be modeled as (Kadaksham et al. 2004; Liu et al. 2005):

$$ \vec{F}_{\text{B}} = \varsigma \sqrt {\frac{{12\pi a\mu k_{\text{B}} T}}{\Updelta t}}. $$

(23)

In this equation, ς is the Gaussian random number with zero mean and unit variance, a is the radius of the particle, μ is viscosity, k _B is Boltzmann constant, T is temperature, and Δt is time step. To find a simple and two-dimensional approximate solution for the electrophoretic force (Eq. 20), the applied electric potential is assumed to be linear in the computational domain. By considering the uniform surface electric charge on the cylindrical nanoparticle (radius a and a unit length), estimation for the electrophoretic force is given by:

$$ \vec{F}_{\text{ep}} = E_{\text{z}} \sigma_{\text{p}} 2\pi a. $$

(24)

The ratio of the Brownian to electrophoretic forces (α) can be found as:

$$ \alpha = \frac{{\vec{F}_{\text{B}} }}{{\vec{F}_{\text{ep}} }} = \frac{C}{{E_{\text{z}} \sqrt {a \times \Updelta t} }}, $$

(25)

where:

$$ C = \varsigma \frac{{\sqrt {12\pi \mu k_{\text{B}} T} }}{{2\pi \sigma_{\text{p}} }}. $$

(26)

In Eq. (25), C is constant that can be found by solving Eq. (26). Using the parameter values listed in Table 1, the maximum value of C becomes ≈1.99 × 10⁻⁸. E _z, Δt, and a are determined by the characteristics of the system in this study. For example, a = 5 × 10⁻⁹ m, Transient period of nanoparticle movement in nanochannels is in the order of 10⁻¹⁵ s (It will be shown at the rest of this article); therefore, Δt = 10⁻¹⁵ s. In most practical applications, such as in electroporation (creating nanopores on cell membrane), even a small electric potential difference (e.g., the trans-membrane potential is about 1 V) over a very short length (e.g., the membrane thickness 5–10 nm) of the nanochannel (nanopore) will generate a very strong electric field in the nanochannels (~10^5–6 V/m). Using these values, the maximum ratio of the Brownian force to the electrophoretic force, Eq. (25), is approximately ≈3 × 10⁻³. Thus, neglecting the Brownian force in comparison with the electrophoretic force is a reasonable assumption for this study. As it can be seen from Eq. (25), the large value of E _z in the nanochannel results in this conclusion. The numerical results of this study, as shown in the following sections, indicate that electrophoretic and hydrodynamic forces are of the same order of magnitude. Thus, without loss of generality, it can conclude that, under the conditions of this study, the effect of Brownian force is negligible in comparison with both electrophoretic and hydrodynamic ones.

Numerical method

This study considers the three-dimensional nanochannel with a circular cross section connected to the two reservoirs at the ends. The nanoparticle is initially located at the center of the nanochannel. The Poisson–Nernst–Plank, the Navier–Stokes, and the continuity equations are solved simultaneously to calculate the electric potential, the ionic concentration, and the fluid flow in the computational domain. These governing equations are highly coupled; the results are affected by all these equations and the corresponding boundary conditions. The numerical simulation was conducted by using the COMSOL Multiphysics 3.5a. A mesh-independent structure is employed to make sure that the results are unique and will not change if any other grid distribution is applied. In order to discretize the solution domain, the structured meshes are applied. The solution domain is broken into small meshes that fully cover the solution domain without overlapping. The reliable numerical results should be grid independent; therefore, in this study, the effect of different number of grids was examined; finally, the number of grids was found with which the numerical results would not change if further increase in grid number was applied.

At each time steps, by simulating the flow field, the ionic concentration, and the electric potential (Eqs. 1–6), the total force on the nanoparticle is computed (Eqs. 19–21); consequently, the Newton second law is utilized to obtain the velocity of the nanoparticle (Eqs. 22, 23). The assumed tolerances for electric potential are 1 × 10⁻³ V and for the other parameters, c (mol/m³), u (m/s), and p (MPa), is 1 × 10⁻⁸. Here, it should mention that that the smallest binary number in the COMSOL that can differentiate from 1 is “eps” = 2.2 × 10⁻¹⁶. To examine the correctness of the proposed numerical method, a simple case of the motion of the rectangular micro-particle in a rectangular microchannel was simulated and the result was compared with the steady state analytical results of Li et al. (2010). Figure 2 depicts this comparison. The key parameters used in this simulation are indicated in this figure. Good agreement in terms of the steady state velocities between both approaches supports the proposed theoretical model and the numerical method.

Fig. 2

Application of the model and the numerical method to a case of electrokinetic motion of a rectangular micro-particle in a rectangular microchannel. The particle velocity at steady state is compared with an analytical solution

Results and discussion

In this study, a cubic nanoparticle is considered in the simulation to mimic the shape of the quantum dots. The electrical and geometrical parameters used in the simulations are summarized in Table 1. The radius of the nanochannel (R) is assumed to be 10–15 nm; the side of the nanoparticle (a) is 5–10 nm; the dimensions of the boundaries in Fig. 1, AB, EF, FG, GH, KL, and LA are 100 nm. The surface electric charge density of the nanoparticle is σ _p = −0.0001 C/m². The surface electric charge density of the walls of the nanochannel (σ _w) is −0.0001 to −0.0005 C/m², and the applied electric potential difference is Δϕ = 1 V.

Effects of the boundary conditions and the reservoirs

As mentioned in the introduction, the correct boundary condition for the non-permeating surface of the particle moving at a velocity $\vec{V}$ should be $n \cdot \vec{N}_{i} = n \cdot (c_{i} \vec{V})$ (Keh and Anderson 1985), i.e., Eq. (13), not $n \cdot \vec{N}_{i} = 0$. The right-hand side of Eq. (13) describes the convective flux on the impermeable surface of the particle due to the particle movement. This difference in the boundary conditions can significantly influence the concentration field, the flow field and the particle’s velocity in the nanochannel. As an example, let us consider one specific case: a NaCl aqueous solution, C = 1 mol/m³, the surface electric charge density on the walls of nanochannel, and the surface electric charge of nanoparticle is −0.0001 C/m², the nanochannel radius is R = 15 nm, the applied electric voltage between boundaries LA and FG is 1 V, and the nanoparticle dimension is 5 nm × 5 nm × 5 nm. As an example, Fig. 3 shows the effects of using these two different boundary conditions on the ionic concentration of the counter-ion (Na⁺). Figure 3a used the correct boundary condition ($n \cdot \vec{N}_{i} = n \cdot (c_{i} \vec{V})$) and Fig. 3b used the incorrect boundary condition ($n \cdot \vec{N}_{i} = 0$) for the non-permeating walls of the moving particle. This figure clearly shows the significant differences in the ionic concentration and the velocity of the nanoparticle.

Fig. 3

The effects of applying a the correct non-permeating boundary condition $(n \cdot \vec{N}_{i} = n \cdot \left( {\vec{V} \times C_{i} } \right)$), and b the incorrect non-permeating boundary condition ($n \cdot \vec{N}_{i} = 0$) at the surface of a moving particle on the ionic concentration distribution and velocity of the nanoparticle. The color bar indicates the concentration of counter-ion (Na⁺) along the channel at the surface across the center line of the channel (z = 0). (Color figure online)

Figure 4 depicts the difference between the concentrations of the positive and the negative ions (counter-ions and co-ions) in the nanochannel region. In this figure, C = 10⁻² mol/m³, σ_w = σ_p = −0.0001 C/m², R = 10 nm, a = 5 nm, Δϕ = 1 V. As indicated in Fig. 1, the applied electric field and consequently the electroosmotic flow are from the left to the right. As it can be seen from this figure, at the exit of the nanochannel to the microchannel (section A–A), this concentration difference increases substantially. Such an accumulation of the counter-ions (here, the positive ions) at the exit of the nanochannel is usually referred as ion polarization effect (Zangle et al. 2010). Without considering the end reservoir effects, i.e., the interface of the microchannel and the nanochannel, such ion polarization effect cannot be modeled and simulated, which will in turn affect the electroosmotic flow and electrophoresis inside the nanochannel.

Fig. 4

The concentration difference of the counter-ions and the co-ions in the nanochannel (C = 10⁻² mol/m³, σ_w = σ_p = −0.0001 C/m², R = 10 nm, a = 5 nm, Δϕ = 1 V). The color bar indicates the ionic concentration difference in mol/m³. The nanoparticle moves from the right to the left at a velocity V _p = −4.94 × 10⁻⁴ m/s. (Color figure online)

Effects of the nanoparticle size

As explained before, the electrophoretic and the hydrodynamic forces act on the nanoparticle. The electrophoretic force is a function of the externally applied electric field, the particle surface electric charge, and dimensions of the nanochannel (Eq. 20). The hydrodynamic force is dependent on the velocity field that is the function of the bulk ionic concentration, the applied electric field, the dimensions of the nanochannel and the nanoparticle, and the surface electric charge of both the channel and the particle. Figure 5 illustrates the induced pressure around the moving nanoparticle. An enlarged view of the flow field in vicinity of the nanoparticle for this specific case is shown in Fig. 5b. Under the assumed parameters of this case, the nanoparticle moves from the right to the left, i.e., opposite to the electroosmotic flow. The electrophoretic movement of the nanoparticle through the nanochannel causes an induced pressure in the nanochannel.

Fig. 5

a The induced pressure field, and b the flow field around the moving cubic particle in the nanochannel. The color bar indicates the induced pressure in Pa. The nanoparticle moves from the right to the left at a velocity V _p = −4.94 × 10⁻⁴ m/s. Δϕ = 1 V, C = 10⁻² mol/m³, σ_w = σ_p = − 0.0001 C/m², R = 10 nm, and a = 5 nm. (Color figure online)

For the same size nanochannels (R = 15 nm), Fig. 6 depicts the velocity field of the two different nanoparticles (a = 5, 10 nm). The bulk ionic concentration, the surface electric charge, and the applied electric field are kept constant (C = 10⁻² mol/m³, σ_w = σ_p = −0.0001 C/m², R = 15 nm, and Δϕ = 1 V). In this case of study, the nanoparticle moves in the direction of electrophoretic force. This figure shows that the bigger nanoparticle moves faster in the same size nanochannels. The same size nanochannels have the same EDL thickness; by increasing the size of the nanoparticles, the gap between the nanoparticle and the wall of nanochannel decreases, consequently, the local electric field in the smaller gap and hence the electrophoresis drive force to the particle increases. Thus, the nanoparticle should move faster.

Fig. 6

The applied external electric field and the velocity vectors around the moving cubic particle in the nanochannel (C = 10⁻² mol/m³, σ_w = σ_p = −0.0001 C/Cm², R = 15 nm, and Δϕ = 1 V). a a = 5 nm, b a = 10 nm. The color bar indicates the externally applied electric field. (Color figure online)

Effects of bulk ionic concentration

Generally, the ionic concentration of the liquid will affect the electric double layer fields of the nanochannel and the nanoparticle, and the applied electric field along the nanochannel. Consequently the ionic concentration affects the velocity of the nanoparticle. Figure 7 illustrates the net velocity variation of the nanoparticle with time for four different values of the bulk ionic concentrations. The negative sign of the velocity of the nanoparticle means that the particle moves in the opposite direction of the x-axis, i.e., from the right to the left (see Fig. 1). It should be realized that, because both the nanoparticle and the nanochannel are negatively charged, the electrophoresis tends to move the nanoparticle towards the left (the positive electrode in Fig. 1); and the electroosmotic flow caused by the negatively charged channel wall tends to move towards the right (the negative electrode in Fig. 1). In this simulation, the surface charge densities of the nanoparticle and the channel wall are the same, −0.0001 C/m². It should be pointed out that the body force for the electroosmotic flow in nanochannels is $\left( {\sum\nolimits_{i} {z_{i} Fc_{i} } } \right)\nabla \phi$, see Eq. (5). This force is function of the bulk ionic concentration c _i . When bulk ionic concentration increases, the body force for electroosmosis increases, and therefore the EOF velocity increases. Thus, the motion of the nanoparticle towards the left will be reduced, and the particle velocity becomes smaller.

Fig. 7

Effects of bulk ionic concentration on the velocity of the nanoparticle. The radius of the nanochannel is 15 nm and the particle size is 5 nm, respectively. Surface electric charge densities on the walls of the nanochannel and on the surface of the nanoparticle are −0.0001 C/m², and Δϕ = 1 V

As explained above, by increasing the bulk ionic concentration, the electroosmotic flow increases, and hence, according to Eq. (21), the hydrodynamic force strengthens. Therefore, increasing the bulk ionic concentration can also change the direction of the nanoparticle movement. As an example, Fig. 7 also shows that the velocity of the nanoparticle can change from negative to positive when the bulk ionic concentration changes from 0.001 to 0.3 mol/m³.

It should emphasize that for the low values of the bulk ionic concentration, the nanoparticle moves in the opposite direction of the flow field, due to the electrophoresis effect; increasing the bulk ionic concentration retards the nanoparticle motion. Further increase of the bulk ionic concentration can reverse the direction of the nanoparticle movement.

Effects of surface electric charge of the nanochannel

As explained before, the two different forces (electrophoretic and hydrodynamic) determine the nanoparticle motion. Direction of the nanoparticle movement is determined by the net force of these two forces. Similar to the bulk ionic concentration, increase of the surface electric charge of the walls of the nanochannel intensifies the electroosmotic flow, and hence the hydrodynamic force on the nanoparticle. Figure 8 shows the effects of the surface electric charge of the nanochannel on the velocity of the nanoparticle. In this simulation, the surface charge density of the nanoparticle is −0.0001 C/m². This figure shows that, for lower values of the surface electric charge on the walls, the nanoparticle moves in the negative direction of x-axis. This implies that the electrophoretic effect is dominant. Increasing the surface electric charge on the channel wall will increase the electroosmotic flow in the positive direction of the x-axis (from the left to the right as shown in Fig. 1). Over a certain value of the surface charge density, the electroosmotic flow is so strong that the associated hydrodynamic force (viscous frictional force on the particle by the moving liquid) will carry the particle to move with the flow (in the positive direction of the x-axis). Therefore, higher values of the surface electric charge can reverse the direction of nanoparticle motion.

Fig. 8

Effects of the surface electric charge density of the nanochannel on the velocity of the nanoparticle. The surface charge density of the nanoparticle is −0.0001 C/m², and Δϕ = 1 V

In summary, it should be noted that for the case of low surface electric charge on the walls of the nanochannel (hence the weaker electroosmotic flow), the nanoparticle moves in the opposite direction of the flow field (dominant by the electrophoresis). Intensifying this surface electric charge of the channel wall slows down the nanoparticle; further increase of the surface electric charge can reverse the direction of the nanoparticle motion.

Effects of the nanochannel cross-sectional area

The effects of the particle size and channel size on the electrophoretic motion of micro-particles in microchannels have been studied previously (Ye and Li 2005; Xuan et al. 2005; Li and Daghighi 2010). For the case of thin EDL, a larger particle moves faster than a smaller particle in a microchannel with a fixed size. This is because the electrophoretic force on the particle or the local applied electric field near the particle is intensified by the smaller gap between the particle and wall of the microchannel. Furthermore, for the case of thin EDL, changing the dimension of the microchannel has no effects on the electroosmotic flow (i.e., the EOF velocity is independent of the microchannel size) and consequently the hydrodynamic force on the particle. However, this story is different for the case of a microchannel with a thick EDL or the case of a small nanochannel where the EDL thickness is comparable with the channel’s dimension. In these cases, the electroosmotic flow velocity field is not independent of the channel size. It has been shown that the particle moves slower in smaller microchannel with thick EDL (Shugai and Carnie1999). For the electrophoretic motion of the particles in the nanochannels, because the EDL thickness is similar to the size of the nanochannel, one should expect the behavior similar to that in the microchannels with the thick EDL: The particle of a fixed size should move slower in the smaller nanochannels.

Figure 9 shows the influences of the nanochannel cross-sectional area on the velocity of the nanoparticle of a fixed size, a = 5 nm. The negative value of particle velocity in this figure indicates that the nanoparticle moves in the negative direction of x-axis, i.e., the opposite direction of the electroosmotic flow. It shows that the velocity of the particle decreases as the nanochannel’s diameter decreases. This may be understood as the following: When the size of the nanochannel is smaller, the EDL overlap increases, and the EDL field is stronger. Consequently the electroosmotic flow is stronger in a smaller nanochannel. Because the electroosmotic flow is in the opposite direction to the electrophoresis of the particle, the particle’s motion from the right to the left is therefore decreased. In brief, if the surface electric charge and the bulk ionic concentrations keep constant, the same size nanoparticles move faster in the bigger nanochannels.

Fig. 9

Effects of nanochannel cross-sectional area on the velocity of nanoparticle. The size of the nanoparticle is 5 nm. Surface electric charge densities on the walls of the nanochannel and the surface of the nanoparticle are the same, −0.0001 C/m², C = 0.01 mol/m³, and Δϕ = 1 V

Figures 7, 8, and 9 show that the nanoparticle accelerates very fast in the nanochannels, and its transient response is in the order of femtosecond. This is too fast to be detected by the current experimental methods. Thus, understanding of the characteristics at steady state will be sufficient for the appreciation of the electrokinetic motion of nanoparticles in nanochannels. Figure 10 shows how the bulk ionic concentration, surface electric charge, and size of the nanochannel impact the steady state velocity of the nanoparticle. This figure represents all the major conclusions of “Effects of the nanoparticle size”, “Effects of bulk ionic concentration”, “Effects of surface electric charge of the nanochannel”, and “Effects of the nanochannel cross-sectional area” sections.

Fig. 10

Effects of bulk ionic concentration (a), surface electric charge on the walls of the nanochannel (b), and the radius of the nanochannel (c) on the steady state velocity of the nanoparticle

Concluding remarks

The electrophoretic motion of a negatively charged cubic nanoparticle in a nanochannel with the circular cross-section was studied. The influences of the reservoirs at the ends of the nanochannel on the electric field, the ionic concentration field, and the flow field were considered. Because of the very large electric field applied over the nanochannel, the Brownian motion of the nanoparticle is negligible in comparison with the electrokinetic effects. Increasing the bulk ionic concentration increases the electroosmotic flow and may change the particle’s motion and carry the particle with the electroosmotic flow. Increasing the surface charge density of the nanochannel wall has the same effect. For a fixed nanochannel size, a larger nanoparticle will move faster than a smaller nanoparticle under the same conditions, because of the stronger local electric field in the smaller gap region between the larger particle and the channel wall. For the nanoparticles of the same size, decreasing the nanochannel size will increase the electric double layer field, and hence the electroosmotic flow in the nanochannel consequently affect the particle’s motion.