Eccentric electrophoretic motion of a sphere in circular cylindrical microchannels

Abstract

The eccentric electrophoretic motion of a spherical particle in an aqueous electrolyte solution in circular cylindrical microchannels is studied in this paper. The objective is to investigate the influences of separation distance and channel size on particle motion. A theoretical model is developed to describe the electric field, the flow field and the particle motion. A finite element based direct numerical simulation method is employed to solve the model. Numerical results show that, when the particle is eccentrically positioned in the channel, the electric field and the flow field are not symmetric, and the strongest electric field and the highest flow velocity occur in the small gap region. It is shown that the rotational velocity of the particle increases with the decrease of the separation distance. With the decrease of the separation distance, the translational velocity increases in a smaller channel; while it decreases first and then increases in a relatively large channel. When a particle moves eccentrically at a smaller separation distance from the channel wall, both the translational velocity and the rotational velocity increase with the decrease of the channel size.

1 Introduction

Electrophoresis is one of the most important electrokinetic phenomena, and it has various applications in colloidal and biomedical sciences. Electrophoretic motion of rigid particles in unbounded electrolyte solutions has been investigated extensively, and mathematical models have been developed to describe this phenomenon in detail. Reviews of electrophoresis can be found in books by Hunter (1981), Lyklema (1991) and Van de Ven (1998). However, with the emergence of microfluidic devices, the study of boundary effects on the electrophoretic motion of particles becomes more and more important. Recent publications on the boundary effects can be classified into two categories: thick electrical double layers (Zydney 1995; Ennis and Anderson 1997; Shugai and Carnie 1999) and thin electrical double layers (Keh and Anderson 1985; Keh and Chen 1988; Keh and Lien 1991; Ye et al. 2002, 2004; Yariv and Brenner 2003a, b).

In most practical applications, the ionic concentration of the buffer solution is high so that the electrical double layer thickness is of the order of nanometers (Stone and Kim 2001). Under the thin electrical double layer consideration, Keh and Anderson (1985) studied a spherical particle moving in the middle of a cylindrical pore using the reflection method; their results are accurate for the separation distance larger than half of the spherical particle radius. Yariv and Brenner (2003a, b) studied a spherical particle eccentrically moving in a cylindrical pore using the reciprocal theorem; their results are restricted to a closely fitted spherical particle in a cylindrical pore.

In practical applications, particles often move in microchannels whose sizes may be very close to the particle’s size or several times larger than the particle size. Furthermore, particles move eccentrically in a microchannel when there is a density difference between the particle and the solution. It is very important to investigate the influences of the separation distance and channel size on the particle electrophoretic motion.

This paper considers a spherical particle moving eccentrically in circular cylindrical microchannels. The objective is to investigate the influence of the separation distance on the particle motion with a constant channel size, and the influence of the channel size on the particle motion when the separation distance is the same. In the following sections, first, a theoretical model governing the electric field, flow field and particle motion is introduced; secondly, a direct numerical simulation method to solve the theoretical model is described; and finally, the numerical results are presented and discussed.

2 Methodology

2.1 Definition of the problem and assumptions

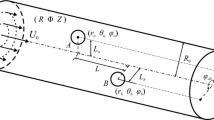
Electrophoretic motion of a spherical particle in a circular cylindrical microchannel filled with an aqueous electrolyte solution is considered. When the density of the particle is larger than that of the solution, the particle will settle down to the channel wall by the gravitational force. Eventually, the particle reaches an eccentric position with a small separation distance from the channel wall, where the gravitational force will be balanced by the buoyancy force, the electrical double layer interaction force and the van der Waals force. Thereafter, under the applied electrical field along the channel length direction, the particle moves steadily in the horizontal direction along the channel. Different densities and sizes of particles will result in different separation distance between the particle and the channel wall (the eccentric position), which can be determined by the force balance on the particle in the vertical direction (Ye and Li 2002). The main focus of this paper is to compute the steady-state eccentric electrophoretic motion of the spherical particle in microchannels in the horizontal direction under the applied electric field. The schematic diagram of the particle-channel system is shown in Fig. 1a, where the channel is positioned horizontally, with x in the horizontal direction and y in the vertical direction. The two ends (i.e., the inlet and the outlet) of the channel are connected to two reservoirs containing electrodes and the electrolyte solution. The two reservoirs are open to the atmosphere, i.e., there is no overall pressure gradient along the microchannel. Electrical potentials can be applied via the electrodes. Both the spherical particle surface and the microchannel surface carry uniform negative charges that are characterized by their respective zeta potentials: ζ_p and ζ_w. To further simplify the analysis, four assumptions have been made:

• 1. The particle and the channel wall are rigid and non-conducting.

• 2. The aqueous electrolyte solution is Newtonian and incompressible, and the flow is a Stokes flow.

• 3. The electrical double layers are thin.

• 4. The Brownian effects are negligible.

Fig. 1

The schematic diagrams of a the particle-channel system, b the outer region, and c the x–y plane sliced in the A–A direction.

2.2 Theoretical model

Under the assumption of the thin electrical double layers, we divide the liquid phase into two regions: an inner region that is defined as the electrical double layers adjacent to the particle and the channel wall and an outer region that is defined as the remainder of the liquid. For the inner region, the characteristic length scale is the Debye length, κ⁻¹. The electroosmotic flow velocity is used to describe the flow in the inner regions adjacent to the particles and the channel wall (Keh and Anderson 1985). In the outer region, as shown in Fig. 1b, Ω denotes the domain of the outer region, Γ_w denotes the outer edge of the electrical double layer adjacent to the channel wall, Γ_p denotes the outer edge of the electrical double layer adjacent to the particle, and Γ_in and Γ_out denote the inlet and the outlet of the channel respectively. The model governing the distribution of electric potential and the flow field in the outer region and the particle motion are described in the following sections.

2.2.1 Distribution of the electric potential

In the outer region, since the local net charge density is zero, the distribution of the electric potential is governed by

$$ \nabla ^2 \psi = 0{\enspace} {\text{in}}\;\Omega $$

(1)

with the following boundary conditions:

$$ {\mathbf{n}} \cdot \nabla \psi = 0{\enspace} {\text{on}}\;\Gamma _{\text{w}} \cup \Gamma _{\text{p}} $$

(2)

$$ \psi = \phi {\enspace} {\text{on}}\;\Gamma _{{\text{in}}} ,\quad \psi = 0{\enspace} {\text{on}}\;\Gamma _{{\text{out}}} $$

(3)

where ψ is the applied electric potential and n is the unit normal vector pointing into the liquid phase.

2.2.2 Flow Field

Under the assumption of thin electrical double layers, the electroosmotic flow velocities are employed to describe the flow in the inner regions adjacent to the particles and the channel wall. In the outer region, since the local net charge density is zero, no electrostatic force acts on the liquid. The steady-state liquid flow in the outer region is governed by

$$ \nabla \cdot {\mathbf{v}} = 0{\enspace} {\text{in}}\;\Omega $$

(4)

$$ \eta \nabla ^2 {\mathbf{v}} + \nabla {\text{p}} = 0{\enspace} {\text{in}}\;\Omega $$

(5)

where v is the liquid flow velocity vector, η is the viscosity of the electrolyte solution, and p is the pressure in the outer region.

Under an applied electric field, a charged particle will be driven to move by the electrostatic force, while the bulk liquid will undergo an electroosmotic flow due to the presence of the electrical double layers near the channel wall and the spherical particle. For the liquid flow, the channel wall is a fixed boundary, while the particle surface is a moving boundary. In addition to the particle’s absolute velocity, the liquid immediately next to the particle surface also experiences an electroosmotic flow (flow slip at the particle surface) due to the presence of the electrical double layer around the charged particle. Therefore, the liquid flow boundary condition at the particle surface is the sum of the particle’s velocity and the liquid electroosmotic flow velocity. Here, the electroosmotic flow velocities at the particle surface and at the channel wall surface are named as the slipping flow boundary velocities. Therefore, the slipping flow boundary conditions for flow field in the outer region are

$$ {\mathbf{v}} = \frac{{\varepsilon \varepsilon _0 \zeta _{\text{w}} }} {\eta }({\mathbf{I}} - {\mathbf{nn}}) \cdot \nabla \psi {\enspace} {\text{on}}\;\Gamma _{\text{w}} $$

(6)

$$ {\mathbf{v}} = {\mathbf{V}}_{\text{p}} + {\mathbf{\omega }}_{\text{p}} \times ({\mathbf{x}}_{\text{p}} - {\mathbf{X}}_{\text{p}} ) + \frac{{\varepsilon \varepsilon _0 \zeta _{\text{p}} }} {\eta }({\mathbf{I}} - {\mathbf{nn}}) \cdot \nabla \psi {\enspace} {\text{on}}\;\Gamma _{\text{p}} $$

(7)

where ɛ is the dielectric constant of the electrolyte solution, ɛ₀ is the permittivity of vacuum, I is the unit dyadic, ${\mathbf{V}}_{\text{p}} ,{\mathbf{\omega }}_{\text{p}} ,{\mathbf{x}}_{\text{p}} ,{\mathbf{X}}_{\text{p}}$ and ζ_p are, respectively, the translational velocity of the particle, the angular velocity of the particle, the position vector on the particle surface, the position vector of the particle center and the zeta potential of the particle. Equation 6 is the slipping flow boundary condition at the channel wall, and Eq. 7 is the flow boundary condition on the particle surface. In Eq. 7, the first term is the particle’s translational velocity, the second term represents the particle’s angular velocity, and the last term is the electroosmotic velocity of the liquid around the particle.

2.2.3 Particle motion

Generally, Newton’s second law governs the particle motion. For steady-state particle motion, the net force acting on the particle equals zero. In cases considered here, the forces responsible for the particle’s motion along the channel are the electrostatic force, F_E, and the hydrodynamic force, F_h. At steady-state, we have

$$ {\mathbf{F}}_{\text{E}} + {\mathbf{F}}_{\text{h}} = 0 $$

(8)

The hydrodynamic force can be divided into two components:

$$ {\mathbf{F}}_{\text{h}} = {\mathbf{F}}_{{\text{ho}}} + {\mathbf{F}}_{{\text{hin}}} $$

(9)

where F_hin is the hydrodynamic force acting on the particle surface by the electroosmotic flow in the inner region, and F_ho is the hydrodynamic force acting on the particle surface by the flow field originated in the outer region.

In this model, we assume that the electrical double layers are so thin that the Debye length can be neglected in comparison with the size of the particle (1–30 μm) and the size of the channel (20–100 μm). For example, in a solution with a high electrolyte concentration such as 10⁻² M, the Debye length is approximately 3 nm. Thus, we do not consider the detailed flow field in the inner region, and simply replace the flow field in the inner region by the electroosmotic velocity as a slipping flow boundary condition for the flow field in the outer region. In this way the flow field around the particle is the flow field which originated in the outer region and is subject to the slipping flow boundary condition at the particle surface. It can be shown that F_E and F_hin have the same value but operate in the opposite directions; therefore, the net force acting on the particle becomes:

$$ {\mathbf{F}}_{{\text{ho}}} = 0 $$

(10)

Similarly, the torque on the particle equals zero:

$$ {\mathbf{T}}_{\text{h}} = 0 $$

(11)

where T_h is the torque on the particle caused by the flow field in the outer region.

The hydrodynamic force and the torque are given by

$$ {\mathbf{F}}_{{\text{ho}}} = \int {\sigma \cdot {\mathbf{n}}\,{\text{d}}\Gamma _{\text{p}} } $$

(12)

$$ {\mathbf{T}}_{\text{h}} = \int {({\mathbf{x}}_{\text{p}} - {\mathbf{X}}_{\text{p}} ) \times (\sigma \cdot {\mathbf{n}})\,{\text{d}}\Gamma _{\text{p}} } $$

(13)

where σ is the stress tensor that is given by

$$ \sigma = - p{\mathbf{I}} + \eta [\nabla {\mathbf{v}} + (\nabla {\mathbf{v}})^{\text{T}} ] $$

(14)

In order to non-dimensionalize the equations, we chose l=a (a is the radius of the particle) as a characteristic length, the electric potential, $\phi = \left. \psi \right|_{\Gamma _{{\text{in}}} }$ as a characteristic electric potential, and U=(ɛ ɛ₀/η)ζ_w (φ/l) as a characteristic velocity. Letting x = lx^*, v = Uv^*, p = (ηU/l)p^* and ψ  =  ϕ ψ^*, we can derive the following dimensionless governing equations:

$$ \nabla ^{*^2 } \psi ^* = 0{\enspace} {\text{in}}\;\Omega $$

(15)

$$ \nabla ^* \cdot {\mathbf{v}}^* = 0{\enspace} {\text{in}}\;\Omega $$

(16)

$$ \nabla ^{*^2 } {\mathbf{v}}^* + \nabla ^* p^* = 0{\enspace} {\text{in}}\;\Omega $$

(17)

The dimensionless boundary conditions become

$$ {\mathbf{n}} \cdot \nabla ^* \psi ^* = 0 \enspace {\text{on}}\;\Gamma _{\text{w}} \cup \Gamma _{\text{p}} $$

(18)

$$ \psi ^* = 1.0{\enspace} {\text{on}}\;\Gamma _{{\text{in}}} ,\quad \psi ^* = 0{\enspace} {\text{on}}\;\Gamma _{{\text{out}}} $$

(19)

$$ {\mathbf{v}}^* = ({\mathbf{I}} - {\mathbf{nn}}) \cdot \nabla ^* \psi ^* {\enspace} {\text{on}}\;\Gamma _{\text{w}} $$

(20)

$$ {\mathbf{v}}^* = {\mathbf{V}}_{\text{p}}^* + {\mathbf{\omega }}_{\text{p}}^* \times ({\mathbf{x}}_{\text{p}}^* - {\mathbf{X}}_{\text{p}}^* ) + \gamma ({\mathbf{I}} - {\mathbf{nn}}) \cdot \nabla ^* \psi ^* {\enspace} {\text{on}}\;\Gamma _{\text{p}} $$

(21)

where γ is the ratio of the zeta potential of the particle to that of the channel.

Defining F_ho=ηUlF ^*_ho , T_h=ηU l² T ^*_h and σ=(ηU/l)σ^* where ${\mathbf{F}}_{{\text{ho}}}^* = \int {\sigma ^* \cdot {\mathbf{n}}\,{\text{d}}\Gamma _{\text{p}}^* } ,\;{\mathbf{T}}_{\text{h}}^* = \int {({\mathbf{x}}_{\text{p}}^* - {\mathbf{x}}_{\text{p}}^* ) \times (\sigma ^* \cdot {\mathbf{n}})\,{\text{d}}\Gamma _{\text{p}}^* }$ and σ^*=− p^* I+[∇^* v^*+(∇^* v^*)^T ], we can write the dimensionless governing equations for the particle motion as follows:

$$ {\mathbf{F}}_{{\text{ho}}}^* = 0 $$

(22)

$$ {\mathbf{T}}_{\text{h}}^* = 0 $$

(23)

The quantities with a star in the above equations are dimensionless variables.

3 Numerical method

To solve the above system of equations, a finite element based direct numerical simulation method is preferable since it evaluates the hydrodynamic interactions with no averaging or approximation. We employed a generalized Galerkin finite element method (Hu 1996; Glowinski et al. 1999), which incorporates both equations of the fluid flow and equations of the particle motion into a single variational equation where hydrodynamic interactions are eliminated and explicit calculation of the hydrodynamic interactions is not required. We use GAMBIT (a mesh generator developed by Fluent Inc.) to generate unstructured tetrahedral meshes. A program based on Taylor-Hood tetrahedral elements (Johnson 1987; Zienkiewicz and Taylor 2000) has been developed to solve the above set of dimensionless equations.

To verify our numerical simulation programs, we considered a test case: a non-conducting spherical particle carrying uniform surface charge is freely suspended in the center of a large circular cylindrical channel. An external electric field is applied along the axis of the channel. The channel wall carries no surface charge and the radius of the channel b is 30 times larger than the radius of the particle, a. Therefore, the channel wall has a negligible boundary effect on the particle motion. Furthermore, we assume that the electrical double layer surrounding the particle is very thin, i.e., κ a  →  ∞, and that the double layer is not affected by the applied electric field. The conditions of this test case match that of Henry’s solution for the electrophoresis of a spherical particle in unbounded solution. For κ a → ∞, according to Henry’s formula, the electrophoretic velocity of the particle is given by:

$$ U_{\text{h}} = \frac{{\varepsilon \varepsilon _0 }} {\mu }\zeta _{\text{p}} E_x $$

(24)

where E_x is the electric field in the x direction. Using U _h as a characteristic velocity, the calculated dimensionless velocity for the spherical particle in the large channel based on our code is V ^*_p =V_p/U_h=0.9988664. The discrepancy between our calculated result and Henry’s solution is approximately 0.113%.

Furthermore, we use our numerical simulation program to test Keh’s solution. Keh and Anderson (1985) considered the electrophoretic motion of a rigid spherical particle with radius a along the axis of a circular cylindrical pore of radius b. Considering a thin electrical double layer, they derived the following approximate solution by a method of reflections:

$$ U_{\text{k}} = \left[ {1 - 1.28987\left( {\frac{a} {b}} \right)^3 + 1.89632\left( {\frac{a} {b}} \right)^5 - 1.02780\left( {\frac{a} {b}} \right)^6 + {\rm O}\left( {\left( {\frac{a} {b}} \right)^8 } \right)} \right]\frac{{\varepsilon \varepsilon _0 }} {\mu }(\zeta _{\text{p}} - \zeta _{\text{w}} )E_z \vec e_z $$

(25)

where U _k is the velocity of the spherical particle. From the above equation, the following dimensionless particle velocity can be derived:

$$ U_{\text{k}}^* = \frac{{U_{\text{k}} }} {{U_{\text{h}} }} = \left[ {1 - 1.28987\left( {\frac{a} {b}} \right)^3 + 1.89632\left( {\frac{a} {b}} \right)^5 - 1.02780\left( {\frac{a} {b}} \right)^6 + {\rm O}\left( {\left( {\frac{a} {b}} \right)^8 } \right)} \right](1 - \gamma ) $$

(26)

We found that the discrepancy between our numerical solution results and Keh’s solution is less than 1.0% when a/b is within the range from 1/4 to 1/30.

However, numerical simulation has its own limitation, i.e., it could not carry out the computation in the case where the separation distance between the particle and the channel is too small (e.g., d<50 nm). This is because both the electric field and the flow field change dramatically in the small gap region so that very fine elements are required to compute the electric field and the flow field with reasonable accuracy. The use of very fine elements introduces at least two concerns: (1) elements which are too small will complicate numerical computation significantly and decrease computation accuracy; and (2) there exists a limit for the finest size of the elements in order to guarantee that the continuum and Stokes equations remain valid in each element. In this study, we consider the particle-channel systems with a separation distance no smaller than 50 nm.

4 Results and discussion

In the system studied here, the electric field (i.e., the gradient of the electric potential) is the driving force for both the particle motion and the flow field in the channel. Since the size of the channel is comparable to the particle size, the boundary effects on the particle motion are significant. In the numerical computation, we consider a spherical particle with a radius of a = 5.25 μm and zeta potential of ζ_p=− 30 mV, and circular cylindrical microchannels with diameters of 16, 20, 30, 50 and 100 μm and a zeta potential of ζ_w=− 50 mV.

4.1 Electric field and flow field

When a spherical particle moves along the axis of a circular cylindrical microchannel, the geometric configuration of the system is axisymmetric. However, when a particle moves eccentrically in a circular cylindrical microchannel, the geometric configuration of this system is not symmetric in the vertical direction. Since both the channel wall and particle surface provide non-conducting boundary conditions to the electric field, the influence of the geometric configuration on the electric field should be significant. Figure 2 shows the electric field near the particle on the x–y plane (see Fig. 1c), where the lines with arrows denote the direction of the electric field and the grey levels denote the relative magnitude of the electric field. The darker area represents the weaker electric field and the lighter area represents the stronger electric field. As seen in Fig. 2, the electric field surrounding the particle is not symmetric in the vertical direction and the electric field is squeezed in the small gap region between the particle and channel wall. The electric field in the small gap is very strong.

Fig. 2

The electric field surrounding a spherical particle (a=5.25 μm) in a 20 μm channel on the x–y plane with a separation distance of 0.75 μm. The lines with arrows denote the direction of the electric field and the grey levels denote the magnitude of the electric field.

Consequently, the geometric configuration and the electric field have a significant influence on the flow field. Figure 3 shows the flow field near the spherical particle on the x–y plane, where the lines with arrows denote the streamlines and the grey contours denote the magnitude of the flow velocity. The flow velocity (v′) in Fig. 3 is the calculated liquid flow velocity subtracting the calculated particle translational velocity, i.e., v′=v − V_p. The darker area represents the lower flow velocity region and the lighter area represents the higher flow velocity region. It can be seen that the flow field surrounding the spherical particle is not symmetric in the vertical direction, and that the flow velocity is very high in the small gap region between the spherical particle and the channel wall.

Fig. 3

The flow field surrounding a spherical particle (a=5.25 μm) in a 20 μm channel on the x-y plane with a separation distance of 0.75 μm. The lines with arrows denote the streamlines and the grey levels denote the magnitude of the flow velocity.

4.2 Particle motion

The influences of separation distance and channel size on particle motion are considered in the following ways: (1) changing the separation distance while the channel size is kept constant; and (2) changing the channel size at a fixed separation distance.

4.2.1 Influence of the separation distance

To capture the influence of the separation distance on the particle motion, a 20 μm (diameter) channel and a 50 μm (diameter) channel are considered. Figure 4 shows the influence of the separation distance on the particle motion in the 20 μm channel. The particle’s radius is 5.25 μm in this case. It can be seen that, with the decrease of the separation distance, both the translational velocity and the rotational velocity of the spherical particle increase. The rotational velocity increases at a much faster rate than the translational velocity. Within the smaller separation distance range, i.e., d < 1.75 μm, both the translational velocity and the rotational velocity increase dramatically with the decrease of the separation distance. At the separation distance d = 4.75 μm, the spherical particle is located in the middle of the channel, and the electric field and the flow field surrounding the spherical particle is symmetric in the vertical direction, and therefore the rotational velocity is negligible.

Fig. 4

Influence of the separation distance on the translational velocity and rotational velocity of the spherical particle (a=5.25 μm) in a 20-μm channel with ζ_p=− 30mV and ζ_w=− 50 mV.

Figure 5 shows the influence of the separation distance on the particle motion in a 50 μm channel. The particle size is the same as in Fig. 4. Compared with Fig. 4, the influence of the separation distance on the rotational velocity in the 50 μm channel shares a similar trend as that in the 20 μm channel, but the influence on the translational velocity in the 50 μm channel has a different trend from that in the 20 μm channel. In Fig. 5, at the separation distance d=19.75 μm, the sphere is located in the middle of the channel. With a decrease of the separation distance, the translational velocity decreases slowly within the relatively large separation distance range, i.e., d > 2.75 μm and then increases dramatically within the relatively small separation distance range, i.e., d < 2.75 μm. A similar trend was reported for a sphere moving parallel to a plane by Keh and Chen (1988). In addition, by comparing Fig. 5 with Fig. 4, it can be seen that the rotational velocity increases at a faster rate with a decrease of the separation distance in the 20 μm channel than that in the 50 μm channel.

Fig. 5

Influence of the separation distance on the translational velocity and rotational velocity of the spherical particle (a=5.25 μm) in a 50-μm channel with ζ_p=− 30 mV and ζ_w=− 50 mV.

The trend that the particle electrophoretic velocity increases with a decrease of the separation distance can be understood as follows. The presence of the non-conducting channel wall gives rise to two competing effects on the electrophoretic velocity: (1) the electric field surrounding the particle is “concentrated” by the wall in the gap region (see Figure 2b), which tends to enhance the particle motion; and (2) the viscous retardation to the liquid flow is enhanced by the wall, which tends to slow down the particle motion. For a particle moving in a relatively large channel with a relatively large separation distance, the second effect is stronger. For a particle moving in a relatively smaller channel or in a relatively large channel with a smaller separation distance, the first effect becomes dominant.

Figure 6 illustrates the spherical particle motion (translation plus rotation) in a 20-μm channel at a 0.75-μm separation distance in 6 s, where a small circular point on the particle is a marker used to illustrate the particle rotation. The trend of the rotational velocity of the particle increasing with the decrease of the separation distance was also reported in other papers (Yariv and Brenner 2003a, b) when the particle is close to making contact with the channel wall.

Fig. 6

The translational and rotational motion of a spherical particle (a=5.25 μm) motion in a 20-μm channel at a 0.75-μm separation distance in 6 s, where a small circular point on the spherical particle is a marker used to illustrate the rotational motion.

4.2.2 Influence of the channel size

To study the influence of channel size on particle motion, five channels with diameters of 16, 20, 30, 50 and 100 μm are considered, and a fixed separation distance is chosen as 50 nm. The particle radius is 5.25 μm. Figure 7 shows the influence of the channel size on the particle motion at a 50 nm separation distance. It can be seen that both the translational velocity and rotational velocity increase with the decrease of the channel size. Comparing the particle velocities between the 100 and 20 μm channels, it can be found that the translational velocity increases by about 12%, and that the rotational velocity increases by 87%. Therefore, the rotational velocity is much more dependent on channel size at the same separation distance.

Fig. 7

Influence of the channel size on translational and rotational velocities of the spherical particle (a=5.25 μm) motion at a 50-nm separation distance with ζ_p=− 30 mV and ζ_w=− 50 mV.

In addition, the influence of the channel size on the particle translational velocities are compared for the following two cases: a spherical particle of 5.25 μm radius which moves: (1) at a 50 nm separation distance in the channels, and (2) along the axis of the channels. As seen in Fig. 8, the two curves show different trends: the particle translational velocity increases with the decrease of channel size at a 50 nm separation distance, while the particle translational velocity along the axis of the channel decreases with the decrease of channel size. As discussed above, the two effects by the presence of a non-conducting channel wall, one enhancing the particle motion and the other slowing down the particle motion, are competing with each other when a particle moves in a microchannel. These two effects are responsible for the behaviors shown in Fig. 8.

Fig. 8

Influence of the channel size on translational velocity of the spherical particle (a=5.25 μm) motion at a 50-nm separation distance and along the axis of channels with ζ_p=− 30 mV and ζ_w=− 50 mV.

4.3 Conclusions

This paper considered the eccentric electrophoretic motion of a spherical particle in circular cylindrical microchannels. When the particle is eccentrically positioned in the channel, the electric field and the flow field are not symmetric; in fact, the strongest electric field and the highest flow velocity occur in the small gap region between the particle and the channel wall. Numerical results show that the rotational velocity of the spherical particle increases with the decrease of separation distance when the particle moves eccentrically in circular cylindrical channels. The translational velocity of the particle increases with the decrease of separation distance in a smaller channel. In a relatively large channel, the translational velocity decreases slightly with the decrease of separation distance when the separation distance is relatively large, and the translational velocity increases with the decrease of the separation distance when the separation distance is relatively small. For the eccentric particle motion, both the translational and rotational velocities increase with the decrease of channel size at smaller separation distances. This is an opposite trend to the case of a particle moving along the axis of the channels, where the translation velocity decreases as the channel size decreases.