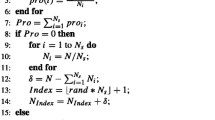A self-adaptive multi-population differential evolution algorithm

Abstract

Differential evolution (DE) is an efficient population-based search algorithm for solving numerical optimization problems. However, the performance of DE is very sensitive to the choice of mutation strategies and their associated control parameters. In this paper, we propose a self-adaptive multi-population differential evolution algorithm, called SAMDE. The population is randomly divided into three equally sized sub-populations, each with different mutation strategies. At the end of each generation, all sub-populations are updated independently and recombined. Each sub-population uses an adaptive mechanism for selecting how current generation control parameters are generated. An improved mutation strategy, “rand assemble/1”, is proposed, its base vector is composed proportionally of three randomly selected individuals. The performance of SAMDE is evaluated on the suite of CEC 2005 benchmark functions. A comparative study is carried out with other state-of-the-art optimization techniques. The results show that SAMDE has a competitive performance compared to several other efficient DE variants.

1 Introduction

Differential evolution (DE), first proposed by Storn and Price (1997), is a simple and efficient evolutionary algorithm (EA) for solving numerical optimization problems. DE is a population-based stochastic search technique, in which mutation, crossover, and selection operators are utilized at each generation to move the population toward the global optimum (Wang et al. 2011). In the last few years, DE has been extended for handling multiobjective, constrained, large scale, dynamic and uncertain optimization problems (Das and Suganthan 2011; Mukherjee et al. 2014) and is now successfully used in various scientific and engineering fields (Plagianakos et al. 2008; Ghasemi et al. 2014; Wang and Cai 2015; Zhao et al. 2014), such as chemical engineering, engineering design, and pattern recognition (Cai and Wang 2015).

When DE is applied to a given optimization problem, there are three crucial associated parameters which significantly affect the performance of DE (i.e., population size NP, scaling factor F, and crossover rate CR). Moreover, there are many trial vector generation strategies, and different strategies have different search capabilities for different problems in different stages of the evolutionary process. An inappropriate setting of these for a particular problem may lead to premature convergence and degrade algorithmic performance. Therefore, in order to apply DE successfully to solve optimization numerical problems, a trial and error search for the strategies and the associated control values is usually required.

Consequently, many enhanced DE variants such as jDE (with self-adapted parameters) (Brest et al. 2006), SaDE (with adapted mutation strategies and parameters) (Qin et al. 2009), JADE (with “current-to-pbest/1” mutation strategy and adaptive parameters) (Zhang and Sanderson 2009), CoDE (with composition of multiple strategies and parameter settings) (Wang et al. 2011), EPSDE (with ensemble of mutation strategies and parameters) (Mallipeddi et al. 2011), SspDE (with self-adapted strategies and control parameters) (Pan et al. 2011), ESADE (with “current-to-pbest/1” mutation strategy and self-adaptive parameters) (Guo et al. 2014), MPEDE (with ensemble of multiple mutation strategies and self-adaptive parameters) (Wu et al. 2016), and DMPSADE (with self-adaptive mutation strategies and parameters) (Fan and Yan 2015), have been proposed.

Although DE’s effectiveness and competitive performance has been demonstrated by many experimental studies and theoretical analysis, DE still quite depends on the settings of control parameters such as scaling factor (F), crossover rate (CR), mutation/crossover strategy and population size (NP), so many variants of DE have proposed, as mentioned above, they all used a similar idea of using different mutation strategies and self-adaptive techniques to control parameter settings (Awad et al. 2016). The proposed variants of DE are classified into 3 types: DE methods with both strategy and control parameter adaptations, DE with only control parameter (F and Cr) adaptation, and DE with population size control (Das et al. 2016). As a very competitive method, the well-known EPSDE (Mallipeddi et al. 2011) is select strategy as well as values of F and Cr from the strategy pool, which is associated with the success rate of the generated trial. EPSDE is developed by a proposed variant of EPSDE where the ensemble of F and Cr values are evolved by using the optimization process of another metaheuristic algorithm called Harmony Search (HS) (Mallipeddi 2013). However, EPSDE and it’s variants can be computationally costlier, especially on large scale problem instances (Das et al. 2016), and the success rate of the generated trial doesn’t all depends on mutation strategies.

It would be a useful attempt that DE consists of multiple populations and each sub-population is evolved using different mutation/crossover strategies and adaptive parameters (Yongjie et al. 2009), individuals may migrate among sub-populations according to certain rules.

In this paper, we propose a self-adaptive multi-population differential evolution, called SAMDE, which aims at improving the search precision and solving numerical optimization problems. The algorithm first randomly divides the population into three equally sized sub-populations. The algorithm then generates trial vectors for each sub-population using three different strategies. A modified mutation strategy uses a linear combination of randomly selected several individuals from the sub-populations. Moreover, two classical mutation strategies (“rand/1” and “best/2”) are used to other two sub-populations, respectively. In addition, parameters such as scaling factor F and crossover rate CR, associated with each mutation strategy are adapted based on iterations. At the end of each generation, each sub-population is updated by random recombination. SAMDE is tested on the suite of CEC 2005 benchmark functions with 10, 30 and 50 variables, respectively. The competitive performance of SAMDE is exhibited by extensive comparisons with several state-of-the-art DE variants.

Recently, population partitioning techniques for enhancing the performance of EAs and swarms, such as particle swarm optimization (PSO) and DE, attracted increasing attention (Wu et al. 2016). Our work is different from previous studies. In all previous works, each sub-population evolved separately for a certain number of generations and then some individuals were randomly selected migrate between sub-populations to share experiences. By contrast, each sub-population in this paper updates at the end of each generation. The application of multi-population technique in our study is aimed to maintain population diversities while enhance algorithmic performance.

The rest of this paper is structured as follows: Sect. 2 gives a brief introduction to classical DE, including its typical mutation operators, crossover, and selection operators. Section 3 reviews the related works in literature. Section 4 introduces details of the implementation of SAMDE. Experimental results and analysis are presented in Sect. 5. Section 6 concludes this paper.

2 Differential evolution

The DE firstly generates a random initial population within the scope of solution, then uses differential mutation, crossover, and selection operation to produce a new generation of population. The DE algorithm, which selects real number coding, generates random initialization population in the feasible solution space. The initial value of the jth decision variable of the ith individual at generation G = 0 is generated within the search space constrained by the prescribed minimum and maximum decision variable’s bounds X_min = {x_min¹, …, x_min^D} and X_max = {x_max¹, …, x_max^D} by:

$$x_{i,0}^{j} = x_{\hbox{min} }^{j} + rand(0,1) \cdot (x_{\hbox{max} }^{j} - x_{\hbox{min} }^{j} ),j = 1,2, \ldots ,D$$

(1)

where D is the dimensions of the problem, rand(0,1) represents a uniformly distributed random variable within the range [0,1].

Constrained numerical optimization problems (CNOPs) is defined as:

$${\text{Min}}\,f\left( {\text{X}} \right),\quad {\text{X}} \in \left[ {{\text{X}}_{\hbox{min} } ,{\text{X}}_{\hbox{max} } } \right]$$

Because of the highly competitive performance showed by DE when solving CNOPs, the researchers have been focused on providing modifications to DE variants, such as self-adaptive parameter control in constrained search spaces, etc.

2.1 Mutation operation

In DE, the variation vector is composed of the difference vector of individual in the population after scaling and other different individuals within the population. A variety of mutation strategies are obtained according to different methods of generating the variation vector. The most commonly used mutation strategies are the followings (Mallipeddi and Lee 2015):

$${\text{``DE}}/{\text{rand}}/1{\text{''}}:\quad V_{i,G} = X_{{r_{1}^{i} ,G}} + F \cdot \left( {X_{{r_{2}^{i} ,G}} - X_{{r_{3}^{i} ,G}} } \right)$$

(2)

$${\text{``DE}}/{\text{rand}}/2{\text{''}}:\quad V_{i,G} = X_{{r_{1}^{i} ,G}} + F \cdot \left( {X_{{r_{2}^{i} ,G}} - X_{{r_{3}^{i} ,G}} } \right) + F \cdot \left( {X_{{r_{4}^{i} ,G}} - X_{{r_{5}^{i} ,G}} } \right)$$

(3)

$${\text{``DE}}/{\text{best}}/1{\text{''}}:\quad V_{i,G} = X_{best,G} + F \cdot \left( {X_{{r_{1}^{i} ,G}} - X_{{r_{2}^{i} ,G}} } \right)$$

(4)

$${\text{``DE}}/{\text{best}}/2{\text{''}}:\quad V_{i,G} = X_{best,G} + F \cdot \left( {X_{{r_{1}^{i} ,G}} - X_{{r_{2}^{i} ,G}} } \right) + F \cdot \left( {X_{{r_{3}^{i} ,G}} - X_{{r_{4}^{i} ,G}} } \right)$$

(5)

$${\text{``DE}}/{\text{rand-to-best}}/1{\text{''}}:\quad V_{i,G} = X_{i,G} + K \cdot \left( {X_{best,G} - X_{i,G} } \right) + F \cdot \left( {X_{{r_{1}^{i} ,G}} - X_{{r_{2}^{i} ,G}} } \right)$$

(6)

$${\text{``DE}}/{\text{rand-to-best}}/2{\text{''}}:\quad V_{i,G} = X_{i,G} + K \cdot \left( {X_{best,G} - X_{i,G} } \right) + F \cdot \left( {X_{{r_{1}^{i} ,G}} - X_{{r_{2}^{i} ,G}} + X_{{r_{3}^{i} ,G}} - X_{{r_{4}^{i} ,G}} } \right)$$

(7)

$${\text{``DE}}/{\text{current - to - rand}}/1{\text{''}}:\quad V_{i,G} = X_{i,G} + K \cdot \left( {X_{{r_{1}^{i} ,G}} - X_{i,G} } \right) + F \cdot \left( {X_{{r_{2}^{i} ,G}} - X_{{r_{3}^{i} ,G}} } \right)$$

(8)

The parameters r₁ⁱ, r₂ⁱ, r₃ⁱ, r₄ⁱ, r₅ⁱ are randomly generated independent integers different from the index i and within the range of [1, NP]. These indexes are randomly generated in each vector. X_best,G is the best individual which has the best fitness value in the Gth generation populations. K is randomly selected in [0, 1]. F is the scale factor.

2.2 Crossover operation

Crossover operator aims to generate trial vectors. The DE algorithm generally employs two kinds of crossover methods: binomial crossover (bin) and exponential crossover (exp).

2.2.1 Binomial crossover

In binomial crossover, at least one component of trial vector is provided by the variation vector with the method of random selection. Operation equation is as follows:

$$u_{i,j,G} = \left\{ {\begin{array}{*{20}l} {v_{i,j,G} } \hfill & {rand(0,1) \le CR\quad or\quad j = j_{rand} } \hfill \\ {x_{i,j,G} } \hfill & {otherwise} \hfill \\ \end{array} } \right.$$

(9)

where j = 1,2,…,D, j_rand is a randomly chosen integer in the range [1,D], CR∈(0,1) is the crossover rate.

2.2.2 Exponential crossover

Exponential crossover operation mode is as follows:

$$u_{i,j,G} = \left\{ {\begin{array}{*{20}l} {v_{i,j,G} } \hfill & {j = < l >_{D} , < l + 1 >_{D} , \cdots , < l + L - 1 >_{D} } \hfill \\ {x_{i,j,G} } \hfill & {otherwise} \hfill \\ \end{array} } \right.$$

(10)

In the exponential crossover, an integer l∈[1,D], which acts as a starting point in the target vector, is chosen randomly from the point at which the crossover or exchange of components with the mutant vector starts. L∈[1,D] denotes the number of components that are contributed by the mutant vector to the target vector. Integer L is drawn from [1,D] depending on the crossover probability (CR). Where the angular brackets <l>_D denote a modulo function with modulus D.

2.3 Selection operation

DE uses a “greed” selection strategy to choose the best individual according to the fitness value of target vector and trial vector. The selection operation can be expressed as follows:

$$X_{i,G + 1} = \left\{ \begin{aligned} \begin{array}{*{20}l} {U_{i,G} } \hfill & {f(U_{i,G} ) < f(X_{i,G} )} \hfill \\ \end{array} \hfill \\ \begin{array}{*{20}c} {X_{i,G} } & {otherwise} \\ \end{array} \hfill \\ \end{aligned} \right.$$

(11)

where X_i,G+1 is target vector of the next generation.

3 Related works

The DE algorithm has became a powerful optimizer for solving global continuous optimization problems, which is simple, high-efficiency, easy to understand and implement, and has less controlled parameters. Meanwhile, it can proceed heuristic search in the continuous space randomly, directly and concurrently (Storn and Price 1997; Qin et al. 2009). However, the performance of the conventional DE algorithm depends on the chosen mutation/crossover strategies and the associated control parameters. In addition, the performance of DE becomes more sensitive to strategies and their associated parameter values as the complexity of the problem increases (Gämperle et al. 2002). In other words, the inappropriate selection of strategies and parameters may lead to a premature convergence, stagnation, or a waste of computational resources (Wu et al. 2016; Gämperle et al. 2002; Lampinen and Zelinka 2000; Price et al. 2005; Zaharie 2003).

In order to improve the performance of DE algorithm, in recent years, some researchers have proposed many improved measures of mutation strategy. In Zhang and Sanderson (2009), a new mutation strategy, named DE/current-to-pbest with optional archive, is proposed to serve as the basis of the adaptive DE algorithm JADE. Li et al. (2012) proposed a new mutation strategy, with the best individual as a guide but not entirely dependent on the best individual, and with a certain probability to the optimal direction of evolution. In Bi and Liu (2012), the base vector selected by the mutation strategy make a compromise between the random individual and the best individual. In Ouyang et al. (2013), a random mutation strategy was proposed. The method of random choice was adopted to implement mutation and disturbance operation, which was aimed at increasing the diversity of population and balancing the local and global search. In Kong et al. (2014), a multi-strategy mutation operator based on symbolic function was designed. In Kong et al. (2014), the global acceleration operator was proposed, which can balance the global search and local search. In Bi et al. (2012), the best global solution and the best previous solution of each individual are utilized in the new mutation strategy to guide the search direction by introducing more effective directional information. This method avoids the search blindness brought by the random selection of individuals in the difference vector. In Qiu et al. (2015), the mutation strategy of DE is proposed and divided into two parts to reflect the changes of the target population trends and their random variations. It consists of an additional mutation factor which is simulated by a different Hurst index fractal Brownian motion. In Ali et al. (2015), a modified mutation strategy was proposed, which called mms, uses a convex linear combination of randomly selected individuals from the population. This novel mutation strategy was used to produce quality solutions to balance exploration and exploitation. In Mukherjee et al. (2016), the mutation phase has been entrusted to a locality-induced operation that retains traits of Euclidean distance-based closest individuals around a potential solution. A locality based DE mutation scheme called ‘DE/current-to-p-local_best/1’ has been devised.

Extensive studies have been done on appropriate setting of the control parameters of DE, such as scaling factor F and crossover rate CR. Initially, Storn and Price (1997) said that F = 0.5 would be a good initial choice, and its adjustable range is from 0.4 to 1. On this basis, Liu and Lampinen (2010) mentioned that F = 0.9 would be a good initial choice, and F∈(0.4,0.95). Ronkkonen et al. (Ronkkonen et al. 2005) set CR∈(0,0.2) in the separable functions. But if parameters are dependent on each other, CR∈(0.9,1). Zielinski et al. (2006) pointed out that F ≥ 0.6 and CR ≥ 0.6 can make the algorithm get better performance. From the above, it can be observed that parameters maintain a fixed value in the process of evolution, which lack sufficient theoretical justification. Therefore, the researchers began to consider the automatic adjustment of DE parameters. Brest et al. (2006) proposed a self-adaptation scheme (jDE), in which control parameters F and CR were encoded into the individuals and are adjusted in the run of DE. Qin et al. (2009) considered allowing F to take different random values in the range (0, 2] with normal distribution of mean 0.5 and standard deviation 0.3 for different individuals in the current population, and accumulating the previous learning experience within a certain generation interval so as to dynamically adapt the value of CR to a suitable range. In Zhang and Sanderson (2009), the parameter adaptation automatically updates the control parameters to appropriate values. In Zou et al. (2013), MDE adjusts scale factor F and crossover rate CR by using Gauss distribution and uniform distribution, respectively.

From the analysis of population structure of DE, the initial population is divided into multiple sub-populations that according to the topology relationship and migrate by the corresponding individual migration mechanism. This form of DE is called distributed DE. In recent years, the distributed DE algorithm has became an important branch of DE. Therefore, the researchers began to pay close attention to the distributed DE. Some researches on the present mainly partition the initial population or swarm into multiple equal smaller sub-populations. As the algorithm proceeds, information exchange among sub-populations and regrouping operators will be triggered with a certain frequency with the aim to maintain the diversity of the whole population and balance the exploitation and exploration capabilities (Wu et al. 2016). Weber et al. (2011) proposed shuffle or update parallel differential evolution (SOUPDE), which is a structured population algorithm characterized by sub-populations employing a differential evolution logic. Two simple mechanisms have been integrated. The first, namely shuffling, consists of randomly rearranging the individuals over the sub-populations. The second consists of updating all the scale factors of the sub-populations. In Ali et al. (2015), the population is divided into four independent sub-groups, each with different mutation and update strategies. The size of each group is fixed and computed by dividing the population size by number of predefined groups. Each sub-group is filled randomly by picking random individuals from the entire population. In Wu et al. (2016), there are three equally sized smaller indicator sub-populations and one much larger reward sub-population. Each constituent mutation strategy has one indicator sub-population. After every certain number of generations, the current best performing mutation strategy will be determined according to the ratios between fitness improvements and consumed function evaluations. Then the reward sub-population will be allocated to the determined best performing mutation strategy dynamically. Shang et al. (2014) proposed a multi-population based cooperative coevolutionary algorithm (MPCCA) to solve the multi-objective capacitated arc routing problem. In MPCCA, population is partitioned into multiple sub-populations with respect to their different direction vectors. These sub-populations evolve separately and search different objective sub-regions simultaneously. The adjacent sub-populations are able to share their information. The differences between our research and other related studies are explained in Sect. 1.

4 Self-adaptive multi-population DE (SAMDE)

The sub-populations quickly exploit some areas of the decision space, thus drastically and quickly reducing the fitness value in the highly multi-variate fitness landscape (Weber et al. 2011). Moreover, the suitable mutation strategies choosing and the reasonable control parameter setting are important to enhance the search ability of DE algorithm. Therefore, in this study, the population is divided into three equally sized sub-populations, each with different mutation strategies. At the end of each generation, all sub-populations are updated by random recombination. Meanwhile, the SAMDE algorithm is proposed to implement the self-adaptive control parameters to ensure the search ability of algorithm.

4.1 Multiple populations

The mechanism of multi-population ensures that each sub-population is not affected by the interference of other sub-populations in the process of evolution. In this work, the formation process of the sub-populations is first initializes the entire population and then calculates fitness value of all individuals, at last, the population is randomly divided into three same size subgroups, called X1, X2, X3. Three sub-populations use different mutation strategies and evolve respectively and concurrently within each sub-population. At the end of each iteration, all individuals are randomly reordered. It is worth mentioning that each sub-population is updated at each generation, which actually share optimization experience with each other and realize the information exchange among sub-populations.

4.2 Parameter adaptation

The choice of numerical values for control parameters F, CR significantly affect the performance of the DE algorithm. Instead of fixing the values of these parameters, the current trend is to use self-adaptive parameter setting mechanisms. In this study, three sub-populations use three sets of scale factor Fk and crossover probabilities CRk, k = 1, 2, 3. In SAMDE, a parameter adaptive approach is proposed that control parameters of each generation can be gradually self-adapted according to the number of iterations. This adaptive scheme can keep both local and global search ability to generate the potential good mutant vector throughout the evolution process.

At each generation t, mutation factor Fk_i^t of each individual xi is independently generated according to a normal distribution of mean μFk^t and standard deviation 0.1 and is bounded in the interval (0, 1) as:

$$Fk_{i}^{t} = randn_{i} (\mu Fk^{t} ,0.1)$$

(12)

In generation t, the location parameter μFk^t of the normal distribution is updated at the end of each generation as:

$$\mu Fk^{t} = o\mu Fk - 0.1 \times e^{{\left( { - \frac{t}{Gm}} \right)}}$$

(13)

Similarly, at each generation t, the crossover probability CRk_i^t of each individual xi is independently generated according to a normal distribution of mean μCRk^t and standard deviation 0.1 and is bounded in the interval (0, 1) as:

$$CRk_{i}^{t} = randn_{i} (\mu CRk^{t} ,0.1)$$

(14)

In generation t, the location parameter μCRk^t of the normal distribution is updated at the end of each generation as:

$$\mu CRk^{t} = o\mu CRk - 0.1 \times e^{{\left( { - \frac{t}{Gm}} \right)}}$$

(15)

where Gm is maximum number of iterations. oμFk is the initial value of μFk, and oμCRk is the initial value of μCRk. Equations (13) and (15) will complete coarse search at beginning of iterations and fine search at ending of iterations.

4.3 Choice of mutation strategies for populations in SAMDE

The choices of different mutation strategies affect the efficiency of DE and accuracy of solution. Therefore, the reasonable selection of mutation strategies is especially important. Several mutation strategies from the DE literature were presented in Sect. 2.1. Two of these strategies are directly used in some sub-populations in SAMDE while one is a modified mutation strategy.

Two standard mutation strategies are used in X1 and X3, that are “rand/1” and “best/2”. “DE/rand/1/bin” is one of the most commonly used strategies in the DE research. It can effectively maintain the diversity of population. For this reason, “DE/rand/1/bin” mutation strategy is used in X1. In contrast, the “DE/best/2/bin” mutation strategy have a faster convergence rate and better searching ability. It can availably ensure optimization ability of the sub-population. Thus, we use “DE/best/2/bin” mutation strategy in X3.

In Ali et al. (2015), a new mutation strategy is proposed. Based on this mutation strategy, we propose a new mutation strategy, call it as “rand assemble/1”, use in X2. In “rand assemble/1”, the choice of the base vector is different from standard DE. It uses a linear combination of randomly selected three individuals from the population, which will carry more paternal genes and pass to their offspring. This modified mutation strategy will produce well distributed solutions with higher convergence rate and increase the diversity of population due to the generational interchange of sub-populations using different mutation strategies.

Mutation strategy 1: “rand/1”

$$V_{i,t} = X_{{r_{1}^{i} ,t}} + F \cdot (X_{{r_{2}^{i} ,t}} - X_{{r_{3}^{i} ,t}} )$$

(16)

Mutation strategy 2: “rand assemble/1”

$$V_{i,t} = (aX_{{r_{1}^{i} ,t}} + bX_{{r_{2}^{i} ,t}} + cX_{{r_{3}^{i} ,t}} ) + F \cdot (X_{{r_{4}^{i} ,t}} - X_{{r_{5}^{i} ,t}} )$$

(17)

Mutation strategy 3: “best/2”

$$V_{i,t} = X_{best,t} + F \cdot (X_{{r_{1}^{i} ,t}} - X_{{r_{2}^{i} ,t}} ) + F \cdot (X_{{r_{3}^{i} ,t}} - X_{{r_{4}^{i} ,t}} )$$

(18)

where r₁, r₂, r₃, r₄, r₅ are all random integers within the interval [1, NP], a, b and c are random numbers selected from the interval (0, 1). Where a + b + c = 1.

According to three mutation strategies and parameter adaptation introduced above, we come to the framework of SAMDE as given in Algorithm 1.

Algorithm 1: Pseudo code of SAMDE

5 Experimental study

5.1 Experimental settings

The proposed SAMDE algorithm was implemented and tested on a set of 25 benchmark functions which proposed in CEC 2005 (Suganthan et al. 2005). The test suite consists of 25 benchmark functions which includes unimodal functions F1–F5, basic multimodal functions F6–F12, expanded multimodal functions F13–F14, and hybrid composition functions F15–F25. The maximum number of function evaluation was set to 2000×D. The population size for this algorithm was set as NP = 60. The initial value of location parameters were set as oμF1 = 1, oμF2 = 0.75, oμF3 = 0.5, oμCR1 = 1.1, oμCR2 = 1 and oμCR3 = 0.9. The crossover operator was set as binomial crossover. Both F and CR are taken in the range (0, 1).

The SAMDE and other DE variants were coded in Matlab environment. The computations were carried out using a PC with Intel(R) Core(TM) i3 - 2350 M @ 2.3 GHz CPU and 2 GB RAM while running Matlab R2012a on 64-bit windows operating system.

5.2 Comparison with state-of-the-art evolutionary algorithms

This section mainly presents 25 real-valued benchmark functions which are used to evaluate the proposed SAMDE algorithm against other DE variants. The computational results obtained by running each of the eight comparative DE variants 25 times on each benchmark function with 10, 30 and 50 variables are reported in Tables 1, 2 and 3, respectively. These tables show statistical results of the mean error and standard deviation values obtained for all these functions. The symbols of “–”, “+”, and “=” in last three rows of each table respectively denote that the performance of the corresponding algorithm is worse than, better than and similar to that of SAMDE. α is level of significance, which is used to determine at which level the null hypothesis H₀ may be rejected, and wins = worse (−)+⌊similar(=)/2⌋.

Table 1 Comparison of the average error for 25 independent runs by different optimization techniques with D = 10 on functions F₁–F₂₅

Table 2 Comparison of the average error for 25 independent runs by different optimization techniques with D = 30 on functions F₁–F₂₅

Table 3 Comparison of the average error for 25 independent runs by different optimization techniques with D = 50 on functions F₁–F₂₅

SAMDE was compared with eight other state-of-the-art DE variants including JADE (Zhang and Sanderson 2009), SaDE (Qin et al. 2009), EPSDE (Mallipeddi et al. 2011), CoDE (Wang et al. 2011), SOUPDE (Weber et al. 2011), SspDE (Pan et al. 2011), ESADE (Guo et al. 2014) and MPEDE (Wu et al. 2016). The reasons we choose these eight DE variants as comparative algorithms are explained as follows. First, JADE, SspDE and ESADE are three DE variants which parameters are set in an adaptive manner. Second, SaDE, EPSDE and CoDE also incorporate multiple mutation strategies as SAMDE. Third, SOUPDE and MPEDE are two DE variants which use evolution of multiple populations as SAMDE, and MPEDE is a recently proposed DE variant that can reflect the latest progress of DE. Hence, it is meaningful to compare SAMDE with them. The settings of each algorithm are as follows:

• 1. JADE with NP = 100.

• 2. SADE with NP = 50, LP=30.

• 3. EPSDE with NP = 50.

• 4. CoDE with NP = 30.

• 5. SOUPDE with NP = 60, ps = 0.5, pu = 0.5, CR = 0.9.

• 6. SspDE with NP = 100, BR = 0.8.

• 7. ESADE with NP = 50, t0 = 1000.

• 8. MPEDE with NP = 250, ng = 20, λ₁ = λ₂ = λ₃ = 0.2.

Let us detail the eight algorithms according to the time order that they were published. All these algorithms have been summarized in Sect. 1.

As indicated in Table 1, SAMDE shows a statistically significant performance when compared with all the contestant algorithms in most of the functions. It is found that SAMDE has the best performance among the other eight classical state-of-the-art DE variants on the 13 test functions with 10D. Regarding the unimodal functions F1–F5, JADE, EPSDE, ESADE and SAMDE show the better performance. SAMDE obtains significantly best results on the 4 test functions (F1, F2, F4 and F5) than all other peers. Only in function F3, JADE performs better than SAMDE. Whereas, compared with the other seven DE variants, SaDE, EPSDE, CoDE, SOUPDE, SspDE, ESADE and MPEDE, SAMDE exhibits better overall performance. For basic multimodal benchmark functions F6–F12, SaDE, EPSDE, CoDE and SAMDE show the better performance. SAMDE has significantly best results on the 3 test functions (F6, F8 and F12) than all the other DE variants. Moreover, SAMDE is better than JADE, SspDE and MPEDE on all simple multimodal functions. SAMDE outperforms SaDE, EPSDE, CoDE, SOUPDE and ESADE on three (F6, F7 and F12), three (F6, F7 and F12), four (F6, F7, F10 and F12), five (F6–F8, F10 and F12) and five (F6, F8–F10 and F12) benchmark functions, respectively. As for expanded multimodal functions, SAMDE generally performs worse than other DE variants (except MPEDE) on function F13 while it outperforms all the other DE variants on function F14. With regard to the more complex hybrid composition functions F15–F25, CoDE, SOUPDE, SspDE and SAMDE show the better performance. SAMDE performs significantly best results on the 5 test functions (F16, F17, F19, F21 and F25) than all other peer DE variants. It outperforms SaDE, EPSDE, CoDE, SOUPDE, SspDE and MPEDE on nine (F16–F19 and F21–F25), nine (F16, F17, F19 and F21–F25), five (F16, F17, F19, F21 and F25), seven (F15–F17, F19, F21, F22 and F25), six (F15–F17, F19, F21 and F25) and ten (F15–F23 and F25) benchmark functions, respectively. Moreover, SAMDE is better than JADE and ESADE on all hybrid composition functions. The performance of MPEDE is better than that of SAMDE only on function F24. However, SAMDE obtains worse performance on functions F18, F20 and F24. And CoDE is superior to SAMDE on functions F15, F18, F20, F22 and F23.

In summary, SAMDE has the best overall performance compared with other eight competitors, namely JADE, SaDE, EPSDE, CoDE, SOUPDE, SspDE, ESADE and MPEDE on all the 25 benchmark functions with 10 variables. Actually, the results of Wilcoxon’s rank sum tests reported in the last three rows indicate that SAMDE is significantly better than JADE, SaDE, EPSDE, CoDE, SOUPDE, SspDE, ESADE and MPEDE on 22, 18, 17, 15, 17, 19, 22 and 24 functions, respectively. It is significantly worse than JADE, SaDE, EPSDE, CoDE, SOUPDE, SspDE, ESADE and MPEDE on 3, 4, 6, 9, 7, 6, 3 and 1 functions and similar to them on 0, 3, 2, 1, 1, 0, 0 and 0 functions, respectively. As the Table 1 states, SAMDE shows a significant improvement over JADE, SaDE, EPSDE, SspDE, ESADE and MPEDE, with a level of significance α = 0.05, and over SOUPDE, with α = 0.1.

Applying the Multiple Sign test, suppose level of significance α = 0.1, the critical value of R_j is 6 for m = 8(m = k − 1) and n = 25 (Derrac et al. 2011), and losses = better(−)+⌈similar(=)/2⌉, since the number of minuses in the pairwise comparison between the control algorithm SAMDE and JADE, SaDE, SspDE, ESADE, MPEDE is equal to 3, 6, 6, 3, 1 in Table 1, respectively, we may conclude that SAMDE has a significantly better performance than them.

As indicated in Table 2, it is found that SAMDE has the best performance among the other eight classical state-of-the-art DE variants on the 9 test functions with 30D. SAMDE shows a statistically significant performance when compared with all the contestant algorithms in most of the functions.

Regarding the unimodal functions F1–F5, JADE and SAMDE show the better performance. SAMDE obtains significantly best results on function F5 than all other peers. JADE performs better than SAMDE on three functions (F2–F4). EPSDE, CoDE and SOUPDE do not show better performance than SAMDE on any unimodal functions.

For basic multimodal benchmark functions F6–F12, SaDE, EPSDE and SspDE show the better performance. SAMDE has significantly best results on the 2 test functions (F8 and F12) than all the other DE variants. Moreover, SAMDE outperforms JADE, SaDE, EPSDE, CoDE, SOUPDE, SspDE, ESADE and MPEDE on five (F6, F8 and F10–F12), four (F6, F7, F9 and F12), three (F9, F10 and F12), five (F6, F7, F9, F10 and F12), four (F6, F7, F10 and F12), five (F6, F7, F9, F10 and F12), six (F6–F9, F11 and F12) and five (F6–F9 and F12) benchmark functions, respectively. As for expanded multimodal functions, SAMDE is inferior to JADE, SaDE, EPSDE, CoDE, SOUPDE, SspDE, ESADE and MPEDE on function F13. In contrast, it outperforms all the other DE variants on function F14.

With regard to the more complex hybrid composition functions F15–F25, ESADE, MPEDE and SAMDE show the better performance. SAMDE performs significantly best results on the 5 test functions (F15, F18, F19, F24 and F25) than all other peer DE variants. It outperforms JADE, SaDE, EPSDE, CoDE, SOUPDE, SspDE, ESADE and MPEDE on nine (F15–F20, F22, F23 and F25), nine (F15–F20, F22, F23 and F25), nine (F15–F20, F22, F23 and F25), seven (F15, F17–F20, F22 and F25), eight (F15–F20, F22 and F25), nine (F15, F17–F23 and F25), six (F15, F17, F19, F21, F24 and F25) and six (F15, F18–F20, F23 and F25) benchmark functions, respectively. However, SAMDE obtains worse performance on functions F16 and F21. And CoDE, SOUPDE, ESADE and MPEDE are superior to SAMDE on three functions (F16, F21 and F23), two functions (F21 and F23), four functions (F16, F20, F22 and F23) and four functions (F16, F17, F21 and F22), respectively.

In summary, SAMDE has the best overall performance compared with other eight competitors, namely JADE, SaDE, EPSDE, CoDE, SOUPDE, SspDE, ESADE and MPEDE on benchmark functions with 30 variables. Actually, the results of Wilcoxon’s rank sum tests reported in the last three rows indicate that SAMDE is significantly better than JADE, SaDE, EPSDE, CoDE, SOUPDE, SspDE, ESADE and MPEDE on 17, 17, 18, 17, 17, 19, 18 and 16 functions, respectively. It is significantly worse than JADE, SaDE, EPSDE, CoDE, SOUPDE, SspDE, ESADE and MPEDE on 7, 5, 5, 5, 5, 4, 6 and 8 functions and similar to them on 1, 3, 2, 3, 3, 2, 1 and 1 functions, respectively. As the Table 2 states, SAMDE shows a significant improvement over SaDE, EPSDE, CoDE, SOUPDE, SspDE and ESADE, with a level of significance α = 0.05, and over JADE, with α = 0.1.

Applying the Multiple Sign test, as mentioned above, since the number of minuses in the pairwise comparison between the control algorithm SAMDE and EPSDE, SspDE is equal to 6, 5 in Table 2, respectively, we may conclude that SAMDE has a significantly better performance than them.

As indicated in Table 3, it is found that SAMDE has the best performance among the other eight classical state-of-the-art DE variants on the 4 test functions with 50D.

Regarding the unimodal functions F1–F5, JADE and MPEDE show the better performance. JADE performs better than SAMDE on three functions (F1–F3). CoDE, SOUPDE and SspDE do not show better performance than SAMDE on any unimodal functions. SAMDE performs better than SaDE, EPSDE, ESADE and MPEDE on four functions (F2–F5), four functions (F2–F5), four functions (F1, F2, F4 and F5), one functions (F1), respectively.

For basic multimodal benchmark functions F6–F12, EPSDE and ESADE show the better performance. SAMDE outperforms JADE, SaDE, EPSDE, CoDE, SOUPDE, SspDE, ESADE and MPEDE on four (F8–F11), three (F7, F9 and F12), two (F9 and F10), five (F6, F7, F9, F10 and F12), four (F6, F7, F10 and F12), five (F7–F10 and F12), three (F7, F8 and F12) and four (F7–F9 and F12) benchmark functions, respectively. As for expanded multimodal functions, SAMDE is superior to JADE, SaDE, EPSDE, CoDE, SspDE and MPEDE on function F13. meanwhile, it outperforms all the other DE variants on function F14.

With regard to the more complex hybrid composition functions F15–F25, CoDE, ESADE and MPEDE show the better performance. SAMDE outperforms JADE, SaDE, EPSDE, CoDE, SOUPDE, SspDE, ESADE and MPEDE on ten (F15–F19 and F21–F25), seven (F15, F16, F18–F20, F22 and F25), seven (F15–F19, F22 and F25), three (F15, F16 and F22), eight (F15–F20, F22 and F25), four (F15, F16, F22 and F25), three (F15, F21 and F25) and five (F15, F19, F21 and F25) benchmark functions, respectively. SAMDE outperforms all the other DE variants on function F14. However, SAMDE obtains worse performance on functions F20, F21 and F23. And CoDE, SspDE and ESADE are superior to SAMDE on seven functions (F17–F21, F23 and F25), six functions (F17–F21 and F23) and seven functions (F16–F20, F22 and F23), respectively.

In summary, the results of Wilcoxon’s rank sum tests reported in the last three rows indicate that SAMDE is significantly better than JADE, SaDE, EPSDE, CoDE, SOUPDE, SspDE, ESADE and MPEDE on 18, 16, 15, 15, 18, 16, 11 and 11 functions, respectively. It is significantly worse than JADE, SaDE, EPSDE, CoDE, SOUPDE, SspDE, ESADE and MPEDE on 7, 7, 8, 8, 5, 8, 13 and 13 functions and similar to them on 0, 2, 2, 2, 2, 1, 1 and 1 functions, respectively. As the Table 3 states, SAMDE shows a significant improvement over other 8 algorithms, with a level of significance α = 0.05.

Applying the Multiple Sign test, as mentioned above, since the number of minuses in the pairwise comparison between the control algorithm SAMDE and JADE, SaDE, EPSDE, CoDE, SOUPDE, SspDE is equal to 4, 6, 6, 6, 5, 5 in Table 3, respectively, we may conclude that SAMDE has a significantly better performance than them.

SAMDE outperforms all the other DE variants on functions F8 and F14 for both 10, 30 and 50 variables. SAMDE obtains best performance on functions F8, F14, F15 and F24 for both 30 and 50 variables that compares with all other peer algorithms. SAMDE outperforms all other peer algorithms on functions F5, F8, F12, F14, F19 and F25 for both 10 and 30 variables.

5.3 Sensitivity analysis

5.3.1 Sensitiveness to the NP values

In this subsection, an experiment is conducted to investigate the sensitivity of the SAMDE algorithm to variations in population size. The population size of all the DE algorithms is set as NP = 30, 60, 90, 120, 150, 180 and 300, respectively. We use those algorithms to solve the 30-dimensional functions and the maximum number of function evaluations was fixed at 2000×D. Table 4 shows the results of this sensitivity tests. Results highlighted in boldface show the best results from the best setting for each parameter. We performed 25 independent runs for every parameters.

Table 4 Sensitivity analysis with respect to population size (NP)

In Table 4, it can be observed that SAMDE is sensitive to parameter NP on many of the benchmark functions. For the unimodal functions F1–F5, SAMDE shows better performance with population size decrease in solving problems F1–F4. However, SAMDE is not sensitive to parameter NP in solving problem F5. With regard to the basic multimodal benchmark functions F6–F12, the better performance of SAMDE concentrate in NP = 60. As for expanded multimodal functions, SAMDE shows better performance with population size decrease. For the hybrid composition functions F15–F25, SAMDE shows better performance with NP=30 in solving problems F16 and F17. And SAMDE is not sensitive to parameter NP in solving problem F18–F25. When NP was equal to 60, the algorithm gave the best results on most of selected benchmarks. So we choose the value of the population size as 60.

5.3.2 Sensitiveness to the F and CR values

In the traditional DE algorithm, the control parameter F and CR will be tuned by a time-consuming trial-and-error procedure for different optimization problems (Zhao et al. 2016). In SAMDE, F is adaptively adjusted by the adaptive parameter μF. μF according to the number of iteration as the search process continues. And three sub-populations have different values of μF. Each μF is decided by the corresponding initial value oμF. In order to study their effects on the performance of SAMDE, some experimental studies are conducted in Fig. 1.

Fig. 1

The influence of oμF on evolution of four representative functions. a1–a3 are the effect of oμF1, oμF2 and oμF3 take different values on function F1, respectively; b1–b3 are related to function F7; c1–c3 are related to function F13; d1–d3 are related to function F20

We choose four benchmark functions as representative ones. They are functions F1, F7, F13 and F20 which respectively as unimodal function, basic multimodal function, expanded multimodal function and hybrid composition function. The horizontal axis is the numbers of iteration, and the vertical axis is the average error values of fitness. From Fig. 1, it can be observed that the effects of the different value of oμF for the evolution results were significant when solving some optimization problem, such as functions F1 and F7. In addition, mutation strategy “best/2” is relatively sensitive to F value with other two mutation strategies. In contrast, the effects of the different value of oμF for the evolution results were not sensitive when solving some optimization problem, such as functions F13 and F20. We can find that the best oμF values for one sub-population are different when solving different optimization problems. For instance, in sub-population X2 (Fig. 1 a2, b2, c2, d2), the best oμF2 values are 0.7 for solving function F1, 1 for solving function F7, 0.5 for solving function F13 and 0.6 for solving function F20. And the best oμF values for different sub-populations are different when solving one optimization problem. For example, when solving function F1 (Fig. 1 a1, a2, a3), the best oμF1 is 0.9, the best oμF2 is 0.7, the best oμF3 is 0.5.

In SAMDE, CR is adaptively adjusted by the adaptive parameter μCR. μCR according to iteration number as the search process continues. And three sub-populations have different values of μCR. Each μCR is decided by the corresponding initial value oμCR. In order to study their effects on the performance of SAMDE, some experimental studies are conducted in Fig. 2.

Fig. 2

The influence of oμCR on evolution of four representative functions. a1–a3 are the effect of oμCR1, oμCR2 and oμCR3 take different values on function F1, respectively; b1–b3 are related to function F7; c1–c3 are related to function F13; d1–d3 are related to function F20

We plot the average values of fitness changes for different oμCR in each sub-population. We select four benchmark functions which same as the setting of experimental studies for oμF. For F1 and F7, the effects of the different value of oμCR for the evolution results were significant. In particular, this phenomenon is more obvious in sub-population X3. In contrast, the average fitness values is not sensitive to parameter oμF in solving problems F13 and F20. From Fig. 2, it can be observed that two point, one is the best oμCR values for one sub-population are different when solving different optimization problems. The other is the best oμCR values for different sub-populations are different when solving one optimization problem.

In summary, the select of appropriate parameters are more important. According to these experimental studies, we choose proper oμCR and oμF to solve 25 numerical optimization problems.

5.3.3 Comparisons between SAMDE and its variants

In this experiment, comparisons between twelve variants of SAMDE and their corresponding SAMDE algorithms are made. They are divided into three groups. The first group is comparison between SAMDE and its variants derived by different setting of update for sub-populations. The second group is comparison between SAMDE and its variants derived by different setting of mutation strategies. The third group is comparison between SAMDE and its variants derived by different setting of evolution methods.

The results for the functions at 30D are shown in Tables 5, 6 and 7. The better values in terms of mean solution error compared between SAMDE and its variants algorithm are highlighted in boldface in Tables 5, 6 and 7.

Table 5 Comparison results between SAMDE and its variants derived by different setting of updation for sub-populations

Table 6 Comparison results between SAMDE and its variants derived by different setting of mutation strategies

Table 7 Comparison results between SAMDE and its variants

SAMDE_T1 indicates that three sub-populations are updated every 10 generations. SAMDE_T2 indicates that three sub-populations are updated every 20 generations. SAMDE_T3 indicates that three sub-populations are updated every 50 generations. SAMDE_T4 indicates that three sub-populations are updated every 100 generations.

From Table 5, we can find that SAMDE significantly outperforms the corresponding variants with respect to the overall performance. Specifically, according to the Wilcoxon’s test, SAMDE significantly improves the performance of SAMDE_T2 on 21 out of 25 functions and losses on only two functions. SAMDE is significantly better than SAMDE_T1, SAMDE_T3 and SAMDE_T4 on 14, 16 and 15 functions, respectively.

SAMDE consists of three different mutation strategies. To show the significant differences between SAMDE and its variants derived by different setting of mutation strategies, the results are shown in Table 6. SAMDE_M1 SAMDE_M2, SAMDE_M3 are SAMDE with “rand/1”, “rand assemble/1” and “best/2”, respectively. They can be thought as special SAMDE variants with a single mutation strategy. SAMDE_MR denotes an SAMDE variant in which three mutation strategies are randomly selected. In this test, we keep all the other parameters fixed at values discussed in earlier subsections.

It can be noted from the Table 6 that the SAMDE outperforms its other variants. For SAMDE_M1, SAMDE is significantly better on 19 functions and worse on only three functions. SAMDE is significantly better than SAMDE_M2 and SAMDE_M3 on 13 and 13 functions and worse than SAMDE_M2 and SAMDE_M3 on 7 and 8 functions, respectively. SAMDE significantly improves the performance of SAMDE_MR on 17 out of 25 functions and losses on five functions. These results clearly show the advantage of SAMDE caused by incorporating three mutation strategies, and by individuals’ migrating among sub-populations based on the fitness value rank. It seems that different mutation strategies and self-adaptive parameter settings were used in different sub-populations, but some individuals were migrated at every iteration among sub-populations to share different mutation strategies and adaptive parameter settings. It is worth noting that SAMDE-M2 shows competitive performance on two unimodal functions F3 and F4 and three hybrid composition functions F15–F17. SAMDE-M3 shows competitive performance on one unimodal function F1, two multimodal functions F6 and F9 and one hybrid composition function F22. SAMDE_MR obtains much better results for F5 and F12 than the other variants.

In this subsection, we compare four different schemes of the proposed SAMDE algorithm. All the algorithms in this section use the same population size and base on the same stopping rule. We tests how adding or changing one component at a time influences the performance.

The first version is the population composed of three sub-populations that based on the fitness value, no use of randomly assigned to individuals. At the end of each generation, all sub-populations are updated based on the new fitness values of its individuals. This version uses the same parameter adaptive strategy as SAMDE. This version is called SAMDE_1. The second scheme (SAMDE_2) of this work is first initializes the entire population and then subdivides the population into three sub-populations that based on the fitness value rank, the first sub-population is called X1 which have better individuals. Then we take X1 as an outstanding sub-population and it no longer involved in later evolution. The other two sub-populations are updated in the same way as SAMDE. The third variant of this work (SAMDE_3) is same as SAMDE_1 in the first 100 generations, after 100 iterations, we take X1 as an outstanding sub-population. At the end of each generation, all sub-populations are updated based on the new fitness values of its individuals. But sub-population X1 is only updated without evolution. The fourth scheme (SAMDE_4) is same as SAMDE in the first 100 generations, after 100 iterations, there are first better nine individuals were extracted and constitute X4. The other individuals are randomly divided into three sub-populations which have the same size. And sub-population X4 is only updated without evolution.

From Table 7, the solution quality of the proposed algorithm SAMDE outperforms all other variants of the proposed work at 30D. For SAMDE_1, SAMDE is significantly better on 17 functions and worse on only four functions. SAMDE is significantly better than SAMDE_2 on 15 functions and worse than SAMDE_2 on 5 functions. SAMDE significantly improves the performance of SAMDE_3 on 16 out of 25 functions and losses on four functions. For SAMDE_4, SAMDE is significantly better on 15 functions out of 25 functions and losses on five functions.

6 Conclusions

This research proposes a self-adaptive multi-population differential evolution algorithm for solving numerical optimization problem. The algorithm divides the population into three sub-populations, each of which employs a certain mutation strategy. These mutation strategies are DE/rand/1/bin, DE/best/2/bin and a our customized mutation strategy that uses a new approach to generate base vector. Because the appropriate control parameters are very important to the performance of DE in the DE algorithm, an adaptive mechanism is also proposed that control parameters Fk_i(t) and CRk_i(t) of each generation can be gradually self-adapted according to the number of iterations. In this paper, the experimental studies on CEC 2005 benchmark suite proved the good performance of SAMDE, SAMDE was compared with other eight state-of-the-art DE variants including JADE, SaDE, EPSDE, CoDE, SOUPDE, SspDE, ESADE and MPEDE. The experimental results show that the overall performance of SAMDE was better than the eight competitors. The parameter sensitivity of SAMDE is also analysed by some experimental studies. We experimentally show that the multiple mutation strategies and adaptive parameters mechanism in this study have obvious advantages and competitiveness compared with other algorithms.

In the future, we intend to further improve the SAMDE to solve high dimensional optimization problems. In addition, multi-populations is still an effective way to improve DE efficiency, we will try to use more, different size sub-populations for parallel computing, and test them on sets of competitive benchmarks like those presented in the CEC 2013 (Li et al. 2013) and CEC 2015 (Chen et al. 2014; García-Martínez et al. 2017) special sessions and competitions.