1 Introduction

Usually, the kinematic pair is regarded as an ideal state when analyzing multibody dynamics, that is, the problems of clearance, friction, wear, and lubrication are not considered. However, due to the influence of manufacturing errors and other factors in practical engineering, it is inevitable to produce clearances at kinematic pairs. The existence of the clearance in a kinematic pair seriously affects the motion accuracy of the mechanism. So in mechanical systems with clearances, lubricate oil will be added to the kinematic pair to improve the dynamic performance and dynamic accuracy reliability of the mechanism [1–3]. The lubricated clearance has a great influence on mechanisms; consequently, it is of great significance to predict and analyze the dynamic response and dynamic accuracy reliability of complex multilink mechanisms with multiple lubricated clearances.

At present, the research on dynamic response of a mechanism with lubricated clearance is often concentrated on simple mechanisms with single clearance, but less research has been done on complex mechanisms with multiple lubricated clearances. Sun et al. [4] explored the impact of buffer action of lubricant on the accuracy of a manipulator with uncertain clearance value. Tian et al. [5] conceived the dynamics of a simple mechanism with dry friction and lubricated joint clearance. Fang et al. [6] established a numerical model of full floating pin bearings of crank-slider mechanism. The application in gasoline engine proves the effectiveness of this model. Zhang et al. [7] derived the impact of clearance value and other factors on the dynamic response of a crank-slider system with lubricated clearance. Krinner et al. [8] presented and compared three different reduction methods of a crank-slider mechanism with lubricated clearances. Daniel et al. [9] used a new method to determine the integral boundary of Reynolds equation, which is applied to solve the fluid force of a mechanism. Flores et al. [10] conducted a new method for modeling lubricated rotating clearance in constrained crank-slider systems. Li et al. [11] used a transition model to emulate the crank-slider system with lubricated clearance. Machado [12] investigated a new transition model to solve the transition problem between lubrication and contact states. Reis et al. [13] discussed the dynamic characteristics of a crank-slider system under two hydrodynamic models. Zhao et al. [14] developed a lubricated model and deduced the hydrodynamic force of the system by the finite element method. Daniel et al. [15] performed a lubricated model under special conditions by considering the interaction between the dynamics of a slider-connecting rod-crank mechanism and lubricated bearing.

In recent years, scholars have done in-depth studies on the motion accuracy reliability of mechanisms with clearance. Nevertheless, most research focusses on the kinematic reliability of a mechanism with dry friction clearance, but less on the dynamic accuracy reliability of mechanisms with lubricated clearance. Sun et al. [16] conceived the kinematic accuracy of the mechanism with clearance with cognitive uncertainty based on the neural network method. Zhang et al. [17] evaluated the kinematic reliability and optimized the design of the radial retractable roof system with rotating clearance. Li et al. [18] set up the model of a spatial deployable mechanism with revolute clearance and then carried out the dynamic solution by the Monte Carlo method. Xiang et al. [19] analyzed the dynamic response and sensitivity of a clearance joint with parameter uncertainty. Geng et al. [20] explored the impact of nonuniform wear clearances on the kinematic accuracy reliability. Gao [21] used the Monte Carlo and Kriging methods to study the kinematic reliability sensitivity with clearance joint in a mechanism. Wu et al. [22] presented an indirect model on reliability evaluation of a crank-slider mechanism with dry friction clearance. Koshy et al. [23] raised a model of contact force of dry friction rotary joint and proved the correctness of the model by experimental research. Li et al. [24] analyzed the numerical and dynamic errors of multibody mechanisms with dry friction clearance and verified the correctness of results by experiments. Erkaya [25] conducted the influence of clearances on the kinematic accuracy of the 6-DOF robot end effector. Geng et al. [26] discussed a reliability evaluation method for mechanisms considering the uncertainty of clearance size and proved the correctness of the method by Monte Carlo simulation. Zhang et al. [27] researched the time-varying reliability of mechanisms with random clearances based on the hybrid dimension reduction method. Lara-Molina et al. [28] explored a method to solve the kinematic accuracy of a parallel manipulator with clearance. Wang et al. [29] derived a synthesis method considering the time-varying reliability of kinematic errors of mechanisms with clearances. Lai et al. [30] discussed the impact of joint wear on the motion accuracy of low-speed planar mechanisms. Zhuang et al. [31] conducted the influence of the wear of the rotary joint of an aircraft locking mechanism on the time-varying reliability of the mechanism and carried out experimental verification.

To sum up, the current studies on dynamic response of multilink mechanism with lubricated clearance are mostly for simple mechanisms, whereas less research has been done on complex mechanisms. Moreover, the research on the dynamic accuracy reliability with lubricated clearance in mechanisms are very rare. Based on this background, in this paper, we take the 2-DOFs 9-bar mechanism as a research object to discuss the dynamic response and dynamic accuracy reliability of complex multilink mechanisms with multiple lubricated clearances. The detailed structure is as follows. In Chap. 2, we establish the “contact-separation-collision” three-state model of dry friction clearance, calculate the contact force at the clearance according to the L-N model and modified Coulomb friction model, and calculate the oil film pressure at the clearance based on the Reynolds equation. In Chap. 3, we establish a dynamic model according to the Lagrange multiplier method. In Chap. 4, we derive the reliability model based on the first-order second-moment method. In Chap. 5, we analyze the effects of dry friction clearances and lubricated clearances on the dynamic response and reliability under different driving speeds and clearance values.

2 Modeling of revolute clearance

2.1 Modeling of dry friction clearance

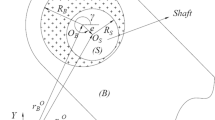
At present, there are three methods to describe the clearance of a revolute pair. One is simulating the clearance as a massless rigid bar, but the impact effect of contact cannot be considered in this model. The other is equating the clearance as a spring damping model element, but it is difficult to accurately define the spring coefficient and damping system. Therefore, in this paper, we adopt the third model, the “contact-separation-collision” three-state model, as shown in Fig. 1. This model considers the three motion states: continuous contact, free, and collision, which could pinpoint the real state of motion. The revolute clearance model is shown in Fig. 2, assuming that the radii of bearing and shaft are \(r_{b}\) and \(r_{s}\), respectively, the center distance is \(r_{d}\), and the clearance value is expressed as

$$ r = r_{b} - r_{s}. $$
(1)

The normal penetration depth of the contact point of bearing and shaft is

$$ \delta _{bs} = r_{d} - r. $$
(2)
Fig. 1
figure 1

Three-state model

Full size image
Fig. 2
figure 2

Revolute clearance model

Full size image

The relationship between the force and displacement in the collision contact process at the revolute clearance is the key factor in modeling of clearance. In the early days, the Hertz contact model was widely accepted. It expressed the contact force as a power function of penetration depth, but the energy dissipation in the contact process was not considered. By comparison, the Lankarani–Nikravesh (L-N) model not only considers the impact contact velocity, the material properties of component, and the geometric characteristics of impact body, but also is conducive to stable solution of dynamics equation, and so it has been widely used [18, 19, 23]. Therefore we adopt the latter in this paper, and the normal contact force \(F_{N}\) of bearing and shaft is expressed as

$$ F_{N} = \left \{ \textstyle\begin{array}{l@{\quad}l} K\delta _{bs}^{n}\left [ 1 + \frac{3\left ( 1 - c_{e}^{2} \right )\delta _{bs}^{\bullet}}{4\delta _{0}^{\bullet}} \right ], & \delta _{bs}^{n} \ge 0, \\ 0, & \delta _{bs}^{n} < 0, \end{array}\displaystyle \right . $$
(3)

where \(n\) is the nonlinear degree, \(c_{e}\) is the coefficient of restitution, \(\dot{\delta}_{0}\) is the initial collision velocity, \(\dot{\delta}_{bs}\) is the relative penetration velocity, and \(K\) is the stiffness coefficient defined as

$$ K = \frac{4}{3(\sigma _{b} + \sigma _{s})}\sqrt{\frac{r_{b}r{}_{s}}{r_{b} + r_{s}},} $$
(4)

with \(\sigma _{i} = \left ( 1 - \nu _{i}^{2} \right ) / E_{i} \left ( i = b,s \right )\), where \(v_{i}\) is Poisson’s ratio, and \(E_{i}\) is the elastic modulus of the material.

The relative motion of shaft and bearing have the friction phenomenon, so it is very important to reasonably express the friction at the clearance. The modified Coulomb friction model is usually applied to describe friction at the clearances and is defined as

$$ F_{t} = - c_{f}c_{d}F_{N}\frac{v_{t}}{\left | v_{t} \right |} = \left \{ \textstyle\begin{array}{l@{\quad}l} 0, & \left | v_{t} \right | \le v_{0}, \\ - c_{f}\frac{\left | v_{t} \right | - v_{0}}{v_{1} - v_{0}}F_{N}sign(v_{t}), & v_{0} \le \left | v_{t} \right | \le v_{1}, \\ - c_{f}F_{N}sign(v_{t}), & \left | v_{t} \right | > v_{1}, \end{array}\displaystyle \right . $$
(5)

where \(c_{f}\) is the sliding friction coefficient, \(c_{d}\) is the dynamic correction coefficient, and \(v_{0}\) and \(v_{1}\) are the speed limits. The parameters of the clearance pair are listed in Table 1.

Table 1 Clearance pair parameters
Full size table

In conclusion, the impact force at the clearance can be expressed as

$$ F_{Dry} = \sqrt{F_{N}^{2} + F_{T}^{2}}. $$
(6)

2.2 Modeling of lubricated clearance

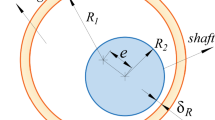
The vector model of lubricated clearance of a revolute pair is shown in Fig. 3. Component \(i\) is bearing, and component \(j\) is shaft. The bearing and shaft are connected by the revolute pair, and the lubricant oil is added between the revolute pair clearance.

Fig. 3
figure 3

Lubricated clearance model

Full size image

The eccentricity vector between bearing and shaft at the lubricated clearance of the revolute pair is

$$ \boldsymbol{e} = \boldsymbol{r}_{j}^{P} - \boldsymbol{r}_{i}^{P}. $$
(7)

The eccentricity represents the offset of the bearing center relative to the shaft center and is expressed as

$$ \varepsilon = \frac{\left | e \right |}{r}. $$
(8)

The offset angle is the angle between the direction of the eccentric vector and positive direction of the \(x\)-axis, expressed as

$$ \gamma = \arctan \left ( \frac{e_{y}}{e_{x}} \right ). $$
(9)

In the lubricated clearance of the revolute pair, the lubricant forms an oil film between the bearing and shaft, and the dynamic load generated by the oil film prevents the bearing and shaft from contacting each other. The Pinkus–Sternlicht model [4, 15] takes into account the pressure field produced by the lubricate oil film, and a general expression of isothermal Reynolds equation under dynamic load is obtained as follows:

$$ \frac{\partial}{\partial x}\left ( \frac{h^{3}}{\mu} \frac{\partial p}{\partial x} \right ) + \frac{\partial}{\partial z}\left ( \frac{h^{3}}{\mu} \frac{\partial p}{\partial z} \right ) = 6U\frac{\partial h}{\partial x} + 12\frac{\partial h}{\partial t}, $$
(10)

where \(x\) and \(z\) represent the radial and axial directions of bearing, respectively, \(h\) is the thickness of the lubricate oil film, \(p\) is the pressure of lubricant, \(\mu \) is the dynamic viscosity, and \(U\) is the relative tangential velocity of bearing and shaft surface. Equation (10) is a nonhomogeneous partial differential equation, which is difficult to solve exactly. However, when we only consider the axial or circumferential direction, formula (10) is a complete partial differential equation. In this paper, because the length-to-diameter ratio \(L\)/\(D\) of bearing is greater than 2, the fluid pressure gradient in clearance changes little along the length direction. Therefore, because of an infinitely short bearing, rewrite formula (10) as

$$ \frac{\partial}{\partial x}\left ( \frac{h^{3}}{\mu} \frac{\partial p}{\partial x} \right ) = 6U\frac{\partial h}{\partial x} + 12\frac{\partial h}{\partial t}, $$
(11)

where the pressure of lubricant \(p\) is expressed as

$$ p = 6\mu \left ( \frac{r_{s}}{r} \right ) + \left \{ \frac{\left ( \omega - 2\dot{\gamma} \right )\left ( 2 + \varepsilon \cos \theta \right )\varepsilon \sin \theta}{\left ( 2 + \varepsilon ^{2} \right )\left ( 1 + \varepsilon \cos \theta \right )^{2}} + \frac{\dot{\varepsilon}}{\varepsilon} \left [ \frac{1}{\left ( 1 + \varepsilon \cos \theta \right )^{2}} - \frac{1}{\left ( 1 + \varepsilon \right )^{2}} \right ] \right \}. $$
(12)

In formula (12) the fluid pressure distribution in the journal bearing can be calculated as a function of the journal bearing parameters and geometry. The force component of the synthetic pressure field can be easily determined in the direction aligned and perpendicular to centerline of the journal and bearing.

We use the Gümbel boundary condition to calculate the oil film bearing capacity, as shown in Fig. 4 [10]. We obtain the oil film pressure by integrating the pressure field around the half-domain \(\pi \). For example, if the pressure of the remaining part is set to zero, then the pressure distribution is integrated only in the positive region.

Fig. 4
figure 4

Gümbel boundary condition

Full size image

When \(\dot{\varepsilon} > 0\), the oil film pressure is decomposed into two forces \(F_{\xi} \) and \(F_{\eta} \), which represent the normal and tangent directions of the bearing and shaft:

$$ \left \{ \textstyle\begin{array}{l}\displaystyle F_{\xi} = \frac{ - 6\mu r_{s}^{3}L}{r^{2}}\frac{\dot{\varepsilon}}{(1 - \varepsilon ^{2})^{1.5}}\left ( \frac{4k\varepsilon ^{2}}{\left ( 2 + \varepsilon ^{2} \right )} + \frac{\pi \left ( k + 3 \right )}{k + 1.5} \right ), \\ \displaystyle F_{\eta} = \frac{6\mu r_{s}^{3}L}{r^{2}}\frac{\pi \varepsilon \left ( \omega - 2\dot{\gamma} \right )}{\left ( 2 + \varepsilon ^{2} \right )\left ( 1 - \varepsilon ^{2} \right )^{0.5}}\frac{k + 3}{k + 1.5}. \end{array}\displaystyle \right . $$
(13)

When \(\dot{\varepsilon} < 0\), the normal and tangential of oil film pressures are expressed as

$$ \left \{ \textstyle\begin{array}{l} \displaystyle F_{\xi} = \frac{ - 6\mu r_{s}^{3}L}{r^{2}}\frac{\dot{\varepsilon}}{(1 - \varepsilon ^{2})^{1.5}}\left ( \frac{4k\varepsilon ^{2}}{\left ( 2 + \varepsilon ^{2} \right )} - \frac{\pi \left ( k + 3 \right )}{k + 1.5} \right ), \\ \displaystyle F_{\eta} = \frac{6\mu r_{s}^{3}L}{r^{2}}\frac{\pi \varepsilon \left ( \omega - 2\dot{\gamma} \right )}{\left ( 2 + \varepsilon ^{2} \right )\left ( 1 - \varepsilon ^{2} \right )^{0.5}}\frac{k}{k + 1.5}, \end{array}\displaystyle \right . $$
(14)

where \(k^{2} = \left ( 1 - \varepsilon ^{2} \right )\left ( \left ( \frac{\omega - 2\dot{\gamma}}{2\dot{\varepsilon}} \right )^{2} + \frac{1}{\varepsilon ^{2}} \right )\), \(L\) is the length of bearing, and \(\omega \) is the relative angular velocity. In actual situations, when the shaft center of mass is very close to the bearing center of mass, that is, when the eccentricity approaches 0, the force at lubricated clearance of the revolute pair will suddenly increase, causing numerical instability. Therefore it is necessary to revise the Pinkus–Sternlicht model:

$$ F_{\xi m} = \left \{ \textstyle\begin{array}{l@{\quad}l} F_{\xi} & \mbox{if }\varepsilon _{0} < \varepsilon < 1, \\ \varepsilon ^{m}F_{\xi} & \mbox{if }0 < \varepsilon < \varepsilon _{0}. \end{array}\displaystyle \right . $$
(15)
$$ F_{\eta m} = \left \{ \textstyle\begin{array}{l@{\quad}l} F_{\eta} & \mbox{if } \varepsilon _{0} < \varepsilon < 1, \\ \varepsilon ^{m}F_{\eta} & \mbox{if } 0 < \varepsilon < \varepsilon _{0}, \end{array}\displaystyle \right . $$
(16)

where \(m\) is the correction coefficient, which is a positive real number between 0 and 1. The specific value is determined by the system parameters. The value of \(\varepsilon _{0}\) is 2 × 10−6. The projections of the force components onto the tangent and normal directions to the \(x\) and \(y\) directions are expressed as

$$ \left \{ \textstyle\begin{array}{l} F_{x} = F_{\xi m}\cos \gamma - F_{\eta m}\sin \gamma , \\ F_{y} = F_{\xi m}\sin \gamma + F_{\eta m}\cos \gamma . \end{array}\displaystyle \right . $$
(17)

The numerical value is unstable when the eccentricity is close to 1. The transition force model is used to guarantee the numerical stability of transition from the lubricated state to the dry friction state [10], which is shown in Fig. 5 and is expressed as

$$ F = \left \{ \textstyle\begin{array}{l@{\quad}l} F_{Lubrication} & \mbox{if }e < r, \\ \frac{r + e_{0} - e}{e_{0}}F_{Lubrication} + \frac{e - r}{e_{0}}F_{\mathit{Dry}} & \mbox{if }r \le e \le r + e_{0}, \\ F_{\mathit{Dry}} & \mbox{if }e > r + e_{0}, \end{array}\displaystyle \right . $$
(18)

where \(F_{\mathit{Lubrication}}\) is the oil film pressure of lubricated clearance, \(F_{\mathit{Dry}}\) is the collision force of dry friction clearance, and \(e_{0}\) indicates eccentricity deviation. This transitional force model can make a smooth transition of the state from the lubricated clearance to the dry friction clearance.

Fig. 5
figure 5

Transition force model

Full size image

3 Dynamics modeling of 2-DOFs 9-bar mechanism with lubricated clearances

The diagram of 2-DOFs 9-bar mechanism with lubricated clearance is shown in Fig. 6. There are eight movable members and a fixed frame in the mechanism, including cranks 1 and 4, connecting rods 2, 3, 7, and 8, frame 5, rocker 6, and slider 9. Cranks 1 and crank 4 are the original moving parts connected with frame 5 by the revolute pair. Connecting rods 2 and 3 are connected with cranks 1 and 4 through the revolute pair, respectively. Connecting rods 2, 3, and 7 are connected by a composite hinge. One end of rocker 6 is connected to the frame by the revolute pair, and the other end is connected to connecting rods 7 and 8 through a composite hinge. The end of connecting rod 8 is connected to slider 9 by the revolute pair. Meanwhile we consider the existence of lubricated clearances at joints A and B and study the effect of lubricated clearances in the mechanism on dynamic response and dynamic accuracy reliability.

Fig. 6
figure 6

Schematic diagram of mechanism with lubricated clearances

Full size image

The reference point coordinate method is used to establish global coordinate system of system, and the local coordinate system is established at the centroid of the component. The 2-DOFs 9-bar mechanism has eight movable components and the generalized coordinates of each component expressed as

$$ \boldsymbol{q}_{i} = \left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c} x_{i} & y_{i} & \theta _{i} \end{array}\displaystyle \right )^{\mathrm{T}} \quad \left ( i = 1, \ldots ,9, i \ne 5 \right ) $$
(19)

The first- and second-order differentials of the global generalized coordinates are obtained for time, and the generalized velocity and acceleration of every member is expressed as

$$ \boldsymbol{\dot{q}}_{i} = \left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c} \dot{x}_{i} & \dot{y}_{i} & \dot{\theta}_{i} \end{array}\displaystyle \right )^{\mathrm{T}} \quad \left ( i = 1,\ldots,9,i \ne 5 \right ), $$
(20)
$$ \boldsymbol{\ddot{q}}_{i} = \left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c} \ddot{x}_{i} & \ddot{y}_{i} & \ddot{\theta}_{i} \end{array}\displaystyle \right )^{\mathrm{T}} \quad \left ( i = 1,\ldots,9,i \ne 5 \right ). $$
(21)

Without considering the clearance, each kinematic pair should introduce two constraint equations. Therefore adding a kinematic pair clearance will reduce two constraint equations. Ideally, there are 10 revolute pairs and one moving pair in the mechanism, 22 constraint equations will be introduced, and the system also has two driving constraints. Then, considering the existence of lubricated clearance at A and B, the constraint of this two kinematic pairs is invalid, so the constraint equations are reduced by 4. The constraint equation of the mechanism is shown as follows:

$$ \boldsymbol{\Phi} \left ( \boldsymbol{q},t \right ) = \left ( \textstyle\begin{array}{l} x_{1} - L_{s1}\cos \theta _{1} \\ y_{1} - L_{s1}\sin \theta _{1} \\ x_{2} - L_{s2}\cos \theta _{2} - x_{1} - L_{s1}\cos \left ( \theta _{1} \right ) \\ y_{2} - L_{s2}\sin \theta _{2} - y_{1} - L_{s1}\sin \left ( \theta _{1} \right ) \\ x_{4} - L_{s4}\cos \theta _{4} \\ y_{4} - L_{s4}\sin \theta _{4} + l_{5} \\ x_{7} - L_{s7}\cos \theta _{7} - x_{2} - L_{s2}\cos \left ( \theta _{2} \right ) \\ y_{7} - L_{s7}\sin \theta _{7} - y_{2} - L_{s2}\sin \left ( \theta _{2} \right ) \\ x_{7} - L_{s7}\cos \theta _{7} - x_{3} - L_{s3}\cos \left ( \theta _{3} \right ) \\ y_{7} - L_{s7}\sin \theta _{7} - y_{3} - L_{s3}\sin \left ( \theta _{3} \right ) \\ x_{7} + L_{s7}\cos \theta _{7} - x_{8} + L_{s8}\cos \left ( \theta _{8} \right ) \\ y_{7} + L_{s7}\sin \theta _{7} - y_{8} + L_{s8}\sin \left ( \theta _{8} \right ) \\ x_{7} + L_{s7}\cos \theta _{7} - x_{6} - L_{s6}\cos \left ( \theta _{6} \right ) \\ y_{7} + L_{s7}\sin \theta _{7} - y_{6} - L_{s6}\sin \left ( \theta _{6} \right ) \\ x_{6} - L_{s6}\cos \theta _{6} - h_{x} \\ y_{6} - L_{s6}\sin \theta _{6} - h_{y} \\ x_{9} - h_{x} \\ \theta _{9} - 90^{\circ} \\ \theta _{1} - \omega _{1}\mathrm{t} + 36.84^{{\circ}} \\ \theta _{4} - \omega _{4}\mathrm{t} - 24.31^{{\circ}} \end{array}\displaystyle \right ) = \mathbf{0}. $$
(22)

Equation (19) seeks the first derivative with respect of time, so the velocity constraint equation is expressed as

$$ \boldsymbol{\Phi}_{q}\boldsymbol{\dot{q}} = - \boldsymbol{\Phi}_{t} \equiv \boldsymbol{\upsilon}. $$
(23)

Among them, \(\boldsymbol{\Phi}_{q}\) means Jacobian matrix, \(\boldsymbol{\Phi}_{t}\) means partial derivative of constraint equation in respect of time, \(\boldsymbol{\dot{q}}\) means generalized velocity vector.

Equation (19) seeks the second derivative in respect of time, so acceleration constraint equation is expressed as

$$ \boldsymbol{\Phi}_{q}\boldsymbol{\ddot{q}} = - \left ( \boldsymbol{\Phi}_{q}\boldsymbol{\dot{q}} \right )_{q}\boldsymbol{\dot{q}} - 2\boldsymbol{\Phi}_{qt}\boldsymbol{\dot{q}} - \boldsymbol{\Phi}_{tt} \equiv \boldsymbol{\gamma} $$
(24)

where \(\boldsymbol{\Phi}_{qt}\) is the partial derivative of the Jacobian matrix with respect to time, and \(\boldsymbol{\Phi}_{tt}\) is the second-order partial derivative of the constraint equation with respect to time.

According to the Lagrangian multiplier method, the rigid-body dynamics equation of the system is expressed as

$$ \boldsymbol{M\ddot{q}} + \boldsymbol{\Phi}_{q}^{\mathrm{T}}\boldsymbol{\lambda} = \boldsymbol{g}, $$
(25)

where \(\boldsymbol{M}\) is the mass matrix of the system, \(\boldsymbol{\lambda} \) is the Lagrangian multiplier, and \(\boldsymbol{g}\) is the generalized force of the system.

According to the default stability algorithm, we introduce the displacement and velocity constraints to the dynamic equation of the system, obtaining the rigid-body dynamic equation

$$ \left ( \textstyle\begin{array}{c@{\quad}c} \boldsymbol{M} & \boldsymbol{\Phi}_{q}^{\mathrm{T}} \\ \boldsymbol{\Phi}_{q} & 0 \end{array}\displaystyle \right )\left ( \textstyle\begin{array}{c} \boldsymbol{\ddot{q}} \\ \boldsymbol{\lambda} \end{array}\displaystyle \right ) = \left ( \textstyle\begin{array}{c} \boldsymbol{g} \\ \boldsymbol{\gamma} - 2\alpha \dot{\boldsymbol{\Phi}} - \beta ^{2}\boldsymbol{\Phi} \end{array}\displaystyle \right ), $$
(26)

where \(\dot{\boldsymbol{\Phi}} = \frac{d\boldsymbol{\Phi}}{dt}\), and \(\alpha \) and \(\beta \) are the correction coefficients; according to [32], we take \(\alpha = \beta = 50\).

4 Modeling of dynamic accuracy reliability

The first-order second-moment method is convenient to reckon and can be used to solve the reliability of the mechanism. The mean and standard deviation of errors are used to quantitatively express the reliability index of the mechanism under different parameter conditions. Assuming that both actual errors of slider output and the allowable errors of engineering practice meet the normal distribution, we will address the reliability under different situations based on strength-stress interference theory. For the reliability of motion accuracy of the mechanism, actual errors and allowable errors represent the stress and strength, respectively:

$$ R = P\left ( \Delta - \delta > 0 \right ) = P\left ( \varepsilon > 0 \right ) $$
(27)

where \(\Delta \) represents the allowable errors, and \(\delta \) represents the actual errors. Assuming that the actual and allowable errors of the slider obey the normal distribution, based on the nature of normal distribution, \(\varepsilon \) also obeys the normal distribution, which can be expressed as

$$ f\left ( \varepsilon \right ) = \frac{1}{\sqrt{2\pi} \sigma _{\varepsilon}} \exp \left [ - \frac{1}{2}(\frac{\varepsilon - \mu _{\varepsilon}}{\sigma _{\varepsilon}} )^{2} \right ], $$
(28)

where \(\mu _{\varepsilon} = \mu _{\Delta} - \mu _{\delta} \) and \(\sigma _{\varepsilon} = \left ( \sigma _{\Delta}^{2} + \sigma _{\delta}^{2} \right )^{1 / 2}\), \(\mu _{\Delta} \) and \(\sigma _{\Delta} \) are the mean and standard deviation of allowable errors, and \(\mu _{\delta} \) and \(\sigma _{\delta} \) are the mean and standard deviation of actual errors.

So the reliability is expressed as follows:

$$ R = P\left ( \varepsilon > 0 \right ) = \int _{0}^{\infty} \frac{1}{\sqrt{2\pi} \sigma _{\varepsilon}} \exp \left [ - \frac{1}{2}(\frac{Z - \mu _{\varepsilon}}{\sigma _{\varepsilon}} )^{2} \right ]d\varepsilon . $$
(29)

Let \(\varepsilon _{0} = \frac{Z - \mu _{\varepsilon}}{\sigma _{\varepsilon}} \), and convert formula (26) into a standard normal distribution form:

$$ R = \int _{0}^{\infty} f\left ( \varepsilon \right )d\varepsilon = \int _{ - \beta}^{\infty} \frac{1}{\sqrt{2\pi}} \exp \left ( - \frac{1}{2}\varepsilon _{0}^{2} \right )d\varepsilon _{0} = \Phi \left ( \beta \right ), $$
(30)

where \(\beta = \frac{\mu _{\varepsilon}}{\sigma _{\varepsilon}} = \frac{\mu _{S} - \mu _{s}}{\sqrt{\sigma _{S}^{2} + \sigma _{s}^{2}}} \) is the reliability index, \(\mu _{S}\) and \(\sigma _{S}\) are the mean and square deviation of allowable errors, and \(\mu _{s}\) and \(\sigma _{s}\) are the mean and square deviation of actual errors. The mean value and square deviation of the actual error are obtained from the rigid-body dynamics model of the mechanism with clearance, whereas the mean value and square deviation of the allowable errors are determined as

$$ \mu _{S} = \frac{\Delta u + \Delta v}{2}, $$
(31)
$$ \sigma _{S} = \frac{\Delta u - \Delta v}{6}, $$
(32)

where \(\Delta \mu \) and \(\Delta \nu \) represent the upper and lower limits of the allowable error, respectively.

5 Dynamic response and dynamic accuracy reliability analysis of mechanism

The clearance values and driving speeds are important parameters that affect the dynamic performance of mechanisms and have great effect on dynamic accuracy reliability of mechanisms. Therefore, in this chapter, the dynamic equation of a mechanism (the design parameters are shown in Tables 2 and 3) is solved by the Runge–Kutta algorithm. We study the impact of distinct clearance values and driving speeds on dynamic response and reliability of a mechanism with multiple lubricated clearances.

Table 2 The parameters of mechanisms
Full size table
Table 3 The parameters of components
Full size table

The flow chart of solving the dynamic response and reliability of a mechanism with multiple lubricated clearances is shown in Fig. 7. Firstly, the initial parameters of a mechanism are determined, and the parameters are substituted into the dynamic model to acquire the output response errors of a mechanism. Secondly, according to engineering practice, taking the slider displacement error range is [0, 0.004 m], the velocity error range is [0, 0.6 m/s], and the acceleration error range is [0, 200 m/s], and according to formulas (31) and (32), the mean and standard deviation of allowable errors of displacement, velocity, and acceleration are determined as 0.002 m, 0.00067 m, 0.3 m/s, 0.1 m/s, 100 m/s2 and 33.33 m/s2, respectively. Finally, the reliability index of the slider can be obtained by the reliability model, and then the reliability of the slider can be acquired by consulting the normal distribution table.

Fig. 7
figure 7

Flow chart of dynamic response and reliability solution

Full size image

5.1 Impact of clearance values on dynamic response and dynamic accuracy reliability of mechanism

In this section, we discuss the dynamic response and dynamic accuracy reliability of a mechanism when the clearance values are 0.3 mm and 0.5 mm, as shown in Fig. 8. The driving speed of cranks 1 and 4 is \(\omega _{1} = \omega _{4} = - 5\pi \mbox{ rad}/\mbox{s}\).

Fig. 8
figure 8figure 8

Dynamics response of a mechanism with different clearance values

Full size image

In Fig. 8(a), the displacement response of the slider is shown when the clearance values of dry friction clearance are 0.3 mm and 0.5 mm, the error peak of displacement of the slider occurs simultaneously at 0.207 s, and the peak values are 5.601e-04 m and 9.714e-04 m, respectively. When the clearance values of the lubricated clearance are 0.3 mm and 0.5 mm, the error peak of displacement of a slider occurs simultaneously at 0.220 s, and the peak values are 8.677e-04 m and 4.399e-04 m, respectively. The velocity response of the slider is shown in Fig. 8(b) when the clearance values of dry friction clearance are 0.3 mm and 0.5 mm, the error peak of velocity of the slider occurs at 0.295 s and 0.111 s, and the peak values are 0.282 m/s and 0.358 m/s, respectively. When the clearance values of the lubricated clearance are 0.3 mm and 0.5 mm, the error peak of velocity of the slider occurs simultaneously at 0.152 s, and the peak values are 0.013 m/s and 0.056 m/s, respectively. The acceleration response of the slider is shown Fig. 8 (c) when clearance values of dry friction clearance are 0.3 mm and 0.5 mm, the error peak of acceleration of the slider occurs at 0.154 s and 0.120 s, and the peak values are −345.3 m/s2 and 1537 m/s2, respectively. When the clearance values of the lubricated clearance are 0.3 mm and 0.5 mm, the error peak of acceleration of the slider occurs simultaneously at 0.273 s, and the peak values are −0.881 m/s2 and −6.074 m/s2, respectively.

To sum up, the larger the clearance value, the larger the displacement, velocity, and acceleration errors of the slider, and the lubricated clearances effectively reduce the errors of the mechanism, and the reduction of the acceleration error is particularly obvious.

The shaft center motion trajectories of clearances A and B are plotted when the clearance values are 0.3 mm and 0.5 mm, respectively. We can see from Figs. 9 and 10 that the shaft center trajectory movement at the dry friction clearance is confusing, whereas the shaft center trajectory movement at the lubricated clearance is relatively smooth, because the existence of a lubricant in the clearance provides a buffer for the movement of bearing and shaft. The larger the clearance value, the larger the motion range of the shaft center trajectory, and the shaft center trajectory becomes more confused. The reason is that the larger the clearance value, the more the free state of the shaft in the bearing, and the greater the contact impact force between the shaft and bearing.

Fig. 9
figure 9

Shaft center motion trajectory when clearance value is 0.3 mm

Full size image
Fig. 10
figure 10

Shaft center motion trajectory when clearance value is 0.5 mm

Full size image

Based on the analysis of dynamic response, the changing trend of the reliability index of the slider at different angles of crank in a motion cycle is studied. By consulting the normal distribution table we obtain the reliability of the slider, as shown in Fig. 11.

Fig. 11
figure 11

Dynamic accuracy reliability of slider

Full size image

To verify that the minimum reliability of mechanism in each motion cycle occurs at the same angle, the displacement reliability of slider in three motion cycles is studied in Fig. 11(a). From the figure, when the dry friction clearances are 0.3 mm, the minimum displacement reliability appears at 198°, 558°, and 918°, and it is 0.9842, 0.9843, and 0.9843, respectively. When the lubricated clearances are 0.3 mm, the minimum displacement reliability appears at 216°, 576°, and 936°, and it is 0.9898, 09901, and 0.9901, respectively. When the dry friction clearances are 0.5 mm, the minimum displacement reliability appears at 198°, 558°, and 918°, and it is 0.9468, 09470, and 0.9468, respectively. When the lubricated clearances are 0.5 mm, the minimum displacement reliability appears at 216°, 558°, and 918°, and it is 0.9557, 09563, and 0.9563, respectively. The results indicate that the minimum reliability occurs at the same basic angle in one cycle of the mechanism. Therefore, to save the calculation cost and time, we further study only the reliability in one cycle of the mechanism.

As shown in Figs. 11(b, c), when the dry friction clearance is 0.3 mm and the crank angles are 270°, the indexes of velocity and acceleration are the lowest, 2.282 and 0.484, respectively. The corresponding reliability is the smallest, 0.9887 and 0.6861, respectively. When the dry friction clearance is 0.5 mm and the crank angles are 90°, the indexes of velocity and acceleration are the lowest, 1.412 and −0.098, respectively. The corresponding reliability is the smallest, 0.9210 and 0.4611, respectively.

When the lubricated clearance is 0.3 mm, the crank angles are 270° and 144°, the indexes of velocity and acceleration are the lowest, 2.864 and 2.984, respectively. The corresponding reliability is the smallest, 0.9980 and 0.9983, respectively. When the lubricated clearance is 0.5 mm and the crank angles are 270° and 144°, the indexes of velocity and acceleration are the lowest, 2.419 and 2.823, respectively. The corresponding reliability is the smallest, 0.9922 and 0.9978, respectively.

To sum up, the larger the clearance value, the lower the reliability of displacement, velocity, and acceleration of the mechanism. Moreover, compared with the dry friction clearance, the lubricated clearance can increase dynamic accuracy reliability of the mechanism.

5.2 Impact of driving speeds on dynamic response and dynamic accuracy reliability of mechanism

In this section, we discuss the dynamic response and dynamic accuracy reliability of the mechanism when the driving speeds are 5\(\pi \) rad/s and 8\(\pi \) rad/s, as shown in Figs. 12 and 13, respectively. The clearance value is 0.6 mm.

Fig. 12
figure 12figure 12

Dynamics response of mechanism when driving speed is 5\(\pi \) rad/s

Full size image
Fig. 13
figure 13figure 13

Dynamics response of mechanism when driving speed is 8\(\pi \) rad/s

Full size image

In Fig. 12, when the driving speed is 5\(\pi \) rad/s, the responses of slider are shown in (a), (b), and (c). For dry friction clearance, the error peaks of displacement, velocity, and acceleration of the slider occur at 0.214 s, 0.083 s, and 0.091 s, respectively, and they are 1.106e-03 m, 0.289 m/s, and 1104 m/s2, respectively. For lubricated clearance, the error peaks of displacement, velocity, and acceleration of slider occur at 0.214 s, 0.280 s, and 0.155 s, respectively, and they are 1.059e-03 m, 0.081 m/s, and −7.32 m/s2, respectively.

In Fig. 13, when the driving speed is 8\(\pi \) rad/s, the responses of the slider are shown in (a), (b), and (c). For dry friction clearance, the error peaks of displacement, velocity, and acceleration of the slider occur at 0.141 s, 0.179 s, and 0.200 s, respectively, and they are 1.123e-03 m, −0.364 m/s, and 1163 m/s2, respectively. For lubricated clearance, the error peaks of displacement, velocity, and acceleration of the slider occur at 0.141 s, 0.083 s, and 0.091 s, respectively, and they are 1.072e-03 m, −0.196 m/s, and −39.94 m/s2, respectively.

To sum up, the larger the driving speed, the larger the displacement, velocity, and acceleration errors of the slider. The lubricated clearances can effectively reduce the errors of the mechanism, especially, the acceleration error.

The shaft center motion trajectories of clearances A and B are plotted when the driving speeds are 5\(\pi \) rad/s and 8\(\pi \) rad/s, as shown in Figs. 14 and 15, respectively. We can see that the shaft center trajectory movement at the dry friction clearance is confusing, whereas the shaft center trajectory movement at the lubricated clearance is relatively smooth. The larger the driving speed, the larger the motion range of the shaft center trajectory, and the shaft center trajectory becomes more confused. This is because the greater the driving speed, the more intense the collision between the shaft and bearing, and the more disordered the movement of the shaft in bearing.

Fig. 14
figure 14

Shaft center motion trajectory when driving speed is 5\(\pi \) rad/s

Full size image
Fig. 15
figure 15

Shaft center motion trajectory when driving speed is 8\(\pi \) rad/s

Full size image

Based on the analysis of dynamic response, we study the changing trend of reliability index of the slider at different angles of the crank in a motion cycle. By consulting the normal distribution table we obtain the reliability of the slider in Fig. 16.

Fig. 16
figure 16

Dynamic accuracy reliability of slider

Full size image

In Fig. 16, when the driving speed is 5\(\pi \) rad/s and there is a dry friction clearance, the crank angles are 198°, 90°, and 90°, and the indexes of displacement, velocity, and acceleration are the lowest, 1.358, 1.412, and −0.098, respectively. The corresponding reliabilities are the smallest, 0.9127, 0.9210, and 0.4611, respectively. When the driving speed is 8\(\pi \) rad/s and there is a dry friction clearance, the crank angles are 216°, 270°, and 180°, the indexes of displacement, velocity, and acceleration are the lowest, 1.325, 1.027, and −0.6811, respectively. The corresponding reliabilities are the smallest, 0.9074, 0.8471, and 0.2480, respectively.

When the driving speed is 5\(\pi \) rad/s and there is a lubricated clearance, the crank angles are 198°, 144°, and 144°, and the indexes of displacement, velocity, and acceleration are the lowest, 1.431, 2.434, and 2.834, respectively. The corresponding reliabilities are the smallest, 0.9226, 0.9926, and 0.9977, respectively. When the driving speed is 5\(\pi \) rad/s and there is a lubricated clearance, the crank angles are 216°, 270°, and 270°, and the indexes of displacement, velocity, and acceleration are the lowest, 1.398, 1.635, and 2.151, respectively. The corresponding reliabilities are the smallest, 0.9190, 0.9489, and 0.9842, respectively.

In summary, the larger the driving speed, the lower the reliability of mechanism. Moreover, compared with the dry friction clearance, the lubricated clearance can increase the dynamic accuracy reliability of the mechanism.

6 Conclusion

The dynamic response and reliability of the 2-DOFs 9-bar mechanism with multiple lubricated clearances are studied, and the influence of different clearance values and driving speeds on dynamic response and dynamic accuracy reliability of the mechanism are discussed. The following conclusions are acquired:

(1) A dynamic model of the 2-DOFs 9-bar mechanism with multiple lubricated clearances is developed based on the Lagrange multiplier method, and a novel reliability model of dynamic accuracy is derived according to the first-order second-moment method.

(2) The different clearance values and driving speeds on dynamic response and dynamic accuracy reliability of the mechanism are studied. When the clearance values are 0.5 mm, the reliability of the displacement, velocity, and acceleration of the slider is lower than that when the clearance values are 0.3 mm. When the driving speeds are 8\(\pi \) rad/s, the reliability of the velocity and acceleration of the slider is lower than that when the driving speeds are 5\(\pi \) rad/s, whereas different the driving speeds have little effect on the displacement reliability of the slider.

(3) The effects of dry friction clearances and lubricated clearances on dynamic response and dynamic accuracy reliability of the mechanism under different conditions are compared and analyzed. The results show that the lubricated clearances can effectively reduce the output errors of the mechanism and make the shaft center motion trajectory smoother. Lubricated clearances can also improve the dynamic accuracy reliability of the mechanism, especially the acceleration reliability.