Correlation dimension and bifurcation analysis for the planar slider-crank mechanism with multiple clearance joints

Abstract

Joint clearance serves as a crucial element of nonlinearity in multibody systems. The quantization of the system chaos is conducive to not only the understanding of the nonlinear nature but the rationalization of system controlled parameters. In the present work, the system dynamics for the planar slider-crank mechanism with multiple clearance joints is depicted by the correlation dimension and bifurcation actions. Considering the obliqueness of the slider, the general configuration of the planar joint is proposed. Generalized coordinates and the Lagrangian approach are adopted to derive the dynamic motion equations. The effects of clearance size and driving speed on the bifurcations of the dynamic response are investigated. Furthermore, the fractal dimension of the strange attractor is identified by the correlation dimension from time series. Based on the Cao method, the Mutual Information (MI) function, and the Grassberger-Procaccia (G-P) algorithm, the controlled factors in the evaluation of correlation dimension are cautiously determined. Ultimately, the compound effect of translational and revolute clearance joints on the mechanism dynamics is featured. The numerical results testify that the correlation dimension of the slider displacement approximately saturates beyond a specific translational clearance value. Moreover, with the parameters used in this work, the complexity of system response seems to be more sensitive to the variation of translational clearance size than with the revolute joint.

1 Introduction

In general, the existence of clearance in the joints is inevitable but essential for multibody systems. Nonlinear surveys reveal that the introduction of joint clearance could bring a higher precision of mechanism analysis as well as the unpredictability of the system response [1,2,3]. In the classical contact model for clearance joints, the joint elements experience constant collision and separation. With the specific range of parameters, the discontinuous contact forces could contribute to the poor dynamics of the mechanism and lead the global behaviors into chaos [4, 5].

In the literature, the revolute joint with clearance is often introduced as an example to depict the effect of clearance joints [6,7,8,9]. Moreover, the prevailing studies have included multiple revolute clearance joints, flexible multibody systems, and the practical application of clearance joint [1]. Based on the numerical simulation and experimental results, Zheng et al. [10] introduced the lubrication forces and revolute joints in flexible multi-link systems, claiming that the consideration of joint collision was essential. Wang et al. [11] noticed the uncertain joint clearance and explored the influence in the rigid-flexible multibody system by the bifurcation diagram. A modified extended delayed feedback control (EDFC) method was implemented in their work to maintain continuous contact in the joint, which finally stabilized the chaotic motion. The same mechanism was investigated by Rahmanian et al. [12] as well, where the bifurcation and the period-doubling phenomenon were presented more in detail. Ma et al. [13] analyzed the dynamic characteristics of the slider-crank mechanism with three revolute clearance joints. Through a close examination of the contact forces in every revolute joint, they emphasized that the joint between the ground and crank should be paid more attention. Similarly, a typical planar four-bar mechanical system with multiple revolute clearance joints was presented by Bai et al. [14]. The nonlinear evolutions of the contact forces and angular acceleration of the crank demonstrated the strong interaction between the revolute clearance joints. The bifurcation analysis of a similar mechanism was proposed by Farahan et al. [15] recently.

Regarding the translational clearance joint, Flores [16] proposed a general methodology to describe the planar issue. Based on the collision situation of the slider corners, four different configurations of contact forces on the slider were conducted. Wu et al. [17] extended the work into a spatial translational clearance joint and modified the stiffness item, which considered the geometrical change in contact regions. It was also stated that undesirable torques could be observed on the slider due to the obliqueness. An experimental rig of slider-crank mechanism with multiple clearance joints was presented by Erkaya et al. [18], where the vibrations and noise characteristics were investigated to feature the compound effects of clearance joints.

Compared with the relatively intuitive judgments of system behaviors from phase portraits or time series diagrams, recent research has progressively put the interests in the characterization of the chaotic response. Kappaganthu and Nataraj [19] investigated a rolling bearing with clearance, where Lyapunov exponents and Poincaré mappings were employed to analyze dynamic behaviors of the mechanism and determine the regions of chaotic response. Concerning the harmonically excited one-degree-of-freedom mechanical system, Serweta et al. [20, 21] successively detailed the bifurcation action for the system possessing one or two symmetrical amplitude constraints. By determining the corresponding spectra of Lyapunov exponents, the research identified the influence of excitation force frequency on the dynamic behavior in a wide range of control parameters. Liu et al. [22] studied the smooth bifurcation and grazing non-smooth bifurcation of a periodic motion for a three-degree-of-freedom vibro-impact system with clearance. The discontinuous jumping phenomenon and co-existing multiple solutions near the grazing bifurcation point were revealed. More recently, Yousuf [23] focused on the rich nonlinear phenomena of the experimental platform for a polydyne cam and roller follower mechanism. The Lyapunov exponents obtained from test data were utilized to quantify the chaos.

In chaos theory, the correlation dimension is an invariant measure of the scale-invariant property and self-similarity of a strange attractor [24]. Evaluation of the correlation dimension can contribute to the description of system complexity. The main object of this paper is to explore the compound effect and interaction of translational and revolute clearance joints on the dynamic response of slider-crank mechanism. On account of the extensive research on the mechanism with a revolute clearance joint in previous studies, the presented work will focus on the effects of the translational clearance joint primarily. Then, the dynamics of clearance joints are modeled by the modified Lankarani-Nikravesh (L-N) contact model [25] and the LuGre friction model [26]. The Lagrangian approach is utilized to derive the dynamic motion equations, based which the system response is reconstituted in discrete phase space. The correlation dimension and bifurcation diagrams, as well as the probability distribution function (PDF), are served as the probes to feature the system chaos. Additionally, the bifurcation analysis illustrates stability ranges of controlled parameters, including clearance size and driving speed. Ultimately, the compound effect of revolute and translational clearance joint is featured by the correlation dimension.

2 Modeling the planar translational joint with clearance

For an ideal translational kinematic joint, the motion trajectory of the slider coincides with the line of translation due to the geometrical limitation of the guide. The introduction of clearance to a planar translational joint removes three DOFs (degrees of freedom) of the slider, namely two translation motion and one revolute motion. Instead of kinematic constraints, the local dynamic behavior of the joint is governed by the generated contact forces, i.e. the kinematic joint is transformed into the “force joint” [27]. Then the contact forces are introduced into the system’s dynamic equations as external generalized forces to evaluate the global system behavior.

3 Kinematics of translational joint with clearance

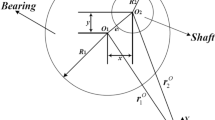
Before the formulation of impact forces in the motion equations, kinematics of the joint should be conducted first. In this section, the methodology proposed by Flores [16] is modified to describe the contact event. It is assumed that the colliding bodies penetrate each other in a dry contact manner during the impact action. Figure 1 presents a representative translational clearance joint where the slider collides with the guide obliquely. It shows that the phenomenon of contact could generate at any corner of the slider, and the collision occurred at corner $B$ is selected as an illustrative example. Let $PQ$ and $RS$ denote the upper and bottom geometrical limits of the guide, respectively.

Fig. 1

Generic planar translational joint with clearance in a multi-body system

Relative to the origin of inertial reference frame, the global position vector for a given point $H$ of body $k$ can be represented by

$$ \mathbf{r}_{H} = \mathbf{r}_{Ok} + \mathbf{R}_{k}^{T}\mathbf{s}_{k}^{H}, \left ( k = i,j \right ), $$

(1)

where $\mathbf{r}_{Ok}$ is the global position vector of the mass center ($O_{k}$) in body $k$. $\mathbf{R}_{k}$ denotes the rotation matrix of the frame ($\xi _{k}O_{k}\eta _{k}$) with respect to the inertial coordinate and is evaluated by

$$ \mathbf{R}_{k} = \mathbf{R}_{k}\left ( \theta _{k} \right ) = \left [ \textstyle\begin{array}{l} \cos \theta _{k}\quad \sin \theta _{k} \\ - \sin \theta _{k}\quad \cos \theta _{k} \end{array}\displaystyle \right ]. $$

(2)

The global position vector from point $H$ to point $K$ is defined as

$$ \mathbf{r}_{HK} = \mathbf{r}_{K} - \mathbf{r}_{H}. $$

(3)

The penetration depth between the slider corner and guide upper surfaces is given by

$$ \delta _{B} = \mathbf{n}_{PQ}^{T}\mathbf{r}_{BQ} = \mathbf{n}_{PQ}^{T}\left ( \mathbf{r}_{Oi} + \mathbf{R}_{i}^{T}s_{i}^{OB} - \mathbf{r}_{Oj} - \mathbf{R}_{j}^{T}s_{j}^{OQ} \right ), $$

(4)

where $\mathbf{n}_{PQ}$ is the unit vector normal to the upper guide surface ($PQ$), i.e., the vector is orthogonal to vector $\mathbf{r}_{PQ}$ and is evaluated by

$$ \mathbf{n}_{PQ} = \left [ \textstyle\begin{array}{l} 0\quad 1 \\ - 1\quad 0 \end{array}\displaystyle \right ]\frac{\mathbf{r}_{PQ}}{\left \| \mathbf{r}_{PQ} \right \| }. $$

(5)

Let the positive sign of the penetration depth present the generation of collisions. Then the orientation of the normal unit vector for the guide surface is stipulated, as shown in the sketch. The penetration vector $\boldsymbol{\delta }_{B}$ is formulated by

$$ \boldsymbol{\delta }_{B} = \left ( \mathbf{n}_{PQ}^{T}\mathbf{r}_{BQ} \right )\mathbf{n}_{PQ}. $$

(6)

Furthermore, the impact velocity, which is essential to evaluate the damping item of normal contact forces, is obtained by differentiating Eq. (6) to time, yielding

$$ \dot{\boldsymbol{\delta }}_{B} = \left ( \dot{\mathbf{n}}_{PQ}^{T}\mathbf{r}_{BQ} + \mathbf{n}_{PQ}^{T}\dot{\mathbf{r}}_{BQ} \right )\mathbf{n}_{PQ} + \left ( \mathbf{n}_{PQ}^{T}\mathbf{r}_{BQ} \right )\dot{\mathbf{n}}_{PQ}. $$

(7)

Assuming that the guide is attached to the ground, the factor $\dot{\mathbf{n}}_{PQ}$ is identically zero vector and the impact velocity is reformulated by

$$ \renewcommand{\arraystretch}{1.5} \left \{ \textstyle\begin{array}{l} \dot{\boldsymbol{\delta }}_{B} = \left ( \mathbf{n}_{PQ}^{T}\dot{\mathbf{r}}_{BQ} \right )\mathbf{n}_{PQ} \\ \dot{\mathbf{r}}_{BQ} = \dot{\mathbf{r}}_{Oj} + \dot{\mathbf{R}}_{j}^{T}\mathbf{s}_{j}^{OB} - \dot{\mathbf{r}}_{Oi} - \dot{\mathbf{R}}_{i}^{T}\mathbf{s}_{i}^{OQ} \end{array}\displaystyle \right .. $$

(8)

The tangential velocity at the contact point, which is requisite to determine the friction, can be represented by the vector difference between the global velocity of corner $B$ and impact velocity, yielding

$$ \mathbf{v}_{T} = \dot{\mathbf{r}}_{Oi} + \dot{\mathbf{R}}_{i}^{T}\mathbf{s}_{i}^{OB} - \left ( \mathbf{n}_{PQ}^{T}\dot{\mathbf{r}}_{BQ} \right )\mathbf{n}_{PQ}. $$

(9)

4 Dynamics of the translation joint with clearance

Generally, the contact forces consist of normal impact force and tangential force, which is also known as the friction force. Considering the energy dissipation and nonlinear nature of the collision, the impact force model proposed by Lankarani is widely accepted [25]. However, the description of this model for the translational clearance joint fails to estimate the stiffness precisely, which is attributed to the neglect of geometrical variation of the contact region. As depicted in Fig. 1, the contact region could be considered as a rectangular characterized by the length $L_{c}$ and penetration depth $\delta _{B}$. The impact force can be evaluated by [25]

$$ F_{N} = K\delta ^{n}\left [ 1 + \frac{3\left ( 1 - c_{e}^{2} \right )}{4\dot{\delta }^{\left ( - \right )}}\dot{\delta } \right ], $$

(10)

where $n$ is the nonlinear exponent and the value is 1.5 for metal-to-metal collisions. The generalized stiffness $K$ is formulated as [17]

$$ K \doteq \frac{\sqrt{S}}{(\sigma _{i} + \sigma _{j})}\frac{1}{11.15\left ( L_{s}/L_{c} + 15.72 \right )^{ - 1} + 0.2854}, $$

(11)

where $S$ denotes the area of contact region and $L_{s}$ represents the length of the slider. Take contact region illustrated in Fig. 1 as the example, the length $L_{c}$ can be estimated by the penetrations of two adjacent corners as

$$ L_{c} = \left \{ \textstyle\begin{array}{l@{\quad }l} L_{s} & \text{if} \delta _{A}, \delta _{B} > 0 \\ 0&\text{if} \delta _{A}, \delta _{B} \le 0 \\ L_{s}\max \left ( \delta _{A}, \delta _{B} \right )/\left | \delta _{A} - \delta _{B} \right | & \text{else} \end{array}\displaystyle \right . $$

(12)

The parameters $\sigma _{i}$ and $\sigma _{j}$ denote the material parameter of the colliding elements $i$ and $j$, respectively,

$$ \sigma _{k} = \frac{1 - \nu _{k}^{2}}{E_{k}}\quad \left ( k = i,j \right ). $$

(13)

Note that the orientation of the normal force vector $\mathbf{F}_{N}$ is parallel to the penetration vector $\boldsymbol{\delta }_{B}$.

For the description of collision, the friction force can be a significant factor to estimate the resultant contact forces. The classical Coulomb friction law could represent the most fundamental principles of friction in the dry sliding condition. However, the model is incapable to represent the physics of the stick-slip effect, which regularly generates in the relative motion of the interfaces. In this work, the sliding friction, stiction friction, and the stick-slip transition motion in the contact region are considered. The LuGre friction law is utilized to simulate the stick-slip friction in the translational joint, and we have [26]

$$ \mathbf{F}_{f} = - \mu \mathbf{F}_{N}\frac{\mathbf{v}_{T}}{\left \| \mathbf{v}_{T} \right \| }. $$

(14)

The instantaneous coefficient of friction $\mu$ in Eq. (14) is represented as

$$ \mu = \sigma _{0}z + \sigma _{1}\dot{z} + \sigma _{2}v_{T}. $$

(15)

The differential equation for the average bristle deflection $z$ is obtained from

$$ \dot{z} = v_{T} - \frac{\sigma _{0}\left | v_{T} \right |}{\mu _{k} + \left ( \mu _{s} - \mu _{k} \right )e^{ - \left | v_{T}/v_{s} \right |\gamma }} z. $$

(16)

Submitting Eq. (16) to Eq. (17), the friction coefficient is reformulated as

$$ \mu = \sigma _{0}z\left [ 1 - \frac{\sigma _{0}\left | v_{T} \right |}{\mu _{k} + \left ( \mu _{s} - \mu _{k} \right )e^{ - \left | v_{T}/v_{s} \right |\gamma }} \right ] + \left ( \sigma _{1} + \sigma _{2} \right )v_{T}. $$

(17)

The normal contact force and friction force act on the mass center of the contact region, which is denoted by point $W$ in the diagrammatic sketch of Fig. 1. The resultant contact force vector together with its magnitude and orientation is evaluated by

$$ \left \{ \textstyle\begin{array}{l} \mathbf{Q}_{c} = \mathbf{F}_{N} + \mathbf{F}_{f} \\ Q_{c} = \left \| \mathbf{Q}_{c} \right \| = K\sqrt{1 + \mu ^{2}} \delta ^{n}\left ( 1 + \frac{3\left ( 1 - c_{e}^{2} \right )}{4\dot{\delta }^{\left ( - \right )}}\dot{\delta } \right ) \\ \varphi = \tan ^{ - 1}\left ( \mu \operatorname{sign} \left ( \mathbf{v}_{T}\mathbf{r}_{PQ} \right ) \right ) + \theta _{j} \end{array}\displaystyle \right .. $$

(18)

The moment vector $\mathbf{M}_{c}$ acting on the slider is represented by the cross multiplication of the contact force and penetration position vector

$$ \mathbf{M}_{c} = \mathbf{r}_{OiW} \times \mathbf{Q}_{c}. $$

(19)

During the evaluation of resultant contact forces, four different contact scenarios proposed by Flores et al [16] are considered. In the numerical integration routines, the collisions generated in the four corners of the slider are the criterion determining the contact configuration.

5 Dynamic equations of the multibody system

In this section, the motion equations for the unconstrained multibody systems are derived based on the generalized coordinates and Lagrangian approach. Due to the introduction of clearance joints, the kinematic translational constraints along the Y-axis and the revolute constraints are removed. Then, the dynamic characteristic of the joint is governed by the contact forces. For a non-conservative multibody system, the Lagrange motion equations are generally obtained by [15]

$$ \frac{d}{dt}\left ( \frac{\partial L}{\partial \dot{q}_{k}} \right ) - \frac{\partial L}{\partial q_{k}} = Q_{nc,k}\quad \left ( k = 2,3,4 \right ), $$

(20)

where $L = T - U$ is the Lagrangian function. $Q_{nc,k}$ is the generalized force corresponding to the generalized coordinate $q_{k}$ and is given by

$$ Q_{nc,k} = \sum _{i = 2}^{4} \left ( \mathbf{F}_{i}^{*} \cdot \frac{\partial \mathbf{v}_{i,c}}{\partial \dot{q}_{k}} + \mathbf{M}_{i}^{*} \cdot \frac{\partial \boldsymbol{\omega }_{i}}{\partial \dot{q}_{k}} \right ), $$

(21)

where $\mathbf{F}_{i}^{*}$ and $\mathbf{M}_{i}^{*}$ denote the vector of resultant external forces and moments acting on the mass center of the body $i$, respectively. $\mathbf{v}_{i,c}$ and $\boldsymbol{\omega }_{i,c}$ indicate the translational and revolute velocity of the mass center of body $i$, respectively.

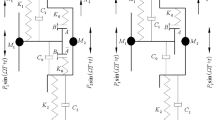
Considering the slider-crank mechanism with a translational clearance joint shown in Fig. 2, the generalized coordinates are chosen as $\mathbf{q} = [\theta _{2}\mbox{;}\ \theta _{3}\mbox{;}\ \theta _{4}]$, responding to the revolute angle of the mass center of the crank, connecting rod and slider, respectively. The geometrical relationship between the markers of each body is evaluated by

$$ \mathbf{OA} + \mathbf{AB} - \mathbf{y}_{4} = \mathbf{x}_{4}. $$

(22)

Let vector $\mathbf{j}$ represent the global unit vector along the Y-axis, and the penetration depth derived from Eq. (4) is given by

$$ \delta _{k} = \left \| \left [ \mathbf{y}_{4} + \left ( \mathbf{R}\left ( \theta _{4} \right )\mathbf{s}_{Bk} \right ) \right ]\mathbf{j} \right \| - c_{t}, $$

(23)

where $k=A$, $B$, $C$, $D$, denoting the corners of the slider respectively. And the positive sign of penetration depth is the metric of the collision generation in the corresponding position. To evaluate the non-conservative forces and the kinetic potential of the slider, the translational velocity of slider mass center is

$$ \renewcommand{\arraystretch}{1.5} \mathbf{v}_{4,c} = \left ( \textstyle\begin{array}{l} - L_{2}\dot{\theta }_{2}\sin \theta _{2} - L_{3}\dot{\theta }_{3}\sin \theta _{3} \\ L_{2}\dot{\theta }_{2}\cos \theta _{2} + L_{3}\dot{\theta }_{3}\cos \theta _{3} \end{array}\displaystyle \right ). $$

(24)

Then, the system kinetic and potential energies are obtained by Eq. (25):

$$ \left \{ \textstyle\begin{array}{l} T = \frac{1}{2}\left [ I_{G2} + m_{2}b_{2}^{2}L_{2}^{2} + \left ( m_{3} + m_{4} \right )L_{2}^{2} \right ]\dot{\theta }_{2}^{2} + \frac{1}{2}\left [ I_{G3} + \left ( b_{3}^{2}m_{3} + m_{4} \right )L_{3}^{2} \right ]\dot{\theta }_{3}^{2} \\ \quad \quad{} + \left ( b_{3}m_{3} + m_{4} \right )L_{2}L_{3}\dot{\theta }_{2}\dot{\theta }_{3}\cos \left ( \theta _{2} - \theta _{3} \right ) + \frac{1}{2}I_{G4}\dot{\theta }_{4}^{2} \\ U = \left ( b_{2}m_{2} + m_{3} + m_{4} \right )gL_{2}\sin \theta _{2} + \left ( b_{3}m_{3} + m_{4} \right )gL_{3}\sin \theta _{3} \end{array}\displaystyle \right .. $$

(25)

Substituting Eqs. (18) and (19) to Eq. (21), the generalized forces responding to the selected coordinates can be cast in the form

$$ \renewcommand{\arraystretch}{1.5} \left \{ \textstyle\begin{array}{l} Q_{\theta _{2}} = Q_{c}L_{2}\sin \left ( \varphi - \theta _{2} \right ) + M_{2} \\ Q_{\theta _{3}} = Q_{c}L_{3}\sin \left ( \varphi - \theta _{3} \right ) \\ Q_{\theta _{4}} = M_{c} \end{array}\displaystyle \right.. $$

(26)

Fig. 2

Configuration of the slider-crank mechanism with a translational clearance joint

The dynamic behavior of the crank is determined by the constant angular velocity $\omega$. Therefore, the system response is evaluated by the equations of motion for the connecting rod and slider, which are derived as follows:

$$ \renewcommand{\arraystretch}{1.5} \left \{ \textstyle\begin{array}{l} \left [ I_{G3} + \left ( b_{3}^{2}m_{3} + m_{4} \right )L_{3}^{2} \right ]\ddot{\theta }_{3} + \left ( b_{3}m_{3} + m_{4} \right )L_{2}L_{3}\omega ^{2}\sin \left ( \theta _{3} - \theta _{2} \right ) \\ \quad \quad + \left ( b_{3}m_{3} + m_{4} \right )gL_{3}\cos \theta _{3} + Q_{c}L_{3}\sin \left ( \theta _{3} - \varphi \right ) = 0 \\ I_{G4}\ddot{\theta }_{4} = M_{c} \end{array}\displaystyle \right .. $$

(27)

And the driving torque acting on the crank is given by

$$ \begin{aligned} M_{2} &= \left ( b_{3}m_{3} + m_{4} \right )L_{2}L_{3}\left [ \ddot{\theta }_{3}\cos \left ( \theta _{2} - \theta _{3} \right ) + \dot{\theta }_{3}^{2}\sin \left ( \theta _{2} - \theta _{3} \right ) \right ] \\ &\quad {}+ \left ( b_{2}m_{2} + m_{3} + m_{4} \right )gL_{2}\cos \theta _{2} + Q_{c}L_{2}\sin \left ( \theta _{2} - \varphi \right ) \end{aligned} . $$

(28)

The motion solution solved by Eqs. (27) and (28) is started with a proper set of initial conditions obtained from the simulation where all the joints are assumed to be perfect, yielding

$$ \left \{ \textstyle\begin{array}{l} \theta _{2,t = 0} = \theta _{3,t = 0} = \theta _{4,t = 0} = 0 \\ \dot{\theta }_{2,t = 0} = \omega ;\dot{\theta }_{3,t = 0} = - \omega L_{2}/L_{3};\dot{\theta }_{4,t = 0} = 0. \end{array}\displaystyle \right . $$

(29)

The MATLAB code is conducted to solve the differential equations, where the fourth-order Runge–Kutta method is employed. The geometrical and initial properties of the mechanism are given by Table 1, while the same mechanism was investigated by Flores [16]. Based on the previous studies [10, 11, 28], the parameters utilized in the simulation are determined by Table 2. In the simulations, the integration time step is set as $1\times 10^{-6}$ s and all the computations are performed on the computer with 6 processors of 3 GHz and a RAM of 8 GB.

Table 1 Properties of the slider-crank mechanism

Table 2 Parameters in the simulation of the mechanism with a translational clearance joint

6 Bifurcation and chaos

As illustrated in Fig. 3, the trajectory of the slider for various translational clearance size is investigated primarily. The numerical results demonstrate that a minor clearance seems to correspond to a more periodical system response, which indicates the low complexity of the mechanism. According to Fig. 3(e) and (f), the simulation adopting the variable-stiffness model share a similar shape of slider trajectory with the constant-stiffness case. However, the penetration depth is larger for the variable-stiffness case. Since the stiffness item evaluated by Eq. (11) depends on the variation of contact region, the minor contact area during collision actions indicates that the guide is easy to be penetrated.

Fig. 3

Slider trajectory for the mechanism with a translational clearance joint varying clearance sizes ($\omega =5000$ rpm, $\mu _{s} =0.1$): (a) 0.5 mm; (b) 0.3 mm; (c) 0.2 mm; (d) 0.1 mm; (e) 0.01 mm; (f) numerical results from Flores for $c_{t}=0.01$ mm [16]

By characterizing the dynamic response in discrete phase space, the system regularity affected by various clearance size is analyzed. The bifurcation diagrams for the slider displacement versus the clearance size are depicted in Fig. 4. For a specific clearance, 1000 periods of system responses are obtained and 50 end-periods representing the steady-state behavior are characterized in the bifurcation diagram. In the presented work, 120 values of clearance size linearly distributed from 0.01 to 0.6 mm are investigated. Concentrative distribution of the sampling points is observed in Fig. 4 when the clearance is minor than 0.07 mm, corresponding to the periodic system response. The point distribution also suggests that the slider contacts the guide bottom surface when reaching the bottom dead center (BDC). For a greater clearance (around 0.1 to 0.15 mm), the densely distributed area of the points gradually expands to the X-axis and system irregularity occurs. As the clearance continues to magnify, the slider motion becomes rather aperiodic. It is suggested that the sampling points fill up the scope defined by the clearance value. Furthermore, the dynamic response appears to be chaotic within a wide range of clearance. Compared with the revolute clearance joint in the same mechanical system [12], period-doubling and bifurcation phenomena are not noticeable for the translational clearance joint case.

Fig. 4

Bifurcation diagram varying the clearance sizes ($\omega =5000$ rpm): (a) distribution of the sampling data; (b) PDF of (a)

The concentrate of sampling data may indicate that the system response is more predictable [29]. The probability distribution of the data points in the bifurcation diagram is shown in Fig. 4(b). For every specific clearance, 500 endpoints in the discrete phase space are obtained to evaluate the PDF. It is revealed that when the clearance is greater than 0.3 mm, the probability distribution basically stabilized and the concentration area gradually moves towards the X-axis. On the contrary, the distribution is concentrated for a low clearance value, while the evolution seems unpredictable with the varying clearance.

System driving speed is another factor that should be given high status. With different crank speeds, the contact events are constantly in flux and the system behavior could transform from the predictable state into chaos [30]. The presented work explores 150 values of crank speed linearly distributed within the range from 500 to 5000 rpm to investigate the system periodicity. Different values of the clearance sizes are selected in the simulation, respectively, namely 0.1 mm, 0.2 mm, 0.3 mm, and 0.5 mm. Similarly, 500 points in the Poincaré portrait are employed to conduct the probability density, as shown in Fig. 5 (a) to (d). For a clearance equal to 0.1 mm, the densely periodic points in Fig. 5 (a) suggest the regularity in the dynamic response for a crank speed lower than 1000 rpm. Uniform distribution and bimodal distribution are detected with the increase of the crank speed. The concentrations of the sampling points, which shows the exact position where the slider locates in each period, is mainly focused below the X-axis. When the clearance is enlarged to 0.2 mm and 0.3 mm, the more extensive range of the bimodal distribution is generated for virtually any speed. However, in the case where the clearance is 0.2 mm and crank rotary speed is chosen to be 628 rpm, the clustered points indicate that the dynamic response is periodic. As the clearance size continues to grow to 0.5 mm, the concentrated zones are relatively stable and approach the X-axis with the increase of crank speed.

Fig. 5

Probability density distribution of the bifurcation for the mechanism featured by various crank speeds and translational clearance sizes. (a) $c_{t} = 0.1$ mm; (b) $c_{t} = 0.2$ mm; (c) $c_{t} = 0.3$ mm; (d) $c_{t} = 0.5$ mm

Through the overall observation of Fig. 5, it seems that the system behavior performs unpredictably within a wide range of crank speeds and clearance sizes. The uniform distribution is also detected in the diagrams, which may be an indicator of stochastic systems. However, the slider’s vertical displacement is plotted versus the velocity in Fig. 6, the strange attractors are manifested in the Poincaré map. By projecting the time series into discrete phase space, Fig. 6 illustrates the system behaviors concerning four different values of the clearance. Note that each portrait includes 10,000 points, and the driving speed is selected as 5000 rpm. The numerical results indicate that the structures of the attractors seem to remain unchanged regarding the increase of clearance size. The fractal structure is featured by a finite scope and infinite details, which denote the main characteristic of chaotic motion. The point concentration demonstrates that the trajectories are stretching and folding in theses bounded regions, implying the possible intricate composition. Thus, the complexity of the strange attractors could not be evaluated precisely through visual observation only. And mathematical methods for estimating and qualifying the complexity of the attractors is required.

Fig. 6

Poincaré portraits for difference translational clearance size for $\omega =5000$ rpm (10,000 points): (a) 0.1 mm; (b) 0.2 mm; (c) 0.3 mm; (d) 0.5 mm

Within the simulation parameter range chosen in Table 2, the computation costs turn out to be about 20 minutes (1280.41s) for conducting each bifurcation diagram and 409.97s for every Poincaré portrait.

7 Quantify the chaos

The time signal from the chaotic system is often, using only visual information, indistinguishable from a stochastic process, despite being driven by deterministic dynamics. Generally, a time-domain analysis of the time series could not represent the dynamics of chaotic systems comprehensively [31, 32].

By projecting the time series to a higher dimension, nonlinear dynamic analysis has provided an effective technique of phase space reconstitution to extract the nature and the rules of the system. Let $x\left ( i \right )$ with $i = 1, \ldots ,N$, be the time series with $N$ samples, and the dataset in the $m$-dimensional phase space is conducted by

$$ X_{i}\left ( m \right ) = \left [ x\left ( i \right ),x\left ( i + \tau \right ), \ldots x\left ( i + \left ( m - 1 \right )\tau \right ) \right ]. $$

(30)

Then $M$ points are created in the phase space, i.e., $i = 1, \ldots ,M; M = N - \left ( m + 1 \right )\tau$. According to the Takens-Mañé embedding theorem [33], the selection of the time delay could significantly influence the reliability and effectiveness of space reconstruction. In this work, the mutual information (MI) method is employed to estimate the optimum time delay, due to its superiority in the nonlinear analysis [34]. The mutual information function is evaluated by

$$ I\left ( \tau \right ) = \sum _{x\left ( i \right ),x\left ( i + \tau \right )} p\left ( x\left ( i \right ),x\left ( i + \tau \right ) \right )\ln \frac{p\left ( x\left ( i \right ),x\left ( i + \tau \right ) \right )}{p\left ( x\left ( i \right ) \right )p\left ( x\left ( i + \tau \right ) \right )}, $$

(31)

where $p\left ( x\left ( i \right ) \right )$ and $p\left ( x\left ( i + \tau \right ) \right )$ denote the probabilities for series $x\left ( i \right )$ and $x\left ( i + \tau \right )$, respectively. $p\left ( x\left ( i \right ),x\left ( i + \tau \right ) \right )$ is the joint probability density for the two time series. The optimal time delay is defined by the first minimum of the average mutual information.

A higher correlation dimension usually represents the concretization of a complex chaotic system, and vice versa [35]. For an $m$-dimensional phase space, the correlation function $C\left ( \varepsilon \right )$ is given by Theiler [36]

$$ C\left ( \varepsilon \right ) = \frac{2}{M\left ( M - 1 \right )}\sum _{1 \le i < j \le M} H\left ( \varepsilon - \left \| X_{i} - X_{j} \right \| _{p} \right ), $$

(32)

where $\left \| \cdot \right \| _{p}$ represent the $p$ norm, and the infinite norm is chosen in this paper. $H(k)$ represents the Heaviside function, with $H\left ( k \right ) = 1$ for $k \geq 0$ and $H\left ( k \right ) = 0$ otherwise. According to the G-P algorithm [37], the dimension $D$ is evaluated by the slope in the logarithmic diagram of $C\left ( \varepsilon \right )$ versus $\varepsilon$, yielding

$$ D = \lim _{\varepsilon \to 0}\frac{\ln C\left ( \varepsilon \right )}{\ln \varepsilon }. $$

(33)

For a chaotic process, the dimension $D$ saturates beyond a certain $m$ [38]. When the value of $D$ is non-integral or greater than 2, the chaotic oscillation sensitive to the initial conditions will be generated in the system behaviors [35]. In this paper, Cao’s method is adopted to obtain the proper embedding dimension due to its objective evaluation [39]. The parameter $E_{1}$ ($m$) is addressed to determine the minimum $m$

$$ \renewcommand{\arraystretch}{1.5} \left \{ \textstyle\begin{array}{l} a\left ( i,m \right ) = \frac{\left \| X_{i}\left ( m + 1 \right ) - X_{n\left ( i,m \right )}\left ( m + 1 \right ) \right \| _{p}}{\left \| X_{i}\left ( m \right ) - X_{n\left ( i,m \right )}\left ( m \right ) \right \| _{p}} \\ E\left ( m \right ) = \frac{1}{N - d\tau } \sum _{i = 1}^{N - d\tau } a\left ( i,m \right ) \\ E_{1}(m) = E\left ( m + 1 \right ) / E\left ( m \right ) \end{array}\displaystyle \right ., $$

(34)

where $n$($i$, $m$) is the index that responds to $X_{n\left ( i,m \right )}\left ( m \right )$ being the nearest neighbor of $X_{i}\left ( m \right )$. The saturation of $E_{1}$ ($m$) beyond a specific $m$ implies the minimum embedding dimension has achieved. Moreover, another parameter $E_{2}$ ($m$) is also established to distinguish deterministic data from random data and is evaluated by

$$ \renewcommand{\arraystretch}{1.5} \left \{ \textstyle\begin{array}{l} E^{ *} \left ( m \right ) = \frac{1}{N - m\tau } \sum _{i = 1}^{N - m\tau } \left | x_{i + m\tau } - x_{n\left ( i,m \right ) + m\tau } \right | \\ E_{2}\left ( m \right ) = E^{ *} \left ( m + 1 \right ) / E^{ *} \left ( m \right ) \end{array}\displaystyle \right .. $$

(35)

For the time series of a deterministic system, $E_{2}(m)$ is not constant to 1 for any embedding dimension $m$.

8 Results and discussion

Primarily, the correlation dimension for the mechanism with different translational clearance sizes is investigated. Time series of vertical slider displacement for 5 continuous periods are selected to be the original data, where the crank speed is 5000 rpm. Figure 7 (b) illustrates the evolution of the MI function varying time delays, where the function reaches the first minimum for $\tau =18$. The original dynamic behavior represented by the phase portrait is depicted in Fig. 7 (a), while Fig. 7 (c) demonstrates the result of phase space reconstitution. The similar graphs indicate that the methodology could restitute the original system behaviors effectively. When the embedding dimension increases from 1 to 12, the corresponding correlation functions are evaluated and displayed in Fig. 7 (d). It shows that the correlation exponent increases before the embedding dimension reaches $m=6$, and the stable correlation dimension is 2.24 in this case. The non-integral fractal dimension authenticates the chaos in the local dynamic response of translational clearance joint. Moreover, the parameters $E_{1}$ and $E_{2}$ in Cao’s method are evaluated for various embedding dimensions simultaneously, of which the saturation is observed in Fig. 7 (f) for $m=6$. As introduced in Sect. 5, the amplitude variation of parameter $E_{2}$ testifies that the contact phenomenon in the clearance joint is described by a determined process, instead of the stochastic system.

Fig. 7

Correlation dimension determination for the dynamic response of the slider: (a) phase portrait of the original system response; (b) evaluation of the proper time delay; (c) phase portrait of the reconstituted phase space; (d) correlation function for different embedding dimensions; (e) correlation dimension varying embedding dimension; (f) the two essential metrics in Cao’s method

It should be noted that before the time series of the slider displacement is considered, the program conducted in MATLAB to obtain the correlation dimension has been verified by two classical chaotic strange attractors beforehand. The Lorenz attractor and Henon attractor were applied to validate the program, and the results corroborated well with Ref. [40].

For the mechanism characterized by different clearance sizes, the correlation dimension is investigated to estimate the system complexity. Simulations are carried out for 120 values of clearance size, and the parameters listed in Table 2 are employed. Figure 8 (a) and (b) illustrate the factor $E_{2}$ and the dimensions obtained from the numerical results, respectively. When the clearance size is magnified, the mutation of factor $E_{2}$ suggests that dynamic performance in the translational clearance joint is determinable invariably. In the previous studies, a large clearance size was considered to correspond to a more unpredictable system [1, 28]. However, the dimension $D$ indicates that system behavior does not always become more complicated with the expansion in clearance size. This finding challenges the conclusion drawn in the literature [16]. The prior study mainly focused on time-domain analysis, including high peaks in the acceleration-time chart and trajectory branches in the phase portraits. This conclusion was based on the investigation for five values of clearance size. The presented work quantifies the chaotic motion and includes a broader scope of clearance size (120 values). Therefore, the conclusion proposed may be more reliable than based on the limited information from visual observation only. It is also detected that the fractal dimension is maintained at a lower level when the translational clearance size is approximately 0.2 mm. The mechanism is supposed to have a low complexity within this range, although the periodicity is not explicit in the bifurcation diagram.

Fig. 8

Measurement of the correlation dimension of the slider dynamics for various clearance sizes: (a) Parameter $E_{2}$ obtained from the Cao method; (b) corresponding correlation dimension

With a small clearance size, the kinematic joint is considered to share a similar dynamic response with the ideal joint case [16]. Yet when the clearance is 0.01 mm, dimension $D$ is still non-integral, which demonstrates that the single periodic state is not achieved. It is non-deterministic; this phenomenon is attributed to the nature of the clearance joint or the rounding errors in the simulation.

The dimension $D$ of the system behavior effected by the two quantities, namely crank speed and clearance size, is depicted in Fig. 9. With regard to the variation of clearance, the dimension achieves saturation approximately beyond a specific clearance (about 0.3 mm). With the increase of the driving speed, the evolution of the dimension seems unpredictable and unstable within the range of a small clearance size. However, steady growth in the dimension is observed as the crank speed intensifies for the clearance greater than 0.3 mm.

Fig. 9

Correlation dimensions of the slider’s vertical displacement for different clearance sizes and crank speeds

The evaluation of correlation dimension by the G-P method involves the determination of the curve slope. Thus, the selection of a linear scope can generate errors to some extent. The slope of the correlation function versus the radius $\varepsilon$ is determined through manual observation to reduce the error.

As mentioned in Sect. 1, the introduction of multiple clearance joints has a complex compound influence on the system responses. In this part, the translational joint and revolute joint between connecting rod and slider are modeled to be imperfect simultaneously. In the planar revolute joint with clearance, the journal and bearing are assumed to penetrate each other in a dry contact manner as illustrated in Fig. 10. The penetration depth is determined by the clearance and center distance between the joint elements. The contact forces generated in the joint are evaluated by the L-N dissipative contact model and LuGre friction model. For the slider-crank mechanism with a revolute clearance joint, the equations of motion can be addressed by the Lagrangian approaches reported in Refs. [2, 12]. The reader can find a more comprehensive investigation of this issue in Tian’s work [1].

Fig. 10

Representation of the planar revolute joint with clearance

Prior to the estimation of correlation dimension from time series, the simulation performed in the presented work should be validated. The numerical results are compared with those obtained by Flores [4] and Wang et al. [11], as illustrated in Fig. 11. In Ref. [15], strange attractors are discovered in the revolute clearance joint, and the friction forces could “smooth” the dynamics-time curve to some extent. Consequently, the system behavior is supposed to be more stable and predictable. In this work, we aim to explore the combined effect of the two strange attractors. Therefore, the friction action in the revolute joint ought to be weakened, and the static friction coefficient is then selected as 0 and 0.05, respectively.

Fig. 11

System response of the slider-crank mechanism with a revolute clearance joint: (a) relative motion trajectory of the journal center relative to the bearing ($c_{r}=0.01$ mm, $\mu =0$); (b) corresponding results obtained by Wang [11]; (c) phase portrait of the slider’s dynamic response ($c_{r}=0.5$ mm, $\mu _{s}=0.1$); (d) the corresponding results presented in Ref. [4]

With the changes in friction coefficient and clearance sizes, the correlation dimension for the slider’s vertical displacement in the mechanism with two clearance joints is investigated. Figure 12 illustrates the numerical results for the system with different combinations of the parameters. When the translational clearance achieves $c_{t} =0.2$ mm, the valley in the dimension evolution occurs. The variation of the friction coefficient and clearance size for the revolute joint seems to have a slight influence on the dimension. It shows that the translational clearance joint has a more stimulating effect on the system outputs than in the revolute case. By examining the journal trajectories shown in Fig. 13, it is easy to see that the journal and bearing maintain in the state of continuous penetration contact fairly, even when the two clearances reach the maximum value simultaneously. The observation is corroborated by the previous numerical results [4, 12]. However, the relative motion between the slider and guide experiences different configurations, including “free flight”, “contact” and “penetrated contact” shown in Fig. 3. When the clearance joint is of the nature of a continuous contact, the dynamic response of the slider-crank mechanism is similar to the ideal joint case [1]. Thus, the system complexity may be more likely controlled by the translational clearance joint.

Fig. 12

Correlation dimensions for the mechanism with different friction coefficient ($\omega =5000$ rpm): (a) friction coefficient in the revolute clearance joint equals 0; (b) static friction coefficient in the revolute clearance joint equals 0.05

Fig. 13

Trajectory of the journal center in the slider-crank mechanism with multiple clearance joints ($\omega =5000$ rpm, $c_{t}=0.5$ mm): (a) $c_{r}=0.1$ mm; (b) $c_{r}=0.5$ mm

9 Conclusions

The system chaos of the planar slider-crank mechanism with multiple clearance joints is examined in this paper. The dynamics of the clearance joint is described by the modified L-N contact model and the LuGre friction model, and the general formulation of the planar translational clearance joint is proposed. Then the Lagrangian approach is adopted to derive the system equations of motion. Time series of the system behaviors are projected into the discrete phase space to obtain the Poincaré portraits and bifurcation diagrams, which play a fundamental role in recognizing the periodicity of nonlinear systems. And the presence of strange attractors signals the chaos character of the mechanism. Parameter analysis is carried out to investigate the effects of clearance size and driving speed on the system’s generic behaviors as well. Furthermore, the system chaos is quantified by the fractal dimension, where a series of methods are employed to rationalize the controlled parameters.

The numerical results demonstrate that, for a relatively large clearance, the dimension saturates for the variation of clearance size but increases with the acceleration of the crank. The valley of the correlation dimension is observed, which indicates that the system complexity is maintained at a low level within this scope of clearance. When the revolute and translational clearance joints are introduced to the system simultaneously, the correlation dimension of the slider vertical displacement is likely to be governed by the translation joint. This phenomenon may be caused by the constant transition from penetrated contact to free flight motion in the translational clearance joint.