1 Introduction

Origami is an art of paper folding that turns flat pieces of paper into 3D structures. Origamis exhibit interesting shape morphing and have inspired numerous applications in engineering such as deployable space solar sails (Miura 1985; Zirbel et al. 2013), novel mechanisms (Zhang and Chen 2018; Nelson et al. 2019), energy-absorbing devices (Ma and You 2013; Lee et al. 2019), meta-materials (Schenk and Guest 2013; Zhai et al. 2018; Pratapa et al. 2019), etc. To date, polyhedral origamis composing of triangular and quadrilateral facets are most widely used in engineering. The deformation of origami involves that of the facet and crease folding. General speaking, the facet undergoes large displacement large rotation but small strain and, if possible, small curvature. To simulate the origami deformation, a classical approach is to adopt the rigid facet assumption in which only crease folding is allowed (Tachi 2009; Wei et al. 2013). The deformed configuration can be obtained efficiently at the expense of setting up geometric constraints which often requires a high level of mathematical skill. Recent emphasis on origami modelling is on deformable facets and elastic creases. The finite element method widely used in the structural analysis has been considered in crushing analysis and the facets can readily be modelled as plate/shell elements (Ma et al. 2018; Song et al. 2012). However, there are a few obstacles for analyzing origamis which can fold and unfold repeatedly using the finite element method.

Firstly, plate/shell elements with rotation dofs are quite often slow in convergence in large rotation analyses, probably because finite rotation is not commutative and special treatment is required to update the rotation (Crisfield 2000). Partly because of this reason and partly because 3D constitutive models can be directly adopted, considerable research effort has gone into solid-shell elements (Park et al. 1995; Kim and Lee 1988; Bischoff and Ramm 1998; Hauptmann and Schweizerhof 1998; Sze et al. 2002; Sze 2002; Kim et al. 2003, Bischoff et al. 2018; Kulikov and Plotnikova 2008) and other rotation-free elements (Guo et al. 2002; Flores and Oñate 2011; Zhou and Sze 2012) which possess only translational dofs. As an illustration, the popular benchmark problem in which a slit annular plate with inner radius 6 and outer radius 10 (Sze et al. 2004) meshed into 6 × 30 elements is analyzed by using the four-node shell element models S4 and S4R as well as the 8-node solid-shell element model SC8R of ABAQUS. A line force is applied at the free end of the radial slit while the other end of the slit is fully clamped. Figure 1 shows the undeformed and the final deformed configurations at the maximum line force at 0.8 unit of force per unit length. The default time increment in ABAQUS is adopted, i.e., the initial, minimum, and largest time increment sizes are 1, 10–5, and 1, respectively. The default automatic time increment option, see the first paragraph in Sect. 5, is employed. The analyses were conducted in a laptop PC with Intel(R) Core(TM) i9-9880H CPU (8 cores, 2.30 GHz) and 64 GB RAM. The predictions of S4, S4R and SC8R are practically identical. The analysis data are given in Table 1. It can be seen that SC8R consumed far less number of time increments, number of iterations and CPU time than the S4 and S4R shell element models. Another example comparing S4R and SC8R can also be found in Sect. 5.1.

Fig. 1
figure 1

a The undeformed and b the final deformed mesh of the slit annular plate problem

Full size image
Table 1 Analysis data for different element models in the slit annular plate problem in Fig. 1
Full size table

The thickness, elasticity modulus and Poisson’s ratio of the plate are 0.03, 21 × 106 and 0, respectively.

Secondly, the elastic hinge needed for modelling the elastic crease is not readily available in most, if not all, commercial finite element programs. Taking ABAQUS as an example, it provides 3 types of spring elements, i.e., SPRING1, SPRING2 and SPRINGA. SPRING1 is a grounded spring defined by only one globally or locally defined dofs. SPRING2 can connect any two globally or locally defined dofs. In principle, an elastic hinge can be realized by coupling two local rotations defined about the hinge using SPRING2. However, ABAQUS requires the local coordinate system used to define the local rotation to be fixed even in large displacement analysis. However, creases in origamis undergoing large displacement and their orientations vary. SPRINGA can adopt the line between two end nodes as the axis which can rotate and translate in large displacement analysis but it can only model extensional/compressive springs.

Thirdly, modelling origami with plate/shell elements with rotational dofs will couple the nodal rotations and the hinge angles. A possible workaround is to define the nodes of adjacent plate/shell elements at the same crease vertex and constrain the equality of the nodal translations. The drawback of this approach can be understood by considering, e.g., a crease vertex shared by 4 facets. While the 3 × 4 translational dofs can be trimmed down to 3 by constraints, the 3 × 4 rotational dofs remain active. In the origami simulation methods to be reviewed below, there are only 3 translation dofs per node. The impact of using 15 instead of 3 dofs per crease vertex on the computational efficiency can be considerable.

The bar-hinge approach can be regarded as a simplified finite element method which can consider deformable facets and elastic creases (Schenk and Guest 2011). In the model, the origami is first represented by a network of bar or truss elements along creases with the element nodes at the endpoints of creases only. Without introducing additional nodes, quadrilateral or higher-order polyhedral facets are then divided into triangles by additional bar elements. The membrane deformation, also known as the shearing/stretching deformation and in-plane deformation, is accounted for by the axial deformation of the bar elements. All inter-facet and intra-facet bar elements are also elastic hinges whilst the stiffness of the latter is derived from the bending stiffness of facets, respectively (Schenk and Guest 2011; Filipov et al. 2017; Gillman et al. 2018). The dihedral angle of the crease is an inverse sine or cosine function of the displacements at nodes defining the adjacent facets. Thus, derivatives of the dihedral angle contain the cosine or sine function in the denominator. The 0/0, zero divided by zero, points need to be removed by expressing the derivatives using algebraic terms (Liu and Paulino 2017; Schenk and Guest 2011; Bekker 1996). To avoid the complication, the arctan2 function, instead of arccos or arcsin functions, was also suggested for computing the dihedral angle at the expense of using two arguments in the function (Gillman et al. 2018). To trace the large displacement which may involve bistability and bifurcations, advanced solution techniques have also been incorporated into the bar-hinge models. Other features such as material nonlinearity, fold stiffness with penalty near the fully-folded state to avoid penetration can also be noted (Liu and Paulino 2017; Gillman et al. 2018). Recently, the bar-hinge models have been adopted to uncover some unique mechanistic properties of the origami structures (Grey et al. 2019; Liu et al. 2019).

This paper develops a simplified FEM approach in which the origami is modelled by ad hoc developed bending and elastic crease elements. Since origamis with pentagonal and higher-order polygonal facets are seldom used in engineering applications, triangular and quadrilateral facets are considered here. Each of these facets would be modelled by 3-node triangle (T3) or 4-node quadrilateral (Q4) with only translational nodal dofs. The membrane deformation in T3 and Q4 can be accounted for by any geometric nonlinear 3D membrane elements of the same nodal configurations. Since creases are practically straight due to the large membrane stiffness of the adjacent non-coplanar facets, bending deformation is not possible in T3 facet whilst there is only one bending deformation mode in the Q4 facet. In this light, a Q4 bending element is developed based on the corotational concept. Under the large-displacement, large-rotation but small strain small curvature assumption, it will be shown that the bending deformation mode can be quantified by the distance between the two straight lines connecting the opposite corners of the quadrilateral. A point of remark is that the two straight lines lie on the flat Q4 facet but would detach from the facet when the facet becomes curved. The salient feature of the elastic energy in the Q4 bending element is that it is quadratic in nodal displacements. Thus, the pertinent tangential stiffness matrix is a constant which does not needs to be updated in the iterative solution process. For the elastic energy in the crease, a 4-node crease element is derived in which the dot product of two vectors connecting the crease and the adjacent nodes are used to determine the fold angle which is the complement of the dihedral angle of the crease. A similar way of computing the dihedral angle can be noted in (Bekker 1996). Here, the large-displacement but small-strain and small-curvature assumption for the facet is invoked to simplify the derivatives of the fold angle with respect to the nodal displacement. The 4-node crease element is equally applicable to model elastic hinges or, equivalently, hinges loaded with torsional springs. To manoeuver the origami into its deformed configuration, the rest angles which define the zero elastic energy states of the creases are changed to their target values incrementally.

The presented Q4 bending element and the 4-node crease element are implemented in ABAQUS thru two user-defined element subroutines. They together with the nonlinear T3 and Q4 3D membrane elements in ABAQUS realize the origami simulation in a finite element environment. Examples are presented to validate the two developed elements for modelling elastic hinges, origami, and kirigami structures.

2 Facet modelling

It will be assumed as in the bar-hinge approach that creases are straight and nodes carrying the dofs in the computation are located only at the endpoints of creases. As specified earlier, only triangular and quadrilateral facets will be considered. Unlike the bar-hinge approach, facets are treated as 2D continua and the material properties can be directly used in the computation.

2.1 Membrane deformation

The membrane deformation of the triangular and quadrilateral facets can be considered by any geometric nonlinear 3D T3 and Q4 membrane elements, respectively. Since ABAQUS does not have solely geometric nonlinear membrane element, its M3D3 T3 and M3D4 Q4 3D membrane elements for general nonlinearity are employed whilst the material is taken to be linear elastic and isotropic. In the two elements, membrane deformation is quantified by the in-plane logarithmic strain. Though logarithmic strain is unnecessarily complicated for small strain problems, M3D3 and M3D4 are adopted because ABAQUS does not display the user-defined element in its post-processor. The presence of the adjacent non-coplanar facets allows one to assume that the creases are straight due to the large membrane stiffness. The assumption implies the T3 facet cannot be bent and it is not necessary to consider its bending deformation. For the Q4 facet, the following subsection will derive a method to quantify the bending deformation under large displacement large rotation but small strain and small curvature assumption using a corotational consideration.

2.2 Bending deformation of quadrilateral facet

Figure 2 shows the initial, corotated and deformed configurations of a quadrilateral facet. In the initial configuration, the element is flat whilst P and Q are the overlapping points along the straight lines 1–3 and 2–4, respectively. The deformed and corotated configurations are obtained from initial configuration through respectively the displacement U and a rigid body displacement Uc defined with respect to the global coordinate (X, Y, Z). The location of node/point i (= 1, 2, 3, 4, P and Q) in the two configurations are denoted by i’ and ic. Since Uc is a rigid body displacement, 1c–2c–3c–4c is flat whilst Pc and Qc remain overlapping. A local Cartesian coordinate system (x, y, z) is set up in the initial configuration and becomes (xc, yc, zc) in the corotated configuration. Thus, the two sets of nodal coordinates (xi, yi) and \((x_{i}^{c} ,y_{i}^{c} )\) are identical. The deformed configuration can be obtained from the corotated configuration through the displacement u = {u,v,w}T defined with respect to (xc, yc, zc) of unit vectors (\({\mathbf{e}}_{x}^{c}\),\({\mathbf{e}}_{y}^{c}\),\({\mathbf{e}}_{z}^{c}\)) defined with respect to (X,Y,Z), i.e.

$$ {\mathbf{U}} = {\mathbf{U}}^{c} + [{\mathbf{e}}_{x}^{c} ,{\mathbf{e}}_{y}^{c} ,{\mathbf{e}}_{z}^{c} ]^{T} {\mathbf{u}} $$
(1)
Fig. 2
figure 2

a Initial, corotated and deformed configurations of the Q4 bending element, b P and Q are along the diagonals in the initial configuration

Full size image

The rigid body displacement Uc is chosen such that it brings 1c–2c–3c–4c close to 1′–2′–3′–4′ such that the small displacement assumption is applicable to u for deriving the strain and curvature. Its idea is similar to the approach for deriving curvatures in fabric materials (Sze and Liu 2009; Zhou and Sze 2012).

The interpolated (xc, yc) and u in terms of the parametric coordinates of the element ξ, η ∈ [− 1, + 1] can be expressed as

$$ \begin{aligned} \left\{ {\begin{array}{*{20}c} {x^{c} } \\ {y^{c} } \\ \end{array} } \right\} & = \sum\limits_{i = 1}^{4} {N_{i} \left\{ {\begin{array}{*{20}c} {x_{i}^{c} } \\ {y_{i}^{c} } \\ \end{array} } \right\}} = \sum\limits_{i = 1}^{4} {N_{i} \left\{ {\begin{array}{*{20}c} {x_{i} } \\ {y_{i} } \\ \end{array} } \right\}} = \left\{ {\begin{array}{*{20}c} {a_{0} + a_{1} \xi + a_{2} \xi \eta + a_{3} \eta } \\ {b_{0} + b_{1} \xi + b_{2} \xi \eta + b_{3} \eta } \\ \end{array} } \right\} \\ {\mathbf{u}} & = \left\{ {\begin{array}{*{20}c} u \\ v \\ w \\ \end{array} } \right\} = \sum\limits_{i = 1}^{4} {N_{i} {\mathbf{u}}_{i} } = \sum\limits_{i = 1}^{4} {N_{i} \left\{ {\begin{array}{*{20}c} {u_{i} } \\ {v_{i} } \\ {w_{i} } \\ \end{array} } \right\}} , \\ \end{aligned} $$
(2a,b)

where

$$ \left[ {\begin{array}{*{20}c} {N_{1} } \\ {N_{2} } \\ {N_{3} } \\ {N_{4} } \\ \end{array} } \right] = \frac{1}{4}\left[ {\begin{array}{*{20}c} {(1 - \xi )(1 - \eta )} \\ {(1 + \xi )(1 - \eta )} \\ {(1 + \xi )(1 + \eta )} \\ {(1 - \xi )(1 + \eta )} \\ \end{array} } \right],\quad \left[ {\begin{array}{*{20}c} {a_{0} } & {b_{0} } \\ {a_{1} } & {b_{1} } \\ {a_{2} } & {b_{2} } \\ {a_{3} } & {b_{3} } \\ \end{array} } \right] = \frac{1}{4}\left[ {\begin{array}{*{20}c} { + 1} & { + 1} & { + 1} & { + 1} \\ { - 1} & { + 1} & { + 1} & { - 1} \\ { + 1} & { - 1} & { + 1} & { - 1} \\ { - 1} & { - 1} & { + 1} & { + 1} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{1} } & {y_{1} } \\ {x_{2} } & {y_{2} } \\ {x_{3} } & {y_{3} } \\ {x_{4} } & {y_{4} } \\ \end{array} } \right]. $$

It can be checked that the deformed element edge, at ξ =  ± 1 or η =  ± 1, is linearly interpolated from the two edge end nodes. Hence, the straight crease assumption is always fulfilled by the element. From the interpolation in (2a), the chain rule of differentiation can be derived as

$$ \frac{\partial }{{\partial x^{c} }} = \frac{1}{j}\left( {(b_{2} \xi + b_{3} )\frac{\partial }{\partial \xi } - (b_{2} \eta + b_{1} )\frac{\partial }{\partial \eta }} \right),\quad \frac{\partial }{{\partial y^{c} }} = \frac{1}{j}\left( { - (a_{2} \xi + a_{3} )\frac{\partial }{\partial \xi } + (a_{2} \eta + a_{1} )\frac{\partial }{\partial \eta }} \right), $$
(3)

in which \(j = \frac{{\partial x^{c} }}{\partial \xi }\frac{{\partial y^{c} }}{\partial \eta } - \frac{{\partial x^{c} }}{\partial \eta }\frac{{\partial y^{c} }}{\partial \xi } = j_{0} + j_{1} \xi + j_{2} \eta\) is the Jacobian determinant and

$$ j_{0} = a_{1} b_{3} - a_{3} b_{1} ,\quad j_{1} = a_{1} b_{2} - a_{2} b_{1} ,\quad j_{2} = a_{2} b_{3} - a_{3} b_{2} . $$

The 3D Q4 element possesses 12 dofs and 6 rigid body modes. Hence, the element possesses 6 deformation modes among them 5 are membrane deformation modes. For a square element on the xc–yc–plane and with edges parallel to the xc- or yc-axis, the five membrane deformation modes are

$$ {\mathbf{u}} = \left\{ {\begin{array}{*{20}c} {x^{c} } \\ 0 \\ 0 \\ \end{array} } \right\},\quad {\mathbf{u}} = \left\{ {\begin{array}{*{20}c} 0 \\ {y^{c} } \\ 0 \\ \end{array} } \right\},\quad {\mathbf{u}} = \left\{ {\begin{array}{*{20}c} {y^{c} } \\ {x^{c} } \\ 0 \\ \end{array} } \right\},\quad {\mathbf{u}} = \left\{ {\begin{array}{*{20}c} {x^{c} y^{c} } \\ 0 \\ 0 \\ \end{array} } \right\},\quad {\mathbf{u}} = \left\{ {\begin{array}{*{20}c} 0 \\ {x^{c} y^{c} } \\ 0 \\ \end{array} } \right\}. $$
(4)

The remaining deformation mode is a bending mode. By applying the differential operator to the interpolated w in (2b), the following curvature components can be worked out

$$ \begin{aligned} \frac{{\partial^{2} w}}{{\partial^{2} x^{c} }} & = - \frac{{(b_{2} \xi + b_{3} )(b_{2} \eta + b_{1} )}}{{j^{3} }}j_{0} \Delta w;\quad \frac{{\partial^{2} w}}{{\partial^{2} y^{c} }} = - \frac{{(a_{2} \xi + a_{3} )(a_{2} \eta + a_{1} )}}{{j^{3} }}j_{0} \Delta w \\ 2\frac{{\partial^{2} w}}{{\partial x^{c} \partial y^{c} }} & = \frac{{(a_{1} \xi + a_{2} \xi \eta + a_{3} \eta )b_{2} + (b_{1} \xi + b_{2} \xi \eta + b_{3} \eta )a_{2} + a_{1} b_{3} + a_{3} b_{1} }}{{j^{3} }}j_{0} \Delta w \\ \end{aligned} $$
(5)

where

$$ \Delta w = \frac{{j_{0} + j_{1} + j_{2} }}{{2j_{0} }}w_{1} + \frac{{ - j_{0} + j_{1} - j_{2} }}{{2j_{0} }}w_{2} + \frac{{j_{0} - j_{1} - j_{2} }}{{2j_{0} }}w_{3} + \frac{{ - j_{0} - j_{1} + j_{2} }}{{2j_{0} }}w_{4} . $$
(6)

Hence, the bending mode is featured by Δw. To stabilize the bending mode, it would be sufficient to evaluate the bending energy using one point quadrature which samples the curvature at ξ = η = 0. Effectively, one takes

$$ \frac{{\partial^{2} w}}{{\partial^{2} x^{c} }} = \frac{{ - b_{3} b_{1} }}{{j_{0}^{2} }}\Delta w,\quad \frac{{\partial^{2} w}}{{\partial^{2} y^{c} }} = \frac{{ - a_{3} a_{1} }}{{j_{0}^{2} }}\Delta w,\quad 2\frac{{\partial^{2} w}}{{\partial x^{c} \partial y^{c} }} = \frac{{a_{1} b_{3} + a_{3} b_{1} }}{{j_{0}^{2} }}\Delta w. $$
(7)

For most papers, it is reasonable to assume isotropy. Thus, elastic energy of the Q4 bending element is

$$ U_{b} = \frac{1}{2}D\int\limits_{ - 1}^{ + 1} {\int\limits_{ - 1}^{ + 1} {\left\{ {\begin{array}{*{20}c} {\partial^{2} w/\partial^{2} x^{c} } \\ {\partial^{2} w/\partial^{2} y^{c} } \\ {2\partial^{2} w/\partial x^{c} \partial y^{c} } \\ \end{array} } \right\}\left[ {\begin{array}{*{20}c} 1 & \nu & 0 \\ \nu & 1 & 0 \\ 0 & 0 & {(1 - \nu )/2} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\partial^{2} w/\partial^{2} x^{c} } \\ {\partial^{2} w/\partial^{2} y^{c} } \\ {2\partial^{2} w/\partial x^{c} \partial y^{c} } \\ \end{array} } \right\}jd\xi d\eta } } = \frac{{D^{e} }}{2}(\Delta w)^{2} $$
(8)

where D = Eh3/(1−ν2)/12 is the bending rigidity, E is the elastic modulus E, ν is the Poisson’s ratio, h is the paper thickness and \(D^{e} = 2D[2(b_{3} b_{1} + a_{3} a_{1} )^{2} + (1 - \nu )j_{0}^{2} ]/j_{0}^{3}\). More complicated material models can also be considered.

A physical interpretation of \(\Delta w\) in (7) is then identified by referring to points Pc and Qc in Fig. 2b. As a point of remark, Pc is along 1c–3c, Qc is along 2c–4c and the two points are intersecting. It can be solved that

$$ \left\{ {\begin{array}{*{20}c} {x_{P}^{c} } \\ {y_{P}^{c} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {x_{Q}^{c} } \\ {y_{Q}^{c} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {x_{P}^{{}} } \\ {y_{P}^{{}} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {x_{Q}^{{}} } \\ {y_{Q}^{{}} } \\ \end{array} } \right\} = \frac{1}{{j_{0} }}\left\{ {\begin{array}{*{20}c} {a_{0} j_{0} - a_{1} j_{1} - a_{3} j_{2} } \\ {b_{0} j_{0} - b_{1} j_{1} - b_{3} j_{2} } \\ \end{array} } \right\}. $$
(9)

Now, u of Pc is linearly interpolated from those at 1c and 3c whilst the displacement of Qc is linearly interpolated from those of 2c and 4c. Thus,

$$ {\mathbf{u}}_{P} - {\mathbf{u}}_{Q} = \left\{ {\begin{array}{*{20}c} {u_{P} - u_{Q} } \\ {v_{P} - v_{Q} } \\ {w_{P} - w_{Q} } \\ \end{array} } \right\} = \frac{{l_{1P} {\mathbf{u}}_{3} + l_{P3} {\mathbf{u}}_{1} }}{{l_{13} }} - \frac{{l_{2Q} {\mathbf{u}}_{4} + l_{Q4} {\mathbf{u}}_{2} }}{{l_{24} }} = M_{1} {\mathbf{u}}_{1} + M_{2} {\mathbf{u}}_{2} + M_{3} {\mathbf{u}}_{3} + M_{4} {\mathbf{u}}_{4} $$
(10)

where \(l_{ij} = \sqrt {(x_{i} - x_{j} )^{2} + (y_{i} - y_{j} )^{2} }\) and \(M_{1} = \frac{{l_{P3} }}{{l_{13} }},\;M_{2} = - \frac{{l_{Q4} }}{{l_{24} }},\;M_{3} = \frac{{l_{1P} }}{{l_{13} }},\;M_{4} = - \frac{{l_{2Q} }}{{l_{24} }}\). Recalling.

\(\left( {\frac{{l_{1P} }}{{l_{13} }},\frac{{l_{P3} }}{{l_{13} }}} \right) = \left( {\frac{{x_{1} - x_{P} }}{{x_{1} - x_{3} }},\frac{{x_{P} - x_{3} }}{{x_{1} - x_{3} }}} \right)\) for \(x_{1} \ne x_{3}\), \(\left( {\frac{{l_{1P} }}{{l_{13} }},\frac{{l_{P3} }}{{l_{13} }}} \right) = \left( {\frac{{y_{1} - y_{P} }}{{y_{1} - y_{3} }},\frac{{y_{P} - y_{3} }}{{y_{1} - y_{3} }}} \right)\) for \(y_{1} \ne y_{3}\),

\(\left( {\frac{{l_{2Q} }}{{l_{24} }},\frac{{l_{Q4} }}{{l_{24} }}} \right) = \left( {\frac{{x_{2} - x_{Q} }}{{x_{2} - x_{4} }},\frac{{x_{Q} - x_{4} }}{{x_{2} - x_{4} }}} \right)\) for \(x_{2} \ne x_{4}\) and \(\left( {\frac{{l_{2Q} }}{{l_{24} }},\frac{{l_{Q4} }}{{l_{24} }}} \right) = \left( {\frac{{y_{2} - y_{Q} }}{{y_{2} - y_{4} }},\frac{{y_{Q} - y_{4} }}{{y_{2} - y_{4} }}} \right)\) for \(y_{2} \ne y_{4}\),

further manipulations can show that

$$ w_{P} - w_{Q} = \Delta w $$
(11)

which provides a physical interpretation of \(\Delta w\) defined in (6). For thin beam/plate under small displacement, it is well-known that the out-of-plane displacement will dominate in general. A simple illustration is given in Fig. 3. Unless the tip force is applied axially to the cantilever (α = 0), otherwise the out-of-plane displacement would be far larger than the in-plane displacement for thin beams. Thus, u would be dominated by w and a good approximation to (11) after taking the magnitude is

$$ \left| {\Delta w} \right| = \left| {w_{P} - w_{Q} } \right| = \left| {{\mathbf{u}}_{P} - {\mathbf{u}}_{Q} } \right|. $$
(12)
Fig. 3
figure 3

A cantilever with an inclined tip force acting and the ratio of its out-of-plane to in-plane deflection at the tip. For thin bean L2 >  > I/A

Full size image

Applying the same method of interpolation of u in the corotated configuration, see (10), to U in the initial configuration, one obtains

$$ {\mathbf{U}}_{P} - {\mathbf{U}}_{Q} = \frac{{l_{1P} {\mathbf{U}}_{3} + l_{P3} {\mathbf{U}}_{1} }}{{l_{13} }} - \frac{{l_{2Q} {\mathbf{U}}_{4} + l_{Q4} {\mathbf{U}}_{2} }}{{l_{24} }} = [M_{1} {\mathbf{I}}_{3} ,M_{2} {\mathbf{I}}_{3} ,M_{3} {\mathbf{I}}_{3} ,M_{4} {\mathbf{I}}_{3} ]\left\{ {\begin{array}{*{20}c} {{\mathbf{U}}_{1} } \\ \vdots \\ {{\mathbf{U}}_{4} } \\ \end{array} } \right\} $$
(13)

By invoking (1),

$$ {\mathbf{U}}_{P} - {\mathbf{U}}_{Q} = ({\mathbf{U}}_{P}^{c} + [{\mathbf{e}}_{x} ,{\mathbf{e}}_{y} ,{\mathbf{e}}_{z} ]^{T} {\mathbf{u}}_{P} ) - ({\mathbf{U}}_{Q}^{c} + [{\mathbf{e}}_{x} ,{\mathbf{e}}_{y} ,{\mathbf{e}}_{z} ]^{T} {\mathbf{u}}_{Q} ) = [{\mathbf{e}}_{x} ,{\mathbf{e}}_{y} ,{\mathbf{e}}_{z} ]^{T} ({\mathbf{u}}_{P} - {\mathbf{u}}_{Q} ) $$
(14)

in which \({\mathbf{U}}_{P}^{c}\) and \({\mathbf{U}}_{Q}^{c}\) cancel each other because Pc and Qc are overlapping. By incorporating (12), (13), (13) and the property of the orthogonal matrix \([{\mathbf{e}}_{x}^{c} ,{\mathbf{e}}_{y}^{c} ,{\mathbf{e}}_{z}^{c} ]\), (8) can be expressed as

$$ \begin{aligned} U_{b} & = \frac{{D{}^{e}}}{2}(\Delta w)^{2} = \frac{{D{}^{e}}}{2}({\mathbf{u}}_{P} - {\mathbf{u}}_{Q} )^{T} ({\mathbf{u}}_{P} - {\mathbf{u}}_{Q} ) = \frac{{D^{e} }}{2}({\mathbf{U}}_{P} - {\mathbf{U}}_{Q} )^{T} ({\mathbf{U}}_{P} - {\mathbf{U}}_{Q} ) \\ & = \frac{1}{2}\left\{ {\begin{array}{*{20}c} {{\mathbf{U}}_{1} } \\ {{\mathbf{U}}_{2} } \\ {{\mathbf{U}}_{3} } \\ {{\mathbf{U}}_{4} } \\ \end{array} } \right\}^{T} \left( {D^{e} \left[ {\begin{array}{*{20}c} {M_{1} M_{1} {\mathbf{I}}_{3} } & {M_{1} M_{2} {\mathbf{I}}_{3} } & {M_{1} M_{3} {\mathbf{I}}_{3} } & {M_{1} M_{4} {\mathbf{I}}_{3} } \\ {M_{2} M_{1} {\mathbf{I}}_{3} } & {M_{2} M_{2} {\mathbf{I}}_{3} } & {M_{2} M_{3} {\mathbf{I}}_{3} } & {M_{2} M_{4} {\mathbf{I}}_{3} } \\ {M_{3} M_{1} {\mathbf{I}}_{3} } & {M_{3} M_{2} {\mathbf{I}}_{3} } & {M_{3} M_{3} {\mathbf{I}}_{3} } & {M_{3} M_{4} {\mathbf{I}}_{3} } \\ {M_{4} M_{1} {\mathbf{I}}_{3} } & {M_{4} M_{2} {\mathbf{I}}_{3} } & {M_{4} M_{3} {\mathbf{I}}_{3} } & {M_{4} M_{4} {\mathbf{I}}_{3} } \\ \end{array} } \right]} \right)\left\{ {\begin{array}{*{20}c} {{\mathbf{U}}_{1} } \\ {{\mathbf{U}}_{2} } \\ {{\mathbf{U}}_{3} } \\ {{\mathbf{U}}_{4} } \\ \end{array} } \right\} \\ \end{aligned} $$
(15)

where the matrix inside the braces is the tangential stiffness matrix of the Q4 bending element. Unlike most tangential stiffness matrix used in nonlinear analysis, the present one is a constant matrix which does not need to be updated in the iterative solution procedure and is in line with that for quantifying the bending energy in fabrics in (Sze and Liu 2009; Zhou and Sze 2012). Unlike the conventional corotational formulation, the choice of the corotational configuration is purely notional here as the above energy is independent of Uc.

3 Crease modelling

Inter-facet edges are creases which are often modelled as spring-loaded hinges. Previous determinations of the dihedral angle involve using simultaneous dot and cross products of selected vectors (Liu and Paulino 2017; Schenk and Guest 2011; Bekker 1996). Alternatively, the arctan2 function is used at the expense of using two arguments in the function (Gillman et al. 2018). Based on the large-displacement but small-strain and small-curvature assumption, an approximate method is here devised that can considerably simplify the fold angle, a complement of dihedral angle, and its derivatives with respect to the nodal displacement.

Left-hand side of Fig. 4 shows the initial crease 1–3 between the flat facets 1–2-3 and 1–3–4–E. Among nodes 4 and E, the one closer to the mid-point of 1–3, i.e. node 4, is used to determine the initial fold angle θo which is normally zero. P and Q are points along 1–3 such that P-4 and Q-2 are perpendicular to 1–3. Thus, the position vectors XP and XQ can be expressed as:

$$ {\mathbf{X}}_{P} = {\mathbf{X}}_{1} + s_{P} ({\mathbf{X}}_{3} - {\mathbf{X}}_{1} ).\quad {\mathbf{X}}_{Q} = {\mathbf{X}}_{1} + s_{Q} ({\mathbf{X}}_{3} - {\mathbf{X}}_{1} ) $$
(16)

where the non-dimensional coordinates sp and sQ can be solved from the orthogonality relations \(({\mathbf{X}}_{3} - {\mathbf{X}}_{1} ) \cdot ({\mathbf{X}}_{4} - {\mathbf{X}}_{P} ) = 0\) and \(({\mathbf{X}}_{3} - {\mathbf{X}}_{1} ) \cdot ({\mathbf{X}}_{2} - {\mathbf{X}}_{Q} ) = 0\) to be

$$ s_{P}^{{}} = \frac{{({\mathbf{X}}_{3} - {\mathbf{X}}_{1} ) \cdot ({\mathbf{X}}_{4} - {\mathbf{X}}_{1} )}}{{|{\mathbf{X}}_{3} - {\mathbf{X}}_{1} |^{2} }},\quad s_{Q}^{{}} = \frac{{({\mathbf{X}}_{3} - {\mathbf{X}}_{1} ) \cdot ({\mathbf{X}}_{2} - {\mathbf{X}}_{1} )}}{{|{\mathbf{X}}_{3} - {\mathbf{X}}_{1} |^{2} }}. $$
(17)
Fig. 4
figure 4

The crease 1–3 between the facets 1–2–3 and 1–3–4–E in its initial and deformed configurations. The fold angle changes from θo to θ

Full size image

Thus,

$$ \underline{P4} = {\mathbf{X}}_{4} - {\mathbf{X}}_{P} = {\mathbf{X}}_{4} - (1 - s_{P} ){\mathbf{X}}_{1} - s_{P} {\mathbf{X}}_{3} ,\quad \underline{Q2} = {\mathbf{X}}_{2} - {\mathbf{X}}_{Q} = {\mathbf{X}}_{2} - (1 - s_{Q} ){\mathbf{X}}_{1} - s_{Q} {\mathbf{X}}_{3} . $$
(18)

In the equation, IJ denotes the vector from I to J where I, J = 1, 2, 3, 4, P and Q. The initial fold angle θo can be obtained as

$$ \cos \theta_{o} = - \frac{{\underline{P4} \cdot \underline{Q2} }}{{\left| {\underline{P4} } \right| \cdot \left| {\underline{Q2} } \right|}}\quad {\text{and}}\quad \theta_{o} = \left\{ {\begin{array}{*{20}c} {\cos^{ - 1} \left( { - \frac{{\underline{P4} \cdot \underline{Q2} }}{{\left| {\underline{P4} } \right| \cdot \left| {\underline{Q2} } \right|}}} \right)} & {{\text{for (}}\underline{P4} \times \underline{Q2} ) \cdot ({\mathbf{X}}_{3} - {\mathbf{X}}_{1} ) > 0} \\ { - \cos^{ - 1} \left( { - \frac{{\underline{P4} \cdot \underline{Q2} }}{{\left| {\underline{P4} } \right| \cdot \left| {\underline{Q2} } \right|}}} \right)} & {{\text{otherwise}}} \\ \end{array} } \right. $$
(19)

in which cos−1 returns the principal value of the angle between 0 and π. It is trivial that the fold angle and dihedral angle are complementary, i.e. their sum is π. A similar way of computing the dihedral angle can be noted in (Bekker 1996).

After displacement U, J moves to J′ whose position vector is XJ’ = XJ + UJ. Following (18), the displaced P4 and Q2 become

$$ {\mathbf{p}} = \underline{P^{\prime}4^{\prime}} = \underline{P4} + {\mathbf{U}}_{4} - (1 - s_{P} ){\mathbf{U}}_{1} - s_{P} {\mathbf{U}}_{3} ,\quad {\mathbf{q}} = \underline{Q^{\prime}2^{\prime}} = \underline{Q2} + {\mathbf{U}}_{2} - (1 - s_{Q} ){\mathbf{U}}_{1} - s_{Q} {\mathbf{U}}_{3} . $$
(20)

The deformation due to crease folding often dominates the overall deformation to which the facet membrane and bending deformations also contribute. Under the large-displacement but small-strain and small-curvature assumption for the facet, close approximations to the fold angle θ and the unit vector n along p × q can be taken to be

$$ \cos \theta = - \frac{{{\mathbf{p}} \cdot {\mathbf{q}}}}{pq}\quad {\text{and}}\quad \theta = \left\{ {\begin{array}{*{20}c} {\cos^{ - 1} \left( { - \frac{{{\mathbf{p}} \cdot {\mathbf{q}}}}{pq}} \right)} & {{\text{for (}}{\mathbf{p}} \times {\mathbf{q}}) \cdot \underline{1^{\prime}3^{\prime}} > 0} \\ { - \cos^{ - 1} \left( { - \frac{{{\mathbf{p}} \cdot {\mathbf{q}}}}{pq}} \right)} & {{\text{otherwise}}} \\ \end{array} } \right. $$
(21a,b)

and

$$ {\mathbf{n}} = \frac{{{\mathbf{X}}_{3^{\prime}}^{{}} - {\mathbf{X}}_{1^{\prime}}^{{}} }}{{|{\mathbf{X}}_{3^{\prime}}^{{}} - {\mathbf{X}}_{1^{\prime}}^{{}} |}} = \frac{{{\mathbf{X}}_{3}^{{}} + {\mathbf{U}}_{3}^{{}} - {\mathbf{X}}_{1}^{{}} - {\mathbf{U}}_{1}^{{}} }}{{|{\mathbf{X}}_{3}^{{}} + {\mathbf{U}}_{3}^{{}} - {\mathbf{X}}_{1}^{{}} - {\mathbf{U}}_{1}^{{}} |}}, $$
(22)

where p =|p| and q =|q|. By invoking the relations in (20), derivative in (21a) with respect to UC is

$$ \frac{\partial \theta }{{\partial {\mathbf{U}}_{4} }} = \frac{1}{\sin \theta }\left( {\frac{{\mathbf{q}}}{pq} - \frac{{{\mathbf{p}} \cdot {\mathbf{q}}}}{{p^{2} q}}\frac{\partial p}{{\partial {\mathbf{U}}_{4} }}} \right) = - \frac{{({\mathbf{p}} \cdot {\mathbf{q}}){\mathbf{p}} - ({\mathbf{p}} \cdot {\mathbf{p}}){\mathbf{q}}}}{{p^{3} q\sin \theta }}. $$
(23)

By substituting a = b = p and c = q substituted into the identity a × (b × c) = (a·c)b − (a·b)c, one gets p × (p × q) = (p·q)p − (p·p)q and

$$ \frac{\partial \theta }{{\partial {\mathbf{U}}_{4} }} = - \frac{{{\mathbf{p}} \times ({\mathbf{p}} \times {\mathbf{q}})}}{{p^{3} q\sin \theta }} = - \frac{{\mathbf{p}}}{{p^{2} }} \times \left( {\frac{{{\mathbf{p}} \times {\mathbf{q}}}}{pq\sin \theta }} \right) = - \frac{{{\mathbf{p}} \times {\mathbf{n}}}}{{p^{2} }}. $$
(24)

Similarly, one can derive

$$ \frac{\partial \theta }{{\partial {\mathbf{U}}_{2} }} = - \frac{{{\mathbf{n}} \times {\mathbf{q}}}}{{q^{2} }}. $$
(25)

By invoking (20), it can be shown that

$$ \frac{\partial \theta }{{\partial {\mathbf{U}}_{1} }} = - (1 - s_{P} )\frac{\partial \theta }{{\partial {\mathbf{U}}_{4} }} - (1 - s_{Q} )\frac{\partial \theta }{{\partial {\mathbf{U}}_{2} }},\quad \frac{\partial \theta }{{\partial {\mathbf{U}}_{3} }} = - s_{P} \frac{\partial \theta }{{\partial {\mathbf{U}}_{4} }} - s_{Q} \frac{\partial \theta }{{\partial {\mathbf{U}}_{2} }}. $$
(26)

From (22), (24), (25) and (26), all the first order derivatives of θ with respect to the nodal displacement are determined.

Before proceeding to the second order derivatives of θ, the following identities for any arbitrary vectors a = {ai} and b = {bi} are recalled:

$$ {\mathbf{a}} \times {\mathbf{b}} = [{\mathbf{a}}]_{ \times } {\mathbf{b}},\quad {\mathbf{a}} \otimes ({\mathbf{a}} \times {\mathbf{b}}) - ({\mathbf{a}} \times {\mathbf{b}}) \otimes {\mathbf{a}} = ({\mathbf{a}} \cdot {\mathbf{a}})[{\mathbf{b}}]_{ \times } - ({\mathbf{a}} \cdot {\mathbf{b}})[{\mathbf{a}}]_{ \times } , $$
(27a,b)

where

$$ [{\mathbf{c}}]_{ \times } = \left[ {\begin{array}{*{20}c} 0 & { - c_{3} } & {c_{2} } \\ {c_{3} } & 0 & { - c_{1} } \\ { - c_{2} } & {c_{1} } & 0 \\ \end{array} } \right]{\text{for}}\,{\text{ any}}\,{\text{ vector}}\,{\mathbf{c}} = \left\{ {c_{i} } \right\}\, {\text{and}}\, {\mathbf{a}} \otimes {\mathbf{b}} = [a_{i} b_{j} ]. $$

By taking a = p and b = n, and invoking the approximation p·n = 0, (27b) becomes

$$ {\mathbf{p}} \otimes ({\mathbf{p}} \times {\mathbf{n}}) - ({\mathbf{p}} \times {\mathbf{n}}) \otimes {\mathbf{p}} = p^{2} [{\mathbf{n}}]_{ \times } . $$
(28)

Noting that n in (22) is independent of U2 and U4, (28) leads to

$$ \frac{{\partial^{2} \theta }}{{\partial {\mathbf{U}}_{4}^{T} \partial {\mathbf{U}}_{4} }} = \frac{{[{\mathbf{n}}]_{ \times } }}{{p^{2} }} + \frac{2}{{p^{4} }}({\mathbf{p}} \times {\mathbf{n}}) \otimes {\mathbf{p}} = \frac{1}{{p^{4} }}[({\mathbf{p}} \times {\mathbf{n}}) \otimes {\mathbf{p}} + {\mathbf{p}} \otimes ({\mathbf{p}} \times {\mathbf{n}})] $$
(29)

By invoking q·n = 0, one can similarly obtain

$$ \frac{{\partial^{2} \theta }}{{\partial {\mathbf{U}}_{2} \partial {\mathbf{U}}_{2} }} = - \frac{{[{\mathbf{n}}]_{ \times } }}{{q^{2} }} - \frac{2}{{q^{4} }}({\mathbf{q}} \times {\mathbf{n}}) \otimes {\mathbf{q}} = - \frac{1}{{q^{4} }}[({\mathbf{q}} \times {\mathbf{n}}) \otimes {\mathbf{q}} + {\mathbf{q}} \otimes ({\mathbf{q}} \times {\mathbf{n}})] $$
(30)

By recalling (20), other second-order derivatives of θ with respect to the nodal displacement can be expressed as

$$ \begin{aligned} \frac{{\partial^{2} \theta }}{{\partial {\mathbf{U}}_{4}^{T} \partial {\mathbf{U}}_{2}^{{}} }} & = {\mathbf{0}},\quad \frac{{\partial^{2} \theta }}{{\partial {\mathbf{U}}_{4}^{T} \partial {\mathbf{U}}_{1} }} = - (1 - s_{P} )\frac{{\partial^{2} \theta }}{{\partial {\mathbf{U}}_{4}^{T} \partial {\mathbf{U}}_{4} }},\quad \frac{{\partial^{2} \theta }}{{\partial {\mathbf{U}}_{4}^{T} \partial {\mathbf{U}}_{3} }} = - s_{P} \frac{{\partial^{2} \theta }}{{\partial {\mathbf{U}}_{4}^{T} \partial {\mathbf{U}}_{4} }}, \\ \frac{{\partial^{2} \theta }}{{\partial {\mathbf{U}}_{2}^{T} \partial {\mathbf{U}}_{1} }} & = - (1 - s_{Q} )\frac{{\partial^{2} \theta }}{{\partial {\mathbf{U}}_{2}^{T} \partial {\mathbf{U}}_{2} }},\quad \frac{{\partial^{2} \theta }}{{\partial {\mathbf{U}}_{2}^{T} \partial {\mathbf{U}}_{3} }} = - s_{Q} \frac{{\partial^{2} \theta }}{{\partial {\mathbf{U}}_{2}^{T} \partial {\mathbf{U}}_{2} }}, \\ \frac{{\partial^{2} \theta }}{{\partial {\mathbf{U}}_{1}^{T} \partial {\mathbf{U}}_{1} }} & = (1 - s_{P} )^{2} \frac{{\partial^{2} \theta }}{{\partial {\mathbf{U}}_{4}^{T} \partial {\mathbf{U}}_{4} }} + (1 - s_{Q} )^{2} \frac{{\partial^{2} \theta }}{{\partial {\mathbf{U}}_{2}^{T} \partial {\mathbf{U}}_{2} }}, \\ \frac{{\partial^{2} \theta }}{{\partial {\mathbf{U}}_{1}^{T} \partial {\mathbf{U}}_{3} }} & = s_{P} (1 - s_{P} )\frac{{\partial^{2} \theta }}{{\partial {\mathbf{U}}_{4}^{T} \partial {\mathbf{U}}_{4} }} + s_{Q} (1 - s_{Q} )\frac{{\partial^{2} \theta }}{{\partial {\mathbf{U}}_{2}^{T} \partial {\mathbf{U}}_{2} }}, \\ \frac{{\partial^{2} \theta }}{{\partial {\mathbf{U}}_{3}^{T} \partial {\mathbf{U}}_{3} }} & = s_{P}^{2} \frac{{\partial^{2} \theta }}{{\partial {\mathbf{U}}_{4}^{T} \partial {\mathbf{U}}_{4} }} + s_{Q}^{2} \frac{{\partial^{2} \theta }}{{\partial {\mathbf{U}}_{2}^{T} \partial {\mathbf{U}}_{2} }}. \\ \end{aligned} $$
(31)

The elastic energy of the crease can be assumed to be

$$ U_{c} = \frac{kl}{2}(\theta - \theta_{o} )^{2} $$
(32)

where k is the fold stiffness per unit length of the crease and l =|X3—X1| is the initial length of the crease. The internal force and tangent stiffness matrix are

$$ {\mathbf{f}}_{c} = \left\{ {\begin{array}{*{20}c} {{\mathbf{f}}_{1} } \\ {{\mathbf{f}}_{2} } \\ {{\mathbf{f}}_{3} } \\ {{\mathbf{f}}_{4} } \\ \end{array} } \right\}\quad {\text{and}}\quad {\mathbf{k}}_{c} = \left[ {\begin{array}{*{20}c} {{\mathbf{k}}_{11} } & {{\mathbf{k}}_{12} } & {{\mathbf{k}}_{13} } & {{\mathbf{k}}_{14} } \\ {} & {{\mathbf{k}}_{22} } & {{\mathbf{k}}_{23} } & {{\mathbf{k}}_{24} } \\ {} & {} & {{\mathbf{k}}_{33} } & {{\mathbf{k}}_{34} } \\ {sym.} & {} & {} & {{\mathbf{k}}_{44} } \\ \end{array} } \right] $$
(33)

in which

$$ {\mathbf{f}}_{i} = \frac{{\partial U_{c} }}{{\partial {\mathbf{U}}_{i} }} = kl(\theta - \theta_{o} )\frac{\partial \theta }{{\partial {\mathbf{U}}_{i} }}\quad {\text{and}}\quad {\mathbf{k}}_{ij} = \frac{{\partial^{2} U}}{{\partial {\mathbf{U}}_{i}^{T} \partial {\mathbf{U}}_{j} }} = kl\frac{\partial \theta }{{\partial {\mathbf{U}}_{i} }} \otimes \frac{\partial \theta }{{\partial {\mathbf{U}}_{j} }} + kl(\theta - \theta_{o} )\frac{{\partial^{2} \theta }}{{\partial {\mathbf{U}}_{i}^{T} \partial {\mathbf{U}}_{j} }} $$
(34)

in which derivatives of θ has been derived in (24) to (26) and (29) to (31). As the crease involves nodes 1, 2, 3 and 4, it would be termed and implemented as a 4-node crease element. It is trivial that the crease element is equally applicable to model elastic hinges.

4 Prescribing fold angles

In origami simulation, it is sometimes more convenient to prescribe the fold angle θ to its rest angle θrest which defines the zero energy configuration of the crease (Ghassaei et al. 2018). Furthermore, it is often necessary to apply the prescribed θrest incrementally to minimize divergence in the nonlinear solution procedure. To effect θ = θrest incrementally, the elastic energy of the crease can be modified to

$$ U_{c} = \frac{kl}{2}(\theta - \overline{\theta })^{2} $$
(35)

where \(\overline{\theta } = (1 - t)\theta_{o} + t\theta_{rest}\) and t varies from 0 (start of the analysis step) to 1 (end of the analysis step). The related element internal force vector and tangential stiffness matrix can be obtained by replacing θo with \(\overline{\theta }\) in (34). In reality, multiple creases would be prescribed with their rest angles and θs may only be approximately equal to \(\overline{\theta }\) s in the converged solution. For simplicity, prescription of the rest angle as the means to deform an origami would be termed as the rest angle loading.

5 Numerical examples

The Q4 bending element and the 4-node crease element are incorporated into ABAQUS thru its user-defined element or UEL subroutines. They are co-used with ABAQUS’s 3D membrane elements M3D4 and M3D3 to realize the origami simulations. Modification of the subroutine is needed for specifying the rest-angle loading. In the automatic time increment feature of ABAQUS, the prescribed loading is applied incrementally as a function of time t which varies from 0 (start of the analysis step) to 1 (end of the analysis step). For each increment, the Newton–Raphson method is used to refine the iterative solution until the default convergence criteria, i.e. the 0.5% force tolerance and the 1% displacement tolerance, are met simultaneously. Unless specified otherwise, the default automatic time increment is employed with the initial and minimum time increment set to be 1 and 10–5, respectively. In the automatic time increment process, if the solution cannot converge within 16 iterations, the scheme abandons the increment and starts again with the time increment reduced to one-quarter of the present value. If the solution still fails to converge, the scheme reduces the increment again. If the time increment becomes smaller than the minimum or the solution fails after 5 reductions, the analysis will be aborted. On the other hand, the time increment increases by 50% if the last two converged solutions are both attained within 5 iterations. The computation is conducted in the same laptop PC, with Intel(R) Core(TM) i9-9880H CPU (8 cores, 2.30 GHz) and 64 GB RAM, used to produce the results in Fig. 1 and Table 1.

In the description of the examples and the ABAQUS calculations, SI units are employed and would not be further specified. The properties of paperboard E = 3 × 109, ν = 0.3 and h = 0.27 × 10–3 are adopted (Filipov et al. 2017; Schulgasser 1983). The fold stiffness per unit crease length is taken to be proportional to the bending rigidity, i.e., k = D/L* where L* is a length scaling factor (Lechenault et al. 2014). For paperboards, L* varies typically from 1.6 × 10–3 to 133 × 10–3 m, see Table 1 of reference (Filipov et al. 2017). In Sects. 5.1, 5.2, 5.3 and 5.6, k = 0.1 is used which corresponds to L* = 54 × 10–3. The video animation files for the examples are provided as Online Resources. They are prepared by the post-processor of ABAQUS with at least 60 time increments to enhance the visual smoothness.

5.1 Elastic hinge

This example considers two identical panels connected by an elastic hinge and aims at illustrating the efficacy of the proposed crease element. It also serves to compare the convergence of different elements used to model the panels. The dimensions of the panels are: L = 2, W = 1 and H = 0.05. Practically, no strain will be induced in the panels. The nonlinearity of the problem mainly comes from the large displacement and rotation experienced by the elements. Here, four modelling methods are considered.

In the first method of modelling, the panels are modelled by ABAQUS’s SC8R solid-shell element model which possesses no rotation dof. Eight elements are employed as shown in Fig. 5. B1 to B5 are pinned. C1 and C2 are restrained from moving along the X-direction. An elastic hinge is realized by having four nodes along A1A3 common to the two panels. The crease element A1A2A3A4 with initial fold angle θo = π, see Fig. 5a, provides the elastic effect to the hinge. A rest angle loading with θrest = 0 is applied to unfold the panels. An intermediate configuration at θ ≈ 2π/3 and the final configuration at θ = 0 are shown in Fig. 5b, c, respectively. The animation video is given in Online Resource 1.

Fig. 5
figure 5

Two panels connected by an elastic hinge. a The initial, b an intermediate and c the final configurations predicted by the 8-node solid-shell element model SC8R. The crease element A1A2A3A4 is defined using nodes on the faces of the two panels

Full size image

In the second method of modelling, A2 and A4 that define the crease element are then changed to nodes on the side edges of the panels, See Fig. 6. In other words, the crease element is initially flat (θo = 0) and fully folded in the final configuration (θrest = π). The animation video is given in Online Resource 2.

Fig. 6
figure 6

Two panels connected by an elastic hinge. a The initial, b an intermediate and c the final configurations predicted by the 8-node solid-shell element model SC8R. The crease element A1A2A3A4 is defined using nodes on the side edges of the two panels

Full size image

In the third method of modelling, the S4R shell element model in ABAQUS is employed, see Fig. 7. The element possesses 4-node on the mid-surface of the plate/shell and each node has 3 translational and 3 rotational dofs. The boundary conditions prescribed to Bis and Cis are the same as those in SC8R. To avoid coupling the rotational dofs of the elements modelling the two panels, the two panels are created separately. The translational dofs of Eis and Fis are then tied by using the Multi-Point Constraint of PIN type in ABAQUS so that Eis and Fis share the same translational dofs. The crease element E2A2E4A4 with initial fold angle θo = π–0.1 is defined to provide the elastic effect to the hinge between the two panels. It should be remarked that the more natural setting θo = π is not used because it would cause all Bis and Cis lying on the same vertical line. The two fully folded panels can spin freely about the vertical line leading to the singular of the initial global stiffness matrix. Again, rest angle loading with θrest = 0 is employed to unfold the panels. After the first few time increments, the time increments of ABAQUS remain to be ~ 0.0014 throughout the simulation, see Table 2. An intermediate configuration θ ≈ 2π/3 and the final configuration are shown in Fig. 7b, c, respectively. The animation video is given in Online Resource 3.

Fig. 7
figure 7

Two panels connected by an elastic hinge. a The initial, b an intermediate and c the final configurations predicted by the 4-node shell element model S4R

Full size image
Table 2 Numbers of time increments and CPU times consumed in the elastic hinge problem
Full size table

In the fourth method of modelling, the M3D4 3D membrane element model in ABAQUS, the Q4 bending element and crease elements are employed. The initial mesh is same as the one shown in Fig. 7a whilst the two panels share the same nodes at the elastic hinge. In other words, nodes Eis and Fis in Fig. 7b are identical and they need not be separately defined. Again, E2A2E4A4 is the crease element providing the elastic hinge effect. For 20 common element edges shared by adjacent elements within each panel, crease elements with a large stiffness (k = 1000) are defined to maintain the coplanarity of the panels. The predicted configurations are identical to those of the S4R shell element model in Fig. 7. The animation video is given in Online Resource 4.

The numbers of time increment and the CPU time consumed by the four methods of modelling are summarized in Table 2. The result echoes that the discussion in Sect. 1 on the relative convergence of the elements with and without rotational dofs. S4R shell element model consumes far more computing resource than the SC8R solid-shell element model which, in turn, is less computationally efficient than using the membrane element and the developed elements.

5.2 Simple pop-up Kirigami

This example considers the simple pop-up kirigami shown in Fig. 8. The kirigami is made from a square paper with two straight cuts B2B4 and C2C4. Initially, the paper is flat, i.e., θo = 0 for all creases. Nodes B0 and B3 are at the two sides of B2B4 whilst nodes C0 and C3 are at the two sides of C2C4. Nodes B1, B2, C1 and C2 are fixed. Both the displacement and rest angle loading are prescribed to pop up the kirigami. Same as the last example, strain inside the facets is negligible and the nonlinearity comes from the large displacement and rotation experienced by the elements. It can also be considered by solid-shell element readily at the expense of high computational cost.

Fig. 8
figure 8

a The initial configuration of a simple pop-up kirigami. B0 and B3 are at the two sides of the cut B2B4, C0 and C3 are at the two sides of the cut C2C4. b The final configuration

Full size image

For the displacement loading, the applied displacements are listed in Table 3. ABAQUS takes 18 increments and 1.4 s of CPU time to complete the computation. The final configuration is shown in Fig. 8b. The animation video is given in Online Resource 5. For the rest angle loading, the following rest fold angles are prescribed:

$$ \theta_{rest} = \left\{ {\begin{array}{*{20}l} { - \pi /2} \hfill & {{\text{for crease B}}_{{0}} {\text{C}}_{{0}} } \hfill \\ {\pi /2} \hfill & {{\text{for creases B}}_{{2}} {\text{C}}_{{2}} {\text{, B}}_{{4}} {\text{C}}_{{4}} {\text{, A}}_{{3}} {\text{B}}_{{3}} {\text{ and C}}_{{3}} {\text{D}}_{{3}} } \hfill \\ 0 \hfill & {\text{for other creases}} \hfill \\ \end{array} } \right.. $$
(36)
Table 3 Displacement loading conditions for the pop-up kirigami, see Fig. 8
Full size table

ABAQUS takes 8 increments and 0.8 s of CPU time to complete the computation. The final folded form is graphically indistinguishable from Fig. 8b. The animation video is given in Online Resource 6.

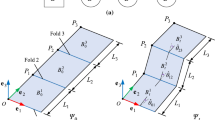
5.3 Crane

As the crane is a symbol of happiness and eternal youth in most Asian countries, it is probably the most popular origami. Crane folding is considered in this example (Ghassaei et al. 2018). Figure 9a shows the crease pattern which consists of triangular and quadrilateral facets. The zero displacement boundary conditions (1) U = 0 for A1, (2) V = 0 for A1 and A2, (3) W = 0 for A2, A3 and A4 are prescribed to prevent the rigid body movement of the origami. Same as the last example, both displacement and rest angle loadings are employed to deform the flat piece of paper in Fig. 9a, i.e. θo = 0, into the final folded form in Fig. 9b.

Fig. 9
figure 9

Crane. a The crease pattern where the valley folds (θrest > 0) and mountain folds (θrest < 0) are indicated by chained and solid lines, respectively. b A paper model of the folded form

Full size image

In the displacement loading, several nodes are prescribed with vertical displacements estimated from the final folded form in Fig. 9b listed in Table 4. The predicted final configuration is shown in Fig. 10a, b in different views. ABAQUS takes 11 increments and 0.7 s of CPU time to complete the computation. Figure 10b shows that the largest value of the maximum principal membrane strain is around 1.41%, justifying the small strain assumption. The animation video is given in Online Resource 7.

Table 4 Displacement loading conditions for the crane
Full size table
Fig. 10
figure 10

Crane under displacement loading (a) and (b): a isometric view of the final configuration and the Z-displacement plot, b top view of the final configuration and the maximum principal membrane strain plot. c and d are the predictions under rest angle loading

Full size image

In the rest angle loading case, the final rest angles for mountain and valley creases in Fig. 9a are set to be

$$ \theta_{{{\text{rest}}}} = \left\{ {\begin{array}{*{20}c} {\pi /2} & {{\text{for}}\,{\text{valley}}\,{\text{creases}}} \\ { - \pi /2} & {{\text{for}}\,{\text{mountain}}\,{\text{creases}}} \\ \end{array} } \right. $$

ABAQUS takes 13 increments and 1.2 s of CPU time to complete the computation. The final configuration is shown in Fig. 10c, d which resembles that of the displacement loading in Fig. 10a, d. The maximum principal membrane strain is plotted in Fig. 10d and the largest value is 1.37%. The animation video is given in Online Resource 8. Since whether a crease is a valley or mountain type can be told readily, it is more straightforward to prescribe rest angles than the nodal displacements at the expense of higher computational cost.

To reduce the computational cost, it is straight forward to use symmetric condition in the displacement loading but slave image nodes would be needed in the rest angle loading. However, origami simulation often aims at seeing the whole origami. Hence, we choose to model the whole origami.

5.4 Compressing the Miura-ori and the derived Kirigami

This example considers the folding of a Miura-ori and its derived kirigami under displacement compression (Liu and Paulino 2017). Figure 11a shows the flat Miura unit cell which is made up of four identical parallelograms with a = b = 0.02 and α = 60°.

Fig. 11
figure 11

a The flat Miura-ori unit cell: a = b = 0.02, α = 60°; θis are fold angles at the creases. b The Miura-ori with 5 × 5 unit cells and β = 118.27°. c The kirigami obtained by cutting away 32 facets from the Miura-ori

Full size image

The Miura-ori consists of 5 × 5-unit cells. In the flat configuration, β = 120°, L = Lflat = 0.1√3 ≈ 0.173 and W = Wflat = 0.2. To avoid the buckling instability under the compressive loading, the initial configuration in Fig. 11b is taken to be nearly flat (β = 118.27°) but not perfectly flat. On the supporting conditions, node O is fixed; the nodes at X = 0 are on the same vertical plane and their X-displacements are fixed. The nodes at the other end of X (≈ 0.172) are on another vertical plane and their X-displacements are prescribed to be − 0.16 under the compressive loading. For nodes on the X–Y-plane at the two ends, their Z-displacements are fixed.

The kirigami in Fig. 11c is obtained by cutting away 32 facets from the Miura-ori. Here, the paperboard is still adopted as the facet material. For the structures to behave like a mechanism with rigid panels connected by hinges, the ratio k/D should be small (Liu and Paulino 2017). To benchmark the predictions with the analytical solution based on the rigid facet assumption, the fold stiffness is reduced to k = 10–4. With the setting, the kirigami experiences convergence problem. In this light, its initial time increment is set to be 0.01 whilst that of the Miura-ori remains to be 1.

The width and height against the folding ratio are plotted in Fig. 12a for Miura-ori. The predictions agree well with the analytical solutions based on the rigid facet assumption (Wei et al. 2013). The dimensional changes of the kirigami are similar to those of the complete tessellation. The two partially folded configurations at L/Lflat = 0.87 and 0.55 are shown in Fig. 12b, c. Figure 13a, b show the histories of the crease energy and the reaction force (X-component) at the compressed end, respectively. They are essentially identical to the analytical solutions. Since the stiffness of the crease is much smaller than that of the facet, the deformation is confined to crease folding whilst the membrane and bending energies are negligible. Based on the rigid facet assumption, it is known that θ3 = -θ1 (minor folds) and θ4 = θ2 (major folds), see Fig. 11a for the labels, during the folding process (Lang and Howell 2018). The Miura-ori has 90 minor and major folds whilst this number decreases to 26 for the kirigami. Thus, Uc for the Miura-ori: Uc for the kirigami = 90: 26. The numerical predictions are in good agreement with this ratio, see Fig. 13a. The same ratio also holds for the magnitude of the reaction force which is shown in Fig. 13b. The animation videoes for Miura-ori and the derived kirigami are given in Online Resources 9 and 10, respectively.

Fig. 12
figure 12

a The width W and height H of the Miura-ori against the folding ratio (L/Lflat). “○” and “*”are the numerical predictions whilst the solid lines are the analytical solutions. b and c are partially folded configurations of the Kirigami at L/Lflat = 0.87 and 0.55, respectively

Full size image
Fig. 13
figure 13

a The crease energy and b the reaction force (X-component) at the compressed end for the Miura-ori and the Kirigami

Full size image

5.5 Pinching the Miura-ori and the derived Kirigami

This example considers the Miura-ori and its derived kirigami pinched at nodes A and B, see Fig. 14a, b. Node B is fixed whilst node A is prescribed with U = W = 0 and V = − 0.03. Node C is restrained from moving along the X-direction to avoid the rigid body rotation about the Y-axis. The crease stiffness per unit length is k = 1 and β equals 90° in the initial configuration. The other settings are the same as the previous example except that the initial time step for the kirigami resumes to 1. Figure 15a shows the final configuration for the Miura-ori which resembles a saddle and is in agreement with the experiment (Schenk and Guest 2011). To quantify the curved surface, a polynomial surface of degree 2 in both X and Y is constructed by least-square fit using the marked nodes in Fig. 14a, b. The curvatures κx and κy at node C are evaluated (Liu and Paulino 2017). The histories of the curvatures and reaction force (Y-component) are plotted against the displacement-VA in Fig. 15b. The results for the kirigami are shown in Fig. 15c, d. For both structures, κx and κy vary almost linearly with the displacement. Due to the removed facets, the reaction force of the kirigami is much lower than that of the Miura-ori. Moreover, the final configuration of kirigami is shallower than that of the Miura-ori, see Fig. 15a, c. This is also reflected by the magnitudes of the curvature in Fig. 15b, d. The animation videos for Miura-ori in the two different views are given in Online Resources 11 and 12 whilst those for the derived kirigami are given in Online Resources 13 and 14.

Fig. 14
figure 14

The initial configurations of a the Miura-ori and b the kirigami in which β = 90°

Full size image
Fig. 15
figure 15

The Miura-ori under pinching: a the isometric and side views of final configuration with the contour showing the Z-displacement, b the history of the reaction force (Y-component) at node A and the curvatures κx and κy. c, d are the predictions for the kirigami

Full size image

5.6 Kresling tube under compression

The Kresling pattern is a well-known origami pattern for deployable cylindrical tubes (Kresling 2008; Guest and Pellegrino 1994). The tube considered here consists of three layers along Z-axis and each layer is made up of 16 identical triangular facets as shown in Fig. 16a. There is no quadrilateral facet. The initial configuration is folded. It is specified by the height of the layer H = 0.05 and the radius of circumscribed circle R = H, see Fig. 16b. The Z-displacement W of the bottommost nodes A1 to A8 at Z = 0 are set to zero. To avoid rigid body movements, U at A3 and A7 are set to zero whilst V at A1 is set to zero. The topmost nodes at Z = 3H are prescribed with W = − 3H for compressing the tube. Figure 17a–c plot the vertical reaction force, energies and maximum principle stress against the normalized vertical displacement of the topmost nodes, respectively. Since this problem converges very rapidly, the initial and maximum time increments are respectively set to be 0.01 and 0.02 to enable a fine tracing of the load history. The reaction force first decreases from 0 to the minimum − 1300 at W/H ≈ − 0.27. The force then increases and becomes positive at W/H ≈ − 1 and thereafter. The reaction force equals to zero at W/H = 0, ≈ − 1 and = − 3. For 0 > W/H > − 1, a download force is required to compress the tube. For − 1 > W/H > −3, the tube would continue to retract by itself. From the reaction force and the total energy plots, the equilibriums are stable at W/H = 0 and − 3 whilst the equilibrium is unstable at W/H ≈ − 1. Hence, the tube is bi-stable (Cai et al. 2015; Liu and Paulino 2017). The animation video is given in Online Resource 15.

Fig. 16
figure 16

a The initial Kresling tube. The bottommost and topmost nodes are constrained with the Z-displacement 0 and – 3H, respectively. b The bottommost layer of the tube. H = R = 0.05

Full size image
Fig. 17
figure 17

Results for the Kresling tube plotted against the deflection: a the vertical reaction force; b the crease and total energies; c the maximum principal membrane strain

Full size image

5.7 Small strain small curvature assumption

The small strain small curvature assumption is adopted in the derivation of the Q4 bending and the 4-node crease elements. To justify the assumption, the maximum first principal membrane strain ε1 and the maximum ∆w/√j0 among all the elements at the end of last all successfully completed time increments are traced and listed in Table 5. It can be seen that the maximum ε1 is only 3.34% which is acceptable for small strain assumption. The small curvature assumption is more complicated. One should look at the ratio of the element size and the radius of curvature but not the curvature alone. In Appendix 1, the square element geometry is assumed for simplicity and the maximum ∆w/√j0 = 0.424 is employed to compare the curvatures computed by the small curvature assumption in (5) and obtained by fitting the deformed surface with circular arcs. The curvatures obtained by the two approaches differ only by 0.33%. Though the analysis involves approximations, the difference in the two curvatures is sufficiently small for adopting the small curvature assumption.

Table 5 Maximum ε1 and maximum ∆w/√j0 among all the elements
Full size table

6 Closure

A Q4 bending element and a 4-node crease element are developed in this paper for origami simulation. To account for the bending energy in the Q4 bending element, a corotational consideration is taken. Based on large displacement/rotation but small strain/curvature behaviour of the facet, the energy turns out to be a quadratic function of the nodal displacement. Thus, the relevant tangential stiffness matrix is constant and requires no update in the iterative solution process. On the other hand, the fold angle in the crease element is quantified by using the dot product of two vectors connecting the crease and the nodes defining the two adjacent facets. The complexity in the derivatives of the fold angle with respect to the nodal displacement is considerably reduced by invoking the small strain/curvature behaviour of the facet. The crease element is equally applicable to elastic hinge modelling. The proposed elements are implemented in ABAQUS thru two user-defined element subroutines, see Appendix 2, and co-used with of 3D membrane elements in ABAQUS. Indeed, it is straight forward to program a comprehensive Q4 element which takes both the membrane and bending deformations into account. Since ABAQUS does not show user-defined elements in its post-processor, the 3D membrane elements of ABAQUS are purposely employed such that the predicted geometry can be displayed by the software. Validation examples including elastic hinge, origami and kirigami are presented whilst the pertinent videos are provided in the Online Resources 1 to 15. The ABAQUS input (.INP) files and FORTRAN source (.FOR) files required to run the example on the crane in Sect. 5.3 are provided in Online Resources 16 and 17 for the displacement loading and 18 and 19 for the rest-angle loading. Interested readers may contact the authors for files on other examples. Though not explored in this paper, instability of the origami can also be studied using the built-in Riks solution method in ABAQUS.