1 Instruction

With the development of the mechanical products built for heavy load, high speed and high precision, the requirement for dynamic performance of mechanism is becoming higher and higher [1, 2]. Due to the manufacturing tolerances, material deformations or wear, these joints are not perfect and have some clearances. The clearance joint changes the movement performance of the mechanical system, which causes a deviation between the actual movement and the anticipated movement of the mechanism [3, 4]. In addition, the clearance of the joint brings violent collisions between the elements of the motion pair, it makes mechanical system response chaotic and unpredictable instead of being periodic and regular [5, 6]. Therefore, it is necessary to study the dynamic behavior of multi-link mechanism with multiple clearances.

The effects of a joint clearance on the dynamic response of a mechanical system have been studied by many researchers over the last few decades [7,8,9,10]. However, most previous studies only focused on the planar 1-DOF simple mechanism with one revolute clearance. Research on multi-link mechanisms with multiple clearances is rare. And comparative analyses of the influence of LuGre model and modified Coulomb friction model on dynamic response of mechanism are even scarcer. Bai et al. [11, 12] explored the dynamic behavior of planar mechanical systems containing a clearance joint. The contact force model of the clearance joint was built by adopting the novel nonlinear hybrid continuous contact force model. Tan et al. [13] built the motion differential equations by using Newton–Euler method. Then, the Baumgarte stabilization approach has been utilized to enhance numerical stability. The influence of different clearance values on the dynamic response was also studied. Ma et al. [14] presented a general procedure for dynamic modeling and simulation of a slider–crank mechanism considering multiple revolute clearances. The validity of the proposed method has been confirmed through a comparison with ADAMS simulation results. Megahed et al. [15] reported the effect of revolute joint clearances on the dynamic performance of a slider–crank mechanism by using ADAMS. Muvengei et al. [16, 17] discussed the behavior of a slider–crank mechanism containing multiple clearance joints. A stick–slip friction force model was utilized in clearance joints. Gummer et al. [18] presented a method to simulate the slider–crank mechanism with one clearance joint in RecurDyn. A detailed research of already existing contact, damping and friction force model and different methods of establishing revolute pair model in RecurDyn has been analyzed. Marques et al. [19] put forward a new formulation to build spatial revolute joints with axial and radial clearances. Equations of motion that govern the dynamic response of the slider–crank mechanism have been established by using the Newton–Euler method. Marques et al. [20] presented an investigation on the dynamic response of a spatial four bar mechanism with spherical clearance joints including friction, and studied the influence of various friction force models, clearance values and friction coefficients. Wang et al. [21] researched the dynamic characteristics of the slider–crank mechanism with clearance by adopting the novel nonlinear contact force model, and the modified Coulomb friction model has been utilized to analyze the friction of clearance joint. Reis et al. [22] introduced the development of the dynamics for the slider–crank mechanism with a revolute joint clearance between the piston and pin. The dynamic equations of the mechanism were obtained by using Lagrange method. The influence of friction, contact and lubrication at the clearance elements was investigated in this research. Geng et al. [23] proposed a new time-dependent reliability assessment methodology with insufficient uncertainty information to quantify uncertainty influence of the clearances and dimensions on the kinematic performance. Marques et al. [24] offered a general and comprehensive method to eliminate constraints violation at the position and velocity levels. The conservation of total energy and computational efficiency were studied and compared using standard Lagrange multipliers’ method, Baumgarte stabilization method, augmented Lagrangian formulation, and so on. Bai et al. [25] presented a design optimization method to reduce undesirable vibrations of the dual-axis driving mechanism containing clearances, which was solved by a Generalized Reduced Gradient algorithm. Xu et al. [26] discussed the influence of the clearance joint on the dynamic response of the 2 DOFs pick-and-place planar mechanism.

As is well known, chaos phenomenon often occurs at the clearance joint, which has an important effect on the dynamic behavior of the system. Nevertheless, research identifying chaotic phenomena of the clearance joints for a planar multi-link mechanism is rare. Bifurcation research of revolute clearance joints with different changing variables in a multiple DOF complex mechanism containing a multiple clearance joint is even scarcer. In recent years, scholars have carried on the discussion and research on the nonlinear characteristics of the mechanism with clearances [27, 28]. Farahan et al. [29] researched the nonlinear dynamic behavior of the four bar mechanism containing clearance, which appears between the connecting rod and rocking bar. Bifurcation analysis was conducted by changing the clearance value corresponding to different crank speed. Rahmanian et al. [30] studied the nonlinear dynamic behavior of the slider–crank mechanism system with revolute clearance, which is a non-autonomous system. The Poincaré map is the criterion that is used to detect chaos phenomenon. The influence of different clearance values on the bifurcation analysis is investigated by looking at different velocity values of the driving component. Yaqubi et al. [31] analyzed the characteristics of the slider–crank mechanism containing single and multiple clearances. The nonlinear dynamic of the mechanical system was addressed by utilizing bifurcation diagrams and Poincaré maps. The influence of friction on nonlinear dynamic behavior of the mechanism has also been researched. Nan et al. [32] developed a nonlinear model of the rotor-bearing with internal clearance between the rolling elements and races, and carried out the nonlinear dynamic analysis. With the help of the bifurcation diagrams, Poincare maps and shaft center trajectory, the effects of the rotating velocity, clearance values and stiffness on the dynamic behavior were researched.

Traditional studies are mainly focused on investigating the planar simple mechanism with one revolute clearance by using modified Coulomb friction model; few researchers studied 2 DOF planar multi-link mechanisms with multiple revolute clearances by using both modified Coulomb friction and LuGre models, and few studies systematically analyzed nonlinear characteristics in the revolute clearance joints of planar multi-mechanism by employing phase diagram, Poincaré map, LLE and bifurcation diagram. Thus, the main goal of this paper is to study the effects of multiple revolute clearances and different friction models (such as LuGre and modified Coulomb friction models) on the dynamics response of a planar multi-DOF mechanism; we want to grasp the nonlinear characteristics of the revolute clearance joints by using phase diagram, Poincaré map, LLE and bifurcation diagrams. A 2-DOF nine bar planar mechanism is selected as the research object. The dynamic model of a 2 DOF nine bar planar mechanism with two revolute clearances is built by using Lagrange equation. The influence of LuGre and modified Coulomb friction models on dynamic response of the nine bar mechanism is studied. The effects of the number of clearance joints, clearance values, driving speeds and friction coefficients on the dynamic responses of the mechanism are analyzed. The chaos phenomenon existing in revolute clearance joints is identified by the phase diagram, Poincaré map and LLE in details. Bifurcation diagrams of revolute clearance joints with changing clearance values, driving speeds and friction coefficients are also drawn. The arrangement of this paper is as follows. In Sect. 2, the joint clearance and contact force models are both established. In Sect. 3, the nonlinear dynamic model nine bar mechanical system with two revolute clearance joints is built by using Lagrange equation. In Sect. 4, the influence of LuGre and modified Coulomb friction models on dynamic response of the nine bar mechanism is studied. The effects of the number of clearance joints, clearance values, driving speeds and friction coefficients on the dynamic response of the mechanism are analyzed. In Sect. 5, the nonlinear characteristics of the clearance joints are investigated systematically. Chaos phenomenon existing in the clearance joints is identified through the phase diagram, Poincaré map and LLE. Bifurcation diagrams obtained by changing clearance values, driving speeds and friction coefficients are also drawn.

2 Modeling of the revolute joint with clearance

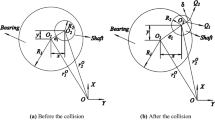
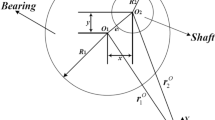
A planar revolute joint with clearance is depicted in Fig. 1. There are two different cases of contact: When there is no contact between the bearing and shaft, the contact force becomes zero. When a contact or impact occurs, the contact force will exist, and it can be divided into the normal force \(F _{\mathrm{n}}\) and tangential force \(F _{ \mathrm{t}}\), as shown in Fig. 2. Both cases could be expressed as follows:

$$ \left \{ \textstyle\begin{array}{l@{\quad }l} F = 0 & \mbox{if } \delta < 0, \\ F = F_{n} + F_{t} & \mbox{if } \delta \ge 0 , \end{array}\displaystyle \right . $$
(1)

where \(\delta \) represents penetration depth. According to the contact condition, \(\delta \) could be expressed as

$$ \delta = e - c $$
(2)

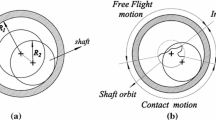
where \(e\) is the eccentricity of the shaft center relative to the bearing center, its value is \(\sqrt{x^{2} + y^{2}}\), \(x\) and \(y\) are vertical and horizontal displacement of shaft’s center relative to the bearing, respectively; \(c\) is the clearance size, its value is \(R_{1} - R_{2}\), where \(R_{1}\) and \(R_{2}\) respectively represent the radii of the bearing and shaft. When \(\delta \) is less than 0, there is no contact between the bearing and shaft, that is, we have a free flight mode. When \(\delta \) is 0, the shaft and bearing are in permanent contact, that is, in continuous contact mode. When \(\delta \) is greater than 0, there is contact between the shaft and bearing, that is, we have impact mode [40].

Fig. 1
figure 1

Revolute joint with clearance

Full size image
Fig. 2
figure 2

Joint contact forces

Full size image

2.1 The normal force model

Herz and Goldsmith contact force models are both pure elastic contact force models, which do not consider energy loss. Kelvin–Voigt contact force model is suitable for contact situation with very small material damping. A contact force model put forward by Lankarani and Nikravesh is suitable for general mechanical contact collisions with high coefficient of restitution, especially when the energy dissipation is relatively small [41]. And as a nonlinear viscoelastic model, the L–N model conforms to experimental results well, and application of this model is more efficient when the restitution coefficient is close to unity. This model is also straightforward for a numerical integration algorithm. In order to consider energy loss during the collision process, the Lankarani–Nikravesh model is used in this paper [33,34,35]:

$$ F_{n} = K\delta ^{n} + D\dot{\delta } $$
(3)

where \(K\) is a stiffness parameter, and \(D\) is a hysteresis damping coefficient; \(n\) is a constant depending on material properties of contact surfaces; \(\dot{\delta } \) represents penetration velocity, \(\dot{\delta } = \frac{x\dot{x} + y\dot{y}}{\sqrt{x^{2} + y^{2}}} \).

The stiffness parameter \(K\) is given by

$$ K = \frac{4}{3\pi (\sigma _{1} + \sigma _{2})} \biggl( \frac{R_{1}R_{2}}{R _{2} + R_{1}} \biggr)^{\frac{1}{2}} $$
(4)

where \(\sigma _{1} = ( 1 - \nu _{1}^{2} )/ ( \pi E _{1} )\), \(\sigma _{2} = ( 1 - \nu _{2}^{2} )/ ( \pi E_{2} )\), \(\nu _{1}\), \(\nu _{2}\) respectively represent Poisson’s ratios of bearing and shaft; \(E_{1}\), \(E_{2}\) represent the elastic moduli of the bearing and shaft, respectively. The radius is negative for the concave surfaces and positive for the convex surface.

The hysteresis damping coefficient \(D\) is given as

$$ D = \frac{3K ( 1 - c_{e}^{2} )\delta ^{n}}{4\dot{\delta } ^{ ( - )}} $$
(5)

where \(c_{e}\) denotes the recovery coefficient, \(\dot{\delta }^{ ( - )}\) is the initial impact velocity.

2.2 The tangential force model

An application of the original Coulomb’s friction law in a general purpose computational program may lead to numerical difficulties because it is a highly nonlinear phenomenon that may involve switching between sliding and stiction conditions. In order to avert such difficulties, Ambrosio presented a modification for the Coulomb’s friction law, which is used in [36,37,38], namely

$$ F_{t} = - c_{f}c_{d}F_{n} \frac{v_{t}}{ \vert v_{t} \vert } $$
(6)

where \(c_{f}\) represents the friction coefficient, while \(c_{d}\) represents the dynamic correction coefficient given by

$$ c_{d} = \left \{ \textstyle\begin{array}{l@{\quad }l} 0, & \vert v_{t} \vert < v_{0} , \\ \frac{ \vert v_{t} \vert - v_{0}}{v_{1} - v_{0}}, & v_{0} \le \vert v_{t} \vert \le v_{1} , \\ 1, & \vert v_{t} \vert > v_{1} , \end{array}\displaystyle \right . $$
(7)

where \(v_{0}\) and \(v_{1}\) represent the limit values of a given velocity.

LuGre model was proposed by Canudas de Wit et al. and this model is capable of capturing Stribeck and stiction effects [16, 17, 36]. Because the normal contact force could be obtained from the contact force models as shown in Eq. (3), according to classical definition, the friction can be expressed as

$$ F_{t} = \mu F_{n}. $$
(8)

The instantaneous coefficient of friction \(\mu \) is viewed as a function of tangential velocity and an internal state \(z\) in the LuGre friction model, which is defined as

$$ \mu = \bar{\sigma }_{0}z + \bar{\sigma }_{1}\dot{z} + \bar{\sigma } _{2}v_{t} $$
(9)

where \(\bar{\sigma }_{0}\) is bristle stiffness, \(\bar{\sigma }_{1}\) is the microscopic damping coefficient, and \(\bar{\sigma }_{2}\) is the viscous friction coefficient.

The evolution differential equation for the average bristle deflection is

$$ \dot{z} = \frac{dz}{dt} = v_{t} - \frac{\bar{\sigma }_{0} \vert v _{t} \vert }{\mu _{k} + ( \mu _{s} - \mu _{k} )e^{ - \vert \frac{v_{t}}{v_{s}} \vert \gamma }} z $$
(10)

where \(\mu _{k}\) is the coefficient of kinetic friction, which is a measure of the Coulomb friction force, and \(\mu _{s}\) is the coefficient of static friction, which is a measure of the stiction friction force.

3 Dynamic modeling of the nine bar mechanism with two revolute clearances

A nine bar mechanism is composed of nine sections which are the frame, crank 1, link 2, link 3, crank 4, rocking-bar 6, triangular panel 7, link 8, and slider 9. Link 5 is a part of the frame. The mechanism has 2 DOF, cranks 1 and 4 are driven by two motors. A structure diagram of the nine bar mechanism is shown in Fig. 3.

Fig. 3
figure 3

Nine bar mechanism with two clearances

Full size image

In the model, crank 1 and link 2 are connected by a clearance revolute joint which is denoted by \(A\), while another clearance revolute joint, denoted by \(B\), is utilized to connect crank 4 and link 3. Locally enlarged drawings of \(A\) and \(B\) correspond to \(A'\) and \(B'\) in Fig. 3. Motion pairs of the mechanism are composed of revolute pairs and translational pair; among them, the number of revolute pairs is the largest. Due to the two cranks, which are driving components, being directly driven by the motors, the clearances at \(A\) and \(B\) can better reflect the effect of clearances on the dynamic behavior.

3.1 Kinematic modeling of the nine bar mechanism with revolute clearances

When the mechanism has two revolute clearances, the closed equations are as follows:

$$ \left \{ \textstyle\begin{array}{l} L_{1}\cos \theta _{1} + L_{2}\cos \theta _{2} + x_{1} = L_{5} + L_{4} \cos \theta _{4} + L_{3}\cos \theta _{3} + x_{2}, \\ L_{1}\sin \theta _{1} + L_{2}\sin \theta _{2} + y_{1} = L_{4}\sin \theta _{4} + L_{3}\sin\theta _{3} + y_{2} , \\ L_{1}\cos \theta _{1} + x_{1} + L_{2}\cos \theta _{2} = L_{11}\cos \theta _{11} + L_{6}\cos \theta _{6} + L_{71}\cos \theta _{7} , \\ L_{1}\sin \theta _{1} + y_{1} + L_{2}\sin \theta _{2} = L_{11}\sin \theta _{11} + L_{6}\sin \theta _{6} + L_{71}\sin\theta _{7} , \\ L_{6}\cos \theta _{6} + L_{72}\cos (\theta _{7} + \beta ) + L_{8}\cos \theta _{8} + S_{9} = S_{0} , \\ L_{6}\sin \theta _{6} + L_{72}\sin (\theta _{7} + \beta ) + L_{8}\sin \theta _{8} = 0 . \end{array}\displaystyle \right . $$
(11)

According to the coordinate perturbation approach [39], all rotation angles of the mechanism and displacement of the slider with clearances can be regarded as having a small disturbance value added to the normal value:

$$ \left \{ \textstyle\begin{array}{l} \theta _{i} = \theta _{i0} + \Delta \theta _{i} \\ S_{9} = S_{90} + \Delta S_{9} \end{array}\displaystyle \right .\quad (i = 2,3,6,7,8) $$
(12)

where \(\theta _{i0}\ (i = 2,3,6,7,8)\) and \(S_{90}\) represent the rotation angle of each member and the displacement of slider 9, when the mechanism is without clearances, respectively.

The velocity and acceleration models of the nine bar mechanism with revolute clearances are as follows:

$$\begin{aligned} &\left \{ \textstyle\begin{array}{l} \dot{\theta }_{i} = \dot{\theta }_{i0} + \Delta \dot{\theta }_{i} \\ \dot{S}_{9} = \dot{S}_{90} + \Delta \dot{S}_{9} \end{array}\displaystyle \right .\quad (i = 2,3,6,7,8), \end{aligned}$$
(13)
$$\begin{aligned} &\left \{ \textstyle\begin{array}{l} \ddot{\theta }_{i} = \ddot{\theta }_{i0} + \Delta \ddot{\theta }_{i} \\ \ddot{S}_{9} = \ddot{S}_{90} + \Delta \ddot{S}_{9} \end{array}\displaystyle \right .\quad (i = 2,3,6,7,8) \end{aligned}$$
(14)

where \(\dot{\theta }_{i0}\ (i = 2,3,6,7,8)\) and \(\dot{S}_{90}\) represent the rotation angle velocity of each member and the velocity of slider 9, when the mechanism is without clearances, respectively; \(\ddot{\theta }_{i0}\ (i = 2,3,6,7,8)\) and \(\ddot{S}_{90}\) represent the rotation angle acceleration of each member and the acceleration of slider 9, when the mechanism is without clearances, respectively.

3.2 Dynamic equation modeling of the nine bar mechanism with revolute clearances

For each revolute clearance joint, two kinematic constraints will be removed, which are the vertical and horizontal displacements of the shaft’s center. Therefore, when the mechanism is complemented with two revolute clearances, the whole mechanism has 6 DOF.

According to Lagrange equation, the dynamic model of the nine bar mechanism with clearances is given by

$$ \frac{d}{dt} \biggl(\frac{\partial T}{\partial \dot{q}_{k}} \biggr) - \frac{\partial T}{\partial q_{k}} + \frac{\partial U}{\partial q_{k}} = Q_{k} \quad (k = x _{1},y_{1},x_{2},y_{2},1,4) $$
(15)

where \(T,U,Q_{k}\) represent the kinetic energy, potential energy and general force, respectively; \(q_{k}\) represents generalized coordinates. The corresponding variables are \(x_{1},y_{1},x_{2},y_{2}, \theta _{1}\) and \(\theta _{4}\).

The expression of the kinetic energy of the mechanism can be expressed as

$$ T = \frac{1}{2} \sum_{{\scriptstyle i = 1 \atop\scriptstyle i \ne 1,4,5,6}}^{9} m_{i}v_{si}^{2} + \frac{1}{2} \sum _{{\scriptstyle i = 1 \atop\scriptstyle i \ne 5,9}}^{9} J_{i} \dot{\theta }_{i}^{2}. $$
(16)

The potential energy of mechanism can be written as

$$ U = \sum_{{\scriptstyle i = 1 \atop\scriptstyle i \ne 5}}^{9} m_{i}gx _{si} $$
(17)

where \(x_{si}\) represents the centroid coordinate in the \(X\) direction of component \(i\).

The generalized force of the system can be expressed as

$$ Q_{k} = \sum_{{\scriptstyle i = 1 \atop\scriptstyle i \ne 5}}^{9} \biggl( \bar{F}_{i}\frac{\partial r_{i}}{\partial q_{k}} + \bar{M}_{i} \frac{ \partial \theta _{i}}{\partial q_{k}} \biggr) $$
(18)

where \(\bar{F}_{i}\) is the external force and \(\bar{M}_{i}\) is the external torque acting on component \(i\); \(r_{i}\) is the position vector of body \(i\).

Equations (16), (17) and (18) are substituted into Eq. (15), and the second-order nonlinear differential equations (see Eq. (19)) with variable coefficients are derived:

$$ \left \{ \textstyle\begin{array}{l} \ddot{x}_{1} = f_{1}(t,x_{1},y_{1},x_{2},y_{2},\dot{x}_{1},\dot{y} _{1},\dot{x}_{2},\dot{y}_{2}) , \\ \ddot{y}_{1} = f_{2}(t,x_{1},y_{1},x_{2},y_{2},\dot{x}_{1},\dot{y} _{1},\dot{x}_{2},\dot{y}_{2}) , \\ \ddot{x}_{2} = f_{3}(t,x_{1},y_{1},x_{2},y_{2},\dot{x}_{1},\dot{y} _{1},\dot{x}_{2},\dot{y}_{2}) , \\ \ddot{y}_{2} = f_{4}(t,x_{1},y_{1},x_{2},y_{2},\dot{x}_{1},\dot{y} _{1},\dot{x}_{2},\dot{y}_{2}) . \end{array}\displaystyle \right . $$
(19)

Equation (19) derived in the previous section contains four second order nonlinear equations. According to Eq. (2), a negative value of the penetration depth \(\delta \) means that there is no contact between the bearing and shaft. Otherwise, a positive value of the penetration depth \(\delta \) means that there is contact between the bearing and shaft [8]. Therefore, if \(\delta ( t_{n} )\delta ( t_{n + 1} ) \le 0\), \(\delta ( t_{n} ) < 0\) and \(\delta ( t_{n + 1} ) > 0\), and contact occurs between the two discrete times, \(t_{n}\) and \(t_{n + 1}\), and the penetration velocity at moment \(t_{n + 1}\) is the initial impact velocity \(\dot{\delta }^{ ( - )}\) [40]. It is supposed that the shaft and bearing have been in contact mode for a long time, when the mode of the shaft and bearing changes from the free flight mode to the impact mode at the beginning of this long contact process, the collision speed at this moment is the initial impact velocity \(\dot{\delta }^{ ( - )}\). Since the equations of the system are complicated, it is almost impossible to solve them analytically. Thus, in order to ensure the efficiency and accuracy of the calculation, the Runge–Kutta method is utilized which converts the four second-order differential equations of motion into eight first order differential equations through MATLAB programming. The core i7-4700 CPU is used for the simulation calculation. The integration step length is \(10^{-3}~\mbox{s}\). The relative error is set as \(10^{-6}\).

4 Dynamic response of multi-link mechanism with two revolute clearances

4.1 System parameters of the nine bar mechanism

The system parameters of the 2 DOF nine bar mechanism are depicted in Tables 1, 2 and 3.

Table 1 Dimensions and mass properties for the 2 DOF nine bar mechanism
Full size table
Table 2 Moments of inertia for the 2 DOF nine bar mechanism
Full size table
Table 3 Clearance joints and integration parameters
Full size table

4.2 The influence of different friction models on the dynamic response of the nine bar mechanism

The driving speeds of the two cranks are set as \(\omega _{1} = - 2.5 \pi ( \mathrm{rad}/\mathrm{s} ),\omega _{4} = 2.5 \pi ( \mathrm{rad}/\mathrm{s} )\), the clearances of joints \(A\) and are both set as 0.5 mm. In order to investigate the difference of the friction models, the influence of the modified Coulomb friction and LuGre models on the dynamic response of the nine bar mechanism is researched. The modified Coulomb’s friction law can solve numerical difficulties when the relative tangential velocity is in the vicinity of zero. The LuGre law could capture variation of the friction force with slip velocity, thus making it suitable for studies involving stick–slip motions. Besides, LuGre law could be observed to capture Stribeck effect, which is a phenomenon related with the stick–slip friction. The velocity and acceleration of the slider, driving torques of cranks, the shaft center’s trajectory of clearance joints are also studied. From Figs. 4–9, it is shown that the effects of LuGre and modified Coulomb friction models on the dynamic response for this mechanism are slightly different, and the time point of collision is basically consistent. There are some differences in the peak magnitude of the dynamic response: when LuGre model is used, the peak magnitude of the dynamic response is higher than that of modified Coulomb friction model. When the modified Coulomb friction model is utilized, the peak values of the slider’s velocity and acceleration, contact force and driving torques of cranks 1 and 4 are \(- 1.938~\mbox{m}/\mbox{s}\), \(- 213.5~\mbox{m}/\mbox{s}^{2}\), \(1253~\mbox{N}\), \(74.55~\mbox{N}\,\mbox{m}\) and \(- 197.7~\mbox{N}\,\mbox{m}\), respectively. While when LuGre model is utilized, the peak values of the slider’s velocity and acceleration, contact force and driving torques of cranks 1 and 4 are \(- 2.179~\mbox{m}/\mbox{s}\), \(- 380.9~\mbox{m}/\mbox{s}^{2}\), \(2270~\mbox{N}\), \(- 163.5~\mbox{N}\,\mbox{m}\) and \(291.9~\mbox{N}\,\mbox{m}\), respectively. When the modified Coulomb’s friction method is used, it takes about 20.05 s to run one cycle. When the LuGre model method is used, it takes about 37.29 s to run one cycle. When the LuGre model is adopted, the computation time is longer than that of the modified Coulomb’s friction method. When the modified Coulomb’s friction model is used, the efficiency is slightly higher. This section is mainly to make a comparative analysis of the two friction models, which provides a reference for other researchers to study dynamics.

Fig. 4
figure 4

Velocity of slider

Full size image
Fig. 5
figure 5

Acceleration of slider

Full size image
Fig. 6
figure 6

Driving torque of crank 1

Full size image
Fig. 7
figure 7

Driving torque of crank 4

Full size image
Fig. 8
figure 8

Shaft center’s trajectory of revolute joint \(A\)

Full size image
Fig. 9
figure 9

Shaft center’s trajectory of revolute joint \(B\)

Full size image

4.3 The influence of the number of clearance joints on the dynamic response

The following studies are based on the modified Coulomb friction model. In order to research the effect of the number of clearance joints on the dynamic response, one clearance joint (joint \(A\)) and two clearance joints (joint \(A\) and joint \(B\)) are both considered. The acceleration of the slider, contact force of clearance joint \(A\), the driving torques of the two cranks and the shaft center’s trajectory of joint \(A\) are used to illustrate the influence of the number of clearance joints on the dynamic response of the nine bar mechanism, as shown in Figs. 10, 11, 12, 13 and 14. It is supposed that the driving speeds of cranks 1 and 4 are \(\omega _{1} = - 2 \pi~( \mbox{rad}/\mbox{s} )\) and \(\omega _{4} = 2 \pi~( \mbox{rad}/\mbox{s} )\), respectively, the friction coefficient is \(c_{f} = 0.01\), and the clearance value is \(c = 0.1~( \mbox{mm} )\).

Fig. 10
figure 10

Acceleration of slider

Full size image
Fig. 11
figure 11

Contact force of joint \(A\)

Full size image
Fig. 12
figure 12

Driving torque of crank 1

Full size image
Fig. 13
figure 13

Driving torque of crank 4

Full size image
Fig. 14
figure 14

Shaft center’s trajectory of revolute joint \(A\)

Full size image

As shown in Fig. 10, the two clearance joints have a greater effect on acceleration of the slider than just one clearance joint. Multiple clearances can produce larger peaks and more violent fluctuations on the slider’s acceleration. From the Figs. 11, 12 and 14, when only one clearance at joint \(A\) is considered, the peak values of the contact force of joint \(A\) and driving torque of crank 1 are larger than when two clearance joints are used. And the shaft center’s trajectory of joint \(A\) is also more chaotic, when only one clearance is considered. The reason is that multi-clearance has a certain coupling effect to reduce the vibration at joint \(A\). It is shown in Fig. 13 that two-clearances have a greater influence on the driving torque of crank 4 than a single clearance at joint \(A\). The main reason is that when only one clearance is considered, joint \(B\) is an ideal pair of motion, whereas when two clearances are considered, B is a clearance joint, so the effect of two clearance joints on the driving torque of crank 4 is greater than with just one clearance joint. For the end effector of the mechanism, the effect of multi-clearance joints on the dynamic response is larger than that of a single clearance joint. When only one revolute clearance is considered, it takes about 14.66 s to run one cycle. When two revolute clearances are considered, it takes about 29.05 s to run one cycle. The calculation of multiple clearances is more complicated than that of a single clearance. So the calculation of multiple clearances takes longer.

4.4 The influence of clearance value on the dynamic response

The effect of two different clearance values on the dynamic response is investigated. It is supposed that the driving speeds of cranks 1 and 4 are \(\omega _{1} = - 2 \pi~( \mbox{rad}/\mbox{s} )\) and \(\omega _{4} = 2 \pi~( \mbox{rad}/\mbox{s} )\), while the friction coefficient is \(c_{f} = 0.01\).

Figure 15 shows the acceleration of the slider corresponding to the clearance values of 0.01 and 0.08 mm, respectively. From Fig. 15, when the mechanism contains clearances, the slider’s acceleration fluctuates violently and has a great peak. With the increase of the clearance value, the peak value of the acceleration increases from −20.39 to \(- 22.97~\mbox{m}/\mbox{s}^{2}\), which shows that clearances have a great influence on the acceleration of the slider. Figures 16 and 17 show variations of the input driving torques of the two cranks. It is shown that collision causes an instant increase in the peak value of the driving torques. The time point of the fluctuation of the input driving torque is consistent with the fluctuation time point of the slider’s acceleration. The bigger the clearance size, the higher the peak value of the driving torques caused by collision: the peak value of the driving torque of crank 1 increases from −14.22 to \(- 14.94~\mbox{N}\,\mbox{m}\), the peak value of the driving torque of crank 4 increases from −19.41 to \(33.79~\mbox{N}\,\mbox{m}\). Figures 18 and 19 show the contact force of joints \(A\) and \(B\), respectively. It is show that the bigger the clearance value, the bigger the peak value of the contact force caused by collision: the peak value of the contact force at joint \(A\) increases from 176.3 to \(186.1~\mbox{N}\), the peak value of the contact force at joint \(B\) increases from 235.4 to \(242.7~\mbox{N}\). The larger the clearance size, the more unstable the mechanical system.

Fig. 15
figure 15

Acceleration of slider for different clearance values

Full size image
Fig. 16
figure 16

Driving torque of crank 1

Full size image
Fig. 17
figure 17

Driving torque of crank 4

Full size image
Fig. 18
figure 18

Contact force of joint \(A\)

Full size image
Fig. 19
figure 19

Contact force of joint \(B\)

Full size image

4.5 The influence of the driving speed of the crank on the dynamic response

The driving speed significantly influences the working efficiency, two different velocity pairs \(\omega _{1} = - \pi~( \mbox{rad}/ \mbox{s} ),\omega _{4} = \pi~( \mbox{rad}/\mbox{s} )\) and \(\omega _{1} = - 2.5\pi~( \mbox{rad}/\mbox{s} ), \omega _{4} = 2.5\pi~( \mbox{rad}/\mbox{s} )\) are compared in the dynamic performance of the mechanism. It is supposed that the clearance sizes at joints \(A\) and \(B\) are both set as 0.1 mm, the friction coefficient is \(c_{f} = 0.01\). The influence of different driving speeds on the driving torques of both the cranks and shaft center’s trajectory are analyzed.

Figures 20 and 21 show the variations of the driving torques of two cranks at two different driving speeds. The bigger the driving speed, the higher the peak value of the crank driving torque. The peak value of the driving torque of crank 1 increases from −9.005 to \(31.73~\mbox{N}\,\mbox{m}\), the peak value of the driving torque of crank 4 increases from −17.56 to \(73.46~\mbox{N}\,\mbox{m}\). Figures 22 and 23 show the variations of the shaft center’s trajectory of the clearance joints for two different driving speeds. As shown in Figs. 22 and 23, with the increase of the driving speed, the shaft center’s trajectory becomes more and more chaotic, and the collision phenomenon is more serious. It is show that the penetration depth between the shaft and bearing increases, and the impact between the shaft and bearing is becoming more serious, while the driving speeds of cranks increase.

Fig. 20
figure 20

Driving torque of crank 1: (a) \(\omega _{1} = - \pi~(\mbox{rad}/\mbox{s})\), \(\omega _{4} = \pi~(\mbox{rad}/\mbox{s})\), (b) \(\omega _{1} = - 2.5\pi~( \mbox{rad}/\mbox{s})\), \(\omega _{4} = 2.5\pi~(\mbox{rad}/\mbox{s})\)

Full size image
Fig. 21
figure 21

Driving torque of crank 4: (a) \(\omega _{1} = - \pi~(\mbox{rad}/\mbox{s})\), \(\omega _{4} = \pi~(\mbox{rad}/\mbox{s})\), (b) \(\omega _{1} = - 2.5\pi~( \mbox{rad}/\mbox{s})\), \(\omega _{4} = 2.5\pi~(\mbox{rad}/\mbox{s})\)

Full size image
Fig. 22
figure 22

Shaft center’s trajectory of revolute joint \(A\)

Full size image
Fig. 23
figure 23

Shaft center’s trajectory of revolute joint \(B\)

Full size image

4.6 The influence of the friction coefficient on the dynamic response

It is supposed that the driving speeds of cranks 1 and 4 are \(\omega _{1} = - 2\pi~( \mbox{rad}/\mbox{s} )\) and \(\omega _{4} = 2\pi~( \mbox{rad}/\mbox{s} )\), respectively, the clearance values at \(A\) and \(B\) are both 0.02 mm, the friction coefficients are selected as 0.01 and 0.1, respectively. The effects of different friction coefficients on the contact force and shaft center’s trajectory are studied.

The contact forces of revolute joints \(A\) and \(B\) are respectively shown in Figs. 24 and 25 for different friction coefficients. The greater the friction coefficient, the smaller the peak of the collision force. The reason is that with the increase of the friction coefficient, the loss of the energy will be increased, and the peak value of the collision force will be reduced. Shaft center’s trajectories of revolute joints \(A\) and \(B\) are respectively shown in Figs. 26 and 27 for different friction coefficients. As shown in Figs. 26 and 27, when the friction coefficient gets larger, the confusion of center’s trajectory gradually decreases, and the stability of the mechanism is enhanced. However, the shock and collision still exist between the bearing and shaft.

Fig. 24
figure 24

Contact force of joint \(A\)

Full size image
Fig. 25
figure 25

Contact force of joint \(B\)

Full size image
Fig. 26
figure 26

Shaft center’s trajectory of revolute joint \(A\)

Full size image
Fig. 27
figure 27

Shaft center’s trajectory of revolute joint \(B\)

Full size image

5 Nonlinear characteristics of a multi-link mechanism with two revolute clearances

5.1 Chaos identification

Chaotic motions always lead to lower motion precision and high-frequency vibration. These behaviors always deteriorate the mechanism performance and reduce its life. The phase diagram, Poincaré map and Lyapunov exponent of clearance joints are shown in Figs. 28, 29 and 30. The periodic motion repeats the previous motion every other cycle, and its phase diagram is a closed curve. The chaotic motion is aperiodic, so its phase diagram is not a closed curve. When the Poincaré cross-section has only one isolated Poincaré mapping point or a few discrete points, the motion of the system is periodic. When the Poincaré cross-section has some patchy distribution of the point set, the system is in a chaos. As can be seen from Fig. 28, the phase diagrams are chaotic, and there is no closed curve. As shown in Fig. 29, the Poincaré mapping points are scattered and not duplicated. Therefore, it can be judged that the clearance joint is in chaos.

Fig. 28
figure 28

Phase diagram of clearance for: (a) joint \(A\) in the \(x_{1}\) direction; (b) joint \(A\) in the \(y_{1}\) direction; (c) joint \(B\) in the \(x_{2}\) direction; (d) joint \(B\) in the \(y_{2}\) direction

Full size image
Fig. 29
figure 29

Poincaré map of the clearance for: (a) joint \(A\) in the \(x_{1}\) direction; (b) joint \(A\) in the \(y_{1}\) direction; (c) joint \(B\) in the \(x_{2}\) direction; (d) joint \(B\) in the \(y_{2}\) direction

Full size image
Fig. 30
figure 30

Lyapunov exponent of clearance for: (a) joint \(A\) in the \(x_{1}\) direction; (b) joint \(A\) in the \(y_{1}\) direction; (c) joint \(B\) in the \(x_{2}\) direction; (d) joint \(B\) in the \(y_{2}\) direction

Full size image

Wolf et al. proposed looking at the Lyapunov exponent, which can be estimated directly based on the phase trajectory, plane and volume. This method is collectively called the Wolf method and is widely applied in the study of chaos [42, 43].

The Wolf method is used to calculate LLE, setting time series data for \(z _{1},z_{2},z_{3},\ldots,z_{n}\), which correspond to the data of \(x_{1}\), \(y_{1}\), \(x_{2}\) and \(y_{2}\) obtained by solving the dynamic equations (see Eq. (19)), its corresponding average period, embedding dimension \(m\), time delay \(\tau \) and length \(N\) are all calculated, and then, its corresponding phase space could be express as:

$$ Z ( t_{i} ) = \bigl( z ( t_{i} ),z ( t _{i} + \tau ),\ldots,z \bigl( t_{i} + ( m - 1 ) \tau \bigr) \bigr)\quad ( i = 1,2,\ldots,N ). $$

Taking the initial point as \(Z ( t_{0} )\), and then taking any point \(Z_{0} ( t_{0} )\) near the initial point \(Z ( t_{0} )\), the distance between the two points is \(L = \vert Z ( t_{0} ) - Z_{0} ( t_{0} ) \vert \). If the value of \(L\) is more than the specified value \(\varepsilon ( \varepsilon > 0 )\) at time point \(t_{1}\), that is, \(L'_{0} = \vert Z ( t_{1} ) - Z_{0} ( t_{0} ) \vert > \varepsilon \), \(Z ( t_{1} )\) is reserved, and then one finds a point \(Z_{1} ( t_{1} )\) near point \(Z ( t_{1} )\), satisfying \(L_{1} = \vert Z ( t_{1} ) - Z_{1} ( t_{1} ) \vert < \varepsilon \), and lets the angle between the two points be as small as possible, and then the above processes are repeated again and again. When \(Z ( t )\) reaches the end of time series \(N\), the LLE could be obtained by

$$ \chi = \frac{1}{t_{M} - t_{0}}\sum_{i = 0}^{M} \ln \frac{L'_{i}}{L _{i}} $$

where \(M\) is total number of iterations during the tracing evolution process, \(t_{M}\) is the time corresponding to the \(M\)th iteration, \(t_{0}\) is the initial time, \(L\) is the distance of the two adjacent points in the phase space. All of these variables are determined by the time series data.

When the LLE is negative, the system is in periodic motion. When the LLE is positive, the system has chaotic motion. As can be seen from Fig. 30, the LLEs in the \(x_{1}\), \(y_{1}\), \(x_{2}\) and \(y_{2}\) directions of clearance joints are 0.6089, 0.1373, 0.5943 and 0.4645, respectively. Since the LLEs in the four directions are all greater than 0, it can be also judged that the clearance joints are both in chaos at this time.

5.2 The influence of different parameters on nonlinear characteristics of the nine bar mechanism

Bifurcation diagrams with changing clearance values of clearance joints in the \(x_{1}\), \(y_{1}\), \(x_{2}\) and \(y_{2}\) directions are depicted in Figs. 31(a)–(d). With the increase of clearance value, the impact between the shaft and bearing becomes more and more serious, which has a great influence on the dynamic performance of the mechanism. Moreover, it could be observed from Figs. 31(a)–(d), clearance joints generally become more chaotic for the range of clearance size from 0.01 to 0.1 mm. The reason is that, as the clearance value increases, the contact force of the clearance joint increases, so that chaos phenomenon of the clearance joint is magnified.

Fig. 31
figure 31

Bifurcation diagram of clearance with changing clearance value for: (a) joint \(A\) in the \(x_{1}\) direction; (b) joint \(A\) in the \(y_{1}\) direction; (c) joint \(B\) in the \(x_{2}\) direction; (d) joint \(B\) in the \(y_{2}\) direction

Full size image

Bifurcation diagram with changing driving speed of clearance joints in the \(x_{1}\), \(y_{1}\), \(x_{2}\) and \(y_{2}\) directions are shown in Figs. 32(a)–(d). The horizontal coordinates in Figs. 32(a)–(d) are the driving speed of crank 4. The driving speeds of cranks 1 and 4 are equal in size and opposite in direction. According to Figs. 32(a)–(d), it can be shown that, as the driving speed of crank 4 increases from \(0.1\pi~(\mbox{rad}/\mbox{s})\) to \(1.7\pi~(\mbox{rad}/ \mbox{s})\) while the driving speed of crank 1 decreases from \(- 0.1\pi~(\mbox{rad}/\mbox{s})\) to \(- 1.7\pi~(\mbox{rad}/ \mbox{s})\), the chaos phenomenon is relatively weakened, and the mechanism is in a relatively stable motion state in this range. While the driving speed of crank 4 increases from \(1.72\pi~(\mbox{rad}/ \mbox{s})\) to \(3\pi~(\mbox{rad}/\mbox{s})\) (whereas the driving speed of crank 1 decreases from \(- 1.72\pi~(\mbox{rad}/\mbox{s})\) to \(- 3\pi~(\mbox{rad}/\mbox{s})\)), the chaos phenomenon of clearance joints is gradually increasing. It has a greater impact on the revolute clearance joints, which makes the mechanism have poor stability.

Fig. 32
figure 32

Bifurcation diagram of clearance joints with changing driving speed for: (a) joint \(A\) in the \(x_{1}\) direction; (b) joint \(A\) in the \(y_{1}\) direction; (c) joint \(B\) in the \(x_{2}\) direction; (d) joint \(B\) in the \(y_{2}\) direction

Full size image

Bifurcation diagram with changing friction coefficients of clearance joints in the \(x_{1}\), \(y_{1}\), \(x_{2}\) and \(y_{2}\) direction are shown in Figs. 33(a)–(d). According to Figs. 33(a)–(d), with the increase of friction coefficients, the chaos phenomenon of the clearance joints in the four directions is gradually weakened, the bifurcation diagram tends to converge, and the motion changes from chaotic to periodic. Thus, it can be concluded that the dynamic behavior will become more stable for the range of the friction coefficients from 0.01 to 0.25. The reason is that, as the friction coefficient increases, more energy is dissipated and contact forces of clearance joint are reduced. So, the mechanism becomes stable.

Fig. 33
figure 33

Bifurcation diagram of clearance with changing friction coefficient for: (a) joint \(A\) in the \(x_{1}\) direction; (b) joint \(A\) in the \(y_{1}\) direction; (c) joint \(B\) in the \(x_{2}\) direction; (d) joint \(B\) in the \(y_{2}\) direction

Full size image

6 Virtual simulation results

In order to verify the correctness of the numerical results, the virtual prototype simulation of 2 DOF nine bar mechanism containing two revolute clearances was carried out by ADAMS software. The clearance values of revolute clearances were both set to 0.5 mm, the driving speed of cranks 1 and crank 4 were assumed to be \(- 4\pi~(\mbox{rad}/\mbox{s})\) and \(4\pi~(\mbox{rad}/\mbox{s})\), respectively. The virtual simulation results of the slider’s displacement, velocity and acceleration are shown in Figs. 34, 35 and 36. The virtual simulation results of the contact force of revolute clearance joints are shown in Figs. 37 and 38.

Fig. 34
figure 34

Displacement of slider

Full size image
Fig. 35
figure 35

Velocity of slider

Full size image
Fig. 36
figure 36

Acceleration of slider

Full size image
Fig. 37
figure 37

Driving torque of crank 1

Full size image
Fig. 38
figure 38

Driving torque of crank 4

Full size image

From Figs. 34–38, the results of Adams virtual simulation are slightly different from those of MATLAB, which is mainly due to the different modeling and solving methods and the integration error [44]. It can be seen from Figs. 34 and 35 that the clearances have little influence on the slider’s displacement and velocity, and the vibration of these two curves is not very intense. According to Figs. 36, 37 and 38, the clearances of the revolute joints have a great influence on the slider’s acceleration and contact forces of revolute clearance joints. Although the curves are slightly different, they have similar regularity and have near peak value. Therefore, it can be proved that the theoretical model is correct.

7 Conclusions

The dynamic equation of a nine bar mechanism with two revolute clearances is built by the Lagrange equation. By using MATLAB programming, motion differential equations are solved by the Runge–Kutta method. The shaft center’s trajectory, contact forces of clearance joints, input driving torques of the cranks and kinematics characteristics of the slider are obtained. It can be indicated that the clearances reduce the dynamics stability of the mechanism and lead to vibration.

The influence of LuGre and modified Coulomb friction models on the dynamic response of the nine bar mechanism is compared. When LuGre model is used, the peak magnitude of the dynamic response is higher than that of the modified Coulomb friction model. The effects of the number of clearance joints, clearance values, driving speeds and friction coefficients on the mechanism behavior are investigated. With the increase of the number of the clearance joints, the vibration and fluctuation of the end-effecter will become more vigorous. The bigger the joint clearance values and the driving speeds of the cranks, the higher the amplitudes of acceleration of the slider, driving torques of cranks and the contact forces of clearance joints caused by collision. And when the friction coefficient gets larger, the fluctuation of the center’s trajectory gradually decreases, and the stability of the mechanism is enhanced. The chaos phenomena of the clearance joints are also identified by phase diagrams, Poincaré maps and LLEs. Bifurcation diagrams of the clearance joints with changing clearance values, friction coefficients and driving speeds of the cranks are also drawn. With the increase of clearance values and driving speeds, the chaos phenomenon of the clearance joints is gradually enhanced. With the increase of friction coefficients, the motion states of clearance joints change from chaotic to periodic motion, and chaos phenomenon gradually weakens. A virtual prototype model of 2 DOF nine bar mechanism containing two revolute clearances is modeled by ADAMS software, and numerical calculation results are verified by comparing them with virtual simulation results. The results prove that the theoretical model is reasonable and correct. This paper has certain theoretical significance and practical application value for the design and control of high reliability equipment.