1 Introduction

Since the direct measurement of muscle and joint contact forces without invasive procedures is infeasible, complex computational models of the musculoskeletal system are attractive and powerful alternatives with the potential to assist in many clinical problems within rehabilitation and orthopedics [1, 8, 12, 16]. Typical musculoskeletal models assume the skeletal system as a system of rigid bodies, constrained by mechanical joints that represent the anatomical joints. The skeletal system movement is enabled by the action of the muscles, which are represented by a set of bundles that may wrap around anatomical elements in a complicated fashion [5]. Because the number of muscles is usually larger than the number of degrees-of-freedom of the biomechanical model, optimization techniques are often applied to solve the redundancy of the muscle force distribution problem [7–9, 19, 21, 29].

Depending on the goals and the availability of experimental data, the redundancy problem may be addressed through an inverse dynamics approach, usually based on Static Optimization (SO), or through a forward dynamics approach, also known as dynamic optimization (DO) [8, 24, 27]. The SO finds, for each instant of time, the set of muscle forces that minimize a selected physiological criterion and fulfill constraints such as the equations of motion and the physiological boundaries of the muscle forces, whereas the DO determines a set of physiological muscle forces that produce a desired movement. From the biomechanical point of view, the DO is more powerful than the SO because it may be formulated regardless of the availability of experimental data, it may comprise the time-dependent physiological nature of the muscles, and it may include time-dependent physiological criteria [3, 13, 17]. However, unlike the SO, the DO requires multiple integrations of the equations of motion, which very often renders the procedure impractical due to the high computational cost [1, 27]. For that reason, the SO is the approach most often applied to estimate the muscle and joint reaction forces of the human body [4, 8, 17].

Considering the computational efficiency of the SO, two methods based on inverse dynamic formulations have been proposed to overcome some of the limitations of the SO while requiring less computational effort than the DO [1, 25]. The first method, named Extended Inverse Dynamics (EID), solves the muscle force redundancy problem as a large-scale optimization problem, in which all instants of time are solved simultaneously [1, 25]. The EID allows the use of time-dependent physiological criteria, as well as time-dependent constraints, such as those given by the muscle contraction and activation dynamics. However, the size of the optimization problem is geometrically proportional to the number of time instants in the analysis, which constitutes a limitation to the level of discretization that can be realistically considered. The second method, named Modified Static Optimization (MSO), is similar to the SO, but the muscle contraction and activation dynamics may be taken into account by considering the results of the previous instant of time [1]. Even though the MSO may include the time-dependent physiological nature of the muscles, it does not allow time-dependent physiological criteria.

The purpose of this study is to propose a new method based on an inverse dynamic formulation that allows both the use of time-dependent physiological criteria and constraints without any limitation on the size of the redundant muscle force distribution problem. The new method, here referred to as Window Moving Inverse Dynamics Optimization (WMIDO), considers a window of arbitrary size \(k\), which moves iteratively across all instants of time. For each window position, the muscle force redundancy problem is solved simultaneously for the \(k\) instants of time that compose the window. Because the window size can be much smaller than the number of time instants of the motion under analysis, the level of discretization does not limit the application of the WMIDO. Note that the WMIDO is not expected, by itself, to bring any new insight into the muscle distribution problem but, instead, it is expected to allow more detailed and complex modeling strategies of the redundant problem. In order to demonstrate the proposed methodology, the solutions to the muscle force distribution problem and the computational efforts of the SO, EID, and WMIDO are compared for an abduction motion in the frontal plane of a musculoskeletal model of the upper limb [21, 22]. In this work it is shown that the proposed method leads to results similar to those obtained with the currently available inverse dynamic based methods when these can be applied, but it does not have their limitations.

2 Redundant muscle force distribution problem: working example with a musculoskeletal model of the upper limb

2.1 Upper limb model

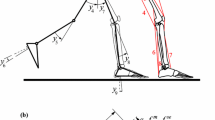
The muscle force distribution problem of an abduction motion in the frontal plane of a musculoskeletal model of the upper limb is used here as the working example case to demonstrate the use of inverse dynamics optimization methods. The musculoskeletal model considered, described in detail in [21, 22], is briefly outlined here. The skeletal system is composed of 7 rigid bodies, including the thorax, rib cage, clavicle, scapula, humerus, ulna, and radius, constrained by 6 anatomical joints, as shown in Fig. 1(a). The thorax and rib cage are assumed to be static, while the relative motion of the remaining bodies is constrained by the sternoclavicular, acromioclavicular (AC), and glenohumeral (GH) joints, modeled as 3 degrees-of-freedom spherical joints; the scapulothoracic (ST) joint, described by two holonomic constraints that impose the movement of the scapula over the rib cage; and the humeroulnar and radioulnar joints, modeled as 1 degree-of-freedom hinge joints. Overall, the upper limb comprises 9 degrees-of-freedom. The muscular system includes 22 muscles, represented by 74 muscle bundles, which are outlined in Fig. 1(b). The muscle paths are defined as a series of straight- and curved-line segments through the obstacle-set method [11]. Simple geometric surfaces are considered to model the shape of constraining anatomical structures. The muscle behavior is simulated by a Hill-type muscle model, composed of a contractile element (CE) in parallel with a passive elastic element (PE). On the basis of the greater computational efficiency, and the negligible loss of accuracy when simulating short tendons, the elasticity of the tendon is neglected by assuming a rigid tendon [14, 30]. For a muscle \(m\), its force is expressed as:

$$ \left \{ \textstyle\begin{array}{l} \displaystyle F^{m} = F_{\mathrm{CE}}^{m} \bigl( L^{m},\dot{L}^{m},a^{m} \bigr) + F_{\mathrm{PE}}^{m} \bigl( L^{m} \bigr) \\ \displaystyle F_{\mathrm{CE}}^{m} = \frac{F_{L} ( L^{m} )F_{\dot{L}} ( \dot{L}^{m} )}{F_{0}^{m}}a^{m} \end{array}\displaystyle \right . $$
(1)

where \(L^{m}\) is the length, \(\dot{L}^{m}\) is the velocity of contraction, \(a^{m}\) is the activation, and \(F_{0}^{m}\) is the maximum isometric force of muscle \(m\). The functions \(F_{L}\) and \(F_{\dot{L}}\) are the muscle force–length and force–velocity relationships, respectively [29]. Since the muscle model assumes a rigid tendon, all kinematic quantities, i.e., muscle length and velocity of contraction, are obtained directly from the kinematic data. The only unknown in Eq. (1) is the muscle activation \(a^{m}\). From the mathematical point of view, the muscles are introduced into the musculoskeletal model as kinematic driver constraints, i.e., each muscle is associated with a constraint equation that describes how its path changes during the motion. The Lagrange multipliers associated with these constraints may represent muscle force or muscle activation, if the constraint equations are multiplied by proper scalar factors. Considering that the muscle lengths are known, the passive components of the muscle forces, which only depend on muscle length, are treated as externally applied forces, while the active components are treated as reaction forces, for which the Lagrange multipliers represent muscle activations [21, 29].

Fig. 1
figure 1

Description of the skeletal (a) and muscular (b) systems of the multibody model of the upper limb. The 22 muscles modeled are represented by 74 muscle bundles, which may wrap around biomechanical obstacles, i.e., bony elements or other muscles

Full size image

The motion analyzed in this study, which serves as the demonstrative case used here to present the proposed methodology, was acquired at the Lisbon Biomechanics Laboratory (LBL) for a 25 year-old male subject with height 170 cm and weight 75 kg. The recommendations from the International Society of Biomechanics were followed to acquire an unloaded motion of abduction in the frontal plane with a sampling frequency of 100 Hz [34]. The dynamic tracking of the scapula was accomplished through the methodology of Senk and Chèze [26]. For the definition of the humerus orientation, the GH joint center was estimated using the algorithm of Gamage and Lasenby [10], while, for the clavicle, its axial orientation was estimated through the minimization of the AC joint rotations [32].

2.2 Inverse dynamics optimization

When defining the biomechanical model and acquiring its motion and external forces, the only unknowns are the internal forces, i.e., the joint reaction forces and muscle forces. Both sets of these unknowns are defined here as design variables in the context of an optimization problem. In particular, for each instant of time \(t\), the design variables of the optimization problem are the Lagrange multipliers \(\boldsymbol{\lambda}_{t}\) associated with the joint reaction forces resulting from the kinematic constraints, and the muscle activations \(\mathbf{a}_{t}\). Since the musculoskeletal model considered in this work includes 33 Lagrange multipliers and 74 muscle segments, there are 107 design variables for each instant of time. For \(k\) instants of time, the design variables are given as

$$ \mathbf{x} = \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \boldsymbol{\lambda}_{1} & \mathbf{a}_{1} & \boldsymbol{\lambda}_{2} & \mathbf{a}_{2} & \boldsymbol{\lambda}_{3} & \mathbf{a}_{3} & \cdots & \boldsymbol{\lambda}_{k} & \mathbf{a}_{k} \end{array}\displaystyle \right ]. $$
(2)

Considering the redundant muscle force distribution problem subjected to the physiological boundaries of the muscle forces, the fulfillment of the equations of motion, and the stability of the GH and ST joints [6, 21], the optimization problem is mathematically stated as:

$$ \min_{\mathbf{x}}J(\mathbf{x}), $$
(3)

subject to

$$\begin{aligned} & \bigl[ \boldsymbol{\varPhi}_{\mathbf{q}}^{T}\mathbf{x} + ( \mathbf{M}\ddot{\mathbf{q}} - \mathbf{g} ) = \mathbf{0} \bigr]_{t},\quad t = 1,\ldots,k, \end{aligned}$$
(3a)
$$\begin{aligned} & \bigl[ \mathbf{0} \le \mathbf{a}_{t} \le \mathbf{1} \bigr]_{t},\quad t = 1,\ldots,k, \end{aligned}$$
(3b)
$$\begin{aligned} & \bigl[ \mathbf{0} \le \mathbf{u}_{t} \le \mathbf{1} \bigr]_{t},\quad t = 1,\ldots,k, \end{aligned}$$
(3c)
$$\begin{aligned} & \biggl[ \biggl( \frac{\mathbf{f}_{\mathrm{GH}}^{T}\boldsymbol{\tau}_{\mathrm{GH}_{d}}}{\mathbf{f}_{\mathrm{GH}}^{T}\mathbf{n}_{\mathrm{GH}}} \biggr) \le \mathit{th}_{d} \biggr]_{t},\quad t = 1,\ldots,k,\ d = 1,2,3,4, \end{aligned}$$
(3d)
$$\begin{aligned} & \bigl[ \mathbf{f}_{\mathrm{ST}}^{T}\mathbf{n}_{\mathrm{ST}} > 0 \bigr]_{t},\quad t = 1,\ldots,k, \end{aligned}$$
(3e)

where Eq. (3) represents the minimization of a physiological criterion \(J\). Equation (3a) represents the equations of motion of the biomechanical model, for which \(\boldsymbol{\varPhi} _{\mathbf{q}}\) is the Jacobian matrix of the kinematic constraint equations, \(\mathbf{M}\) is the mass matrix, q̈ is the acceleration vector, and \(\mathbf{g}\) is the generalized vector of external forces. Equations (3b) and (3c) represent the physiological boundaries of the muscle activations and muscle excitations, respectively, while Eq. (3d) represents the stability condition of the GH joint, for which \(\mathbf{f}_{\mathrm{GH}}\) is the GH reaction force, \(\mathbf{n}_{\mathrm{GH}}\) is the normal to the glenoid plane, and \(\boldsymbol{\tau}_{\mathrm{GH}_{d}}\) is the unitary vector in the glenoid plane describing the direction \(d\), illustrated in Fig. 2, with stability threshold \(\mathit{th}_{d}\) [6]. Finally, Eq. (3e) describes the stability of the ST joint, for which \(\mathbf{f}_{\mathrm{ST}}\) is the ST joint reaction force, and \(\mathbf{n}_{\mathrm{ST}}\) is the directional vector of compression between the scapula and thorax. The GH and ST joint reaction forces are obtained directly from the Jacobian of the constraint equations and the Lagrange multipliers associated with these joints. A more detailed treatment of these forces is provided in [21].

Fig. 2
figure 2

Direction of the GH dislocation force threshold ratios \(\mathit{th}_{d}\), presented in parentheses

Full size image

The compatibility of the muscle force predictions with the muscle force–length–velocity properties and the activation dynamics is ensured by Eqs. (3b) and (3c), respectively. Note that the activation dynamics describes the delay between the neural excitation arriving at a muscle, or ceasing, and the development, or decay, of muscle activation, respectively [18, 29]. Accordingly, the constraints in Eq. (3b) control the lower and upper bounds of the muscle forces, while the constraints in Eq. (3c) control the maximum changes in the muscle forces that are physiologically admissible. The constraints in Eq. (3b) are easily defined since the muscle activations are design variables of the optimization problem described in Eq. (3). The constraints in Eq. (3c) are defined by assessing the time history of the neural excitations \(\mathbf{u}\) through the inversion of the activation dynamics. The activation dynamics of a muscle \(m\) is usually described by a first-order ordinary differential equation that relates the rate of change in muscle activation and the muscle excitation, i.e.,

$$ \dot{a}^{m} = f \bigl( a^{m},u^{m} \bigr). $$
(4)

Considering the first-order equation presented by Winter and Starks [33] for the activation dynamics, and after some algebraic manipulation, the neural excitation at an instant of time \(t\) can be written as [23, 28]

$$ u_{t}^{m} = \left \{ \textstyle\begin{array}{l@{\quad }l} \frac{a_{t}^{m} T_{1} - T_{2} \pm \sqrt{ ( a_{t}^{m} T_{1} + T_{2} )^{2} + 4\dot{a}_{t}^{m} T_{1}}}{2T_{1}} & \dot{a}_{t}^{m} \ge 0, \\ \frac{\dot{a}_{t}^{m} + T_{2}a_{t}^{m}}{T_{2}} & \dot{a}_{t}^{m} < 0, \end{array}\displaystyle \right . $$
(5)

where \(\dot{a}_{t}^{m}\) is the activation rate of the muscle \(m\) at the instant of time \(t\), and \(\mathrm{T}_{1}\) and \(\mathrm{T}_{2}\) are given as:

$$ \begin{aligned} &T_{1} = \frac{1}{\tau_{\mathrm{act}}} - T_{2}, \\ &T_{2} = \frac{1}{\tau_{\mathrm{deact}}}. \end{aligned} $$
(6)

The activation and deactivation time constants \(\tau_{\mathrm{act}}\) and \(\tau_{\mathrm{deact}}\) can be defined as 10 and 50 ms, respectively [19], and the activation rates \(\dot{a}_{t}^{m}\) can be estimated by numerical differentiation of the muscle activations using finite differences, as proposed by Ackermann [1].

The optimization problem posed by Eq. (3) can be solved by a wide variety of optimization methods, including Sequential Quadratic Programming algorithms [15, 17], interior-point algorithms [31], or genetic algorithms [15], just to name a few. All inverse dynamic procedures discussed in this study can be considered regardless of the method used to solve the optimization problem. Therefore, the use of the best optimization method is not addressed here, and the optimization problem is solved with the interior-point algorithm of the fmincon function of Matlab®. Due to the form of Eq. (3) and Eqs. (3a) to (3e), the gradients of the objective function and of the constraint equations are available analytically and are ready to be used in the optimization method.

2.3 Physiological criteria

Two physiological criteria are alternatively considered in this study. The first is an instantaneous measure of the energy-consuming processes in a muscle [20], whereas the second is an integral form of the muscle effort [2]. For \(k\) instants of time, the two criteria are respectively formulated as:

$$\begin{aligned} J_{1} =& \sum_{t = 1}^{k} \sum_{m = 1}^{n_{m}} \biggl( c_{1}\frac{V^{m}{F_{\mathrm{CE}}^{m}}_{t}}{\mathrm{PCSA}^{m}} + c_{2}V^{m}a_{t}^{m} + c_{3}V^{m} \bigl( a_{t}^{m} \bigr)^{2} \biggr), \end{aligned}$$
(7a)
$$\begin{aligned} J_{2} =& \sum_{m = 1}^{n_{m}} V^{m}\int_{t_{1}}^{t_{k}} \bigl( a^{m} \bigr)^{2}\,dt, \end{aligned}$$
(7b)

where \(n_{m}\) is the number of muscles, \(V^{m}\) is the volume of muscle \(m\), \(\mathrm{PCSA}^{m}\) is the physiological cross-sectional area of muscle \(m\), and \(a^{m}\) is the activation level of muscle \(m\). The weighting factors \(c_{1}\), \(c_{2}\), and \(c_{3}\) are defined according to Praagman et al. [20]. The optimization problem is formulated by solving Eq. (3), in which the physiological criterion is either Eq. (7a) or Eq. (7b), subjected to the constraints described by Eqs. (3a) through (3e). Note that the criterion in Eq. (7a) is stated as a sum over \(k\) instants of time only to make its application suitable for all methods applied here.

3 Solution methods

The muscle force distribution problem is solved using the Static Optimization (SO), Extended Inverse Dynamics (EID), and Window Moving Inverse Dynamics Optimization (WMIDO) methods, which are further explained hereafter. Three simulations starting from randomly-generated initial solutions are performed for each method and for each physiological criterion, and the average of the optimal solution cost function and of the computation time required to reach the solution are compared. The analyses were performed on an Intel® Core™ i7 2600k CPU with 16 GB of RAM.

3.1 Static Optimization (SO)

The SO considers muscles as instantaneously available actuators whose forces only depend on the current activation levels so that the muscle force distribution problem can be solved independently at each instant of time. Considering Eqs. (3a) to (3e) and Eq. (7a), the number of instants of time \(k\) equals 1, and \(n\) independent problems are solved for a motion discretized into \(n\) instants of time. Since the SO cannot handle time varying physiological criteria or constraints, the integral form of the muscle effort, described by Eq. (7b), and the activation dynamics constraints, described by Eq. (3c), are excluded from the optimization problem when using this method.

3.2 Extended Inverse Dynamics (EID)

The EID solves all instants of motion at the same time rather than each instant of time independently. Accordingly, \(k = n\) instants of time, and only one problem is solved. The EID can handle all the physiological criteria and constraints described, but the size of the optimization problem is geometrically proportional to the number of instants of time in the analysis, which limits its applicability. Despite the motion under analysis, in the demonstrative case used here, comprising 701 instants of time, only the first half of these are analyzed here because the EID cannot solve them all simultaneously due to memory limitations. Note that, for the sake of comparison, the SO and WMIDO also analyze only the first half of the motion, even though they have no limitations from this point of view. The activation dynamics constraints, described by Eq. (3c), are also excluded from the analyses of the EID because their addition into the muscle force distribution problem makes the problem too large, decreasing the number of instants of time that the EID can solve to less than 200.

3.3 Window Moving Inverse Dynamics Optimization (WMIDO)

Instead of solving each instant of time independently, or all instants of time at once, the procedure proposed here solves the muscle force distribution problem for all \(k\) instants of time bounded within a moving window of size \(k\). At the beginning of the analysis, the window comprises the first \(k\) instants of time, for which the redundancy problem is solved simultaneously. Once the solution is found for the current window position, the window is moved forward \(l\) instants of time, and the procedure is repeated until all instants of time are solved. The number of instants of time \(l\) that the window can move forward, i.e., the marching step, can be as large as the window size \(k\). If \(l\) is smaller than \(k\), then only the first \(l\) instants of time of the window are saved as the optimal solution, as exemplified in Fig. 3 for a \(k\) of 10 and an \(l\) of 5. For each window position, the optimal solution defined for previous instants of time may be used, if needed, to compute time-dependent criteria or constraints. At the end of the analysis, the window size is adjusted to the size of the remaining instants of time.

Fig. 3
figure 3

Window Moving Inverse Dynamics Optimization (WMIDO) procedure for a window of size 10 and a marching step of 5 instants of time in each problem. At the beginning of the analysis, in position 1, the muscle force distribution problem is solved for the first 10 instants of time that compose the window of the WMIDO. Once the solution is found, the window moves forward 5 instants of time to position 2, and the next 10 instants of time are solved. This procedure is repeated until the optimal solution is found for all instants of time

Full size image

The WMIDO can handle all the physiological criteria and constraints described. The number of optimization problems to be solved is dependent on the size and the marching of the window. Interestingly, for specific choices of \(k\) and \(l\), the proposed procedure resembles the MSO and EID [1, 25]. In particular, if \(k\) and \(l\) are chosen to be 1, the WMIDO is similar to the MSO, whereas if \(k\) and \(l\) are the same as the total number of instants of time of the motion under analysis, the WMIDO is similar to the EID.

In this study, the WMIDO analyses are performed considering a window of size 10 frames and a marching step of 5 instants of time in each update. For the sake of comparison, the WMIDO is applied considering both the inclusion (WMIDOac) and exclusion (WMIDOc) of the activation dynamics, described by Eq. (3c). In order to evaluate the robustness of the proposed procedure, additional simulations are performed for the WMIDOac for different window sizes and marching steps. Assuming a marching step of half the size of the window, window sizes of 4, 10, and 20 instants of time are evaluated, and for a window size of 10 instants of time, marching steps of 1, 5, and 10 instants of time are evaluated.

4 Results and discussion

The redundant muscle force distribution problem of an abduction motion of the upper limb is used here to discuss the proposed methodology. The number of instants of time used and the constraints are sized in order to ensure that the SO, EID, and WMIDO methods are able to solve the muscle force distribution problem of the motion under analysis. The average of the optimal solution cost function and of the computation time of the three simulations performed for each method are presented in Fig. 4. Note that, for the sake of comparison, the cost functions of the optimal solutions are computed over all instants of time, regardless of the method applied. Moreover, the results presented in Fig. 4 are normalized by those of the EID.

Fig. 4
figure 4

Optimal solution cost function and computation time of the Static Optimization (SO), Extended Inverse Dynamics (EID), and Window Moving Inverse Dynamics Optimization (WMIDOc and WMIDOac) for which the physiological criterion is: (a) the instantaneous measure of the energy-consuming processes in a muscle (\(J_{1}\)); and (b) the integral form of the muscle effort (\(J_{2}\)). The results are presented as an average of the three simulations performed, and are normalized by those of the EID. The WMIDOc does not include the muscle activation dynamics, similarly to the SO and EID, whereas the WMIDOac does

Full size image

The muscle force distribution problem solved by the WMIDOac is different from that of the SO, EID, and WMIDOc due to the inclusion of the muscle activation dynamics. Therefore, the results of the WMIDOac are not used to compare the inverse dynamic procedures discussed here, but are primarily presented to show that the WMIDO is able to include time-dependent physiological properties of the muscles, and to show the influence of the muscle activation dynamics on the muscle force predictions.

For all three starting solutions, the optimal solutions estimated by the SO, EID, and WMIDOc present the same physiological cost. Accordingly, similar muscle and joint reaction forces are predicted by all, as illustrated in Fig. 5 for the GH joint reaction force. Although the simulation of the muscle activation dynamics did not produce a noticeable change in the physiological costs of the WMIDOac, a smoothing effect to avoid fast variations in the muscle forces is observed, as depicted in Fig. 6 for the predictions of the objective function \(J_{1}\) regarding the clavicular part of the trapezius muscle and the most superior bundle of the infraspinatus muscle. As expected, the first-order model of the activation dynamics behaves as a low-pass filter that controls the rate of force change [18]. The small impact of the muscle activation dynamics on the muscle forces is likely due to the characteristics of the motion under analysis, which is a standard motion of the upper limb, performed at a slow speed. For more complex and fast-paced motions, a more pronounced influence of the muscle activation dynamics is expected.

Fig. 5
figure 5

Glenohumeral joint reaction force for (a) the instantaneous measure of the energy-consuming processes in a muscle (\(J_{1}\)), and (b) the integral form of the muscle effort (\(J_{2}\)). The results are presented as an average of the three simulations performed for the Static Optimization (SO), the Extended Inverse Dynamics (EID), and the Window Moving Inverse Dynamics Optimization (WMIDOc and WMIDOac). The WMIDOc does not include the muscle activation dynamics, similarly to the SO and EID, whereas the WMIDOac does. The humeral elevation is described with respect to the thorax

Full size image
Fig. 6
figure 6

Muscle forces of the clavicular part of the trapezius muscle and of the most superior bundle of the infraspinatus muscle for the instantaneous measure of the energy-consuming processes in a muscle (\(J_{1}\)): (a) force for all instants of time evaluated; (b) zoom of force in selected areas to highlight the influence of the muscle activation dynamics simulation (WMIDOac). The results are presented as an average of the three simulations performed for the Static Optimization (SO), the Extended Inverse Dynamics (EID), and the Window Moving Inverse Dynamics Optimization (WMIDOc and WMIDOac). The WMIDOc does not include the muscle activation dynamics, similarly to the SO and EID, whereas the WMIDOac does. The humeral elevation is described with respect to the thorax

Full size image

Regarding the computation time, the EID is significantly more time-consuming than the SO and WMIDOc, regardless of the objective function considered. In particular, the EID requires 37 times more time than the SO for the \(J_{1}\) and 21 times more time than the WMIDOc for the \(J_{2}\). Even though the EID solves only a single optimization problem, as opposed to the SO and WMIDOc that solve several, the computational effort of the EID is greater due to the dimension of the optimization problem. Note that the optimization problem of the EID includes 351 times more design variables and constraint equations than the low-dimension optimization problems of the SO. In other words, solving several low-dimension problems is more attractive from the computational point of view than solving a single high-dimension problem, as also observed by Ackermann [1]. The computational effort of the WMIDOc decreased significantly compared to the EID, but it is still larger than that required by the SO. Considering only time-independent physiological criteria, and disregarding the time-dependent behavior of the muscles, these results clearly highlight why the SO is the method most often applied to estimate the muscle and joint reaction forces [4, 8, 17]. Yet, if a global, time-dependent physiological criterion or the time-dependent physiological nature of the muscles are to be considered in the framework of an inverse dynamic formulation, only the EID and WMIDO overcome the limitations of the SO, and only these can be used [1]. Under these conditions, the superiority of the method proposed becomes clear. Both the EID and WMIDOc reach similar optimal solutions, but the WMIDOc is significantly less computationally expensive. For the objective functions \(J_{1}\) and \(J_{2}\), the EID is 15 and 21 times more time-consuming than the WMIDOc. Compared to the SO, the WMIDOc is only 3 times more time-consuming. Additionally, it must be noted that the EID cannot solve all 701 instants of time of the motion under analysis while disregarding the muscle activation dynamics, or the 351 instants of time analyzed if the activation dynamics is considered. For such cases, the limited memory capacity of the computer used precluded the EID from solving the optimization problem. The WMIDO, on the other hand, is able to solve all 701 instants of time while taking into account all the optimization constraints described in Eqs. (3a) to (3e).

The WMIDOac simulations for different window sizes and marching steps show no relevant effect of these features on the optimal solution of the muscle force distribution problem, which provides further confidence in the proposed method. However, significant differences are observed in the computation time, as shown in Fig. 7. The increase in window size increases the computational effort due to the increase in the optimization problem size. An increase from a window size of 4 to a window size of 20 instants of time resulted in a ninefold and threefold increase in the computation time for \(J_{1}\) and \(J_{2}\), respectively. On the other hand, the increase in the marching step decreases the computational effort because the number of optimization problems that must be solved also decreases. For a marching step of 10 instants of time, i.e., the size of the window considered, the optimal solutions for \(J_{1}\) and \(J_{2}\) were computed ten and seven times faster, respectively, than for a marching step of 1 instant of time.

Fig. 7
figure 7

Optimal solution cost function and computation time of the Window Moving Inverse Dynamics Optimization (WMIDOac) for different window sizes and marching steps for (a) the instantaneous measure of the energy-consuming processes in a muscle (\(J_{1}\)); and (b) the integral form of the muscle effort (\(J_{2}\)). For the analysis of different marching steps, a window of size 10 instants of time is considered, while for the analysis of different window sizes, a marching step of half the size of the window is considered. The results are presented as an average of the three simulations performed for each case, and are normalized by those of the EID. The WMIDOac includes the muscle activation dynamics, whereas the EID does not

Full size image

The EID and WMIDO overcome the limitations of the SO in using time-dependent physiological criteria or constraints, but the WMIDO is significantly more efficient than the EID, and it also overcomes the limitation of the EID in the level of the discretization that can be realistically considered. It must be noted that, even though the elastic properties of tendons were not considered in this study, their contribution can be accounted for in the same way as the activation dynamics. A detailed description of the implementation of tendon elasticity is provided by Ackermann [1]. One limitation of the proposed procedure, and also of the EID, is the need to estimate time derivatives by finite differences, as described for the determination of the neural excitations, which can lead to inaccuracies if the time steps are not sufficiently small. Additionally, it must be pointed that Ackermann [1] reported infeasibilities when applying the Modified Static Optimization (MSO) method, a particular case of the WMIDO for a window size of 1 frame and a marching step of 1 instant of time, due to restrictive constraints that could not be satisfied as a result of the fixed values at previous instants of time. Accordingly, despite the simulations performed in this study for different window sizes and marching steps not showing any infeasibilities, the authors recommend the use of a marching step always smaller than the window size. Under this condition, the procedure saves only the solution for part of the instants of time of the current window, as illustrated in Fig. 3, which means that the solution to these is estimated while taking into account future instants of time. The influence of the size and marching step of the window on the performance of the proposed procedure should be further investigated in future studies, especially for more complex and fast-paced motions and other biomechanical models.

Considering that the selection of the best optimization method to solve the redundant muscle force distribution problem is transversal to the SO, EID, and WMIDO, the research for the best optimization method, or the most suitable, was not focused in this work. Nevertheless, to avoid or at least limit the possibility of the method identifying local minima, three cases, starting from randomly-generated initial solutions, were always analyzed. The solution reached was always similar for all, which suggests that the local minimum found is in fact global.

5 Concluding remarks

A new method based on an inverse dynamic formulation was proposed here. The Window Moving Inverse Dynamic Optimization (WMIDO) consists in considering a moving window of \(k\) instants of time for which the optimization problem is solved. The window moves iteratively across all instants of time until all of them are analyzed. In order to evaluate the potential of the proposed procedure, the Static Optimization (SO), Extended Inverse Dynamics (EID), and WMIDO methods were applied to solve the muscle force distribution problem of an abduction motion in the frontal plane of a musculoskeletal model of the upper limb. A time-dependent and a time-independent physiological criteria were considered. Despite the SO limitations, the results show that it is the most effective method, from the computational cost point of view, to estimate the muscle and joint reaction forces when an instantaneous physiological criterion is considered and the time-dependent nature of the muscles is disregarded. For a more realistic estimation of the muscle forces, including a global, time-dependent physiological criteria or the time-dependent physiological nature of the muscles, only the EID and WMIDO can be applied. Under these conditions, the results clearly show the superiority of the WMIDO over the EID. In particular, the WMIDO is not limited by the level of discretization of the motion under analysis, and it is more computationally efficient.