Weakly and fully coupled methods for structural optimization of flexible mechanisms

Abstract

The paper concerns a detailed comparison between two optimization methods that are used to perform the structural optimization of flexible components within a multibody system (MBS) simulation. The dynamic analysis of flexible MBS is based on a nonlinear finite element formulation. The first method is a weakly coupled method, which reformulates the dynamic response optimization problem in a two-level approach. First, a rigid or flexible MBS simulation is performed, and second, each component is optimized independently using a quasi-static approach in which a series of equivalent static load (ESL) cases obtained from the MBS simulation are applied to the respective components. The second method, the fully coupled method, performs the dynamic response optimization using the time response obtained directly from the flexible MBS simulation. Here, an original procedure is proposed to evaluate the ESL from a nonlinear finite element simulation, contrasting with the floating reference frame formulation exploited in the standard ESL method. Several numerical examples are provided to support our position. It is shown that the fully coupled method is more general and accommodates all types of constraints at the price of a more complex optimization process.

1 Introduction

Since the early 1960s, structural optimization has undergone considerable evolution. Nowadays, the achieved developments are such that optimization techniques are embedded in commercial software tools and are daily used to solve industrial problems. Even if the majority of real loads are dynamic in essence, optimization techniques are usually applied to the design of structural components under (quasi-)static or vibration design criteria due to the intrinsic difficulties of evaluating the dynamic response and then incorporating it in an optimization problem.

Historically, design of mechanisms first considered a component-based approach, wherein the standard methods of static response optimization are used. Saravanos and Lamancusa [20] selected several configurations of the mechanism, whereupon structural optimization was performed based on representative loading conditions coming from the designer experience for each posture. This approach is not rational since a few configurations can hardly represent the overall motion and the optimal design strongly depends on the designers’ choices. Moreover, the coupling between rigid and elastic motions are omitted, which causes an inaccuracy on the displacements and stresses.

With the evolution of multibody system (MBS) analysis, Bruns and Tortorelli [6] proposed an approach combining rigid MBS analysis and optimization techniques to design optimal components. The component-based approach is thusly extended toward a system-based approach, which better captures the behavior of the whole system. The optimization procedure is performed with load cases evaluated directly during the MBS analysis. The method is illustrated on the design of a slider–crank mechanism loaded with the maximum tensile force calculated during the simulation. This breakthrough is essential since the optimal design may be very sensitive to the support and loading conditions [2].

Using a system-based approach to perform the dynamic response optimization of components, two optimization methods can currently be identified, the weakly and fully coupled methods.

The weakly coupled method reformulates the dynamic response optimization problem in a two-level approach. First, a rigid or flexible MBS simulation computes the loads applied to each component, and second, each isolated component is optimized independently using a quasi-static approach, in which a series of equivalent static load cases obtained from the MBS simulation are applied to the respective components. An important development has been made by Kang et al. [18], who proposed a rational method to define equivalent static loads (ESLs) to optimize flexible mechanisms. During the static response optimization process, whereas ESLs are implicit functions of the dynamic simulation response, they are not updated. Thus, cycles are needed to account for the ESL dependency on design variables. Häussler [13] showed the importance of considering the update of quasi-static loads at each cycle due to the property changes of component inertia since these interactions might be significant. The weakly coupled method is used in e.g. [14–16, 23].

The fully coupled method considers a more integrated approach of the optimization problem wherein the optimization is performed using the time response directly obtained from the MBS simulation. Oral and Kemal Ider [19] proposed a methodology to consider the coupled rigid-elastic motion of the MBS system and the time-dependency of the constraints. They investigated the representation of global constraints either by the most critical constraint or aggregated with a Kresselmeier–Steinhauser function. Later on, Brüls et al. [5] took advantage of the evolution of numerical simulations and topology optimization tools to design structural components within a flexible MBS simulation. They showed the feasibility and convenience of integrating the optimization loop directly to the flexible MBS simulation. Doing so, the dynamic effects are naturally taken into account. However, the resulting optimization problem is not a simple extension of structural optimization. The influence of the changes of component inertial property on vibrations and the interactions between flexible components generally result in complex design problems. Moreover, treating time-dependent responses coming from the MBS analysis in the optimization process is rather complex. The formulation of the optimization problem is essential to obtain good convergence properties [28]. The fully coupled method is used in e.g. [15, 21, 27].

The objective of this paper is to investigate the performance of the weakly and fully coupled methods. In addition, the standard ESL method was developed for flexible MBS described using a floating reference frame formulation [18]. This formalism facilitates the derivation of the equivalent static loads notably as this formulation deals with body-attached frame. However, in our previous developments of the fully coupled method [5, 28], we adopted a nonlinear finite element formalism [12]. In order to realize a fair comparison between both optimization methods, it is preferable to use a unique MBS formalism. Therefore, another contribution of this paper is to adapt the ESL method to the nonlinear finite element formulation because the ESL method proposed by Kang et al. [18] cannot be simply translated and directly applied to the latter formalism.

The first part of the paper briefly discusses the flexible MBS analysis, that is, the derivation of the equations of motion and the time integration algorithm. Afterwards, the ESL method is presented in three parts: the ESL definition, the ESL derivation for a floating reference frame formalism, and the proposed method to derive the ESL for a nonlinear finite element formalism. The fully coupled method is then described. The following part introduces the general framework of the dynamic response optimization problem and different approaches to solve it. Several standard examples are investigated to compare both approaches, to illustrate the similarities and differences and to support our discussion before drawing our conclusions.

2 Flexible multibody systems approach

2.1 Equations of motion of flexible multibody systems

In this paper, flexible MBS are modeled using a nonlinear finite element formulation as proposed by Géradin and Cardona [12], which is based on an inertial frame approach. Absolute nodal coordinates that correspond to the displacements and orientations of each node of the finite element mesh are gathered in the generalized coordinate vector $\mathbf {q}$.

The motion of the system is subject to kinematic constraints $\boldsymbol{\Phi}(\mathbf {q},t)$ that ensure the connections between bodies due to kinematic joints such as hinges, spherical joints, etc. They introduce nonlinear kinematic constraints between generalized coordinates.

The constrained dynamic problem is formulated using an augmented Lagrangian approach based on the kinetic and potential energies of the system. The augmented Lagrangian approach introduces a penalty term $p\boldsymbol{\Phi}_{q}^{T}\boldsymbol{\Phi}$ with penalty coefficient $p$ in the formulation of the constraints notably for convergence reasons. Nevertheless, since this term vanishes at convergence, the response of the system is independent of the choice of $p$.

Following [12], the motion of the system is obtained by solving the following differential-algebraic equation system (DAE):

$$ \begin{aligned} \mathbf {M}(\mathbf {q}) \ddot{\mathbf {q}} + \boldsymbol{\Phi}_{q}^{T}(\mathbf {q},t) \bigl(k\boldsymbol{\lambda} + p \boldsymbol{\Phi} (\mathbf {q},t ) \bigr) & = \mathbf {g}(\dot{\mathbf {q}},\mathbf {q},t), \\ k\boldsymbol{\Phi}(\mathbf {q},t) & = \mathbf {0}, \end{aligned} $$

(1)

subject to the initial conditions

$$ \mathbf {q}(0) = \mathbf {q}_{0} \quad \text{and}\quad \dot{\mathbf {q}}(0) = \dot{\mathbf {q}}_{0}. $$

(2)

In this system, $\mathbf {M}$ is the mass matrix, $\ddot{\mathbf {q}}$, $\dot{\mathbf {\nonumber q}}$, and $\mathbf {q}$ are respectively the acceleration, velocity, and displacement vectors, the vector $\mathbf {g}$ gathers the external, internal and complementary inertia forces, $k$ is a scaling factor, $\boldsymbol{\lambda}$ is the Lagrange multiplier vector and the subscript $(\cdot)_{\mathbf {q}}$ denotes the derivative with respect to $\mathbf {q}$. It should be noted that the mass matrix can depend on the generalized coordinates.

2.2 Time integration

To solve the set of nonlinear DAE (1), Géradin and Cardona [12] consider the generalized-$\alpha$ time integration scheme initially developed by Chung and Hulbert [9]. Arnold and Brüls [1] demonstrated that, despite the presence of algebraic constraints and the nonconstant character of the mass matrix, this integration scheme leads to accurate and reliable results with a small amount of numerical damping.

According to the generalized-$\alpha$ method, a vector $\mathbf {a}$ of acceleration-like variables is defined by the recurrence relation

$$ ( 1-\alpha_{m} ) \mathbf {a}_{n+1} + \alpha_{m} \mathbf {a}_{n} = ( 1-\alpha_{f} ) \ddot{\mathbf {q}}_{n+1} + \alpha_{f}\ddot{\mathbf {q}}_{n} $$

(3)

with $\mathbf {a}_{0} = \ddot{\mathbf {q}}_{0}$. The vector $\mathbf {a}_{n}$ is an auxiliary variable used by the algorithm and can be interpreted as an approximation of the true acceleration $\ddot{\mathbf {q}}(t)$ at time $t=t_{n}+ (\alpha_{m}-\alpha_{f} )h$.

The integration scheme is subsequently obtained by employing the pseudo-acceleration $\mathbf {a}_{n}$ in the Newmark integration formulae:

$$\begin{aligned} \mathbf {q}_{n+1} =& \mathbf {q}_{n} + h\dot{\mathbf {q}}_{n} + h^{2} \biggl( \frac {1}{2}-\beta \biggr) \mathbf {a}_{n} + h^{2}\beta \mathbf {a}_{n+1}, \end{aligned}$$

(4)

$$\begin{aligned} \dot{\mathbf {q}}_{n+1} =& \dot{\mathbf {q}}_{n} + h ( 1-\gamma ) \mathbf {a}_{n}+h\gamma \mathbf {a}_{n+1}, \end{aligned}$$

(5)

where $h$ denotes the time step. If the parameters $\alpha_{f}$, $\alpha _{m}$, $\beta$, and $\gamma$ are properly chosen according to [9], second-order accuracy and unconditional stability are guaranteed for linear problems. It is convenient to define these parameters in terms of the spectral radius at infinite frequencies $\rho _{\infty} \in [0,1 ]$ as

$$ \begin{aligned} &\alpha_{m}=\dfrac{2\rho_{\infty}-1}{\rho_{\infty}+1}, \quad \quad \alpha_{f}=\dfrac {\rho_{\infty}}{\rho_{\infty}+1}, \\ &\gamma= \dfrac{1}{2}-\alpha_{m}+\alpha_{f}, \quad \quad\beta= \dfrac{1}{4} \biggl(\gamma+\dfrac{1}{2} \biggr)^{2}. \end{aligned} $$

(6)

The choice $\rho_{\infty} = 0$ annihilates high-frequency response, whereas $\rho_{\infty} = 1$ corresponds to no numerical damping.

At time step $n+1$, the variables $\ddot{\mathbf {q}}_{n+1}$, $\dot{\mathbf {q}}_{n+1}$, $\mathbf {q}_{n+1}$, and $\boldsymbol{\lambda}_{n+1}$ must satisfy the system of nonlinear equations (1). To solve this dynamic equilibrium problem, a Newton–Raphson procedure associated with the linearized form (7) of (1) is employed, which brings the residual of (1), that is, $\mathbf {r} = \mathbf {M}\ddot {\mathbf {q}} + \boldsymbol{\Phi}_{\mathbf {q}}^{T} (k \boldsymbol{\lambda}+p \boldsymbol{\Phi} ) - \mathbf {g}$ and $\boldsymbol{\Phi}$, close to zero. More precisely, around an approximate solution $\ddot {\mathbf {q}}$, $\dot{\mathbf {q}}$, $\mathbf {q}$, $\boldsymbol{\lambda}$, the following linearized residual equations are solved:

$$ \begin{aligned} &\mathbf {r} (\mathbf {q}+\Delta \mathbf {q},\dot{\mathbf {q}}+\Delta\dot{\mathbf {q}}, \ddot{\mathbf {q}}+\Delta\ddot{\mathbf {q}}, \boldsymbol{\lambda} + \Delta\boldsymbol{\lambda} ) \\ & \quad\simeq \mathbf {r} (\mathbf {q}, \dot{\mathbf {q}}, \ddot{\mathbf {q}}, \boldsymbol{\lambda} )+ \mathbf {M}\Delta\ddot{\mathbf {q}} + \mathbf {C}_{t} \Delta\dot{\mathbf {q}}+\mathbf {K}_{t} \Delta \mathbf {q} + \boldsymbol{\Phi}_{\mathbf {q}}^{T} (k \Delta\boldsymbol{\lambda} + p \boldsymbol{\Phi}_{\mathbf {q}} \Delta \mathbf {q} ) = \mathbf {0}, \\ &k \boldsymbol{\Phi} (\mathbf {q}+\Delta \mathbf {q} ) \simeq k \boldsymbol{\Phi} (\mathbf {q} ) + k \boldsymbol{\Phi}_{\mathbf {q}} \Delta \mathbf {q} = \mathbf {0}, \end{aligned} $$

(7)

where $\mathbf {C}_{t}=\partial \mathbf {r} / \partial\dot{\mathbf {q}}$ and $\mathbf {K}_{t}=\partial \mathbf {r}/ \partial \mathbf {q}$ denote the tangent damping and tangent stiffness matrices, respectively.

3 Weakly coupled approach: Equivalent static load method

3.1 Introduction and definition

In the context of dynamic response, the optimization problem formulation involves time-dependent functions. The purpose of the equivalent static load method is to remove the time component from the problem, that is, to transform the dynamic response optimization problem into a static optimization problem with multiple load cases [8]. Indeed, all the advantages of static response optimization and all the standard methods can thus be used, whereas the problems related to time-dependent functions are circumvented.

In [18], the authors define an equivalent static load as follows.

Definition 1

When a dynamic load is applied to a structure, the equivalent static load is defined as the static load that produces the same displacement field as the one created by the dynamic load at an arbitrary time.

In order to introduce the concept of equivalent static loads, let us consider the following equilibrium equation of a linear structure¹ subject to a dynamic load $\mathbf {g} (t )$:

$$ \mathbf {M}(\mathbf {p})\ddot{\mathbf {q}}(\mathbf {p},t) + \mathbf {K}(\mathbf {p})\mathbf {q}(\mathbf {p},t)=\mathbf {g}(t), $$

(8)

where $\mathbf {p}$ is the design variable vector, $\mathbf {q}$ and $\ddot{\mathbf {q}}$ are the displacement and acceleration vectors, respectively, and the damping effect is neglected. Terms of Eq. (8) can be rearranged as

$$ \mathbf {K}(\mathbf {p})\mathbf {q}(\mathbf {p},t) = \mathbf {g}(t)- \mathbf {M}(\mathbf {p})\ddot{ \mathbf {q}}(\mathbf {p},t). $$

(9)

The left-hand-side of (9) has a similar layout as the classical static equilibrium equation of a structure. By identification and according to the previous definition, the equivalent static load at time $t$ is defined as

$$ \mathbf {g}_{\mathrm{eq}}(t) = \mathbf {g}(t)- \mathbf {M}(\mathbf {p})\ddot{\mathbf {q}}(\mathbf {p},t). $$

(10)

It should be noticed that the equivalent static load $\mathbf {g}_{\mathrm{eq}}(t)$ is an implicit function of the design variables and that it involves the external loads and inertia forces. From an analysis point of view, equivalent static loads seem useless, but they are developed in order to elaborate a static response optimization problem. In lieu of considering the dynamic loading, they offer the possibility of considering a series of static loads that give at each time step the same displacement field as the one given by the dynamic loading. Therefore, the dynamic optimization problem is transformed into a optimization problem subject to multiple static load cases with a load case for each integration time step.

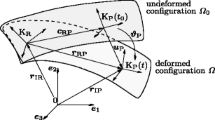
3.2 Derivation of the equivalent static loads using a floating frame of reference formalism

Initially, the ESL method has been developed for flexible MBS modeled using a floating reference frame formulation [18]. In order to develop the ESL derivation, the equations of motion and the notation corresponding to this formalism are first reminded.

According to [22], the equations of motion that govern a flexible multibody system using a floating frame of reference formalism can be expressed as

$$\begin{aligned} &\left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \mathbf {m}_{xx}^{b} & \mathbf {m}_{x\theta}^{b} & \mathbf {m}_{x f}^{b}\\ & \mathbf {m}_{\theta\theta}^{b} & \mathbf {m}_{\theta f}^{b}\\ & & \mathbf {m}_{ff}^{b} \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{c} \ddot{\mathbf {x}}_{0}^{b}\\ \ddot{\boldsymbol{\theta}}_{0}^{b}\\ \ddot{\mathbf {q}}_{f}^{b} \end{array}\displaystyle \right ] + \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \mathbf {0} & \mathbf {0} & \mathbf {0}\\ \mathbf {0} & \mathbf {0} & \mathbf {0}\\ \mathbf {0} & \mathbf {0} & \mathbf {K}_{ff}^{b} \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{c} \mathbf {x}_{0}^{b}\\ \mathbf {\boldsymbol{\theta}}_{0}^{b}\\ \mathbf {\mathbf {q}}_{f}^{b} \end{array}\displaystyle \right ] \\ &\quad = - \left [ \textstyle\begin{array}{c} \mathbf {C}_{x^{b}}^{T}\\ \mathbf {C}_{\theta^{b}}^{T}\\ \mathbf {C}_{q_{f}^{b}}^{T} \end{array}\displaystyle \right ] \boldsymbol{\lambda} + \left [ \textstyle\begin{array}{c} (\mathbf {Q}_{e}^{b} )_{x}\\ (\mathbf {Q}_{e}^{b} )_{\theta}\\ (\mathbf {Q}_{e}^{b} )_{f} \end{array}\displaystyle \right ]+ \left [ \textstyle\begin{array}{c} (\mathbf {Q}_{v}^{b} )_{x}\\ (\mathbf {Q}_{v}^{b} )_{\theta}\\ (\mathbf {Q}_{v}^{b} )_{f} \end{array}\displaystyle \right ], \quad b=1,2, \ldots, n_{b}, \end{aligned}$$

(11)

where $n_{b}$ is the number of bodies, $\mathbf {q}_{f}$ is the nodal deformation, $\mathbf {x}_{0}^{b}$ is a set of Cartesian coordinates that defines the origin location of the floating body reference frame, and $\boldsymbol{\theta}_{0}^{b}$ is a set of rotational coordinates that describes the orientation of the floating body reference frame. The right-hand-side terms of (11) are respectively the reaction force vector from the joint constraints, the external load vector, and the quadratic velocity vector including the effect of Coriolis and centrifugal forces. As with the nonlinear finite element formalism, all the terms depend on time, and the flexible MBS expressed by (11) is subject to dynamic loads.

According to Definition 1, the equation system (11) must be solved to obtain the ESL. The last row can be rearranged as

$$ \mathbf {K}_{ff}^{b} \mathbf {q}_{f}^{b} = - \mathbf {m}_{xf}^{b} \ddot{\mathbf {x}}_{0}^{b} - \mathbf {m}_{f\theta}^{b} \ddot{\boldsymbol{\theta}}_{0}^{b} -\mathbf {m}_{ff}^{b} \ddot{\mathbf {q}}_{f}^{b} - \mathbf {C} _{q_{f}^{b}}^{T} \boldsymbol{\lambda} + \bigl(\mathbf {Q}_{e}^{b} \bigr)_{f} + \bigl( \mathbf {Q}_{v}^{b} \bigr)_{f}. $$

(12)

Thus, from Definition 1, the ESL of body $b$ at time step $t_{n}$ in the body-attached frame for a flexible MBS system described using a floating reference frame formulation is

$$ \mathbf {K}_{ff}^{b} \mathbf {q}_{n,f}^{b} = \mathbf {g}_{n,\mathrm{eq}}^{b}, $$

(13)

where

$$ \mathbf {g}_{n,\mathrm{eq}}^{b} = -\mathbf {m}_{xf}^{b} \ddot{\mathbf {x}}_{n,0}^{b} - \mathbf {m}_{f\theta}^{b} \ddot{\boldsymbol {\theta}}_{n,0}^{b} -\mathbf {m}_{ff}^{b} \ddot{\mathbf {q}}_{n,f}^{b} - \mathbf {C} _{q_{n,f}^{b}}^{T} \boldsymbol{\lambda}_{n} + \bigl(\mathbf {Q}_{n,e}^{b} \bigr)_{f} + \bigl(\mathbf {Q}_{n,v}^{b} \bigr)_{f}. $$

(14)

In (14), the first two terms represent the effect of the coupling between rigid-body motion and elastic deformation, whereas the third term represents the inertia force vector caused by elastic deformation of flexible bodies. The fourth term is the reaction force vector from the joint constraints, the fifth term is the external load vector, and the last term includes the effect of the Coriolis and centrifugal forces.

From the previous developments initially made by Kang et al. [18] we observe that the resulting equations of motion resulting from the floating reference frame formalism are suitable to obtain directly the ESL.

3.3 Derivation of the equivalent static loads using a nonlinear finite element formalism

In [18], the derivation of the ESL for flexible MBS is straightforward due to inherent properties of the floating reference frame formulation. First, we point out that the stiffness matrix is constant in the body-attached frame during the entire motion. Thus, independently of the system configuration, a single stiffness matrix per body is considered in the optimization process, that is, for all the time steps. Second, the component deformation is computed in the body-attached frame and is readily extracted for the ESL computation.

These essential characteristics do not exist in a standard nonlinear finite element formalism. The equations of motion are developed in an inertial frame, that is, the forces are not expressed in a body-attached frame. Furthermore, no decoupling exists between rigid-body motion and elastic deformation, which is usually one of its key points.

Hereafter, we propose a method to recover these characteristics in a post-processing step of the MBS simulation wherein ESL are obtained. We note that the proposed method does not alter the MBS analysis.

At a converged time step $t_{n}$, linearizing the equations of motion (1) leads to

$$ \begin{aligned} \mathbf {M}\Delta\ddot{\mathbf {q}} + \mathbf {C}_{t} \Delta\dot{\mathbf {q}}+\mathbf {K}_{t} \Delta \mathbf {q} + \boldsymbol{\Phi}_{\mathbf {q}}^{T} (k \Delta\boldsymbol{\lambda} + p \boldsymbol{\Phi}_{\mathbf {q}} \Delta \mathbf {q} ) &= \Delta \mathbf {r}, \\ k \boldsymbol{\Phi}_{\mathbf {q}} \Delta \mathbf {q} &= \Delta\boldsymbol{\Phi}. \end{aligned} $$

(15)

At first sight, it would be possible to obtain a similar expression as in (9). However, several problems are encountered when trying to apply Definition 1. First, the tangent stiffness matrix is related to the whole system, and it evolves with the system configuration. It would be very inefficient to store this matrix for each time step. Second, the body tangent stiffness matrix $\mathbf {K}_{t}^{b}$ of body $b$ is needed to derive the ESL of body $b$. Third, the generalized coordinate vector $\mathbf {q}(t_{n})$ exhibits no decoupling between rigid-body motion and elastic deformation, whereas the knowledge of deformation is required to derive ESL.

The key idea of the method is to introduce a corotational frame per body in a post-processing step so that the required characteristics can be recovered. We note that several definitions of the corotational frame exist such as, for example, a definition based on the minimization of the strain energy, a chord frame, or a tangent frame definition [29].

The above-mentioned problems are circumvented as follows. (1) A single tangent stiffness matrix for a chosen reference state $\mathbf {K}_{t}(t_{\mathrm{ref}})$ is stored whereupon appropriate transformations must be applied to the vector $\mathbf {q}(t_{n})$ in order to bring it back to the reference configuration for all other time steps. Based on the corotational frame, transformation rules can be established to switch from the actual configuration to the reference configuration and vice versa. (2) For each body $b$, the body tangent stiffness matrix $\mathbf {K}_{t}^{b}(t_{\mathrm{ref}})$ is extracted from $\mathbf {K}_{t}(t_{\mathrm{ref}})$ of the reference state. This is easily performed by identifying the coordinates related to the nodes of body $b$ and then extracting the body tangent stiffness matrix from the complete matrix. This technique is possible because, in our implementation of the finite element formalism, each body has its own set of nodal rotation and translation coordinates, which are not shared with other bodies. (3) Component deformation measure is defined with respect to the body-attached frame, that is, the corotational frame.

For each body $b$, a corotational frame definition is adopted and defined by $\mathbf {x}_{0}^{b}$ and $\boldsymbol{\theta}_{0}^{b}$, the position of the body-attached frame in the inertial frame and the relative rotation vector of the body-attached frame compared to its reference configuration. As illustrated in Fig. 1, the relationship between the absolute position $\mathbf {x}_{i}$ and orientation $\mathbf{\varPsi}_{i}$ of node $i$ of a flexible component and its local displacement $\mathbf {u}_{i}$ and rotation $\boldsymbol{\psi}_{i}$ with respect to the corotational frame is given by

$$\begin{aligned} \mathbf {x}_{i} =& \mathbf {x}_{0}^{b} + \mathbf {R}_{0}^{b} (\mathbf {X}_{i}+\mathbf {u}_{i}), \end{aligned}$$

(16)

$$\begin{aligned} \mathbf{\varPsi}_{i} =& \boldsymbol{\theta}_{0}^{b} \circ\boldsymbol{\psi}_{i}, \end{aligned}$$

(17)

where $\mathbf {R}_{0}^{b} (\boldsymbol{\theta}_{0}^{b})$ is the rotation matrix between the inertial frame and the corotational frame, $\mathbf {X}_{i}$ is the position of node $i$ in the body-attached frame for the nondeformed configuration, and the operation ∘ symbolizes the composition of rotations. Amongst others, Cardona and Géradin [7] provide a comprehensive definition of corotational frames.

Fig. 1

Kinematic description of a corotational frame

By (16)–(17), a local generalized displacement vector $\mathbf {u}_{n}^{b}$ with respect to the corotational frame for body $b$ at time step $t_{n}$ is defined as

$$ \mathbf {u}_{n}^{b} = \bigl[\mathbf {u}_{1}^{T} \boldsymbol{\psi}_{1}^{T} \ldots \mathbf {u}_{i}^{T} \boldsymbol{\psi}_{i}^{T} \ldots \mathbf {u}_{nn}^{T} \boldsymbol{\psi }_{nn}^{T} \bigr]^{T}, $$

(18)

where $nn$ numbers the nodes of body $b$. The size of the vector $\mathbf {u}_{n}^{b}$ is $(n_{u}+n_{\psi} ) nn \times1$, where $n_{u}$ and $n_{\psi}$ represent the dimensions of the local displacement and rotation vectors, respectively. For planar problems, $n_{u} = 2$ and $n_{\psi} = 1$, and for spatial problems, $n_{u} = n_{\psi} = 3$.

For MBS modeled using a standard nonlinear finite element formalism, the ESL $\mathbf {g}_{n,\mathrm{eq}}^{b}$ in the corotational frame at time $t_{n}$ for body $b$ is defined as

$$ \mathbf {g}_{n,\mathrm{eq}}^{b} = \mathbf {K}_{t}^{b}(t_{\mathrm{ref}}) \mathbf {u}_{n}^{b}. $$

(19)

To solve (19), boundary conditions must be enforced to remove the stiffness matrix singularity caused by the rigid-body modes. They mainly depend on the choice of the corotational frame definition. For example, if a tangent frame is used at node $i$, then the local displacement of node $i$ should be zero, that is, clamping conditions must be enforced in (19). A parallel reasoning can be drawn with the floating reference frame formulation wherein boundary conditions must be imposed to components in order to introduce flexibility in the MBS analysis; see e.g. the component mode synthesis method [22].

In summary, to define ESL for MBS modeled using a standard nonlinear finite element formalism, five steps must be followed:

• 1. Select a reference configuration.

• 2. For each body $b$, extract the tangent stiffness matrix $\mathbf {K}_{t}^{b}(t_{\mathrm{ref}})$ of the body out of the global tangent stiffness matrix $\mathbf {K}_{t}(t_{\mathrm{ref}})$.

• 3. For each time step $t_{n}$ and each body $b$.

  • 3.1. Compute $\mathbf {x}_{0,n}^{b}$, $\boldsymbol{\theta}_{0,n}^{b}$, and $\mathbf {R}_{0,n}^{b}$ related to the body-attached frame.

  • 3.2. Construct the vector $\mathbf {u}_{n}^{b}$ via (18).

  • 3.3. Compute $\mathbf {g}_{n,\mathrm{eq}}^{b}$ via (19).

3.4 Remarks

Once the MBS analysis has been realized, ESL can be computed whereupon the optimization process can be performed. We note that the optimization process concerns isolated components whereas the effects of the whole system stem from load cases.

4 Fully coupled method

The fully coupled method naturally incorporates dynamic effects into the optimization process. Cost and constraint functions are formulated with the time responses obtained from the MBS simulation. Hence, the behavior of the whole mechanical system is considered in the optimization process, that is, it is not limited to the behavior of the optimized component isolated from the rest of the system. This approach also offers a global–local view of the optimization problem, which is necessary when designing lighter–more flexible components. Indeed, reducing the mass and thus increasing the flexibility of a lone component can significantly influence the overall mechanical system behavior. The fully coupled approach evaluates the dynamic loading exerted on the considered component (local view) based on a global system-level simulation, and the optimization process also accounts for the system global behavior.

With the fully coupled method, possibilities seem increased compared to an isolated component optimization approach since more complex and coupled behaviors related to the whole system are considered. However, the optimization problem formulation should be carefully addressed to obtain good convergence [28].

5 Optimization of flexible multibody systems

5.1 Formulation of the MBS optimization problem

Engineering design problems can be formulated as a mathematical optimization problem (20) in which an objective function $f_{0} ( \mathbf {p} )$ is minimized subject to $n_{c}$ constraints $f_{j} (\mathbf {p} )$ ensuring the integrity of the structural design and design requirements. The $n_{v}$ independent design variables are gathered in the vector $\mathbf {p}$. Side-constraints $\underline {p}_{i} \leq p_{i} \leq\overline{p}_{i}$ reflect technological considerations.

$$ \begin{aligned} & \underset{\mathbf {p}}{\text{minimize}} & & f_{0} ( \mathbf {p} ) & \\ & \text{subject to} & & f_{j} ( \mathbf {p} ) \leq\overline{f}_{j}, & j = 1,\ldots, n_{c}, \\ &&& \underline{p}_{i} \leq p_{i} \leq\overline{p}_{i}, & i = 1,\ldots , n_{v}. \end{aligned} $$

(20)

This formulation provides a general and robust design framework that can be solved by various types of optimization algorithms.

In MBS optimization, the cost and constraint functions are based on structural properties and responses, that is, mass, displacement, or stress measures at particular points and time steps. The design variables $n_{v}$ can be sizing, shape, or topological variables. Only sizing variables are considered here.

In the paper, the optimization problem concerns the minimization of the mechanical system mass $m(\mathbf {p})$, whereas constraints are enforced at each time step, that is, a local formulation of the constraints is used. This option offers a tight control over the optimal design, but the large number of constraints hinders the optimization process. Local formulations are usually opposed to global formulations that agglomerate parts or entire responses into a few constraints. The reduced number of constraints generally facilitates the optimization convergence, but the precise control of the optimized design is relinquished due to their global nature. The complexity of the treated examples is rather moderate, so that basic local formulations are sufficient.

Particularizing the general formulation (20) to the MBS optimization considered in this paper reads

$$ \begin{aligned} & \underset{\mathbf {p}}{\text{minimize}} & & m ( \mathbf {p} ) & \\ & \text{subject to} & & \mathbf {M}(\mathbf {p}) \ddot{\mathbf {q}}_{n} + \boldsymbol{\Phi}_{q}^{T}(\mathbf {p}) \bigl(k \boldsymbol{\lambda}_{n} + p \boldsymbol{\Phi}(\mathbf {p}) \bigr) = \mathbf {g}(\mathbf {p}), & \\ &&& k\boldsymbol{\Phi}(\mathbf {p}) = \mathbf {0}, & \\ &&& f_{j} ( \mathbf {p},\mathbf {q}_{n},\dot{\mathbf {q}}_{n}, \ddot{\mathbf {q}}_{n},\boldsymbol{\lambda}_{n},t_{n} ) \leq\overline{f}_{j}, & j = 1,\ldots, n_{c}, \\ &&& \underline{p}_{i} \leq p_{i} \leq\overline{p}_{i}, & i = 1,\ldots , n_{v}, \end{aligned} $$

(21)

for $n = 1,\ldots, n_{\mathrm{end}}$, where $n_{\mathrm{end}}$ is the number of simulation time steps.

We note that this formulation can easily be extended to account for global constraints of the form

$$ \sum_{k=1}^{n_{\mathrm{end}}}f_{j}^{k} ( \mathbf {p},\mathbf {q}_{n},\dot{\mathbf {q}}_{n},\ddot{\mathbf {q}}_{n},\boldsymbol{\lambda}_{n},t_{n} )\leq \overline{f}_{j}. $$

(22)

5.2 Optimization algorithm and sensitivity analysis

Mathematical programming tools are used to solve the optimization problem (21). Gradient-based methods have been employed to solve large-scale structural and multidisciplinary optimization problems with great success [10, 24]. The major advantage of these methods is their good convergence rates, which limits the number of function evaluations to obtain an optimal design. However, these methods are sensitive to local optima. In this study, we employ an “active-set” algorithm, which is based on the sequential quadratic programming approach and is part of the optimization toolbox of Matlab^® [17].

Gradient-based optimization methods require a sensitivity analysis to compute the derivatives of the cost and constraint functions. The efficiency of the sensitivity analysis is an essential part of the optimization process because it can drastically affect computation time. Whereas a semi-analytical sensitivity analysis needs less computational efforts in comparison to a finite difference scheme, the latter approach is adopted in this paper. This sensitivity analysis requires one additional simulation per design variable, and thus, CPU time grows by a factor $n_{v}+1$. However, we adopt it to carry out the investigations since this method is easy to use and the computation time is rather small for the examples considered here.

5.3 Weakly coupled method

Employing the weakly coupled method, the optimization problem formulation (21) is reformulated so that the dynamic response of the system is replaced by a series of static responses, that is, at time step $t_{n}$, the component deformation under the dynamic loading is mimicked by an ESL. As proposed in [8], the optimization process repeatedly solves the following static response optimization problem wherein ESL are incorporated:

$$ \textstyle\begin{array}{l@{\quad}l@{\quad}l} \underset{\mathbf {p}}{\text{minimize}} & m ( \mathbf {p} ) & \\ \text{subject to} & \mathbf {K}_{t}^{b}(\mathbf {p},t_{\mathrm{ref}}) \mathbf {u}_{n}^{b} = \mathbf {g}_{n,\mathrm{eq}}^{b}, & b = 1,\ldots n_{b}, \\ & f_{j} \bigl( \mathbf {p},\mathbf {u}_{n}^{b},t_{n}\bigr) \leq\overline{f}_{j}, & j = 1,\ldots, n_{c}, \\ & \underline{p}_{i} \leq p_{i} \leq\overline{p}_{i}, & i = 1,\ldots , n_{v}, \end{array} $$

(23)

for $n = 1,\ldots, n_{\mathrm{end}}$.

In the optimization problem (23), the constraints are formulated with respect to the local generalized displacement vector $\mathbf {u}_{n}^{b}$, that is, responses in the corotational frame. To consider responses in the inertial frame, a relation must be defined to switch from the corotational frame to the inertial frame representation based on (16)–(17). As shown afterward in the examples, the constraints are often formulated as functions of $\mathbf {q}_{n}^{b}$, that is, $f_{j}^{\ast} ( \mathbf {p},\mathbf {q}_{n}^{b}(\mathbf {u}_{n}^{b}),t_{n} ) \leq\overline{f}_{j}^{\ast}$, where $\mathbf {q}_{n}^{b}$ is the generalized coordinate vector related to body $b$ at time step $t_{n}$ in the inertial frame defined as

$$ \mathbf {q}_{n}^{b} = \bigl[\mathbf {x}_{1}^{T} \mathbf{\varPsi}_{1}^{T} \ldots \mathbf {x}_{i}^{T} \mathbf{\varPsi}_{i}^{T} \ldots \mathbf {x}_{nn}^{T} \mathbf{\varPsi}_{nn}^{T} \bigr]^{T}. $$

(24)

We note that after the first iteration of the static optimization process, the assembly of $\mathbf {q}_{n}^{b}$ for all bodies creates a global generalized coordinate vector, which does not respect the kinematic constraints anymore since each component has been optimized independently.

In the optimization problem formulation (23), each body is loaded by as many load cases as the number of time steps. During the static response optimization process, the ESL are not updated. Therefore, cycles between MBS analysis and static response optimization are needed to account for the effects of the design modification over the ESL. Reference [15] shows that doing so is identical to neglecting the time dependency in the sensitivity analysis of (21).

To solve the dynamic response optimization problem using the weakly coupled method, the algorithm proposed in [8], apart from the stopping criteria, is as follows:

• 1. Initialize the design variables and set $\mathit{it}=0$.

• 2. Perform a dynamic MBS analysis.

• 3. Compute the ESL.

• 4. If $\mathit{it}=0$, go to step 5. If $\mathit{it}>0$ and if

  $$ \dfrac{\sum_{n=1}^{t_{\mathrm{end}}} \Vert \mathbf {g}_{n,\mathrm{eq},\mathit{it}}^{b}-\mathbf {g}_{n,\mathrm{eq},\mathit{it}-1}^{b}\Vert}{\sum_{n=1}^{t_{\mathrm{end}}} \Vert \mathbf {g}_{n,\mathrm{eq},\mathit{it}-1}^{b}\Vert} < \varepsilon, $$

  (25)

  then stop. Otherwise go to step 5.

• 5. Solve the static response optimization problem (23). The iterations to solve this optimization problem are hereafter denoted as inner iterations.

• 6. Set $\mathit{it}= \mathit{it}+1$ and go to step 2.

One cycle is composed of steps 2 to 6. Reference [26] discusses the convergence of the solution obtained using this optimization method toward the optimal solution of the original dynamic response optimization problem. Figure 2 illustrates the flowchart of the ESL method.

Fig. 2

Flowchart of the weakly coupled method

5.4 Fully coupled method

Considering the fully coupled method, the optimization problem formulation (21) is employed as it is. The flowchart of the optimization process is illustrated in Fig. 3. The MBS simulation and the optimization process are fully coupled, that is, at each iteration of the optimization process, an MBS analysis is performed. However, as described in Sect. 4, the design problem is quite complex, and the convergence may suffer poor properties if not treated properly. This is due to the existence of significant couplings between vibrations and large amplitude motions, the influence of the changes of component inertial property on the vibrations, and the interactions between flexible components.

Fig. 3

Flowchart of the fully coupled method

Using the fully coupled method, the sensitivity analysis can be costly if not addressed with care. Efficient semi-analytical sensitivity methods have been proposed to compute the response derivatives, that is, $d\mathbf {q}_{n}/d\mathbf {p}$, $d\dot{\mathbf {q}}_{n}/d\mathbf {p}$, $d\ddot{\mathbf {q}}_{n}/d\mathbf {p}$, $d\boldsymbol{\lambda}_{n}/d\mathbf {p}$ [3, 4]. The sensitivity analysis can also be incorporated into the time integration scheme of the MBS analysis whereupon the cost of gradient computation is significantly lessened.

6 Optimization of 2-dof planar robot

6.1 Modeling hypotheses

The first example concerns the mass minimization of a 2-dof planar robot inspired from [18, 19]. Each robot arm has a length of $600~\mbox{mm}$ and is modeled by two equal-length beam elements with a hollow cross section (Fig. 4(a)). The adopted beam element model is described in [12]. The robot is made of aluminum with a Young’s modulus of $E=72~\mbox{GPa}$, Poisson’s ratio of $\nu=0.3$, and mass density of $2700~\mbox{kg}/\mbox{m}^{3}$. Each revolute joint is driven by an ideal motor, which imposes a smooth joint trajectory $\theta_{1}(t)$ and $\theta_{2}(t)$ such that the robot tip deploys along a straight line. The initial joint angles are $\theta_{1}(t_{0}) = 120^{\circ}$ and $\theta_{2}(t_{0}) = -150^{\circ}$. The ideal (rigid MBS) tip displacement corresponds to the following trajectory equation:

$$ \Delta x_{\mathrm{tip}}(t) = \Delta y_{\mathrm{tip}}(t) = \frac{0.5}{T} \biggl( t - \frac {T}{2\pi} \sin\frac{2\pi t}{T} \biggr), $$

(26)

where the period of the deployment motion $T$ is set to $0.5~\mbox{s}$.

Fig. 4

Modeling of the 2-dof robot

The actuator of the second robot arm is located at joint A and has a mass of $2~\mbox{kg}$. The combined mass of the end-effector plus the payload is $1~\mbox{kg}$. The gravity field is considered. The simulation is performed using the generalized-$\alpha$ scheme with a time step $h=5 \times 10^{-4} ~\mbox{s}$ and a spectral radius of $\rho_{\infty}=0.5$.

The design variables $p_{i}$ are the outer diameters of the hollow beam elements whose wall thickness is set to $0.1\times p_{i}$. Initial values of the design variables are set to $50~\mbox{mm}$. Tangent corotational frames are adopted to derive the ESL. Thus, the boundary conditions of each static load case correspond to fixed-free beam conditions.

The optimization problem concerns the mass minimization of the robot $m ( \mathbf {p} )$ subject to $n_{c}$ deviation constraints $\Delta l(\mathbf {p},\mathbf {q}_{n},t_{n})$, where $n_{c}$ equals the number of integration time steps. Mathematically, it is stated as

$$ \textstyle\begin{array}{l@{\quad}l@{\quad}l} \underset{\mathbf {p}}{\text{minimize}} & m ( \mathbf {p} ) & \\ \text{subject to} & \Delta l(\mathbf {p},\mathbf {q}_{n},t_{n})\leq\overline{\Delta l}, & n = 1,\ldots, n_{\mathrm{end}}, \\ & 0.02~\mbox{m} \leq p_{i} \leq0.06~\mbox{m}, & i = 1,\ldots, 4. \end{array} $$

(27)

Two different optimization problems are studied hereafter, which result from two different formulations of the deviation constraints.

6.2 Component-based constraints

Inspired from the initial paper [18] considering the coupling between the ESL method and flexible MBS, the deviation constraint at time step $t_{n}$ reads

$$ \Delta l = \sqrt{ (y_{A}-y_{A_{r}} )^{2}+ \bigl( ( y_{\mathrm{tip}}-y_{\mathrm{tip}_{r}} )- (y_{A}-y_{A_{r}} ) \bigr)^{2}} \leq 0.001~\mbox{m}, $$

(28)

where $y_{A}$ and $y_{\mathrm{tip}}$ are respectively the joint A and tip $y$-positions in the inertial frame (Fig. 4(b)), and the subscript $r$ refers to a reference mechanism, here the same mechanism but whose components are modeled as rigid bodies.

The constraint formulation (28) is not suitable to perform the optimization problem using the weakly coupled method since the terms are related to values in the inertial frame whereas the weakly coupled method makes use of values in the body-attached frame. Based on (16)–(17), (28) is easily reformulated as

$$ \Delta l = \sqrt{ \bigl(\mathbf {R}_{0,n}^{1}\mathbf {u}_{n,A}^{1}\vert _{y} \bigr)^{2} + \bigl(\mathbf {R}_{0,n}^{2} \mathbf {u}_{n,\mathrm{tip}}^{2} \vert _{y} \bigr)^{2} } \leq 0.001~\mbox{m}, $$

(29)

which only contains values related to the body-attached frames. Formulation (28) is employed with the fully coupled method.

The simulation time interval is $0.65~\mbox{s}$ corresponding to 1301 time steps. The fully coupled method is deemed converged when the relative changes of the objective function value and the relative constraint violation are less than $10^{-3}$ and $10^{-6}$, respectively. The weakly coupled method is deemed converged when the stopping criterion (25) with $\varepsilon$ equal to $10^{-2}$ is satisfied. These stopping criteria ensure a tight convergence of the optimization processes so that the comparison is performed on converged solutions.

The optimization results are gathered in Table 1, and the convergence history is illustrated in Fig. 5. For readability reasons of this figure, markers are printed each $0.01~\mbox{s}$. It is observed that both optimization methods converge quickly toward a similar optimal design. The fully coupled method has no inner iteration compared to the weakly coupled method. However, the inner iterations are based on static computations, and static analyses are less CPU-time consuming than dynamic analyses. Moreover, in this example, the weakly coupled method needs less global iterations, that is, MBS analysis, to converge. However, it is not easy to draw a general conclusion about the relative efficiency of the two methods in this case.

Fig. 5

2-Dof robot, formulation (28): objective function history and deviation constraint for the optimal design

Table 1 Numerical results (in kg and mm): 2-dof robot, formulation (28)

6.3 Multicomponent-based constraints

In [19], the authors enforce a trajectory tracking constraint expressed at time step $t_{n}$ as

$$ \Delta l = \sqrt{ (x_{\mathrm{tip}}-x_{\mathrm{tip}_{r}} )^{2}+ (y_{\mathrm{tip}}-y_{\mathrm{tip}_{r}} )^{2}} \leq 0.001~\mbox{m}, $$

(30)

where $x_{\mathrm{tip}}$ and $y_{\mathrm{tip}}$ are respectively the tip $x$- and $y$-positions in the inertial frame. The simulation time interval is still equal to $0.65~\mbox{s}$. Stopping criteria are identical to those used in Sect. 6.2.

In the previous example, each optimized component is subject to component-based constraints, that is, each component is constrained by its own responses. Here, the trajectory tracking constraint enforces a multicomponent-based constraint, that is, by constraining the absolute deflection of the robot tip, all components are constrained. However, the weakly coupled method concerns the optimization of components that are isolated from the rest of the system during the optimization process. Thus, (30) must be reformulated in order to consider the flexibility of the whole system by enforcing component-based constraints.

Due to the open-loop system properties, we formulate the deflection of the tip as a linear combination of all the component deflections. At time step $t_{n}$, the deflection of the tip is stated as

$$ \left [ \textstyle\begin{array}{c} x_{\mathrm{tip}}-x_{\mathrm{tip}_{r}}\\ y_{\mathrm{tip}}-y_{\mathrm{tip}_{r}} \end{array}\displaystyle \right ] = \sum \limits_{k=1}^{n_{b}} \mathbf {R}_{0,n}^{k} \mathbf {u}_{n,\mathrm{ext}}^{k}, $$

(31)

where $k$ is the robot link index, and the subscript ‘$\mathrm{ext}$’ denotes the link extremity.

Using the fully coupled method, multicomponent-based constraints are incorporated in the optimization problem without any difficulty. The generalized coordinates of the MBS analysis are available for the optimization process and naturally account for the flexibility of the whole mechanism.

The optimization results are given in Table 2 and are illustrated in Fig. 6. Markers are again printed each $0.01~\mbox{s}$. The weakly coupled method is deemed converged after five cycles, whereas the fully coupled needs 11 iterations. Although the optimal values of objective functions are similar, the design variable values are slightly different. The effect is observed in Fig. 6, where the time responses of the optimal systems are different. However, the critical time zone around $0.1~\mbox{s}$ exhibits not so much difference between the two optimal solutions in terms of time response.

Fig. 6

2-Dof robot, formulation (30): objective function history and deviation constraint for the optimal design

Table 2 Numerical results (in kg and mm): 2-dof robot, formulation (30)

7 Optimization of a 4-bar mechanism

7.1 Modeling hypotheses

The optimization problem concerns the mass minimization of a 4-bar mechanism inspired from [11, 18, 25]. The 4-bar mechanism consists of three flexible links connected to each other and to the ground by revolute joints (Fig. 7). The three links have a constant solid circular cross section, Young’s modulus of $E=68.95~\mbox{GPa}$, Poisson’s ratio of $\nu=0.3$, and mass density of $\rho=2757~\mbox{kg}/\mbox{m}^{3}$. Each link is modeled by six beam elements [12]. The lengths of the links are $l_{1}=0.3048~\mbox{m}$, $l_{2}=l_{4}=0.9144~\mbox{m}$, and $l_{3}=0.762~\mbox{m}$. Lumped masses of $5~\mbox{kg}$ are located at points A and B. The 4-bar mechanism moves in the horizontal plane so that gravity can be ignored. The input crank is driven by an ideal motor, which imposes the rotation $\theta(t)$ with a linear acceleration from 0 to $10\pi~\mbox{s}^{-1}$ in $0.3~\mbox{s}$ and then maintains a constant angular velocity until $0.5~\mbox{s}$. The simulation is performed using the generalized-$\alpha$ scheme with a time step $h=5 \times 10^{-4} ~\mbox{s}$ and a spectral radius of $\rho_{\infty}=0.5$.

Fig. 7

Kinematic model of the 4-bar mechanism

The design variables $p_{i}$ are the link diameters. The initial values of design variables are set to $250~\mbox{mm}$. The tangent corotational frames are adopted to derive the ESL.

7.2 Optimization problem and numerical results

The optimization problem is to find the mobile link diameters that minimize the total mass of the system subjected to a deviation constraint on point A. Mathematically, it is stated as

$$ \textstyle\begin{array}{l@{\quad}l@{\quad}l} \underset{\mathbf {p}}{\text{minimize}} & m ( \mathbf {p} ) & \\ \text{subject to} & \Delta l(\mathbf {p},\mathbf {q}_{n},t_{n})\leq 0.001~\mbox{m}, & n = 1,\ldots1001, \\ & 0.015~\mbox{m} \leq p_{i} \leq 0.5~\mbox{m}, & i = 1,\ldots, 3, \end{array} $$

(32)

where at time step $t_{n}$,

$$ \Delta l = \sqrt{ (x_{A}-x_{{A}_{r}} )^{2}+ (y_{A}-y_{{A}_{r}} )^{2}}. $$

(33)

In (33), $x_{A}$ and $y_{A}$ are respectively the $x$- and $y$-positions of point A in the inertial frame. The reference mechanism is the same mechanism but with components modeled as rigid bodies. The optimization differs from [11, 18, 25], wherein authors consider stress constraints.

The weakly coupled method can hardly incorporate the loop closure kinematic in the optimization problem formulation due to the component-based characteristics of the method. To overcome this difficulty, the closed-loop system is opened in the optimization problem formulation, and the multicomponent-based constraint is split into two constraints. The first one enforces a limit on the deflection of link 1, and the second one constrains the cumulative deflection of links 2 and 3. At time $t_{n}$, using the values related the body-attached frames, it reads

$$\begin{aligned} \Delta l_{1} =& \bigl( \bigl(\mathbf {R}_{0,n}^{1} \mathbf {u}_{n,A}^{1} \vert _{x} \bigr)^{2} + \bigl(\mathbf {R}_{0,n}^{1} \mathbf {u}_{n,A}^{1} \vert _{y} \bigr)^{2}\bigr)^{\frac{1}{2}} \leq 0.001~\mbox{m}, \end{aligned}$$

(34)

$$\begin{aligned} \Delta l_{2} =& \bigl( \bigl(\mathbf {R}_{0,n}^{2} \mathbf {u}_{n,A}^{2} \vert _{x} + \mathbf {R}_{0,n}^{3} \mathbf {u}_{n,B}^{3} \vert _{x} \bigr)^{2} +\bigl(\mathbf {R}_{0,n}^{2}\mathbf {u}_{n,A}^{2} \vert _{y} + \mathbf {R}_{0,n}^{3} \mathbf {u}_{n,B}^{3} \vert _{y} \bigr)^{2} \bigr)^{\frac{1}{2}} \leq 0.001~\mbox{m}, \end{aligned}$$

(35)

where the last subscript of $\mathbf {u}_{n}^{b}$ denotes the point where the displacement is considered. Note that the loop closure constraint is still enforced in the MBS simulation, it is only discarded at the level of the optimization procedure. On the contrary, the fully coupled method incorporates constraint (33) without any difficulty.

The fully coupled method is deemed converged when the relative changes of the objective function value and design variable values vary less than $10^{-3}$ while the relative constraint violation is less $10^{-6}$. The weakly coupled method is deemed converged when the stopping criterion (25) with $\varepsilon$ equal to $10^{-2}$ is satisfied. These tolerance values ensure a tight convergence of the optimization processes so that the comparison is performed on converged solutions.

The initial design has a mass of $268~\mbox{kg}$ (without the lumped masses) and a maximum deviation around $50~\upmu\mbox{m}$, which is far from the upper bound limit. The optimal design greatly differs depending on the optimization method. The objective function optimal value is seven times larger with the weakly coupled method (Table 3). The ESL method surprisingly needs a large number of iterations to converge. In Fig. 8, it is observed that, in both methods, at least one constraint is active once converged. The optimization processes would seem to be trapped in local optima.

Fig. 8

4-Bar mechanism: objective function history and deviation constraint for the optimal design

Table 3 Numerical results (in kg and mm): 4-bar mechanism

7.3 Trivial optimization

In order to explain the previously obtained behavior, the same optimization process is performed, but the lumped masses at points A and B are removed.

Before performing the optimization, let us get a feeling of the optimal design. The goal is to minimize the deviation of point A, which is mainly guided by the motor through link 1. Links 2 and 3 mainly follow the imposed motion and produce reactions forces at point A. Thus, physical intuition would tend to remove these links.

The optimization results are gathered in Table 4, and the convergence history is illustrated in Fig. 9. The fully coupled method converges toward our predicted design wherein design variables $p_{2}$ and $p_{3}$ reach the lower bounds of their side-constraints. The weakly coupled method also converges, and at least one constraint is active at convergence, but the optimum design is quite different. Links 2 and 3 cannot be removed; they are optimized in order to satisfy (35). However, if this constraint is suppressed, links 2 and 3 can no more be incorporated in the optimization problem. This example illustrates that the weakly coupled is not suitable to consider multicomponent-based constraints in the presence of closed-loops.

Fig. 9

4-Bar mechanism without lumped masses: objective function history and deviation constraint for the optimal design

Table 4 Numerical results (in kg and mm): 4-bar mechanism without lumped masses

8 On some particular behaviors

The 2-dof robot example developed in the previous section concerns the structural optimization of mechanical systems wherein flexibility effects are not predominant. We have illustrated that both optimization methods can converge toward the same optimal design.

In this section, the optimization problem of Sect. 6.2 is reconsidered since it concerns optimization with component-based constraints suitable to both methods. The difference is that the simulation time interval is slightly increased so that the mechanism approaches a singularity as its motion is driven by the tip position. After time $t=0.65~\mbox{s}$, the robot Jacobian $\mathbf {J}$ defined as

$$ \mathbf {J} = \left [ \textstyle\begin{array}{c@{\quad}c} \frac{\partial x_{\mathrm{tip}}}{\partial\theta_{1}} & \frac{\partial x_{\mathrm{tip}}}{\partial\theta_{2}} \\ \frac{\partial y_{\mathrm{tip}}}{\partial\theta_{1}} & \frac{\partial y_{\mathrm{tip}}}{\partial\theta_{2}} \end{array}\displaystyle \right ] $$

(36)

tends to become singular whereupon inertia effects become predominant over the robot, which is already in an extended configuration. As exposed hereafter, difficulties arise when flexibility effects become more important.

8.1 Oscillating phenomenon

Recalling the optimization problem in Sect. 6.2, the deviation constraint formulation reads

$$ \Delta l = \sqrt{ (y_{A}-y_{A_{r}} )^{2}+ \bigl( ( y_{\mathrm{tip}}-y_{\mathrm{tip}_{r}} )- (y_{A}-y_{A_{r}} ) \bigr)^{2}} \leq 0.001~\mbox{m}, $$

(37)

where $y_{A}$ and $y_{\mathrm{tip}}$ are respectively the joint A and tip $y$-positions in the inertial frame. Here, the only difference compared to the study conducted in Sect. 6.2 is that the simulation time interval is set to $0.66~\mbox{s}$ corresponding to 1321 time steps. The same stopping criteria are used.

The convergence history of the weakly coupled method is illustrated in Fig. 10. It is observed that the objective function value oscillates, which prevents the convergence of the optimization, and it reaches the allowed maximum number of iterations. Observing the trajectory tracking constraint evolution during several iterations (Figs. 10(b)–10(e)), we point out that the deviation constraint is always activated for the last time step but oscillating phenomenon appears due to the deviation constraint around $0.125~\mbox{s}$. Between iterations 4 and 5, the optimization process reduces the mass and then tries to converge. However, after performing the MBS analysis and updating the ESL, the optimization process converge toward a design that was previously obtained so that the process enters an infinite loop. Move-limits can be implemented to damp out these oscillations, but the optimal design is thus artificially forced.

Fig. 10

Weakly coupled method: illustration of the oscillating behavior of the optimization process

This example illustrates that in certain circumstances, oscillations prevent the optimization convergence. However, in the present case, this phenomenon seems to appear only for this particular simulation time interval, where there is a strong interaction between the activation of the constraint at the last time step and the activation of constraints around $0.125~\mbox{s}$.

Employing the fully coupled method, the optimization problem smoothly converges without any oscillation (Fig. 11 and Table 5). The optimization is deemed converged after 11 iterations, where a single constraint corresponding to the last time step is active.

Fig. 11

2-Dof robot, fully coupled method, formulation (37): objective function history and deviation constraint for the optimal design

Table 5 Numerical results (in kg and mm): 2-dof robot, formulation (37)

8.2 Initial point influence

A general characteristic of gradient-based algorithms is that they are sensitive to local optima. Thus, depending on the initial value of design variables, several optimal designs can be obtained.

In this section, four different starting points are used: $\mathbf {p}_{0}^{1}=[50, 50, 50, 50]$, $\mathbf {p}_{0}^{2} = [55, 55, 55, 55]$, $\mathbf {p}_{0}^{3} = [55, 45, 35, 25]$, and $\mathbf {p}_{0}^{4} = [45, 45, 45, 45]$. The latter is an infeasible starting point making the optimization process more complex.

Considering the optimization problem treated in Sect. 6.2 and based on the numerical results gathered in Table 6, we conclude that the influence of the initial point on the optimal design is not significant. To support this conjecture, the deviation constraint is given as a function of the design parameters in Fig. 12 for time $t=0.0995~\mbox{s}$, where $p_{1}$ and $p_{3}$ are set to 39.35 and $35~\mbox{mm}$, respectively. The design domain presents similar shape for time steps around. It is observed that the design space domain is relatively smooth whereupon the convergence is facilitated and the optimization process is not very sensitive to local optima.

Fig. 12

Design domain of the deviation constraint at time step 200 (0.0995 s) plotted with respect to design variables $p_{2}$ and $p_{4}$

Table 6 Formulation (28): Numerical results for four initial points (in kg and mm)

Let us now continue with the same optimization problem except that the 2-dof robot undergoes a motion until the final joint angles $\theta_{1}(t_{\mathrm{end}}) = 60^{\circ}$ and $\theta_{2}(t_{\mathrm{end}}) = -30^{\circ}$ corresponding to a simulation time interval of $0.6687~\mbox{s}$ and thus 1338 time steps. Approaching the singularity of the mechanism, inertia effects become more important.

Analyzing the results given in Table 7, the weakly coupled method seems to be rather insensitive to the starting points. Although the number of iterations needed to converge strongly varies, the optimal design remains similar. Using the fully coupled method, optimal designs differ with the initial points. Unlike the weakly coupled method, in Figs. 13–14, it is observed that the fully coupled method generally activates only the constraint related to the last time step at convergence. In Table 8, the history of active constraints is given for $\mathbf {p}_{0} = [55, 55, 55, 55]$, where it is clearly shown that the fully coupled method is more affected by the dynamic effects occurring at the end of the simulation. Using the weakly coupled method, the optimization is less affected by the last time step, and as depicted in Table 8, the last constraint is no more active at convergence within the given tolerance. This behavior can be explained by the fact that design sensitivities are smoother in the weakly coupled method due to their time independence. In this case, this approximation avoids getting stuck in a local minimum created by the last time steps where inertia effects are predominant.

Fig. 13

Influence of the initial point on the optimization process: objective function history and deviation constraint for the optimal design

Fig. 14

Infeasible initial point $\mathbf {p}_{0} = [45, 45, 45, 45]$: objective function history and deviation constraint for the optimal design

Table 7 Influence of the initial point on the optimal design (in kg and mm)

Table 8 History of active constraints, $\mathbf {p}_{0} = [55, 55, 55, 55]$

To explain the difference between optimal designs obtained with the fully coupled method, the design space domain of the deviation constraint as a function of design variables for time step $t=0.6685~\mbox{s}$ is illustrated in Fig. 15, where $p_{1}$ and $p_{3}$ are set to 52.49 and $33.24~\mbox{mm}$, respectively. The design space configuration exhibits a lot of oscillations near the upper bound value of the constraint preventing the convergence toward a unique optimal design.

Fig. 15

Design domain of the deviation constraint at time step 1338 (0.6685 s) plotted with respect to design variables $p_{2}$ and $p_{4}$

Lastly, observing Fig. 14, the convergence history exhibits oscillations. This is expected since the convergence is hardened when the starting point is infeasible combined with a local formulation of the optimization problem [28]. Other formulations can help to work with a feasible domain of the design space more adapted to gradient-based algorithms, but these difficult and important issues are left for future work.

9 Conclusions

Two optimization methods for the structural optimization of mechanisms have been compared. On the one hand, the weakly coupled method uses an MBS simulation to generate ESL whereupon static response optimization with multiple load cases is performed. On the other hand, the fully coupled method solves a dynamic response optimization problem with time responses obtained directly from the MBS analysis.

In order to carry out a fair comparison using a unique MBS formalism, we proposed a method to derive ESL adapted to a standard nonlinear finite element formulation.

When the optimization problem concerns component-based constraints, that is, where each component is optimized subject to its own set of constraints, both methods can converge toward the same optimum. The weakly coupled method generally lessens the CPU time consumption since it avoids the expensive gradient computation of the state variables. Also, less dynamic analyses are usually required to converge. However, this reduction is partly balanced by inner iterations, which are performed at each cycle although the latter are based on static computations.

When multicomponent-based constraints are considered, the weakly coupled method is not suitable except in particular cases, that is, when the multicomponent-based constraints can be properly translated into component-based constraints. The fully coupled method is more general and accommodates all types of component- and multicomponent-based constraints at the price of a more complex optimization process.

The examples illustrate the potential of both methods to perform structural optimization of flexible mechanisms. However, as illustrated by the last section, it is not trivial to obtain convergence for mechanisms wherein flexibility and vibrations are important. The understanding of the physical behavior of the mechanism is fundamental to manage the optimization process and interpret afterward the optimization results.