1 Introduction

Waviness, roughness, and roundness are considered to be the different forms of shaping error of the inner and outer raceway surfaces of rolling element bearings. They are usually regarded as distributed defects in the rolling element bearings. With improvements in processing techniques, the effects of roughness and roundness of the surfaces on bearing vibration have gradually decreased. However, the influence of waviness is still significant, as shown in Fig. 1. Hence, waviness is one of the main factors responsible for vibration in rolling element bearing systems. Bearing vibration directly affects the dynamic performance of a mechanical system. In order to produce stable working mechanical systems, many scholars have carried out research on vibration in a rolling bearing system. Existing research is mainly focused on the effects on the dynamic performance of the rolling element bearing system of nonlinear factors such as unbalanced load [1, 2], clearance [1–4], and local defects [5–9].

Fig. 1
figure 1

Waviness defects on the outer raceway of a deep-groove ball bearing [6]

Full size image

In recent years, the nonlinear dynamics of rolling element bearings affected by waviness defects has attracted more attention. Aktiirk [10] studied the radial and axial vibrations of a rigid shaft supported by a pair of angular contact ball bearings. The effect of the waviness of the bearing’s running surface on the vibration of the shaft was investigated. Tandon [11] developed a theoretical model to predict the vibrational response of a rolling element bearing with waviness on its inner and outer raceways. Sopanen [12, 13] proposed a dynamic model for a deep-groove ball bearing with waviness on the raceways. Harsha [14–16] analyzed the nonlinear dynamic response of a rotor–bearing system due to waviness on the bearing’s surface. Bai [17] presented a dynamic model with 5 degrees of freedom (DOF) to study the dynamic performance of ball bearings due to the effect of both internal clearance and waviness at high speed. The centrifugal force and gyroscopic moment from the balls were also taken into account. Jang [18–20] presented a nonlinear model to analyze ball bearing vibration due to waviness in a rigid rotor supported by two or more ball bearings. The waviness of the balls and each race was modeled using a superposition of sinusoidal functions. Wang [21] deduced an expression for the nonlinear contact forces on a roller bearing under four-dimensional loads. A 4-DOF transient dynamics model of the roller bearings was presented and used to investigate the vibrational behavior of the rotor roller bearing system. The radial clearances and waviness of the bearings were also taken into account in this work. In most of the above work, the bearing–rotor system is usually selected as the research object. The rolling element bearing plays the role of supporting the high-speed rotation of the rotor. However, the rolling element bearing is often used as the connection between moving links, i.e., it constitutes a revolving joint between linkages in the applied engineering field. In fact, one finds that there is not only rotational motion of the bearing to be considered, but also translational motion within the mechanism. Under these conditions, the dynamic load on the bearing is more complex. Furthermore, the nonlinear vibrational effects of the bearing on the dynamic performance of the high-speed mechanism and kinematic accuracy are more prominent.

At present, multibody dynamic systems influenced by nonideal joints have attracted much attention from many scholars worldwide. Many studies have been made on the influence of joint clearance, lubricant films, contact forces, friction, and wear on the mechanical characteristics of the multibody system dynamics. Ravn [22] and Flores et al. [23] proposed a continuous analysis approach that was combined with the contact force model presented by Lankarani and Nikravesh [24] to model clearance revolute joints in planar rigid multibody systems. In follow-up studies, the approach was validated by experimental work [25], and other techniques have also been utilized to guarantee the correctness of the numerical simulations [26]. In subsequent research, Erkaya and Uzmay [27], Flores and Lankarani [28, 29], Liu et al. [30], and Megahed and Haroun [31] discussed the dynamic performance of mechanisms with multiple clearance revolute joints. In practical applications, the joints are designed to operate with a lubricant [32]. A thin lubricant film can not only provide the high pressures required to keep the journal and bearing apart, but also reduce friction and wear, provide load capacity, and add damping to dissipate vibrations. Therefore, a proper description of lubricated revolute joints [33–38] is required to achieve a better understanding of the dynamic performance of such mechanical systems. In general, correctly formulating the contact force and friction models is important for revealing the dynamical characteristics of a clearance joint. For this purpose, Muvengei et al. [39] and Machado et al. [40] presented and discussed several different compliant contact forces models to use in a multibody system dynamics context to model and analyze contact–impact events. Flores et al. [41] proposed a new continuous contact force model for soft materials in multibody dynamics. This approach can be used for contact problems involving materials with low or moderate values of coefficient of restitution. Lee [42] introduced a numerical technique to solve the problem of having a very stiff spring-damper on the contact point. The special feature of this technique is that the equation of motion may be time-integrated with any convenient method valid for solving ordinary differential equations. Also, time step size reduction and penetration threshold need not be considered at the time of impact. Pereira et al. [43] analyzed and discussed several analytical models to study the contact between cylindrical bodies. More recently, Rodriguez and Bowling [44] presented a method for determining the post-impact behavior of a rigid body undergoing multiple, simultaneous impacts including the effects of friction. Muvengei et al. [45] analyzed the dynamic response of a slider–crank mechanism when different friction models are adopted to model the clearance joints. As is well known, exposure to an extended period of the effects of friction will lead to wear of the contact bodies. In order to reveal the wear phenomenon in clearance joints in depth, some researchers have complemented previous studies by integrating wear into the dynamic analysis of multibody systems. In these studies, Gummer [46] developed an analytical and numerically effective method for calculating the stiffness of a revolute joint depending on the geometry and wear state. Flores [47] and Mukras [48] presented an approach for modeling and evaluating wear in multibody systems. The wear model used was based on the generalized Archard equation, which relates the volume of material loss to the physical and geometrical properties of the contacting bodies. The simulation results verified that the wear in a clearance joint is not uniformly distributed around the joint element’s surface. Actually, the mechanism does not necessarily contain a revolute joint. Translational joints, spatial spherical joints, and spatial cylindrical joints are also widely used to connect rigid bodies in multibody systems. Flores et al. [49, 50] presented methods for modeling translational and spherical joints with clearance in rigid multibody systems. Tian et al. [51] analyzed the effect of clearance of a cylindrical joint on the dynamic performance of spatial flexible multibody systems. Furthermore, Qi et al. [52] proposed a methodology for the analysis of the frictional contact of rigid multibody systems with spatial prismatic joints.

However, most of the above work takes sliding bearings as the object of study. If rolling element bearings are applied to the revolute joint connections between components [53], the sliding wear between joint elements can be reduced. However, the vibrations, caused by manufacturing defects in the bearings (such as the waviness defects on the raceway surface), are bound to have an effect on the dynamic performance of the mechanical system. The primary objective of this work is to present an approach for modeling and dynamically analyzing a planar multibody system containing deep-groove ball bearings with waviness defects. The deep-groove ball bearing is modeled by introducing a nonlinear force system that takes into account the elastic deformations of the contact between the ball elements and raceways. Hertzian contact theory is applied to calculate the elastic deflection and the nonlinear contact force. The waviness defect on the bearing’s inner and outer raceways is modeled using a sinusoidal function. The paper is organized as follows. In Sect. 2, the method for modeling the waviness defect in the bearing raceways is introduced. Section 3 offers an approach to modeling a deep-groove ball bearing in a planar multibody system. In Sect. 4, a planar slider–crank mechanism with a deep-groove ball bearing located at different revolute joints is proposed as a numeral example to verify the methodology. In Sect. 5, the variation of the slider acceleration, crank moment, and bearing equivalent reaction force are obtained and discussed. Finally, in the last section, the main conclusions from this study are presented.

2 Modeling of the waviness of bearing raceways

2.1 Kinematic analysis of the ball bearing

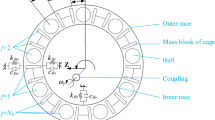
A kinematic analysis of a bearing is used to reveal the relationship between the motion of the rolling elements and the inner and outer raceways. The position of each rolling ball in the bearing at any time t can be subsequently determined. In the process of rotation of the bearing, a rigid cage is often used to equally space the balls—this also enables them to roll on the surfaces of the raceways with equal velocity. If the slipping and sliding that occurs between the bearing rolling balls and raceways are ignored, the velocity of the cage and rolling element set is the mean of the inner and outer raceway velocities [54], as shown in Fig. 2.

Fig. 2
figure 2

Rolling speeds and velocities in the deep-groove ball bearing

Full size image

The velocity of the rolling ball at any time t can therefore be described using

$$ \upsilon_{\mathrm{m}} = \frac{\upsilon_{\mathrm{i}} + \upsilon_{\mathrm{o}}}{2} $$
(1)

with

$$ \upsilon_{\mathrm{i}} = \frac{\omega_{\mathrm{i}}d_{\mathrm{i}}}{2},\quad \upsilon_{\mathrm{o}} = \frac{\omega_{\mathrm{o}}d_{\mathrm{o}}}{2}, $$
(2)

where ω i and ω o are the angular velocities of the bearing’s inner and outer races, respectively, and d i and d o are the bearing’s inner and outer raceway diameters, respectively. Substituting Eq. (2) into Eq. (1) yields

$$ \upsilon_{\mathrm{m}} = \frac{\omega_{\mathrm{i}}d_{\mathrm{i}} + \omega_{\mathrm{o}}d_{\mathrm{o}}}{4}. $$
(3)

Taking into account that

$$ r_{\mathrm{m}} = \frac{d_{\mathrm{i}} + d_{\mathrm{o}}}{4} $$
(4)

and

$$ \omega_{\mathrm{m}} = \frac{\upsilon_{\mathrm{m}}}{r_{\mathrm{m}}} $$
(5)

and substituting Eqs. (3) and (4) into Eq. (5), the angular velocity of the cage and rolling balls can be obtained:

$$ \omega_{\mathrm{m}} = \frac{\omega_{\mathrm{i}}d_{\mathrm{i}} + \omega_{\mathrm{o}}d_{\mathrm{o}}}{d_{\mathrm{i}} + d_{\mathrm{o}}}. $$
(6)

The angular position of the rth ball in the bearing at time t can be represented by

$$ \phi_{r} = \frac{2\pi}{N_{b}} ( r - 1 ) + \omega_{\mathrm{m}}t, \quad ( r = 1,2, \ldots,N_{b} ), $$
(7)

where N b is the number of balls in the bearing. By using the form given in Eq. (7), the ball elements are constrained to distribute uniformly and move around the bearing raceways with equal velocity.

2.2 Waviness of the bearing’s inner and outer raceways

In general, a bearing raceway is formed by grinding. During the grinding process, a continuous and periodic waviness defect is generated on the surface of the bearing raceway due to the effect of the periodic vibration of the grinding wheel spindle. Obviously, the complexity of the bearing waviness defect is determined by the vibrational characteristics of the grinding machine. Due to the fact that an actual vibrational signal in the time domain usually has many frequency components, the real waviness on the bearing raceway surface may be a complex curve formed by the superposition of many simple periodic curves. To simplify the problem, the main vibration component is generally considered. Then, the single waviness defect caused by this main vibration component is usually considered in the vibrational analysis of the rolling element bearings. We can certainly change the wavelength and amplitude of this single waviness to discuss its influence on the dynamic response of the bearing system.

Based on experimental test results [54], the waviness of the bearing raceway can be simplified as a periodic sinusoidal function, as shown in Fig. 3. The corresponding waviness Π at a certain position L in the bearing can be described using

$$ \varPi = \varPi_{\mathrm{p}}\sin \biggl( \frac{2\pi L}{\lambda} \biggr), $$
(8)

where Π p is the maximum amplitude of the waviness, and λ is the mean wavelength of the waviness.

Fig. 3
figure 3

A simplified model for the waviness

Full size image

The waviness of the bearing inner raceway surface is shown in Fig. 4(a). Here, P i is the center of the bearing inner race, and b is the center of the ball. According to Eq. (8) and considering the influence of the initial amplitude, the waviness Π i can be expressed as

$$ \varPi_{\mathrm{i}} = \varPi_{\mathrm{T}} + \varPi_{\mathrm{p}}\sin \biggl( \frac{2\pi L_{\mathrm{i}}}{\lambda_{\mathrm{i}}} \biggr), $$
(9)

where Π T is the amplitude of the waviness when L i=0.

Fig. 4
figure 4

Modeling the waviness defect of the bearing raceways: the bearing’s (a) inner and (b) outer raceways

Full size image

For the inner raceway of the rolling element bearing, the mean wavelength λ i of the waviness can be expressed as

$$ \lambda_{\mathrm{i}} = \frac{\pi d_{\mathrm{i}}}{N_{\mathrm{i}}}, $$
(10)

where N i represents the total number of waviness on the bearing inner raceway. We also have

$$ L_{\mathrm{i}} = \frac{d_{\mathrm{i}}\theta_{i}}{2}, $$
(11)
$$ \theta_{i} = \frac{2\pi}{N_{b}} ( i - 1 ) + ( \omega_{\mathrm{m}} - \omega_{\mathrm{i}} )t \quad ( i = 1,2, \ldots,N_{b} ). $$
(12)

Figure 4(b) shows the waviness on the bearing outer raceway surface, in which P j represents the center of the bearing’s outer race. The waviness at any position on the surface of outer raceway can be described using

$$ \varPi_{\mathrm{o}} = \varPi_{\mathrm{T}} + \varPi_{\mathrm{p}}\sin \biggl( \frac{2\pi L_{\mathrm{o}}}{\lambda_{\mathrm{o}}} \biggr). $$
(13)

The mean wavelength λ o of the waviness on the bearing outer raceway can be expressed as

$$ \lambda_{\mathrm{o}} = \frac{\pi d_{\mathrm{o}}}{N_{\mathrm{o}}}, $$
(14)

where N o denotes the total waviness number on the outer raceway. Also,

$$ L_{\mathrm{o}} = \frac{d_{\mathrm{o}}\theta_{j}}{2}, $$
(15)
$$ \theta_{j} = \frac{2\pi}{N_{b}} ( j - 1 ) + ( \omega_{\mathrm{m}} - \omega_{\mathrm{o}} )t\quad ( j = 1,2, \ldots,N_{b} ). $$
(16)

3 Modeling of a deep-groove ball bearing in planar multibody system

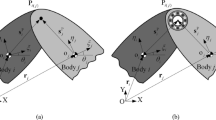
In order to investigate the effect of the waviness defect on the dynamic performance of the multibody system, a dynamic multibody model of the system with rolling bearing elements must first be established. Figure 5 describes an approach for modeling deep-groove ball bearings in a planar multibody system. As shown in the figure, two bodies i and j are connected by a deep-groove ball bearing in the multibody system. It is supposed that the outer race of the bearing is fixed to the bearing housing of rigid body i and that the inner race is fixed to the journal of rigid body j. The existence of the bearing allows the rigid bodies i and j to rotate relative to each other. The centers of mass of bodies i and j are o i and o j , respectively. Body-fixed coordinate systems, ξoη, are attached to the center of mass of each body, while the XOY coordinate frame represents the global coordinate system. The points P i and P j indicate the centers of the bearing outer and inner races, respectively.

Fig. 5
figure 5

Modeling of a deep-groove ball bearing in the planar multibody system

Full size image

During the motion of the mechanical system, the centers of the inner and outer races of the bearing will be relatively offset due to the effect of inertial load. As shown in Fig. 5, the eccentricity vector e connecting the centers of the housing and the journal can be calculated using

$$ \mathbf{e} = \mathbf{r}_{j}^{P} - \mathbf{r}_{i}^{P} = \bigl( \mathbf{r}_{j} + \mathbf{A}_{j}\mathbf{s}_{j}^{P} \bigr) - \bigl( \mathbf{r}_{i} + \mathbf{A}_{i}\mathbf{s}_{i}^{P} \bigr), $$
(17)

where r i and r j are vectors linking the global origin and the centers of mass of the bodies, \(\mathbf{s}_{i}^{P}\) and \(\mathbf{s}_{j}^{P}\) are vectors in the local coordinate system that link the centers of mass to the housing and journal centers, respectively, and A i and A j are matrices that transform the vectors \(\mathbf{s}_{i}^{P}\) and \(\mathbf{s}_{j}^{P}\) from the local coordinate system to the global system.

The velocities of the points P i and P j in the global coordinate system are

$$ \dot{\mathbf{r}}_{k}^{P} = \dot{\mathbf{r}}_{k} + \dot{\mathbf{A}}_{k}\mathbf{s}_{k}^{P},\quad ( k = i,j ). $$
(18)

The relative velocities between points P i and P j can then be computed from

$$ \boldsymbol{\upsilon} = \dot{\mathbf{r}}_{j}^{P} - \dot{ \mathbf{r}}_{i}^{P}. $$
(19)

The magnitude of the eccentricity vector is evaluated as

$$ e = \sqrt{\mathbf{e}^{\mathrm{T}}\mathbf{e}}. $$
(20)

The unit vector n in the direction of eccentricity is therefore

$$ \mathbf{n} = \mathbf{e}/e. $$
(21)

In the eccentricity direction, the contact point between the housing and the bearing outer raceway is marked as Q i . The contact point between the journal and the bearing inner raceway is indicated as Q j .

The locations of the contact points Q i and Q j can be expressed as

$$ \mathbf{r}_{k}^{Q} = \mathbf{r}_{k} + \mathbf{A}_{k}\mathbf{s}_{k}^{P} + R_{k} \mathbf{n},\quad ( k = i,j ) $$
(22)

where R k (k=i,j) are the housing and journal radii.

Considering the effect of bearing clearance and waviness defect, the radial deflection at the rth ball at any angle ϕ r can be written as

$$ \delta_{r} = e_{x}\cos \phi_{r} + e_{y}\sin \phi_{r} - \frac{1}{2}P_{\mathrm{d}} + \varPi_{\mathrm{i}} + \varPi_{\mathrm{o}}, $$
(23)

where e x and e y are components of the eccentricity e in the x and y directions, respectively, and P d is the internal radial clearance of the bearing.

The radial relative velocity at the rth ball at any angle ϕ r is given by

$$ \upsilon_{r} = \upsilon_{x}\cos \phi_{r} + \upsilon_{y}\sin \phi_{r}, $$
(24)

where υ x and υ y are the components of the relative eccentric velocity υ in the x and y directions, respectively.

According to local contact Hertzian theory, taking into account the bearing damping effect, the load–deformation relationship for the point contacts between ball–raceways can be written as

$$ F_{r} = K\delta_{r}^{3 / 2} + C\upsilon_{r}, $$
(25)

where K and C are the total stiffness and damping coefficients for either the inner or outer raceway contacts, respectively. The stiffness coefficients K i,o for the inner and the outer raceway–ball contacts, respectively, can be expressed as follows [54]:

$$ K_{\mathrm{i},\mathrm{o}} = \frac{2\sqrt{2}}{3} \Bigl( \sum \rho_{\mathrm{i},\mathrm{o}} \Bigr)^{ - 1/2} \bigl( \delta_{\mathrm{i},\mathrm{o}}^{*} \bigr)^{ - 3/2} \biggl( \frac{E}{1 - \nu^{2}} \biggr) \quad \bigl(\mathrm{N}/ \mathrm{m}^{3 / 2}\bigr), $$
(26)

where E and ν are the elastic modulus and Poisson ratio of the ball bearing elements, respectively, δ ∗ is the dimensionless deflection factor, and ∑ρ i,o is the curvature sum at the contact point. The value of δ ∗ can be obtained from a graph of the curvature difference function, F(ρ), as shown by Harris [54]. The total stiffness for a single ball element in contact with the inner and outer raceways is written as

$$ K = \bigl( K_{\mathrm{i}}^{ - 2 / 3} + K_{\mathrm{o}}^{ - 2 / 3} \bigr)^{ - 3/2}\quad \bigl(\mathrm{N}/\mathrm{m}^{3 / 2}\bigr). $$
(27)

Generally, estimation of the damping of a ball bearing is very difficult because of the dominant extraneous damping, which swamps the damping of the bearing [55]. Based on experimental and theoretical studies, Dietl et al. [56] pointed out that the major contributions to bearing damping include lubricant film damping in the rolling contacts, material damping due to Hertzian deformation of the rolling bodies, and damping at the interface between the outer ring and bearing housing. Experimental measurement also shows that bearing damping decreases as the rotation speed increases. Mitsuya et al. [57] investigated experimentally the damping of a 6200-type deep-groove ball bearing. The experimental damping ratios ranged between 2 and 4 %, and the damping coefficients between 150 and 350 N s/m. Based on these experimental results, an appropriate damping value can be selected to ensure convergence of the numerical calculation.

Substituting Eqs. (23) and (24) into Eq. (25) yields

$$ \begin{aligned}[b] &F_{r} = K \biggl( e_{x}\cos \phi_{r} + e_{y}\sin \phi_{r} - \frac{1}{2}P_{\mathrm{d}} + \varPi_{\mathrm{i}} + \varPi_{\mathrm{o}} \biggr)_{ +}^{3 / 2} + C ( \upsilon_{x}\cos \phi_{r} + \upsilon_{y} \sin \phi_{r} )_{ +}, \\ &\quad ( r = 1,2, \ldots,N_{b} ). \end{aligned} $$
(28)

The subscript “+” on the first bracket indicates that when the expression inside is less than or equal to zero, the rolling ball is not in the load zone, and the restoring force F r is set to zero. If the expression in the bracket is greater than zero, then the ball at angular location ϕ r is loaded giving rise to a restoring force F r .

It is worth noting that the friction model is not used in the contact analysis in this research. The reason this simplification is used is because the rolling element bearing has multiple point contacts between the rolling elements and raceways. A detailed description of the friction effect in each contact is quite complex, and so the simulation would be very time consuming. In order to simplify the complexity of the computational model further, only the normal contact forces in the bearing’s multipoint contacts are considered. On the other hand, the rolling friction at the ball and raceway contact is usually quite small and has a small effect on the dynamic response of the bearing system. This explains why much of the research on rolling element bearing dynamics neglects the influence of friction.

If the effect of rolling friction force is neglected, the equivalent reaction force in the bearing is the sum of the restoring forces from each of the rolling ball elements. Resolving the total restoring force along the x and y directions, we obtain

$$ \left [ \begin{array}{c} F_{x} \\ F_{y} \end{array} \right ] = \sum_{r = 1}^{N_{b}} F_{r}\left [ \begin{array}{c} \cos \phi_{r} \\ \sin \phi_{r} \end{array} \right ]. $$
(29)

After calculation of the equivalent reaction forces F x and F y , the contributions to the generalized force vectors and moments in the multibody system can be found. The forces that act on the contact points of bodies i and j are transferred to the centers of mass of the bodies, and an equivalent transport moment is applied to the rigid body.

As shown in Fig. 6, the forces f i and moment T i that act on the center of mass of body i due to the eccentricity of the bearing’s inner and outer race centers can be expressed as follows:

$$ \mathbf{f}_{i} = \left [ \begin{array}{c} F_{x} \\ F_{y} \end{array} \right ],\qquad T_{i} = \bigl( y_{i}^{Q} - y_{i} \bigr)f_{i}^{x} - \bigl( x_{i}^{Q} - x_{i} \bigr)f_{i}^{y}. $$
(30)
Fig. 6
figure 6

Force vectors acting at the points of contact

Full size image

The corresponding forces f j and moment T j applied to body j are

$$ \mathbf{f}_{j} = - \left [ \begin{array}{c} F_{x} \\ F_{y} \end{array} \right ],\qquad T_{j} = - \bigl( x_{j}^{Q} - x_{j} \bigr)f_{j}^{y} - \bigl( y_{j}^{Q} - y_{j} \bigr)f_{j}^{x}. $$
(31)

We take these forces and moments as the generalized force and substitute them into the multibody system. Then, we can derive the equations of motion of the multibody system containing deep-groove ball bearings with waviness defects,

$$ \left [ \begin{array}{c@{\quad}c} \mathbf{M} & \boldsymbol{\Phi}_{\mathrm{q}}^{\mathrm{T}} \\ \boldsymbol{\Phi}_{\mathrm{q}} & \mathbf{0} \end{array} \right ]\left [ \begin{array}{c} \ddot{\mathbf{q}} \\ \boldsymbol{\lambda} \end{array} \right ] = \left [ \begin{array}{l} \mathbf{Q}^{\mathrm{A}} \\ \boldsymbol{\gamma} \end{array} \right ]. $$
(32)

Here, M is the mass matrix consisting of the masses and moments of inertia of the system components, Φ q is the Jacobian matrix of the constraint equations, \(\ddot{\mathbf{q}}\) is the acceleration vector, λ is the vector of Lagrange multipliers, Q A is the generalized force vector including the bearing equivalent reaction forces and transport moments applied to the rigid bodies, and \(\gamma = \boldsymbol{\Phi}_{\mathrm{q}}\ddot{\mathbf{q}} = - ( \boldsymbol{\Phi}_{\mathrm{q}}\dot{\mathbf{q}} )_{\mathrm{q}}\dot{\mathbf{q}} - 2\boldsymbol{\Phi}_{\mathrm{q}t} \dot{q} - \boldsymbol{\Phi}_{tt}\) is a vector that groups all the terms in the acceleration reaction equations that depend on the velocities. Figure 7 presents a flowchart of the computational procedure used in the dynamic analysis of the multibody system containing deep-groove ball bearings with waviness defects.

Fig. 7
figure 7

Flowchart of the computational procedure used for dynamic analysis of the multibody system containing deep-groove ball bearings with waviness defects

Full size image

4 Numerical examples: a slider–crank mechanism containing a deep-groove ball bearing with waviness defects on the raceways

In this section, a general slider–crank mechanism is chosen as an example to demonstrate the application of the methodologies presented. The mechanism consists of four rigid bodies (ground, crank, connecting rod, and slider), one nonideal revolute joint, two ideal revolute joints, and one ideal translational joint. A typical deep-groove ball bearing (SKF 98205) with waviness defects on the raceways constitutes the nonideal revolute joint in the mechanism. The dimensions and mass properties of the slider–crank mechanism are shown in Table 1, and the geometric and material properties of the deep-groove ball bearing used in the model are shown in Table 2.

Table 1 Dimensions and mass parameters for the slider–crank mechanism
Full size table
Table 2 Geometric and material properties for the deep groove ball bearing (SKF 98205)
Full size table

It is worth noting that the bearing model introduced in this paper is a simplified approach as the balls are not treated as independent rigid bodies. The bearing joint is modeled by introducing a system of nonlinear force constraints that takes into account the stiffness of the contact interaction between the rolling elements and raceways. A complicated bearing model is not used in the multibody system modeling process because describing each component of the bearing (balls, cage, and inner and outer raceways), and contact between them would lead to a model with a large number of degrees of freedom and nonlinear factors. On the other hand, a simplified approach is effective for revealing the influence of the rolling element bearing on the dynamic response of the mechanical system.

In general, the initial values (including the positions and velocities) of all the bodies in the multibody system need to be accurately specified before solving the equations of motion. In this example, the initial configuration of the slider–crank mechanism is defined as when the crank and connecting rod are collinear and the centers of the bearing’s inner and outer raceways coincide. All the initial positions and velocities necessary to start the dynamic analysis are obtained from kinematic simulations of the mechanism in which all the joints are considered to be ideal.

The ball number is an important geometric parameter of the deep-groove ball bearing. The value of the ball number not only affects the bearing capacity and service life, but also has an important effect on the dynamic performance of the mechanical system. To verify the effect of varying the bearing ball number on the dynamic characteristics of the slider–crank mechanism, it is supposed that there are 8, 9, 10, and 11 rolling balls in the bearing in the analysis that follows. Figure 8 shows the initial angular positions of the balls in the deep-groove ball bearing. When the slider–crank is in its initial position, we suppose that Ball 1 is located in the horizontal position and the others are arranged accordingly in a counterclockwise direction. The calculation step size is selected as 20 μs in the examples given. The integrator scheme utilized in the numerical simulation is the Gear method. This method is capable of dealing with system rigidity and realizes highly efficient changeable step integration in each time interval. Through an exactitude calculation, the equivalent contact stiffness between the rolling ball and the inner and outer raceways is 9.57×109 N/m. Based on experimental studies of bearing damping [57], a damping value of 300 N s/m is selected to ensure the convergence of the numerical calculations in this research.

Fig. 8
figure 8

The initial angular positions of the balls in the bearing

Full size image

4.1 Example 1: bearing located at the revolute joint between crank and ground

Figure 9 illustrates a slider–crank mechanism with a deep-groove ball bearing wherein the bearing is located between the crank and the ground. Generally, in order to achieve fixed-axis rotation of the crank relative to the ground, a shaft is needed through which the rotary motion of the motor can be transferred to the crank. In engineering application, a deep-groove ball bearing is usually used to support the shaft and guarantee its normal rotation. By simulating this example, the influence of bearing ball variation and waviness defect on the dynamic response of the slider–crank mechanism can be analyzed.

Fig. 9
figure 9

A slider–crank mechanism with a deep-groove ball bearing between the crank and ground

Full size image

4.2 Example 2: bearing located at the revolute joint between crank and connecting rod

Figure 10 also shows a slider–crank mechanism with a deep-groove ball bearing. We suppose now that the bearing is located between the crank and the connecting rod and is used to constitute a revolute joint between them. The revolving angular velocity of the rolling ball depends on the angular velocities of the inner and outer races of the bearing. As the bearing’s outer race is fixed to the crank while the inner race is fixed to the connecting rod, the revolving angular velocity of the rolling ball depends on the angular velocities of the crank and connecting rod. Additionally, the bearing in this position not only moves rotationally, but also translationally with the slider–crank mechanism.

Fig. 10
figure 10

A slider–crank mechanism with a deep-groove ball bearing between crank and connecting rod

Full size image

5 Results and discussion

In this section, two examples above are analyzed to determine the dynamic performance of the slider–crank mechanism when the crank rotates at 300 and 600 rpm, respectively. Keeping the analysis of the two examples in the paper is quite necessary. The dynamic response in the two examples may be different because the bearings at the two different positions have different movements and this affects the inertial load. The initial values used when starting the dynamic analysis are listed in Table 3. Through analysis of the variation in slider acceleration, crank moment, and bearing equivalent reaction force, the effects of different ball numbers and waviness defects on the dynamic response characteristics can be discussed.

Table 3 The initial values of the slider–crank mechanism necessary to start the dynamic analysis
Full size table

5.1 Simulation for Example 1, crank rotation speed 300 rpm

When there is no waviness defect on the surface of the bearing raceways, the variation in slider acceleration, crank moment, and bearing equivalent reaction force in the slider–crank mechanism are as shown in Figs. 11, 12, and 13, respectively. By comparison, the dynamic response of the slider–crank mechanism containing a deep-groove ball bearing without waviness defects on the raceways is very close to that of an ideal slider–crank mechanism possessing only ideal joints. When there are only eight rolling balls in the bearing, there are local small-amplitude vibrations in the slider acceleration, crank moment, and bearing equivalent reaction force. With an increase in the number of rolling balls in the bearing, the dynamic response of the slider–crank mechanism approaches that of an ideal slider–crank mechanism.

Fig. 11
figure 11

Variation in the slider acceleration without bearing waviness defects: (a) 8 balls, (b) 9 balls, (c) 10 balls, and (d) 11 balls

Full size image
Fig. 12
figure 12

Variation in the crank moment without bearing waviness defects: (a) 8 balls, (b) 9 balls, (c) 10 balls, and (d) 11 balls

Full size image
Fig. 13
figure 13

Variation in the bearing equivalent reaction force without bearing waviness defects: (a) 8 balls, (b) 9 balls, (c) 10 balls, and (d) 11 balls

Full size image

Including the effect of waviness defects on the surface of the bearing raceways, the variation in slider acceleration, crank moment, and bearing equivalent reaction force of the slider–crank mechanism are as shown in Figs. 14, 15, and 16, respectively. It can be seen that the waviness defect can result in vibration of the slider–crank mechanism in its kinematic process. By varying the bearing ball number, the amplitude of the vibration of the system is different.

Fig. 14
figure 14

Variation in the slider acceleration with bearing waviness defects: (a) 8 balls, (b) 9 balls, (c) 10 balls, and (d) 11 balls

Full size image
Fig. 15
figure 15

Variation in the crank moment with bearing waviness defects: (a) 8 balls, (b) 9 balls, (c) 10 balls, and (d) 11 balls

Full size image
Fig. 16
figure 16

Variation in the bearing equivalent reaction force with bearing waviness defects: (a) 8 balls, (b) 9 balls, (c) 10 balls, and (d) 11 balls

Full size image

Figure 14 shows that when there are eight rolling balls in the bearing, there is severe and large-amplitude vibration in the acceleration of the slider. However, when there are nine rolling balls, the response curve for the slider’s acceleration is close to that of the ideal curve, and the vibration of the slider is very small. In contrast, when there are 10 and 11 rolling balls in the bearing, respectively, there are still large vibrations in the slider acceleration curves, but the amplitude of the vibrations is smaller than that when there are eight balls. Figure 15 shows the variation in the crank moment when the ball numbers in the bearing are different. The figure shows that when there are eight rolling balls, the crank moment vibrates severely. When there are nine rolling balls, the vibration amplitude of the crank moment is at a minimum. When there are 10 and 11 rolling balls, there is still vibration in the crank moment but to different degrees. However, its amplitude is smaller than that when there are eight rolling balls. As can be seen from the variation in the equivalent reaction force of the bearing (Fig. 16), when there are eight rolling balls in the bearing, there are large-amplitude vibrations. If there are nine rolling balls, the vibration amplitude is at a minimum, and the situation is close to the variation in the constraint force of an ideal joint. When there are 10 and 11 rolling balls, there is also large-amplitude vibration in the bearing equivalent reaction force. The results indicate that under the premise of a certain waviness number, if the number of rolling balls in the bearing is different, the vibrational amplitudes of the slider–crank mechanism are different.

5.2 Simulation for Example 1, crank rotation speed 600 rpm

Figures 17, 18, and 19 show the variation in slider acceleration, crank moment, and bearing equivalent reaction force when the crank rotates at 600 rpm, respectively. It can be seen that when there is no waviness defect, the dynamic response of the slider–crank mechanism approaches the ideal result. Varying the ball number has little effect on the dynamic response of the system.

Fig. 17
figure 17

Variation in the slider acceleration without bearing waviness defects: (a) 8 balls, (b) 9 balls, (c) 10 balls, and (d) 11 balls

Full size image
Fig. 18
figure 18

Variation in the crank moment without bearing waviness defects: (a) 8 balls, (b) 9 balls, (c) 10 balls, and (d) 11 balls

Full size image
Fig. 19
figure 19

Variation in the bearing equivalent reaction force without bearing waviness defects: (a) 8 balls, (b) 9 balls, (c) 10 balls, and (d) 11 balls

Full size image

Including the waviness defect, the variation of the same three quantities at 600 rpm are as shown in Figs. 20, 21, and 22. The waviness defect can induce vibration of the slider–crank mechanism in its kinematic processes. However, with different ball numbers, the amplitudes of the vibration of the system are different. When there are nine rolling elements, the dynamic response of the slider–crank mechanism is more ideal, with minimum vibrational amplitude. When there are eight rolling balls, the vibration amplitude of the slider–crank mechanism is the largest. Also, when there are 10 and 11 rolling balls, respectively, there are still vibrations in the kinematic process for the slider–crank mechanism but with different degrees.

Fig. 20
figure 20

Variation in the slider acceleration with bearing waviness defects: (a) 8 balls, (b) 9 balls, (c) 10 balls, and (d) 11 balls

Full size image
Fig. 21
figure 21

Variation in the crank moment with bearing waviness defects: (a) 8 balls, (b) 9 balls, (c) 10 balls, and (d) 11 balls

Full size image
Fig. 22
figure 22

Variation in the bearing equivalent reaction force with bearing waviness defects: (a) 8 balls, (b) 9 balls, (c) 10 balls, and (d) 11 balls

Full size image

5.3 Simulation for Example 2, crank rotation speed 300 rpm

As shown in Fig. 10, we suppose that the deep-groove ball bearing is located between the crank and connecting rod in Example 2. The bearing in this position not only rotates but also translates along with the slider–crank mechanism. When the waviness defect on the surface of the bearing raceways is neglected, the variations in slider acceleration, crank moment, and bearing equivalent reaction force are as shown in Figs. 23, 24, and 25. It is still found that the dynamic response of the slider–crank mechanism with the bearing approaches that of an ideal slider–crank mechanism. When there are only eight rolling balls, there are local small-amplitude vibrations in the slider acceleration, crank moment, and bearing equivalent reaction force. With an increase in number of rolling balls, the dynamic response of the slider–crank mechanism with the bearing approaches that of an ideal slider–crank mechanism.

Fig. 23
figure 23

Variation in the slider acceleration without bearing waviness defects: (a) 8 balls, (b) 9 balls, (c) 10 balls, and (d) 11 balls

Full size image
Fig. 24
figure 24

Variation in the crank moment without bearing waviness defects: (a) 8 balls, (b) 9 balls, (c) 10 balls, and (d) 11 balls

Full size image
Fig. 25
figure 25

Variation in the bearing equivalent reaction force without bearing waviness defects: (a) 8 balls, (b) 9 balls, (c) 10 balls, and (d) 11 balls

Full size image

Adding in the influence of the waviness defect on the surface of bearing raceways, the variation in the slider acceleration, crank moment, and bearing equivalent reaction force are as described in Figs. 26, 27, and 28. It can be seen that the waviness defect can still cause vibration of the slider–crank mechanism. When there are nine rolling balls in the bearing, the vibrational amplitudes of the slider acceleration, crank moment, and bearing equivalent reaction force are the smallest. However, when there are 8, 10, and 11 rolling balls in the bearing, the vibrational response of the slider–crank mechanism is larger.

Fig. 26
figure 26

Variation in the slider acceleration with bearing waviness defects: (a) 8 balls, (b) 9 balls, (c) 10 balls, and (d) 11 balls

Full size image
Fig. 27
figure 27

Variation in the crank moment with bearing waviness defects: (a) 8 balls, (b) 9 balls, (c) 10 balls, and (d) 11 balls

Full size image
Fig. 28
figure 28

Variation in the bearing equivalent reaction force with bearing waviness defects: (a) 8 balls, (b) 9 balls, (c) 10 balls, and (d) 11 balls

Full size image

By comparing the results from Examples 1 and 2, we can see that if we suppose that the bearing is located between the crank and the ground, the vibrational response of the slider–crank mechanism is large. On the other hand, if the bearing is between the crank and the connecting rod, the vibrational response of the slider–crank mechanism under the same conditions is slightly smaller. The results indicate that the ball numbers and waviness defect have different effects on the dynamic performance of the slider–crank mechanism when the bearing is in different positions.

5.4 Simulation for Example 2, crank rotation speed 600 rpm

Figures 29, 30, 31, 32, 33, 34, illustrate the effect of bearing ball number and waviness defect on the slider acceleration, crank moment, and bearing equivalent reaction force when the crank rotation speed is 600 rpm. The dynamic response of the slider–crank mechanism in its kinematic processes is consistent with the results from the former analyses.

Fig. 29
figure 29

Variation in the slider acceleration without bearing waviness defects: (a) 8 balls, (b) 9 balls, (c) 10 balls, and (d) 11 balls

Full size image
Fig. 30
figure 30

Variation in the crank moment without bearing waviness defects: (a) 8 balls, (b) 9 balls, (c) 10 balls, and (d) 11 balls

Full size image
Fig. 31
figure 31

Variation in the bearing equivalent reaction force without bearing waviness defects: (a) 8 balls, (b) 9 balls, (c) 10 balls, and (d) 11 balls

Full size image
Fig. 32
figure 32

Variation in the slider acceleration with bearing waviness defects: (a) 8 balls, (b) 9 balls, (c) 10 balls, and (d) 11 balls

Full size image
Fig. 33
figure 33

Variation in the crank moment with bearing waviness defects: (a) 8 balls, (b) 9 balls, (c) 10 balls, and (d) 11 balls

Full size image
Fig. 34
figure 34

Variation in the bearing equivalent reaction force with bearing waviness defects: (a) 8 balls, (b) 9 balls, (c) 10 balls, and (d) 11 balls

Full size image

6 Conclusions

In this paper, a new approach to the dynamic modeling of a deep-groove ball bearing with waviness defects in a planar multibody system has been presented. The deep-groove ball bearing is modeled by introducing a nonlinear force system. This takes into account the elastic deformation of the contacts between the ball elements and the raceways. Hertzian contact theory is applied to calculate the elastic deflection and the nonlinear contact force. The waviness of the bearing inner and outer raceways is modeled using a sinusoidal function. A planar slider–crank mechanism containing a deep-groove ball bearing with waviness defect on the raceways is chosen as an example to demonstrate the application of the methodologies.

The results indicate that the waviness defect on the surface of the bearing raceways has a great effect on the dynamic response of a slider–crank mechanism. The waviness defect can promote vibration of the slider–crank mechanism in its kinematic process. Such vibration can lead to noise and also influence the stability of the mechanical system’s motion. When the waviness number is constant, bearings with different numbers of rolling balls can lead to different amplitudes of vibration of the slider–crank mechanism. For example, when there are eight rolling balls in the bearing, the vibration amplitude of system is the largest. However, when there are nine balls, the vibration amplitude of the slider–crank mechanism is the smallest, and the dynamic response of the system approaches ideality. This result shows that the effect of the bearing waviness defect on the dynamic response of a mechanical multibody system can be restrained by adjusting the number of rolling balls in the bearing. Furthermore, the influence of varying the rolling ball number and waviness defect on the dynamic performance of the slider–crank mechanism are different if the bearing is in different positions.

In future research, the influence of waviness amplitude and number on the dynamic response of a multibody system will be investigated. At the same time, the relationship between bearing rolling element number and waviness number will be discussed in depth in order to effectively restrain the system vibration caused by bearing waviness defects.