1 Introduction

This paper deals with one-point, ‘hard’ collision with friction in three-dimensional (3D), simple non-holonomic multibody systems, using classical collision theories (alternate approaches involving restoring and dissipative forces, also called ‘soft’ approach, and finite-element-based approach, also called full-deformation approach, described, e.g., by Chatterjee and Ruina in [1] and by Najafabadi et al. in [2], will not be discussed here). Djerassi has shown in [3] that, as far as two-dimensional (2D) systems are concerned, an algebraic, closed form, Poisson’s and Stronge’s hypotheses-related solutions always exist, and are unique, coherent, and energy-consistent.

Unfortunately, this is not the case with collision in 3D systems. If Keller’s idea [4] and Coulomb’s friction law are applied to the solution of collision problems, one obtains a set of five, coupled, nonlinear, first order differential equations, which has a singular point if sticking is reached. Solutions with analytic integrals exist only in special cases (e.g., in the absence of friction, as in [5] and [6], or if the ‘reduced’ 3×3 mass matrix is diagonal [7]). Battle shows in [8] that for what he calls ‘balanced collision’, solutions can be obtained with the integration of a single differential equation, that the remaining unknowns can be evaluated algebraically; and that sliding renewal cannot occur. He shows that, for a given system and collision points, the hodographs (describing the sliding relative velocity components of the colliding points versus one another) spanned by the collision initial conditions are continuous, unique and nonintersecting curves.

Thus, 3D collision problems require in general the solution of the five differential equations, investigated in depth by a small number of authors. Bhatt and Koechling [9] used Keller’s idea ([4]) to formulate the differential equations governing 3D collision of a rigid body hitting a plane, pointing out the singularity encountered if sticking occurs; and, showed that, depending on the coefficient of friction, either sticking prevails, or sliding is resumed in a constant, predictable direction. Battle [10] exploits the mathematical similarity between the description of the hodograph and an autonomous nonlinear flow, and, without solving the associated differential equations, draws a picture of the hodograph behavior during the sliding phase of the collision, and its dependence on five system parameters and on the coefficient of friction. Stronge [11] formulated the differential equations governing collisions between two bodies, and, introducing his coefficient of restitution, solved a number of examples (e.g., ball, rod, triangle and spherical pendulum hitting a plane). Zhen and Liu [12] formulated differential equations for 3D collision of holonomic systems using Keller’s idea, replacing the numerical integration with a difference method. They used a search algorithm to find the sliding direction if sliding resumption occurs.

It may be concluded that these authors provided the building blocks required to produce comprehensive solutions to the 3D, one point collision with friction problem for simple non-holonomic systems, a task undertaken in the present work. Two complete solutions are discussed, the first is based on the numerical integration of the indicated five differential equations, dealing with sliding, sticking and sliding renewal phases; and the second comprises a recursive summation associated with the first.

In both solutions, use is made of the classic collision hypotheses (by Newton [13], Poisson [14] and Stronge/Boulanger [11, 15], introducing, respectively, ‘kinematic’, ‘kinetic’ and ‘energetic’ coefficients of restitutions), a choice requiring elaborations in view of two observations related to these hypotheses. First, these hypotheses capture local effects, i.e., elastic and plastic deformations in the neighborhood of the colliding points. When applied to one point collision problems in multibody systems, they ’disregard’ the effect of the collision on the entire system (namely, on the rise of structural vibrations, friction in joints, restitution in the tangential direction, etc., as noted, e.g., in [16] and [1]), hence are not accurate. Second, Newton’s collision hypothesis can lead to an increase of the system mechanical energy (illustrated by Kane and Levinson in [17]). These observations gave rise to a number of newly defined hypotheses. For example, Chatterjee and Ruina augment in [1] Newton’s hypothesis with a tangential coefficient of restitution, which, among other features, improves the predictions of certain experimental results. Najafabadi et al. propose in [16] a new energy-related coefficient of restitution, which equals the square root of the ratio of the kinetic energy associated with the ‘constrained’ motion before and after the collision, better accommodating multibody systems. Rubin [18] discusses physical restrictions on the coefficient of restitution, concluding that it equals the ratio between the components of the velocity of separation and the velocity of approach in the impulse direction. Ivanov [19] arrives at a similar definition from an energy-related view-point.

In spite of their shortcomings, the classical hypotheses are widely used by numerous authors to conduct their studies. For example, Whittaker [5], Brach [20] and Smith [7] use Newton’s hypothesis, Routh [21], Keller [4] and Zen and Liu [12] use Poisson’s hypothesis, and Stronge [11], Hurmuzlu [22] and Djerassi [3] use Stronge/Boulanger’s hypothesis. Marghitu and Hurmuzlu [23], Smith and Liu [24], Ivanov [19] and others discuss all three hypotheses, showing that they lead to different results. It is understood, therefore, that a real-world problem requires calibration of the coefficient of restitution, validating its value for a limited parameter range (including, as shown by Stoianovici and Hurmuzlu in [25], geometrical ones). Incidentally, parameters associated with ‘soft’ approaches also require calibration (as e.g., in [26] and [27]). Accordingly, the analysis described here rests on the classical hypotheses. The paper starts with preliminaries (Sect. 2), followed by a presentation of the five differential equations and their solution in the events of sliding, sticking and sliding renewal (Sect. 3) in conjunction with the three classical hypotheses (Sect. 4). A 3D two-sled collision example is solved by integration in Sect. 5, and then by a recursive summation in Sect. 6. A short discussion in Sect. 7 concludes this work.

2 Preliminaries

Let

$$ F_{r} + F_{r}^{*} = 0\quad(r= 1,\ldots,p)$$
(1)

be Kane’s equations of motion for S, a simple, non-holonomic system of ν particles P i (i=1,…,ν) of mass m i , possessing p independent generalized speeds u 1,…,u p and n (n>p) generalized coordinates q 1,…,q n , where F r and \(F_{r}^{*}\) are, respectively, the rth generalized active force and the rth generalized inertia force for S (Kane and Levinson [17]). \(\mathbf{v}^{P_{i}}\), the velocity of P i in N, a Newtonian reference frame, can be expressed in terms of u 1,…,u p , q 1,…,q n and time t as

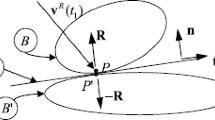
$$ \mathbf{v}^{P_{i}} = \sum_{r = 1}^{p}\mathbf{v}_{r}^{P_{i}}u_{r} + \mathbf{v}_{t}^{P_{i}}\quad (i=1,\ldots,\nu)$$
(2)

where \(\mathbf{v}_{r}^{P_{i}}\), called the rth partial velocity of P i , and \(\mathbf{v}_{t}^{P_{i}}\), called the remainder partial velocity of P i , are vector functions of q 1,…,q n and t. Let B and B′ be bodies of S, and let P be a point of B coming into contact with point P′ of B′ during the collision of B with B′ occurring between two instants t 1 and t 2 (Fig. 1). Under these circumstances, collision hypotheses [11, 13, 14] can be used to bring the effect of this collision into (1). To this end, let v R be the relative velocity of points P and P′, defined as

$$ \mathbf{v}^{R}\hat{=} \mathbf{v}^{P} - \mathbf{v}^{P'},$$
(3)

and note that v R can be written similarly to \(\mathbf{v}^{P_{i}}\) in (2), hence

(4a)
(4b)

where \(\mathbf{v}_{r}^{R}\) is the coefficient of u r in v R. Suppose that, during collision, P′ exerts on P a force R, so that P exerts on P′ a force −R. Then (1) give way to equations that bring into evidence the contributions of R, i.e.,

$$ F_{r} + F_{r}^{*} + \mathbf{R} \cdot \mathbf{v}_{r}^{P} -\mathbf{R} \cdot \mathbf{v}_{r}^{P'} = 0\quad (r= 1,\ldots,p;\ t_{1} \le t \le t_{2})$$
(5)

or, in view of (4a),

$$ F_{r} + F_{r}^{*} + \mathbf{R} \cdot \mathbf{v}_{r}^{R} = 0\quad (r=1,\ldots,p).$$
(6)

During the collision, P is assumed to maintain contact with P′, i.e., to coincide with P′; and a plane \(\tilde{S}\) exists which passes through P′ (≡P) and is tangent to B and B′ at P′ if both are locally smooth, or to B′ at P′ if only B′ is locally smooth. Name B and B′ such that n, a unit vector perpendicular to \(\tilde{S}\), makes v R(t 1)⋅n a non-positive quantity.

Fig. 1
figure 1

3D Collision; side (left) and top views on \(\tilde{S}\)

Full size image

Align t, a unit vector lying in \(\tilde{S}\), with the projection of v R(t 1) on \(\tilde{S}\), making v R(t 1)⋅t a non-negative quantity (see Fig. 1) and v R(t 1)⋅s, where \(\mathbf{s}\hat{ =} \mathbf{n} \times \mathbf{t}\), vanish. Then

(7a)
(7b)
(7c)
(7d)

v R(t 1) and v R(t 2) (at times denoted v A and v S [17]) are called velocity of approach and velocity of separation, respectively. Equation (6) can thus be replaced with

$$ F_{r} + F_{r}^{*} +\mathbf{R} \cdot \mathbf{n}\mathbf{v}_{r}^{R} \cdot \mathbf{n} +\mathbf{R} \cdot \mathbf{t}\mathbf{v}_{r}^{R}\cdot \mathbf{t} + \mathbf{R} \cdot \mathbf{s}\mathbf{v}_{r}^{R} \cdot \mathbf{s} = 0\quad (r=1,\ldots,p;\ t_{1} \le t \le t_{2}).$$
(8)

If it is assumed that t 2−t 1 is ‘small’ compared to time constants associated with the motion of S, and that, consequently, q 1,…,q n and t remain constants between t 1 and t 2, then both sides of (8) can be integrated from t 1 to t≤t 2, yielding

$$ \sum_{s = 1}^{p} m_{rs}\Delta u_{s} + I_{n}\mathbf{v}_{r}^{R} \cdot \mathbf{n} +I_{t}\mathbf{v}_{r}^{R} \cdot \mathbf{t} + I_{s}\mathbf{v}_{r}^{R} \cdot \mathbf{s} = 0\quad (r=1,\ldots,p).$$
(9)

Here, I n , I t and I s are the normal and tangential impulses at time t, defined as

(10a)
(10b)
(10c)

\(\mathbf{v}_{r}^{R}\hat{ =} \mathbf{v}_{r}^{R}(t)\) (t 1≤t≤t 2,r=1,…,p) (see (4a)), Δu s (s=1,…,p) are defined as

$$ \Delta u_{s}\hat{ =} u_{s}(t) - u_{s}(t_{1})\quad (s=1,\ldots,p),$$
(11)

and m rs is the entry in raw r, column s of the mass matrix −M associated with (1) (see (63), Appendix A). Note that n, t and s, defined only for t 1≤t≤t 2, remain fixed in N during the collision. Also note that R⋅n(t 1≤t≤t 2)>0 (P′ cannot ‘pull’ P), hence I n >0. The matrix form of (9), solved for Δu s (s=1,…,p) reads

(12a)
(12b)
(12c)
(12d)

Now, v R(t)−v R(t 1) can be written

$$ \mathbf {v}^{R}(t) - \mathbf {v}^{R}(t_{1}) =\bigl| \Delta u_{1} \cdots \Delta u_{p}\bigr|\bigl|\mathbf {v}_{1}^{R} \cdots \mathbf {v}_{p}^{R} \bigr|^{T}\quad \bigl(\mathbf {v}_{t}^{R}(t)- \mathbf {v}_{t}^{R}(t_{1})\mathop{=}\limits_{(4\mathrm{b})}0\bigr)$$
(13)

when use is made of (2), (4a) and (4b). If both sides of (13) are dot-multiplied by n, t and s, one at a time, and if |Δu 1⋯Δu p | is eliminated with the aid of (12a), one has, defining \(\mathbf {V}\hat{ =} | \mathbf {V}_{n} \mathbf {V}_{t} \mathbf {V}_{s}|^{T}\) \((\Rightarrow \mathbf {V}^{T} = | \mathbf {V}_{n}^{T} \mathbf {V}_{t}^{T} \mathbf {V}_{s}^{T}|)\),

$$ \left|\begin{array}{@{}c@{}}\mathbf {v}^{R}(t) \cdot \mathbf {n}- \mathbf {v}^{R}(t_{1}) \cdot \mathbf {n}\\[1mm]\mathbf {v}^{R}(t)\cdot \mathbf {t}- \mathbf {v}^{R}(t_{1}) \cdot \mathbf {t}\\[1mm]\mathbf {v}^{R}(t) \cdot \mathbf {s}- \mathbf {v}^{R}(t_{1}) \cdot \mathbf {s}\end{array}\right|= - \mathbf {V}\mathbf {M}^{ - 1}\mathbf {V}^{T}\left|\begin{array}{@{}c@{}}I_{n} \\I_{t} \\I_{s}\end{array}\right|.$$
(14)

The coefficients of I n , I t and I s in (14) are functions of q 1,…,q n and t, hence remain constants between t 1 and t 2. Defining m nn , m nt , m tt , m ns , m ts and m ss as

$$ \begin{array}{@{}l}m_{nn}\hat{ =} -\mathbf {V}_{n}\mathbf {M}^{ - 1}\mathbf {V}_{n}^{T} > 0,\quad m_{nt}\hat{=} - \mathbf {V}_{n}\mathbf {M}^{ - 1}\mathbf {V}_{t}^{T},\quad m_{tt}\hat{ = } - \mathbf {V}_{t}\mathbf {M}^{ - 1}\mathbf {V}_{t}^{T} > 0, \\[2mm]m_{ns}\hat{ =} - \mathbf {V}_{n}\mathbf {M}^{ -1}\mathbf {V}_{s}^{T},\quad m_{ts}\hat{ = } - \mathbf {V}_{t}\mathbf {M}^{ - 1}\mathbf {V}_{s}^{T},\quad m_{ss}\hat{ = } - \mathbf {V}_{s}\mathbf {M}^{ - 1}\mathbf {V}_{s}^{T} > 0,\end{array}$$
(15)

v n , v t , v s , v n1, v t1, v s1, v n2, v t2 and v s2, the n, t and s components of v R at times t, t 1 and t 2, and I n2, I t2 and I s2, the n, t and s impulse components at time t 2, as

$$ v_{n}\mathop{\hat{ =}}\limits_{(7\mathrm{a})}\mathbf {v}^{R}(t) \cdot \mathbf {n},\quad v_{t}\mathop{\hat{ =}} \limits_{(7\mathrm{a})}\mathbf {v}^{R}(t) \cdot \mathbf {t},\quad v_{s}\mathop{\hat{ =}} \limits_{(7\mathrm{a})}\mathbf {v}^{R}(t) \cdot \mathbf {s},$$
(16)
$$ v_{n1}\hat{ =} \mathbf {v}^{R}(t_{1}) \cdot \mathbf {n}(\mathop{ <0)}\limits_{(7\mathrm{b})},\quad v_{t1}\hat{ =} \mathbf {v}^{R}(t_{1}) \cdot \mathbf {t}(\mathop{ > 0)}\limits_{(7\mathrm{c})},\quad \mathbf {v}_{s1}\hat{ =}\mathbf {v}^{R}(t_{1}) \cdot \mathbf {s}(\mathop{ = 0)}\limits_{(7\mathrm{d})},$$
(17)
$$ v_{n2}\hat{ =} \mathbf {v}^{R}(t_{2}) \cdot \mathbf {n},\quad \mathbf {v}_{t2}\hat{ =}\mathbf {v}^{R}(t_{2}) \cdot \mathbf {t},\quad v_{s2}\hat{ =} \mathbf {v}^{R}(t_{2}) \cdot \mathbf {s},$$
(18)
$$ I_{n2}\hat{ =} I_{n}(t_{2}),\quad I_{t2}\hat{ =} I_{t}(t_{2}),\quad I_{s2}\hat{ =}I_{s}(t_{2}),$$
(19)

\((I_{n1}\hat{ =} I_{n}(t_{1}) = 0\), \(I_{t1}\hat{ =} I_{t}(t_{1}) = 0\), \(I_{s1}\hat{ =} I_{s}(t_{1}) = 0)\) one can rewrite (14) for t 1≤t≤t 2

$$ v_{n} - v_{n1} = m_{nn}I_{n} + m_{nt}I_{t} +m_{ns}I_{s},$$
(20)
$$ v_{t} - v_{t1} = m_{nt}I_{n} + m_{tt}I_{t} +m_{ts}I_{s},$$
(21)
$$ v_{s} - v_{s1} = m_{ns}I_{n} + m_{ts}I_{t} +m_{ss}I_{s}.$$
(22)

(Equations (20)–(22) reduce to (22)–(23) in [28] for 2D systems; then m ts =m ns =m ss =0.) These so-called ‘reduced equations of motion’ possess a coefficient matrix \(\mathfrak{M}\) shown in Appendix A to be positive definite; and six unknowns I n , I t , I s , v n , v t and v s . Knowledge of I n2, I t2 and I s2 enables the evaluation of Δu 1(t 2)…Δu p (t 2) with (12a), with which simulations (i.e., numerical integrations of (1)) can be kept running. Accordingly, I n2, I t2 and I s2 are generated in the following sections first by integration and then by recursive summation, with the aid of friction- and collision-related hypotheses.

Regarding ΔE 2, the change in the system mechanical energy following a collision, a straightforward extension of the proof given in [28] for the planar case shows that

$$ \Delta E_{2} = 1/2I_{n2}(v_{n2} + v_{n1}) +1/2I_{t2}(v_{t2} + v_{t1}) + 1/2I_{s2}(v_{s2}+ v_{s1})$$
(23)

(\(= 1/2\mathbf {u}_{2}( - \mathbf {M})\mathbf {u}_{2}^{T} - 1/2\mathbf {u}_{1}( - \mathbf {M})\mathbf {u}_{1}^{T}\), where \(\mathbf {u}\hat{ =} | u_{1} \cdots u_{p} |\)) for the 3D case, provided

$$ - I_{n2}\mathbf {v}_{t}^{R} \cdot \mathbf {n}-I_{t2}\mathbf {v}_{t}^{R} \cdot \mathbf {t}- I_{s2}\mathbf {v}_{t}^{R}\cdot \mathbf {s}+ \sum_{i= 1}^{\nu} m_{i}\mathbf {v}_{t}^{P_{i}} \cdot \bigl[\mathbf {v}^{P_{i}}(t_{2}) -\mathbf {v}^{P_{i}}(t_{1})\bigr]\mathop{ =}\limits_{(2)}0,$$
(24)

a condition ‘neutralizing’ specified motions implied by \(\mathbf {v}_{t}^{R}\) and \(\mathbf {v}_{t}^{P_{i}}\) (i=1,…,ν).

3 Solution by integration

One can start with the differential form of (20)–(22) given by

$$ \mathrm{d}v_{n} = m_{nn}\mathrm{d}I_{n} + m_{nt}\mathrm{d}I_{t} + m_{ns}\mathrm{d}I_{s},$$
(25)
$$ \mathrm{d}v_{t} = m_{nt}\mathrm{d}I_{n} + m_{tt}\mathrm{d}I_{t} + m_{ts}\mathrm{d}I_{s},$$
(26)
$$ \mathrm{d}v_{s} = m_{ns}\mathrm{d}I_{n} + m_{ts}\mathrm{d}I_{t} + m_{ss}\mathrm{d}I_{s}.$$
(27)

Let the slip speed s of P relative to P′ and the orientation angle ϕ be defined so that

(28a)
(28b)
(28c)
(28d)

where sϕ=sinϕ and cϕ=cosϕ (Fig. 1); and note that as long as there is slip R⋅t=−μ R⋅n cϕ, R⋅s=−μ R⋅n sϕ ([(R⋅t)2+(R⋅s)2]1/2=μ|R⋅n|), in accordance with Coulomb’s friction law, or, in view of (10a)–(10c),

$$ \mathrm{d}I_{t} = - \mu \mathrm{d}I_{n}c\phi,\quad \mathrm{d}I_{s} = - \mu \mathrm{d}I_{n}s\phi,$$
(29)

where μ is Coulomb’s coefficient of friction. With f,g and h defined as

$$ \begin{array}{@{}l@{\quad}l}f\hat{ =} \mathrm{d}v_{n}/\mathrm{d}I_{n},&g\hat{ =} \mathrm{d}v_{t}/\mathrm {d}I_{n}c\phi+\mathrm {d}v_{s}/\mathrm {d}I_{n}s\phi, \\[1mm]& h\hat{ =} - \mathrm {d}v_{t}/\mathrm {d}I_{n}s\phi+\mathrm {d}v_{s}/\mathrm {d}I_{n}c\phi \end{array}$$
(30)

one can show, dividing (25)–(27) throughout by dI n and using (29), that

$$ f = m_{nn} - \mu m_{nt}c\phi- \mu m_{ns}s\phi,$$
(31)
$$ g = m_{nt}c\phi+ m_{ns}s\phi- \mu m_{tt}c^{2}\phi- \mu m_{ss}s^{2}\phi- 2\mu m_{ts}s\phi c\phi,$$
(32)
$$ h = - m_{nt}s\phi+ m_{ns}c\phi- \mu m_{ts}(c^{2}\phi- s^{2}\phi) +\mu(m_{tt} - m_{ss})s\phi c\phi,$$
(33)

and that dv t and dv s can be eliminated from (25), (28b) and (28d), which reduce to

(34a)
(34b)
(34c)
(34d)
(34e)

Equations (34a)–(34e) comprise five ordinary, coupled, first order differential equations with five dependent variables ϕ, s, v n , I t and I s and one, monotonously increasing, independent variable I n governing the sliding portion of the collision. The right-hand sides of (34a)–(34e) and their partial derivatives with respect to ϕ, s, v n , I t and I s , are continuous functions of ϕ, s, v n , I t and I s in the region s>0. Therefore, a solution of (34a)–(34e) in conjunction with the following initial conditions (when I n =0): ϕ(0)=0, s(0)=v t1 (then, by (28a)–(28d) v t (0)=s(0)=v t1, v s (0)=0), v n (0)=v n1, I t (0)=0 and I s (0)=0, always exists and is unique (see, e.g., [29], p. 267). Moreover, \(\mathrm {d}\Delta E = \mathbf {R}\cdot \mathbf {v}^{R}(t)\mathop{ =} \limits_{(7\mathrm{a}),(16)}(\mathbf {R}\cdot \mathbf{n}\mathbf{n} + \mathbf {R}\cdot \mathbf {t}\mathbf {t}+ \mathbf {R}\cdot \mathbf {s}\mathbf {s}) \cdot(v_{n}\mathbf {n}+ v_{t}\mathbf {t}+v_{s}\mathbf {s})\mathop{ =}\limits_{(10),(28\mathrm{a},\mathrm{c}),(29)}(v_{n} - \mu s)\mathrm {d}I_{n}\). With \(\mathrm{d}\Delta E_{n}\hat{ =} v_{n}\mathrm {d}I_{n}\), (34a)–(34e) can be augmented with the differential equations

(35a)
(35b)

enabling the evaluation of the ‘total’ and the ‘normal’ energy losses during collision.

It is worth noting that (23) is valid for t 1<t≤t 2 if ΔE 2, I n2, v t2, etc. are replaced with ΔE, I n , v t , etc.; then the I n derivative of both sides of (23) can be used to prove the validity of (35a) with the aid of (29), (34b)–(34e) and (20)–(22) in yet a different way. Moreover, d[1/2I n (v n +v n1)]/dI n ≠v n , hence ΔE n ≠1/2I n (v n +v n1). It can be shown this is also the case with 2D systems, except in sliding.

In general (34a)–(34e) cannot be integrated analytically (see, e.g., [9] and [11]). Furthermore, the ‘trivial’ solution ϕ≡0, valid for 2D problems, does not apply: ϕ≡0 implies dϕ/dI n =0; however, during sliding s>0, hence h(μ,ϕ)=0 (see (34a)). This equation has at least two nonzero solutions for ϕ (Appendix B), in contrast with the trivial solution.

Collisions comprise at least the first of the following events.

3.1 Sliding

Suppose that I n2, the normal impulse at t 2 is known, and that the sliding speed s remains positive throughout the integration of (34a)–(34e) from I n =0 to I n =I n2. Then integration underlies the solution for sliding, yielding ϕ(t 2), s(t 2)(>0) (hence, by (28a) and (28c) v t2 and v s2), v n2, I t2 and I s2.

3.2 Sticking

It may occur that s becomes zero, say, at t=t S <t 2, i.e., before I n =I n2. In that event h(μ,ϕ)→0 as s→0, provided g(μ,ϕ)<0; and vice versa. To show this, note that

(36a)
(36b)

hence

$$ \mathrm{d}v_{s}\mathrm{/d}v_{t}=(\mathrm{d}v_{s}/\mathrm{d}I_{n})/(\mathrm{d}v_{t}/\mathrm{d}I_{n}) = (gs\phi+hc\phi)/(gc\phi- hs\phi).$$
(37)

Moreover, \(\lim_{s \to 0}(\mathrm{d}v_{s}/\mathrm{d}v_{t})\mathop{ =}\limits_{(28\mathrm{b},\mathrm{d})}\lim_{s \to 0}[s(\phi)/c(\phi)]\), so that, with (37),

provided at least one solution \(\bar{\phi}\) of h(μ,ϕ)=0 satisfies \(g(\mu,\bar{\phi} )c^{2}\bar{\phi} \ne0\). In fact, when s(>0)→0 then necessarily ds/dI n <0, hence, by (34b), \(\lim_{s \to0 \Rightarrow\phi\to\bar{\phi}} g(\mu,\phi) < 0\), in agreement with Appendix B, showing that at least one such solution exists. Conversely, (34a) and (34b) can be condensed into

$$ \mathrm{d}s/s = g/h\mathrm{d}\phi,$$
(38)

an equation which, when integrated from s=s(0) and ϕ=0 to s and ϕ yields \(s = s(0)\exp\int_{ 0}^{ \phi}g(\mu,\eta)/h(\mu,\eta)\,\mathrm{d}\eta\), showing that if \(\lim_{\phi\to \bar{\phi}} h(\mu,\phi) \to0\) (and, since \(\mathrm{d}\eta/h\mathop{ >}\limits_{(34\mathrm{a})}0\)) and \(\lim_{\phi\to\bar{\phi}} g(\mu,\phi)< 0\), then s(>0)→0 and sticking is approached.

During sticking, (25)–(27) remain valid with

$$ v_{t} \equiv 0,\quad v_{s} \equiv0\quad\Rightarrow\quad \mathrm {d}v_{t}= 0,\quad \mathrm {d}v_{s} = 0,$$
(39)

yielding, when solved for dI n , dI t and dI s ,

(40a)
(40b)
(40c)

where c n ,c t and c s are functions of m nn , m nt ,…,m ss given by

(41a)
(41b)
(41c)
(41d)

Equations (40a)–(40c) govern sticking just as (34c)–(34e) govern sliding. Seeking limit-values of ϕ and μ satisfying both (34c, 34d, 34e) and (40a)–(40c) one finds

$$ \mathrm {d}I_{s}/\mathrm {d}I_{t}\mathop{ =}\limits_{(34\mathrm{d},\mathrm{e})}\tan\phi\mathop{ =}\limits_{(40)}c_{s}/c_{t},$$
(42)
$$\mu\mathop{ =} \limits_{(34\mathrm{d})} -\mathrm {d}I_{t}/\mathrm {d}I_{n}c^{ -1}\phi\mathop{ =} \limits_{(40\mathrm{a},\mathrm{b})} - c_{t}/(c_{n}c\phi),\quad \mu\mathop{ =} \limits_{(34\mathrm{e})} -\mathrm {d}I_{s}/\mathrm {d}I_{n}s^{ -1}\phi\mathop{ =} \limits_{(40\mathrm{a},\mathrm{c})} - c_{s}/(c_{n}s\phi).$$

Here c n >0 (see (41a)) and μ>0, conditions that, given c t and c s , determine μ and (the signs of sϕ and cϕ, hence) ϕ uniquely, namely,

$$ \mu_{c} = \sqrt{c_{t}^{2} + c_{s}^{2}} /c_{n},\quad \phi_{c} = a\tan2( -c_{s}, - c_{t}).$$
(43)

Moreover, dv t /dI n =0 and dv s /dI n =0 ((39)), so that, in view of (36a) and (36b)

$$ g(\mu,\phi) = 0, \quad h(\mu,\phi) = 0.$$
(44)

μ c and ϕ c in (43) satisfy (44), and conversely, if g(μ,ϕ) and h(μ,ϕ) ((32) and (33)) are substituted explicitly in (36a) and (36b), then, in view of (39) and (44), m ns −μm ss sϕ−μm ts cϕ=0 and m nt −μm tt cϕ−μm ts sϕ=0, equations having (μ c ,ϕ c ) as a unique solution. μ c is interpreted as the minimal coefficient of friction for which sticking remains once it has occurred. (In ‘balanced collision’ \(m_{nt} = m_{ns} = 0 \mathop{\Rightarrow} \limits_{(41)}c_{t} = c_{s} = 0\mathop{ \Rightarrow}\limits_{(43)}\mu_{c} = 0\), as indicated by Battle in [8].) That is, if s(t=t S )=0 and μ>μ c then s(t S <t≤t 2)=0; and, for t S <t≤t 2, (34a)–(34e) can be replaced with

(45a)
(45b)
(45c)
(45d)
(45e)

3.3 Sliding renewal

If μ<μ c , and s(t=t S )=0 before I n2 is reached, sliding is resumed; however, I n2, I t2 and I s2 cannot be obtained by the integration of (34a)–(34e), which become singular (\(s(t= t_{S}) = 0 \Rightarrow h(\mu,\bar{\phi} ) = 0\)). One way to navigate the solution through this singularity (see [9]) for t>t S is to let ϕ switch values from \(\phi= \bar{\phi}\) to \(\phi=\hat{\phi}\), the only solution of h(μ,ϕ)=0 satisfying \(\mathrm {d}s/\mathrm {d}I_{n} = g(\mu,\hat{\phi} ) > 0\) (see Appendix B). If, in addition, dϕ/dI n =0 is imposed, then ϕ remains constant \(( = \hat{\phi} )\), \(\mathrm {d}s/\mathrm {d}I_{n} = \mathit{const} = g(\mu,\hat{\phi} ) > 0\) (see (34a) and (34b)), and, for t S <t≤t 2 (34a)–(34e) can be replaced with

(46a)
(46b)
(46c)
(46d)
(46e)

In conclusion, solutions to the 3D collision problem can be obtained by the integration of (34a)–(34e). If s(t=t S )=0, then (34a)–(34e) are replaced by either (45a)–(45e) or (46a)–(46e), according to weather μ>μ c (sticking) or μ<μ c (sliding renewal).

It may occur that \(\mu= \mu_{s}\hat{ =} m_{ns}/m_{ts}\); then initially h(μ,0)=m ns −μm ts =0. In that event ϕ≡0, and the hodograph remains on the v t axis unless sticking occurs with μ s <μ c ; then sliding is renewed in the \(\hat{\phi}\) direction. If μ s >μ c , sticking prevails.

Next, the assumption that I n2 is known is abandoned in favor of collision hypotheses which govern the integration limits. Accordingly, Newton’s [13], Poisson’s [14] and Stronge’s [11] collision hypotheses will be introduced, along with the following assumption, namely, that the collision time comprises a compression phase, starting at t 1 and terminating at t C , the instant of maximum compression, when the normal relative velocity vanishes, i.e.,

$$ v_{nC}\hat{ =} \mathbf {v}^{R}(t_{C}) \cdot \mathbf {n}= 0\quad (t_{1} < t_{C} <t_{2});$$
(47)

and a restitution phase, starting at t C and terminating at t 2, when R(t 2)=0 (see (5)).

4 Newton’s, Poisson’s and Stronge’s hypotheses

4.1 Newton’s hypothesis

In accordance with Newton’s hypothesis, the coefficient of restitution is defined

$$ e\hat{ =} - v_{n2}/v_{n1}\quad (0 \le e\le 1).$$
(48)

Here, the integration proceeds until v n =v n2.

4.2 Poisson’s hypothesis

Let I nC and I nR be parts of I n2 associated with the compression and with the restitution phases, respectively; then (see (10a))

$$ I_{n2} = I_{nC} + I_{nR},\quad I_{nC}\hat{ =}\biggl(\int_{ t_{1}}^{t_{C}}\mathbf {R}\,\mathrm {d}t\biggr) \cdot n,\quad I_{nR}\hat{ =}\biggl(\int_{ t_{C}}^{ t_{2}} \mathbf {R}\,\mathrm {d}t\biggr) \cdot \mathbf {n}.$$
(49)

According to Poisson’s hypothesis, the coefficient of restitution is defined

$$ e\hat{ =} I_{nR}/I_{nC}\quad (0 \le e \le1),$$
(50)

so that, in light of (49) and (50)

$$ I_{n2} = (1 + e)I_{nC}.$$
(51)

Here I nC is recorded for which v n vanishes. I n2 is then evaluated with (51), and the integration proceeds until I n =I n2.

4.3 Stronge’s hypothesis

Let ΔE nC (<0) and ΔE nR (>0) be parts of the ‘normal’ energy loss ΔE n2 (see (35b)) associated with the compression and the restitution phases, respectively; then

$$ \Delta E_{n2} = \Delta E_{nC} + \Delta E_{nR},\quad \Delta E_{nC}\hat{ =} \int_{0}^{ I_{nC}} v_{n}\,dI_{n},\quad \Delta E_{nR}\hat{ =} \int_{I_{nC}}^{I_{n2}} v_{n}\,dI_{n}.$$
(52)

According to Stronge’s hypothesis, the coefficient of restitution is defined

$$ e^{2}\hat{ =} - \Delta E_{nR}/\Delta E_{nC}\quad (0 \le e \le1),$$
(53)

so that, in light of (52) and (53)

$$ \Delta E_{n2} = (1 - e^{2})\Delta E_{nC}.$$
(54)

Here ΔE nC is recorded for which v n vanishes (see (35b)). ΔE n2 is then evaluated with (54), and the integration proceeds until ΔE n =ΔE n2.

The steps underlying the solution by integration can be summarized as follows:

  1. 1.

    Find n, t and s satisfying relations (7b)–(7d), and identify V n , V t and V s ((12a)–(12d)), the members of M ((9)) and \(\mathfrak{M}\) ((18)), c n , c t and c s (41a)–(41c), and μ c , ϕ c ((43)); and \(\hat{\phi}\) satisfying \(h(\mu,\hat{\phi} ) = 0\) with \(g(\mu,\hat{\phi} ) > 0\).

  2. 2.

    Introduce λ, a parameter, and integrate both sides of the expressions

    $$ [\mathrm{Eqs}.(34i)](1 - |\lambda|) +[\mathrm{Eqs}.(45i)]\lambda(\lambda- 1)/2 +[\mathrm{Eqs}.(46i)]\lambda(\lambda+ 1)/2$$
    (55)

    with i playing the roles of a, b, c, d and e, one at a time, and with λ(0)=0, ϕ(0)=0, s(0)=v t1, v n (0)=v n1, I t (0)=0 and I s (0)=0 as initial conditions, switching, if s<ε s , from the initial sliding (λ=0) to sticking (μ>μ c ,λ=−1) or to sliding renewal (μ<μ c ,λ=1). It can be shown that, if ε s is sufficiently small, it has no effect on the integration results.

  3. 3.

    Identify v n2, I n2 or ΔE n2, and stop the integration according to the chosen collision hypothesis; find I n2, I t2 and I s2 and then Δu 1,…,Δu p with (12a).

  4. 4.

    Evaluate the mechanical energy loss with both (23) (two versions) and (35a). Identical results validate of the entire procedure.

These steps need modifications, discussed in Appendix C, when used to solve the 2D problem. With these modifications, all the results reported in Table 3 of [3] for the planar version of the two-sled problem are reproduced with a three-digit precision.

5 The two-sled example ([30], p. 9)

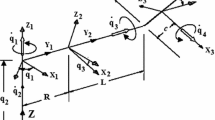
Figure 2 shows two identical sleds A and B comprising rods of length 2l and mass m, supported by massless knife-edges with steering angles γ and δ, touching planes \(\bar{A}\) and \(\bar{B}\) fixed in N at points A s and B s , a distance k from their mass centers A ∗ and B ∗; and supported by two back sliders moving in \(\bar{A}\) and \(\bar{B}\), respectively. \(\bar{A}\) and \(\bar{B}\) are rotated with respect to one another about their intersection line L forming an angle θ<π/2 with \(\bar{\mathbf{a}}_{1}\), a unit vector fixed in \(\bar{A}\), such that lines a and b lying in \(\bar{A}\) and \(\bar{B}\) normal to L form an angle η<π/2; and \(\bar{\mathbf{b}}_{1}|_{\eta=0} = \bar{\mathbf{a}}_{1}\). Let u 1,…,u 6 be generalized speeds, and let the velocities of A ∗ and B ∗, and the angular velocities of A and B in N, expressed as

$$\mathbf {v}^{A*} = u_{1}\mathbf{a}_{1} + u_{2}\mathbf{a}_{2},\quad \omega^{A} = u_{3}\mathbf{a}_{3},\quad \mathbf{v}^{B*} =u_{4}\mathbf{b}_{1} + u_{5}\mathbf{b}_{2},\quad \omega^{B} = u_{6}\mathbf{b}_{3},$$

be subject to the constraints \(\mathbf {v}^{A_{s}} \cdot \mathbf{a}'_{2} = 0\) and \(\mathbf {v}^{B_{s}} \cdot \mathbf {b}'_{2} = 0\) imposed by the knife-edges. Here a i , b i , \(\mathbf {a}'_{i}\) and \(\mathbf {b}'_{i}\) (i=1,2,3) are sets of three dextral, mutually perpendicular unit vectors fixed in A and B, with a 3 and \(\mathbf {a}'_{3}\), and b 3 and \(\mathbf {b}'_{3}\) normal to \(\bar{A}\) and \(\bar{B}\), respectively, as shown in Fig. 2. The indicated constraint equations, when written explicitly and solved for u 2 and u 5, read

$$u_{2} = t\gamma u_{1} - ku_{3},\quad u_{5} = t\delta u_{4} - ku_{6},$$

where t(.)=tan(.), and lead, with u 1, u 3, u 4, and u 6 regarded as independent generalized speeds, to the following equations, governing motions of A and B:

where s(.)=sin(.) and c(.)=cos(.). Defining generalized coordinates q 1,…,q 6 as \(q_{1}\hat{ =} \mathbf {p}^{A*} \cdot \mathbf {a}_{1}\), \(q_{2}\hat{ =} \mathbf {p}^{A*} \cdot \mathbf {a}_{2}\), \(\dot{q}_{3}\hat{ =} u_{3}\) and \(q_{4}\hat{ =} \mathbf {p}^{B*} \cdot \mathbf {b}_{1}\), \(q_{5}\hat{ =} \mathbf {p}^{B*} \cdot \mathbf {b}_{2}\), \(\dot{q}_{6}\hat{ =} u_{6}\), one can replace the constraint equations with

non-integrable differential equations, which make the system non-holonomic. Next, suppose that at time t 1 the endpoint B c of B collides with point A c of A located a distance p from A ∗; and that it is required to evaluate the associated changes in the generalized speeds and in the system kinetic energy. To this end, the velocities of A c and B c are expressed as

$$\mathbf {v}^{A_{c}} = u_{1}\mathbf {a}_{1} +(u_{2} + pu_{3})\mathbf {a}_{2},\quad \mathbf {v}^{B_{c}} = u_{4}\mathbf {b}_{1}+ (u_{5} + lu_{6})\mathbf {b}_{2},$$

and the relative velocity \(\mathbf {v}^{R} = \mathbf {v}^{B_{c}} - \mathbf {v}^{A_{c}}\) of the colliding points is written, with z 1=(k−p)u 3−tγu 1, z 2=(l−k)u 6+tδu 4, z 3=cη+c 2 θ(1−cη), z 4=cη+s 2 θ(1−cη), z 5=sθcθ(1−cη), z 6=z 5 sq 6+z 3 cq 6, z 7=z 5 cq 6−z 3 sq 6, z 8=z 5 cq 6+z 4 sq 6, and z 9=z 5 sq 6−z 4 cq 6, as

With n, t and s identified as n=a 2, t=cφ a 1+sφ a 3 and s=−sφ a 1+cφ a 3, φ can be found that satisfies v R⋅t=v t1>0 and v R⋅s=v s1=0, enabling the evaluation of V n , V t and V s ((12a)–(12d)) and of the members of \(\mathfrak{M}\) ((15)). With m=3 kg, l=1, k=0.75, p=−0.5m, γ=δ=0.2, θ=π/3, η=2π/9 rad, q 3(t 1)=π/4, and q 6(t 1)=7π/4 rad one can show, by substitutions, that φ=3.81, m nn =0.225, m tt =0.236, m ss =0.270, m nt =−0.109, m ts =−0.116, m ns =−0.126 ((18)), c n =42.6, c t =37.3, c s =35.8 ((41a)–(41c)), μ c =1.21, ϕ c =3.76 ((43)) and \(\hat{\phi} = 3.91\) (Sect. 3.3). For u 1(t 1)=u 4(t 1)=1 m/sec, u 3(t 1)=u 6(t 1)=0.1 rad/sec (v n1=−0.9,v t1=1.06,v s1=0m/sec), one obtains, integrating (34a)–(34e), (45a)–(45e) and (46a)–(46e) with ε s =0.1÷0.01, results recorded in Table 1 and Fig. 3 for μ=0.6, 1.1, 1.6 and e=0.8, where ‘○’, ‘+’ and ‘□’ designate collision termination points according Newton’s, Poisson’s and Stronge’s hypotheses, respectively. One can thus follow the hodographs as μ increases. For \(\mu< \mu_{s}\hat{ =} m_{ns}/m_{ts} = 1.086\) (e.g., μ=0.6) there is sliding, with a local maximum approaching the origin. If μ=μ s ⇒h=0 (see end of Sect. 3.3) then ϕ≡0 throughout sliding ((34a)). The sliding part runs along the v t axis, and is followed by a sliding renewal part. The latter becomes ‘shorter’ as μ increases toward μ c , vanishing for μ=μ c . For μ>μ c sliding is followed by sticking for all collision hypotheses; then the three hodograph end-points overlap at the origin. The similarity between the hodographs for the sliding and the sliding renewal cases corroborates the ‘switch’ between \(\bar{\phi}\) and \(\hat{\phi}\) when sliding renewal occurs (Appendix B). Regarding energy gains associated with Newton’s hypothesis, it turns out to be significantly larger than that recorded for 2D systems, e.g. in [17] and [28].

Fig. 2
figure 2

A two-sled collision

Full size image
Fig. 3
figure 3

v s vs. v t (hodograph) and v n and s vs. I n for μ=0.6, 1.1, 1.6, yielding sliding, sliding renewal (\(\bar{\phi} = 0.432\)) and sticking (\(\bar{\phi} = 0.598\)), respectively

Full size image
Table 1 Changes of the motion variables and of the system energy for the example
Full size table

It may occur that the number of collisions become large, as when numerous particles or bodies collide with one another. In that case the use of elaborate numerical integrators to solve (55) can produce prohibitively long simulations, unless exact integrals exist, e.g., when μ=0 ([5] and [6]) or when m nt =m ns =m ts =0. This state of affairs can be alleviated with recursive summation-based solutions, which, taking advantage of the limited integration range of (55), provide a reasonable compromise between accuracy and speed. Such a solution is discussed next.

6 Solution by recursive summation

6.1 Recursive summation

Referring to Euler’s explicit, first order accurate method, described, e.g., in [31], Para. 3, Sect. 9, let I n (1)=0, I n (i)=(i−1)/k, \(D(i)\hat{ =} I_{n}(i) - I_{n}(i - 1)(i =2,3,\ldots)\), where k, an integer, is a refinement factor, and replace (55) with

$$ \phi(i)\mathop{ =}\limits_{(34\mathrm{a}),(45\mathrm{a}),(46\mathrm{a})}\bigl\{ \phi(i - 1) +\bigl[h(i - 1)/s(i - 1)\bigr]D(i)\bigr\}(1 - |\lambda|) + \hat{\phi} \lambda(\lambda + 1)/2,$$
(56a)
$$ f(i)\mathop{ =} \limits_{(31)}m_{nn} - \mu m_{nt}c\phi(i) - \mu m_{ns}s\phi(i),$$
(56b)
$$ g(i)\mathop{ =} \limits_{(32)}m_{nt}c\phi(i) + m_{ns}s\phi(i) - \mu m_{tt}c^{2}\phi(i) - \mu m_{ss}s^{2}\phi(i) - 2\mu m_{ts}s\phi(i)c\phi(i),$$
(56c)
$$ h(i)\mathop{ =} \limits_{(33)} - m_{nt}s\phi(i) + m_{ns}c\phi(i) - \mu m_{ts}[c^{2}\phi(i) - s^{2}\phi(i)] + \mu(m_{tt} -m_{ss})s\phi(i)c\phi(i),$$
(56d)
$$ s(i)\mathop{ =}\limits_{(34\mathrm{b}),(45\mathrm{b}),(46\mathrm{b})}\bigl[s(i - 1) + g(i -1)D(i)\bigr]\bigl[1 - |\lambda| + \lambda(\lambda+ 1)/2\bigr],$$
(56e)
(56f)
(56g)
(56h)
$$ v_{t}(i)\mathop{ =}\limits_{(28\mathrm{a})}s(i)c\phi(i),$$
(56i)
$$ v_{s}(i)\mathop{ =}\limits_{(28\mathrm{c})}s(i)s\phi(i),$$
(56j)
$$ \Delta E(i)\mathop{ =} \limits_{(35\mathrm{a})}\Delta E(i - 1) +\bigl[v_{n}(i) - \mu s(i)\bigr]D(i),$$
(56k)
$$ \Delta E_{n}(i)\mathop{ =}\limits_{(35\mathrm{b})}\Delta E_{n}(i - 1) + v_{n}(i)D(i),$$
(56l)

where λ=0, ϕ(1)=0, s(1)=v t1, v n (1)=v n1, I t (1)=I s (1)=ΔE(1)=ΔE n (1)=0, and f(1)=m nn −μm nt , g(1)=m nt −μm tt , h(1)=m ns −μm ts . Now, by [31] Euler’s method is stable if each of the eigenvectors λ j (j=1,…,5) of the coefficient matrix of the linearized right-hand-sides of (34a)–(34e) about a point ϕ 0, s 0, v n0, I t0 and I s0 ‘close’ to the integration range satisfies the inequalities |1−λ j D|≤1, D=D(i)/k being the summation step. There are two nonzero eigenvector associated with (34a)–(34e), namely \(\lambda_{1,2} = 1/s_{0}(h'_{0} \pm\sqrt{h_{0}^{\prime 2} - 4h_{0}g'_{0}} )\), \(h'_{0}\hat{ =} dh/d\phi|_{\phi= \phi_{0}}\), \(g'_{0}\hat{ =}dg/d\phi|_{\phi= \phi_{0}}\), drifting apart as s 0→0, thus leading to a stiffer system. At the limit s 0=0, hence (Sect. 3.2) \(h_{0} = h(\bar{\phi} ) = 0\) \((\phi_{0} = \bar{\phi})\). Only one nonzero, infinitely large eigenvector remains, which decrees \(0 <h'_{0}/s_{0}D < 1\), and, with a finite summation step, leads to instability accompanied by relatively poor results. One obtains for D(i)=1, k=1 (i.e., 5-8 summation steps) a ∼96% agreement with the results of Sect. 5 for μ=0.6, and (only) ∼70% agreement for μ=1.1,1.6, where s 0=0 (sticking) is reached. Increasing k to 5, one has ∼98% and ∼90% agreement, respectively. Further investigation of this procedure is left for future work.

6.2 Partial integration/recursive summation (i/rs)

Equations (45a)–(45e) and (46a)–(46e) can be integrated analytically. Thus, a one-step evaluation can replace integration or recursive summation for the sticking or the sliding renewal parts of the collision, saving computation time. To show this, suppose again that the normal impulse I n2 is known. If, in the i/rs process, I n2 is reached with s>0, then sliding prevails. If, however, s vanishes before I n2 is reached, then the associated values of v n , I n , I t and I s , denoted v nS , I nS , I tS and I sS , obtained with (34a)–(34e) or (56a)–(56l) (for λ=0) are recorded, and used to identify v n2, I n2, I t2, I s2 and ΔE n2, as follows. If μ>μ c , then sticking prevails, and I n2, I t2 and I s2 can be obtained by the analytic integration of (45a)–(45e) from t S to t C and from t C to t 2 if t C >t S (sticking in compression), yielding

(57a)
(57b)
(57c)
(57d)
(57e)
(57f)

where (47) was used; or from t S to t 2 if t C <t S (sticking in restitution), yielding

(58a)
(58b)
(58c)

relations valid also for sticking in compression. If, on the other hand, μ<μ c , then sliding renewal prevails, and I n2, I t2 and I s2 can be obtained by the analytic integration of (46a)–(46e) from t S to t C and from t C to t 2 if t C >t S (sliding renewal in compression), yielding

(59a)
(59b)
(59c)
(59d)
(59e)
(59f)
(59g)
(59h)
(59i)
(59j)

where (47) was used with \(\hat{f}\mathop{\hat{ =}}\limits_{(31)}f(\mu,\hat{\phi} )\) and \(\hat{g}\mathop{\hat{=}}\limits_{(32)}g(\mu,\hat{\phi} )\); or from t S to t 2 if t C <t S (sliding renewal in restitution), yielding

(60a)
(60b)
(60c)
(60d)
(60e)

relations valid also for sliding renewal in compression.

The use of (57a)–(57f) and (60a)–(60e) can limit the integration or the recursive summation to the sliding part of the collision with the aid of the following collision hypothesis-dependent procedures, all starting with the evaluation of s, v n , I n , I t and I s by i/rs.

6.3 Collision hypotheses

6.3.1 Newton’s hypothesis

If, during i/rs, v n2 is reached with s(v n2)>0, then I n2=I n (v n =v n2), I t2=I t (v n =v n2) and I s2=I s (v n =v n2) are identified. If s(v n <v n2)=0, then v nS , I nS , I tS and I sS are recorded, and used to evaluated I n2, I t2 and I s2 either with (58a)–(58c) or with (60a)–(60c), depending on whether μ>μ c (sticking) or μ<μ c (sliding renewal), respectively.

6.3.2 Poisson’s hypothesis

If, during i/rs, v n =0 occurs before s vanishes (t C <t S ), then I nC is recorded, and I n2 calculated ((51)). The i/rs proceeds until s=0 or I n =I n2. If I n =I n2 occurs first, then sliding prevails, and I n2, I t2=I t (I n =I n2) and I s2=I s (I n =I n2) are identified during the i/rs. If s=0 occurs first, then v nS , I nS , I tS and I sS are recorded. If μ>μ c , then sticking prevails in restitution, and v n2, and then I t2 and I s2 are evaluated with (58a), and then (58b) and (58c), respectively. If μ<μ c , then sliding renewal prevails in restitution, and v n2, and then I t2 and I s2 are evaluated with (60a), and then (60b) and (60c), respectively. Next, if s=0 occurs before v n =0(t C >t S ), then v nS , I nS , I tS and I sS are recorded. If μ>μ c , then sticking prevails in compression. I nC and I n2 are obtained form (57a) and (51); and v n2, and then I t2 and I s2 are evaluated with (58a), and then (58b) and (58c), respectively. Finally, if μ<μ c , then sliding renewal prevails in compression. I nC and I n2 are obtained form (59a) and (51); and v n2, and then I t2 and I s2 are evaluated with (60a), and then (60b) and (60c), respectively.

6.3.3 Stronge’s hypothesis

Here ΔE n is obtained by i/rs (see (35b)/(56l)) as well. If v n =0 occurs before s vanishes (t C <t S ,I nC <I nS ), then ΔE nC is recorded, and ΔE n2 is evaluated ((54)). The i/rs proceeds until s=0 or ΔE n2 is reached. If ΔE n2 is reached first, then sliding prevails, and I n2=I n (ΔE n =ΔE n2), I t2=I t (ΔE n =ΔE n2) and I s2=I s (ΔE n =ΔE n2) are identified during the i/rs. If s=0 occurs first, then v nS , I nS , I tS , I sS and ΔE nS are recorded. Now, if μ>μ c , then sticking prevails in restitution, and one can write \(\Delta E_{n2} - \Delta E_{nS}\mathop{ =}\limits_{(35\mathrm{b})}\int_{ I_{nS}}^{ I_{n2}}v_{n}\,\mathrm{d}I_{n} \mathop{ =}\limits_{(45\mathrm{c)}}c_{n}\int_{v_{nS}}^{v_{n2}}v_{n}\,\mathrm{d}v_{n} = c_{n}(v_{n2}^{2} -v_{nS}^{2})/2\), which yields

$$ v_{n2} = \bigl\{ v_{nS}^{2} + 2/c_{n}\bigl[(1 - e^{2})\Delta E_{nC} - \Delta E_{nS}\bigr]\bigr\} ^{1/2},$$
(61)

in accordance with (54). The positive root was chosen to ensure v n2>0 and ∂v n2/∂e>0; and I n2, I t2 and I s2 are evaluated with (58a)–(58c). If μ<μ c , then sliding renewal prevails in restitution, v n2 is evaluated by (61) with \(1/\hat{f}\) replacing c n (\(\mathrm{d}v_{n}/\mathrm{d}I_{n}\mathop{ =}\limits_{(46\mathrm{c})}\hat{f}[\hat{ =} f(\mu,\hat{\phi} )]\) replaces \(\mathrm{d}v_{n}/\mathrm{d}I_{n}\mathop{ =}\limits_{(45\mathrm{c})}1/c_{n}\)); and I n2, I t2 and I s2 are evaluated with (60a)–(60c). Next, if s=0 occurs while v n <0 (t C >t S ,I nC >I nS ), then v nS , I nS , I tS , I sS and ΔE nS are recorded. If μ>μ c , then sticking prevails in compression, and \(\Delta E_{nC} - \Delta E_{nS}\mathop{ =} \limits_{(35\mathrm{b})}\int_{I_{nS}}^{ I_{nC}} v_{n}\,\mathrm{d}I_{n} \mathop{ =}\limits_{(45\mathrm{c})} c_{n}\int_{v_{nS}}^{v_{nC}}v_{n}\,\mathrm{d}v_{n} \mathop{ =} \limits_{(47)} -c_{n}v_{nS}^{2}/2\), or

$$ \Delta E_{nC} = \Delta E_{nS} - c_{n}v_{nS}^{2}/2.$$
(62)

One can then obtain v n2 by substitution form (62) in (61), and then evaluate I n2, I t2 and I s2 with (58a)–(58c). Finally, if μ<μ c , then sliding renewal prevails in compression. ΔE nC is identified with the aid of (62) with \(1/\hat{f}\) replacing c n . Then (61) is used to evaluate v n2 (again with \(1/\hat{f}\) replacing c n ), which is then used to uncover I n2, I t2 and I s2 with (60a)–(60c).

For the last two cases of Table 1 one obtains, integrating (34a)–(34e) in conjunction with (58a)–(58c), (60a)–(60c), (61) and (62),

the exact results (within four digits) obtained by the integration of (55).

7 Conclusions

Three sets of five differential equations governing 3D one-point collision with friction problems associated with simple, non-holonomic systems were discussed, and shown to possess unique solutions. Ways to speed up the integration were presented, whereby the integration of equations governing the sliding part of the collision was replaced with recursive summation, and the integration of equations governing the sticking and sliding renewal parts were replaced with a one-step evaluation of the impulse components. It was also demonstrated that Newton’s hypothesis can lead to energy discrepancy significantly exceeding the values recorded to-date for planar systems. Finally, it is noted that there is no clear cut proof that Poisson’s hypothesis always lead to energy-consistent solutions in 3D systems, leaving Stronge’s hypothesis the most suitable for the type of solution under consideration.