1 Introduction

According to the rheological theory, creep can be explained as an increase in the strain with the constant stress for a long time. And with the development of time, the material will finally yield to failure (Nopola and Roberts 2016; Mighani et al. 2015). In the rock engineering, the time-dependence of rock creep has attracted lots of attention and the time of rock failure caused by creep cannot be determined (Mauricio 2014; Li et al. 2014; Yang et al. 2017). So many efforts have been put to explore the rule and mechanism of creep under various boundary conditions. Among those explorations, the prediction of creep with time passing is significant and given much importance to study the prediction models for rock (Jiang et al. 2016; Xie et al. 2011). A series of accelerating bending experiments were conducted on the ECC to obtain the creep data under high stress level by Suryanto. And an empirical formula was introduced to predict creep as a function of time, which was based on the damage and plasticity theory (Suryanto 2013). Ghavidel et al. (2014) conducted lots of creep experiments on the salt rock, and the Burgers constitutive model was applied to describe the creep characteristics of the salt rock with time precisely. Zhou et al. (2018) performed many creep experiments of the salt rock, and a creep damage model was proposed to predict the creep with time, which was based on the fractional theory and energy consuming theory.

By reviewing the previous work, it is can be known that the effect of time-dependence and the viscoelastic mechanic behavior of creep are significant during the process of creep. And the remarkable feature of fractional theory is the effect of historical memory. As a consequence, the fractional theory has been applied widely in the description of viscoelastic behavior and the construction of creep constitutive model. Tang et al. (2017) proposed a new creep model with four elements based on the variable-order fractional theory. And this creep model has good agreement with the creep experimental data of salt rock. Arikoglu (2014) introduced a fractional creep model with ten parameters to describe the viscoelastic behavior, which can be identified by the genetic algorithms. Wu et al. (2015) performed lots of creep experiments of salt rock and proposed a fractional Maxwell creep model to describe the behavior of creep, which is based on the variable-order fractional calculus. Kong et al. (2017) studied the mechanical behavior of coal by the method of AE and fractional theory and illustrated the evolution of mechanism and the process of crush. So from those previous researches, the necessity of applying the fractional theory in the depiction of creep behavior is obvious.

However, except for the effect of time-dependence, it is worth paying attention to the damage effect during the total process of creep. The failure and collapse of rock caused by the effect of creep damage is regular in the rock engineering (Cao et al. 2016; Zhao et al. 2017; Shao et al. 2003). Many efforts have been devoted to studying the influence of damage in the process of creep. Kang et al. (2015) proposed a modified nonlinear creep model for depicting the creep behavior of coal under various conditions. Yang et al. (2014) made use of Hooke body, viscoelastic-plastic and viscoplastic body to build nonlinear creep damage model for investigating the time-dependent behavior of rock. Wu et al. (2018) conducted a series of creep experiments on salt rock and based on those experimental data, a nonlinear creep damage model was proposed to describe the nonlinear characteristics of creep. Therefore it can be concluded that the effect of damage is necessary to attach importance in constructing a nonlinear damage creep model of rock.

To sum up, the effect of time-dependence and damage both need to be taken into account when building a creep model. And the current research related to damage creep model focuses on the single rock sample (Zhou et al. 2011). So in this paper, in Sect. 1, based on the first application of Caputo fractional derivative with respect to the Mittag–Leffler (M–L) and power functions and the Scott Blair model, two improved time-varying viscoelastic models are introduced. In Sect. 2, using the form of Norton power law, a new damage function is introduced and then, in conjunction with the two improved viscoelastic models, the nonlinear damage creep models 1 and 2 are proposed to describe the mechanical behavior of rock materials. In Sect. 3, a series of creep experiments of sandstone are carried out to verify the applicability of the proposed models 1 and 2. Meanwhile, the creep experimental data of salt rock and mudstone in other papers are selected to verify the validity of proposed models. The proposed model 2 with a power function is better than model 1 with M–L function in the description of creep mechanical behavior of rock. Comparisons between predictions from model 2 and creep experimental data of rock are given, and the parameters of the proposed model 2 are also shown. Finally, the conclusions of this work are given.

2 Theory of fractional calculus

Definition 1

Let \(\lambda >0\), \(I\in ( a,\ b )\), \(f ( t ) \in L ( I )\) and \(g ( t ) \in C ( I )\), \(g ' ( t ) \neq 0\). The function \(g ( t )\) is assumed increasing for all \(t\in I\). And the fractional integral of \(f ( t )\) with respect to another function \(g ( t )\) is defined as follows:

$$ I_{a+}^{\lambda , g} f ( t ) = \frac{1}{\varGamma ( \lambda)} \int _{a}^{t} g ' ( \tau ) \bigl[ g ( t ) -g ( \tau ) \bigr]^{\lambda -1} f ( \tau ) d\tau $$
(1)

Remark 1

When \(g ( t ) =t\), the Riemann–Liouville fractional integral can be obtained. And if \(g ( t ) = \ln ( t )\), the Hadamard fractional operator appears. Then if \(g ( t ) = t^{{\lambda } / {\beta }}\), the Erdelyi–Kober fractional integral is obtained (Arikoglu 2014; Suryanto 2013).

Definition 2

Let \(\operatorname{Re} ( \lambda ) >0\), \(t>0\), \(\lambda >0\). The Caputo fractional integral is expressed as follows:

$$ {}_{a}^{C} D_{t}^{\lambda } f ( t ) = I_{a}^{n-\lambda } f^{ ( n )} ( t ) = \frac{1}{\varGamma ( n-\lambda )} \int _{a}^{t} \frac{f^{ ( n )} ( t )}{ ( t-\tau )^{\lambda -n+1}} d\tau $$
(2)

where \(n\geq \lambda +1\) and \(f ( t )\) can be differentiated \(n\) times.

Remark 2

It can be known that, when \(a=0\) and \(n=1\), the above function can be expressed as follows:

$$ {}_{0}^{C} D_{t}^{\lambda } f ( t )= \frac{1}{\varGamma ( 1-\lambda )} \int _{0}^{t} \frac{f ' ( t )}{ ( t-\tau )^{\lambda }} d\tau $$
(3)

where \(\varGamma \) is the Gamma function,

$$ \varGamma ( t ) = \int _{0}^{t} e^{-\tau } \tau ^{t-1} d\tau . $$
(4)

Considering the above Eqs. (1)–(2), the Caputo fractional derivative of \(f ( t )\) relative to \(g ( t )\) can be expressed as follows:

$$ {\vphantom{\biggl(}}_{a+}^{C} \biggl( \frac{d}{g ' ( t ) dt} \biggr)^{\lambda } f ( t ) = I_{a+}^{n-\lambda , g} \biggl( \frac{d}{g ' ( t ) dt} \biggr)^{n} f ( t ) $$
(5)

It must be noted that a valuable operator was introduced. And this will make researchers explicitly understand the fractional law of the denominator derivative, i.e., \(\frac{1}{g ' ( t )} \frac{d ( f )}{dt}\).

By applying the famous definition with \(f ( t ) = [ g ( t ) -g ( a+ ) ]^{\upsilon -1}\) in Eq. (5) (Almeida 2017), the new fractional equation can be achieved as follows:

$$ {\vphantom{\biggl(}}_{a+}^{C} \biggl( \frac{d}{g ' ( t ) dt} \biggr)^{\lambda } f ( t ) = \frac{\varGamma ( \nu )}{\varGamma ( \nu -\lambda )} \bigl[ g ( t ) -g ( a+ ) \bigr]^{\upsilon -\lambda -1}. $$
(6)

3 Nonlinear damage creep model based on fractional theory

3.1 The Maxwell model

The Maxwell model is commonly used in the depiction of viscoelastic mechanical behavior during the investigation of creep. And this model is composed by a spring element and dashpot. The constitutive model can be expressed as follows:

$$ \varepsilon ( t ) = \frac{\sigma _{1}}{E} + \frac{\sigma _{1}}{\eta } t $$
(7)

where \(\sigma _{1}\) is the constant stress in the creep, \(E\) is the elastic modulus, \(\eta \) is the viscosity coefficient. If \(t=0\), the constitutive model will generate a Hooke body.

But in the matter, the viscosity coefficient is not only time-dependent, but also has time-varying behavior. And the total process of creep includes elasticity, viscoelasticity, and viscoplasticity. As a consequence, the dashpot element should be modified and the Maxwell model should be improved to depict the creep behavior.

3.2 The modified viscoelastic models with time-varying viscoelasticity based on power and M–L functions

In 1947, G.W. Scott Blair proposed a classical fractional dashpot to describe the viscoelastic behavior, which was based on the fractional theory (Zhou et al. 2011). And the constitutive equation can be shown as follows:

$$ \sigma ( t ) =M \frac{d^{\lambda } \varepsilon ( t )}{d t^{\lambda }} $$
(8)

where \(\sigma ( t )\) is stress and \(\varepsilon ( t )\) is strain, \(\lambda \) is the fractional order, and \(M\) is a material constant parameter.

In a recent paper, Wu et al. derived the constitutive model of Scott Blair model by taking the Riemann–Liouville (R–L) fractional integral calculus (Wu et al. 2015). When the stress is constant, it can be shown as follows:

$$ \varepsilon ( t ) = \frac{\sigma _{1}}{M \varGamma ( 1+\lambda ) t^{-\lambda }}. $$
(9)

It is known that Eq. (9) is the creep constitutive model, which was obtained by the method of Riemann–Liouville fractional calculus. This model can exhibit the time-dependent characteristics with the different stress levels. But it cannot better describe the time-varying property under various stress levels. So in the next step, Eqs. (1) and (5) were used to deduce the modified viscoelastic model with the Caputo fractional calculus:

$$ \sigma ( t ) =M {}_{0}^{C} D^{\lambda } \varepsilon ( t ) =M \biggl( \frac{d}{g ' ( t ) dt} \biggr)^{\lambda } \varepsilon ( t ) $$
(10)

where \(\lambda \) is the fractional order and \(\lambda \in ( 0,\ 1 )\). The function \(g ( t )\) is increasing when \(t>0\).

Then letting the stress be constant \(\sigma ( t ) = \sigma _{2}\) and taking \(n=1\), according to Eqs. (1)–(6), the new creep constitutive model can be obtained as follows:

$$ \varepsilon ( t ) = \frac{\varGamma ( 1- \lambda ) \sigma _{2}}{M} \bigl[ g ( t ) -g ( 0 ) \bigr]^{\lambda +1}. $$
(11)

As we can see in Eq. (11), \(g ( t )\) is the kernel function to describe the time-varying viscoelasticity behavior. In this paper, the power function was regarded as the kernel function, i.e., \(g ( t ) = \frac{t^{\beta +1}}{\beta +1}\) (Zha et al. 2018). So Eq. (11) can be expressed as follows:

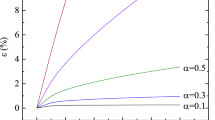
$$ \varepsilon _{p} ( t ) = \frac{\varGamma ( 1- \lambda ) \sigma _{2}}{M} \biggl( \frac{t^{\beta +1}}{\beta +1} \biggr)^{\lambda +1}. $$
(12)

It should be noticed that, when \(\lambda =0\), Eq. (12) describes the creep behavior of a solid body. When \(\lambda =1\), Eq. (12) describes the creep behavior of a fluid body.

Afterwards, the M–L function was used as another kernel function, i.e., \({g} ( {t} ) = \frac{1}{{c}} {E}_{\alpha ,\beta } ( {c} ( {t} ) )\) (Olver and Maximon 2010; Shen et al. 2019). And the normal equation of M–L function can be expressed as follows (Garra et al. 2018):

$$ E_{\alpha , \beta } \bigl( c ( t ) \bigr) = \sum_{k=0}^{\infty } \frac{ ( c ( t ) )^{k}}{\varGamma ( \alpha k+\beta )} $$
(13)

where \(E_{\alpha , \beta } ( c ( t ) )\) is a three-parameter M–L function, \(\alpha \) and \(\beta \) are its parameters, and \(c ( t )\) is a function that can be differentiated.

When \(c ( t ) =ct\) was substituted into Eq. (13), \(g ( t )\) was adjusted as \(g ( t ) = \frac{1}{c} E_{\alpha ,\ \beta } ( ct )\). Then

$$ g ( t ) = \frac{1}{c} E_{\alpha , \beta } ( ct ) = \frac{1}{c} \sum_{k=0}^{\infty } \frac{ ( ct )^{k}}{\varGamma ( \alpha k+\beta )} $$
(14)

where \(c\) is a parameter related to the stress level, \(\alpha \in (0,1]\), and \(\beta \) is a parameter, which is close to 1.

According to Eqs. (2) and (5), Eq. (14) should be derived as follows:

$$ g ' ( t ) = \frac{1}{c} \frac{d}{dt} E_{\alpha , \beta } ( ct ) = \sum_{k=0}^{\infty } \frac{ ( k+1 ) ( ct )^{k}}{\varGamma ( \alpha k+\alpha +\beta )} $$
(15)

where, when \(\beta =1\), \(g ' ( 0+ ) = {1} / {\varGamma ( \alpha +1 )}\), and it has fast convergence.

As a consequence, Eqs. (15) and (14) can be substituted into Eqs. (10) and (11). When the stress in constant, \(\sigma ( t ) = \sigma _{2}\), and \(\beta \) is close to 1, the new creep model equation can be shown as follows:

$$ \varepsilon _{M-L} ( t ) = \frac{\varGamma ( 1-\lambda ) \sigma _{2}}{M} \biggl(\frac{E_{\alpha , \beta } ( ct ) -1}{c} \biggr)^{1+\lambda }. $$
(16)

In short when the power and M–L functions were selected as kernel functions to derive the nonlinear creep models, the creep functions with different kernels are different and those functions can be expressed as follows:

$$ \left \{ \textstyle\begin{array}{l} \varepsilon _{p} ( t ) = \frac{\varGamma ( 1-\lambda ) \sigma _{2}}{M} ( \frac{t^{\beta +1}}{\beta +1} )^{\lambda +1},\\ \varepsilon _{M-L} ( t ) = \frac{\varGamma ( 1-\lambda ) \sigma _{2}}{M} ( \frac{E_{\alpha , \beta } ( ct ) -1}{c} )^{1+\lambda }. \end{array}\displaystyle \right . $$
(17)

3.3 The modified time-dependent damage model

It is known that the damage behavior is along with the total process of creep (Zhou et al. 2017). For the damage theory, Tang et al. proposed a damage factor as follows (Tang and Kaiser 1998):

$$ D=1- e^{- ( \frac{\varepsilon ( t )}{\varepsilon _{0}} )^{m}} $$
(18)

where \(D\) is the damage factor, \(\varepsilon _{0}\) is the referred strain, and \(m\) is a parameter related to the stress level.

For better describing the nonlinear damage behavior of creep, the damage factor should be applied in the construction of a constitutive model. So, considering the effect of stress and strain, based on the Norton power law, the strain rate versus stress can be expressed by Eq. (19) as follows (Zhou et al. 2018; Wu et al. 2018):

$$ \frac{d\varepsilon ( t )}{dt} = M_{1} \biggl( \frac{\sigma ( t )}{\sigma ^{*}} \biggr)^{n} $$
(19)

where \(\gamma \) is the exponential law, \(\frac{d\varepsilon ( t )}{dt}\) is the strain rate, \(M_{1}\) is the material constant, and \(\sigma ^{*}\) is the unit stress.

When the stress is constant, Eq. (19) can be derived as follows:

$$ \varepsilon ( t ) = M_{1} \biggl( \frac{\sigma ( t )}{\sigma ^{*}} \biggr)^{n} t. $$
(20)

And then, considering the influence of stress on the evolution of damage, \(\sigma ^{*}\) can be assumed as the damage factor \(D\), so the time-dependent damage model can be reconstituted as follows:

$$ \varepsilon ( t ) = M_{1} \biggl( \frac{\sigma ( t )}{1- e^{- ( \frac{\varepsilon }{\varepsilon _{0}} )^{m}}} \biggr)^{n} t. $$
(21)

3.4 The new nonlinear damage creep model

It can be seen in Fig. 3 that the total process of creep exhibits three parts: attenuation phase (primary phase), stable phase (steady phase), and accelerating phase (tertiary phase). This phenomenon is similar to the results in a paper by Cai (2006). Considering the presence of damage in the process of creep with time, the damage creep model, based on the fractional theory, can be expressed as follows:

$$ \varepsilon = \varepsilon _{a} + \varepsilon _{b} + \varepsilon _{c} $$
(22)

where \(\varepsilon \) is the total strain. Let the stress be constant, \(\sigma = \sigma _{3}\).

Because of two viscoelastic models, the new nonlinear damage creep models 1 and 2 can be expressed as follows:

$$ \left \{ \textstyle\begin{array}{l} \varepsilon _{1} ( t ) = \frac{\sigma _{3}}{E} + \frac{\varGamma ( 1-\lambda ) \sigma _{3}}{M} ( \frac{E_{\alpha , \beta } ( ct ) -1}{c} )^{1+\lambda } + M_{1} ( \frac{\sigma _{3}}{1- e^{- ( \frac{\varepsilon }{\varepsilon _{0}})^{m}}} )^{n} t,\\ \varepsilon _{2} ( t ) = \frac{\sigma _{3}}{E} + \frac{\varGamma ( 1-\lambda ) \sigma _{3}}{M} ( \frac{t^{\beta +1}}{\beta +1} )^{\lambda +1} + M_{1} ( \frac{\sigma _{3}}{1- e^{- ( \frac{\varepsilon }{\varepsilon _{0}} )^{m}}} )^{n} t. \end{array}\displaystyle \right . $$
(23)

4 Experiment preparation

4.1 Experimental device

The creep experiments were carried out by the five-connected rheological apparatus in the State Key Laboratory for GeoMechanics and Deep Underground Engineering, China University of Mining and Technology (Beijing). As shown in Fig. 1, this device embraces high precision for tests. It can exert vertical force with range from 0 to 600 kN and the axial displacement can vary from 0 to 200 mm. Furthermore, five samples can be tested simultaneously and the experimental data can be automatically collected by the computer software.

Fig. 1
figure 1

Five-connected rheological apparatus in tests

Full size image

4.2 Experimental sample

The tested sandstone samples in the experiments were obtained from the Ningtiao coal mine in Shanxi, China. As shown in Fig. 2, those samples were all drilled from the sound rock sample. The operation must obey the requirements of the “Standard for test methods of engineering rock mass”. The drilled sandstone sample is a cylinder in shape with the height of 100 mm and the diameter of 50 mm. Before the tests, all sandstone samples must be identified by the method of infrared nondestructive testing and the surface of samples must be keep without obvious cracks or damage.

Fig. 2
figure 2

Tested sandstone samples

Full size image

4.3 Experimental program

The experimental steps in this paper can be divided into the following three steps: (1) tests of uniaxial compressive strength of sandstone must be carried out before creep test, which determine the loading level of each test stage; (2) keeping the laboratory quiet and operation platform clean is necessary. And all samples must be wrapped in the plastic films and placed on the platform of the device. The sensors of force and displacement need to be stably installed in the cell room; (3) each loading level can be designed, which increases by 0.25 times the uniaxial compressive strength. And every loading stress must be maintained for more than 24 h. Then if the vertical displacement of each 4 h is lower than 0.001 mm, this step can be thought of as ended.

5 Experimental results and verification of proposed model

5.1 Tested creep data of sandstone

As shown in Fig. 3, the A-1 sandstone sample was selected to present the total process of creep. And the creep can be divided into three phases: decaying creep, stable creep, and accelerating creep. Along with time, the strain increased gradually, and the stable creep was the main stage during the total creep. When we reached a later stage, the strain rate increased rapidly and the sample experienced failure in a short time. So it can be concluded that the main reason for failure of the sample was the fast accumulation of damage inside the sample. And the appearance of accelerating creep phenomenon signifies the failure of a rock sample. It can be explained that the internal cracks of the sample develop rapidly and damage accumulates rapidly.

Fig. 3
figure 3

The curve of total creep of sandstone

Full size image

5.2 Applicability of two proposed creep models for rock materials

In this section, the applicability and rationality of the two proposed models will be verified by applying the nonlinear least squares method. In addition to the creep data of sandstone in this paper, the experimental creep data of salt rock and mudstone were also picked to verify the reasonability of the proposed creep models 1 and 2, which were taken from those classical papers. The comparisons between experimental data and proposed models 1 and 2 are introduced in what follows, and the fitting parameters of the proposed model 2 are also given in Table 1. The maximum relative errors of predicted data obtained from the two proposed models and measured data for the three materials are all less than 5% and those errors are in a reasonable range.

Table 1 Fitting parameters obtained by the proposed model 2 for each material
Full size table

Considering the creep data in the 8th stress level, where constant stress is 39.4 MPa, the proposed model was used to analyze the tested data. As shown in Fig. 4(a), the fitting curve obtained from the proposed model 2 has a good agreement with tested data. And the proposed model 1 cannot match well with the experimental data. Except for the decaying and stable phases, the nonlinear behavior of the accelerating phase can be reflected by the proposed model 2. In Fig. 4(b), the measured and predicted data by models 1 and 2 were compared based on a standard line, and the dependency of model 2 has a high accuracy with measured data. So, to some extent, in addition to taking history of the total stress into account, the proposed model 2 also can well depict and predict the damage creep data of rock materials.

Fig. 4
figure 4

(a) Experimental data of sandstone under stress level of 39.4 MPa and fitting curves from proposed models 1 and 2. (b) Comparison between measured and predicted data obtained from models

Full size image

As shown in Fig. 5, the experimental creep data of salt rock was obtained from Wang’s paper (Wang et al. 2018). The test results were applied to verify the proposed models 1 and 2 based on step by step loading style and the constant stress \(\sigma =26~\mbox{MPa}\). The stable phase in the total creep is not significant and the nonlinear behavior of accelerating creep is obvious. The fitting curve achieved from model 2 has great correlation with the test data, and the relative error between measured and predicted data is in reasonable range. From Fig. 5(b), it can be seen that compared to the measured data, the predicted data by model 2 has a higher accuracy than that from model 1.

Fig. 5
figure 5

(a) Experimental data of salt rock under stress level of 26 MPa and fitting curves from proposed models 1 and 2. (b) Comparison between measured and predicted data obtained from models

Full size image

Following the above overview of salt rock and considering mechanical properties of soft rock, the mechanical behavior of mudstone is similar to salt rock in most respects (Yuan et al. 2015). But in Fig. 6(a), concentrating on the accelerating creep, the nonlinear behavior of mudstone is more obvious than for other rock materials, which can be accounted for the effect of stress level and soft rock. Based on the proposed models 1 and 2, in Fig. 6(b), compared to the proposed models 1 and 2, it can be concluded that the measured data of mudstone and predicted data from the proposed model 2 under constant stress \(\sigma =30~\mbox{MPa}\) has a high correlation.

Fig. 6
figure 6

(a) Experimental data of mudstone under stress level of 30 MPa and fitting curves from proposed models 1 and 2. (b) Comparison between measured and predicted data obtained from models

Full size image

From above comparisons between the proposed models 1 and 2, the advantage of model 2 is more obvious than that of model 1. And the proposed model 2 has higher accuracy than model 1 in the description of the nonlinear behavior of creep. As shown in Table 1, the parameters of the proposed model 2 were determined and shown by the method of least squares. And the rationality of those parameters should be analyzed. The elastic modulus \(E\) can be taken as the initial elastic modulus of the sample, and the strain obtained from Hook’s law based on elastic modulus \(E\) is consistent with the initial sharp strain rate. The parameters \(M\) and \(M_{1}\) are both material parameters. Other parameters relate to the stress level and were determined by using properties of material and various stress levels.

6 Summary

  1. (1)

    Based on the Caputo fractional theory with respect to another function, Mittag–Leffler function with three parameters and power kernel function, two improved viscoelastic models were presented for time-varying viscoelasticity. And a modified damage body was built by using Norton power law and classical damage body. By combining the new viscoelastic elements and modified damage body, two improved nonlinear damage creep models were proposed to describe the nonlinear mechanical behavior of each rock material.

  2. (2)

    A series of creep experiments were conducted on the sandstone employing the step by step loading style. And the experimental creep data of salt rock and mudstone in other classical papers were also obtained. Based on the experimental data, the rationality and applicability of the proposed models 1 and 2 were verified. The parameters of the proposed model 2 were exhibited and analyzed.

  3. (3)

    A comparison between measured data from experiments and predicted data from the proposed models 1 and 2 has been presented. The relative error between the data was given and analyzed. It can be concluded that the proposed nonlinear damage creep model 2 with a power function can better describe and predict the creep data of rocks and soils, compared to model 1 with M–L function.