1 Introduction

The Biot theory of fluid-saturated porous media provides a description of the waves propagating in soils (Biot 1956). Several authors have extended this theory to sound-absorbing materials, such as glass wool and plastic foams, for noise control applications in engineering activities like aeronautics and the automotive industries (Allard 1993). When porous material is bounded inside a vibrating structure or is excited at strong sound levels (Kuntz and Blackstock 1987), the skeleton of the foam cannot be considered rigid anymore, and its acoustical behavior can be described by Biot’s theory where the elastic properties of the solid phase are needed.

Several techniques exist for the experimental determination of the frequency dependence of solids’ viscoelastic moduli (Corsaro and Sperling 1990; Oyadiji and Tomlimson 1985). These techniques can be classified as resonant and non-resonant (Jaouen et al. 2008) and consist generally in measuring the viscoelastic moduli on a narrow frequency range at different temperatures (Sfaoui 1995). To extend the frequency range, the frequency–temperature equivalence (known for polymeric viscoelastic materials) is used (Ferry 1961). The latter was successfully applied for porous acoustic foams (Etchessahar et al. 2005; Sfaoui 1995; Deverge et al. 2009).

Different approaches to analytically model the rheological behavior of a linear viscoelastic solid are available in the literature. The classical approach is a linear combination of springs and dashpots (Tschoegl 1989). For these systems, the stress–strain relationship in a linear regime is commonly expressed in a differential form, and the time-domain material functions derived from such models are expressed by a series of decaying exponentials with characteristic times reflecting the distribution of the relaxation time of the material.

Another way to consider the distribution of the relaxation time in the material is to consider fractional models that received increasing attention and found applications in engineering, physical and even in biomedical sciences (Nonnenmacher and Metzler 1995; Surguladze 2002). They were used to characterize the rheological behavior of linear viscoelastic systems by a number of authors (Caputo and Mainardi 1971a; Bagley and Torvik 1983; Soula et al. 1997; Pritz 1996; Sahraoui et al. 2015). Friedrich (1991) considered the four-parameter Maxwell model. Nonnenmacher and Glockle (1991) solved the stress–strain relationship of the fractional Zener model (FZM) by introducing a Fox function. Atanackovic (2002) studied a modified Zener model of a viscoelastic body by using an internal variable method. More recently Cuenca and Goransson (2012) applied the framework of an augmented Hooke’s law (Dovstam 2000) to anisotropic open-cell foams.

The use of fractional derivative models is primary motivated by their ability to describe the viscoelastic behavior of materials with a limited number of parameters. Moreover, experimental results of Bagley and Torvik (1983) suggested that the rheological properties that give rise to viscoelasticity may have a fundamental behavior based on fractional rather than integer calculus. The rate of creep (compliance) and the rate of relaxation (modulus) play the role of memory functions in the constitutive equations. Linear viscoelasticity is certainly the field of the most extensive applications of fractional calculus in view of its ability to model hereditary phenomena with long memory (Caputo and Mainardi 1971b). More recently, the modeling of memory mechanics by the fractional derivative approach was presented in other fields (Du et al. 2013).

To characterize the mechanical behavior of viscoelastic materials, experiments can be carried out either in the frequency or in the time domain. In the linear regime, the two results are connected to each other. For example, the relaxation or retardation time function is extracted from experimental curves of complex moduli versus frequency (Soula et al. 1997; Bechir and Idjeri 2011). To avoid the long and sometimes difficult series of measurements at several temperatures or in a wide frequency range in vacuum (Sfaoui 1995; Etchessahar et al. 2005; Cuenca et al. 2014), this paper is focused on the experimental determination of the relaxation function \(R(t)\) and the computation of the complex modulus in the frequency domain through a single relaxation test. The originality of the present method lies in the fitting of the relaxation function \(R(t)\) and the resolution of the stress–strain relationship in the time domain. In addition, it has been shown that the use of Mittag–Leffler function, more appropriate for the fitting process, allows for straightforward prediction of the frequency-dependence of the complex modulus.

The analysis of the fractional Zener model in the frequency domain (Pritz 1996) highlights its mathematical and physical background and its ability to describe the viscoelastic behavior of materials in a wide frequency range. Thus, the frequency dependence of the viscoelastic moduli was calculated on a very broad range of frequency and compared to the experimental value obtained by the time–temperature superposition (TTS) method from isotherm dynamic measurements in narrow frequency and temperature domains. The results have shown a very good agreement between the experimental values and the prediction of the FZM.

The manuscript is organized as follows. Section 2 is devoted to a brief overview of viscoelastic models and a theoretical presentation of the four-parameter FZM in the frequency domain as well as in the time domain. In Sect. 3, relaxation tests and dynamic modulus measurements on acoustic foams are presented. The obtained results are compared for the validation of the presented method.

2 Fractional calculus for the stress–strain relationship

We denote by \(\sigma(t)\) the stress response to the applied strain \(\varepsilon(t)\), the relaxation function \(R(t)\) and the strain rate \(\dot{\varepsilon}(t)\), and assume that the stress satisfies the relationship (Ferry 1961):

$$ \sigma(t)= \int^{t}_{-\infty} R(t-\tau)\dot{\varepsilon}(\tau)\,\mathrm{d}\tau, $$
(1)

where \(\tau\) is an integration variable.

Using the Laplace transform for a function \(f(t)\),

$$ L\bigl\{ f(t);p\bigr\} = \tilde{f}(p)= \int^{\infty}_{0} f(t)e^{-\mathit{pt}}\,\mathrm{d} t, $$
(2)

relation (1) becomes

$$ \tilde{\sigma}(p)=\tilde{R}(p)\tilde{\dot{\varepsilon}}(p). $$
(3)

2.1 Classical mechanical models

Viscoelasticity behavior was similarly modeled by ideal springs and dashpots, respectively representing the elasticity and the dissipation phenomenon during material deformation.

To introduce a single dissipation in a solid viscoelastic material, Zener (1948) added a spring in parallel to a Maxwell model (Fig. 1),

Fig. 1
figure 1

Zener model. \(E_{1}\) and \(E_{2}\) are the spring constants, \(\eta\) is the dashpot viscosity

Full size image

The stress–strain relationship for a linear viscoelastic system represented by a spring–dashpot mechanical model is commonly expressed in the differential form (Tschoegl 1989) as

$$ \sigma (t) + \sum_{i = 1}^{N} a_{i} \frac{\mathrm{d}^{i}\sigma (t)}{\mathrm{d}t^{i}} = m\varepsilon (t) + \sum_{i = 1}^{M} b_{i} \frac{\mathrm{d}^{i}\varepsilon (t)}{\mathrm{d}t^{i}}, $$
(4)

where \(t\) is the time, \(i\) is an integer, and \(m\), \(a_{i}\) and \(b_{i}\) are parameters depending on the material. The order of derivation of stress and of strain should satisfy \(M=N\) or \(M=N+1\) (Pritz 1996).

For the Zener model (Fig. 1), the well-known stress–strain relationship

$$ \sigma (t) + \frac{\eta}{E_{2}}\frac{\mathrm{d}\sigma (t)}{\mathrm{d}t} = E_{1}\varepsilon (t) + \eta \biggl(1 + \frac{E_{1}}{E_{2}}\biggr)\frac{\mathrm{d}\varepsilon (t)}{\mathrm{d}t} $$
(5)

can be written (Mainardi 2010) as

$$ \sigma ({t}) + {a}\frac{\mathrm{d}\sigma ({t})}{\mathrm{d}{t}} = {m}\varepsilon ({t}) + {b} \frac{\mathrm{d}\varepsilon ({t})}{\mathrm{d}{t}}, $$
(6)

where \(a\), \(b\), and \(m\) will be used below in the fractional models.

2.2 Fractional derivatives’ models

A model with fractional derivatives is a sort of interpolation between viscous and elastic behavior. Indeed, the spring element connects the stress with the zero-order derivative of the strain, while for a viscous element the stress is proportional to the first time derivative of the strain. Extending the stress–strain relation (Eq. (4)) which is based on integer order derivatives to fractional order of derivation, the fractional derivative models can be described by

$$ \sigma ({t}) + \sum_{{i} = 1}^{{N}} {a}_{{i}} \frac{\mathrm{d}^{\beta_{{i}}}\sigma ({t})}{\mathrm{d}{t}^{\beta_{{i}}}} = {m}\varepsilon ({t}) + \sum _{i = 1}^{{M}} {b}_{{i}} \frac{\mathrm{d}^{\alpha_{{i}}}\varepsilon ({t})}{\mathrm{d}{t}^{\alpha_{{i}}}}, $$
(7)

where \(a_{i}\), \(m\) and \(b_{i}\) are parameters depending on the material, and \(0 < \alpha_{i} < 1\), \(0 < \beta_{i} < 1\).

The \(\alpha\)th order fractional derivative of the function \(\varepsilon (t)\) is defined with the gamma function as

$$ \frac{\mathrm{d}^{\alpha}}{\mathrm{d}{t}^{\alpha}} \varepsilon = \frac{1}{\varGamma (1 - \alpha )}\frac{\mathrm{d}}{\mathrm{d}{t}} \int_{0}^{{t}} \frac{\varepsilon (\tau )}{({t} - \tau )^{\alpha}} \,\mathrm{d} \tau, $$
(8)

where \(\tau\) is an integration variable (Ross 1975).

The complex modulus for a fractional derivative model can be obtained by using the Fourier transformation. We denote by \(\hat{f}(\omega )\) the Fourier transform of the function \(f(t)\). In the frequency domain, relation (7) reads:

$$ \Biggl[1 + \sum_{i = 1}^{N} a_{i} (j\omega )^{\beta_{i}}\Biggr]\hat{\sigma} (\omega ) = \Biggl[m + \sum _{i = 1}^{M} b_{i} (j\omega )^{\alpha_{i}} \Biggr]\hat{\varepsilon} (\omega ). $$
(9)

So, the complex modulus \(G^{*}(\omega )\) of the fractional derivative models is in the form

$$ G^{*}(\omega ) = \frac{m + \sum_{i = 1}^{M} b_{i} (j\omega )^{\alpha_{i}}}{1 + \sum_{i = 1}^{N} a_{i} (j\omega )^{\beta_{i}}}. $$
(10)

2.3 FZM in the frequency and time domains

For the special case of FZM, the stress–strain relation is written as

$$ \biggl[1+ a\frac{\mathrm{d}^{a}}{\mathrm{d}t^{a}}\biggr]\sigma(t)=\biggl[m+ b \frac{\mathrm{d}^{a}}{\mathrm{d}t^{a}}\biggr]\varepsilon (t). $$
(11)

In the frequency domain, we have

$$ \bigl[1+a(j\omega)^{\alpha}\bigr] \hat{\sigma}(\omega)= \bigl[m+ b(j\omega)^{\alpha}\bigr]\hat{\varepsilon}(\omega). $$
(12)

The complex modulus \(G^{*}(\omega ) = \hat{\sigma} (\omega )/\hat{\varepsilon} (\omega )\) is in the form

$$ G^{*}=\frac{m+b(j\omega)^{\alpha}}{1+a(j\omega)^{\alpha}}=G'+jG'', $$
(13)

where the storage modulus \(G'(\omega)\) and loss modulus \(G''(\omega)\) are respectively

$$ G'(\omega) =\frac{m+(b+am) \omega^{\alpha}\cos (\pi\alpha/2)+ab\omega^{2\alpha}}{1+2a\omega^{\alpha}\cos (\pi\alpha/2)+a^{2}\omega^{2\alpha}} $$
(14)

and

$$ G''(\omega) =\frac{(b-am) \omega^{\alpha}\sin (\pi\alpha/2)}{1+2a\omega^{\alpha}\cos (\pi\alpha/2)+a^{2}\omega^{2\alpha}}. $$
(15)

From relation (13), the parameter \(m\) corresponds to the value of the storage modulus at zero frequency; it is also called the static modulus of elasticity. However, we notice that the dimensions of the parameters \(a\) and \(b\) depend on the value of \(\alpha\): the dimension of \(a\) is \(s^{\alpha}\), and the ratio \(b/a\) describes the limit of the storage modulus at high frequency.

In the time domain, the Laplace transform is applied for the determination of the relaxation function. By using the sign ↔ to denote the transformation between the function \(f(t)\) and its Laplace transform \(\tilde{f}(p)\), a Laplace transform pair reads

$$ \tilde{f}(p) \leftrightarrow f(t). $$
(16)

The Laplace transform of Eq. (11) leads to

$$\begin{aligned} \tilde{R}(p) &= \frac{\tilde{\sigma}(p)}{\tilde{\dot{\varepsilon}}(p)} = \frac{1}{p} \frac{m+bp^{\alpha}}{1+ap^{\alpha}} \\ &= \frac{m}{p}+\biggl(\frac{b}{a} -m\biggr)\frac{p^{\alpha-1}}{p^{\alpha}+1/a}, \end{aligned}$$
(17)

which yields

$$ R(t)= m+\biggl(\frac{b}{a}-m\biggr) E_{\alpha}\bigl[-t^{\alpha}/a\bigr], $$
(18)

where \(E_{\alpha}\) is the classical Mittag–Leffler function (Kilbas et al. 2006) defined as

$$ E_{\alpha}\bigl[-t^{\alpha}/a\bigr]= \frac{1}{\pi} \int^{\infty}_{0}\mathrm{e}^{-\tau t} \frac{\tau^{\alpha-1}\sin(\alpha\pi)/a}{1/a^{2}+2\tau^{\alpha}\cos(\alpha\pi)/a+\tau^{2\alpha} }\,\mathrm{d} \tau $$
(19)

and corresponding to its Laplace transform (Mainardi and Gorenflo 2007) \(\frac{p^{\alpha-1}}{p^{\alpha}+1/a}\) (Eq. (17)).

For \(\alpha\) close to 1, \(E_{\alpha}(-t^{\alpha}/a)\approx \mathrm{e}^{t/\tau_{\sigma}} \) with the relaxation time \(\tau_{\alpha}=a^{1/\alpha}\). But for \(\alpha\) close to 0, the Mittag–Leffler function (Fig. 2) exhibit a high slope at small values of \(t\) followed by a slight decrease at large times. This graphic representation (Podlubny 2006) highlights the effectiveness of Mittag–Leffler function in the solution of the fractional Zener model (Eq. (19)) at various values of \(\alpha\) between 0 and 1.

Fig. 2
figure 2

Classical Mittag–Leffler function \(E_{\alpha} ( - t^{\alpha} )\) for some values of \(\alpha\)

Full size image

The relaxation function, Eq. (18), is a generalization of relaxation behavior for any \(\alpha\); for \(\alpha=1\) we obtain the function corresponding to the standard linear solid model (Tschoegl 1989).

3 Experiments and results

Polyurethane (PU) foam, kindly provided by Tramico Company, is considered for relaxation tests in the time domain and for dynamic measurements in the frequency domain. The foam samples were cylinders of 20 mm radius, and 40 mm or 20 mm length for the relaxation experiments or dynamic measurements, respectively.

3.1 Relaxation tests

In relaxation tests, a constant strain (\(\varepsilon_{0} =5~\%\)) was applied to the foam sample which is in the linear regime.

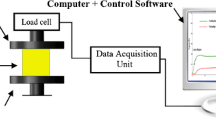
Compression tests were performed at room temperature (20 °C) by means of a tensile machine from Zwick/Roell (Z010) equipped with a 500 N load cell. The sample was compressed between two parallel plates covered with sand paper to avoid any slippage at the interface of the plates. The crosshead speed, fixed at 100 cm min−1, corresponds to the strain rate \(\dot{\varepsilon} = 2.5~\mbox{mm}^{-1}\). At this speed, the loading time necessary to reach a constant speed is about 0.12 s and the imposed strain can be written as

$$ \varepsilon ({t}) = \varepsilon_{0}{H}({t}) $$
(20)

for relatively long relaxation durations (more than 10 min), where \(H\) is the Heaviside function.

In this case, the stress is related to the relaxation function as

$$ \sigma ({t}) = \varepsilon_{0}{R}({t}). $$
(21)

3.2 Extraction of FZM parameters

The inverse estimation of fractional derivatives’ parameters (\(a\), \(b\), \(m\) and \(\alpha\)) consists in numerically fitting the model (Eq. (18)) to experimental stress relaxation.

The vector

$$ \mathbf{x} = ({m},{a},{b},\alpha )^{{T}} $$
(22)

defines a 4-dimensional space in which the model evolves. The properties of a given material are then defined as the set \(\mathbf{x}_{0}\) that minimizes the distance in such space between the model and the experiment.

Assuming that the stress function is extracted from the measurement and replicated using the model with a certain set of parameters, \(\mathbf{x}\), the objective function is defined as

$$ {f}(\mathbf{x}) = \sum_{{n} = 1}^{{N}} \biggl\vert \frac{\sigma ({t}_{{n}},\mathbf{x}) - \sigma^{\exp} ({t}_{{n}})}{\sigma^{\exp} ({t}_{{n}})} \biggr\vert ^{2}, $$
(23)

where \(N\) is the number of time points of stress, and \(\sigma^{\exp} \) and \(\sigma\) respectively denote the experimental and simulated stress. The optimization problem is implemented using the globally convergent method of moving asymptotes (Cuenca and Goransson 2012; Svanberg 2002).

The experimental stress \(\sigma (t)\) is compared to the fitted FZM curve in Fig. 3. By using the estimated parameters (\(a= 0.001~\mbox{SI}\), \(b=29.7~\mbox{kSI}\), \(m=36~\mbox{kPa}\), \(\alpha = 0.2\)), the complex modulus can be predicted over a wide frequency range (Fig. 5). We have already mentioned that the units of the fractional parameters \(a\) and \(b\) depend on the value of \(\alpha\), for this reason the SI notation (International system of units) is used. Furthermore, the chosen relaxation duration was determined by some tests in the time range (1 min–8 h); the relaxation function obtained in just 10 min and the FZM are able to predict the measured stress at a long time as shown by Fig. 3. The relative error of the fitted curve is less than 2 %.

Fig. 3
figure 3

Stress relaxation (experimental and FZM fitted curves). The insert is a zoom of the first 10 minutes

Full size image

In order to validate the time domain method, the predicted complex modulus is compared to the experimental results obtained in the frequency domain in the next section.

3.3 Dynamic moduli measurements

The purpose of this experiment was to determine the complex shear modulus of the foam over a wide frequency range. To do so, the sample was tested in torsion by means of a standard torsional rheometer ARES G2 from TA Instruments equipped with a parallel plate/plate geometry with 40 mm of diameter. The frequency sweep was fixed between 0.16 and 16 Hz; and the strain at 0.1 % is in the linear response of the foam. The temperatures of the experiment were fixed at 20, 10, 0, −10, and −20 °C. The TTS is used to compute the complex shear modulus at a reference temperature (20 °C) over a broader frequency range (Williams et al. 1955; Sfaoui 1995; Etchessahar et al. 2005; Deverge et al. 2009). This method consists in translating horizontally and vertically the curves of \(G'\) and \(G''\) versus frequency obtained on a reduced frequency range at different temperatures, in order to superimpose them at a given temperature. The storage modulus of the foam is presented in Fig. 4 and is discussed in the next section.

Fig. 4
figure 4

Storage modulus: (a) isotherm curves, (b) master curve at 20 °C as a reference temperature. The shift factors are 1, 6, 60, 1800, 250 000 for 20, 10, 0, −10 and −20 °C, respectively

Full size image

3.4 Validation of the time approach method

As shown in Sect. 3.2, the fractional parameters \(a\), \(b\), \(m\) and \(\alpha\) were extracted from the experimental relaxation. These parameters were used for the prediction of the storage and loss moduli (Eqs. (13) and (14)) at every frequency. By using the TTS principle, the complex shear modulus is experimentally determined in a wide frequency range.

By using the assumption that the Poisson ratio of PU foam is real and frequency independent (Etchessahar et al. 2005; Sahraoui et al. 2001), the viscoelastic constants obtained in compression and in torsion have the same frequency dependence. Therefore, the data obtained from static compression and dynamic torsion tests are adjusted only vertically and used below to highlight the performance of the procedure.

A comparison between experimental measurements and the prediction of the viscoelastic moduli over a wide range of frequency using FZM is presented in Fig. 5. For the studied foam, the agreement is very good both for \(G'\) and \(G''\) even though the prediction of the storage modulus is better than that for the loss.

Fig. 5
figure 5

A comparison of storage and loss moduli

Full size image

4 Conclusions

In this work, by adjusting the FZM on the stress relaxation experiments of acoustic foams, we were able to extract the four parameters of the model. It has been shown that the relaxation function obtained in just 10 min in a single static compression test was sufficient to calculate the complex modulus at any frequency. This model was analyzed and its mathematical and physical backgrounds have been outlined. To verify the applicability and the accuracy of the present procedure, the complex modulus was obtained on a wide frequency range using the TTS principle. A comparison between the experimental results and the predicted values of the FZM has shown good agreement in a frequency range between 0.1 and \(10^{6}~\mbox{Hz}\). The proposed method may be considered as an improved alternative to characterize the frequency dependence of polymeric foams especially at high frequencies and could be generalized for other materials.