Theoretical and practical differences between creep and relaxation Poisson’s ratios in linear viscoelasticity

Abstract

Poisson’s ratio is a well-defined parameter in elasticity. For time-dependent materials, multiple definitions based on the ratios between lateral and axial deformations are available. Here, we focus ourselves on the two most widely used definitions in the time domain, which define time-dependent functions that we call relaxation Poisson’s ratio and creep Poisson’s ratio. Those two ratios are theoretically different, but are linked in an exact manner through an equation we derive. We show that those two functions are equal at both initial and large times and that their derivatives with respect to time also are. Based on simple rheological models for both the deviatoric and volumetric creep behaviors, we perform a parametric study and show that the difference between those two time-dependent Poisson’s ratios can be significant. However, based on creep data available in the literature, we show that, for cementitious materials, this difference can be negligible or not, depending on the case.

1 Introduction

For an isotropic body, the elastic Poisson’s ratio $\nu_{0}$ is defined unambiguously as the ratio of the lateral contraction $-\varepsilon_{l}$ to the elongation $\varepsilon_{a}$ in the infinitesimal deformation under uniaxial load, that is,

$$ \nu_{0}=-\frac{\varepsilon_{l}}{\varepsilon_{a}}. $$

(1)

By extension, for linear viscoelastic materials, we can aim at defining a time-dependent Poisson’s ratio (Van der Varst and Kortsmit 1992; Hilton 2001, 2011; Tschoegl et al. 2002; Lakes and Wineman 2006). However, such an aim can generate some ambiguity since Hilton (2001) enumerated five different ways of defining a time-dependent Poisson’s ratio. Here, by using a direct extension of Eq. (1) to a uniaxial creep experiment and to a uniaxial relaxation experiment, we define the creep Poisson’s ratio $\nu_{c}$ and the relaxation Poisson’s ratio $\nu_{r}$:

$$\begin{aligned} \nu_{c}(t) & = -\frac{\varepsilon_{l}(t)}{\varepsilon_{a}(t)} \quad\text{during a uniaxial creep experiment for which }\sigma_{a}(t) = \sigma_{a0}, \end{aligned}$$

(2a)

$$\begin{aligned} \nu_{r}(t) & = -\frac{\varepsilon_{l}(t)}{\varepsilon_{a0}} \quad\text{during a uniaxial relaxation experiment for which } \varepsilon_{a}(t) = \varepsilon_{a0}, \end{aligned}$$

(2b)

where $\varepsilon_{a}(t)$ and $\varepsilon_{l}(t)$ are the time-dependent axial and lateral strains, respectively, $\sigma _{a}(t)$ is the axial load, and $\sigma_{a0}$ and $\varepsilon _{a0}$ are constants. Note that these definitions are specific to the case of creep and relaxation with an instantaneous loading: indeed, even in the case of uniaxial compression only, various load histories lead to various evolutions of the ratio of the lateral dilation to the axial contraction over time.

With respect to the terminology used by Hilton (2001), our creep Poisson’s ratio $\nu_{c}$ corresponds to his type I definition restricted to a uniaxial creep experiment, whereas our relaxation Poisson’s ratio corresponds to his type II definition. These two Poisson’s ratios are not equal (Tschoegl et al. 2002; Lakes and Wineman 2006). However, little is known on how significant the difference between them is. Quantifying such a difference is the main goal of this work.

Better understanding how Poisson’s ratios evolve with time is relevant for a variety of applications, among which we find the estimation of service life of the containment of French nuclear power plants. Indeed, the containment of French nuclear power plants is made of a biaxially prestressed concrete and designed to withstand an internal pressure of 0.5 MPa in case of an accident. In order to avoid tensile stresses in concrete, the applied prestress corresponds to compressive stresses in concrete of around 8.5 MPa and 12 MPa along vertical and orthoradial axes, respectively (Torrenti et al. 2014). To limit cracking of concrete, tensile stresses should remain below the tensile strength of concrete in case of accident. That is why the evolution of prestressing forces with respect to time is critical for the operation of nuclear power plants and for the optimization of their service life. Consequently, a good prediction of the evolution of delayed strains of the containment under a biaxial stress condition is needed.

In this article, starting from the basic equations of linear viscoelasticity, we derive a relationship between the two time-dependent Poisson’s ratios just introduced. We specifically consider how their values and their derivatives can be compared at short and long times. Then, a parametric study of the difference between them over all times is performed, based on common rheological models. In the last section, we consider the practical case of cementitious materials (on which creep data in both axial and lateral directions are available from the literature): for this specific class of materials, the difference between the two time-dependent Poisson’s ratios is scrutinized.

2 Theoretical derivations

This section is devoted to derive analytical relations pertaining to the creep Poisson’s ratio $\nu_{c}$ and the relaxation Poisson’s ratio $\nu_{r}$. First, from the basic equations of viscoelasticity we derive expressions of the two Poisson’s ratios. Then, we derive relation between them and compare their initial and long-time asymptotic values and derivatives with respect to time.

2.1 Viscoelastic constitutive relations

We restrict ourselves to an isotropic nonaging linear viscoelastic solid submitted to infinitesimal strains in isothermal conditions. For such a case, the time-dependent state equations that link the stress tensor $\underline{\underline{\sigma}}$ (decomposed into the volumetric stress $\sigma_{v}= \operatorname{tr}(\underline{\underline{\sigma}})/3$ and the deviatoric stress tensor $\underline{\underline{s}}$ such that $\underline{\underline{\sigma}} = \sigma_{v} \underline{\underline{1}} + \underline{\underline{s}}$, where $\operatorname{tr}$ is the trace operator and $\underline{\underline{1}}$ is the unit tensor) to the strain tensor $\underline{\underline{\varepsilon}}$ (decomposed into the volumetric strain $\varepsilon_{v} = \operatorname{tr}(\underline {\underline{\varepsilon}})$ and the deviatoric strain tensor $\underline{\underline{e}}$ such that $\underline{\underline{\varepsilon }} = (\varepsilon_{v}/3) \underline{\underline{1}} + \underline{\underline {e}}$) are (Christensen 1982):

$$\begin{aligned} \sigma_{v}(t)&=K(t)\otimes\dot{\varepsilon}_{v}(t), \end{aligned}$$

(3a)

$$\begin{aligned} s_{ij}(t)&=2G(t)\otimes\dot{e}_{ij}(t), \end{aligned}$$

(3b)

where ⊗ denotes the convolution product defined as $f\otimes g = \int_{-\infty}^{t}f(t-\tau)g(\tau)\,d\tau$, and $\dot{f}$ is for derivatives with respect to time, $\dot{f}=df(t)/dt$. Those state equations can equivalently be written as (Christensen 1982)

$$\begin{aligned} \varepsilon_{v}(t)&=J_{K}(t)\otimes\dot{ \sigma}_{v}(t), \end{aligned}$$

(4a)

$$\begin{aligned} e_{ij}(t)&=\frac{1}{2}J_{G}(t)\otimes \dot{s}_{ij}(t), \end{aligned}$$

(4b)

where $J_{K}(t)$ and $J_{G}(t)$ are called the bulk creep compliance and the shear creep compliance, respectively. Creep compliances are linked to relaxation moduli through (Christensen 1982)

$$\begin{aligned} s\widehat{J_{K}}&=\frac{1}{s\widehat{K}}, \end{aligned}$$

(5a)

$$\begin{aligned} s\widehat{J_{G}}&=\frac{1}{s\widehat{G}}, \end{aligned}$$

(5b)

where $s$ is the Laplace variable, and $\widehat{f}(s)$ is the Laplace transform of a function $f(t)$.

Starting from the state equations (4a)–(4b), in uniaxial testing, we can show that the axial stress history $\sigma_{a}(t)$ and the axial strain history $\varepsilon_{a}(t)$ are related by (Christensen 1982)

$$\begin{aligned} \sigma_{a}(t)&=E(t)\otimes\dot{\varepsilon}_{a}(t), \end{aligned}$$

(6a)

$$\begin{aligned} \varepsilon_{a}(t)&=J_{E}(t)\otimes\dot{ \sigma}_{a}(t), \end{aligned}$$

(6b)

where $E(t)$ and $J_{E}(t)$ are called the uniaxial relaxation modulus and the uniaxial creep compliance, respectively. For a uniaxial relaxation or creep test, by solving Eqs. (3a), (3b) and (4a), (4b) in the Laplace domain, we obtain an analytic expression for the uniaxial relaxation modulus $E$ and the uniaxial creep compliance $J_{E}$ in the Laplace domain, respectively, the latter being transformed back directly:

$$\begin{aligned} \widehat{E}(s) & =\frac{9\widehat{K}(s)\widehat{G}(s)}{3\widehat {K}(s)+\widehat{G}(s)}, \end{aligned}$$

(7a)

$$\begin{aligned} J_{E}(t) & =\frac{1}{9}J_{K}(t)+ \frac{1}{3}J_{G}(t). \end{aligned}$$

(7b)

In the uniaxial relaxation test, for which $\varepsilon_{a}(t)=\varepsilon _{a0}$, by substituting this condition into Eqs. (3a), (3b) and solving it in Laplace domain, the relaxation Poisson’s ratio is found:

$$ \widehat{\nu_{r}}(s) =\frac{3\widehat{K}(s)-2\widehat{G}(s)}{2s(3\widehat{K}(s)+\widehat{G}(s))}. $$

(8)

For the uniaxial creep test, for which $\sigma_{a}(t)=\sigma_{a0}$, Eqs. (4a), (4b) are solved directly in the time domain, which yields an analytic expression of the creep Poisson’s ratio $\nu_{c}$ in time:

$$ \nu_{c}(t)=\frac{3J_{G}(t)-2J_{K}(t)}{2(3J_{G}(t)+J_{K}(t))}. $$

(9)

In the creep test, the ratio between the Laplace transform $\widehat{\varepsilon_{l}}$ of the lateral strain to the Laplace transform $\widehat{\varepsilon_{a}}$ of the axial strain is evaluated and found to be equal to $-s\widehat{\nu_{r}}$. By transforming this equality back to the time domain we have

$$ \widehat{\varepsilon_{l}}=-s\widehat{\nu_{r}}\widehat{ \varepsilon_{a}} \Rightarrow\varepsilon_{l}(t)=- \nu_{r}(t)\otimes\dot{\varepsilon}_{a}(t). $$

(10)

Comparing Eq. (10) with Eq. (2a) and combining them with Eq. (6b), we get the relation between the two Poisson’s ratios:

$$ \nu_{c}(t)=\frac{\nu_{r}(t)\otimes\dot{J}_{E}(t)}{J_{E}(t)}. $$

(11)

Van der Varst and Kortsmit (1992) also found this relation by writing the equilibrium of a cylindrical bar subjected to a uniaxial load. Salençon (1983) also demonstrated this relation, but in the Laplace domain. Note that this relationship is only valid to relate the creep and relaxation Poisson’s ratios as defined by Eqs. (2a) and (2b), respectively. In contrast, if the loading is not applied instantaneously, then how the ratio between lateral and axial strains evolves over time during the creep phase is related in a different manner to how this same ratio evolves over time during the relaxation phase.

2.2 Comparison of the relaxation Poisson’s ratio and the creep Poisson’s ratio

Equations (8) and (9) indicate that both the relaxation Poisson’s ratio $\nu_{r}$ and the creep Poisson’s ratio $\nu _{c}$ can be expressed as functions of the relaxation moduli, even though they are defined with reference to a specific loading path. In order to evaluate the difference between the relaxation Poisson’s ratio $\nu_{r}$ and the creep Poisson’s ratio $\nu_{c}$, their initial and long-time asymptotic values are compared first.

At time $t=0$, the relaxation modulus and creep compliance are equal to their elastic values, that is, $K(t=0)=K_{0}$, $G(t=0)=G_{0}$, $J_{K}(t=0)=J_{K0}=K_{0}^{-1}$, $J_{G}(t= 0)= J_{G0}= G_{0}^{-1}$. By using the initial value theorem (Auliac et al. 2000), the value of the relaxation Poisson’s ratio $\nu_{r}$ at time 0 is evaluated:

$$ \nu_{r} (0 )=\lim_{s \to+\infty} s\widehat{ \nu_{r}}(s) =\lim_{s \to+\infty} \frac{3\widehat{K}-2\widehat{G}}{6\widehat{K}+2\widehat {G}} \frac{s}{s}=\frac{3K_{0}-2G_{0}}{6K_{0}+2G_{0}}=\nu_{0}. $$

(12)

What concerns the creep Poisson’s ratio $\nu_{c}$, evaluating Eq. (9) at time $t=0$ is straightforward:

$$ \nu_{c} (0 )=\frac{3J_{G0}-2J_{K0}}{6J_{G0}+2J_{K0}}=\frac{3K_{0}-2G_{0}}{6K_{0}+2G_{0}}=\nu_{0}. $$

(13)

Therefore, the value of both the relaxation Poisson’s ratio $\nu_{r}$ and the creep Poisson’s ratio $\nu_{c}$ at time 0 is equal to the elastic Poisson’s ratio $\nu_{0}$.

At large times (i.e., as $t \rightarrow+\infty$), the bulk and shear relaxation moduli tend toward $K_{\infty}$ and $G_{\infty}$, respectively. Hence, an asymptotic Poisson’s ratio $\nu_{\infty}$ can be defined:

$$ \nu_{\infty}=\dfrac{3K_{\infty}-2G_{\infty}}{6K_{\infty}+2G_{\infty}}. $$

(14)

The asymptotic value of the relaxation Poisson’s ratio is evaluated by using the final value theorem (Auliac et al. 2000):

$$ \lim_{t \to+ \infty} \nu_{r}(t) =\lim_{s \to0} s\widehat{\nu_{r}}(s) =\lim_{s \to0} \dfrac{3\widehat{K}-2\widehat{G}}{6\widehat{K}+2\widehat{G}} \dfrac{s}{s}=\dfrac{3K_{\infty}-2G_{\infty}}{6K_{\infty}+2G_{\infty }}=\nu_{\infty}, $$

(15)

whereas since $\lim_{t \to+ \infty}J_{K}(t) = 1/K_{\infty}$ and $\lim_{t \to+ \infty}J_{G}(t) = 1/G_{\infty}$,

$$ \lim_{t \to+\infty} \nu_{c}(t) =\dfrac{3/G_{\infty}-2/K_{\infty }}{6/G_{\infty}+2/K_{\infty}}= \dfrac{3K_{\infty}-2G_{\infty}}{6K_{\infty }+2G_{\infty}}=\nu_{\infty}. $$

(16)

Therefore, both relaxation Poisson’s ratio $\nu_{r}$ and creep Poisson’s ratio $\nu_{c}$ tend toward the same value $\nu_{\infty}$ at large times.

The relation between their derivatives with respect to time will be derived from Eq. (11). The uniaxial creep compliance $J_{E} (t )$ is a continuous function for times $t \geq0$ but exhibits a discontinuity at $t=0$: $J_{E}(t<0) = 0$, whereas $J_{E}(t=0)=J_{E0} >0$. The existence of this discontinuity implies that the convolution integral on the right-hand side of Eq. (11) is a hereditary integral. By multiplying both sides of Eq. (11) by $J_{E}$ and simplifying the hereditary integral, we get

$$ \nu_{c} (t )J_{E} (t )=\nu_{r} (t )J_{E} (0 )+\int_{0^{+}}^{t}{ \nu_{r} (t-\tau )\frac{ dJ_{E} (\tau )}{d\tau}\, d\tau}. $$

(17)

Differentiating this equation with respect to time yields

$$ \dot{\nu_{c}} (t )J_{E} (t )+\nu_{c} (t )\dot {J_{E}} (t )=\dot{\nu_{r}} (t )J_{E} (0 )+\nu _{r} (t )\dot{J_{E}} (t ), $$

(18)

which, after evaluation at $t=0$, yields $\dot{\nu_{r}} (0 )=\dot{\nu_{c}} (0 )$.

The relaxation Poisson’s ratio $\nu_{r}$ and creep Poisson’s ratio $\nu _{c}$ are known to be bounded. In addition, in most cases, considering that, after a certain time, those two Poisson’s ratios are monotonic functions of time is a reasonable assumption. Under such an assumption, we can therefore conclude that their derivatives with respect to time must tend to zero, that is, $\lim_{t \to\infty}\dot{\nu_{r}} (t )=\lim_{t \to\infty}\dot{\nu_{c}} (t )=0$.

In conclusion, the initial values of the relaxation Poisson’s ratio $\nu _{r}$ and of the creep Poisson’s ratio $\nu_{c}$ are equal to each other. So are their long-time asymptotic value, their initial derivative with respect to time, and the long-time asymptotic values of their derivatives with respect to time. However, in spite of these similarities, over all times, those two Poisson’s ratios differ from each other. Quantifying how different those quantities are is the main objective of the next section.

3 Difference between relaxation and creep Poisson’s ratios in rheological models

This section is devoted to assessing how different the relaxation Poisson’s ratio $\nu_{r}$ and the creep Poisson’s ratio $\nu_{c}$ are over all times. To do so, we perform a parametric study in which the shear and volumetric behaviors are modeled with the most common rheological units.

Here, we consider virtual materials for which the volumetric behavior and the deviatoric behavior are modeled with either the Maxwell unit (to model a creep behavior that diverges with time) or the Kelvin–Voigt unit (to model a creep behavior with an asymptotic value). All four combinations of those units are considered (see Fig. 1). For simplicity, when the Kelvin–Voigt unit is considered, the stiffness of the two springs it contains are set equal to each other.

Fig. 1

Rheological models used in the parametric study: (a) Both volumetric and deviatoric behaviors governed by the Maxwell unit; (b) Volumetric behavior and deviatoric behavior governed by the Maxwell unit and the Kelvin–Voigt unit, respectively; (c) Volumetric behavior and deviatoric behavior governed by the Kelvin–Voigt unit and the Maxwell unit, respectively; (d) Both volumetric and deviatoric behaviors governed by the Kelvin–Voigt unit

If the bulk behavior is modeled with the Maxwell unit, then the bulk relaxation modulus $\widehat{K}(s)$ in the Laplace domain and the bulk creep compliance $J_{K}(t)$ in the time domain read

$$\begin{aligned} \widehat{K} (s )&= \biggl(\frac{s}{K_{0}}+\frac{1}{\eta_{K}} \biggr)^{-1}, \end{aligned}$$

(19a)

$$\begin{aligned} J_{K} (t )&=\frac{t}{\eta_{K}}+\frac{1}{K_{0}}. \end{aligned}$$

(19b)

In contrast, if the bulk behavior is modeled with the Kelvin–Voigt unit, the bulk relaxation modulus $\widehat{K}(s)$ in the Laplace domain and the bulk creep compliance $J_{K}(t)$ in the time domain read

$$\begin{aligned} \widehat{K} (s )&= \biggl(\frac{s}{K_{0}}+\frac{s}{K_{0}+s\eta _{K}} \biggr)^{-1}, \end{aligned}$$

(20a)

$$\begin{aligned} J_{K} (t )&=\frac{1}{K_{0}} \biggl(2-\exp \biggl(- \frac{K_{0}}{\eta _{K}}t \biggr) \biggr). \end{aligned}$$

(20b)

Equivalent equations can be derived for the shear behavior.

For every combination of rheological units considered (see Fig. 1), by applying the inverse Laplace transform to Eq. (8), in which the corresponding time-dependent moduli have been injected, we obtain the relaxation Poisson’s ratio $\nu_{r}$ over all times. The creep Poisson’s ratio $\nu_{c}$ is obtained by injecting the corresponding creep compliances into Eq. (9). Details of all calculations are provided in Appendix A.

The relaxation Poisson’s ratio $\nu_{r}$ and the creep Poisson’s ratio $\nu_{c}$ depend on the stiffnesses $K_{0}$ and $G_{0}$ of the springs and on the viscosities $\eta_{K}$ and $\eta_{G}$ of the dashpots. In fact, dimensional analysis shows that those two Poisson’s ratios $\nu_{r}$ and $\nu_{c}$ can be expressed with the following dimensionless parameters:

$$\begin{aligned} \nu_{c}(t, K_{0}, G_{0}, \eta_{K}, \eta_{G}) = & \nu_{c} (\tilde{t}, \nu_{0}, \eta _{K}/\eta_{G}), \end{aligned}$$

(21)

$$\begin{aligned} \nu_{r}(t, K_{0}, G_{0}, \eta_{K}, \eta_{G}) = & \nu_{r} (\tilde{t}, \nu_{0}, \eta _{K}/\eta_{G}), \end{aligned}$$

(22)

where $\tilde{t} = t G_{0} / \eta_{G}$ is a dimensionless time. This dimensional analysis defines the rationale for the parametric study: For the four combinations of rheological units considered, the difference between the two Poisson’s ratios is studied for various values of the elastic initial Poisson’s ratio $\nu_{0}\in[-1,0.5]$ and for a wide range of values of the ratio $\eta_{K}/\eta_{G}$ (i.e., $\eta _{K}/\eta_{G} \in[0.01, 100]$).

Figure 2 displays the two Poisson’s ratios $\nu_{r}$ and $\nu_{c}$ for the specific case of a material whose both the volumetric and deviatoric behaviors are governed by the Maxwell unit and for which $\nu_{0}=0.1$ and $\eta_{K}/\eta_{G}=10$. We observe that, in this case, the relaxation Poisson’s ratio $\nu_{r}$ increases more rapidly and reaches its asymptotic value earlier than the creep Poisson’s ratio $\nu_{c}$.

Fig. 2

Relaxation Poisson’s ratio $\nu_{r}(t)$ and creep Poisson’s ratio $\nu_{c}(t)$ for a material whose volumetric and deviatoric behaviors are governed by the Maxwell unit and for which $\nu_{0}=0.1$ and $\eta_{K}/\eta_{G}=10$

In the following parametric study, the difference in the evolutions of the two Poisson’s ratios over time is characterized by two parameters, a characteristic difference $\Delta\nu$ and a retard factor $f_{\Delta t}$ that captures the retard of the creep Poisson’s ratio $\nu_{c}$ with respect to the relaxation Poisson’s ratio $\nu_{r}$:

$$\begin{aligned} \Delta\nu& = \nu_{r}(t_{m})-\nu_{c}(t_{m}), \end{aligned}$$

(23a)

$$\begin{aligned} f_{\Delta t} & = \frac{t_{c}}{t_{r}}, \end{aligned}$$

(23b)

where $t_{m}$ is such that ${\lvert\nu _{r}(t_{m})-\nu_{c}(t_{m})\rvert= \max_{t} \lvert\nu_{r}(t)-\nu_{c}(t)\rvert}$, and $t_{r}$ and $t_{c}$ are such that $\nu_{r}(t_{r})=\nu_{c}(t_{c})=(\nu_{0} + \nu_{\infty})/2$.

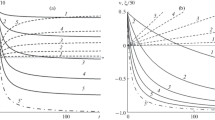
Figure 3 displays the characteristic difference $\Delta \nu$. For a material whose both volumetric and deviatoric behaviors are governed by the Maxwell unit (see Figs. 3a and 1a), the characteristic difference $\Delta\nu$ is an increasing function of the ratio $\eta_{K}/\eta_{G}$ and a decreasing function of the initial Poisson’s ratio $\nu_{0}$. For this material, the characteristic difference $\Delta\nu$ is comprised between −0.3 and 0.3. For a material whose volumetric and deviatoric behaviors are governed by the Maxwell unit and the Kelvin–Voigt unit, respectively (see Figs. 3b and 1b), the characteristic difference $\Delta\nu$ is a decreasing function of the initial Poisson’s ratio $\nu_{0}$. The minimum characteristic difference is equal to −0.3 and is observed for the material for which $\nu_{0} = 0.5$. For a material whose volumetric and deviatoric behaviors are governed by the Kelvin–Voigt unit and the Maxwell unit, respectively (see Figs. 1c and 3c), the characteristic difference $\Delta\nu$ is an increasing function of the initial Poisson’s ratio $\nu_{0}$. The maximum characteristic difference is equal to 0.3 and is observed for the material for which $\nu_{0} \rightarrow -1$. For a material whose both volumetric and deviatoric behaviors are governed by the Kelvin–Voigt unit (see Figs. 1d and 3d), the characteristic difference $\Delta\nu$ is almost 0. The observation of such a small characteristic difference is likely due to the fact that we chose identical stiffnesses for the two springs of the Kelvin–Voigt unit, for both the volumetric and deviatoric behaviors.

Fig. 3

Characteristic difference $\Delta\nu$ between relaxation Poisson’s ratio $\nu_{r}(t)$ and creep Poisson’s ratio $\nu_{c}(t)$: (a) Both volumetric and deviatoric behaviors governed by the Maxwell unit (see Fig. 1a); (b) Volumetric behavior and deviatoric behavior governed by the Maxwell unit and the Kelvin–Voigt unit, respectively (see Fig. 1b); (c) Volumetric behavior and deviatoric behavior governed by the Kelvin–Voigt unit and the Maxwell unit, respectively (see Fig. 1c); (d) Both volumetric and deviatoric behaviors governed by the Kelvin–Voigt unit (see Fig. 1d)

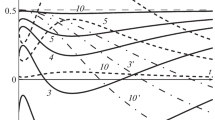
Figure 4 displays the retard factor $f_{\Delta t}$. For a material whose both volumetric and deviatoric behaviors are governed by the Maxwell unit (see Figs. 1a and 4a), the retard factor $f_{\Delta t}$ is constant and equal to 1.44 for the various values of the initial Poisson’s ratio $\nu_{0}$ and the ratio $\eta_{K}/\eta_{G}$. For a material whose volumetric and deviatoric behaviors are governed by the Maxwell unit and the Kelvin–Voigt unit, respectively (see Figs. 1b and 4b) and for a material whose volumetric and deviatoric behaviors are governed by the Kelvin–Voigt unit and the Maxwell unit, respectively (see Figs. 1c and 4c), the retard factor $f_{\Delta t}$ is a monotonic function of neither the initial Poisson’s ratio $\nu_{0}$ nor the ratio $\eta_{K}/\eta_{G}$. For each of those two types of materials, the retard factor $f_{\Delta t}$ is comprised between 1.44 and 2.08. For the material whose both volumetric and deviatoric behaviors are governed by the Kelvin–Voigt unit (see Figs. 1d and 3d), since the characteristic difference $\Delta\nu$ between the two Poisson’s ratios is almost 0, the retard factor is not studied.

Fig. 4

Retard factor $f_{\Delta t}$ of the creep Poisson’s ratio $\nu _{c}(t)$ with respect to the relaxation Poisson’s $\nu_{r}(t)$: (a) Both volumetric and deviatoric behaviors governed by the Maxwell unit (see Fig. 1a); (b) Volumetric behavior and deviatoric behavior governed by the Maxwell unit and the Kelvin–Voigt unit, respectively (see Fig. 1b); (c) Volumetric behavior and deviatoric behavior governed by the Kelvin–Voigt unit and the Maxwell unit, respectively (see Fig. 1c)

To sum up this parametric study, for some materials, the creep Poisson’s ratio $\nu_{c}(t)$ can differ significantly from the relaxation Poisson’s ratio $\nu_{r}(t)$ (see, e.g., the case of a material whose both volumetric and deviatoric behaviors are governed by the Maxwell unit in Fig. 3a). In contrast, for other materials, the difference can be negligible (see, e.g., the case of a material whose both volumetric and deviatoric behaviors are governed by the Kelvin–Voigt unit in Fig. 3d). For all cases considered, the characteristic difference $\Delta\nu$ between the two Poisson’s ratios lies in the range $[-0.3, 0.3]$. In terms of kinetics, the creep Poisson’s ratio $\nu_{c}(t)$ always evolves slower than the relaxation Poisson’s ratio $\nu_{r}(t)$: for all cases for which the difference between the two Poisson’s ratios is not negligible, the retard factor $f_{\Delta t}$ that we introduced is always comprised in the range $[1.44, 2.08]$.

4 Discussions

This section discusses the difference between the two Poisson’s ratios $\nu_{r}$ and $\nu_{c}$, first in practice in the case of multiaxial creep tests on cementitious materials, and then with respect to the elastic–viscoelastic correspondence principle (Christensen 1982). A brief conclusion on the different usage of the two Poisson’s ratios is drawn at the end of this latter section, in which the influence of the duration of the loading phase on the creep strains is also discussed.

4.1 Poisson’s ratio from multiaxial creep tests on cementitious materials

In order to compare the two Poisson’s ratios $\nu_{r}$ and $\nu_{c}$ in practice, we consider cementitious materials (i.e., cement paste, mortar, and concrete), for which multiaxial creep tests are available in Gopalakrishnan et al. (1969), Jordaan and Illson (1969), Parrott (1974), Kennedy (1975), Neville et al. (1983), Bernard et al. (2003), Kim et al. (2005). The tests here considered characterize the so-called “basic” creep of the cementitious materials (Neville 1995), which is measured in absence of any hydric transfer and to which any time-dependent deformation observed on a nonloaded specimen (i.e., autogenous shrinkage) is subtracted.

We consider that the coordinate frame is oriented in the principal directions, which are numbered from 1 to 3. The principal stresses and strains in those principal directions are denoted $\sigma_{i}(t)$ and $\varepsilon_{i}(t)$, respectively, with $i=1,2,3$. For a multiaxial creep test, the stresses are kept constant over time, that is, $\sigma _{i}(t)=\sigma_{i0}$. For such a test, the linearity of the material makes it possible to extend Eqs. (2a) and (10) to find out the viscoelastic stress–strain relations valid in the case of multiaxial solicitation, expressed in terms of either the relaxation Poisson’s ratio $\nu_{r}(t)$ or the creep Poisson’s ratio $\nu_{c}(t)$:

$$\begin{aligned} \varepsilon_{i}(t)&=J_{E}(t)\sigma_{i0}-( \sigma_{j0}+\sigma_{k0})\nu _{r}(t)\otimes \dot{J}_{E}(t), \quad\text{where } i \neq j \neq k \in\{1,2,3\}, \end{aligned}$$

(24a)

$$\begin{aligned} \varepsilon_{i}(t)&=J_{E}(t)\sigma_{i0}-( \sigma_{j0}+\sigma_{k0})\nu _{c}(t)J_{E}(t), \quad\text{where } i \neq j \neq k \in\{1,2,3\}. \end{aligned}$$

(24b)

Here, we consider experimental results available in the literature (see Fig. 5), and by using Eqs. (24a) and (24b) we compute the experimental values of the Poisson’s ratios $\nu_{r}$ and $\nu_{c}$. The details of the computation are given in Appendix B. Note that the Poisson’s ratios displayed on Figs. 5a–c exhibit very different trends over time: some increase, one decreases, and one remains constant. For such a variety of cases, we compare the relaxation and creep Poisson’s ratios with each other.

Fig. 5

Experimental data of multiaxial creep experiments on cementitious materials: (a) Biaxial creep test on cubic concrete sample (Jordaan and Illson 1969); (b) Uniaxial creep test on a cuboid sample of cement paste (Parrott 1974); (c) Triaxial creep tests on cylindrical specimens of leached cement paste and mortar (Bernard et al. 2003)

Figure 5a displays results of a biaxial creep test on a cubic concrete sample (Jordaan and Illson 1969). The two Poisson’s ratios reach their asymptotic value in less than 10 days, during which they vary by about 0.004. The difference between them is smaller than 0.0002, which is negligible: they can be considered as equal to each other. Note that such a trend of almost constant Poisson’s ratios is observed with other experimental data on concrete available in the literature (i.e., namely the data in Kennedy 1975; Stockl et al. 1989; Kim et al. 2005): with such data, relaxation and creep Poisson’s ratio can again be considered as equal to each other. The results from a uniaxial creep test on a cuboid sample of cement paste (Parrott 1974) are displayed in Fig. 5b. Both Poisson’s ratios decrease by about 0.05 in about a dozen of days. The difference between the two Poisson’s ratios is always smaller than 0.004, which, depending on the applications, can be considered as negligible or not. The last case displayed in Fig. 5c is that of triaxial creep tests on cylindrical specimens of leached cement paste and mortar (Bernard et al. 2003). In this last case, the Poisson’s ratios are increasing functions of time and vary by about 0.157 for the cement paste specimen and by about 0.218 for the mortar specimen.¹ Here, the difference between the two Poisson’s ratios can be as large as 0.017 for the cement paste specimen and 0.025 for the mortar specimen: for those specimens, the difference between the relaxation Poisson’s ratio and the creep Poisson’s ratio is no more negligible. From this back-analysis of creep tests on cementitious materials we conclude that if the Poisson’s ratios vary little over time, then the difference between the relaxation Poisson’s ratio and the creep Poisson’s ratio is negligible. In contrast, when the Poisson’s ratios vary significantly over time, the difference between the two Poisson’s ratios can be no more negligible: whether this difference must be taken into account in practice needs to be assessed case by case, that is, for each application considered.

The significance of the difference between the two Poisson’s ratios must also be assessed by keeping in mind the accuracy of the measurement of creep strains, which results from the accuracy of strain gauges and of temperature control. For instance, the accuracy of the strain gauges that were used in the biaxial creep test reported on concrete sample (see Fig. 5a) is $1\times10^{-6}$ (Jordaan and Illson 1969): this accuracy leads to an uncertainty on the creep Poisson’s ratio of about 0.002, which is ten times larger than the difference between the two Poisson’s ratios in that experiment. The temperature was controlled with an accuracy of $\pm1$ °C in that experiment. Considering a thermal dilatation coefficient of $14.5 \times10^{-6}~\mbox{K}^{-1}$ for concrete, uncorrected variations of temperatures would lead to an uncertainty on the measured strain that would be 15 times larger than the accuracy of the strain gauges. However, in that experiment, variations of temperature were corrected so that the uncertainty induced by variations of temperatures would be much smaller than 15 times the accuracy of the strain gauges, although probably nonnegligible. Also, what concerns the uniaxial creep test reported on cement paste (see Fig. 5b), for which the accuracy of the strain gauges they used was $3\times10^{-6}$ (Parrott 1974), we found an uncertainty on the creep Poisson’s ratio of about 0.003, which is of the same order of magnitude as the maximum difference between the two Poisson’s ratios in that experiment. In contrast, what concerns the experiments performed on leached specimens (see Fig. 5c), since the strains are about two orders of magnitude greater than the strains in the experiments displayed in Figs. 5a and 5b, the uncertainty on the Poisson’s ratio becomes truly negligible: with respect to this uncertainty, the difference between the creep and relaxation Poisson’s ratios in that experiment is significant.

4.2 The elastic–viscoelastic correspondence principle

For an isotropic elastic material with bulk modulus $K_{0}$ and shear modulus $G_{0}$, the stress–strain relations read

$$\begin{aligned} \sigma_{v}&=K_{0}\varepsilon_{v}, \end{aligned}$$

(25a)

$$\begin{aligned} s_{ij}&=2G_{0}e_{ij}. \end{aligned}$$

(25b)

We observe that these elastic relations are analogous to the viscoelastic stress–strain relations (3a), (3b) and (4a), (4b). In fact, we could have inferred these latter viscoelastic stress–strain relations in the Laplace domain directly from the elastic stress–strain relations (25a), (25b) simply by replacing all elastic coefficients by the $s$-multiplied Laplace transform (also called the Carson transform) of their corresponding viscoelastic relaxation functions (Tschoegl et al. 2002).

In terms of Poisson’s ratio, for an isotropic elastic material, we have the following relation

$$ \nu_{0}=\frac{3K_{0}-2G_{0}}{2(3K_{0}+G_{0})}. $$

(26)

We observe that applying the correspondence principle to this equation makes it possible to retrieve Eq. (8) if one replaces the elastic Poisson’s ratio $\nu_{0}$ with the $s$-multiplied Laplace transform of the relaxation Poisson’s ratio $\nu_{r}(t)$. Therefore, we infer that the corresponding viscoelastic operator of the elastic Poisson’s ratio is the relaxation Poisson’s ratio $\nu _{r}(t)$ and not the creep Poisson’s ratio $\nu_{c}(t)$; in other words, the correspondence principle can be applied to elastic relations that involve the Poisson’s ratio if this latter is replaced with the $s$-multiplied Laplace transform $s\widehat{\nu}_{r}(s)$ of the relaxation Poisson’s ratio $\nu_{r}(t)$ in the corresponding viscoelastic equation.

The validity of correspondence principle is due to the fact that the viscoelastic relations are “of the convolution type whose integral transforms lead to algebraic relations similar to the elastic ones” (Hilton 2001). Considering the specific example of a uniaxial creep test, we observe that the lateral strain $\varepsilon_{l}(t)$ and the axial strain $\varepsilon_{a}(t)$ can be related through the use of either the relaxation Poisson’s ratio $\nu_{r}(t)$ or the creep Poisson’s ratio $\nu_{c}(t)$ through Eqs. (10) or (2a), respectively. Of those two equations, the former involves a convolution, whereas the latter does not, which shows that the correspondence principle is not applicable to the creep Poisson’s ratio $\nu_{c}$, as already noted by Hilton (2001, 2009, 2011) and Tschoegl et al. (2002). Note that Lakes and Wineman (2006) found a relationship between the two Poisson’s ratios $\nu_{r}$ and $\nu_{c}$ that differs from that given in Eq. (11). We believe that their equation is not valid and that the error in their derivation stems from the fact that they applied the correspondence principle not only to the relaxation Poisson’s ratio $\nu _{r}$ (which is valid), but also to the creep Poisson’s ratio $\nu_{c}$ (which is not valid) (Tschoegl et al. 2002). This example shows that we can easily get confused in how to manipulate the various Poisson’s ratios that can be defined; in consequence, in the generic case, to perform a viscoelastic characterization, avoiding as much as possible the use of viscoelastic Poisson’s ratios and restricting oneself to the use of creep compliances and relaxation moduli seems to be a wise choice.

Since the relaxation Poisson’s ratio $\nu_{r}$ is the only Poisson’s ratio to which the correspondence principle can be applied, solving viscoelastic problems analytically can be performed much more easily by using the relaxation Poisson’s ratio rather than the creep Poisson’s ratio. In contrast, since the relationship between the creep Poisson’s ratio $\nu_{c}$ and the time-dependent strains does not involve any convolution (see Eq. (24b) in comparison with Eq. (24a)), back-calculating the creep Poisson’s ratio from experimental data is more straightforward than back-calculating the relaxation Poisson’s ratio. This is the reason why, when experimentalists report a Poisson’s ratio, they almost exclusively report the creep Poisson’s ratio (see, e.g., Benboudjema 2002; Torrenti et al. 2014; Hilaire 2014).

For a uniaxial experiment performed on an elastic material, the lateral strain $\varepsilon_{l}$ is linked to the axial strain $\sigma_{a}$ through $\varepsilon_{l} = - (\nu/E) \sigma_{a}$. Based on this elastic relation, the fact that the correspondence principle is applicable to the relaxation Poisson’s ratio makes it possible to derive how, for a uniaxial experiment with a generic load history $\sigma_{a}(t)$ performed on a viscoelastic solid, the lateral strain $\varepsilon_{l}(t)$ must evolve over time. Thus, we find that, in the Laplace domain, the following relation holds:

$$ \widehat{\varepsilon}_{l}=-s\widehat{\nu}_{r} (s \widehat{J}_{E}\widehat {\sigma}_{a} ). $$

(27)

This relation can be translated back into the time domain:

$$ \varepsilon_{l}(t)=-\nu_{r}(t) \otimes \biggl( \frac{d}{dt}\bigl(J_{E}(t)\otimes\dot {\sigma}_{a}(t) \bigr) \biggr). $$

(28)

Thus, for a uniaxial experiment with a generic load history, we can use the relaxation Poisson’s ratio to calculate the evolution of the lateral strain over time. Note that we did not succeed in deriving such an equation based on the creep Poisson’s ratio, which is a direct consequence of the fact that the correspondence principle cannot be applied to the creep Poisson’s ratio.

For triaxial loadings with a generic load history, starting from Eqs. (6b) and (28), using the principle of superposition makes it possible to derive the following equation:

$$ \varepsilon_{i}(t)=J_{E}(t)\otimes\dot{ \sigma}_{i}(t)-\nu_{r}(t)\otimes \biggl(\frac{d}{dt} \bigl(J_{E}(t)\otimes\bigl(\dot{\sigma}_{j}(t)+\dot{\sigma }_{k}(t)\bigr) \bigr) \biggr)\quad\text{where } i \neq j \neq k \in\{1,2,3 \}, $$

(29)

which is a direct extension of Eq. (24a). Thus, if we know the uniaxial creep compliance and the relaxation Poisson’s ratio of the material, this equation makes it possible to predict the evolution of the principal strains over time from the history of the triaxial stresses. Note that, again, we did not succeed in deriving such an equation based on the creep Poisson’s ratio.

4.3 Influence of duration of loading phase on apparent creep Poisson’s ratio

In order to identify the creep Poisson’s ratio, we may want to perform a creep experiment and calculate the ratio $- \varepsilon _{l}(t)/\varepsilon_{a}(t)$ of the lateral dilation to the axial contraction measured during the creep phase. By doing so, we identify a time-dependent function to which we will refer as to an “apparent” creep Poisson’s ratio since, in practice, for any creep experiment, the duration of the loading phase is finite, whereas the creep Poisson’s ratio was defined with respect to a creep experiment with an instantaneous loading (see Eq. (2a)). Therefore, we can wonder by how much an apparent creep Poisson’s ratio identified on an actual creep experiment differs from the creep Poisson’s ratio of the material. The study of such a difference is the focus of this section.

To study this difference, we consider two virtual materials whose rheological behaviors are those described in Figs. 1a and 1b in the specific case where $\eta_{K} \rightarrow +\infty$. Therefore, the volumetric behavior of the two virtual materials is elastic since they only creep deviatorically. The deviatoric behavior of the first virtual material is governed by the Maxwell unit (see Fig. 1a), whereas the deviatoric behavior of the second virtual material is governed by the Kelvin–Voigt unit (see Fig. 1b). Their characteristic viscous time is $\tau_{G} = \eta_{G} / G_{0}$. The elastic stiffnesses are chosen such that the elastic Poisson’s ratio is $\nu_{0}=0.2$.

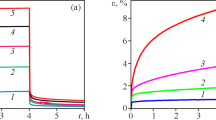
On each of those two materials, we consider creep experiments in which the load is increased linearly over time in a duration $\tau_{L}$, after which the load is kept constant. For various durations $\tau_{L}$ of the loading phase, Fig. 6 displays what the ratio of the lateral dilation to the axial contraction is, together with the creep Poisson’s ratio of the material. We observe that the apparent creep Poisson’s ratio differs from the creep Poisson’s ratio: the slower the loading, the greater this difference. Also, this difference is maximum at the end of the loading phase (i.e., at the dimensionless time $t / \tau_{L} =1$), but we note that this difference is significant only for times that are smaller than about 10 times the duration of the loading phase: at times greater than 10 times the duration of the loading phase, the difference between the creep Poisson’s ratio and the apparent creep Poisson’s ratio is negligible.

Fig. 6

Ratio $-\varepsilon_{l}(t)/\varepsilon_{a}(t)$ of the lateral to the axial strain (black lines) observed during creep experiments with various durations $\tau_{L}$ of the loading phase, and creep Poisson’s ratio $\nu_{c}$ (gray lines) for a material that creeps deviatorically and whose deviatoric creep behavior is modeled by (a) the Maxwell unit or (b) the Kelvin–Voigt unit

In conclusion, if we aim at identifying the creep Poisson’s ratio as the ratio $- \varepsilon_{l}(t)/\varepsilon_{a}(t)$ of a lateral dilation to an axial contraction measured during the creep phase of an actual creep experiment, we will commit some error. However, the difference between the creep Poisson’s ratio and the apparent one may only be significant for times smaller than about 10 times the duration of the loading phase; for larger times, this difference will be negligible.

5 Conclusions

Two time-dependent Poisson’s ratios are defined for linear viscoelastic materials: the relaxation Poisson’s ratio $\nu_{r}(t)$ and the creep Poisson’s ratio $\nu_{c}(t)$. Those two Poisson’s ratios are defined with respect to creep or relaxation experiments with an instantaneous loading. The following conclusions are drawn on their differences, in both theory and practice:

• Those two Poisson’s ratios are not equal to each other. They can be expressed as functions of the creep compliances and relaxation moduli and are linked to each other through the exact expression (11).

• At the initial time of loading, both Poisson’s ratios are equal to the elastic Poisson’s ratio. Their long-time asymptotic values are identical. Their initial derivatives with respect to time are also identical, and so are their long-time asymptotic derivatives.

• The parametric study of virtual materials based on simple rheological models indicates that the two Poisson’s ratios can differ significantly from each other. The maximum characteristic difference $\Delta\nu$ between them at a given time can be as large as 0.3. The creep Poisson’s ratio evolves slower than the relaxation Poisson’s ratio by a retard factor $f_{\Delta t}$, which is in the range $[1.44, 2.08]$.

• A study of multiaxial creep data on cementitious materials showed that if the Poisson’s ratios vary little over time, then their difference is negligible. When the Poisson’s ratios vary significantly over time, whether their difference must be taken into account in practice should be assessed with respect to the application considered. The significance of the difference must also be assessed by keeping in mind the accuracy of the measurement of creep strains.

• The use of each of the two Poisson’s ratios is of interest: solving viscoelastic problems analytically can be performed much more easily by using the relaxation Poisson’s ratio rather than the creep Poisson’s ratio since the elastic–viscoelastic correspondence principle is applicable to this former parameter; in contrast, back-calculating the creep Poisson’s ratio from experimental data is more straightforward than back-calculating the relaxation Poisson’s ratio.

• For materials subjected to a triaxial loading, even if the load history is generic, from the uniaxial creep compliance $J_{E}(t)$ and the relaxation Poisson’s ratio $\nu_{r}(t)$ we can calculate the evolution of the principal strains over time (see Eq. (29)). However, given all confusion in the literature on how to manipulate viscoelastic Poisson’s ratios, in the generic case, a wise choice to perform viscoelastic characterization or analytical calculations in viscoelasticity is to restrict oneself to the use of unambiguously defined creep compliances and relaxation moduli.

• The creep Poisson’s ratio was defined on a creep experiment with an instantaneous loading. If the loading phase of the creep experiment is not instantaneous (which is the case in practice), then the ratio of the lateral dilation to the axial contraction during the creep phase differs from the creep Poisson’s ratio. This difference may be significant only for times that are smaller than about 10 times the duration of the loading phase.

We calculated how the relaxation and creep Poisson’s ratios of cementitious materials evolved over time. The analysis of those parameters could be translated in terms of volumetric and deviatoric creep behaviors, thus paving the way for a more rational choice of creep models for those materials.

Appendices

Appendix A: Relaxation and creep Poisson’s ratios in rheological models

This section is devoted to present an analytical expression of the relaxation Poisson’s ratio $\nu_{r}$ and the creep Poisson’s ratio $\nu _{c}$ based on the rheological models that are presented in Fig. 1. For a material whose both volumetric and deviatoric behaviors are governed by the Maxwell units (see Fig. 1a), the Poisson’s ratios read as follows:

$$\begin{aligned} \nu_{r} (t ) =&-\frac{ (G_{0}+3K_{0} ) (2\eta_{G}-3\eta _{K} )+9 (\eta_{G}K_{0}-\eta_{K}G_{0} )\exp (-\frac{G_{0}K_{0} (\eta_{G}+3\eta_{K} )}{\eta_{G}\eta_{K} (G_{0}+3K_{0} )}t )}{2 (\eta_{G}+3\eta_{K} ) (G_{0}+3K_{0} )} , \end{aligned}$$

(30)

$$\begin{aligned} \nu_{c} (t ) =&-\frac{\eta_{G}\eta_{K} (2G_{0}-3K_{0} )+G_{0}K_{0} (2\eta_{G}-3\eta_{K} )t}{\eta_{G}\eta_{K} (G_{0}+3K_{0} )+G_{0}K_{0} (\eta_{G}+3\eta_{K} )t}. \end{aligned}$$

(31)

For a material whose volumetric and deviatoric behaviors are governed by the Maxwell unit and the Kelvin–Voigt unit, respectively (see Fig. 1b), the Poisson’s ratios are expressed as follows:

$$\begin{aligned} \nu_{r} (t ) =&-1+\frac{9K_{0}}{2 (G_{0}+3K_{0} )}\exp (-\varOmega_{1}t ) \bigl(\cosh (\varOmega_{2}t )+\varOmega_{3}\sinh ( \varOmega_{2}t ) \bigr), \end{aligned}$$

(32)

$$\begin{aligned} \nu_{c} (t ) =&-\frac{2\eta_{K}G_{0}-6\eta_{K}K_{0}+2G_{0}K_{0}t+3\eta_{K}K_{0}\exp (-\frac{G_{0}}{\eta_{G}}t )}{2 (\eta_{K}G_{0}+6\eta _{K}K_{0}+G_{0}K_{0}t-3\eta_{K}K_{0}\exp (-\frac{G_{0}}{\eta_{G}}t ) )}, \end{aligned}$$

(33)

where the parameters $\varOmega_{1}, \varOmega_{2}, \varOmega_{3}$ are functions of $K_{0}, G_{0}, \eta_{K}, \eta_{G}$:

$$\begin{aligned} \varOmega_{1} &= \frac{G_{0} (6K_{0}\eta_{K}+\eta_{G}K_{0}+G_{0}\eta_{K} )}{2\eta _{G}\eta_{K} (G_{0}+3K_{0} )}, \\ \varOmega_{2} &=\frac{\sqrt{G_{0}^{2} (36\eta_{K}^{2}K_{0}^{2}+12\eta_{K}^{2}G_{0}K_{0}+\eta _{G}^{2}K_{0}^{2}-2\eta_{G}\eta_{K}G_{0}K_{0}+\eta_{K}^{2}G_{0}^{2} )}}{2\eta_{G}\eta_{K} (G_{0}+3K_{0} )}, \\ \varOmega_{3} &= \frac{ (3\eta_{K}G_{0}+6\eta_{K}K_{0}-\eta_{G}K_{0} )}{\sqrt { (36\eta_{K}^{2}K_{0}^{2}+12\eta_{K}^{2}G_{0}K_{0}+\eta_{G}^{2}K_{0}^{2}-2\eta_{G}\eta _{K}G_{0}K_{0}+\eta_{K}^{2}G_{0}^{2} )}}. \end{aligned}$$

For a material whose volumetric and deviatoric behaviors are governed by the Kelvin–Voigt unit and the Maxwell unit, respectively (see Fig. 1c), the Poisson’s ratios read as follows:

$$\begin{aligned} \nu_{r} (t ) =&\frac{1}{2}-\frac{3G_{0}}{2 (G_{0}+3K_{0} )}\exp (- \varOmega_{4}t ) \bigl(\cosh (\varOmega_{5}t )- \varOmega_{6}\sinh (\varOmega_{5}t ) \bigr) , \end{aligned}$$

(35)

$$\begin{aligned} \nu_{c} (t ) =&\frac{3\eta_{G}K_{0}-4\eta_{G}G_{0}+3K_{0}G_{0}t+2\eta_{G}G_{0}\exp (-\frac{K_{0}}{\eta_{K}}t )}{2 (3\eta_{G}K_{0}+2\eta _{G}G_{0}+3K_{0}G_{0}t-\eta_{G}G_{0}\exp (-\frac{K_{0}}{\eta_{K}}t ) )} , \end{aligned}$$

(36)

where the parameters $\varOmega_{4}, \varOmega_{5}, \varOmega_{6}$ are functions of $K_{0}, G_{0}, \eta_{K}, \eta_{G}$:

$$\begin{aligned} \varOmega_{4} &= \frac{K_{0} (3K_{0}\eta_{G}+3\eta_{K}G_{0}+2G_{0}\eta_{G} )}{2\eta_{G}\eta_{K} (G_{0}+3K_{0} )}, \\ \varOmega_{5} &=\frac{\sqrt{K_{0}^{2} (9\eta_{G}^{2}K_{0}^{2}-18\eta_{K}\eta _{G}K_{0}G_{0}+12\eta_{G}^{2}K_{0}G_{0}+9\eta_{K}^{2}G_{0}^{2}+4\eta_{G}^{2}G_{0}^{2} )}}{2\eta _{G}\eta_{K} (G_{0}+3K_{0} )}, \\ \varOmega_{6} &= \frac{K_{0} (3\eta_{K}G_{0}-9\eta_{G}K_{0}-2\eta_{G}G_{0} )}{\sqrt{K_{0}^{2} (9\eta_{G}^{2}K_{0}^{2}-18\eta_{K}\eta_{G}K_{0}G_{0}+12\eta _{G}^{2}K_{0}G_{0}+9\eta_{K}^{2}G_{0}^{2}+4\eta_{G}^{2}G_{0}^{2} )}}. \end{aligned}$$

For a material whose both volumetric and deviatoric behaviors are governed by the Kelvin–Voigt units (see Fig. 1d), the Poisson’s ratios read as follows:

$$\begin{aligned} \nu_{r}(t) =&\frac{3K_{0}-2G_{0}}{2(3K_{0}+G_{0})}+\frac{9K_{0}G_{0}}{3K_{0}+G_{0}}\varOmega _{9}\exp(-\varOmega_{7}t)\sinh\biggl(\frac{\varOmega_{8}}{\eta_{K}\eta_{G}(3K_{0}+G_{0})} \biggr), \end{aligned}$$

(38)

$$\begin{aligned} \nu_{c} (t ) =&\frac{6K_{0}-4G_{0}-3K_{0}\exp (-\frac{K_{0}}{\eta _{K}}t )+2G_{0}\exp (-\frac{G_{0}}{\eta_{G}}t )}{2 (6K_{0}+2G_{0}-3K_{0}\exp (-\frac{K_{0}}{\eta_{K}}t )-G_{0}\exp (-\frac {G_{0}}{\eta_{G}}t ) )}, \end{aligned}$$

(39)

where the parameters $\varOmega_{4}, \varOmega_{5}, \varOmega_{6}$ are functions of $K_{0}, G_{0}, \eta_{K}, \eta_{G}$:

$$\begin{aligned} \varOmega_{7} &= \frac{3K_{0}^{2}\eta_{G}+6K_{0}G_{0}\eta_{K}+G_{0}^{2}\eta_{K}+2K_{0}G_{0}\eta _{G}}{2\eta_{K}\eta_{G}(3K_{0}+G_{0})}, \\ \varOmega_{8} &=9K_{0}^{4}\eta_{G}^{4}-36K_{0}^{3}G_{0} \eta_{K}\eta_{G}-18K_{0}^{2}G_{0}^{2} \eta_{K}\eta _{G}+12K_{0}^{3}G_{0} \eta_{G}^{2} \\ &\quad{} +36K_{0}^{2}G_{0}^{2} \eta_{K}^{2}+12K_{0}G_{0}^{3} \eta_{K}^{2}+G_{0}^{4} \eta_{K}^{2}-4K_{0}G_{0}^{3} \eta _{K}\eta_{G}+4K_{0}^{2}G_{0}^{2} \eta_{G}^{2}, \\ \varOmega_{9} &= \frac{G_{0}\eta_{K}-K_{0}\eta_{G}}{\varOmega_{8}}. \end{aligned}$$

Appendix B: Calculation of the two Poisson’s ratios from the experimental results

This section is devoted to present how the relaxation Poisson’s ratio $\nu_{r}$ and the creep Poisson’s ratio $\nu_{c}$ are calculated from the experimental results. By using Eq. (24b) the creep Poisson’s ratio $\nu_{c} (t )$ and the uniaxial creep compliance $J_{E}$ are computed directly from the experimental measurement of principals strains $\varepsilon_{1} (t )$, $\varepsilon_{2} (t )$, $\varepsilon_{3} (t )$ and applied stress values $\sigma_{10}$, $\sigma_{20}$, $\sigma_{30}$. Then, to the experimental values of the uniaxial creep compliance $J_{E}$ the following analytical expression is fitted:

$$ J_{E} (t )=\alpha_{1}t+\alpha_{2}+ \alpha_{3}\exp \biggl(-\frac {t}{\tau_{1}} \biggr), $$

(41)

where $\alpha_{1}$, $\alpha_{2}$, $\alpha_{3}$, and $\tau_{1}$ are fitted parameters.

Further, in order to capture the asymptotic behavior of the Poisson’s ratio, we assumed that the relaxation Poisson’s ratio $\nu_{r} (t )$ has the exponential form

$$ \nu_{r} (t )=\nu_{f}+\alpha_{0}\exp \biggl(- \frac{t}{\tau_{0}} \biggr), $$

(42)

where $\nu_{f}$, $\alpha_{0}$, and $\tau_{0}$ are parameters to fit.

Substituting Eqs. (41) and (42) into Eq. (17), the creep Poisson’s ratio $\nu_{c}$ is computed analytically. By changing the parameters $\nu_{f}$, $\alpha_{0}$, and $\tau_{0}$ in Eq. (42), a best fit that gives the minimum variance for the fitted creep Poisson’s ratio $\nu_{c}$ is obtained.