Abstract
In today’s Internet era, group communications in multimedia applications are becoming more and more popular. The issues of controlling illegal access to multimedia contents require efficient and secure mechanisms for distribution of common key called scrambling key or group key. In order to provide secure delivery of multimedia contents in digital pay-TV systems, a large number of keying information messages are exchanged for group key/scrambling key updates in the traditional key distribution schemes. In this paper we propose a Chinese Remainder Theorem (CRT) based key distribution protocol which is highly secure and computationally efficient. The proposed protocol, 1) has drastically reduced the computational complexity of Group Manager (GM) and members for updating the keys, 2) has greatly increased the security by using an additional secret parameter at Group Manager and members areas, 3) can efficiently handle large and dynamically updating groups and, 4) can update the group key in one message, without updating member’s key. With our proposed key distribution scheme, only legal members can access the multimedia contents correctly and the illegal access can be prevented. The proposed scheme is applicable in Conditional Access System (CAS) of digital pay-TV systems without increasing storage and communication overheads on GM and members. The comparative analysis of our proposed scheme with existing schemes in terms of computational cost assures the effectiveness of our scheme. As a proof of concept, we implement our scheme to a decentralized architecture-based key management system and demonstrate that the proposed scheme significantly reduces the computational complexity.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
With the growing popularity of group communications and the rapid growth of the Internet, certain multimedia multicast services like Pay-TV, video conferences, stock quotes, group games, distance learning, etc. require confidentiality during communication [3, 6, 18, 22, 26, 27]. For such kind of group oriented services it is necessary to develop the access control mechanism so that only legal group members can access the multicast communication. In digital pay-TV systems, the members are able to select and purchase their favourite programs. The Conditional Access System (CAS) provides access of selected programs to only authorized members who have paid for the digital pay-TV programs. For these reasons, the problem of illegal access of pay-TV systems has become important and researchers have attracted a lot of attention to solve these problems. In digital pay-TV systems, the CAS is a type of security system which guarantees that only legal members can access multimedia multicasting. In CAS, the Key Management System (KMS) is an important component which prevents illegal access to digital pay-TV. systems. Whether the key management system is suitable or not can directly affect the performance and security of the CAS. The KMS is responsible to generate and distribute group key to authorized members which is used to scramble/descramble the media contents. The scramble and encryption techniques are normally used for channel protection and delivery of multimedia contents to prevent illegal access in digital pay-TV multicasting systems. The scramble/encryption keys are distributed to all members in the group so that they can obtain and descramble/ decrypt the multicast data for which they are entitled [7].
As the groups may be dynamic in nature and the group membership may change over time. The members may join/leave the group any time. In order to provide the privacy in the multicast communication, the group key must be refreshed and redistributed securely to the members if there is any change in group membership. The updating and redistributing of group key over time is known as re-keying. In the present scenario of subscription of services, the membership of short-period services is growing. Therefore, the key management system implemented on short-period services, the group key is refreshed frequently. The frequently update in the group key leads the security problems related to backward and forward secrecy and expeditiously grow the rekeying cost [9]. For secure distribution of group key to members, forward and backward secrecy are initial security requirements of a group key management system. The backward secrecy means that new group members must not be able to access previously used group keys. Similarly, the forward secrecy means that the old group members must not be able to access new group keys [19].
The scrambling is the main function of CAS, which is a cryptographic operation and needs a key called Control Word (CW) to shuffle the media contents for pay-TV systems. When the Service Provider (SP) multicasts the digital signals of the program, CAS uses source digital signal and CW to produce digital signals in jumbled form and multicast the media contents in its jumbled form. This allows digital signals to be transmitted securely via open channels. Regularly changing CW and securely sending them are key problems of CAS. If CAS is not secure, then an adversary can easily discover CW, which can be used in descrambling the multicast digital signals. In order to provide the higher security for CAS, the CW must be changed regularly about every 5–20 s so that the attacker is not able to descramble the signals. Therefore, a secure technique to multicast updated CW is much more serious than preventing illegal members to capture CW. The CAS sends secret key to each member at the time of registration in the system. The capture of secret key by attacker is equivalent to crack the CAS. In order to prevent the attackers from obtaining the secret key, the KMS of CAS must be highly secured. Moreover, the descramble algorithm which run at member area should be efficient because digital pay-TV system is a real time application.
Various key management schemes for secure multicast communication have been designed till now. According to whether a trusted GM exists or not, all the group key management schemes are mainly classified into two types: group key distribution and group key agreement schemes. There is no GM in the key agreement protocols to generate and distribute the group key to all members. Because of not presence of GM, all group members contribute equally to establish a common key called group key. As there is no GM in the key agreement schemes and all members are responsible to contribute equally, higher communication overhead is needed during key establishment. In group key distribution protocols, a single trusted entity called GM is exists. The GM is responsible to generate and distribute the group key and other essential keys to the group members. We have proposed a key management scheme for access control of media delivery in Pay-TV systems using GM because a Pay-TV system have a SP like a GM which is responsible to manage the necessary keys and handle the subscribers. The key management schemes without a GM may increase computation and communication complexity of key update phase and hence the performance of Pay-TV systems may be degraded. Therefore, the use of key management schemes without a GM is not efficient in Pay-TV systems. However, distributing a group key in CAS of pay-TV is not easy due to the following reasons:
-
1)
The computational, communication and storage complexities of CAS should be as minimal as possible.
-
2)
A common group key is transferred to several members at one go; therefore, it is easy to intercept during key transmission.
-
3)
Group membership may change over time. At every join/leave, the group key requires to be updated and redistributed.
-
4)
Even though the group membership does not change for a long time, the group key still needs to be refreshed after a certain period of time.
Till now, many key management protocols have been presented in the literature to address above mentioned issues. Previously we have also proposed many key management and other cryptographic protocols [8,9,10,11,12]. In [9], a centralized group key distribution scheme based on RSA has been proposed which reduces the computation complexity key server. The storage complexity of key server has also reduced. To enhance the scalability, the protocol is implemented on clustered tree based architecture. In this protocol most of the computations are performed in initialization phase to minimize the rekeying cost. Moreover, it removes vulnerabilities of [14] such as eliminating factorization attack, decryption exponent attack, timing attack and Wiener attack etc. The protocol [9] requires slightly higher computation and communication cost for key update and it cannot be implemented in four level hierarchical structures by which it is not suitable to implement in pay-TV system for key distribution and hence the work presented in this manuscript is more efficient and highly scalable as compared the protocol presented in [9]. In [30], a fast key distribution protocol based on CRT has been proposed in which some keys parameters are computed and stored in initialization phase to reduce the key updating cost. In [10], a group key computation protocol based on polynomial for multicast communications has been presented in which group key is computed without interaction among the members. The scheme has reduced the computation, communication and storage complexities. However, the scheme is only suitable for small groups and not suitable for pay-TV systems because it is not highly scalable. In [25], a centralized key management scheme to reduce the key updating cost has been presented in which most of the computations are performed in initialization phase to compute key parameters for group members.
In [8], the improvements in RSA public key cryptosystem for higher security using CRT have been introduced in which the functions of encryption/decryption are more secure than conventional RSA. In order to generate the private/public key pairs, the protocol has used four prime numbers instead of two. Moreover, it removes the weaknesses of traditional RSA cryptosystem such as eliminating Factorization attack, Decryption exponent attack, Timing attack and Wiener attack etc., The protocol presented in [8] cannot be implemented in pay-TV system for key distribution because it is not a key management scheme. Therefore, the proposed research work is completely dissimilar from [8]. In [11], a novel fully homomorphic encryption protocol based on Euler’s theorem which requires less encryption overhead has been proposed. In the protocol, the computational complexity of decryption function has reduced greatly. In [12], a ternary tree based key establishment protocol for distributed environment has been proposed in which a common key is established using secret shares of each group member. Additionally, the scheme [12] is only suitable for distributed environment. In the distributed key management schemes, the computation and communication cost of group members is increased. Therefore, the scheme [12] is not suitable to implement in pay-TV systems for key distribution. Moreover, the work presented in this manuscript is differs from the protocol presented in [12] in many characteristics such as applicability, efficiency and scalability etc. Apart from these protocols many other protocols [6, 14, 18, 19, 22] etc. have been proposed for key distribution in Pay-TV systems. But most of the existing protocols suffer from the problem of high computation, storage overheads and security. The protocols [8,9,10,11,12] do not support three or four level decentralized architecture, as a result these protocols cannot be implemented in Pay-TV systems. Therefore, the design of a computationally and memory efficient key distribution protocol is necessary, which can be implemented in Pay-TV systems and handle large and dynamically updating groups while providing higher level of security.
The main contribution of this paper is to design a new centralized key distribution protocol for secure group communication with dynamic membership changes. In the proposed scheme, the computational complexity of GM for updating the keys is minimized by pre-computing alternative keys at the initialization phase so that it can be implemented in digital Pay-TV systems and provides efficient results. The proposed protocol consists of initialization, members joining, members leaving, massively joining & leaving members and periodically updates phases. The contribution of this paper can be summarized as follows:
-
1)
The proposed protocol minimizes the computational complexity of GM for updating the keys.
-
2)
It drastically reduces the computational and storage complexity of each member of the group.
-
3)
When a new member joins into group, then to distribute the new Group Key (GK), the GM requires executing only three basic operations: one addition, one multiplication and one modulus operation. Also, at member leave it performs one subtraction, one multiplication, and one modulus operation to broadcast new GK.
-
4)
Every group member requires executing only one multiplication and one modulus operation to recover the new GK.
-
5)
The proposed protocol can efficiently deal with massive membership changes.
The remaining sections of the paper are organized as follows: Section 2 presents literature survey of the related work. Section 3 provides preliminaries which include symbol definition, system and adversary models and a brief review of Chinese Remainder Theorem. In section 4, we describe our proposed protocol in detail. Section 5 presents the security analysis. The performance analysis is presented in section 6. Section 7 presents the implementation results. Finally, we conclude this paper in section 8.
2 Literature Survey
The key management for secure group communication has a lot of attention in the field of cryptography. A variety of group key management protocols for secure group communication have been proposed. The main challenges of various existing key management protocols are higher computation, communication and storage overheads. The key management protocols also encounter the problem of scalability and security. In order to explore above mentioned issues, it is essential to analyse the various key management protocols have been proposed in the literature. The brief review of related key management protocols is given as follows.
O. Pal et al., [18] recently introduced a key distribution protocol for secure conditional access systems. The scheme is based on Extended Euclidean algorithm and has efficient technique for balancing the load of Group Controller (GC). However, scheme has many drawbacks such as it will work only if GCD(η, δ) = 1, and for other cases it will not work at all. Therefore, the scheme has lots of failure cases since the keys are selected from \( {\mathbb{Z}}_p^{\ast } \) for which the condition GCD(η, δ) = 1 will rarely true. Moreover, the scheme is vulnerable to impersonation attack since product of all subscriber’s keys or multiple of product of all member’s keys can easily be computed by each subscriber. Therefore, the forward secrecy is also not maintained and member who has left the channel package can easily subscribe the channel and enjoy the multimedia content without having subscription. R. Varalakshmi et al., [22] proposed key management scheme for CAS based on Huffman encoding technique. In the scheme it is possible that private key of one member may divide other member’s keys since the keys are selected from\( {\mathbb{Z}}_p^{\ast } \). Therefore, if private key of one member is a factor of another member’s private keys then that member can access multimedia contents after leaving the group. Consequently, the forward secrecy is also not maintained in the scheme. The scheme is also vulnerable to impersonation attack. Another demerit of the scheme is that the channel selection procedure is not efficient since the users are not able to select channels as per his/her choice.
M. Y. Joshi et al., [6] proposed a key distribution scheme based on CRT for single and multiple access control. To update the group key, the scheme requires only one message. However, the computational overhead for key updates is very high because it is necessary to solve the sets of congruence equations for every key update. In case of multimedia multicast the group key is updated very frequently. Therefore, the scheme is not applicable in CAS. The protocol for multiple access control is also required high computational cost. Therefore, the protocol cannot be integrated with CAS. P. Vijaykumar et al., [26] proposed an effective key management scheme for secure pay-TV system. The scheme is vulnerable to impersonation attack and does not maintain forward secrecy. Therefore, the scheme is suitable for secure CAS system. He D. et al., [3] analysed Wang H. et al., [27] scheme and prove that it is vulnerable to impersonation attack. They have also proposed new solution that eliminates security weaknesses of Wang H. et al., scheme. McGrew et al. [16] proposed a key establishment protocol for large and dynamic groups using one-way function trees. The keys stored at members side, the size of broadcast messages and the computational cost of group members are logarithmic proportional to the size of the group. On the other hand, the protocol is vulnerable to collusion attack, in which joining and leaving members may use the information about their group keys to find the old and new group keys.
Mingyan Li et al. [13] explored the key distribution problems in secure multicast group with one-to-many communications. In proposed scheme the author’s point out the issues in the designing of model for key distribution with known communication budget can be determined as a constraint optimization problem. The author’s also point out that how the memory space required by the GC is minimized. However, due to more complexity of the solution of constraint optimization problem, the Key Server (KS) and members computation cost is increased. M. S. Farash et al., [2] presented weaknesses of Yeh and Tsaur’s [28] scheme and indicates that the scheme is vulnerable to impersonation attack. An adversary can impersonate both head-end system and mobile devices. To eliminate these security weaknesses of Yeh and Tsaur’s scheme, the authors proposed an efficient and provably secure authentication protocol for CAS using bilinear pairings. S. Chen et al., [1] studied various key management models for Pay-TV systems and conclude that the four-key management model is more efficient for Pay-Per-Channel (PPC) programs, and three-key management model is appropriate for Pay-Per-View (PPV) programs. The protocol requires less memory space. However, it requires a more complex algorithm for four-key management model. J. Kim et al., [7] analyzed security weaknesses of Sun et al. [20] scheme. Sun et al. scheme does not preserve backward secrecy. The authors have simple changes in Sun et al. protocol to make it capable for maintaining backward secrecy.
J.A.M. Naranjo et al. [17] have proposed key management protocol for secure communication in centralized multicast environments based on extended Euclidean algorithm. For every rekeying operation, the protocol generates only one rekeying message for entire group. Each group member is needed to store only one key. However, when a member wants to join or leave the group, the time requires to determine a new multiplicative group is very high. Moreover, in this scheme, two values δ and L are computed in the intermediary steps of group controller which should be relatively primes, otherwise the scheme is failed and members are unable to recover the secret message sent by GC. Zenghui Liu et al. [15] have investigated an efficient and secure protocol based on Logical Key Hierarchy(LKH) tree to rekey group key. The scheme reduced the rekeying cost and it can handle large-scaled group efficiently. Vijayakumar P. et al. [24] have presented key tree approach based on rotations to balance the tree, even if the batch leaving requests are involved in more operations than the batch joins. The protocol has reduced the batch rekeying overhead, if batch leave request are larger than batch join. By comparing with the other existing schemes, it reduced the rekeying overhead up to 20% − 30%. However, when batch join requests are larger than batch leave, the performance of the protocol is poor.
Dong-Hyun Je et al., [5] have presented a batch rekeying protocol which minimized total rekeying cost per unit time. The protocol configures batch rekeying intervals dynamically. In comparison with periodic batch rekeying protocol, the protocol has reduced the rekeying complexity by more than 50%. Shaohua Tang et al. [21] proposed hyper-sphere based provably secure key distribution protocol which is efficient and scalable for large groups. In the proposed approach every key has no any dependency on future and previously used keys. The protocol has greatly reduced the storage and computational complexity of group members. However the GC’s computation and storage overhead is increased linearly with the group size. Zheng et al., [30] have presented two variations named Chinese Remainder GK (CRGK) and Fast Chinese Remainder GK (FCRGK) for key distribution protocol. The protocol has also minimized the memory load and key recovery cost of group members. However, the storage and computational complexity of key server has increased. Lin et al., [14] have presented a group key management approach to solve the rekeying problem. The approach has eliminated the rekeying operating cost of the key server. The protocol has minimized the memory load of members. However, the computation and memory load of key server is increased.
Saravanan K. et al., [19] proposed an efficient multicast key management algorithm based on star topology in which the private key is computed by individual member. The computation overhead of KS is reduced by distributing the KS load amongst the members. The rekeying overhead is completely reduced. However in some cases the forward Secrecy is not maintained. VijayaKumar, P. et al., [23] proposed a key management protocol which reduces computation and storage cost during key updates. To enhance the scalability, the protocol has implemented on clustered tree base structure. However, the storage and communication overhead of key server has increased. Vijayakumar, P. et al., [25] have introduced a key management protocol which minimized the computation complexity of key server and group members. The protocol can handle batch join and batch leave operations efficiently. However, the initialization and storage cost of key server has increased. J. Zhang et al., [29] have investigated various key management schemes for secure communication in wireless sensor network. Yu-Lun Huang et al., [4] proposed key distribution scheme for securely distribution of encryption keys to the legal subscribers. The scheme requires only one multicast message to update the encryption key. It also reduced the computational cost since it needs to perform simple operations for key updating.
Most of the above mentioned protocols have poor performance in the process of joining / leaving of members and required higher storage space at member’s area to store the keys. This paper proposes an Efficient and Scalable Key Management Scheme (ESKMS) for secure multicast communication in multimedia applications to overcome these shortcomings. We summarize the characteristics of our proposed protocol for key distribution in secure group communication as below.
-
1)
The GM needs to share private keys with each group members in privacy during registration.
-
2)
Each group members will drive a common group key from encrypted message sent by GM.
-
3)
When some new members join the group, they can’t obtain any information regarding older group keys. Similarly, if some members exit the group, they can’t obtain any information regarding new group keys.
-
4)
The group key distribution process is separated into initialization, members joining, members leaving, massively joining and leaving members phase. The GM performs most of computation in the initialization phase, so that it can distributes the group key to group members very quickly.
-
5)
Our protocol drastically minimizes the computation load of GM and members and can efficiently deal with membership changes on a large scale.
-
6)
To protect the privacy of group key, it is updated periodically.
-
7)
Each key is fully independent from the keys which are generated in the future and have been used earlier.
-
8)
The presented scheme is secured against the various security attacks such as passive attack, impersonation attack, and collusion attack and preserves backward and forward secrecy.
3 Preliminaries
This section, presents symbol definition, the concept of our system model and adversary model. The brief review of the Chinese remainder theorem which is mainly used for key distribution is also presented.
3.1 Symbol Definition
The notations used throughout this paper are summarized in Table 1.
3.2 System Model
All the entities in the proposed ESKMS protocol are classified into three categories: 1) GM, 2) Member and 3) Adversary. The GM is a trusted authority. It issues private keys  to each group member. The GM generates and distributes the re-keying message to group members when a group membership is changed. To achieve fast rekeying, the GM performs most of the computations in initialization phase. A member is an entity who receives its private key \( {\mathcal{PK}}_{\mathcal{i}} \) from GM during joining phase. The members are expected to preserve the secrecy of own private key all the time, because the private keys are reused to recover the group key again when there is a change in the group membership. The members of the group are entitled to receive the common secret message sent by GM. The members recover a common group key from secret message sent by GM. An adversary is an entity who may perform various attacks on the proposed protocol. The adversaries may be insiders or outsiders according to whether they are group members or not. Our system model is based on key start architecture, where a group of legal members is directly linked with GM. The number of members considered for secure group communication in our system model is
to each group member. The GM generates and distributes the re-keying message to group members when a group membership is changed. To achieve fast rekeying, the GM performs most of the computations in initialization phase. A member is an entity who receives its private key \( {\mathcal{PK}}_{\mathcal{i}} \) from GM during joining phase. The members are expected to preserve the secrecy of own private key all the time, because the private keys are reused to recover the group key again when there is a change in the group membership. The members of the group are entitled to receive the common secret message sent by GM. The members recover a common group key from secret message sent by GM. An adversary is an entity who may perform various attacks on the proposed protocol. The adversaries may be insiders or outsiders according to whether they are group members or not. Our system model is based on key start architecture, where a group of legal members is directly linked with GM. The number of members considered for secure group communication in our system model is  + 1, which includes one GM and \( \mathcal{n} \) group members. In the proposed system model for secure key distribution, the group members are named as \( {\mathcal{M}}_i \) for \( i=1,2,3,\dots ..,\mathcal{n} \). The group key encryption key used to encrypt the group key is computed by the GM and is known only to GM itself. The private keys of the members are generated by GM in the initialization phase and distributed to group members at the time of joining into group. The private keys \( {\mathcal{PK}}_{\mathcal{i}} \) are known only to GM and members. The group key encryption key and member’s private keys are used within group for secure key distribution. In the proposed system model, it is assumed that there is no communication take place among members of the group. The system model is presented in Fig. 1.
+ 1, which includes one GM and \( \mathcal{n} \) group members. In the proposed system model for secure key distribution, the group members are named as \( {\mathcal{M}}_i \) for \( i=1,2,3,\dots ..,\mathcal{n} \). The group key encryption key used to encrypt the group key is computed by the GM and is known only to GM itself. The private keys of the members are generated by GM in the initialization phase and distributed to group members at the time of joining into group. The private keys \( {\mathcal{PK}}_{\mathcal{i}} \) are known only to GM and members. The group key encryption key and member’s private keys are used within group for secure key distribution. In the proposed system model, it is assumed that there is no communication take place among members of the group. The system model is presented in Fig. 1.
3.3 Adversary Model
Some reasonable assumptions are considered in proposed ESKMS protocol which are necessary for secure communication and are already employed in most of the protocols for key distribution. The GM is always trustworthy and has authentication system for the members of the group. For authentication, the system makes use of valid certificate which is issued by certification authority (CA) to the group members. The adversary  is assumed to be a probabilistic polynomial time adversary. We assume that an adversary \( \mathcal{A} \) never participates in the protocol as a member of the group. It is also assumed that the information about keys is kept secret by GM and group members in their database. The information related to key of any group member may be computed by an adversary \( \mathcal{A} \) using all information that it possesses and all capabilities that it owns. To obtain the private key \( {\mathcal{PK}}_{\mathcal{i}} \) of a member of the group, adversary \( \mathcal{A} \) may apply brute force attack. In our proposed protocol, the communicating parties (GM & group members) exchange secret messages over an insecure channel. Therefore, adversary capabilities usually include eavesdropping the transmitted messages over the public insecure channel and he/she can modify, insert, delete or replying it. It is also assume that all the communications between GM and members are authenticated. Therefore, it is not possible for adversary \( \mathcal{A} \) to initiate attacks by inserting, updating, deleting and replaying the message.
is assumed to be a probabilistic polynomial time adversary. We assume that an adversary \( \mathcal{A} \) never participates in the protocol as a member of the group. It is also assumed that the information about keys is kept secret by GM and group members in their database. The information related to key of any group member may be computed by an adversary \( \mathcal{A} \) using all information that it possesses and all capabilities that it owns. To obtain the private key \( {\mathcal{PK}}_{\mathcal{i}} \) of a member of the group, adversary \( \mathcal{A} \) may apply brute force attack. In our proposed protocol, the communicating parties (GM & group members) exchange secret messages over an insecure channel. Therefore, adversary capabilities usually include eavesdropping the transmitted messages over the public insecure channel and he/she can modify, insert, delete or replying it. It is also assume that all the communications between GM and members are authenticated. Therefore, it is not possible for adversary \( \mathcal{A} \) to initiate attacks by inserting, updating, deleting and replaying the message.
3.4 Chinese Remainder Theorem
The Chinese Remainder Theorem is used to find a common value from a system of congruences.
Theorem 3.1: Let m1, m2………. mn ∈ ℕ be a collection of pair wise co-prime integers ( i. e. gcd(mi, mj) = 1 for i ≠ j) and consider the following correspondence
Then for any given positive integers k1, k2, k3………kn, the system of following congruence equations
have a unique solution X modulo N; where N = m1 × m2 × ⋯⋯ × mn. For solution, the group members required to compute\( {N}_i=\frac{N}{m_i}\ for\ 1\le i\le n \). The Ni and mi be relatively prime( i. e. gcd(mi, Ni) = 1 for 1 ≤ i ≤ n). There exists two integers ai and bi such that\( {a}_i\ {N}_i+{b}_i{m}_i=1 \). The desired solution for the system of congruence equations is \( X\equiv {\sum}_{i=1}^n{k}_i{a}_i{N}_i\left(\mathit{\operatorname{mod}}\ N\right) \).
4 The Proposed ESKMS Protocol
This section presents a detailed description of our proposed ESKMS protocol, which is based on Chinese remainder theorem. The proposed protocol is divided into five phases. The initialization of GM is completed in the first phase of the protocol where the GM generates private keys \( {\mathcal{PK}}_{\mathcal{i}} \) and secret γi for each group member. In addition that the GM computes the group key encryption key  . The second phase is members joining phase where GM distributes private keys \( {\mathcal{PK}}_{\mathcal{i}} \) and secret number
. The second phase is members joining phase where GM distributes private keys \( {\mathcal{PK}}_{\mathcal{i}} \) and secret number  to the group members. Moreover, GM generates the group key and distributes it to the group members. The third phase is members leaving phase where GM updates group key encryption key and redistributes updated group key to the group members. The fourth phase is known as massively joining and leaving members phase, in which the massive changes in the group membership are handled efficiently. The massive changes in the group membership are possible if there are large requests from the members for joining and leaving. The last & fifth phase is periodically update phase in which the group key is updated after some fixed period of time regularly.
to the group members. Moreover, GM generates the group key and distributes it to the group members. The third phase is members leaving phase where GM updates group key encryption key and redistributes updated group key to the group members. The fourth phase is known as massively joining and leaving members phase, in which the massive changes in the group membership are handled efficiently. The massive changes in the group membership are possible if there are large requests from the members for joining and leaving. The last & fifth phase is periodically update phase in which the group key is updated after some fixed period of time regularly.
4.1 Initialization of System
First, the GM selects a large prime number  to define the multiplicative group
to define the multiplicative group  . Next, the GM selects private keys \( {\mathcal{PK}}_{\mathcal{i}} \) from multiplicative group \( {\mathbb{Z}}_{\mathcal{p}}^{\ast } \) for \( ^{\prime}\mathcal{n}^{\prime } \) number of members. The selected private keys \( {\mathcal{PK}}_{\mathcal{i}} \) should be primes or pairwise coprime positive numbers. Apart from this, all the selected private keys \( {\mathcal{PK}}_{\mathcal{i}} \) of group members should be greater than the group key
. Next, the GM selects private keys \( {\mathcal{PK}}_{\mathcal{i}} \) from multiplicative group \( {\mathbb{Z}}_{\mathcal{p}}^{\ast } \) for \( ^{\prime}\mathcal{n}^{\prime } \) number of members. The selected private keys \( {\mathcal{PK}}_{\mathcal{i}} \) should be primes or pairwise coprime positive numbers. Apart from this, all the selected private keys \( {\mathcal{PK}}_{\mathcal{i}} \) of group members should be greater than the group key  (i.e. \( {\mathcal{PK}}_{\mathcal{i}} \) \( >\mathcal{GK} \)) generated by GM. Furthermore, the GM selects \( ^{\prime}\mathcal{n}^{\prime } \) large and distinct prime numbers \( {\mathcal{p}}_i \) for the group members. To initialize the system, GM performs the steps given below.
(i.e. \( {\mathcal{PK}}_{\mathcal{i}} \) \( >\mathcal{GK} \)) generated by GM. Furthermore, the GM selects \( ^{\prime}\mathcal{n}^{\prime } \) large and distinct prime numbers \( {\mathcal{p}}_i \) for the group members. To initialize the system, GM performs the steps given below.
-
Step 1:
The GM compute
 = \( {\prod}_{i=1}^n \) \( {\mathcal{PK}}_{\mathcal{i}} \) and
= \( {\prod}_{i=1}^n \) \( {\mathcal{PK}}_{\mathcal{i}} \) and  , where \( {\mathcal{m}}_{\mathcal{i}} \) =
, where \( {\mathcal{m}}_{\mathcal{i}} \) =  for\( i=1,2,3,\dots ..,\mathcal{n} \).
for\( i=1,2,3,\dots ..,\mathcal{n} \). -
Step 2:
Next, the GM computes
 , such that \( {\mathcal{m}}_{\mathcal{i}}\times {\mathcal{n}}_{\mathcal{i}}\equiv 1\ \mathit{\operatorname{mod}} \) \( {\mathcal{PK}}_{\mathcal{i}} \). Here \( {\mathcal{n}}_{\mathcal{i}} \) is the multiplicative inverse of \( {\mathcal{m}}_{\mathcal{i}} \) with the modulus \( {\mathcal{PK}}_{\mathcal{i}} \).
, such that \( {\mathcal{m}}_{\mathcal{i}}\times {\mathcal{n}}_{\mathcal{i}}\equiv 1\ \mathit{\operatorname{mod}} \) \( {\mathcal{PK}}_{\mathcal{i}} \). Here \( {\mathcal{n}}_{\mathcal{i}} \) is the multiplicative inverse of \( {\mathcal{m}}_{\mathcal{i}} \) with the modulus \( {\mathcal{PK}}_{\mathcal{i}} \). -
Step 3:
Next, the GM computes γi, such that \( {\gamma}_i={\mathcal{p}}_i\times {\mathcal{m}}_{\mathcal{i}}\times {\mathcal{n}}_{\mathcal{i}} \). Here γi is the secret share of group key encryption key δℊ for the group member \( {\mathcal{m}}_{\mathcal{i}} \).
-
Step 4:
Finally, the GM computes group key encryption key δℊ such that

Initially, the GM executes initialization phase for the group of size \( \mathcal{n} \) (i.e. | | = \( \mathcal{n} \)). If the members in the group are reached up to \( \mathcal{n} \) (total size), then GM again executes initialization phase to compute \( \mathcal{M} \), \( {\gamma}_i \), and δℊ for
| = \( \mathcal{n} \)). If the members in the group are reached up to \( \mathcal{n} \) (total size), then GM again executes initialization phase to compute \( \mathcal{M} \), \( {\gamma}_i \), and δℊ for  number of members where \( {\mathcal{n}}_{\mathcal{m}} \) = \( \mathcal{n}\times \mathcal{t} \) (i.e., for
number of members where \( {\mathcal{n}}_{\mathcal{m}} \) = \( \mathcal{n}\times \mathcal{t} \) (i.e., for  times of \( \mathcal{n} \) members) without changing secrets \( {\mathcal{p}}_i \) and private keys \( {\mathcal{PK}}_{\mathcal{i}} \) of existing \( \mathcal{n} \) members . The value of \( \mathcal{t} \) is not fixed. It may be changed depending on the dynamic nature of the group i.e., it depends on the rate of new members joining the group. In this research work, the value of \( \mathcal{t} \) is assumed to be \( \mathcal{t}\le 10 \) because at a time, large number of subscribers may join Pay-TV system to subscribe the channels. Therefore, dynamic nature of the group plays major role to select the value of \( \mathcal{t} \). If the group expands beyond the maximum size (the group size taken at the initialization of the system for example \( \mathcal{n} \)) then GM expands the group by computing new \( \mathcal{M} \), \( {\gamma}_i \), and δℊ and storing them in its database for large set of members without changing the key parameters already assigned to the existing members. To reduce the computational cost of key update process, the GM performs most of the computations in initialization phase in offline mode before group is formed. Therefore, computation complexity of initialization phase in the online mode is negligible. Therefore, our scheme can efficiently handle very large groups i.e. groups of millions of members because it requires few computations for updating the keys.
times of \( \mathcal{n} \) members) without changing secrets \( {\mathcal{p}}_i \) and private keys \( {\mathcal{PK}}_{\mathcal{i}} \) of existing \( \mathcal{n} \) members . The value of \( \mathcal{t} \) is not fixed. It may be changed depending on the dynamic nature of the group i.e., it depends on the rate of new members joining the group. In this research work, the value of \( \mathcal{t} \) is assumed to be \( \mathcal{t}\le 10 \) because at a time, large number of subscribers may join Pay-TV system to subscribe the channels. Therefore, dynamic nature of the group plays major role to select the value of \( \mathcal{t} \). If the group expands beyond the maximum size (the group size taken at the initialization of the system for example \( \mathcal{n} \)) then GM expands the group by computing new \( \mathcal{M} \), \( {\gamma}_i \), and δℊ and storing them in its database for large set of members without changing the key parameters already assigned to the existing members. To reduce the computational cost of key update process, the GM performs most of the computations in initialization phase in offline mode before group is formed. Therefore, computation complexity of initialization phase in the online mode is negligible. Therefore, our scheme can efficiently handle very large groups i.e. groups of millions of members because it requires few computations for updating the keys.
4.2 Members Joining
Whenever a new member \( {\mathcal{M}}_i \) is authorized to join the group \( \mathcal{G} \) for the first time, the GM sends a private key \( {\mathcal{PK}}_i \) and a unique secret number \( {\mathcal{p}}_i \) to the member using secure channel like SSL. The private key \( {\mathcal{PK}}_i \) and secret number \( {\mathcal{p}}_i \) are only known to member \( {\mathcal{M}}_i \) and GM. After receiving \( {\mathcal{PK}}_i \) and \( {\mathcal{p}}_i \) from GM, the member \( {\mathcal{M}}_i \) computes \( {\mathcal{q}}_i \) the multiplicative inverse of \( {\mathcal{p}}_i \) modulus \( {\mathcal{PK}}_i \) such that \( {\mathcal{p}}_i\times {\mathcal{q}}_i\equiv 1\ \mathit{\operatorname{mod}} \) \( \left({\mathcal{PK}}_i\right) \). Next, the GM generates and distributes the \( \mathcal{GK} \) to the group member using the procedure given below.
-
Step 1:
Initially, the GM selects \( \mathcal{GK} \), a random element
 \( ^{\prime}\mathcal{K}^{\prime } \) such that
\( ^{\prime}\mathcal{K}^{\prime } \) such that 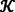 < \( {\mathcal{PK}}_{\mathcal{i}} \) for\( i=1,2,3,\dots ..,\mathcal{n} \).
< \( {\mathcal{PK}}_{\mathcal{i}} \) for\( i=1,2,3,\dots ..,\mathcal{n} \). -
Step 2:
Next, the GM encrypt the newly generated \( \mathcal{GK} \) with the help of group key encryption key δℊ and generates cipher-text
 by using following eq. (1).
by using following eq. (1).

-
Step 3:
Finally, the cipher-text \( \mathcal{CT} \) generated in step-2 is sent by GM to the group members using multicast. After obtaining the cipher-text \( \mathcal{CT} \) from GM, an authorize member \( {\mathcal{M}}_i \) of the group can obtain the \( \mathcal{GK} \) \( ^{\prime}\mathcal{K}^{\prime } \) by using the following eq. (2).

Therefore, the members of the group can find the updated \( \mathcal{GK} \), \( {\mathcal{K}}^{\prime } \) by performing one multiplication and one modulus operation. The Diagrammatic sketch of proposed key management scheme for secure multicast communication is presented in Fig. 2.
4.3 Members Leaving
Whenever, member \( {\mathcal{M}}_i \) leaves the group, the GM removes his/her private key \( {\mathcal{PK}}_{\mathcal{i}} \) and secret number \( {\mathcal{p}}_i \) from the database of active group members and update the group encryption key δℊ. After that the GM generate new \( \mathcal{GK} \), \( \mathcal{K}^{\prime } \) and broadcast it to remaining members. To perform leave operation, the GM needs to perform the steps given below.
-
Step 1:
Initially, GM updates group key encryption key δℊ and computes new group key encryption key
 with help of secret share γi of leaving member as shown in (3)
with help of secret share γi of leaving member as shown in (3)

-
Step 2:
Next, the GM generates new \( \mathcal{GK} \), \( \mathcal{K}^{\prime } \). To generate new encrypted rekeying message, the GM encrypts newly generated \( \mathcal{K}^{\prime } \) using updated group key encryption key \( {\delta}_{\mathcal{g}}^{\prime } \) as shown in (4).

-
Step 3:
Finally, the cipher-text \( \mathcal{CT}^{\prime } \) generated in step-2 is sent by GM to available group members using multicast. The existing group members compute the updated \( \mathcal{GK} \), \( \mathcal{K}^{\prime } \) by performing one multiplication and one modulus operation as shown in following eq. (5)

The leaving member \( {\mathcal{M}}_i \) is not able to find the refreshed \( \mathcal{GK} \), \( \mathcal{K}^{\prime } \), because his/her secret share γi is not incorporated in \( {\delta}_{\mathcal{g}}^{\prime } \). Therefore, our ESKMS scheme ensures that only the members whose γi values are used to generate the rekeying message are able to recover the updated \( \mathcal{GK} \). Therefore, the proposed protocol fulfils the initial requirement of forward and backward secrecy.
4.4 Massively Joining and Leaving Members
Let \( \left(\mathcal{n}-\mathcal{m}\right) \) members are presently available in the group, where \( \mathcal{n}>0 \) and \( \mathcal{n}>\mathcal{m}>0 \), and a set of \( \mathcal{m} \) members join the group, where \( \mathcal{m}>0 \). After joining of \( \mathcal{m} \) new members, the group consist of \( \mathcal{n} \) members which are represented by \( {\mathcal{M}}_1,{\mathcal{M}}_2,{\mathcal{M}}_3,\dots \dots ..{\mathcal{M}}_n \). In general, if a set of \( \mathcal{m} \) members join the group then GM requires to execute \( \mathcal{m} \) number of addition operations for updating the \( \mathcal{GK} \). Suppose a batch of five members \( {\mathcal{M}}_6,{\mathcal{M}}_7,{\mathcal{M}}_8,{\mathcal{M}}_9\ \mathrm{and}\ {\mathcal{M}}_{10} \) join the group, then the GM directly selects the values of secret shares γ6, γ7, γ8, γ9 and γ10 of joining members from database that are computed in system initialization phase. In the proposed protocol the values of secret shares for the entire group of size \( \mathcal{n} \) is computed in the initialization phase rather than computing at the time of joining. After that the GM compute updated group key encryption key \( {\delta}_{\mathcal{g}}^{\prime }\ \mathrm{as}\kern0.50em {\delta}_{\mathcal{g}}^{\prime }={\delta}_{\mathcal{g}}+\left({\gamma}_6+{\gamma}_7+{\gamma}_8+{\gamma}_9+{\gamma}_{10}\right) \). Next, the GM needs to update old \( \mathcal{GK} \) and generate the new \( \mathcal{GK} \), \( \mathcal{K}^{\prime } \). After that, GM encrypt newly generated \( \mathcal{GK} \) with the help of updated \( {\delta}_{\mathcal{g}}^{\prime } \) to form new rekeying message for members as shown in (4). The cipher text \( \mathcal{CT}^{\prime } \) of encrypted \( \mathcal{GK} \) is transmitted to all existing and newly added group members by GM using multicast. After obtaining \( \mathcal{CT}^{\prime } \), sent by the GM, the members of the group need to perform one multiplication and one modulus operation to recover the updated \( \mathcal{GK} \), \( \mathcal{K}^{\prime } \) as shown in (5). All legal members of the group are able to recover the updated \( \mathcal{GK} \), \( \mathcal{K}^{\prime } \) from cipher-text \( \mathcal{CT}^{\prime } \)since their γi are included in \( {\delta}_{\mathcal{g}}^{\prime } \). Therefore, if a set of \( \mathcal{m} \) members join the present group then to update old \( \mathcal{GK} \), the GM needs to perform \( \mathcal{m} \) addition operations.
Similarly, let \( \left(\mathcal{n}+\ell \right) \) members presently available in the group, where \( \mathcal{n}>0 \) and ℓ > 0, and a set of ℓ members leave the group, where ℓ > 0. After leaving of ℓ members, the group has \( \mathcal{n} \) members. The remaining members in the group are represented by \( {\mathcal{M}}_1,{\mathcal{M}}_2,{\mathcal{M}}_3,\dots \dots ..{\mathcal{M}}_n \). In general, if a set of ℓ members exits from the group, the GM requires to execute ℓ − 1 number of addition operations and one subtraction operation for updating the \( \mathcal{GK} \). Suppose a batch of five members \( {\mathcal{M}}_6,{\mathcal{M}}_7,{\mathcal{M}}_8,{\mathcal{M}}_9\ \mathrm{and}\ {\mathcal{M}}_{10} \) leaves the group, then instead of updating the \( \mathcal{GK} \) encryption key of the individual member leaving the group, the GM directly update the \( \mathcal{GK} \) encryption key \( {\delta}_{\mathcal{g}}^{\prime } \) such that \( {\delta}_{\mathcal{g}}^{\prime }={\delta}_{\mathcal{g}}-\left({\gamma}_6+{\gamma}_7+{\gamma}_8+{\gamma}_9+{\gamma}_{10}\right) \). Next, the GM needs to update old \( \mathcal{GK} \) and generate the new \( \mathcal{GK} \), \( \mathcal{K}^{\prime } \). After that the GM encrypts updated \( \mathcal{GK} \) with the help of \( {\delta}_{\mathcal{g}}^{\prime } \) to form new rekeying message for remaining members as shown in (4). The cipher text \( \mathcal{CT}^{\prime } \) of encrypted \( \mathcal{GK} \) is transmitted to all the remaining group members by GM using multicast. After obtaining \( \mathcal{CT}^{\prime } \), sent by GM, the members of the group needs to perform one multiplication and one modulus operation to recover the updated \( \mathcal{GK} \), \( \mathcal{K}^{\prime } \)as shown in (5). The leaving members \( {\mathcal{M}}_6,{\mathcal{M}}_7,{\mathcal{M}}_8,{\mathcal{M}}_9\ \mathrm{and}\ {\mathcal{M}}_{10} \) are not able to recover the refreshed \( \mathcal{GK} \), \( \mathcal{K}^{\prime } \) from cipher-text \( \mathcal{CT}^{\prime } \), since their γi parameter values are not included in \( {\delta}_{\mathcal{g}}^{\prime } \). Therefore, if a set of ℓ members exits from the group then to update the old \( \mathcal{GK} \), the GM needs to perform ℓ − 1 addition operations and one subtraction operation.
Our scheme is highly scalable i.e., it handles large groups efficiently and large number of members may join/ leave the group because it requires few computations for updating the keys. Therefore, our scheme can efficiently handle very large groups i.e. groups of millions of members. The proposed ESKMS scheme has drastically reduced the computational complexity of GM for key update operation performed to handle mass join and mass leave. The procedures for massive join/leave and group key extraction are given in Algorithm 1 and Algorithm 2.
4.5 Periodically Update
To ensure the information security, the group key \( \mathcal{K} \) should be updated periodically. If due to not changing in the group membership from long period of time, the group key \( \mathcal{K} \) is not updated within the time period, then to update the group key \( \mathcal{K} \), the periodically update process is initiated. In order to provide the confidentiality for communication in the group, the GM starts periodically update process to change the group key before exceed the given time frame. In each periodically update process, the GM needs to re-generate a new group key \( \mathcal{K}^{\prime } \), and computes new rekeying message which is transmitted to the group members.


4.6 Hierarchal Key Management Scheme for CAS
The proposed ESKMS scheme can be easily integrated into CAS of digital pay-TV system because it can be represented into three or four level hierarchical structure. In order to provide the efficiency and higher level security, the key management system of CAS organised the keys in a hierarchical structure. In digital pay-TV systems the media contents are encrypted with Control Words (CWs). For higher security of media contents the CWs are updated frequently after about 5–20 s. The CWs are encrypted with Authorization Key (AK) called channel key to generate Entitlement Control Message (ECM) using symmetric key algorithm. From the security point of view the authorization key is updated weekly or monthly. Each subscriber has unique private key issued by SP and it will never be updated. The AK is encrypted by private keys of members. In our proposed scheme, the Subgroup Key Encryption Key is generated which is used to encrypt the AK. The encrypted AK form a message called the Entitlement Management Message (EMM). The subscriber can obtain the AK using his/her private key while receiving EMM. Then, the subscriber can use AK to obtain CWs in order to descramble the media contents. The concept of key hierarchy used in a CAS is presented in Fig. 3.
Therefore, in the key hierarchy structure a second level key is needed to protect the first level key. Similarly, a third level key is needed to protect the second level key. Whenever key needs to be exchanged, another key from one level up is used to encrypt this message.
4.7 Correctness Analysis of ESKMS Scheme
Theorem 4.1: All the authorized members of the group can recover group key\( \mathcal{K} \), from the cipher-text \( \mathcal{CT} \) sent by GM i.e. K = ((CT mod () × IIi) mod (.))
Proof
The proposed ESKMS scheme generates rekeying messages for every change in the group membership by using eq. (1) and generates cipher-text \( \mathcal{CT} \). The GM transmitted the cipher-text \( \mathcal{CT} \) to members of the group using multicast. After getting \( \mathcal{CT} \), the legal members of the group are able to recover the \( \mathcal{GK} \), \( \mathcal{K} \) by using the following equation.

Therefore, all the authorized members of the group can recover group key \( \mathcal{K} \)
5 Security Analysis
This section presents the detailed security analysis of our proposed ESKMS scheme. Our security analysis is mainly focuses on how the proposed ESKMS scheme is secured against various security attacks such as passive attack, collusion attack and impersonation attack etc. Moreover, the analysis is also focus on how our scheme fulfils the initial security requirements of group backward and forward secrecy and how it achieves confidentiality in the group communication. In the scheme, it is assumed that the GM keeps secret the values of \( {\mathcal{PK}}_{\mathcal{i}} \), \( {\gamma}_i \)and δℊ in its own database. Moreover, the members keep secret the values of \( {\mathcal{PK}}_{\mathcal{i}} \) and \( {\mathcal{q}}_i \) in its own database. It is also assumed that adversary \( \mathcal{A} \) may sometimes be a member of the group.
5.1 Forward Secrecy
The forward secrecy is the security technique which ensures that the leaving members are unable to use the upcoming communications which will be done after executing leave operation. In the proposed scheme, the members leaving procedure satisfies the properties of forward secrecy.
Theorem 5.1:
A leaving member removes from the group at time frame
\( \mathcal{t} \)
, then he/she cannot access any keys used to encrypt the group key
 after
\( \mathcal{t} \)
.
after
\( \mathcal{t} \)
.
Proof: Suppose at time frame \( \mathcal{t} \), a member \( {\mathcal{m}}_{\mathcal{i}} \) leaves the group and he/she try to compute newer group key by performing possible attacks to read the communication of GM and group members which take place at time frame (\( \mathcal{t}+1 \)). To obtain the updated GK, the leaving members may try to attempt possible attacks in the system. The evicted member can easily read the cipher-text \( \mathcal{CT} \) of newer group key sent by GM to group members through open channel. However, it is impossible for evicted members to obtain newer group key GK from \( \mathcal{CT} \), since their private keys \( {\mathcal{PK}}_{\mathcal{i}} \) and \( {\gamma}_i \) has been deleted by the GM from active list. Therefore, the evicted members are unable to recover new GK in a feasible manner, since their private keys \( {\mathcal{PK}}_{\mathcal{i}} \) and \( {\gamma}_i \) are not used to encrypt the new GK. To obtain new GK, the evicted members required to know the private key \( {\mathcal{PK}}_{\mathcal{i}} \) and secret  of current group members which are kept secret by GM and members in their database.
of current group members which are kept secret by GM and members in their database.
To know \( {\mathcal{PK}}_{\mathcal{i}} \) and \( {\mathcal{q}}_{\mathcal{i}} \), the evicted members may try to make use of any impracticable procedure. It is assumed that an evicted member may be an adversary in the system. Therefore, it is impracticable for an adversary A to obtain \( {\mathcal{PK}}_{\mathcal{i}} \) and \( {\mathcal{q}}_{\mathcal{i}} \) since, these parameters are sent by GM to members using unicast via Secure Sockets Layer (SSL) channel at the time of joining. Even though adversary A somehow knows \( {\mathcal{PK}}_{\mathcal{i}} \), after that to compute newer GK, he/she required to know \( {\mathcal{q}}_{\mathcal{i}} \) or if he/she knows \( {\mathcal{q}}_{\mathcal{i}} \) then required to know \( {\mathcal{PK}}_{\mathcal{i}} \). Therefore, to compute GK, both \( {\mathcal{PK}}_{\mathcal{i}} \) and \( {\mathcal{q}}_{\mathcal{i}} \) should be known. An adversary A may try to make use of brute force attack to obtain both \( {\mathcal{PK}}_{\mathcal{i}} \) and \( {\mathcal{q}}_{\mathcal{i}} \). To compute \( {\mathcal{PK}}_{\mathcal{i}} \), an adversary A required to perform \( {\left\{0,1\right\}}^{{\mathcal{pk}}_{\mathcal{bs}}} \) attempts, where  is the length of \( {\mathcal{PK}}_{\mathcal{i}} \) in bits. Similarly, to compute \( {\mathcal{q}}_{\mathcal{i}} \), he/she required to perform \( {\left\{0,1\right\}}^{{\mathcal{q}}_{\mathcal{bs}}} \) attempts, where
is the length of \( {\mathcal{PK}}_{\mathcal{i}} \) in bits. Similarly, to compute \( {\mathcal{q}}_{\mathcal{i}} \), he/she required to perform \( {\left\{0,1\right\}}^{{\mathcal{q}}_{\mathcal{bs}}} \) attempts, where  is the length of \( {\mathcal{q}}_{\mathcal{i}} \) in bits. Therefore, it is not easily possible to find group key information by a feasible method for an adversary to read the future communication. As a result our proposed ESKMS scheme fulfils the initial requirement of forward secrecy. The total time required to break forward secrecy of our scheme is described in the following Eq. (6)
is the length of \( {\mathcal{q}}_{\mathcal{i}} \) in bits. Therefore, it is not easily possible to find group key information by a feasible method for an adversary to read the future communication. As a result our proposed ESKMS scheme fulfils the initial requirement of forward secrecy. The total time required to break forward secrecy of our scheme is described in the following Eq. (6)

Where,
- τforward secrecy:
-
Total time required to break the forward secrecy of the proposed scheme
 :
:-
Time taken to obtain the private key \( {\mathcal{PK}}_{\mathcal{i}} \) of a present group member using brute force attack
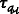 :
:-
Time taken to obtain the secret parameter \( {\mathcal{q}}_{\mathcal{i}} \) of a present group member using brute force attack
Finally, it is concluded that adversary A cannot decipher the cipher-text \( \mathcal{CT} \) of encrypted GK in the reasonable amount of time. Therefore, adversary A cannot read the future communications, which means scheme fulfil first initial security requirement of forward secrecy.
5.2 Backward Secrecy
The backward secrecy is the security technique which prevents the newly joining members from having access of previous communications. In the proposed scheme, the members joining procedure satisfies the properties of backward secrecy.
Theorem 5.2: A joining member added in the group at time frame \( \mathcal{t} \) then he/she cannot access any keys used to encrypt the group key GK before \( \mathcal{t} \) .
Proof: Suppose, at time frame \( \mathcal{t} \), a member \( {\mathcal{m}}_{\mathcal{i}} \) joins the group and he/she may try to compute the older group key GK, by performing possible attacks to access the communication of GM and members which take place at time frame (\( \mathcal{t}-1 \)) i.e. the communication happened before joining the group. In proposed scheme, the private keys \( {\mathcal{PK}}_{\mathcal{i}}\in {\mathbb{Z}}_{\mathcal{p}}^{\ast } \) and secret \( {\mathcal{p}}_{\mathcal{i}} \) are distributed by the GM to the members at the time of joining using secure unicast channel. In the scheme it is assumed that the \( {\mathcal{PK}}_{\mathcal{i}} \) should be distinct and large so that no private keys of the members are common. Similarly, the secret \( {\mathcal{p}}_{\mathcal{i}} \) should not be common for any group member. The \( {\mathcal{PK}}_{\mathcal{i}} \) and \( {\mathcal{p}}_{\mathcal{i}} \) are kept secret by members and GM. The value of \( {\mathcal{q}}_{\mathcal{i}} \) is computed by member \( {\mathcal{m}}_{\mathcal{i}} \) at his/her area using congruence \( {\mathcal{p}}_i\times {\mathcal{q}}_i\equiv 1\ \mathit{\operatorname{mod}}\ \left({\mathcal{PK}}_i\right) \) . The \( {\mathcal{q}}_i \) is kept secret by member \( {\mathcal{m}}_{\mathcal{i}} \) in his/her database. Therefore, the \( {\mathcal{q}}_i \) is also secured.
The member joins the group at time frame \( \mathcal{t} \) cannot access the past communication happened earlier at time frame (\( \mathcal{t}-1 \)) since, the private key \( {\mathcal{PK}}_{\mathcal{i}} \) of newly joined member is not used to distribute the old group key GK. Suppose, at time frame (\( \mathcal{t}+1 \)), an adversary A gets authentication and becomes a member of the group for some time then in order to read old communication, he/she may try to compute old \( \mathcal{GK} \). In the proposed scheme, it is not feasible for adversary \( \mathcal{A} \) to derive old \( \mathcal{GK} \) even if he/she has become a member of the group because the old \( \mathcal{GK} \) is not used for any purpose. To encrypt the updated \( \mathcal{GK} \), the group key encryption key δℊ and member’s private keys \( {\mathcal{PK}}_{\mathcal{i}} \) are used. Likewise, to derive the updated \( \mathcal{GK} \), the member’s \( {\mathcal{PK}}_{\mathcal{i}} \) and \( {\mathcal{q}}_{\mathcal{i}} \) are used. The cipher-text \( \mathcal{CT} \) of updated \( \mathcal{GK} \) is transmitted through open channel, therefore, an adversary can easily obtain \( \mathcal{CT} \) and try to derive the updated \( \mathcal{GK} \). The adversary \( \mathcal{A} \) could not decrypt it because his/her \( {\mathcal{PK}}_{\mathcal{i}} \) and  are not used earlier to transmit the old \( \mathcal{GK} \) as well as he/she does not have \( {\mathcal{PK}}_{\mathcal{i}} \) and \( {\mathcal{q}}_{\mathcal{i}} \) of any old group member. Therefore, to access the old communications, the adversary \( \mathcal{A} \) may try to compute \( {\mathcal{PK}}_{\mathcal{i}} \) and \( {\mathcal{q}}_{\mathcal{i}} \) of any old group member.
are not used earlier to transmit the old \( \mathcal{GK} \) as well as he/she does not have \( {\mathcal{PK}}_{\mathcal{i}} \) and \( {\mathcal{q}}_{\mathcal{i}} \) of any old group member. Therefore, to access the old communications, the adversary \( \mathcal{A} \) may try to compute \( {\mathcal{PK}}_{\mathcal{i}} \) and \( {\mathcal{q}}_{\mathcal{i}} \) of any old group member.
The \( {\mathcal{PK}}_{\mathcal{i}} \), \( {p}_{\mathcal{i}} \) and \( {\mathcal{q}}_{\mathcal{i}} \) are kept secret by GM and members. Therefore, to compute \( {\mathcal{PK}}_{\mathcal{i}} \) and \( {\mathcal{q}}_{\mathcal{i}} \), the adversary \( \mathcal{A} \) may try to make use of brute force attack. In our ESKMS scheme, it is impossible for an adversary \( \mathcal{A} \) to compute \( {\mathcal{PK}}_{\mathcal{i}} \) and \( {\mathcal{q}}_{\mathcal{i}} \) in a reasonable amount of time using brute force attack. To compute \( {\mathcal{PK}}_{\mathcal{i}} \), an adversary A required to perform \( {\left\{0,1\right\}}^{{\mathcal{pk}}_{\mathcal{bs}}} \) attempts, where \( {\mathcal{pk}}_{\mathcal{bs}} \) is the length of \( {\mathcal{PK}}_{\mathcal{i}} \) in bits. Suppose, an adversary requires 1 to perform one attempt then he/she requires 2
to perform one attempt then he/she requires 2 ηs, where
ηs, where  is bit size of \( {\mathcal{PK}}_{\mathcal{i}} \), to compute the \( {\mathcal{PK}}_{\mathcal{i}} \). Similarly, to compute \( {\mathcal{q}}_{\mathcal{i}} \), he/she required to perform \( {\left\{0,1\right\}}^{{\mathcal{q}}_{\mathcal{bs}}} \) attempts, and requires
is bit size of \( {\mathcal{PK}}_{\mathcal{i}} \), to compute the \( {\mathcal{PK}}_{\mathcal{i}} \). Similarly, to compute \( {\mathcal{q}}_{\mathcal{i}} \), he/she required to perform \( {\left\{0,1\right\}}^{{\mathcal{q}}_{\mathcal{bs}}} \) attempts, and requires  ηs, where \( {\mathcal{q}}_{\mathcal{bs}} \) is the length of \( {\mathcal{q}}_{\mathcal{i}} \) in bits to compute \( {\mathcal{q}}_{\mathcal{i}} \). Therefore, it is not easily possible to find group key information by a feasible method for an adversary to read the future communication. As a result our proposed ESKMS scheme fulfils the initial requirement of forward secrecy. The total time taken to break backward secrecy of our scheme is given by the Eq.(7)
ηs, where \( {\mathcal{q}}_{\mathcal{bs}} \) is the length of \( {\mathcal{q}}_{\mathcal{i}} \) in bits to compute \( {\mathcal{q}}_{\mathcal{i}} \). Therefore, it is not easily possible to find group key information by a feasible method for an adversary to read the future communication. As a result our proposed ESKMS scheme fulfils the initial requirement of forward secrecy. The total time taken to break backward secrecy of our scheme is given by the Eq.(7)

Where,
- τBackward secrecy:
-
Total time taken to break the backward secrecy of the proposed scheme
- \( {\tau}_{{\mathcal{PK}}_{\mathcal{i}}} \):
-
Time required to obtain the private key \( {\mathcal{PK}}_{\mathcal{i}} \) of an old group member using brute force attack
- \( {\tau}_{{\mathcal{q}}_{\mathcal{i}}} \):
-
Time required to obtain the secret parameter \( {\mathcal{q}}_{\mathcal{i}} \) an old group member using brute force attack
Finally, it is concluded that adversary A can neither obtain old group key \( \mathcal{GK} \) nor \( {\mathcal{PK}}_{\mathcal{i}} \) & \( {\mathcal{q}}_{\mathcal{i}} \) of any old group member in the reasonable amount of time. Therefore, adversary A cannot read the old communications, which means scheme fulfil second initial security requirement of backward secrecy.
5.3 Passive Attack
A passive attack on a scheme is one in which the adversaries cannot interact with any of the member involved in the group communication. In passive attack, adversaries can break the privacy of a scheme by capturing messages distributed among authorized members.
Theorem 5.3: Outsider cannot recover the group key and no adversary can obtain the private keys of legal group members by passive attack.
Proof: Suppose, the GM sends the cipher-text \( \mathcal{CT} \) as a broadcast message through an open channel to all group members to compute updated group key. In order to compute the updated group key, an adversary is possible to capture this \( \mathcal{CT} \) and he/she can store it in his/her storage area. To compute the group key from \( \mathcal{CT}, \) an adversary needs the private key \( {\mathcal{PK}}_{\mathcal{i}} \) and secrets \( {\mathcal{q}}_{\mathcal{i}} \) of any member presently involved in group communication. For an adversary, it is impracticable to get \( {\mathcal{PK}}_{\mathcal{i}}\ \mathrm{and}\ {\mathcal{q}}_{\mathcal{i}} \) of a present group member in a reasonable amount of time because the GM has transmitted \( {\mathcal{PK}}_{\mathcal{i}}\ \mathrm{and}\ {\mathcal{q}}_{\mathcal{i}} \) through secure channel like SSL and every group member kept secret these parameters in its storage area. Even if an adversary is an evicted member and he/she contains its own \( {\mathcal{PK}}_{\mathcal{i}\mathrm{old}}\ \mathrm{and}\ {\mathcal{q}}_{\mathcal{i}\mathrm{old}} \) then he/she is not able to compute the updated group key from the cipher-text \( \mathcal{CT} \) as

From Eq. (8) it is clear that any evicted member is not able to obtain the updated group key since his/her secret parameters, \( {\mathcal{PK}}_{\mathcal{i}\mathrm{old}}\ \mathrm{and}\ {\upgamma}_{\mathcal{i}\mathrm{old}} \) are expelled from active list. Therefore, an outsider can neither obtain the group key nor private key of a member by using the passive attack.
5.4 Collusion Attack
A Collusion attack is a type of attack in which multiple members may collude and try to share their keys to compute unknown keys. Many legitimate members who are participated in the group as members for sometime but after leaving from the group they may collide to derive the new group key and existing member’s private keys.
Theorem 5.4: By sharing previously used private keys and group keys, multiple evicted members cannot derive any private key and group key of present group members.
Proof: Let the group members  1, m2, m3, ………. mk have their private key
1, m2, m3, ………. mk have their private key  1, \( {\mathcal{PK}}_2,{\mathcal{PK}}_3,\dots \dots \dots .{\mathcal{PK}}_{\mathrm{k}} \) and secret
1, \( {\mathcal{PK}}_2,{\mathcal{PK}}_3,\dots \dots \dots .{\mathcal{PK}}_{\mathrm{k}} \) and secret  1, q2, q3, ………. qk respectively. The value of \( {\gamma}_i \) of each group member is kept secret by GM. Suppose there are
1, q2, q3, ………. qk respectively. The value of \( {\gamma}_i \) of each group member is kept secret by GM. Suppose there are  members present in the group at time frame \( \mathcal{t} \). Let the member m1 leaves the group at time frame (\( \mathcal{t}+1 \)) and he/she knows the values of \( \mathcal{GK},{\mathcal{PK}}_1,{\mathcal{q}}_1 \) and \( {\mathcal{p}}_1 \). At the same time the GM updates GK encryption key δℊ as \( {\delta}_{\mathcal{g}}^{\prime } \) = δℊ − γ1, where γ1is the secret share of group key encryption key δℊ of member m1. And the GM generates new \( {\mathcal{GK}}^{\prime } \) and transmit it to remaining (\( \mathcal{k}-1 \)) group members. Next, at time frame (\( \mathcal{t}+2 \)), another member m3 leaves the group who knows the values of \( \mathcal{GK} \), \( {\mathcal{GK}}^{\prime },{\mathcal{PK}}_3,{\mathcal{q}}_3 \) and\( {\mathcal{p}}_3 \). And the GM updates \( {\delta}_{\mathcal{g}}^{\prime } \) as
members present in the group at time frame \( \mathcal{t} \). Let the member m1 leaves the group at time frame (\( \mathcal{t}+1 \)) and he/she knows the values of \( \mathcal{GK},{\mathcal{PK}}_1,{\mathcal{q}}_1 \) and \( {\mathcal{p}}_1 \). At the same time the GM updates GK encryption key δℊ as \( {\delta}_{\mathcal{g}}^{\prime } \) = δℊ − γ1, where γ1is the secret share of group key encryption key δℊ of member m1. And the GM generates new \( {\mathcal{GK}}^{\prime } \) and transmit it to remaining (\( \mathcal{k}-1 \)) group members. Next, at time frame (\( \mathcal{t}+2 \)), another member m3 leaves the group who knows the values of \( \mathcal{GK} \), \( {\mathcal{GK}}^{\prime },{\mathcal{PK}}_3,{\mathcal{q}}_3 \) and\( {\mathcal{p}}_3 \). And the GM updates \( {\delta}_{\mathcal{g}}^{\prime } \) as  = \( {\delta}_{\mathcal{g}}^{\prime } \) − γ3 and generates and distributes new \( {\mathcal{GK}}^{\prime \prime } \). After leaving, the members m1 and m3 may collide and share GK, \( {\mathcal{PK}}_1,{\mathcal{q}}_1,{\mathcal{p}}_1,{\mathcal{GK}}^{\prime },{\mathcal{PK}}_3,{\mathcal{q}}_3 \) and\( {\mathcal{p}}_3 \) in order to compute \( {\mathcal{GK}}^{\prime \prime \prime }, \), \( {\mathcal{PK}}_{\mathcal{i}} \) and \( {\mathcal{q}}_{\mathcal{i}} \) of existing group members at time frame (\( \mathcal{t}+3 \)). Therefore, both members m1 and m3 have all the keys transmitted by GM to group members between the time intervals from (\( \mathcal{t}+1 \)) to (\( \mathcal{t}+2 \)).
= \( {\delta}_{\mathcal{g}}^{\prime } \) − γ3 and generates and distributes new \( {\mathcal{GK}}^{\prime \prime } \). After leaving, the members m1 and m3 may collide and share GK, \( {\mathcal{PK}}_1,{\mathcal{q}}_1,{\mathcal{p}}_1,{\mathcal{GK}}^{\prime },{\mathcal{PK}}_3,{\mathcal{q}}_3 \) and\( {\mathcal{p}}_3 \) in order to compute \( {\mathcal{GK}}^{\prime \prime \prime }, \), \( {\mathcal{PK}}_{\mathcal{i}} \) and \( {\mathcal{q}}_{\mathcal{i}} \) of existing group members at time frame (\( \mathcal{t}+3 \)). Therefore, both members m1 and m3 have all the keys transmitted by GM to group members between the time intervals from (\( \mathcal{t}+1 \)) to (\( \mathcal{t}+2 \)).
Using these known key values, the collision of multiple leaving members cannot be used to get information related to congruence system and to compute the updated \( {\mathcal{GK}}^{\prime \prime \prime } \) which is transmitted at time frame (\( \mathcal{t}+3 \)) in a practicable amount of time because their secret shares γ1 and γ3 are subtracted from group key encryption key δℊ. Using collision, it is also not possible to compute \( {\mathcal{PK}}_{\mathcal{i}} \) and \( {\mathcal{q}}_{\mathcal{i}} \) of any remaining group member since \( {\mathcal{PK}}_{\mathcal{i}} \) and \( {\mathcal{p}}_{\mathcal{i}} \) are sent by GM to group members at the time of joining using secure SSL channel and which are kept secret by GM as well as group members. The value of \( {\mathcal{q}}_{\mathcal{i}} \) is computed using congruence \( {\mathcal{p}}_i\times {\mathcal{q}}_i\equiv 1\ \mathit{\operatorname{mod}}\ \left({\mathcal{PK}}_i\right) \) by member \( {\mathcal{m}}_{\mathcal{i}} \) at his/her area and kept secret in his/her database. In the proposed scheme, by sharing previously used \( {\mathcal{PK}}_{\mathcal{i}} \), \( {\mathcal{p}}_{\mathcal{i}} \), \( {\mathcal{q}}_{\mathcal{i}} \) and \( \mathcal{GK} \), multiple evicted members cannot cooperatively derive \( {\mathcal{PK}}_{\mathcal{i}} \) and \( {\mathcal{q}}_{\mathcal{i}} \) of any remaining group member and updated group key \( \mathcal{GK} \). Therefore, the collision attack cannot be successfully performed in our proposed scheme.
5.5 Impersonation Attack
Impersonation attack is an attack in which an entity can pretends to another. In proposed scheme an adversary can pretends to GM for generating and distributing the fake group key. The proposed scheme is secured against the impersonation attack.
Theorem 5.5: An adversary \( \mathcal{A} \) cannot distribute a fake group key to group members by impersonation attack.
Proof: In proposed scheme, an adversary may sometimes be a member of the group and he/she may has its own private key \( {\mathcal{PK}}_{\mathcal{i}} \), secrets \( {\mathcal{p}}_{\mathcal{i}} \) & \( {\mathcal{q}}_{\mathcal{i}} \) and may be compute the group key from cipher-text \( \mathcal{CT} \) sent by GM. In order to perform impersonation attack, upon receiving \( \mathcal{CT} \), an adversary may try to compute \( \mathcal{M} \), where \( \mathcal{M}={\prod}_{i=1}^n\left({\mathcal{PK}}_i\right) \) and δℊ, where \( {\delta}_{\mathcal{g}}={\sum}_{i=1}^n{\gamma}_i \) that the GM holds. In proposed scheme, it is impossible for an adversary to compute aforementioned parameters from known private key \( {\mathcal{PK}}_{\mathcal{i}} \), secrets \( {\mathcal{p}}_{\mathcal{i}} \) & \( {\mathcal{q}}_{\mathcal{i}} \) and \( \mathcal{CT} \) in a reasonable amount of time. Thus the impersonation attack is infeasible to the proposed scheme.
6 Performance Analysis
The performance of the proposed ESKMS scheme is analyzed through numerical analysis and implementations in terms of computation complexity, communication complexity and storage complexity. The notations used in performance analysis are given in Table 2.
6.1 Security Features Comparison
The comparison of security features of our scheme with the related schemes and present the same in Table 3. From Table 3 it is observed that our proposed and existing M.Y. Joshi et al., [6] scheme provides all security features. Other existing schemes [14, 18, 19, 22] are not secured against the various security attacks and hence are not capable to securely distribute the \( \mathcal{GK} \) in Pay-TV systems.
6.2 Computational Complexity
The computational complexity of system initialization is computed by the time taken to execute required operations in startup phase. Table 4 illustrates the comparisons of computational complexity of system initialization of our proposed ESKMS scheme and various existing schemes [6, 14, 18, 19, 22]. In our scheme, some basic operations require to initialize the system are as follows: \( 3\mathcal{n} \) multiplications, \( \mathcal{n} \) divisions and \( \mathcal{n} \) additions operations. Therefore, in our scheme, the computational complexity of GM to initialize the system is \( \left(4\mathcal{n}{\mathcal{t}}_{md}+\mathcal{n}{\mathcal{t}}_{gxm}+{\mathcal{nt}}_{as}\right) \) which is high as compared to other scheme [6, 14, 18, 19, 22] but it is insignificant because in our protocol, all the computations of initialization phase take place offline before any group is formed. Therefore, computational complexity of initialization phase is unimportant and may be considered as negligible in our protocol. However, in case of other schemes [6, 14, 18, 19, 22] all the computations of system initialization take place online after formation of group. Therefore, in our protocol, the computation complexity of initialization phase in online mode (i.e., at the time of group formation, communication in the group and at the time of members joining or leaving the group) is negligible.
On the other hand, the computation complexity of members in our proposed and other schemes [6, 14, 18, 22] is nil because in the initialization phase, either the members are not required to perform any computation or some of the required computations are performed offline. However, in case of protocol [19], the GM and members simultaneously perform required computations online for initialization of the system. Therefore, the computational complexity of GM and each group member for system initialization in scheme [19] is  cmm \( +\mathcal{n}{\mathcal{t}}_{gxm} \) and \( 2{\mathcal{t}}_{md}+{\mathcal{t}}_{cmm}+2{\mathcal{t}}_{as}+2{\mathcal{t}}_{iee} \) respectively. However, the computation cost of each group member is constant and not dependent on the size of the group.
cmm \( +\mathcal{n}{\mathcal{t}}_{gxm} \) and \( 2{\mathcal{t}}_{md}+{\mathcal{t}}_{cmm}+2{\mathcal{t}}_{as}+2{\mathcal{t}}_{iee} \) respectively. However, the computation cost of each group member is constant and not dependent on the size of the group.
The computational complexity of key updating phase is determined by the time taken by GM and members to update the group key GK, whenever a new member joins or existing member leaves the group \( \mathcal{G} \). Table 5 illustrates the comparisons of computational complexity of our proposed ESKMS scheme and various existing schemes [6, 14, 18, 19, 22] at the time of member’s joining. In the proposed scheme, if any new member \( {\mathcal{M}}_i \) joins into group then the system needs to refreshes a new group key and GM require to perform only few basic operations. Only three basic operations are required to perform by GM: one addition, one multiplication and one mod operation, which require low computational power. As a result, the computational complexity of GM is \( \left({\mathcal{t}}_{as}+{\mathcal{t}}_{md}+{\mathcal{t}}_{gxm}\right) \). To obtain the refreshed GK, only two basic operations are required to perform by each group member: one multiplication and one mod operation. Thus each member’s computational complexity is \( \left({\mathcal{t}}_{md}+{\mathcal{t}}_{gxm}\right) \). Table 5 shows that the computational complexity of GM and members in our ESKMS scheme is less than that of existing schemes [6, 14, 18, 19, 22].
Table 6 illustrates the comparisons of computational complexity of our scheme with various existing schemes [6, 14, 18, 19, 22] on member’s leaving. When an existing member leaves the group, the scheme needs to update the group key and GM required to perform only three basic operations: one subtraction, one multiplication and one mod operation. Thus the computational complexity of GM is \( \left({\mathcal{t}}_{as}+{\mathcal{t}}_{md}+{\mathcal{t}}_{gxm}\right) \). To obtain refreshed GK, only two basic operations required to perform by each group member: one multiplication and one mod operation. As a result, the computational complexity of each group member is \( \left({\mathcal{t}}_{md}+{\mathcal{t}}_{gxm}\right) \). Table 6 clearly illustrates that when an existing member exits from the group, the computational complexity of proposed ESKMS scheme is less than that of schemes proposed in [6, 14, 18, 19, 22].
6.3 Communication Complexity
The communication complexity only involves the transmission of rekeying messages from GM to group members in order to refreshes the GK in different rekeying processes (joining/leaving/periodically updates). Therefore, to determine the communication complexity, we estimate the transmission size of rekeying messages. Table 7 illustrates the detailed analytical comparisons of communication complexity of our scheme with some of the relevant schemes [6, 14, 18, 19, 22]. In order to send the refreshed GK to the group members, the GM needs to multicast \( \mathcal{CT} \), where \( \mathcal{CT}=\left(\mathcal{K}\times {\delta}_{\mathcal{g}}\ \right)\mathit{\operatorname{mod}} \)  \( {\mathcal{PK}}_i \) and \( \mathcal{CT}\in \)
\( {\mathcal{PK}}_i \) and \( \mathcal{CT}\in \)  . If it is assumed that the average length of member’s private key \( {\mathcal{PK}}_i \) is Ssp bits. Therefore, the average size of transmission message \( \mathcal{CT} \) is
. If it is assumed that the average length of member’s private key \( {\mathcal{PK}}_i \) is Ssp bits. Therefore, the average size of transmission message \( \mathcal{CT} \) is  \( {\mathcal{n}}_{\mathcal{r}}\times {S}_{sp} \), where \( {\mathcal{n}}_{\mathcal{r}} \) is the number of receivers. From Table 7, it is observed that the transmission load (Size of Broadcast, Multicast and Unicast message) of our ESKMS scheme at member is less than that of other existing schemes [6, 14, 18, 19, 22]. Moreover, when an existing member leaves from the group, the transmission load (Broadcast and Multicast message size) of our scheme is less as compared to the schemes [6, 18, 22]. However, it is similar to the protocols [14, 19].
\( {\mathcal{n}}_{\mathcal{r}}\times {S}_{sp} \), where \( {\mathcal{n}}_{\mathcal{r}} \) is the number of receivers. From Table 7, it is observed that the transmission load (Size of Broadcast, Multicast and Unicast message) of our ESKMS scheme at member is less than that of other existing schemes [6, 14, 18, 19, 22]. Moreover, when an existing member leaves from the group, the transmission load (Broadcast and Multicast message size) of our scheme is less as compared to the schemes [6, 18, 22]. However, it is similar to the protocols [14, 19].
6.4 Storage Complexity
Storage complexity is determined by computing the memory size taken to store keying information by the GM and members. The amount of keying information necessary to be stored by GM and members in our proposed scheme and existing schemes has been calculated and are shown in Table 8. In our scheme, the storage complexity of GM and members are \( \left(3\times \mathcal{n}+1\right){S}_{sp} \) Ssp and 2 × Ssp respectively. Therefore, the GM needs to store \( 3\mathcal{n}+1 \) key parameters which is linear and depends on the size of the group. Moreover, each group member requires storing only two key parameters which is constant and not depends on the size of the group. From Table 8, it is evident that the storage complexity of GM in our scheme is less than that of other existing SKTPCRT and SBMK and it is similar to ESTMKM scheme. However, it is slightly more in comparison with ESCAS and HCASKD. Furthermore, it is also less for each group member in comparison with existing ESCAS, HCASKD, SKTPCRT and ESTMKM schemes and it is similar to SBMK scheme.
7 Implementation Results and Discussions
In this section, we verify the performance of proposed ESKMS scheme through empirical analysis. The scheme is implemented using Java Big Integer library functions. Big Integer library provides the functionality of various modular arithmetic operations like modular multiplicative inverse, modular exponentiation, prime generation, GCD calculation and other miscellaneous operations. The details of experimental environment and conditions are given in Table 9. The results of proposed ESKMS scheme and reference schemes [6, 14, 18, 19, 22] have been tasted with varying size of keys (64 bits to 1024 bits) and 1000 members in the group. The results have been also tested for varying size of groups from 500 to 8000 members with keys of size 256 bits. We compared the computational, communication and storage costs of our proposed ESKMS scheme with reference schemes. The computational cost for the GM is to update the GK, which includes computation of new group key encryption key and encryption of new GK. Similarly, the computational cost of each member is to recover the refreshed GK, which includes computation of private key, other secret parameters and decryption of refreshed GK. In the implementation of scheme, the computational time of our proposed and reference schemes has computed for GM and members, which is required to refresh the KG. For comparative study, the computational time of all the schemes is computed in milliseconds (ms).
Figures 4 and 5 illustrate the comparisons of computational time of the proposed ESKMS scheme with reference schemes at member’s joining for the group of 1000 members with varying size of keys from 64 bits to 1024 bits. Similarly, Figs. 6 and 7 illustrate the comparisons of computational time at member’s leaving. Figure 8 illustrates computation time of GM for initialization of the system in our proposed scheme and other related schemes. Figures 9 and 10 illustrate the comparisons of computational time of our and reference schemes at member’s joining for varying size of groups from 500 to 8000 members with keys of size 256 bits. Similarly, Figs. 11 and 12 illustrate the comparisons of computational time at member’s leaving. The graphical results illustrated in Fig. 4, clearly shows that if the size of keys is 64 bits and 1024 bits, the GM’s computation time of our proposed scheme at member join is 19.22 ms and 68.02 ms respectively, which is better as compared to reference schemes [6, 14, 18, 19, 22]. Figure 5, clearly illustrates that if the keys are of length 64 bits and 1024 bits, the member’s computation time of our scheme at joining is 1.29 ms and 5.43 ms respectively, which is more desirable as compared with existing schemes [6, 14, 18, 19, 22].
The results illustrated in Fig. 6, clearly shows that if the size of keys is 64 bits and 1024 bits, the GM’s computation time of our proposed scheme at member leave is 18.02 ms and 66.02 ms respectively, which is better as compared to reference schemes [6, 14, 18, 19, 22]. Figure 7, clearly illustrates that if the keys are of length 64 bits and 1024 bits, the member’s computation time of our scheme at leaving is 1.01 ms and 4.23 ms respectively, which is also superior as compared with existing schemes [6, 14, 18, 19, 22]. Form Fig. 8, it is clear that the computation time of GM is constant for the schemes [18, 22] but it is rising according to increasing the size of the group in our proposed and other schemes [6, 14, 19]. Figure 8 indicates that if there are 500 to 8000 members in the group, the computation time of GM for system initialization in the proposed scheme is 124,230.78 ms and 1,987,680.29 ms respectively, which are high in comparison with existing schemes [6, 14, 18, 19, 22]. This increased computation time of GM for system initialization is not important because all the computations of initialization phase are completed offline in our proposed scheme. However, in case of other related schemes [6, 14, 18, 19, 22], all computations are done online after formation of group. Therefore, computation complexity of initialization phase is unimportant and may be considered as negligible in our protocol.
The experimental results given in Fig. 9 clearly indicate that when there are 500 and 8000 members in the group, the computation time of GM at member’s joining in the proposed scheme is 129.72 ms and 1113.09 ms respectively, which is more suitable as compared to reference schemes. It can clearly be seen from Fig. 10 that the member’s computation time at member’s joining in the proposed ESKMS scheme is 1.02 ms and 7.52 ms when there are 500 and 8000 members in the group which is far better as compared to reference schemes.
It can clearly be seen from Fig. 11 that the GM computation time at member’s leave in the proposed ESKMS scheme is 192.72 ms and 913.09 ms when there are 500 and 8000 members in the group which is more suitable as compared to reference protocols.
Figure 12 clearly illustrates that the member’s computation time at member leave in the proposed ESKMS scheme is 1.02 ms and 6.52 ms when there are 500 and 8000 members in the group which is far better as compared to reference protocols. Hence, from experimental results we are confirmed that our proposed ESKMS scheme is efficient as compared to other existing schemes in terms of computational complexity of GM and members.
8 Conclusion
To solve the key distribution problems of multicast communication, a computationally efficient and highly secure ESKMS scheme based on Chinese remainder theorem has been proposed. The proposed scheme has significantly reduced the computational complexity of GM and members for key update procedure. The communication complexity of our proposed scheme is much better as compared to reference schemes. Moreover, the storage complexity of GM and group members is also minimized. The proposed scheme also handles the issues related to scalability and massive membership change of multimedia multicasts in large and dynamic groups. In order to provide the information of refreshed GK to members, the proposed scheme requires only one multicast message. Compared to the reference schemes, our scheme provides far better results. The scheme is secure against various attacks like passive attack, impersonation attack, and collusion attack. The group backward and forward secrecy is also ensured by the proposed scheme. Both theoretical and experimental analysis has shown that our ESKMS has much lower rekeying complexity as compared to existing schemes.
Change history
10 October 2020
Tables 1, 3, 4, 5, 6, 7, 8 and the body texts in the original publication contain incorrect symbols. The original article article has been corrected.
References
Chen SM, Yang CY, Hwang MS (2017) Using a new structure in group key management for pay-TV. International Journal of Network Security 19(1):112–117
Farash MS, Attari MA (2016) A provably secure and efficient authentication scheme for access control in mobile pay-TV systems. Multimed Tool Appl 75(1):405–424
He D, Kumar N, Shen H, Lee JH (2016) One-to-many authentication for access control in mobile pay-tv systems. Sci China Inf Sci 59. https://doi.org/10.1007/s11432-015-5469-5
Huang Y-L, Shieh S, Ho F-S, Wang J-C (Oct. 2004) Efficient key distribution schemes for secure media delivery in pay-TV systems. in IEEE Transactions on Multimedia 6(5):760–769. https://doi.org/10.1109/TMM.2004.834861
Je DH, Kim H-S, Choi Y-H, Seo SW (2014) Dynamic configuration of batch rekeying interval for secure multicast service, 2014 International Conference on Computing, Networking and communications (ICNC), Honolulu, HI, pp. 26–30. doi: https://doi.org/10.1109/ICCNC.2014.6785299.
Joshi MY, Bichkar RS (2013) Scalable Key Transport Protocol Using Chinese Remainder Theorem‖, The Proceedings of International symposium on Security in Computers and Communications (SSCC), Mysore, pp 397–402
Kim J, Choi H (June 2010) Improvements on Sun 's conditional access system in pay-TV broadcasting systems. in IEEE Transactions on Multimedia 12(4):337–340. https://doi.org/10.1109/TMM.2010.2046362
Kumar V, Kumar R, Pandey SK, An Enhanced and Secured RSA Public Key Cryptosystem Algorithm Using Chinese Remainder Theorem, third International Conference, NGCT 2017, Smart and Innovative Trends in Next Generation Computing Technologies, Communications in Computer and Information Science(CCIS), pp. 1–12, doi: https://doi.org/10.1007/978-981-10-8660-1_42.
Kumar V, Kumar R, Pandey SK (2018) A computationally efficient centralized group key distribution protocol for secure multicast communications based upon RSA public key cryptosystem. Journal of King Saud University – Computer and Information Sciences. https://doi.org/10.1016/j.jksuci.2017.12.014
Kumar V, Kumar R, Pandey SK (2018) Polynomial based non-interactive session key computation protocol for secure communication in dynamic groups, International Journal of Information Technology pp 1–6, doi:https://doi.org/10.1007/s41870-018-0140-1.
Kumar V, Kumar R, Pandey SK, Alam M Fully homomorphic encryption scheme with probabilistic encryption based on euler’s theorem and application in cloud computing. In: Aggarwal, V.B., Bhatnagar, V., Mishra, D.K. (eds.) Big Data Analytics. AISC, vol. 654, pp. 605–611. Springer, Singapore (2018). https://doi.org/10.1007/978-981-10-6620-7_58.
Kumar V, Kumar R, Pandey SK (2020) An Efficient and Scalable Distributed Key Management Scheme Using Ternary Tree for Secure Communication in Dynamic Groups. In: Singh P., Panigrahi B., Suryadevara N., Sharma S., Singh A. (eds) Proceedings of ICETIT 2019. Lecture notes in electrical engineering, vol 605. Springer, Cham doi: https://doi.org/10.1007/978-3-030-30577-2_13
Li M, Poovendran R, Berenstein C (2002) Design of Secure Multicast key Management Schemes with communication budget constraint. IEEE communication letters 6(3):108–110. https://doi.org/10.1109/4234.991148
Lin I-C, Tang S-S, Wang C-M (September 2010) Multicast key management without rekeying processes. Comput J 53(7):939–950
Z. Liu, Y. Lai, X. Ren and S. Bu (2012) An Efficient LKH Tree Balancing Algorithm for Group Key Management, 2012 International conference on control engineering and communication technology, Liaoning, pp.1003–1005. doi: https://doi.org/10.1109/ICCECT.2012.213.
McGrew DA, Sherman AT (2003) Key establishment in large dynamic groups using one-way function trees. IEEE Trans Softw Eng 29(5):444–458
Naranjo JAM, Lopez-Ramos JA, Casado LG (2010) Applications of the extended Euclidean algorithm to privacy and secure communications, in: proceedings of the 10th international conference on computational and mathematical methods in science and engineering, CMMSE
Pal O, Alam B (2019) Efficient and secure conditional access system for pay-TV systems. Multimed Tools Appl 78:18835–18853. https://doi.org/10.1007/s11042-019-7257-5
Saravanan K, Purusothaman T (2012) Efficient star topology based multicast key management algorithm. J Comput Sci 8(6):951–956
Sun HM, Chen CM, Shieh CZ (2008) Flexible-pay-per-channel: a new model for content access control in pay-TV broadcasting systems. IEEE Trans Multimed 10(6):1109–1120
Tang S, Xu L, Liu N, Huang X, Ding J, Yang Z (Dec. 2014) Provably secure group key management approach based upon hyper-sphere. in IEEE Transactions on Parallel and Distributed Systems 25(12):3253–3263. https://doi.org/10.1109/TPDS.2013.2297917
Varalakshmi R, Rhymend Uthariaraj V (2013) Huffman based conditional access system for key distribution in digital. TV multicast Multimed Tools Appl 74(9):2899–2912. https://doi.org/10.1007/s11042-013-1753-9
Vijaya Kumar P, Bose S, Kannan A (2013) Centralized Key Distribution Protocol using the Greatest Common Divisor Method, Computers & Mathematics with Applications, 2013 Volume 65, Issue 9. Pages: 1360–1368, doi:https://doi.org/10.1016/j.camwa.2012.01.038.
VijayaKumar P, Bose S, Kannan A (2012) Rotation based secure multicast key management for batch rekeying operations. Netw Sci 1(1–4):39–47
VijayaKumar P, Bose S, Kannan A (2014) Chinese remainder theorem based centralized group key management for secure muticast communication. IET Inf Secur 8(3):179–187. https://doi.org/10.1049/iet-ifs.2012.0352
Vijayakumar P, Naresh R, Islam SK, Deborah LJ (2016) An effective key distribution for secure internet pay-TV using access key hierarchies. J Secur Commun Netw. https://doi.org/10.1002/sec.1680
Wang H, Qin B (Dec. 2012) Improved one-to-many authentication scheme for access control in pay-TV systems. in IET Information Security 6(4):281–290. https://doi.org/10.1049/iet-ifs.2011.0281
Yeh L, Tsaur W (2012) A secure and efficient authentication scheme for access control in Mobile pay-TV systems. in IEEE Transactions on Multimedia 14(6):1690–1693. https://doi.org/10.1109/TMM.2012.2199290
Zhang J, Varadharajan V (2010) Wireless sensor network key management survey and taxonomy. Journal of Network and Computer Applications 33(2):63–75
Zheng XL, Huang CT, Matthews M (2007) Chinese remainder theorem based group key management, in Proc. 45th ACMSE, Winston-Salem, NC, USA, 266–271.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original version of this article was revised: Table 1 contains incorrect symbols.
Rights and permissions
About this article
Cite this article
Kumar, V., Kumar, R. & Pandey, S.K. A Computationally Efficient and Scalable Key Management Scheme for Access Control of Media Delivery in Digital Pay-TV Systems. Multimed Tools Appl 80, 1–34 (2021). https://doi.org/10.1007/s11042-020-08904-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11042-020-08904-8



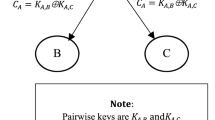


 =
=  , where
, where  for
for , such that
, such that 

 <
<  by using following eq. (
by using following eq. (
 with help of secret share γi of leaving member as shown in (3)
with help of secret share γi of leaving member as shown in (3)
 :
: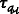 :
:







