1 Introduction

Digital imaging has enabled people to save memorable moments in their lives. However, when they are being captured, images can be contaminated by various effects such as noise [34], blurring [6, 13, 15, 17, 21, 28,30,31,31, 34, 36], hazing [24, 25], fogging [26], barcode de-blurring [22] and sequential ocular images from multi-spectral imaging [16] etc. These undesirable effects may occur for a number of reasons; for example, camera movement while the picture is being taken is a common problem that can produce a blurred image. Based on the characteristics, image de-blurring algorithms are mainly divided into two types. In first type of image de-blurring, the blur kernel is known. In the second type, the blur kernel is unknown; this is known as blind image de-blurring. In this paper, we focus on blind image de-blurring and, more specifically, on kernel estimation. The estimated kernel can be further used with any image de-blurring method to recover an image.

There are two phases to blind image de-blurring:1) kernel estimation, and 2) image de-blurring. Both phases play an equally important role in the recovery of a clear image. Kernel estimation is an effective means of dealing with a blurred image. The better the estimation of the kernel, the better will be the recovered image., blind image de-blurring has attained the researchers’ attention. Blind image de-blurring has been successfully applied in different fields such as audio signal processing, astronomical and medical image processing.

Based on different properties, kernel estimation techniques are broadly categorized into two types: (1) Variational Bayes (VB) [6, 13, 28, 29] and (2) Maximum A Posterior (MAP) [3, 15, 17, 21, 23, 30, 31, 34, 36]. VB-based methods have the ability to evade trivial solutions; however, the computational cost is higher compared to MAP. Two variants have been proposed to estimate the kernel based on MAP: (1) Kernel estimation achieved by using the salient structures of an object is known as Salient Structures-Based Kernel Estimation [2, 3, 12, 17, 23, 30, 36] and (2) Sparse Regularization-Based Kernel Estimation [9, 11, 15, 21, 31, 34, 35]. The main focus of this paper is on the second type of MAP-based image de-blurring method.

Earlier, single image de-blurring did not perform well because of kernel priors and different latent variables [3, 30]. Although researchers used Gaussian priors, the estimated kernels were not able to preserve the structures of salient objects and did not provide compact, sparse representation. This led to a noise-contaminated image with dense structures. Salient edges are detected from a gradient image by the use of l1-norm [2]. Image priors obtained in this way can produce better results only under certain conditions [2, 15, 21]. To improve the quality of the image, a combination of l1-norm and a new ring suppressing term was employed [23]. To suppress the small structures, l1/l2-norm regularization term was introduced [11] where a l1 to l2 norm ratio was applied to high frequencies of an image. This regularization term was unable to produce images with sharp edges, as the ratio of the l1 to l2 does not have this property.

A new method for generalized sparse representation for uniform and non-uniform motion de-blurring was proposed by [31]. Here, the authors mathematically proved the soundness of l0-norm for sparse representation. Moreover, the proposed system requires fewer iterations to converge the system because no extra filtering is needed during the optimization process. However, the proposed technique did not perform well on real images containing text.

To handle the outlier, a new effective kernel estimation method was proposed which considered the data fidelity term to suppress the effect of outliers [7]. The estimated kernel was further used to recover the degraded image. However, the computational cost increased due to outlier detection. Row-Column sparsity has been used for blind image de-blurring [18]. Authors proposed to solve a new type of sparsity optimization problem by including rows and columns to estimate the kernel. Singular value decomposition was used to recover the kernel and latent image from the blurred image.

To remove the noise and recover the blurred image, a new inverse Radon transform-based kernel was estimated [34]. Multiple directional filters with different orientations were applied to the input image and a true Radon transform was estimated for each image. However, multiple directional filters produced significant ringing artifacts in the recovered images. To preserve the smooth structure of an object for blind image de-blurring, an iteration-wise generalized shrinkage–threshold method was proposed [36]. Here, the authors extended the generalized shrinkage–thresholding (GST) that is used to sharpen the salient edges of an object while eliminating the small details. However, the elimination of small details can lead to an inaccurate estimation of the blind kernel.

A single-image blind de-blurring based on the color image priors has been proposed to better preserve the sharp edges of an object [12]. The normalized color line was used to estimate the blur kernel instead of the original color line that is not effective for estimation. A method was proposed for the selection of effective centroids, which was more effective compared to K-means method. A new generalized MAP-estimation framework for blind image de-blurring was proposed [35], in which the scene specific edge priors were used. Dark channel image priors were proposed by [9] who assumed that the dark channel image priors are less sparse.

The salient structure of an image plays an important role in estimating the kernel. Most of the existing methods neglect the small texture structures when estimating the kernel for convolution with the image. The neglect of such structures can lead to the problem of over-smoothed edges of an object within the image. Better contrast information gives a more accurate estimation of the blurred kernel. Two well-known approaches are used to determine the contrast of an image: maximum likelihood estimation (MLE) and probability weighted moments (PWM). PWM has the proven ability to provide better contrast information while preserving the edges of an object even for a small sample size as compared to MLE which is further used for image classification [4].

This paper presents an effective image regularization method whereby a new type of image regularization approach is introduced that recovers sharp images from blurry images. The kernel estimated by using the PWMR has the ability to preserve the trivial structures that are further used to recover the image. This allows an extremely cost-effective formulation to be used for the blind de-convolution model, consequently obviating the need for additional methods. The salient contributions of this work are as follows:

a) New image regularization term by utilizing the PWM to preserve the small textures of an object which helps to recover an improved, sharper image.

b) The proposed PWMR has the ability to identify the outliers and disregard them during the estimation of the kernel, and also reduces the ringing effect with comparable computational cost.

2 Background knowledge

In this section, a brief introduction to PWM is presented.

2.1 Probability weighted moments

PWM has the ability to uniquely determine the distribution of given data. MLE can be used to capture the tails of distribution, which can affect the estimation because the tails or ending points may be the outliers. However, the PWM can be used to better capture the middle of the distribution, thereby providing a better estimation of given data.

Below is a better linear estimate of standard deviation for the normal distribution [5]:

$$ PWM=\frac{\sqrt{\pi }}{n}\sum \limits_{i=1}^n\left[{X}_i-2\left(1-\frac{i-0.5}{n}\right){X}_i\right] $$

where Xi refers to the ordered observations within the sample of size n. The estimation of the standard deviation using PWM is also a function of ordered observations. The expression (i − 0.5)/n denotes the empirical distribution function; π is 3.1416.

PWM has been successfully applied in different fields for better estimation such as in image classification [4], in Heteroscedastic Linear Regression Model for adaptive estimation [20] and estimation for the better-quality control charts [19].

3 Probability weighted moments based regularization

PWM as the linear function of the sample space has less influence on the sample variability. PWM renders a better estimation of the parameters compared to the conventional moments in the presence of outliers within the sample space. The closed form of a cumulative distribution function provides unbiased, stable and particularly attractive PWM. This property improves our estimation of the blind kernel for recovering the corrupted image.

The local relationships among the textures of image objects are investigated to estimate the blind kernel named PWM-based Regularization (PWMR). More precisely, each pixel is considered to estimate the kernel by utilizing efficient and effective PWMR defined as follows:

$$ PWMR=\frac{PW{M}_x}{PW{M}_y}, $$

Where PWMxrefers to the estimated variance in the direction of x derivate, and PWMy denotes the estimated variance in the direction of y derivate. As PWM are less sensitive to the outliers when considering the coefficient in the direction of the x-axis, and the y-axis has the ability to preserve the salient edges of an object. The terms PWMx and PWMyin the equation above provide the horizontal and vertical structures in a given blurred image. The ratio of these terms provides the compact value of a given structure which is neither a noisy value nor the motion blur caused due to motion. Different regularization techniques have been proposed to find the best estimate of a kernel. However, neglecting the small salient regions by considering the outliers/ noise does not produce the better kernel which can then be used recover the latent image. Most of regularization techniques approach the problem as a non-convex problem, which needs an optimization technique to solve it.

4 Proposed framework

Commonly, image de-blurring models are defined as follows:

$$ \mathrm{y}=\mathrm{k}x+\mathrm{n}, $$

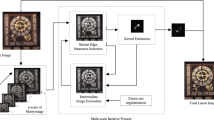
Where y is the obtained blurred image, n is the additive Gaussian i.i.d noise, x and k denote the unknown sharp image and blurring matrix used to blur the sharp image x, respectively. Blind image de-blurring is considered to be a greatly ill-posed inverse problem, in which there is a need to estimate the sharp image x and the blurring matrix k, simultaneously The blind image de-blurring algorithm is mainly divided into two parts: unknown kernel estimation and image de-blurring. A better estimation of the unknown kernel can improve the quality of the recovered image. A standard blind image de-blurring is presented in Algorithm 1.

figure h
  1. A.

    Kernel Estimation

Kernel estimation is accomplished for the high frequency of an image as in [11]. High frequency image I is obtained from the blurry image, which is actually the combination of derivatives in the x and y direction. More precisely, the following filters are used to obtain the high frequency images in horizontal (x-axis) and vertical (y-axis) directions as,

$$ {\nabla}_x=\left[1,\kern1em -1\right];\kern1.12em {\nabla}_y={\left[1,\kern1em -1\right]}^T. $$

Where ∇x filter used in horizontal direction, and ∇y filter used in vertical direction (which is the transpose (T) of ∇x). The de-blurring model can be defined as

$$ \underset{x,k}{\min}\lambda\ {\left\Vert x\otimes k-I\right\Vert}_2^2+ PWMR+\beta {\left\Vert k\right\Vert}_1 $$
(1)

Where k and x represent the unknown kernel and sharp image, respectively. PWMR is the proposed regularization term for image de-blurring, λ and βare the trade-off parameters used to optimize the stability of kernel and image regularization terms, and is the 2D convolution operator. l1-norm as regularization term is applied on k to reduce the noise during the kernel estimation which also presents a good, sparse representation. In consideration of the physical principles for blur formation, k is bounded by two restrictions: k ≥ 0 and \( \sum \limits_i{k}_i=1 \). Due to the high convexibility of Eq. 1, in order to optimize the solution, an initialization is assumed on both x and k; after that, x and k are alternatively updated. To update x and k, the altering method suggested by [11] is employed.

To update x and k, Eq. 1 can be divided into two parts as follows:

$$ \underset{x,k}{\min}\lambda\ {\left\Vert x\otimes k-I\right\Vert}_2^2+ PWMR $$
(2)
$$ \underset{x,k}{\min}\lambda\ {\left\Vert x\otimes k-I\right\Vert}_2^2+\beta {\left\Vert k\right\Vert}_1 $$
(3)

The new term, PWMR, in Eq. 2 makes it a convex problem. The Iterative Shrinkage-Thresholding Algorithm (ISTA) [1] is used to solve the general linear inverse problem. The algorithm applied to update x is presented as follows:

figure i

Where k is the blurring matrix obtained after last iteration of k and t = 0.001 is the threshold value used for ISTA. M and N denote the maximum number of inner and outer iterations, respectively and considered as 2 in the proposed algorithm. S represents the vector soft shrinkage operator to decrease the input vector towards zero as presented in Eq. 4.

$$ {S}_x{(x)}_i=\max \left(\left|{x}_i\right|-\alpha, 0\right)\mathit{\operatorname{sign}}\left({x}_i\right) $$
(4)

The ISTA algorithm is used for the inner iteration updating of x, and the outer iteration is used only for the re-estimation of the likelihood term in eq. 2.

It is necessary to update k after updating x by using eq. 3. An unconstrained Iterative Re-weighted Least Squares method [14] is used to estimate the kernel by using the weights obtained from the previous updated matrix of k (with single outer iteration). The estimated kernel may have negligible values at the finest level, which are normalized to zero to enhance the efficiency of obtained kernel against noise. Coarse-to-fine pyramid of image resolutions is used for the multi-scale estimation of the kernel.

  1. B.

    Image De-blurring

Once the fine kernel has been obtained, any non-blind image de-blurring algorithm can be used to recover the sharp image [10, 14]. A fast image de-convolution algorithm is used to recover the sharp image, which employs Hyper-Laplacian priors after the estimated kernel has been obtained. The underlying algorithm [10] is robust against small kernel errors, and is as follows:

$$ \underset{x}{\min}\lambda\ {\left\Vert x\otimes k-I\right\Vert}_2^2+{\left\Vert {\nabla}_x\right\Vert}_b+{\left\Vert {\nabla}_y\right\Vert}_b $$

Where ∇x and ∇y are the derivative filters used aforesaid section A. Where b = 0.8 and λ = 3000 as in [11]. Non-blind de-convolution is far lower ill-posed problem as compared to blind de-convolution. Therefore, in the current scenario, a lp-type regularization term is used to solve the aforementioned cost function as defined in [10].

5 Results and discussion

To validate the effectiveness of the proposed method, results are obtained for both synthetic and real-world images with well-known performance measures. This section is further subdivided into three sub-sections: performance measures, experimental results, and discussion of the synthetic dataset and real-world images.

5.1 Performance measure

The performance of the PWMR method was evaluated using well-known performance measures: Peak signal to Noise Ratio (PSNR), Structural Similarity Index Measure (SSIM), Error ratio, and time in seconds. The PSNR was obta ined with

$$ PSNR=10.{\log}_{10}\left(\frac{{\mathit{\operatorname{MAX}}}^2}{MSE}\right) $$

Where 'MAX' represents the maximum possible value present in an image. 'MSE' is the mean squared error between the original image (pure image) 'O' and restored image 'R'as follows:

$$ MSE=\left(\frac{1}{M\times N}\right)\sum \limits_{i=1}^M\sum \limits_{j=1}^N{\left(O-R\right)}^2 $$

M′ × N′ is the size of the original and restored image, where 'M' is the total number of rows and 'N' is the total number of columns. The similarity structure between the original image and restored image is obtained by Structural Similarity Index method (SSIM) as follows:

$$ SSIM=\frac{\left(2{\mu}_O{\mu}_R+{c}_1\right)\left(2{\sigma}_{OR}+{c}_2\right)}{\left({\mu}_O^2+{\mu}_R^2\right)\left({\sigma}_O^2+{\sigma}_R^2+{c}_2\right)} $$

Where 'c1' and 'c2' are constant values.\( {}^{\prime }{\mu}_O^{\prime },{}^{\prime }{\mu}_R^{\prime },{}^{\prime }{\sigma}_O^{\prime },{}^{\prime }{\sigma}_R^{\prime } \) and ′σOR′represent the means, variances and co-variances. The subscript ‘o’ and ‘r’ represents the original and restored images, respectively. The error ratio is defined as follows:

$$ {r}_{error}= std\left({I}_{EK},{I}_R\right)/ std\left({I}_{RK},{I}_R\right) $$

IEKandIRK represents the image recovered by using the estimated kernel and true kernel respectively. IR shows the real image and std. () is the standard deviation.

5.2 Synthetic data

A well-known standard benchmark dataset [15] for synthetic images was used to evaluate the PWMR against other state-of-the-art methods. In all experiments, the same images were used to validate the effectiveness of the PWMR. This dataset contained four 255 × 255 images as well as eight different blur kernels varying in size from13 × 13 to 27 × 27. After convolving the kernels with the images, a total of 32 images were obtained. The given dataset contained the blurry images, ground-truth kernels and ground-truth images.

Table 1 shows a detailed comparison of the synthetic dataset provided by [15]. The results of PWMR are compared in terms of PSNR, SSIM, computational time and the error ratio with baselines [3, 9, 11, 15, 30, 32]. PWMR outperforms existing methods in terms of PSNR and SSIM except for [9]. However, the computational cost of [9] is little higher than PWMR. The capability of PWMR to preserve the small texture while estimating the kernel gives a better reconstruction of an image.

Table 1 Comparison of Levin et al.’s dataset (Levin et al. [15]) using Mean PSNR, SSIM, computational time (In seconds) and Error Ratio
Full size table

Figure 1 depicts the visual comparison of results between PWMR and other state-of-the-art methods on dataset given by [15] for one image. Visual evaluation indicates that the kernel estimated by employing PWMR has comparable results with other methods [3, 9, 13, 21, 23, 30, 31]. The image recovered by PWMR has better visualization except for [9, 21]. The dark image prior with sparsity preserves the edges better than PWMR. However, PWMR is faster than [9]. The image recovered by [23] has strong ringing effects and is still somewhat blurred compared to the image recovered by [3].

Fig. 1
figure 1

Example of de-blurring results for Levin et al. [15] (27 × 27 Kernel size.) (a) Original image, (b) image recovered by Shan et al. [23], (c) Cho and Lee [3], (d) Xu et al. [30], (e) Levin et al. [13], (f) Xu et al. [31], (g) Perrone et al. [21], (h) Jinsha et al. [9] and (i) PWMR

Full size image

5.3 Real-world images

Real-world standard images are also evaluated in order to compare the proposed regularization method with state-of-the-art methods. The real-world images have no ground truth, enabling them to be compared visually. To ensure a fair comparison, we have used all methods with their proposed parameters.

Figure 2 depicts the comparison of PWMR with [9, 27, 31, 33, 36] for a real-world image of fish. Although images recovered by the methods proposed by [9, 31, 36] are somewhat fine, the recovered images have over-smoothened the local texture of the object. Therefore, the local geometry of objects has not been preserved. The image recovered by [33] is over-sharp and the ringing effect on the image is amplified. Similarly, the image recovered by [27] has a strong ringing effect. PWMR has less ringing effect compared to that produced by state-of-the-art methods, and also better preserves the fine textures during the removal of the blur.

Fig. 2
figure 2

Visual results for the fish image (a) image recovered by Whyte et al. [27], (b) image recovered by Xu et al. [31], (c) image recovered by Zhang et al. [33] (d) image recovered by Jinsha et al. [9], (e) image recovered by Zuo et al. [36], (f) image recovered by PWMR

Full size image

Figure 3 presents the results for the Lyndsey image (with the zoomed area of an image to show the effectiveness of image de-blurring methods) of PWMR with [6, 11, 21, 28, 30]. The zoomed area of an image recovered by PWMR preserved the small texture structures compared to results produced by the aforementioned methods. The image recovered by other methods either over-smoothed [11, 28, 30] or increased the contrast [21] with a strong ringing effect. It is also clear that image recovered by [6] still has a strong ringing effect.

Fig. 3
figure 3

Visual results on Lyndsey image. Image recovered by (a) Fergus et al. [6], (b) Xu et al. [30] (c) Krishnan et al. [11], (d) Zhang et al. [28] (e) Perrone et al. [21] (f) PWMR

Full size image

Figure 4 shows the visual results for the Mukta image as well as the kernel recovered by Michaeli et al. [17], Zhong et al. [34], Zuo et al. [36], Krishnan et al. [11], Jinsha et al. [8] and PWMR. The visual images of the recovered kernels shows the effectiveness of PWMR compared with the kernels recovered by other methods. The kernel recovered by PWMR is less sparse and the neighboring pixels are more compact, which can help to recover a better image during the convolution process while preserving a better texture. The image recovered by Zuo et al. [36] produced a strong ringing effect and also increased the contrast of the image. The image recovered by Jinsha et al. [38] neglected the small texture during image recovery, causing an over- smoothed image.

Fig. 4
figure 4

Visual results for Mukta image also showing the estimated kernel. Image recovered by (a) Krishnan et al. [11] (b) Zhong et al. [34], (c) Michaeli et al. [17], (d) Jinsha et al. [8], (e) Zuo et al. [36], (f) PWMR

Full size image

6 Conclusion

An efficient and effective image regularization term based on Probability Weighted Moments is proposed as a means of estimating kernel function for blind image de-blurring. It is concluded that PWM has the ability to preserve the small textures regardless of the outliers in a small sample space. One can also see that the kernel estimated by using the proposed PWMR has the ability to restore the edges of objects much better and with less ringing effect compared to other methods. The effectiveness of PMWR on synthetic and real-world images, in terms of visually plausible de-blurring, PSNR, SSIM, Error ratio and computational cost has been confirmed.

For the future, when restoring an image, a better estimation of kernel can be considered while taking into the global and local textures of the image.