An efficient optimal multilevel image thresholding with electromagnetism-like mechanism

Abstract

Segmentation process is considered a major part of various image-processing applications due to its extreme inspiration on the subsequent image analysis. Thresholding is one of the simplest techniques for segmentation. In this paper, Renyi’s entropy is combined with electromagnetism-like mechanism optimization (EMO) to perform multilevel thresholding based color image segmentation. For statistical independent subsystems, Renyi’s entropy shows an extensive property and is applied to find best threshold value for image segmentation. The entropic parameter α can handle the additive information that is existent in the image. The feasibility of the EMO-Renyi’s based approach has been tested on various satellite and standard color images with bat algorithm (BAT), backtracking search algorithm (BSA), firefly algorithm (FA), particle swarm optimization (PSO), and wind driven optimization (WDO) for solving the multilevel color image thresholding problem. The analysis based on statistics of different optimization algorithms indicates the proposed EMO-Renyi’s algorithm to be more robust and precise for multilevel color image segmentation problem. These claims have been confirmed by comparing fidelity parameters such as mean error (ME), mean squared error (MSE), peak signal-to-noise ratio (PSNR), feature similarity index (FSIM), structure similarity index (SSIM) and entropy. Experiments on standard daily-life color images are conducted to prove the effectiveness of the proposed scheme. The results show that the proposed method can produce more promising segmentation results from the aspect of objective and subjective observations.

1 Introduction

The classification of pixels into two or more regimes defines segmentation. The region of interest in the image can be efficiently extracted and analyzed using image segmentation. To carry out the segmentation of an image, the presence of mutual information in the sub-regions is necessary. The mutual information could be any of the attributes such as texture, color, and shape [1]. The successful implementation of image segmentation in several areas such as agriculture [15], image denoising [27], industrial production [20], medical image processing [21, 48], and pattern recognition [58] has made. Segmentation methods can be categorized into region-based segmentation [16, 32], threshold-based segmentation [3, 26], edge-based segmentation [4, 5, 47], and clustering techniques [2] to name a few. Image segmentation based on thresholding [53] has its application on a histogram of the image [14]. This results in the consumption of less storage space, proficient processing speed and easy handling which makes the thresholding based segmentation approach as the most frequently used method for segmentation.

Generally, the thresholding techniques are classified into two parts named as bi-level and multilevel thresholding. The process of dividing the entire image into two non-overlapping regimes using a single threshold is termed as bi-level thresholding. According to the predefined threshold value th, the pixels representing the gray levels below the intensity value th belongs to one class viz. background while other pixels belong to another class. On the other hand, multilevel thresholding is done using more than one threshold which implies that there are more than 2 classes. Although bi-level thresholding method is one of the simplest and easiest technique however, for daily life color images and remote sensing data set it doesn’t give appropriate results. As a consequence, multi-level thresholding has a strong obligation for color image segmentation. Thresholding methods can be categorized into non-parametric methods and parametric methods. The parameter estimation of a probability density function (PDF) is a necessity in parametric approaches. Such an approach is resource-intensive. On the contrary, a non-parametric technique employs statistical properties for threshold selection [51] based on the image histogram such as between-class variance-based methods [40], moment-based technique [56] and entropy-based approach [33].

These statistical parameters must be optimized to determine the optimum threshold values. The non-parameterized approach opens a striking option due to its exactness and robustness [6]. Counter production of between-class variance adds to the consumption in the computational cost of an algorithm specifically in multi-level threshold selection. Amongst all the remarkable thresholding methods, thresholding based on entropy is an absorbing subject. Kapur et al. [33] proposed a method that uses the model of entropy maximization to determine the homogeneousness between classes. The information in the image can be treated as either additive or the non-additive. A maximum entropy method has been proposed on the basis of non-extensive Tsallis entropy [23] whose entropic parameter q enables the Tsallis entropy to handle the non-additive information.

In 1997, Sahoo [52] has proposed a method for thresholding based on Renyi’s entropy. Renyi’s entropy can handle the additive property using the tuneable entropic parameter α [31, 50]. The value of α and q can be varied to maximize the Renyi’s and Tsallis entropy respectively. A simple implementation of Renyi’s entropy is the motivation behind its exploitation. The easy extension of Renyi’s entropy to multilevel thresholding problems sums up the advantage of less computation cost. The results show that the accuracy of Renyi’s entropy surpasses that of Tsallis entropy and Kapur’s entropy. Therefore, in this paper, Renyi’s entropy is selected for the entropy computation due to its superlative accuracy and enhanced performance for the purpose of color image segmentation. However, the classical multilevel color image thresholding methods based on entropy results in the huge consumption of time when the thresholding level increases. A substitute for traditional methods, the multi-level thresholding problems have also been managed through swarm-based evolutionary optimization methods. Over the last few years, the success of utilization of meta-heuristic algorithms is one to note. The swarm and evolutionary methodologies have been successful in solving the problem of multilevel image segmentation to achieve the optimum multilevel threshold.

Furthermore, numerous optimization based thresholding techniques have been established which use the features of swarm and evolutionary techniques viz. artificial bee colony (ABC) inspired from the searching behaviour of swarm of honey bees [7, 9, 30], genetic algorithm (GA) which is motivated from the notion of survival of the fittest given by Darwin [9], PSO based on public behaviour of fish schooling or bird flocking [11]. In addition to this, FA is based on flashing phenomenon of fireflies of tropical areas during summer season [28, 29], WDO other optimization methodology which is grounded on the atmospheric behaviour of earth [8, 11], EMO has been inspired from the attraction-repulsion mechanism of the electromagnetism theory [38, 39].

The concept on which the BAT algorithm relates to the echolocation of the bats [36, 41]. In 2017, a new color image multilevel thresholding has been proposed by exploiting the backtracking search algorithm (BSA) for satellite images [22, 25, 44]. In favor of color image multilevel thresholding, another new approach has been given [45] through the modification of fuzzy entropy and further the proposed modified entropic parameters are optimized by Levy flight firefly algorithm to get more accurate results for satellite image segmentation. On the other hand, a new grey-level co-occurrence matrix [46] has been introduced first time as an objective function to get accurate multilevel thresholding for multiband remote sensing images as well as daily life color images. Ant colony optimization (ACO) [25], cuckoo search (CS) [8, 43], bacterial foraging optimization (BFO) [49], differential evolution (DE) [13], and honey bee mating optimization [57] have been reported explicitly to many multilevel color image segmentation problems for evaluation of optimal thresholds.

The swarm-based algorithms [11] and evolutionary computing approaches [12, 42] outstand due to their ability to search superlative solution from any of the objective functions. In 2015, Bhandari et al. [10] has proposed a novel method based on CS methodology for the problem of color image segmentation which is supported by Tsallis entropy. Renyi’s entropy has been used by Soham et al. [53] while proposing a technique to segment the hyper-spectral images with the aid of differential evolution. Again in 2016, a comparative performance analysis [41] using two new optimization algorithms, social spiders optimization (SSO) and flower pollination algorithm (FPA) has been done by taking Kapur’s and Otsu’s as the fitness functions. The two functions, Kapur’s and Otsu’s have also been used to perform multilevel color image thresholding using EMO [38] technique, which shows that EMO algorithm gives more satisfactory results with Otsu as objective function when compared with that of Kapur’s.

Again in 2015, Oliva et al. [39] has used the electromagnetism-like mechanism optimization method to speed up the segmentation process and this time Tsallis entropy has been used as a fitness function. Multilevel thresholding for iris images has been done based on the artificial bee colony [19]. Recently, a modified PSO [35] based multilevel thresholding is applied for the segmentation of medical image segmentation. PSO has been used again in Glioma detection based on multi-fractal features in the medical field to segmented brain MRI images [34]. Lifan et al. [29] presented a work of multilevel color image thresholding by modifying the firefly algorithm and used Kapur’s, minimum cross-entropy and Otsu’s as objective (or fitness) function.

Shilpa et al. have proposed an effectual CS algorithm based thresholding for segmentation of remote sensing images using various objective functions [54] and also proposed multilevel thresholding that is based on chaotic Darwinian PSO for segmentation of satellite images [55]. In 2016, Pare et al. proposed a technique for multilevel color image segmentation using CS and energy curve concept [43]. Unlike segmentation for satellite images, segmentation of dental X-ray images has been proposed based on cooperative semi-supervised fuzzy clustering [48]. Satellite images have always been a study of interest in fields such as astronomical studies, geoscience studies, a survey of climate, forest monitoring, geographical system, agriculture and marine environment [9, 11]. Therefore, for providing the solutions to such king of problems, in this paper, BAT algorithm, BSA, FA, PSO, WDO and EMO based satellite image segmentation using Kapur’s, Tsallis and Renyi entropy is inspected. The schemes are used to maximize the entropy as a fitness function.

This paper is focused on EMO algorithm is used for the proposed approach due to its novelty and an ability of the solving real constraints. The electromagnetism-like mechanism optimization method is used to speed up the segmentation process. This optimization technique generates good results for test functions such as unimodal, multi-modal, and composite and balances global and local search during optimization. In addition to this Renyi’s entropy has selected for entropy computation because of the easiest implementation. The Renyi’s entropy has additive features. The entropic parameter α is used to maximize the entropy. The easy extension of Renyi’s entropy along with producing accurate results as compared to Kapur’s and Tsallis entropy so it is nominated for the entropy computation. Furthermore, by incorporating Renyi’s entropy with EMO technique, it reduces the complexity cost and produces accurate segmented enhanced result. Hence, several researchers are focused on EMO algorithm in their respective research areas for good results with high convergence rate.

The remainder of the paper is organized as follows: Section 2 describes the concepts related to the proposed scheme and the problem statement. Section 3 presents the EMO and Renyi entropy-based proposed framework. Section 4 highlights the comparison of the entropy using each optimization algorithm. Finally, conclusion and future work are drawn in Section 5.

2 Problem statement for optimal multilevel thresholding

Global thresholding can be defined using Eq. (1). If g(x, y) is the original image and f(x, y) represents the thresholded version of the original image then at some global threshold Th can be expressed as:

$$ f\left(x,y\right)=\left\{\begin{array}{l}0;\mathrm{g}\left(x,y\right)\le Th\\ {}1;\mathrm{g}\left(x,y\right)> Th\end{array}\right\}, $$

(1)

where, (x, y) represents the pixel location. The variation of Th over the entire image gives variable thresholding. When Th is a function of the pixel location (x, y) adaptive thresholding can be done and if Th has a dependency on the neighboring pixels, regional thresholding or local thresholding can be evaluated.

2.1 Thresholding

The pixels of a gray-scale or colored image are classified into regions or sets on account of their intensity level (L). For the selection of fitting neighborhoods in a test image, the optimum threshold value Th should be obtained in a routine, which obeys the simple law of the following equations:

$$ {\displaystyle \begin{array}{l}{C}_0\leftarrow i\kern0.5em if\kern0.5em 0\le i\le Th,\\ {}{C}_1\leftarrow i\kern0.5em if\kern0.5em Th\le i\le L-1\end{array}} $$

(2)

and

$$ {\displaystyle \begin{array}{l}{C}_0\leftarrow i\kern0.5em if\kern0.5em 0\le i<{Th}_1\\ {}{C}_1\leftarrow i\kern0.5em if\kern0.5em {Th}_1\le i<{Th}_2,\\ {}{C}_2\leftarrow i\kern0.5em if\kern0.5em {Th}_2\le i<{Th}_3,\\ {}{C}_n\leftarrow i\kern0.5em if\kern0.5em {Th}_n\le i\le L-1,\end{array}} $$

(3)

where, C₀ to C_n defines the classes of the image after thresholding operation is done, i represent the intensity value of the image with the maximum intensity value L and {Th₁, Th₂, Th₃, …., Th_n} represents multiple thresholds.

Segmentation of pixels in their respective classes is done using Eqs. (2) and (3) for bi-level thresholding and multilevel thresholding respectively. The core idea is to choose threshold values that properly classify the different regions in the image using either of bi-level or multilevel thresholding algorithms. When the problem’s formulation is considered, it has been observed that the two-level thresholding is a simple technique for the purpose of obtaining a threshold for segmentation. However, estimating thresholds for multilevel thresholding requires higher computational works.

2.2 Kapur’s entropy-based segmentation

The Kapur’s method aims at maximizing the entropy such that each different region has greater centralized distribution. Kapur’s entropy [33] based thresholding methodology is cited as an effective method. Furthermore, Kapur’s entropy [8] has been extended for multilevel thresholding problem [37] as represented by Eq. (4):

$$ {\displaystyle \begin{array}{l}{E}_{k0}=-\sum \limits_{i=0}^{Th_1-1}\frac{h_i}{w_0}\ \ln\ \frac{h_i}{w_0},{w}_0=\sum \limits_{i=0}^{Th_1-1}{h}_i,\\ {}{E}_{k1}=-\sum \limits_{i={Th}_1}^{Th_2-1}\frac{h_i}{w_1}\ \ln\ \frac{h_i}{w_1},{w}_1=\sum \limits_{i={Th}_1}^{Th_2-1}{h}_i,\\ {}{E}_{km}=-\sum \limits_{i={Th}_m}^{Th_{m+1}-1}\frac{h_i}{w_m}\ \ln\ \frac{h_i}{w_m},{w}_m=\sum \limits_{i={Th}_m}^{Th_{m+1}-1}{h}_i,\\ {}{E}_{kn}=-\sum \limits_{i={Th}_n}^{L-1}\frac{h_i}{w_n}\ \ln\ \frac{h_i}{w_n},{w}_n=\sum \limits_{i={Th}_n}^{L-1}{h}_i,\end{array}} $$

(4)

where, E_ki represents the Kapur’s entropy of i_th class, w_i represents the probability of i_th class and n represents the maximum number of classes.

The optimal multilevel segmentation problem is solved by considering it as an n-dimensional problem of optimization. Now, to solve the multilevel thresholding problem, n-dimensional optimal thresholds are obtained by Eq. (5), which is used for the maximization of the objective function as:

$$ (t)\ast =\arg\ \max \left(\sum \limits_{i=0}^n{E}_{ki}\right). $$

(5)

2.3 Concept of Tsallis entropy for segmentation

Constantino Tsallis have proposed the Tsallis entropy. The concept of Tsallis entropy is based on the Shannon’s entropy. Discrete probabilities make up the fundamental principle for Tsallis entropy where the sum of total of all discrete probabilities is 1. Tsallis entropy is capable of handling non-additive or non-extensive information [9, 10]. The entropy for a class is calculated using Eq. (6):

$$ {E}_T=\frac{1}{1-q}\left[\sum \limits_{i=0}^{Th}{\left(\frac{h_i}{w_0}\right)}^q-1\right]. $$

(6)

The maximized Tsallis entropy can be achieved by using Eq. (7) which can be presented as:

$$ {E}_T={E}_{T0}+{E}_{T1}+{E}_{T2}+\dots +{E}_{Tn}+\left(1-q\right)\ {E}_{T0}{E}_{T1}{E}_{T2}\dots {E}_{Tn}, $$

(7)

where,

$$ {\displaystyle \begin{array}{l}{E}_{T0}=\frac{1}{1-q}\left[\sum \limits_{i=0}^{Th_1-1}{\left(\frac{h_i}{w_0}\right)}^q-1\right],{w}_0=\sum \limits_{i=0}^{Th_1-1}{h}_i,\\ {}{E}_{T1}=\frac{1}{1-q}\left[\sum \limits_{i={Th}_1}^{Th_2-1}{\left(\frac{h_i}{w_1}\right)}^q-1\right],{w}_1=\sum \limits_{i={Th}_1}^{Th_2-1}{h}_i,\\ {}{E}_{T2}=\frac{1}{1-q}\left[\sum \limits_{i={Th}_2}^{Th_3-1}{\left(\frac{h_i}{w_2}\right)}^q-1\right],{w}_2=\sum \limits_{i={Th}_2}^{Th_3-1}{h}_i,\\ {}{E}_{Tn}=\frac{1}{1-q}\left[\sum \limits_{i={Th}_n}^{L-1}{\left(\frac{h_i}{w_n}\right)}^q-1\right],{w}_n=\sum \limits_{i={Th}_n}^{L-1}{h}_i,\end{array}} $$

(8)

where, E_Ti represents the Tsallis entropy of i_th class and n represents the maximum number of classes. The values of Eq. (8) give the Tsallis entropy of each region (or class) and these values are used in Eq. (7) to get the maximum entropic value. This degree of non-additivity is represented by the variable q which behaves as an entropic parameter. When the value of q is taken to be 1, the Tsallis entropy reduces to the Shannon entropy which implies that the Tsallis entropy is derived from of Shannon entropy. In this paper, the value of q is considered as 0.8 for each optimization algorithm to maximize the Tsallis entropy. In this context, the BAT [36, 41], BSA [22, 25, 44], FA [28, 29], PSO [11], and WDO [8] algorithms are used as optimization techniques to determine the optimum thresholds for segmentation which are obtained by maximizing each entropy as fitness functions. Through which evaluation of precision of the segmented image has been done.

3 Proposed algorithm

In this paper, the segmentation process is carried out with an optimization methodology that is presented as:

$$ \operatorname{maximize}\ {f}_{Kapur}(Th)\ \mathrm{or}\ {f}_{Tsallis}(Th), Th=\left[{Th}_1,{Th}_2,\dots, {Th}_n\right], $$

(9)

where, Th₁, Th₂,…,Th_n define the thresholds which are used for segmentation purpose. In the presented method, the segmentation of an image is processed with an optimization technique that is formulated as Eq. (10):

$$ \operatorname{maximize}\ {f}_{Renyi}(TH), Th=\left[{Th}_1,{Th}_2,\dots, {Th}_n\right],\mathrm{where}, TH\in X=\left\{{R}^k|\ 0\le {Th}_i\le 255\right\}. $$

(10)

Where i = [1, 2,…,n] and X denotes the constrained region which is valid for the interval 0 to 255.

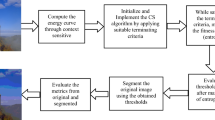
Therefore, the Renyi’s entropy-based EMO algorithm is utilized in order to search the gray level values (TH), which can resolve the formulated problem of multilevel thresholding. Optimization refers to the process of obtaining the best possible outcome for a method, which should be better than the previous result. A block diagram for an overall process of optimal color image multilevel thresholding using optimization techniques is demonstrated in Fig. 1.

Fig. 1

Block diagram of the multilevel thresholding using optimization techniques

3.1 Renyi based thresholding

Alfred Renyi proposed a definition for the measure of information that preserves the expansively for independent events which later termed as Renyi’s entropy. This entropy quantifies the randomness, uncertainty or diversity of a system. Renyi entropy is used as a diversity index in statistics and ecology and also essential in quantum information where it is used to measure entanglement [31, 52]. The entropic parameter α defines the amount of extensive information that is present in the image. In a system, the value of α determines which events contribute to the calculation of Renyi’s entropy. For example, if the value of α tends to 0, almost all the events are weighted equally by Renyi’s entropy and if a value of α tends to infinity, Renyi entropy is evaluated using the events that have the highest probability.

Similarly, in the case of image processing, the events represent the classes of the image whose probabilities are used to determine Renyi’s entropy. When the value of α is closer to zero, regardless of the probability of each class, Renyi entropy weighs all possible events more equally and when α is one, Renyi entropy reduces to Shannon entropy. This entropy yields maximum result when the value of α is taken to be 0.8. Renyi entropy can be presented using Eq. (11)

$$ {E}_R=\frac{1}{1-\alpha}\ln \sum \limits_{i=0}^{Th}{\left(\frac{h_i}{w_0}\right)}^{\alpha }, $$

(11)

where, E_R defines the entropy of a class.

Renyi entropy is a monotonically decaying function of given probability distribution in accordance with α [31]. As already detailed, Renyi entropy satisfies the additive property which can be expressed as then the total Renyi entropy of the system is given by

$$ {E}_R\left({C}_0+{C}_1\right)={E}_R\left({C}_0\right)+{E}_R\left({C}_1\right), $$

(12)

where, E_R(C₀) represents Renyi entropy of class C₀. This additive property can be extended to n independent classes C0, C1, C2, ...,C_n by

$$ {E}_R\left({C}_0+{C}_1+{C}_2+\dots +{C}_n\right)={E}_R\left({C}_0\right)+{E}_R\left({C}_1\right)+{E}_R\left({C}_2\right)+\dots +{E}_R\left({C}_n\right), $$

(13)

where

$$ {\displaystyle \begin{array}{l}{E}_{R0}=\frac{1}{1-\alpha}\ln \sum \limits_{i=0}^{Th_1-1}{\left(\frac{h_i}{w_0}\right)}^{\alpha },{w}_0=\sum \limits_{i=0}^{Th_1-1}{h}_i,\\ {}{E}_{R1}=\frac{1}{1-\alpha}\ln \sum \limits_{i={Th}_1}^{Th_2-1}{\left(\frac{h_i}{w_0}\right)}^{\alpha },{w}_1=\sum \limits_{i={Th}_1}^{Th_2-1}{h}_i,\\ {}{E}_{R2}=\frac{1}{1-\alpha}\ln \sum \limits_{i={Th}_2}^{Th_3-1}{\left(\frac{h_i}{w_0}\right)}^{\alpha },{w}_2=\sum \limits_{i={Th}_2}^{Th_3-1}{h}_i,\\ {}{E}_{Rn}=\frac{1}{1-\alpha}\ln \sum \limits_{i={Th}_n}^{L-1}{\left(\frac{h_i}{w_0}\right)}^{\alpha },{w}_3=\sum \limits_{i={Th}_n}^{L-1}{h}_i.\end{array}} $$

(14)

3.2 Electromagnetism-like mechanism

Electromagnetism-like mechanism optimization (EMO) is an evolutionary method having grounds on population. Initially, Birbil et al. [17] introduced the EMO algorithm to solve the problems related to unconfined optimization. Unlike other evolutionary optimization methodologies, EMO shows fast convergence and keeps its ability to avoid local minima in the presence of high modality surroundings [24]. Many researchers [18] have revealed that the EMO algorithm provides the superlative balance between the demand for evaluation of functions and the results from optimization. The EMO method is designed to crack the problem of searching for a global solution. When implementing EMO, it uses N number of n-dimensional points x_{i, t} where, i = 1, 2,…,n and t defines the number of generation (or iteration) used in the algorithm. To search the feasible set in the n-dimensional points can be formulated by Eq. (15):

$$ X=\left\{x\in {R}^n|{l}_i\le x\le {u}_i\right\}. $$

(15)

The initial population is expressed by using S_{p, t} = {x_{1, t}, x_{2, t}, …, x_{N, t}}. When the value of t is taken as 1, it shows that the samples in the search region X are distributed uniformly. S_p,t denotes the population class at t_th iteration and as the value of t changes the members of S_p,t varies. After S_p,t is initialized, an EMO algorithm will continue its looping process until a halting criterion such as the maximum number of iterations is encountered. EMO’s iteration mainly comprises two steps: firstly, each point in the initial population travels to a different position on the basis of attraction-repulsion mechanism. In the second step, electromagnetic an attraction-repulsion principle moves the points which are further agitated locally by a search which makes them the members of S_pt + 1 in the iteration t + 1_th. The local search of EMO and the electromagnetism principle drive the members S_p,t and x_i,t closest to the optimal value.

Concerning the theory of the electromagnetics related to charged particles, each in the search space X is considered a charged particle and on the basis of fitness function’s value, where the charge of a point is calculated. The charge obtained for a point is directly proportional to the objective (or fitness) function value. The principle of attraction-repulsion technique defines that the points with more charge attract others, whereas the points with lesser charge repel others. At last, a sum of total force vector F_i,t which is exerted on a point can be evaluated by adding the attraction-repulsion forces, and each x_i,t that belongs to S_p,t is moved in the direction of its total force to the location y_i,t. A localized search is used to browse the surroundings of each and every particle in accordance with its objective value. The members, x_{i, t + 1} belonging to S_p,t, of t + 1_th iteration are searched by the use of Eq. (16):

$$ {x}_{i,t+1}=\left\{\begin{array}{l}{y}_{i,t};f\left({y}_{i,t}\right)\le f\left({z}_{i,t}\right)\\ {}{z}_{i,t}; else\end{array}\right.. $$

(16)

The pseudo algorithm for EMO is given below as:

In addition, the detail steps of the proposed EMO based multilevel thresholding scheme have been also offered. The following are the steps involved in the implementation of electromagnetism-like mechanism optimization (EMO) algorithm:

• Step 1: Define the input parameters: Initialize the maximum length of iterations iter_max. In case of local search stage, n × iter_local gives the z_i,t which is representing the maximum number of positions, within the δ distance of y_i,t, for each dimension i.

• Step 2: Initialize: Select the (points) x_{i, t}, at t = 1 uniformly in X, i.e., x_{i, 1} ≈Unif (X), I = 1, 2,...,N, where Unif is representing the uniform distribution. Compute the fitness function values f (x_{i, t}) and identify the best point for minimization and maximization, which can be done using Eqs. (17) and (18):

$$ {x}_t=\arg \underset{X_{i,t}\in {s}_t}{\min}\left\{f\left({x}_{i,t}\right)\right\} $$

(17)

and

$$ {x}_t=\arg \underset{X_{i,t}\in {s}_t}{\max}\left\{f\left({x}_{i,t}\right)\right\}. $$

(18)

• Step 3: Calculate the force after assigning a charge like value (q_{i, t}) to each and every point (x_{i, t}). The charge q_{i, t} has a dependency on f (x_{i, t}) which implies that, if a point has more charge, it has a better fitness value. Use Eq. (19) to compute the charge:

$$ {q}_{i,t}=\exp \left\{-n\frac{f\left({x}_{i,t}\right)-f\left({x}_t\right)}{\sum \limits_{j=1}^Nf\left({x}_{i,t}\right)-f\left({x}_t\right)}\right\}. $$

(19)

• Step 4: For each t, determine the force between i_th point x_i,t and j_th point x_j,t using the equation given as:

$$ {F}_{i,\mathrm{j}}=\left\{\begin{array}{l}\left({x}_{j,t}-{x}_{i,t}\right)\frac{q_{j,t}.{q}_{i,t}}{{\left\Vert {x}_{j,t}-\left.{x}_{i,t}\right\Vert \right.}^2};f\left({x}_{j,t}\right)<f\left({x}_{i,t}\right)\\ {}\left({x}_{i,t}-{x}_{j,t}\right)\frac{q_{j,t}.{q}_{i,t}}{{\left\Vert {x}_{j,t}-\left.{x}_{i,t}\right\Vert \right.}^2};f\left({x}_{j,t}\right)\ge f\left({x}_{i,t}\right)\end{array}\right. $$

(20)

and calculate the total force for each t as:

$$ {F}_i=\sum \limits_{j=1,j\ne i}^N{F}_{i,\mathrm{j}}. $$

(21)

• Step 5: Except x_t, each point x_i,t is to be moved along F_i utilizing the Eq. (22)

$$ {x}_{i,t}={x}_{i,t}+\lambda \frac{F_i}{\left\Vert {F}_i\right\Vert }(RNG),i=1,2,\dots, N, $$

(22)

where, λ≈Unif (0, 1) for each and every point x_i,t and the allowable movement range towards the upper and lower bound for a respective dimension is defined by RNG.

• Step 6: For each y_{i, t}, generate a maximum of iter_local points for every direction of coordinate which should remain in the δ neighborhood of y_i,t. Continue the process until either a better z_i,t is obtained or the iteration reaches its maximum value i.e., n × iter_local.

• Step 7: For the selection of the next iteration x_{i, t + 1}, which belongs to S_pt + 1 are selected from z_i,t and y_i,t using Eq. (16) to identify the extreme point using Eq. (17) for minimization or Eq. (18) for maximization.

The aim of this paper is to maximize the Renyi’s objective (or fitness) function using electromagnetism-like mechanism optimization (EMO). A complete systematic flowchart routine of the proposed EMO-Renyi’s based multilevel color image thresholding is shown in the Fig. 2.

Fig. 2

Flowchart of the proposed EMO-R based multilevel thresholding scheme

4 Experiment results and discussion

In this section, experiment outcomes have been demonstrated to estimate and validate the performance of the proposed (EMO-R) methodology along with Kapur’s and Tsallis based existing approaches using each optimization algorithm for normal as well as satellite images. In satellite images, different bands with different frequency regions make the algorithms inefficient and containing high resolution is an additional source of inadequacy. In satellite image segmentation, the presence of intrinsic uncertainty makes the search of interested domain imprecise. Multi-level thresholding can be used for efficient satellite image segmentation. Therefore, in this paper, optimizing techniques with Kapur’s, Tsallis, and Renyi’s entropy as an objective function has been presented towards accurate and fast multilevel based segmentation for daily-life and satellite images.

4.1 Image dataset

With a view to obtaining a better estimation of the segmented output of the proposed (EMO-R) scheme, the performance of Kapur’s and Tsallis entropies are compared using each optimization algorithm. Therefore, experimental results of each selected methods such as BAT, BSA, FA, PSO, WDO, and EMO algorithm with Kapur’s entropy, Renyi’s entropy, and Tsallis entropy have been shown separately. Moreover, for better discrimination of each method, the trials have been steered on 10 entirely diverse images with distinct histogram characteristic. To check the robustness of the proposed (EMO-R) scheme for different feature images, the first five test images are included as well-known standard color images and the next five are considered as high-resolution satellite images which are shown in Fig. 3(1–10). Each of the images depicts a histogram which is exclusive in itself which is indicated in Fig. 3(1′-10′). All the 10 images have diverse features that add on to the result of the segmented image.

Fig. 3

Images (1–10) depict standard and satellite test images, (1′-10′) represent respective histogram images

4.2 Measurement parameters to assess image quality

This section represents different prominent fidelity factors such as structural-similarity index (SSIM) and feature-similarity index (FSIM), misclassification error (ME), mean-squared error (MSE) and peak signal-to-noise ratio (PSNR), which have been utilized to show the quality of the proposed and compared methods. The image fidelity parameters like mean error (ME), mean squared error (MSE), peak signal to noise ratio (PSNR), structural similarity index module (SSIM), feature similarity index module (FSIM) and Entropy values are taken to test the efficiency of the proposed method.

These parameters are used to represent the quality of the segmented image. MSE calculates the difference between the expected value and actual value. PSNR is used to calculate the peak signal to noise ratio between original and segmented image. SSIM is the structural similarity index needed to calculate the structural similarity and FSIM used to evaluate the feature similarity of the segmented and original image. Higher values of SSIM and FSIM indicate higher performance. The formulae for all these parameters are defined in Table 1. The values of important parameters of each of the optimization algorithm are presented in Table 2. The determination of the proper value of the entropic parameter is important. The parameter q and α represents the variable for Tsallis and Renyi’s entropy respectively. The value of q is fixed at 0.8, which is an endorsed value in literature such as [50]. The optimum value for α and q is set after several experiments. The value of α is set to 0.8 and the value of q is also set to 0.8. The values of α beyond 1 give poor results. When q is set from 0.5 to 0.9 the same results are obtained. The optimum results are obtained, when α is 0.8.

Table 1 Different metrice to test the efficiency of each methods

Table 2 Parameters and their respective values used in optimization algorithms

4.3 Performance evaluation and comparison

The simulation results are arranged in the form of separate tables and invisulats graphical plots for each parameter to examine a different aspect of the thresholded images. To evaluate the overall performance different parameters are examined which are shown quantitatively in Tables 3, 4, 5, 6, 7, 8, 9, 10, and 11. Furthermore, CPU time (in seconds) is computed in Table 12, to estimate the computational difficulties or efficiency of the proposed EMO-R approach.

Table 3 Comparison of ME and best objective values (entropy) computed by different algorithm using Kapur’s entropy

Table 4 Comparison of ME and best objective values (entropy) computed by different algorithm using Tsallis entropy

Table 5 Comparison of ME and best objective values (entropy) computed by different algorithm using Renyi entropy

Table 6 Comparison of MSE, and PSNR computed by different algorithm using Kapur’s entropy

Table 7 Comparison of MSE, and PSNR computed by different algorithm using Tsallis entropy

Table 8 Comparison MSE, and PSNR computed by different algorithm using Renyi entropy

Table 9 Comparison of SSIM, and FSIM computed by different algorithm using Kapur’s entropy

Table 10 Comparison of SSIM, and FSIM computed by different algorithm using Tsallis entropy

Table 11 Comparison SSIM, and FSIM computed by different algorithm using Renyi entropy

Table 12 Comparison of CPU Timing obtained by using different methods for each sample images

Figures 4, 5, 6, 7, 8, 9, 10, and 11 visually evaluate the overall segmented results and illustrate the pictorial view demonstration of thresholded images. The proposed method has been shown the best-segmented images in a thorough examination of the qualitative evaluation part. A comparison with other nature-inspired optimization algorithms (BAT, BSA, FA, PSO, and WDO) are incorporated using Kapur’s, Tsallis, and Renyi’s entropy at 3, 5, 8 and 16 levels of threshold, to adjudicate the performance of the proposed EMO-Renyi’s scheme. However, among all methods, EMO-Renyi’s based approach is superior, but BAT, BSA, FA, PSO, and WDO are also producing satisfactory results with Renyi’s entropy.

Fig. 4

The 3-levels thresholded test images obtained by BAT, BSA, FA, PSO, WDO and EMO techniques using Kapur’s entropy

Fig. 5

The 5-levels thresholded test images obtained by BAT, BSA, FA, PSO, WDO and EMO techniques using Kapur’s entropy

Fig. 6

The 3-levels thresholded test images obtained by BAT, BSA, FA, PSO, WDO and EMO techniques using Tsallis entropy

Fig. 7

The 5-levels thresholded test images obtained by BAT, BSA, FA, PSO, WDO and EMO techniques using Tsallis entropy

Fig. 8

The 3-levels thresholded test images obtained by BAT, BSA, FA, PSO, WDO, and EMO techniques using Renyi’s entropy

Fig. 9

The 5-levels thresholded test images obtained by BAT, BSA, FA, PSO, WDO, and EMO techniques using Renyi’s entropy

Fig. 10

The 3, 5, 8, and 16-levels thresholded test image 2 obtained by BAT, BSA, FA, PSO, WDO, and EMO techniques using Kapur’s, Tsallis and Renyi’s entropy

Fig. 11

The 3, 5, 8, 16-levels thresholded test image 7 obtained by BAT, BSA, FA, PSO, WDO, and EMO techniques using Kapur’s, Tsallis, and Renyi’s entropy

Figures 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, and 29 depict the graphical plots of numerical parameters together, whereas Figs. 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, and 29 report the comparison plots of ME, MSE, PSNR, SSIM, FSIM, and CPU time using Kapur’s Tsallis and Renyi’s entropy for 8-level of threshold using BAT, BSA, FA, PSO, WDO, and EMO correspondingly. Figures 30 and 31 represent the computational efficiency of the proposed scheme for a different level of threshold. To test the effectiveness, efficiency, and robustness of the proposed EMO and Renyi based algorithm, three different objective (or fitness) functions are examined. They are presented separately as follows:

Fig. 12

Comparison of 8-level ME values for Kapur’s entropy

Fig. 13

Comparison of 8-level ME values for Tsallis entropy

Fig. 14

Comparison of 8-levelME values for Renyi ‘s entropy

Fig. 15

Comparison of 8-level MSE values for Kapur’s entropy

Fig. 16

Comparison of 8-level MSE values for Tsallis entropy

Fig. 17

Comparison of 8-level MSE values for Renyi ‘s entropy

Fig. 18

Comparison of 8-level PSNR values for Kapur’s entropy

Fig. 19

Comparison of 8-level PSNR values for Tsallis entropy

Fig. 20

Comparison of 8-level PSNR values for Renyi ‘s entropy

Fig. 21

Comparison of 8-level SSIM values for Kapur’s entropy

Fig. 22

Comparison of 8-level SSIM values for Tsallis entropy

Fig. 23

Comparison of 8-level SSIM values for Renyi ‘s entropy

Fig. 24

Comparison of 8-level FSIM values for Kapur’s entropy

Fig. 25

Comparison of 8-level FSIM values for Tsallis entropy.

Fig. 26

Comparison of 8-level FSIM values for Renyi ‘s entropy

Fig. 27

Comparison of 8-level CPU time for Kapur’s entropy

Fig. 28

Comparison of 8-level CPU time for Tsallis entropy

Fig. 29

Comparison of 8-level CPU time for Renyi ‘s entropy

Fig. 30

Comparison of CPU time required by EMO algorithm using Kapur’s, Tsallis and Renyi’s entropy at 8-level threshold

Fig. 31

Comparison of CPU time required by EMO algorithm using Kapur’s, Tsallis and Renyi’s entropy at 16-level threshold

4.4 Experiment 1: Kapur’s entropy maximization

This part of the paper discusses the outcomes obtained for various satellite and daily-life test images using Kapur’s as a fitness function. Table 3 portrays the misclassification error and objective values obtained by BAT algorithm, BSA, FA, PSO, WDO, and EMO. It is examined that the misclassification error evaluated by the EMO method produces the lowest value amongst all the techniques, which are being compared for almost all the images. MSE and PSNR values obtained using the optimization methods have been listed in Table 6 and the comparison is done with the results acquired using BSA, BAT algorithm, FA, PSO, WDO, and EMO methods. Adding to the quality assessment results, the feature assessment parameters such as SSIM and FSIM also show better results for EMO-Kapur’s based segmentation in comparison to other optimization methods, when implemented using Kapur’s entropy. This can be seen in Table 9. Table 12 compares the computation efficiency of all the algorithms. This table confirms that the EMO algorithm is the most suitable when it comes to efficiency. Figures 4 and 5 depict the segmented results for all the images obtained at 3-level and 5-level thresholding. Figures 12, 15, 18, 21, 24, shows the plots for the metrics stated above and it can be clearly seen from the plots that the EMO algorithm and Kapur’s entropy-based method outperforms all other optimization (BAT algorithm, BSA, FA, WDO, and PSO) techniques with Kapur’s entropy for most of the images. The plot for CPU timing is depicted by Fig. 27.

4.5 Experiment 2: Tsallis entropy maximization

In this section, an evaluation of the optimum threshold values from the aid of Tsallis entropy has been discussed for the desired problem. The misclassification error (ME), fitness function values calculated for all the optimization methods used in this paper are listed in Table 4. PSNR and mean square error (MSE) valuation obtained using the BAT algorithm, BSA, FA, PSO, WDO, and EMO with Tsallis entropy is shown in Table 7. A simple observation from Tables 4 and 7 verifies, for most of the images, the best results are obtained when Tsallis entropy is used with electromagnetism-like mechanism optimization. Table 10 compares the similarity in features of the original image and segmented image from the results obtained by using the mentioned methods with Tsallis entropy as an objective function respectively. Figures 6 and 7 portray the segmented results of all considered images for threshold levels3, and 5 acquired for BAT-Tsallis, BSA-Tsallis, FA-Tsallis, PSO-Tsallis, WDO-Tsallis, and EMO-Tsallis. Figures 13, 16, 19, 22, 25, and 28 report the plots for the ME, MSE, PSNR, SSIM, FSIM, and CPU timing respectively from which it is clear that the EMO algorithm and Tsallis entropy-based method outperforms all other optimization techniques with Tsallis as a fitness function.

4.6 Experiment 3: Renyi’s entropy maximization

In this section of the paper, the results achieved for various test images by using Renyi’s entropy as objective (or fitness) function are discussed. Table 5 depicts the objective values and the ME values obtained by BAT algorithm, PSO, WDO, BSA, FA, and EMO algorithm. It has been tested that the misclassification error evaluated by the proposed method i.e. EMO with Renyi entropy harvests the lowest value among all the techniques that are being compared for different standard and satellite images. SSIM and FSIM are the metrics that show the feature similarity between the images being tested. MSE and peak signal to noise ratio PSNR values that have been attained using the proposed Renyi entropy-based EMO method show its supremeness over other methods.

Table 8 contains the comparison of MSE and PSNR of the listed methods whereas Table 11 illustrates the SSIM and FSIM values. Table 12 shows the time required to compute the optimum thresholds by using BSA algorithm, PSO, WDO, FA, BSA, and EMO. From Tables 11 and 12, it has been made sure that EMO-Renyi’s beats BAT-Renyi, BSA-Renyi, FA-Renyi, PSO-Renyi, and WDO-Renyi in terms of feature similarity as well as computational efficiency. It can be clearly observed from the segmented images in Figs. 8 (3-level) and 9 (5-level) that the proposed EMO-Renyi’s based technique offers superior segmentation when compared with other evolutionary algorithms such as BSA, BAT algorithm, PSO, FA, and WDO. From the plots presented in Figs. 14, 17, 20, 23, 26, and 29 depict the qualitative and computational supremacy of the proposed method over other methods.

4.7 Comparative analysis of Renyi’s, Tsallis, and Kapur’s entropy

Keeping the view of all the fidelity assessment from Tables 3, 4, 5, 6, 7, 8, 9, 10, and 11, EMO-Kapur’s, EMO-Tsallis, and EMO-Renyi’s have performed outstandingly in comparison to BAT algorithm, BSA, FA, PSO, and WDO. In addition, Fig. 10 shows the segmented results of the second test image at 3-level, 5-level, 8-level, and 16-level thresholding from which it can be deduced that EMO-Renyi’s method surpasses the EMO-Kapur’s and EMO-Tsallis. The same can be concluded from Fig. 11 which shows segmented results for test image 7 which is a satellite image, it has been clarified that Renyi’s entropy-based segmentation performs in a better manner in comparison with Kapur’s and Tsallis entropy-based multilevel thresholding approaches. Table 12 has been computed to show the computational efficiency among all algorithms when implemented with the aid of Renyi’s, Tsallis, and Kapur’s entropy as fitness (or objective) function. From Table 12, it can be clearly visualized that Renyi’s entropy outsmarts Kapur’s and Tsallis and also that the proposed method i.e. EMO-Renyi’s is the absolute suitable when the time is the most important matter of concern. The same has also been depicted in the plot in Fig. 30 for 8-level and Fig. 31 for 16-level which implies the computational supremacy of EMO-Renyi’s based color image segmentation. The convergence plots at 8-level for input images 3, 4, 8, and 10 have been shown in Fig. 32a–d. From the convergence graph plots for each objective function, it can be easily observed that for mostly all the images EMO-Renyi’s technique is converging faster than rest of the algorithms used in this paper.

Fig. 32

a-d Convergence plot for BAT, BSA, FA, PSO, WDO and EMO at 8-level threshold for input image 3, 4, 8, and 10 respectively

In order to measure the performance of the proposed approach, mean square error (MSE), misclassification error (ME), SSIM, FSIM, and PSNR have been utilized to assess the quality of segmentation, considering the coincidences in between the original images and respective segmented images. After the analysis of the convergence rate of different images using EMO, FA, PSO, BAT algorithm, BSA, and WDO algorithms, it is concluded that EMO is very fast as compared to other algorithms. The order of computational efficiency has been sorted in the order as EMO > FA > WDO > PSO > BAT algorithm > BSA. Even if individual entropies are considered, EMO outperforms all other optimization techniques considered in this paper. Hence, EMO has been proven to be superior to the rest of algorithms and also the EMO-Renyi’s beats EMO-Tsallis and EMO-Kapur’s i.e. in terms of efficiency and robustness Renyi’s > Kapur’s > Tsallis.

In addition, convergence plots have been drawn in Fig. 32 for Kapur’s, Tsallis and Renyi’s entropy. As seen from all of the convergence plots, the optimum value (maximum value) is attained in the case of proposed EMO-Renyi’s method. Proposed EMO-Renyi computes maximum value efficiently in comparison with the BAT, BSA, FA, PSO, and WDO algorithms.

4.8 Merits of the proposed method

The color image multilevel thresholding outcomes of proposed EMO-Renyi’s method are encouraging and it inspires future works. For statistical independent subsystems, Renyi’s entropy shows an extensive property and is applied to find the best threshold value for image segmentation. However, EMO belongs to old optimization technique but by combining this technique with Renyi’s entropy this produces efficient segmentation results with high accuracy. This technique has a fast convergence rate. Renyi’s entropy has selected for energy calculations because of the easiest implementation and the highest accuracy. The easy extension of Renyi’s entropy to multilevel thresholding problems sums up the advantage of less computation cost. The proposed work has noteworthy application in the area of expert and intelligent systems which includes machine learning, medical image processing, object recognition, traffic monitoring practice, video investigation, the study of thermal imaging, pattern analysis, image and computer vision domain. So far, multilevel-based image segmentation approaches have been effectively utilized in several fields of expert and intelligent systems applications with a different purpose. Few of them may consider as face recognition, image retrieval, and object detection for example. Satellite images are often segmented in the presence of unpredictability. This randomness is due to the factors that are highly dependent on environmental conditions, deprived resolution, very low spatial resolution, and poor illumination.

5 Conclusion

This paper has focused on color image multilevel thresholding for normal data and satellite test images using current optimization algorithms. In this paper, EMO, BAT algorithm, BSA, FA, PSO, and WDO methods have been employed to maximize Renyi’s, Tsallis, and Kapur’s entropy to solve the problem of multilevel thresholding by determining the optimum multilevel threshold values. Based on qualitative and quantitative assessments, it can expose that the proposed EMO-Renyi’s algorithm can be efficiently and effectively useful in multilevel thresholding for satellite and daily-life color images. The outcomes emphasize that the EMO outperforms the BAT algorithm, BSA, FA, PSO, and WDO when implemented with each of the objective function. The best part of EMO is its computational proficiency for multilevel color image segmentation over existing approaches. The experimental outcomes are encouraging and motivate futuristic research areas to apply the EMO algorithm to other image processing applications such as image enhancement and image denoising for remote sensing images, image classification and in various computer-related problems. Furthermore, the proposed scheme can be extended for medical image segmentation due to fast segmentation ability.