1 Introduction

High-dimensional data are commonly generated in a range of real-world applications, including computer vision, pattern recognition, data mining and machine learning. However, the use of high-dimensional data can not only increase storage costs, but also introduce redundancy and irrelevant information [9, 32, 36], that degenerates the performance of learning tasks. Accordingly, feature selection, which aims to select the most representative feature set from the original features is preferred in these instances [6, 17, 20, 23, 29, 31]. Since practical large-scale data are usually collected without labels being appended, and annotating these data is a dramatically expensive and time-consuming process [2, 11], unsupervised feature selection has become a ubiquitous and challenging problem [5]. In recent years, the development of various unsupervised feature selection methods has significantly facilitated the performance of many machine learning tasks, such as classification, clustering, retrieval, and ranking [7, 8, 13, 14, 16].

In this letter, we focus on the family of graph-based unsupervised feature selection (GUFS) methods, in which the manifold geometry structure of the whole feature set is characterized in graph form. A range of typical GUFS methods have been proposed over the past decade, including Laplacian Score (LS) [9], Spectral Feature Selection (SPEC) [37], Multi-Cluster Feature Selection (MCFS) [1], and Robust Unsupervised Feature Selection (RUFS) [28]. However, most traditional GUFS methods focus on learning task performance while neglecting the underlying computational complexity, which is of great importance given the ever-increasing size of data. This complexity arises primarily due to two aspects: the first is the graph construction, and the second is the feature selection on the graph. Both of these processes are time-consuming for large-scale data, and have a time complexity of at least O(n2d), where n and d denote the number of samples and features, respectively.

To address this issue, and inspired by recent works that have scaled up graph-based learning models using anchors [3, 4, 18, 19], we propose a novel approach named Fast Unsupervised Feature Selection (FUFS) incorporating an anchor graph and ℓ2,1-norm regularization. The main contributions of our work are as follows. First, the anchor graph is constructed using a parameter-free adaptive neighbor assignment strategy. Meanwhile, an approximate nearest neighbor search (ANNS) technique is introduced to speed up the construction of the anchor graph. Second, the ℓ2,1-norm regularization [22, 26, 34] is performed in order to select more valuable features, and a simple yet efficient iterative algorithm is designed to optimize the proposed objective function. Thirdly, the computational complexity of the FUFS algorithm can be reduced to O(ndmt), where m and t are the number of anchors and iteration, respectively, giving our proposed method a great advantage over conventional GUFS methods. Comprehensive experiments on several large-scale data sets demonstrate the efficiency and effectiveness of the proposed FUFS algorithm.

2 The FUFS algorithm

In this section, we introduce our FUFS method for large-scale data sets. First, the anchor graph is constructed, after which the ℓ2,1-norm regularization is adopted to select more valuable features on this graph.

2.1 Graph construction

Let \(\boldsymbol {X}=[\boldsymbol {x}_{1},\boldsymbol {x}_{2},\cdots ,\boldsymbol {x}_{n}]^{T}\in \mathbb {R}^{n\times d}\) represent the data matrix, where n and d denote the number of data points and the dimension of features, respectively. Each data point xi is represented as a vertex on the affinity graph, while each edge represents the similarity relationship of one pair of vertexes. The weight of the edge between xi and xj is defined as aij and \(\boldsymbol {A} =\{a_{ij}\}\in \mathbb {R}^{n\times n}\) denotes the similarity matrix of the affinity graph.

2.1.1 Traditional graph construction

The first step of all the traditional GUFS methods is to construct the similarity graph by computing all pairwise similarity between the data points. There are usually three different similarity graphs:

  1. 1.

    Theε-neighborhood graph: We connect all points whose pairwise distances are smaller than ε.

  2. 2.

    k-nearest neighbor graph: The vertexes xi and xj are connected if xi is among the k-nearest neighbors of xj or xj is among the k-nearest neighbors of xi.

  3. 3.

    The fully connected graph: All points are connected with positive similarity with each other.

We can apply all graphs mentioned above to weight the edges by the similarity, while the choice of different graphs may result in different learning performance. Since local geometric structure of data can usually get better performance than global geometric structure, and the value of positive integer k is easier to tune than ε, almost all the graph-based methods tend to apply k-nearest neighbor graph (KNN) to construct similarity graph. A reasonable way to define the weight aij is by using the Gaussian kernel function, then we can define

$$a_{ij} = \left\{ \begin{array}{ll} \text{eps}(-\frac{\|\boldsymbol x_i-\boldsymbol x_j\|^2}{2\sigma^2}) & \boldsymbol x_i\in\mathcal{N}{(\boldsymbol x_{j})} \text{or} \ \boldsymbol x_j\in\mathcal{N}{(\boldsymbol x_{i})}\\ 0 & \text{otherwise}, \end{array} \right. $$

where \(\mathcal {N}(\boldsymbol x)\) denotes the set of k-nearest neighbors of x, σ is a parameter that controls the width of the neighborhoods. Since the extra parameter σ in the Gaussian kernel function is very sensitive [24, 33] and is difficult to tune in practice, we are more likely to adopt a parameter-free method to construct similarity graph.

2.1.2 Anchor graph construction

Recent studies have adopted an anchor-based strategy to construct the similarity matrix A. Generally, this strategy requires two steps to construct A: first, m (m ≪ n) anchors are generated from data points, after which the similarity between data points and anchors are measured by the matrix \(\boldsymbol {Z}\in \mathbb {R}^{n\times m}\).

Anchor generation can be achieved either by random selection or by using the k-means method [3, 4, 18, 19]. Random selection selects m anchors by random sampling from data points and takes O(1) computational complexity. Although random selection cannot guarantee that the selected m anchors are always good, it is extremely fast for large-scale data sets. The k-means method makes use of m clustering centers as anchors. Although use of these clustering centers results in more representative anchors, the k-means method needs O(ndmt) computational complexity , where t is the number of iterations, which makes its use for large-scale data sets impossible.

After the anchors are generated, the similarity matrix Z needs to be constructed. Conventional methods usually use kernel-based neighbor assignment strategy (e.g., Gaussian similarity function), which typically requires extra parameters. To avoid this, we adopt an adaptive neighbor assignment strategy [24] to obtain the the similarity matrix Z. Let \(U=[\boldsymbol u_{1},...,\boldsymbol u_{m}]^{T}\in \mathbb {R}^{m\times {d}}\) denotes the set of anchor points. The similarity zij between xi and uj can be defined as probability that ui is to be the neighbor of xi. We use the square of Euclidean distance \(\|\boldsymbol {x}_{i}-\boldsymbol {u}_{j}\|_{2}^{2}\) as the distance measure. For the i-th data point xi, all the anchor points can be connected to xi with probability zij. Evoked by the intuition that nearby points should have similar properties [10, 25], a smaller distance should be assigned a larger probability. Thereby, a natural method to obtain neighbor probabilities for the i-th sample is by solving following problem

$$ \min_{\boldsymbol {z_{i}^{T}}\textbf{1}= 1,z_{i}\geq{0}} \sum\limits_{j = 1}^{m}\|\boldsymbol x_{i}-\boldsymbol u_{j}\|_{2}^{2}z_{ij}. $$
(1)

However, Eq. (1) has a trivial solution, only the nearest anchor point can be the neighbor of xi. To avoid this dilemma, a regularization term is added to Eq. (1), then we have

$$ \min_{\boldsymbol{z}_{i}^{T}\textbf{1}= 1,z_{ij}\geq0} \sum\limits_{j = 1}^{m}\|\boldsymbol{x}_{i}-\boldsymbol{u}_{j}\|_{2}^{2}z_{ij}+\gamma\sum\limits_{j = 1}^{m}z_{ij}^{2}, $$
(2)

where \(\boldsymbol {z}_{i}^{T}\) denotes the i-th row of Z, zij is the j-th element of \(\boldsymbol {z}_{i}^{T}\) and γ is the regularization parameter. Let \(d_{ij}=\|\boldsymbol {x}_{i}-\boldsymbol {u}_{j}||_{2}^{2}\), while \(\boldsymbol {d}_{i}\in \mathbb {R}^{m\times 1} \) is a vector with the j-th element as dij, Eq. (2) can be rewritten in vector form as

$$ \min_{\boldsymbol{z}_{i}} \|\boldsymbol{z}_{i}+\frac{\boldsymbol{d}_{i}}{2\gamma}\|_{2}^{2}~~~s.t.~\boldsymbol{z}_{i}^{T}\textbf{1}= 1, z_{ij}\geq0. $$
(3)

In light of [24], it is preferred to learn a sparse zi which has exactly k nonzero values. Thus, the learned Z is sparse, and the computation burden of subsequent spectral analysis can be largely alleviated. The parameter γ can be set as \(\gamma =\frac {k}{2}d_{i,k + 1}-\frac {1}{2}{\sum }_{j = 1}^{k}d_{ij} \), such that optimal solution to Eq. (3) is

$$ z_{ij}=\frac{d_{i,k + 1}-d_{ij}}{kd_{i,k + 1}-{\sum}_{j = 1}^{k}d_{ij}}. $$
(4)

For detail derivation, see [24]. The computational complexity of calculating matrix Z using Eq. (4) is O(ndm). To improve the efficiency of the anchor graph construction, we investigate an ANNS technique so as to achieve k-nearest neighbors matching. Thus, the process of computing the matrix Z can be efficiently implemented in O(nd log(m)) [21].

Accordingly, the similarity matrix A can be obtained by [18]

$$ \boldsymbol{A}=\boldsymbol{Z}\boldsymbol{\Delta}^{-1}\boldsymbol{Z}^{T}, $$
(5)

where the diagonal matrix \(\boldsymbol {\Delta }\in \mathbb {R}^{m\times {m}}\) is defined as \({\Delta }_{jj}={\sum }_{i = 1}^{n}z_{ij}\).

2.2 Feature selection with anchor graph and ℓ 2,1-norm regularization

According to the manifold learning theory, high-dimensional data lies in or is close to a low-dimensional manifold, and there is always a matrix \(\boldsymbol {W}\in \mathbb {R}^{d\times l}\) that can preserve the manifold structure after projection, where d is the original dimension, l is the projection dimension. A typical dimensionality reduction algorithm is proposed in [12, 27] to solve the following problem:

$$ \min_{\boldsymbol{W}^{T}\boldsymbol{W}=\boldsymbol{I}}Tr(\boldsymbol{W}^{T}\boldsymbol{X}^{T}\boldsymbol{L}\boldsymbol{X}\boldsymbol{W}), $$
(6)

where I denotes the identity matrix, \(\boldsymbol L\in \mathbb {R}^{n\times n}\) is Laplacian matrix which is defined by L = D −A, D is a diagonal matrix, and the i-th entry is defined as \(D_{ii}={\sum }_{j = 1}^{n}a_{ij}\). Problem (6) is a dimensionality reduction model and the projected feature is a linear combination of all original features. However, in many applications, we are more interested in the feature selection model. Since only a few important features are involved in the projection and the i-th row of matrix W could be used to measure the importance of i-th feature of original data. The task of our proposed method is to find the optimal projection matrix that is constrained to be a row sparse matrix, which can be achieved by means of ℓ2,1-norm regularization. Therefore, problem (6) can be rewritten as follows for feature selection:

$$ \min_{\boldsymbol{W}^{T}\boldsymbol{W}=\boldsymbol{I}}Tr(\boldsymbol{W}^{T}\boldsymbol{X}^{T}\boldsymbol{L}\boldsymbol{X}\boldsymbol{W})+\alpha\|\boldsymbol{W}\|_{2,1}, $$
(7)

where α is the regularization parameter, ∥W∥2,1 is defined as \({\sum }_{i = 1}^{d}\|\boldsymbol {w}_{i}\|_{2}\), where \(\boldsymbol {w}_{i}\in \mathbb {R}^{l\times 1} \) is the transpose of the i-th row of W. From (5), A can be written as A = BBT, where \(\boldsymbol {B}=\boldsymbol {Z}\boldsymbol {\Delta }^{-\frac {1}{2}}\). For the degree of each data point, we have \(D_{ii}={\sum }_{sj}Z_{is}({\Delta }_{ss})^{-1}Z_{js}={\sum }_{s}Z_{is}= 1\). Therefore, it is easy to see that A is a double stochastic matrix, and we obtain the diagonal matrix D = I and L = I −BBT. Accordingly, we propose our fast unsupervised feature selection (FUFS) model by solving the following problem:

$$ \min_{\boldsymbol{W}^{T}\boldsymbol{W}=\boldsymbol{I}}Tr[\boldsymbol{W}^{T}\boldsymbol{X}^{T}(\boldsymbol{I}-\boldsymbol{B}\boldsymbol{B}^{T})\boldsymbol{X} \boldsymbol{W}]+\alpha\sum\limits_{i = 1}^{d}\|\boldsymbol{w}_{i}\|_{2}. $$
(8)

Obviously, ∥wi∥2 can be zero in theory, however, this will make Eq. (8) non-differentiable. To avoid this issue, ∥wi∥2 is replaced by \(\sqrt {\boldsymbol {w}_{i}^{T}\boldsymbol {w}_{i}+\varepsilon }\) to make Eq. (8) differentiable, where ε is a small enough constant. Therefore, we obtain

$$ \min_{\boldsymbol{W}^{T}\boldsymbol{W}=\boldsymbol{I}}Tr[\boldsymbol{W}^{T}\boldsymbol{X}^{T}(\boldsymbol{I}-\boldsymbol{B}\boldsymbol{B}^{T})\boldsymbol{X} \boldsymbol{W}]+\alpha\sum\limits_{i = 1}^{d}\sqrt{\boldsymbol{w}_{i}^{T}\boldsymbol{w}_{i}+\varepsilon}, $$
(9)

which is evidently equal to problem (8) when ε is infinitely close to zero. The Lagrangian function of problem (9) is

$$\begin{array}{@{}rcl@{}} \mathcal{L}(\boldsymbol{W},\boldsymbol{\Lambda})&=&Tr[\boldsymbol{W}^{T}\boldsymbol{X}^{T}(\boldsymbol{I}-\boldsymbol{B}\boldsymbol{B}^{T})\boldsymbol{X}\boldsymbol{W}]\\ &&+\alpha\sum\limits_{i = 1}^{d}\sqrt{\boldsymbol{w}_{i}^{T}\boldsymbol{w}_{i}+\varepsilon} +Tr(\boldsymbol{\Lambda}(\boldsymbol{W}^{T}\boldsymbol{W}-\boldsymbol{I})), \end{array} $$
(10)

where Λ is the Lagrangian multiplier. By taking the derivative of \(\mathcal {L}(\boldsymbol {W},\boldsymbol {\Lambda })\) w.r.t W, and set the derivative to zero, we obtain

$$ \frac{\partial{\mathcal{L}(\boldsymbol{W},\!\boldsymbol{\Lambda})}}{\partial{\boldsymbol{W}}}\,=\, \boldsymbol{X}^{T}\!(\boldsymbol{I}\,-\,\boldsymbol{B}\boldsymbol{B}^{T})\boldsymbol{X}\boldsymbol{W}\,+\,\alpha\boldsymbol{Q}\boldsymbol{W} \,+\,\boldsymbol{W}\boldsymbol{\Lambda}\,=\,0. $$
(11)

where \(\boldsymbol {Q}\in \mathbb {R}^{d\times d}\) is a diagonal matrix, and the i-th element is defined as

$$ \boldsymbol{Q}_{ii}=\frac{1}{2\sqrt{\boldsymbol{w}_{i}^{T}\boldsymbol{w}_{i}+\varepsilon}}. $$
(12)

Note that Q is also a unknown variable and dependent on W. We now propose an alternative iterative algorithm to solve problem (9). When W is fixed, then Q is obtained by Eq. (12). When Q is fixed, solving Eq. (11) is equivalent to solving

$$ \min_{\boldsymbol{W}^{T}\!\boldsymbol{W}\,=\,\boldsymbol{I}}Tr[\boldsymbol{W}^{T}\!\!\boldsymbol{X}^{T}\!(\boldsymbol{I}\,-\,\boldsymbol{B}\!\boldsymbol{B}^{T}\!)\boldsymbol{X}\!\boldsymbol{W}] \,+\,\alpha Tr(\boldsymbol{W}^{T}\!\boldsymbol{Q}\boldsymbol{W}), $$
(13)

and problem (13) can be solved directly to obtain W. Let M = XT(I −BBT)X; as such, the details of this algorithm are summarized in Algorithm 1. The convergence of Algorithm 1 has been proved in our previous work. For detail and proof, see lemma 1 in [26].

figure f

2.3 Computational complexity analysis

Our proposed method (FUFS) consists of four steps:

  1. 1.

    We need O(1) and O(ndmt) to generate m anchors by random selection and the k-means method respectively, where t is the iterative number of the k-means.

  2. 2.

    We need O(nd log(m)) to obtain the matrix Z.

  3. 3.

    We need O(ndm + nd2 + d2m) to calculate M.

  4. 4.

    We need O(d2l) to obtain projection matrix W by performing eigenvalue decomposition on (M + γQ).

Considering that d ≪ m ≪ n for very large-scale data sets, l and the iterative number of our proposed iterative algorithm are usually fairly small; the overall computational complexity of FUFS-R and FUFS-K is O(ndm) and O(ndmt) respectively.

3 Experiments

In this section, several experiments are performed to demonstrate the effectiveness and efficiency of our proposed method (FUFS), and then show several analysis of experimental results. As there are two common ways to generate anchor points, FUFS can be further subdivided into FUFS-R and FUFS-K, where anchor points are generated by random selection and the k-means method respectively.

3.1 Experimental setup

We conduct experiments on four benchmark data sets in terms of clustering and running time. These data sets include one face data set (MSRA25), three hand written digit image data sets (USPS, MNIST and Extended MNIST). The above four data sets can be categorized into small, medium and large sizes. In our experiment, we regard MSRA25 and USPS as small-sized data sets, MNIST as medium-sized data set, while Extended MNIST is considered large-sized data sets. The important statistics of these data sets are summarized in Table 1.

Table 1 Data Set Description
Full size table

For our proposed method (FUFS), there are two unique parameters that need to be set in advance: projection dimension (i.e., l) and the number of anchor points (i.e., m). In our experiment, we set the projection dimension as the number of clusters for FUFS-R and FUFS-K, then set the number of anchor points as 500 for small-sized data sets, 1000 for medium-sized data sets, and 2000 for large-sized data sets. To ensure a fair comparison between the different unsupervised feature selection algorithms, we fix k = 5 for all data sets to specify the size of neighborhoods. The number of selected features is set from half of the total number to the full feature size, while all other parameters are tuned from {10− 3,10− 2,10− 1,1,10,102,103}. After the different combinations of parameters are fixed, each feature selection algorithm is first executed to rank features, after which the k-means was repeated 30 times in the selected feature subspace and compute the average results to alleviate the stochastic effect. Owing to space limitations, only the best results from the optimal parameters are reported here. All these compared methods are implemented in MATLAB R2015b, and run on a Windows 7 machine with 3.40 GHz i7-6700 CPU, 16 GB main memory.

3.2 Evaluation metrics

To evaluate the clustering results, we adopt two widely used evaluation metrics to measure the learning performance:

Clustering Accuracy

(ACC) discovers the one-to-one relationship between clusters and classes and measures the extent to which each cluster contained data points from the corresponding class. Clustering Accuracy is defined as follows:

$$ ACC=\frac{{\sum}_{i = 1}^{n}\delta(map(r_{i}),l_{i})}{n}, $$
(14)

where ri denotes the cluster label of xi and li denotes the true class label, n is the total number of samples, δ(x,y) is the delta function that equals one if x = y and equals zero otherwise, and map(ri) is the permutation mapping function that maps each cluster label ri to the equivalent label from the data set. The larger the value of ACC is, the better performance is.

Normalized Mutual Information

(NMI) is used for determining the quality of clusters. According to the definition in [30], NMI is estimated by

$$ NMI=\frac{{\sum}_{i = 1}^{c}{\sum}_{i = 1}^{c} n_{i,j}\log\frac{n_{i,j}}{n_{i} \hat{n}_{j}}}{\sqrt{({\sum}_{i = 1}^{c} n_{i} \log\frac{n_{i}}{n})({\sum}_{j = 1}^{c} \hat{n}_{j}\log\frac{\hat{n}_{j}}{n})}}, $$
(15)

where ni is the number of data contained in the cluster Ci(1 ≤ i ≤ c), which is generated by a clustering algorithm. While \(\hat {n}_{j}\) is the number of data belonging to the j-th ground truth cluster, and ni,j denotes the number of data that are in the intersection between cluster Ci and the class Lj. Similarly,a larger NMI indicates a better clustering result.

3.3 Compared algorithms

In the experiments, we have compared our methods (FUFS-R and FUFS-K) with following unsupervised feature selection approaches:

  • Baseline: All original features are adopted as the baseline in the experiments.

  • LS: Laplacian Score [9] where features are ranked according to their power of locality preserving in a descending order.

  • MCFS: Multi-Cluster Feature Selection [1] which selects those features that can best preserve multi-cluster structure of the data by using spectral regression with ℓ1-norm regularization.

  • UDFS: Unsupervised Discriminative Feature Selection [35] which simultaneously exploits discriminative information and feature correlations.

  • NDFS: Nonnegative Discriminative Feature Selection [15] which selects features by a joint framework of nonnegative spectral analysis and ℓ2,1-norm regularized regression.

3.4 Results and analysis

The average running time of all methods is shown in Table 2, while the clustering performance is shown in Tables 3 and 4. From the results, the following observations can be made. First, feature selection can not only make the subsequent processing more efficient by selecting a subset of original features, but also significantly improves the learning performance. All feature selection methods exhibit better performance than Baseline in terms of ACC. This is mainly caused by the removal of redundant and noisy features. Second, for small-sized data sets, our FUFS method has no obvious advantages over traditional graph-based unsupervised feature selection methods; however, the performance is much better than LS, which has the lowest computational complexity of all the compared methods. Moreover, for medium-sized and large-sized data sets, the proposed FUFS-R and FUFS-K achieve significant improvements in running time. FUFS-R and FUFS-K only need 33.474 and 95.466 seconds, respectively, which is 28 and 6 times faster than the third-fastest method (LS) on the medium-sized data set (MNIST). Meanwhile, our methods achieve competitive performance for almost all data sets, and FUFS-K achieves the best performance on USPS and Extended MNIST. In addition, we can expect to obtain a more accurate similarity matrix as the number of anchor points increases, meaning that the performance of both FUFS-R and FUFS-K could conceivably achieve even higher performance. Third, although FUFS-R selects anchor points randomly, its performance is not significantly lower than that of FUFS-K, while the running time is much smaller than that of FUFS-K. Compared with FUFS-R, the extra running time of FUFS-K is derived from the use of the k-means method to generate anchors, and this method may require a large number of iterations to converge in some cases. Therefore, considering both accuracy and efficiency, FUFS-R is the best unsupervised feature selection method among all of the compared approaches, especially for very large-scale data sets.

Table 2 Running time (in seconds) for different selection methods
Full size table
Table 3 Clustering results (ACC%) for different selection methods
Full size table
Table 4 Clustering results (NMI%) for different selection methods
Full size table

3.5 Studies on parameter sensitivity and convergence

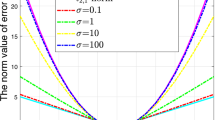
In this subsection, we first evaluate parameter sensitivity for our proposed method FUFS-R. From the results shown in Figs. 1 and 2, we can see that different combinations of parameters may result in different learning performance. To illustrate the influence of the regularization parameter and number of features on the learning performance, we conduct experiments to assess Clustering Accuracy on four benchmark data sets. Figure 1 shows that our method is robust to the parameter α with wide ranges, while comparatively sensitive to the number of selected features. We also study the parameter sensitivity with regard to the number of anchor points. Figure 2 shows that as the number of anchor points increases, the performance does not always improve, while the running time increases in a linear fashion. Thus, we can make a tradeoff between computational complexity and learning performance by selecting an appropriate number of anchor points. Theoretically, the optimal number of anchor points is larger corresponding to a larger scale data set; however, determining the optimal number of anchor points for different data sets is still an open problem.

Fig. 1
figure 1

Clustering Accuracy versus of different α and feature numbers on four data sets

Full size image
Fig. 2
figure 2

ACC and Running time versus number of anchors on MNIST

Full size image

To solve the objective function, we have developed an efficient iterative algorithm. And now we experimentally study the speed of its convergence. Figure 3 shows the objective function values versus the number of iteration. From the figure, we can see that the convergence curves of the objective value monotonically decreases with a faster speed, and our algorithm converges to the optimum, almost within four iterations. The fast convergence of Algorithm 1 validates the efficiency of our proposed method.

Fig. 3
figure 3

Convergence curves of the proposed algorithm (FUFS-R)

Full size image

4 Conclusion

In this paper, we propose a fast graph-based unsupervised feature selection method, which applies an anchor-based strategy to construct a similarity graph by means of a parameter-free adaptive neighbor assignment strategy with fast approximate nearest neighbor matching, then adds a ℓ2,1-norm regularization into the objective function. To solve the optimization problem of FUFS, an efficient iterative algorithm was executed to obtain the projection matrix. Extensive experiments have shown that FUFS-R overcomes the limitations of existing graph-based strategy in dealing with extremely large-scale data sets.