1 Introduction

Data security plays an important role in the development of hospital information system (HIS) [8]. Medical image security has become a major concern in recent years; it usually involves the following aspects: confidentiality (only authorized individuals can access patient data), integrity (proof that the medical information has not been modified) and authentication (which is concerned with identification; the two communication participants should identify each other, allowing the information’s origin to be proven) [1, 26, 30].

A variety of methods can be applied to provide information security for medical images, including steganography, watermarking and encryption. Steganography and watermarking can imperceptibly embed authentication information so that unauthorized users have no access to the hospital information system [15, 19, 22]. There is a large number of image encryption methods because different applications require different levels of security. Gutub has proposed a variety of methods in which the scarcity of resources plays an effective role; each method has achieved good results [3].

In recent years, among others, the following image encryption schemes have been proposed [24]. 1. Arnold’s cat map [9] schemes have low computational complexity, but they do not alter the pixel values of the image; therefore, their security level is not high enough. 2. Discrete cosine transform (DCT) [12, 17] schemes have low computational complexity and high-level security. However, computer calculation precision is limited; thus, these schemes will lose accuracy when using the transform and inverse transform. Therefore, the decrypted image will not be exactly the same as the original image. 3. Chaos-based methods, have a high sensitivity to initial conditions and parameters; their irrelevance, random-like nature and unpredictability can help considerably in improving the security of transmitted communications [28].

There are several problems with traditional chaos-based image encryption algorithms. First, traditional chaotic systems are easy to analyze and predict. For example, the most commonly used chaotic systems for generating pseudorandom sequences are one-dimensional chaotic maps, which include the tent map, the logistic map, and the Chebyshev map. These simple chaotic maps can be attacked via a nonlinear prediction method based on phase–space reconstruction [4, 7]. Second, discrete chaotic systems can exhibit computationally based dynamic degradation [13], which renders these encryption schemes unreliable. Thus, it is more suitable to construct pseudorandom sequence generators using high-dimensional chaotic systems.

In this paper, a new simple chaotic system based on the hyperbolic sine is proposed. Furthermore, a decorrelation operation is used to enhance the performance of the chaotic sequence. Statistical testing verifies that the system has good pseudorandom characteristics, which indicates that this system is more suitable for image encryption than are traditional chaotic maps. With four initial conditions and six control parameters, the proposed system has a large key space that makes brute-force attacks infeasible. Key sensitivity and pseudorandom behavior make this scheme resistant to known-plaintext attacks, chosen ciphertext attacks, statistical attacks, and differential attacks.

The rest of the paper is organized as follows: In Section 2, a new simple chaotic system is introduced, followed by its analysis. Section 3 provides an analysis of a pseudorandom sequence after the decorrelation operation. The proposed image encryption scheme is shown in Section 4. Simulation results and performance analyses are reported in Section 5. Finally, conclusions are drawn in Section 6.

2 A new simple chaotic system

Finding a simple example of chaos is an interesting task. For cryptographic purposes, using a design based on a simple chaotic system can reduce the computational complexity and increase the speed of calculation. Over decades, there had been ongoing debate over which system was the “simplest” example of chaos until Piper and Sprott proposed three simplicity metrics: mathematical simplicity, circuit simplicity, and practical simplicity [21]. Based on these characteristics, a special class of dynamical systems—the so-called jerk systems—proposed to at minimum provide mathematical simplicity. Their functional forms are described by \( \overset{\dddot{}}{\mathrm{X}}=\mathrm{J}\left(X,\dot{X},\ddot{X}\right) \), where the first derivative of the position is called velocity \( \dot{X} \), the second derivative of the position is called acceleration \( \ddot{X} \), and the third and higher order derivatives of the position is called jerk \( \overset{\dddot{}}{X} \) In 2011, Sprott and Munmuangsaen proposed a jerk system with an exponential nonlinearity [16, 23]; this system provides a good foundation for exploring the hyperbolic sine chaotic system.

2.1 Equations and phase space plot

The simplest dissipative chaotic flow with a hyperbolic sine nonlinearity is [14]

$$ \overset{\dddot{}}{x}+0.75\ddot{x}+x+1.2\times {10}^{-6}\sinh \left(\dot{x}/0.026\right)=0. $$
(1)

It can be rewritten as three first-order ordinary differential equations

$$ \left\{\begin{array}{l}\dot{x}=y\\ {}\dot{y}=z\\ {}\dot{z}=-0.75z-1.2\times {10}^{-6}\sinh \left(y/0.026\right)-x.\end{array}\right. $$
(2)

We upgraded this system to a simple fourth-order chaotic system and removed some of the coefficients, such as 1.2 × 10−6 and 1/0.026. By searching its control parameter space, we found an example of a simple chaotic system with a hyperbolic sine nonlinearity, which is described by

$$ \left\{\begin{array}{l}\dot{\mathrm{x}}=6y-x\\ {}\dot{y}=z\\ {}\dot{z}=u\\ {}\dot{u}=-u-\sinh (z)-6x.\end{array}\right. $$
(3)

Figure 1 shows some phase-space plots with distinct initial conditions. When the initial conditions are set to (x0, y0, z0, u0) = (−0.7, −0.9, −1, −1.3) and (x0, y0, z0, u0) = (0.7, 0.9, 1, 1.3), the system shows period-1 behavior. The attractors are antisymmetric about the origin. Moreover, the system could also show chaotic behavior under the initial conditions (x0, y0, z0, u0) = (−7, −9, −10, −13) and (x0, y0, z0, u0) = (7, 9, 10, 13), which are also antisymmetric about the origin. Therefore, the system has four coexisting attractors [10, 11, 20, 25].

Fig. 1
figure 1

Numerically calculated phase space plot of the system under different initial conditions

Full size image

2.2 Analysis

To find the equilibrium point, we set every time-derivative to zero. Therefore, the equilibrium point of this system is (x, y, z, u) = (0, 0, 0, 0), for which the corresponding Jacobian matrix is

$$ \mathrm{J}(s)=\left(\begin{array}{l}\begin{array}{cc}-1& 6\\ {}0& 0\end{array}\ \begin{array}{cc}0& 0\\ {}1& 0\end{array}\\ {}\begin{array}{cc}0& 0\\ {}-6& 0\end{array}\ \begin{array}{cc}0& 1\\ {}0& -1\end{array}\end{array}\right). $$
(4)

The resulting eigenvalues are λ1 = −2.2685 + 1.6963i, λ2 = −2.2685 − 1.6963i, λ3 = 1.2685–1.6963i, and λ4 = 1.2685 + 1.6963i. Because λ1 and λ2 are a pair of complex conjugate eigenvalues with a negative real part, and λ3 and λ4 are a pair of complex conjugate eigenvalues with positive real parts, the origin is a 2-D stable manifold and a 2-D unstable manifold, which suggests that the system is chaotic.

Lyapunov exponents characterize the rate of separation of infinitesimally close trajectories in state space as time tends to infinity. A positive large Lyapunov exponent indicates chaos. In this system, the Lyapunov exponents are (0.1268, 0, −0.9999, −1.1269) under the initial conditions (x, y, z, u) = (7, 9, 10, 13), thereby suggesting that the system is chaotic.

3 The generation of a pseudorandom sequence and its analysis

By analyzing the sequences generated by Eq. (3), the authors realized that the randomness of the sequence is not ideal. Figure 2 shows the probability distribution of the variables x, y, z and u under the initial conditions (x0, y0, z0, u0) = (7, 9, 10, 13). This illustrates that the sequence generated directly by Eq. (3) is not a uniform distribution.

Fig. 2
figure 2

The probability distributions of x, y, z and u

Full size image

To generate sequences of uniformly distributed random variables and enhance the random statistical properties, we used the decorrelation operation, which is defined by the following equations:

$$ {S}_{out}={S}_{in}\ast {10}^4- floor\left({S_{in}}^{\ast }{10}^4\right), $$
(5)

where Sin is the input sequence (which could be the variables (x, y, z or u) generated by Eq. (3)) and Sout is the output sequence. Figure 3 shows the waveform and probability distribution between Sin and Sout. In this case, we chose the variable u as the input sequence.

Fig. 3
figure 3

The waveform and distribution of Sin and Sout

Full size image

To further evaluate the performance of the chaotic sequence and the de-correlation operation, we used a test run of the SP 800–22 suite to test the random statistical characteristics of the sequence [4, 7]. The results are shown in Table 1.

Table 1 Statistical performance
Full size table

After the de-correlation operation, the sequence exhibits improved randomness and ensures that the image encryption scheme will have improved resistance against known attacks. The results are shown in Table 1 and Fig. 3.

4 Image encryption scheme

In this section, an image encryption scheme will be proposed using the pseudorandom sequence from Section 3.

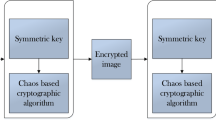
A flowchart of the encryption scheme is shown in Fig. 4.

Fig. 4
figure 4

A flowchart of the encryption scheme

Full size image

The detailed encryption process includes the following steps.

  • Input: Plain image; Initial conditions for chaotic system; Control parameter for chaotic system

  • Output: Ciphered image

  • Step 1: Calculate the average pixel value of the plain image and generate the pseudorandom sequence.

  • Step 2: Transform the pseudorandom sequence and change pixel value of the image via XOR

  • Step 3: Sort the pseudorandom sequence for permutation

  • Step 4: Shift the pixel positions by column using the sorted elements.

  • Step 5: Shift the pixel positions by row using the sorted elements.

To provide a better understanding of this scheme, the pseudocode is provided in Table 2.

Table 2 Image encryption scheme
Full size table

The decryption process of the proposed algorithm is the reverse process of the encryption algorithm. A flowchart of the decryption process is shown in Fig. 5.

Fig. 5
figure 5

The flowchart of the decryption scheme

Full size image

The detailed decryption process includes the following steps.

  • Input: Plain image; Initial conditions for the chaotic system; Control parameter for the chaotic system; Average pixel value of the plain image

  • Output: Decrypted image

  • Step 1: Generate a pseudorandom sequence via the initial conditions and the average pixel values of the plain image

  • Step 2: Sort the pseudorandom sequence for row and column recovery.

  • Step 3: Shift the pixel positions by row

  • Step 4: Shift the pixel positions by column

  • Step 5: Transform the pseudorandom sequence and recover the pixel values of the image via XOR

To provide a better understanding of this scheme, the pseudo-code is provided in Table 3.

Table 3 Image decryption scheme
Full size table

Because this cryptosystem is designed for use with grayscale images, it is suitable for encrypting all kinds of medical images. Figures 6, 7, and 8 show the encryption and decryption results of a 512*512 grayscale mammography image, a CT image and an MRI image, respectively. All the images are from a hospital and the DICOM database.

Fig. 6
figure 6

Encryption and decryption results for a mammography image: (a) Plain image; (b) Encrypted image; (c) Decrypted image

Full size image
Fig. 7
figure 7

Encryption and decryption results for a CT image: (a) Plain image; (b) Encrypted image; (c) Decrypted image

Full size image
Fig. 8
figure 8

Encryption and decryption results for an MRI image: (a) Plain image; (b) Encrypted image; (c) Decrypted image

Full size image

5 Performance analysis

As is well-known, an outstanding cryptosystem should resist all types of known attacks, including known-plaintext attacks, ciphertext attacks, statistical attacks, differential attacks, and various brute-force attacks. A corresponding security analysis has been performed on the proposed algorithm, including a key space analysis, a statistical analysis and a differential analysis.

5.1 Key space analysis

For a secure image cipher, the key space should be large enough to render a brute force attack infeasible. In this system, all the initial conditions and control parameters can be considered as secret keys. Because the basin of attraction of each initial condition is greater than 1, it could have more than 1015∗4 = 1060 choices via a resolution of 10−15, in terms of a numeric calculation. Moreover, if a range of control parameters were to be considered for the key space, the key space of this system would far exceed 1090. Such a large key space provides sufficient security against brute-force attacks.

5.2 Key sensitivity analysis

The key space includes all initial conditions and control parameters. Due to the mutual independence of the secret keys, the practical approach is to analyze each key with a tiny change while leaving the other keys unchanged.

To perform a sensitivity analysis using the initial condition (x, y, z, u) = (7, 9, 10, 13), we made a slight change of Δx = 10^(−15). The modified key is (x + Δx, y, z, u) = (7 + 10^ (−15), 9, 10, 13). The difference in the output sequence between the two initial conditions is shown in Fig. 9.

Fig. 9
figure 9

The difference between two variables of x and x + Δx

Full size image

In Fig. 9, the sequence of the differences between the two variables is a pseudorandom sequence, and we verified that the distribution has random statistical characteristics.

To test the key sensitivity further, we used these two keys to encrypt the same image. The results show that 95% of the pixels are different. The difference between the two encrypted images is shown in Fig. 10.

Fig. 10
figure 10

The difference between the two encrypted images

Full size image

Therefore, the difference between ciphertexts encrypted via different keys is sufficiently large to maintain high security against this kind of known-plaintext attack.

5.3 Histogram analysis

The histogram of an image reveals the distribution of its pixel values. An ideal encrypted image should have a uniform but completely different histogram compared to the plain image to prevent the adversary from extracting any meaningful information from the fluctuating histogram of the cipher image [29].

Figure 11 shows the histograms of the plain and ciphered images of a CT image.

Fig. 11
figure 11

Histograms of plain and encrypted images of a CT image

Full size image

For the quantitative analyses of histograms, we employ variances of histograms to evaluate the uniformity of the ciphered images. Lower variance values indicate a higher uniformity in the encrypted images. The variance of the histograms is presented as follows:

$$ \operatorname{var}\left(\mathrm{Z}\right)=\frac{1}{n^2}\sum \limits_{i=1}^n\sum \limits_{j=1}^n\frac{1}{2}{\left({\mathrm{z}}_{\mathrm{i}}-{z}_j\right)}^2 $$
(6)

where Z is the vector of the histogram values and zi and zj are the numbers of pixels whose gray values are equal to i and j, respectively. In this experiment, we used an initial condition of (x, y, z, u) = (7, 9, 10, 13) and calculated the variances of the plain images and the encrypted images.

The variance value is 1,293,577.2343 for the histogram of the plaintext image “Lena” and 3903.0000 for the histogram of the ciphered image. Therefore, these simulation results indicate that any statistical attack on the proposed scheme are useless.

5.4 Correlation analysis

A high correlation typically exists between pixels of an image, and this correlation is an intrinsic feature. Thus, a secure encryption scheme should obscure this relationship to improve the resistance against statistical analysis. For this calculation, we use the following equations:

$$ \left\{\begin{array}{l}\mathrm{E}(x)=\frac{1}{N}\sum \limits_{i=1}^N{x}_i\\ {}D(x)=\frac{1}{N}\sum \limits_{i=1}^N{\left({x}_i-E(x)\right)}^2\\ {} Cov\left(x,y\right)=\frac{1}{N}\sum \limits_{i=1}^N\left(x{}_i-E(x)\right)\left({y}_i-E(y)\right)\\ {}{\gamma}_{xy}=\frac{Cov\left(x,y\right)}{\sqrt{D(x)D(y)}}\end{array}\right.. $$
(7)

The correlations between adjacent pixels in the plain image and the encrypted image are shown in Fig. 12. Table 4 provides the correlation coefficients of the original and encrypted images shown in Fig. 10. This correlation analysis proves that the encryption scheme satisfies zero co-correlation, which is a private high-level security.

Fig. 12
figure 12

Correlation analysis for plain and encrypted CT image versions: (a) Correlations of the horizontal adjacent pixels for the plain image; (b) Correlations of the horizontal adjacent pixels for the encrypted image; (c) Correlations of vertical adjacent pixels for the plain image; (d) Correlations of the vertical adjacent pixels for the encrypted image

Full size image
Table 4 Correlation coefficients of adjacent pixels in the plain and encrypted image
Full size table

5.5 Differential attack analysis

In general, the relationship between a plain image and an encrypted image can be traced to the differences caused by a specific change to the plain image. Two evaluating indicators are usually used to test the effect of a 1-bit change in the plain-image on the corresponding cipher-image. They are the number of pixel change rates (NPCR) and the unified average changing intensity (UACI) [27]. NPCR and UACI are calculated as follows:

$$ {\displaystyle \begin{array}{l}\mathrm{NPCR}=\frac{\sum_{i,j}D\left(i,j\right)}{\mathrm{W}\times \mathrm{H}}\times 100\%\mathrm{and}\ \\ {} UACI=\frac{1}{W\times H}\left[{\sum}_{i,j}\frac{\left|{c}_1\left(i,j\right)-{c}_2\left(i,j\right)\right|}{255}\right]\times 100\%,\end{array}} $$
(8)

where c1 and c2 are two images with the same size (M × N). If c1 (i, j) = c2 (i, j), then D(i, j) = 1; otherwise D(i, j) = 0. The NPCR and UACI score of CT image are 99.5804% and 33.3227%.

5.6 Overall performance

As revealed in Sections 5.1–5.5, the proposed scheme has a large key space (> > 2100), which can provide sufficient security against brute-force attacks. The key is highly sensitive, which provided a high level of security against known plaintext attacks. Histogram and correlation analysis indicate that the proposed scheme removes the intrinsic features of plain images; thus, any statistical attacks on the proposed scheme are useless. Finally, the NPCR and UACI scores are close to ideal values, which indicates that the proposed scheme provides sufficient security against differential attack. Therefore, this proposed scheme provides sufficient security against all known attacks.

5.7 Comparison results, discussion and future work

5.7.1 Comparison results

In this section, we compared the performance of our algorithm to several typical image encryption algorithms. We evaluate the performance of our proposed method by conducting several tests based on image quality and other evaluation metrics. To compare the correlation values, we used the following equation

$$ \mathrm{CC}=\frac{\left|{C}_h\right|+\left|{C}_v\right|+\left|{C}_d\right|}{3}. $$
(9)

The image encryption method described in [29] uses a chaotic system of mixed linear–nonlinear coupled map lattices for diffusion of the image encryption. In [6], a secure video summarization framework was introduced that used a 2-D chaotic map to generate a set of permutation keys to shift the positions of the plain keyframe pixels, followed by a diffusion per block using arithmetic matrix multiplication over the finite field. A novel image encryption scheme proposed in [5] was based on the Zaslavsky chaotic map, while [18] described a cryptosystem using a newly enhanced chaotic map designed from an existing one-dimensional chaotic economic map.

A performance comparison of all these algorithms is shown in Tables 5 and 6.

Table 5 Comparison of the proposed image encryption method with recent state-of-the-art encryption algorithms (the test image is “Lena”)
Full size table
Table 6 Comparison of the proposed image encryption method with recent state-of-the-art encryption algorithms (the test image is an MRI image)
Full size table

5.7.2 Discussion

Tables 5 and 6 show that the key space of the proposed algorithm is the smallest of the compared algorithms. This is because we could not determine the exact key space value but could estimate only the most conservative value. We have tried and failed to figure out the basin of the attraction and the whole control parameter space, which would allow us to estimate the exact value of the key space. Because using Lyapunov exponents is the most reliable method of indicating chaos and is defined via infinite time, the algorithm does not run very fast. Assuming that the entire initial condition space and control parameter space is 1; the key space would be 1060. Assuming that it would take 1 ms to calculate the Lyapunov exponent of every secret key, more than 1.15*1042 days would be required to calculate the key space. Our estimate shows the most conservative values; however, the true key space may be far greater that the value found in this paper.

The entropy, correlation coefficient, NPCR and UACI scores of the proposed algorithm are not the highest among the compared algorithms, but its scores are very close to the ideal values of those metrics. The differences in score between our algorithm and the ideal value are 0.0048% (entropy), 0.0014% (NPCR), and 0.24%. Because this encryption scheme is very simple and can encrypt an image in a single round, we believe that only the chaotic system described in Section 2 and the pseudorandom sequence generated in Section 3 have this good performance.

5.7.3 Future work

Chaos theory can be applied outside of the natural sciences. For example, chaotic invariants and relevance vector machines (RVM) could be used in human action recognition [2]. Because this paper has proposed a new simple chaotic system, one could attempt to use this system to solve problems of action recognition.

6 Conclusion

In this paper, a new simple chaotic system with a hyperbolic sine and its encryption scheme are proposed. Because the chaotic sequence does not fit a uniform distribution and the randomness of the sequence is not quite ideal, a decorrelation operation is used to improve the randomness of the sequence. Due to the given features in the dynamics of the pseudorandom proposed sequence, cryptosystem security has been enhanced. A key space analysis, key sensitivity analysis, histogram analysis, correlation analysis and differential attack analysis showed that this algorithm is highly resistant to known attacks such as known-plaintext attacks, ciphertext attacks, statistical attacks, differential attacks, and various other brute-force attacks.

Based on these advantages, the proposed method could be used as an assistive tool for telemedical systems or in secure medical systems. In future work, we intend to implement the method in hardware or extend it via parallel execution to reduce the execution time of the encryption algorithm. Although the proposed scheme focuses on medical image encryption, it is not limited to this area. Additional future work could explore related applications in other information security fields.