SRIHASS - a similarity measure for discovery of hidden time profiled temporal associations

Abstract

Mining and visualization of time profiled temporal associations is an important research problem that is not addressed in a wider perspective and is understudied. Visual analysis of time profiled temporal associations helps to better understand hidden seasonal, emerging, and diminishing temporal trends. The pioneering work by Yoo and Shashi Sekhar termed as SPAMINE applied the Euclidean distance measure. Following their research, subsequent studies were only restricted to the use of Euclidean distance. However, with an increase in the number of time slots, the dimensionality of a prevalence time sequence of temporal association, also increases, and this high dimensionality makes the Euclidean distance not suitable for the higher dimensions. Some of our previous studies, proposed Gaussian based dissimilarity measures and prevalence estimation approaches to discover time profiled temporal associations. To the best of our knowledge, there is no research that has addressed a similarity measure which is based on the standard score and normal probability to find the similarity between temporal patterns in z-space and retains monotonicity. Our research is pioneering work in this direction. This research has three contributions. First, we introduce a novel similarity (or dissimilarity) measure, SRIHASS to find the similarity between temporal associations. The basic idea behind the design of dissimilarity measure is to transform support values of temporal associations onto z-space and then obtain probability sequences of temporal associations using a normal distribution chart. The dissimilarity measure uses these probability sequences to estimate the similarity between patterns in z-space. The second contribution is the prevalence bound estimation approach. Finally, we give the algorithm for time profiled associating mining called Z-SPAMINE that is primarily inspired from SPAMINE. Experiment results prove that our approach, Z-SPAMINE is computationally more efficient and scalable compared to existing approaches such as Naïve, Sequential and SPAMINE that applies the Euclidean distance.

1 Introduction

Time profiled temporal association mining is one of the challenging areas of research interest in temporal data mining. The problem of mining interesting seasonal or temporal trends, emerging patterns hidden in time stamped temporal data throws several challenges for researchers to address approaches for improving computational efficiency. One of the drawbacks is the dearth of similarity measures that can address high dimensionality challenges of time stamped temporal data. This area of research is comparatively understudied when compared to its counterparts such as temporal clustering, classification, search & retrieval [8]. The pioneering work that addressed mining temporal associations in time stamped temporal data is SPAMINE by Jin Soung Yoo and Shashi Shekhar [59,60,61]. Yoo and Shashi Shekhar uses the Euclidean distance measure and propose approaches for support estimation of temporal associations. No effort has been made to devise new dissimilarity measure and this was coined as the future work of authors [60]. It is known that the Euclidean distance measure is sensitive to high dimensional data [34] and hence it is not suitable for efficient mining of temporal associations from time stamped temporal data. Studies and research addressed in [59,60,61] is extended in our previous research by devising novel fuzzy Gaussian-based dissimilarity measures [8, 44,45,46]. However, the design of dissimilarity measures proposed in all the previous studies [8, 23, 34, 44,45,46,47, 49, 50, 56, 59,60,61] is not based on the standard score and normal probability. To the best of our knowledge this research proposes a novel approach for mining time profiled associations applying the concept of standard score and probability distribution. In this paper, a dissimilarity measure based on the concept of normal distribution is introduced. i.e. the design of dissimilarity measure is now extended to suit the possibility of mining time profiled temporal association patterns through computing standard scores and normal probability. The basic idea is to transform support value and support sequences into equivalent z-score value and z-score sequences. For these z-score sequences, the probability value is computed using a normal distribution chart. Finally, temporal patterns are expressed as sequences of z-score probability values. This paper extends our previous research studies with a novel contribution by proposing a new dissimilarity measure for retrieving all possible and valid time profiled temporal association patterns from the given input time stamped temporal database.

This paper is outlined as follows: Section-1 explores some of the important and significant studies related to frequent pattern mining, association rule mining, temporal association rule mining, closest related works to time profiled temporal association mining. The scope for present research, basic terminology and notations are also outlined in this section. The proposed prevalence estimation approach and z-score based dissimilarity measure are discussed in section-2 and section-3 respectively. Section-4 outlines the algorithm design and Section-5 gives the time profiled association mining algorithm, Z-Spamine. Experiment results and discussions are discussed in Section-6 by considering various test cases that study algorithm scalability and performance. Section-7 gives the normal distribution chart used to design the dissimilarity measure in this research. Section-8 concludes this paper.

1.1 Related works

1.1.1 Mining associations in transaction databases

Some important algorithms that address discovery of frequent items in a transaction database are discussed in this subsection. Discovery of association rules in transaction database is initially addressed by introducing two algorithms called AIS and SETM [3]. Both AIS and SETM algorithms generate candidate itemsets on the fly in a given pass as and when data is being read. The idea of AIS and SETM is to verify for itemsets that are found to be large in the previous pass and then extend itemsets in the current pass that contain itemsets from previous pass. In otherwords, the supports are computed for these items in the current pass. The drawback of these two algorithms is that all unnecessary combinations are also considered for generation and counts too many candidate items that are actually not large. This drawback of AIS and SETM algorithms has been well addressed and overcome in the later research by agarwal and srikant [2] which is considered as the significant milestone in the field of data mining. The pioneering work is the apriori [2] and aprioriTid [2] algorithms addressed for mining frequent itemsets and hidden association rules in a transaction database. These algorithms only consider itemsets that are found to be large in the previous pass and generate candidate itemsets in the next pass with out scanning the database. The limitation of apriori (or aprioriTid) algorithm is that it does not consider the structural properties of frequent itemsets.

Zaki (in year, 2000) proposed scalable algorithm for mining association rules that consider structural properties of frequent items called Eclat algorithm [62]. Eclat algorithm uses lattice traversal technique for finding frequent itemsets and aims at minimizing I/O costs. This work was later extended by Zaki (in year, 2001) by coming with a vertical mining based approach called Dclat algorithm [63] for frequent itemset mining. Dclat algorithm uses novel vertical data representation called Diffset. Mining frequent patterns in time series databases and transaction databases have been extensively studied in data mining and most of the earlier studies use candidate set generation and test such as apriori which is computationally expensive.

Han [21] proposed a compressed tree based approach for finding frequent patterns called FP-tree approach. The advantages of FP-tree approach are i) it generates a highly compact FP-tree that is substantially smaller than original transaction database ii) it avoids costly candidate generation and test process by concatenating the frequent-1 itemsets present in the conditional FP-trees iii) the partitioning based divide and conquer approach reduces the size of the conditional patterns. The FP-tree approach of frequent pattern mining [21] is extended in [11] which applies recursive elimination principle. The advantage of this approach is simple tree structure. Following works of [2] several works on association rule mining have been addressed that includes generalized association rule mining [52], multiple-levl association rule mining [19], quantitative association rule mining [53], high-dimensional association rule mining [58], constraint based and multiple minimum support based ARM [36, 55], incremental association rule mining [16, 30], parallel association rule mining [1, 38]. An interesting work (in year, 2001) carried by cohen [17] address correlation based association rule mining that is useful in many data mining applications such as clustering web data, finding similar web documents, colloborative filtering and other data mining related applications. Association rules may be extended to web data amalgation [22] w.r.t cloud and concept of similarity measure may be extended to find outliers.

1.1.2 Temporal association rule mining

The fundamental objective of traditional association rule mining (ARM) is to retreive the set of all rules that satisfy certain constraints such as support, confidence of an itemset and the interestingness. Association rule mining for non-temporal databases is extended to temporal databases by introducing the concept of time and the rules so obtained are termed as temporal association rules [4]. The conventional support in ARM does not consider the lifespan of an itemset because of which all transactions are considered irrespective of the lifespan of itemset. This limitation is overcome by considering lifespan of an itemset in which it is valid and introducing the concept of temporal support and confidence. The apriori algorithm for non-temporal databases [2] is extended for temporal databases in [4]. This is followed by several approaches for mining association rules from subset database that consider the time aspect [10, 12, 13, 18, 20, 32, 57]. Although, algorithms such as FP-tree and constraint based approaches exist unfortunately, all these algorithms do not help to discover interesting rules from publication databases. An approach called “progressive partioned miner” [31] is addressed to discover temporal association rules from publication databases and causal relationalship between itemsets that are actually infrequent.

Another type of temporal association rules called cyclic association rules [37] are proposed by Ozden, Ramaswamy, and Silberschatz. Cyclic association rules are association rules that satisfy periodicity. i.e. if an association rule satisfies at a given time point or time instant, then this rule also holds good for all other cycles at that particular instant. Similarly, if a rule does not hold true for a time instance, then for all cycles it also does not hold good. On the otherhand, most of the real life patterns are actually not perfect and the objective is to find all imperfect patterns. Another limitation is that they are not addressed for multiple time granularities but have only been addressed to a single time point. Hence, these cannot at least address a query of the form, “second holiday of every year”. Given a time stamped transaction dataset, the problem of mining association rules in calendar schema is addressed in [32, 33].

Most of these studies did not address time profiled temporal association mining that has various applications in stock market exchange, analyzing sales trends in market-basket, climate measurement (such as temperature, moisture, precipitation etc) to mention a few of them. Although, studies [28, 29, 33, 51, 64] have considered transaction data that is implicitly related to time, all these studies did not address approaches that can discover special regulation patterns such as “emerging temporal patterns”, “seasonal temporal patterns” or diminishing patterns which consider “actual prevalence similarity”. Studies [59,60,61] addressed the problem of “similarity-based temporal association mining” but they were restricted to the use of Euclidean distance measure for mining time profiled associations. Mining temporal patterns from interval databases is addressed in [14] that proposed Gaussian based similarity measure. Summary, detailed information and implementation of various data mining algorithms and respective synthetic and real time data sets for sequential pattern mining, sequential rule mining, sequence prediction, frequent itemset mining, periodic itemset mining, high utility pattern mining, association rule mining, time series mining, clustering and classification are available as open source (http://www.philippe-fournier-viger.com/spmf).

1.2 Time profiled temporal association mining

Similarity profiled temporal association pattern mining is one of the topics of wide research interest in the context of temporal data mining. The pioneering work to address the solution in this direction is by the authors, Jin Soung Yoo and Shashi Shekhar [59,60,61]. All these studies use Euclidean distance measure. From the extensive literature survey performed and to the best of our knowledge, there are no significant findings recorded in the literature in the direction of proposing new measures to address the above said problem. This fact has motivated us to come up with new similarity measures, so that these measures can be used to retrieve all valid similar temporal patterns w.r.t any chosen reference pattern. Some of our earlier studies [5, 15, 39,40,41,42,43, 48] proposed new similarity (or dissimilarity) measures that extend the basic Gaussian function and the approaches to estimate the supports of temporal association patterns.

In [39], we come up with a dissimilarity measure for mining temporal association patterns, all those patterns whose prevalence variations are same as prevalence variations of reference pattern. The drawback [39], is that it is not addressed as to what deviation must be chosen for applying the dissimilarity measure. This drawback was later overcome and addressed by proposing the expression for computing deviation [8, 44,45,46,47, 56] and for choosing proper threshold value corresponding to the deviation. Approaches for estimating supports of temporal association patterns are discussed in [15, 48,49,50]. These similarity measures designed may also be applied to different applications related to [6, 7, 9]. Application of similarity measures for dimensionality reduction is discussed in [25,25,26,27].

1.3 Research scope

The present research is inspired from [23, 34, 59,60,61]. Past research [49, 50, 59,60,61] that addressed mining time profiled temporal associations considered the widely known Euclidean distance measure. It is a well-known fact that the Euclidean distance falls prey to high dimensionality and hence does not suit for time profiled association mining, which have the support sequences that are implicitly highly dimensional. Some of our previous works [5, 8, 42,43,44,45,46,47, 56] propose the fuzzy Gaussian based distance measures for finding similarity between temporal trends and patterns. However, all these distance measures that are proposed does not consider transforming support time sequences to a different time space. The following are several findings that lead to the following research

• a. There is a scope for research to find the similarity of temporal associations to a given query time sequence in transforming space. This scope for research has motivated the present work. The idea is to find the standard score of support time sequences of time stamped temporal patterns and then transform these sequences to z-score probability sequences.

• b. There is also scope for coming out with a dissimilarity measure that can find the similarity between the temporal pattern in z-space. Our research thus addresses a novel dissimilarity measure to find similarity between time stamped temporal patterns in such transforming space.

• c. There is a scope for proposing a method for estimating prevalence time sequence limits of temporal associations that can address computational complexity and is compatible with proposed similarity/distance measure

1.4 Problem statement

Given a time stamped transaction database and subset constraints that include i) reference time sequence ii) allowable dissimilarity threshold and iii) a dissimilarity function that maps the prevalence time sequence of temporal itemset and reference time sequence onto a transformed space in which the similarity between two given temporal associations can be accurately estimated. The problem of time profiled temporal association mining is to discover set of all valid time profiled associations that satisfy all those subset constraints through estimating prevalence time sequence of temporal associations by performing a minimum number of true support computations to achieve improved computational efficiency.

1.5 Basic terminology

In this section, we introduce the basic terms and notations followed in this paper.

1.5.1 Time stamped transaction database

It is defined as the transaction data that is defined over a finite number of ‘n’ disjoint time slots where each time slot is a point in time.

1.5.2 Temporal item or itemset

An item or itemset present in a given transaction (or transactions) of a time stamped temporal database.

1.5.3 Positive temporal item (or positive itemset)

A positive temporal item or itemset denotes the existence of itemset in the time stamped transaction database. A positive itemset is also called as the positive temporal pattern. Unless specified, the default itemset is considered as a positive temporal item or itemset. A positive itemset say ‘I’ is denoted using T _I where T denotes temporal nature of itemset.

1.5.4 Negative temporal item (or negative itemset)

A negative temporal item or itemset denotes the non-existence of itemset in the time stamped transaction database. A negative itemset is also called as the negative temporal pattern. A negative temporal itemset is denoted using $\overline{T_I}$ where T denotes temporal nature of itemset.

1.5.5 Prevalence (or support)

Let ‘t_i’ denote i^th time slot and the transaction database defined at t_i be represented using the notation, D_i. Prevalence of an itemset, I at timeslot, t_i is denoted using ${T}_{I_i}$ and is equal to the fraction of transactions that contain the itemset in D_i. It is also called as the support of itemset. The prevalence value is always between 0 and 1. For example, if a particular time slot, t₃ contains 100 transactions and a given item is present in 40 transactions, then the prevalence value of itemset at the time slot, t₃ is equal to 40/100 = 0.4.

1.5.6 Positive prevalence (or support)

Let t_i be the i^th time slot and the transaction database defined at t_i be denoted as D_i. The positive prevalence of a temporal item or itemset in a given time slot, t_i is defined as the fraction of transactions that contain the temporal item or itemset in the time slot, t_i. It is also called as support of itemset. The positive prevalence value always lies between 0 and 1. For example, if a particular time slot say, t₁ contains 250 transactions and a given item is present in 25 transactions, then the prevalence value at the time slot considered is 25/250 = 0.1.

1.5.7 Negative prevalence (or support)

Let ‘t_i’ denote i^th time slot and the transaction database defined at t_i be represented using the notation, D_i. The negative prevalence of an itemset, I at timeslot, t_i is denoted using $\overline{T_{I_i}}$ and is equal to the fraction of transactions that do not contain the itemset in the database, D_i. Negative prevalence value defines the probability of non-existence of an item or itemset. For example, if a particular time slot, t₃ contains 100 transactions and a given item is present in 40 transactions, then the negative prevalence value of itemset at the time slot, t₃ is equal to 60/100 = 0.6.

1.5.8 Positive prevalence time sequence$\left(\overrightarrow{T_I}\right)$

Let I be any itemset, then the prevalence time sequence is the sequence of prevalence values of a time stamped temporal item or itemset defined over ‘n’ disjoint time slots and is denoted using $\overrightarrow{T_I}$. The prevalence time sequence corresponding to positive itemset is defined as positive prevalence time sequence. A prevalence time sequence is also called positive prevalence time sequence.

1.5.9 Negative prevalence time sequence $\left(\overrightarrow{\overline{T_I}}\right)$

Let I be any itemset, then the negative prevalence time sequence is the sequence of prevalence values of a time stamped temporal item or itemset defined over ‘n’disjoint time slots for a negative temporal itemset and is denoted using $\overrightarrow{\overline{T_I}}$.

2 Prevalence bounds estimation

One of the important challenges that are to be addressed when discovering all the valid similar temporal association patterns from a time stamped temporal database of disjoint transactions is the number of true support computations that are required to be performed. For example, for ‘N’ items, there exists 2^N item set combinations and hence the complexity is O(2^N). This means that the total number of true support computations required is 2^N in the worst case. Hence, if we can come up with approaches for estimating prevalence bounds of association patterns (or item sets) by devising a suitable procedure then, it shall help to reduce the total number of true support scans that must be carried out. Sections 2.2 and 2.3 give the approaches for estimating prevalence values of temporal associations.

Let ‘N’ be the number of items in the finite itemset, ‘I’ and pattern size be represented using notation ‘S’. Suppose that P and Q are any two items chosen from ‘I’. Then, notations T_P and T_Q each denote corresponding positive temporal pattern for P and Q respectively. Similarly, notations $\overline{T_P}$ and $\overline{T_Q}$ each denote corresponding negative temporal pattern. For estimating prevalence bounds of patterns, the complete set of possible patterns are mainly divided into three categories, each representing, temporal patterns of sizes, S = 1, S = 2 and S > 2. Necessary expressions which are required to estimate support bounds of temporal association patterns of size (i) |S| = 2 and (ii) |S| > 2 are discussed in subsections below.

2.1 Prevalence bounds for single time slot

Let, T_P and T_Q are any singleton temporal patterns and T _PQ is temporal association pattern generated from temporal patterns, T_P and T_Q. The support bounds for temporal association pattern, T _PQ are computed using expressions defined in Eq. (1)

$$ {T}_{PQ}=\left\{\begin{array}{c}{T}_{p_1}-\min \left({T}_{p_1},1-{T}_{Q_1}\right)\\ {}{T}_{p_1}-\max \left({T}_{p_1}-{T}_{Q_1},0\right)\end{array}\right. $$

(1)

The expression to compute the minimum prevalence bound is given by Eq. (2)

$$ {T}_{PQ}^{min}={T}_{p_1}-\min \left({T}_{p_1},1-{T}_{Q_1}\right) $$

(2)

The expression to compute the maximum prevalence bound is given by Eq. (3)

$$ {T}_{PQ}^{max}={T}_{p_1}-\max \left({T}_{p_1}-{T}_{Q_1},0\right) $$

(3)

Throughout this discussion, the notation ${T}_{I_k}$ represents support value of temporal item or itemset at k^th time slot.

2.2 Prevalence bounds for level-2 temporal pattern (size, S = 2)

Let, T_P and T_Q are any two temporal patterns defined over ‘n’ time slots. For ‘n’ time slots, we denote respective pattern support time sequences as $\overrightarrow{T_P}$ = (${T}_{P_1},{T}_{P_2},{T}_{P_3},\dots \dots \dots \dots, {T}_{P_n}$) and$\overrightarrow{\ {T}_Q}$ = (${T}_{Q_1},{T}_{Q_2},{T}_{Q_3},\dots \dots \dots \dots, {T}_{Q_n}$). The bounds for all temporal association patterns (i.e of the form T_PQ) at level-2, are obtained applying Eq. (4),

$$ \overrightarrow{T_{PQ}}=\left\{\begin{array}{c}\left(\left({T}_{P_1}-\min \left({T}_{P_1},1-{T}_{Q_1}\right)\right),\left({T}_{P_2}-\min \left({T}_{P_2},1-{T}_{Q_2}\right)\right),\dots, \left(\ {T}_{P_n}-\min \left({T}_{P_n},1-{T}_{Q_n}\right)\right)\right)\\ {}\left(\left({T}_{P_1}-\max \left({T}_{P_1}-{T}_{Q_1},0\right)\right),\left({T}_{P_2}-\max \left({T}_{P_2}-{T}_{Q_2},0\right)\right),\dots .,\left({T}_{P_n}-\max \left({T}_{P_n}-{T}_{Q_n},0\right)\right)\right)\end{array}\right. $$

(4)

For a temporal pattern of the form, T _PQ , the minimum prevalence time sequence is denoted by $\overrightarrow{T_{PQ}^{min}}$ and is given by Eq. (5),

$$ \overrightarrow{T_{PQ}^{min}}=\left({T}_{PQ_1}^{min},{T}_{PQ_2}^{min},{T}_{PQ_3}^{min},\dots \dots \dots \dots \dots \dots \dots \dots \dots \dots, {T}_{PQ n}^{min}\right) $$

(5)

where

$$ {\displaystyle \begin{array}{l}{T}_{PQ_1}^{min}={T}_{P_1}-\min \left({T}_{P_1},1-{T}_{Q_1}\right)\\ {}{T}_{PQ_2}^{min}={T}_{P_2}-\min \left({T}_{P_2},1-{T}_{Q_2}\right)\\ {}\dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots .\\ {}{T}_{PQ_n}^{min}={T}_{P_n}-\min \left({T}_{P_n},1-{T}_{Q_n}\right)\end{array}} $$

In similar lines, its maximum prevalence sequence bound is given by Eq. (6),

$$ \overrightarrow{T_{PQ}^{max}}=\left({T}_{PQ_1}^{max},{T}_{PQ_2}^{max},{T}_{PQ_3}^{max},\dots \dots \dots \dots \dots \dots \dots \dots \dots \dots, {T}_{PQ n}^{max}\right) $$

(6)

where

$$ {\displaystyle \begin{array}{l}{T}_{PQ_1}^{max}=\left({T}_{P_1}-\max \left({T}_{P_1}-{T}_{Q_1},0\right)\right)\\ {}{T}_{PQ_2}^{max}=\left({T}_{P_2}-\max \left({T}_{P_2}-{T}_{Q_2},0\right)\right)\\ {}\dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots .\\ {}{T}_{PQ_n}^{max}=\left({T}_{P_n}-\max \left({T}_{P_n}-{T}_{Q_n},0\right)\right)\end{array}} $$

2.3 Pattern support bound for ‘n’ time slots and S > 2

Let, P and Q are any two items of sizes equal to (S-1) and 1 respectively, in a time stamped transaction database of ‘n’ number of disjoint time slots. Then, notations T _P and T _Q each denote temporal itemset (or pattern) of size, equal to (S-1) and 1 respectively. The respective support time sequence of T _P and T _Q over ‘n’ time slots are denoted by $\overrightarrow{T_P}$ = (${T}_{P_1},{T}_{P_2},{T}_{P_3},\dots \dots \dots \dots, {T}_{P_n}$) and$\overrightarrow{\ {T}_Q}$ = (${T}_{Q_1},{T}_{Q_2},{T}_{Q_3},\dots \dots \dots \dots, {T}_{Q_n}$).

A temporal association pattern T _PQ is generated from itemset association PQ (or may be viewed as generated from temporal patterns, T _P and T _Q ). The size of temporal association pattern, T _PQ is equal to |S| (or S) while the size of patterns T _P and T _Q is equal to (|S|-1) and 1 respectively. Let, Ss(PQ) be the subset itemset of size equal to (|S|-1) and S(PQ) denotes the singleton item of size equal to 1 which are obtained from their superset itemset association, PQ of size equal to |S|. It should be noted that, itemset represented by Ss(PQ) and S(PQ) together form the itemset association PQ and the corresponding temporal pattern is denoted using T _PQ , i.e. for some randomly chosen itemset association PQ, we have Ss(PQ) ≡ P whose size is equal to (S-1) and S(PQ) ≡ Q of size equal to 1 respectively such that Ss(PQ) ∩S(PQ)=∅. Here, Ss(PQ) and S(PQ) represents all possible subset combinations possible at level (l-1) and level-1 using which superset itemset combination PQ at level ‘l’ can be generated.

For example, consider the itemset ABC of size equal to 3, then the possible size-2 itemset are AB, AC and BC while the size-1 itemset are C, B and A. Itemset ABC may be obtained by considering any of these three possible combinations. It can be easily verified that {A, B}∩ {C} = ∅ where Ss(ABC) ≡ AB and S(ABC)≡ C. Similarly, {A, C}∩ {B} = ∅ and {B, C}∩ {A} = ∅. To find the support bounds for temporal itemset ABC, i.e. T _ABC we consider all these possible subset combinations.

In general, notations, ${T}_{\mathrm{Ss}{(PQ)}_t}$and ${T}_{\mathrm{S}{(PQ)}_t}$ are used to represent the support value of subset temporal patterns, T _Ss(PQ) and T _S(PQ) at t^th time slot. The support time sequence bounds (maximum possible and minimum possible) for such temporal associations of size greater than two are obtained for each time slot by considering every possible subset of size equal to (S-1), and 1 as discussed above. Subsection 2.4.4 demonstrates the computation of support bounds of temporal itemset association, ABC.

2.3.1 Minimum support time sequence

The minimum possible support time sequence of temporal association pattern, T _PQ of size equal to |S| (i.e at level ‘l’) for ‘n’ time slots is obtained by considering each possible k^th subset (i.e Ss ^k(PQ)) of size, |S|-1 at previous level, i.e. (l-1) and singleton item, S(PQ) at level-1 such that Ss^k(PQ) ∩S(PQ)=∅. Equation (7) represents the support time sequence of temporal association pattern, T _PQ obtained from the k^th possible subset denoted by Ss(PQ) of size equal to |S|-1 and singleton pattern S(PQ).The minimum support time sequence of temporal association pattern, T _PQ obtained over ‘n’ time slots by considering k^th subset (i.e Ss ^k(PQ)) is given by (7)

$$ \overrightarrow{{\left({\mathrm{T}}_{\mathrm{PQ}}^{\mathrm{k}}\right)}^{min}}=\left({T}_{PQ_1}^k,{T}_{PQ_2}^k,{T}_{PQ_3}^k,\dots \dots \dots \dots \dots ..,{T}_{PQ_n}^k\right) $$

(7)

where

$$ {\displaystyle \begin{array}{c}\hfill {T}_{PQ_1}^k=\left({T}_{Ss^k{(PQ)}_1}-\mathrm{minimum}\left\{{T}_{Ss^k{(PQ)}_1},1-{T}_{S{(PQ)}_1}\right\}\right)\hfill \\ {}\hfill {T}_{PQ_2}^k=\left({T}_{Ss^k{(PQ)}_2}-\mathrm{minimum}\left\{{T}_{Ss^k{(PQ)}_2},1-{T}_{S{(PQ)}_2}\right\}\right)\hfill \\ {}\hfill \begin{array}{l}\dots \dots \dots \dots \dots .\\ {}{T}_{PQ_n}^k=\left({T}_{Ss^k{(PQ)}_n}-\mathrm{minimum}\left\{{T}_{Ss^k{(PQ)}_n},1-{T}_{S{(PQ)}_n}\right\}\right)\end{array}\hfill \end{array}} $$

From all possible support time sequences obtained by applying Eq. (7) through considering each subset itemset association denoted by Ss ^k(PQ) and S(PQ), the minimum support time sequence is obtained by considering maximum support value at every time slot over all possible subsets of itemset association, PQ. The minimum support time sequence, $\overrightarrow{{T_{PQ}}^{min}}$ of temporal association pattern, T _PQ is given by Eq. (8)

$$ \overrightarrow{{T_{PQ}}^{min}}=\left({T}_{PQ_1}^{min},{T}_{PQ_2}^{min},{T}_{PQ_3}^{min},\dots \dots \dots \dots \dots, {T}_{PQ_n}^{min}\right) $$

(8)

where

$$ {\displaystyle \begin{array}{c}\hfill {T}_{PQ_1}^{min}=\mathrm{maximum}\left\{{T}_{PQ_1}^1,{T}_{PQ_1}^2,.\dots, {T}_{PQ_1}^k\right\}\hfill \\ {}\hfill {T}_{PQ_2}^{min}=\mathrm{maximum}\left\{{T}_{PQ_2}^1,{T}_{PQ_2}^2,.\dots, {T}_{PQ_2}^k\right\}\hfill \\ {}\hfill \dots ..\hfill \\ {}\hfill {T}_{PQ_n}=\mathrm{maximum}\left\{{T}_{PQ_n}^1,{T}_{PQ n}^2,.\dots, {T}_{PQ_n}^k\right\}\hfill \end{array}} $$

2.3.2 Maximum support time sequence

The maximum possible support time sequence of temporal association pattern, T _PQ of size equal to |S| (i.e at level ‘l’) for ‘n’ time slots is obtained by considering each possible k^th subset (i.e Ss ^k(PQ)) of size |S|-1 at previous level, i.e. (l-1) and singleton item, S(PQ) at level-1 such that Ss(PQ) ∩S(PQ)=∅. Equation (9) represents the support time sequence of temporal association pattern T _PQ obtained by considering the k^th possible subset denoted by Ss ^k(PQ) of size equal to |S|-1 and the singleton pattern S(PQ)

$$ \overrightarrow{{\left({T}_{PQ}^k\right)}^{max}}=\left({T}_{PQ_1}^k,{T}_{PQ_2}^k,{T}_{PQ_3}^k,\dots \dots \dots \dots \dots ..,{T}_{PQ_n}^k\right) $$

(9)

where

$$ {\displaystyle \begin{array}{c}\hfill {T}_{PQ_1}^k=\left({T}_{Ss^k{(PQ)}_1}-\max \left(\left\{{T}_{Ss^k{(PQ)}_1}-{T}_{S{(PQ)}_1}\right\},0\right)\right)\hfill \\ {}\hfill {T}_{PQ_2}^k=\left({T}_{Ss^k{(PQ)}_2}-\max \left(\left\{{T}_{Ss^k{(PQ)}_2}-{T}_{S{(PQ)}_2}\right\},0\right)\right)\hfill \\ {}\hfill \dots \dots \dots \dots \dots .\hfill \\ {}\hfill {T}_{PQ_n}^k=\left({T}_{Ss^k{(PQ)}_n}-\max \left(\left\{{T}_{Ss^k{(PQ)}_2}-{T}_{S{(PQ)}_n}\right\},0\right)\right)\hfill \end{array}} $$

In all the expressions above ${T}_{Ss^k{(PQ)}_t}$ and T _S(PQ)t refers to support of k^th itemset combination denoted by Ss(PQ) and singleton pattern at t^th time slot respectively. From all possible support time sequences obtained by applying Eq. (9) through considering each subset itemset associations denoted by Ss ^k(PQ) and S(PQ), the maximum support time sequence is obtained by considering minimum support value at every time slot over all possible subsets of itemset association, PQ. The maximum support time sequence, $\overrightarrow{{T_{PQ}}^{max}}$ is given by Eq. (10)

$$ \overrightarrow{{T_{PQ}}^{max}}=\left({T}_{PQ_1}^{max},{T}_{PQ_2}^{max},{T}_{PQ_3}^{max},\dots \dots \dots \dots \dots, {T}_{PQ_n}^{max}\right) $$

(10)

where

$$ {\displaystyle \begin{array}{c}\hfill {T}_{PQ_1}^{max}=\mathrm{minimum}\left\{{T}_{PQ_1}^1,{T}_{PQ_1}^2,.\dots, {T}_{PQ_1}^k\right\}\hfill \\ {}\hfill {T}_{PQ_2}^{max}=\mathrm{minimum}\left\{{T}_{PQ_2}^1,{T}_{PQ_2}^2,.\dots, {T}_{PQ_2}^k\right\}\hfill \\ {}\hfill \dots \dots \hfill \\ {}\hfill {T}_{PQ_n}^{max}=\mathrm{minimum}\left\{{T}_{PQ_n}^1,{T}_{PQ n}^2,\dots, {T}_{PQ_n}^k\right\}\hfill \end{array}} $$

In sub-expressions of Eq. (9) the representation ${T}_{PQ_t}^k$ denotes the support value obtained by considering the k^th possible subset itemset combination at t^th time slot and ${T}_{PQ_t}^{max}$ denotes the maximum possible support value of temporal association pattern T _PQ at t^th time slot.

2.4 Case study

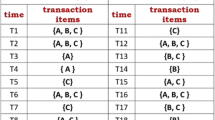
This section explains the approach for estimating prevalence time sequence bounds of temporal association patterns by applying the method discussed in sections 2.1 to 2.3. For this, the time stamped transaction database generated using IBM data generator [8, 44] as shown in Fig. 1a is considered. The database is defined over two-time slots (denoted by T2). It consists of ten transactions per each time slot (denoted by TD10). The total number of transactions is 20 (D20). The total number of items in finite itemset is three (I3) with average transaction size equal to two (L2). The temporal dataset is denoted as TD10-D20-I3-L2-T2. The database is defined over three items A, B and C which form the finite set of items. Figure 1b shows the lattice diagram depicting the distance computations using proposed similarity function. Table 1 shows prevalence values of level-1 (singleton) positive and negative temporal patterns. Notations, T _A , T _B , T _C represent positive temporal pattern and $\overline{T_A}$, $\overline{T_B}$ and $\overline{T_C}$ are negative temporal pattern of itemset size equal to one at level-1. ${T}_{A_1}$, ${T}_{B_1}$are positive supports of patterns at time slot t₁ and ${T}_{A_2}$, ${T}_{B_2}$ are positive supports of patterns at time slot t₂. Similarly, $\overline{T_{A_1}}$, $\overline{T_{B_1}}$ are negative supports at time slot t₁ and $\overline{T_{A_2}}$, $\overline{T_{B_2}}$ are negative supports at time slot t₂.

Fig. 1

a Example dataset. b monotonicity property of proposed dissimilarity measure w.r.t ${D}_Z^{\mathit{\max}-\mathit{\min}}$ showing distance values in the form: ${D}_Z^{true}$ (${D}_Z^{\mathit{\max}-\mathit{\min}}$)

Table 1 Support values of singleton temporal items

In subsections 2.4.1 to 2.4.4, the proposed approach for estimating support bounds of temporal association patterns is explained by considering itemset associations AB, AC_, BC and ABC.

2.4.1 Prevalence bound of temporal itemset, AB i.e. T_AB

Consider the temporal itemset, T_AB. The computation of prevalence sequence bounds of temporal patterns can be obtained by applying Eqs. (5) and (6). Figure 2a shows the maximum possible support sequence bound and minimum possible support sequence bound for the temporal itemset, T_AB.

Fig. 2

Support bounds for temporal associations

Maximum support time sequence of T_{AB, (} $\overrightarrow{T_{AB}^{max}}$)

The temporal support sequence of temporal itemset, T_AB is denoted by $\overrightarrow{T_{AB}^{max}}$and can be computed using $\overrightarrow{T_{AB}^{max}}=\left(\ {T}_{AB_1}^{max},{T}_{AB_2}^{max}\ \right)$ where ${T}_{AB_1}^{max}$ = ${T}_{A_1}-\max \left({T}_{A_1}-{T}_{B_1},0\right)$ and ${T}_{AB_2}^{max}$= ${T}_{A_2}-\max \left({T}_{A_2}-{T}_{B_2},0\right)$. In expressions for ${T}_{AB_1}^{max}$and ${T}_{AB_2}^{max}$ the notation${T}_{A_1}$and ${T}_{B_1}$ represent positive supports of temporal pattern at time slot, t₁ and ${T}_{A_2}$, ${T}_{B_2}$ are positive supports of temporal patterns at time slot, t₂. In the present example, we have ${T}_{A_1}$=0.6, ${T}_{A_2}=$0.4, ${T}_{B_1}$=0.3, ${T}_{B_2}=$0.7. So, ${T}_{AB_1}^{max}$ = ${T}_{A_1}-\max \left({T}_{A_1}-{T}_{B_1},0\right)$ = 0.6 – maximum (0.6–0.3, 0) = 0.6- maximum (0.3, 0) = 0.6–0.3 = 0.3. Similarly, ${T}_{AB_2}^{max}$ = ${T}_{A_2}-\max \left({T}_{A_2}-{T}_{B_2},0\right)$ = 0.4 – maximum (0.4–0.7, 0) = 0.4 – maximum (−0.3, 0) = 0.4–0 = 0.4. Hence,$\overrightarrow{T_{AB}^{max}}=\left(\ 0.3,0.4\ \right).$

Minimum support time sequence of T_AB, ($\overrightarrow{T_{AB}^{min}}$)

The minimum temporal support sequence of temporal itemset, T_AB is denoted by $\overrightarrow{T_{AB}^{min}}$and can be computed using $\overrightarrow{T_{AB}^{min}}=\left(\ {T}_{AB_1}^{min},{T}_{AB_2}^{min}\ \right)$ where ${T}_{AB_1}^{min}$ =${T}_{A_1}-$ $\min \left({T}_{A_1},1-{T}_{B_1}\right)$ and ${T}_{AB_2}^{min}$= ${T}_{A_2}-$ $\min \left({T}_{A_2},1-{T}_{B_2}\right)$. In the present example, we have ${T}_{A_1}$=0.6, ${T}_{A_2}=$0.4, ${T}_{B_1}$=0.3, ${T}_{B_2}=$0.7. So, ${T}_{AB_1}^{min}$ =${T}_{A_1}-$ $\min \left({T}_{A_1},1-{T}_{B_1}\right)$ = 0.6− min(0.6, 0.7) = 0. Similarly, ${T}_{AB_2}^{min}$ = ${T}_{A_2}-$ $\min \left({T}_{A_2},1-{T}_{B_2}\right)$ = 0.4− min(0.4, 0.3) = 0.1. So, $\overrightarrow{T_{AB}^{min}}=\left(\ 0.0,0.1\ \right)$

From Fig. 2a, it can be verified that the true support sequence of temporal itemset, T_AB lies between the maximum possible support sequence ($\overrightarrow{T_{AB}^{max}}$) and minimum possible support sequence ($\overrightarrow{T_{AB}^{min}}$) as represented by the shaded region. The shaded region in Fig. 2a is used to represent the fact that the true support of temporal pattern, T_AB can only belong to this region.

2.4.2 Prevalence bound of temporal pattern, AC i.e. T_AC

The computation of prevalence sequence bounds of temporal pattern, T_AC can be obtained by applying Eqs. (5) and (6). Figure 2c shows the maximum possible support sequence bound and minimum possible support sequence bound for the temporal itemset, T_AC.

Maximum support time sequence of T_AC, $\Big(\overrightarrow{T_{AC}^{max}}$)

The maximum support time sequence of temporal itemset, T_AC is denoted by $\overrightarrow{T_{AC}^{max}}$and can be computed using $\overrightarrow{T_{AC}^{max}}=\left(\ {T}_{AC_1}^{max},{T}_{AC_2}^{max}\ \right)$ where ${T}_{AC_1}^{max}$ = ${T}_{A_1}-\max \left({T}_{A_1}-{T}_{C_1},0\right)$ and ${T}_{AC_2}^{max}$=${T}_{A_2}-\max \left({T}_{A_2}-{T}_{C_2},0\right)$. In the expressions for ${T}_{AC_1}^{max}$and ${T}_{AC_2}^{max}$ the notations${T}_{A_1}$, ${T}_{C_1}$ represent positive supports of temporal patterns at time slot, t₁ and ${T}_{A_2}$, ${T}_{C_2}$ are positive supports of temporal patterns at time slot, t₂ . In the present example, we have ${T}_{A_1}$=0.6, ${T}_{A_2}=$0.4, ${T}_{C_1}$=0.8, ${T}_{C_2}=$0.8. So, ${T}_{AC_1}^{max}$ = ${T}_{A_1}-\max \left({T}_{A_1}-{T}_{C_1},0\right)$ = 0.6 – maximum (0.6–0.8, 0) = 0.6- maximum (−0.2, 0) = 0.6–0.0 = 0.6. Similarly, ${T}_{AC_2}^{max}$ = ${T}_{A_2}-\max \left({T}_{A_2}-{T}_{C_2},0\right)$ = 0.4 – maximum (0.4–0.8, 0) = 0.4 – maximum (−0.4, 0) = 0.4–0 = 0.4. Hence,$\overrightarrow{T_{AC}^{max}}=\left(\ 0.6,0.4\ \right)$

Minimum support time sequence of T_AC, ($\overrightarrow{T_{AC}^{min}}$)

The minimum support time sequence of temporal itemset, T_AC is denoted by $\overrightarrow{T_{AC}^{min}}$and can be computed using $\overrightarrow{T_{AC}^{min}}=\left(\ {T}_{AC_1}^{min},{T}_{AC_2}^{min}\ \right)$ where ${T}_{AC_1}^{min}$ =${T}_{A_1}-$ $\min \left({T}_{A_1},1-{T}_{C_1}\right)$ and ${T}_{AC_2}^{min}$= ${T}_{A_2}-$ $\min \left({T}_{A_2},1-{T}_{C_2}\right)$. In the present case, ${T}_{A_1}$=0.6, ${T}_{A_2}=$0.4, ${T}_{C_1}$=0.8, ${T}_{C_2}=$0.8. So, ${T}_{A{C}_1}^{min}$ =${T}_{A_1}-$ $\min \left({T}_{A_1},1-{T}_{C_1}\right)$ = 0.6− min(0.6, 0.2) = 0.4. Similarly, ${T}_{AC_2}^{min}$ = ${T}_{A_2}-$ $\min \left({T}_{A_2},1-{T}_{C_2}\right)$ = 0.4− min(0.4, 0.2) = 0.2. Hence,$\overrightarrow{T_{AC}^{min}}=$(0.4, 0.2)

2.4.3 Prevalence bound of temporal pattern, T_BC

The computation of prevalence time sequence bounds of temporal patterns can be obtained by applying Eqs. (5) and (6). Figure 2b shows the maximum possible support time sequence and minimum possible support time sequence for the temporal itemset, T_BC

Maximum support time sequence of T_BC, $\Big(\overrightarrow{T_{BC}^{max}}$)

The temporal support sequence of temporal itemset, T_BC is denoted by $\overrightarrow{T_{BC}^{max}}$and may be computed using $\overrightarrow{T_{BC}^{max}}=\left(\ {T}_{BC_1}^{max},{T}_{BC_2}^{max}\ \right)$ where ${T}_{BC_1}^{max}$ = ${T}_{B_1}-\max \left({T}_{B_1}-{T}_{C_1},0\right)$ and ${T}_{BC_2}^{max}$=${T}_{B_2}-\max \left({T}_{B_2}-{T}_{C_2},0\right)$. In the expressions for ${T}_{BC_1}^{max}$and ${T}_{BC_2}^{max}$ the notations${T}_{B_1}$, ${T}_{C_1}$ represent positive supports of temporal patterns at time slot, t₁ and ${T}_{B_2}$, ${T}_{C_2}$ are positive supports of temporal patterns at time slot, t₂. From the given dataset, we have ${T}_{B_1}$=0.3, ${T}_{B_2}=$0.7, ${T}_{C_1}$=0.8, ${T}_{C_2}=$0.8. So, ${T}_{BC_1}^{max}$ = ${T}_{B_1}-\max \left({T}_{B_1}-{T}_{C_1},0\right)$ = 0.3 – maximum (0.3–0.8, 0) = 0.3- maximum (−0.5, 0) = 0.3–0.0 = 0.3. Similarly, ${T}_{BC_2}^{max}$ = ${T}_{B_2}-\max \left({T}_{B_2}-{T}_{C_2},0\right)$ = 0.7 – maximum (0.7–0.8, 0) = 0.7 – maximum (−0.1, 0) = 0.7. Hence, $\overrightarrow{T_{BC}^{max}}=$(0.3, 0.7)

Minimum support time sequence bound of T_BC, ($\overrightarrow{T_{BC}^{min}}$)

The minimum temporal support sequence of temporal itemset, T_BC is denoted by $\overrightarrow{T_{BC}^{min}}$and can be computed using $\overrightarrow{T_{BC}^{min}}=\left(\ {T}_{BC_1}^{min},{T}_{BC_2}^{min}\ \right)$ where ${T}_{BC_1}^{min}$ =${T}_{B_1}-$ $\min \left({T}_{B_1},1-{T}_{C_1}\right)$ and ${T}_{BC_2}^{min}$= ${T}_{B_2}-$ $\min \left({T}_{B_2},1-{T}_{C_2}\right)$. In the present case, ${T}_{B_1}$=0.3, ${T}_{B_2}=$0.7, ${T}_{C_1}$=0.8, ${T}_{C_2}=$0.8. So, ${T}_{BC_1}^{min}$ =${T}_{B_1}-$ $\min \left({T}_{B_1},1-{T}_{C_1}\right)$ = 0.3− min (0.3, 0.2) = 0.1. Similarly, ${T}_{BC_2}^{min}$ = ${T}_{B_2}-$ $\min \left({T}_{B_2},1-{T}_{C_2}\right)$ = 0.7- min (0.7, 0.2) = 0.5. Hence,$\overrightarrow{T_{BC}^{min}}=$(0.1, 0.5)

2.4.4 Prevalence bound of temporal pattern, T_ABC

The computation of prevalence sequence bounds of temporal pattern, T _ABC can be obtained by applying Eqs. (7) to (10). Figure 2d shows the maximum possible support sequence bound and minimum possible support sequence bound for the temporal itemset, T_ABC.

Maximum support time sequence of T_ABC, $\Big(\overrightarrow{T_{ABC}^{max}}$)

The maximum support sequence of temporal association pattern, T _ABC at level-3 is computed by considering all possible size-2 subset patterns of level-2 and singleton patterns at level-1. This gives following three cases

• 1. Case-1: k = 1, Ss ¹( ABC) =AB, S(ABC) = C i.e. ${T}_{Ss^1\left(\ ABC\right)}\equiv {T}_{AB}$ and T _S( ABC) ≡ T _C

$$ {\displaystyle \begin{array}{c}\hfill \overrightarrow{{\mathrm{T}}_{\mathrm{ABC}}^1}=\left({T}_{{AB C}_1}^1,{T}_{{AB C}_2}^1\right)\hfill \\ {}\hfill =\left({T}_{AB_1}-\max \left({T}_{AB_1}-{T}_{C_1},0\right),{T}_{AB_2}-\max \left({T}_{AB_2}-{T}_{C_2},0\right)\right)\hfill \\ {}\hfill =\left(0.3-\max \left(0.3-0.8,0\right),0.3-\max \left(0.3-0.8,0\right)\right)=\left(0.3,0.3\right)\hfill \end{array}} $$

• 2. Case-2: k = 2, Ss ²( ABC) =AC, S(ABC) = B i.e. ${T}_{Ss^2\left(\ ABC\right)}\equiv {T}_{AC}$ and T _S( ABC) ≡ T _B

$$ {\displaystyle \begin{array}{c}\overrightarrow{{\mathrm{T}}_{\mathrm{ABC}}^2}=\left({T}_{AB{C}_1}^2,{T}_{AB{C}_2}^2\right)\kern1.00em \\ {}\kern1.00em =\left({T}_{A{C}_1}-\max \left({T}_{A{C}_1}-{T}_{B_1},0\right),{T}_{A{C}_2}-\max \left({T}_{A{C}_2}-{T}_{B_2},0\right)\right)\kern1.00em \\ {}\kern3.00em =\left(0.4-\max \left(0.4-0.3,0\right),0.4-\max \left(0.4-0.7,0\right)\right)=\left(0.3,0.4\right)\kern1.00em \end{array}} $$

• 3. Case-3: k = 3, Ss ³( ABC) =BC, S(ABC) = A i.e. ${T}_{Ss^3\left(\ ABC\right)}\equiv {T}_{BC}$ and T _S( ABC) ≡ T _A

$$ {\displaystyle \begin{array}{c}\kern1.00em \overrightarrow{{\mathrm{T}}_{\mathrm{ABC}}^3}=\left({T}_{AB{C}_1}^3,{T}_{AB{C}_2}^3\right)\kern1.00em \\ {}\kern1.00em =\left({T}_{B{C}_1}-\max \left({T}_{B{C}_1}-{T}_{A_1},0\right),{T}_{B{C}_2}-\max \left({T}_{B{C}_2}-{T}_{A_2},0\right)\right)\kern1.00em \\ {}\kern3.00em =\left(0.3-\max \left(0.3-0.6,0\right),0.5-\max \left(0.5-0.4,0\right)\right)=\left(0.3,0.4\right)\kern1.00em \end{array}} $$

$$ \overrightarrow{{T_{AB C}}^{max}}=\left({T}_{AB{C}_1}^{max},{T}_{AB{C}_2}^{max}\right)=\left(\min \left(0.3,\mathrm{0.3.0.3}\right),\min \left(0.3,0.4,0.4\right)\right)=\left(0.3,0.3\right) $$

So, $\overrightarrow{{T_{ABC}}^{max}}=\left({T}_{ABC_1}^{max},{T}_{ABC_2}^{max}\right)=$(0.3, 0.3)

Minimum support time sequence of T_{ABC, (} $\overrightarrow{T_{ABC}^{min}}$)

The minimum support sequence bound of temporal association pattern, T _ABC at level-3 is computed by considering all possible size-2 subset patterns of level-2 and singleton patterns at level-1. This gives following three cases

• 1 Case-1: k = 1, Ss ¹( ABC) =AB, S(ABC) = C i.e. ${T}_{Ss^1\left(\ ABC\right)}\equiv {T}_{AB}$ and T _S( ABC) ≡ T _C

$$ {\displaystyle \begin{array}{c}\hfill \overrightarrow{{\mathrm{T}}_{\mathrm{ABC}}^1}=\left({T}_{{AB C}_1}^1,{T}_{{AB C}_2}^1\right)\hfill \\ {}\hfill =\left({T}_{AB_1}-\min \left({T}_{AB_1},1-{T}_{C_1}\right),{T}_{AB_2}-\min \left({T}_{AB_2},1-{T}_{C_2}\right)\right)\hfill \\ {}\hfill =\left(0.3-\min \left(0.3,0.2\right),0.3-\min \left(0.3,0.2\right)\right)\hfill \\ {}\hfill =\left(0.1,0.1\right)\hfill \end{array}} $$

• 2 Case-2: k = 2, Ss ²( ABC) =AC, S(ABC) = B i.e. ${T}_{Ss^2\left(\ ABC\right)}\equiv {T}_{AC}$ and T _S( ABC) ≡ T _B

$$ {\displaystyle \begin{array}{c}\hfill \overrightarrow{{\mathrm{T}}_{\mathrm{ABC}}^2}=\left({T}_{ABC_1}^2,{T}_{ABC_2}^2\right)\hfill \\ {}\hfill =\left({T}_{AC_1}-\min \left({T}_{AC_1},1-{T}_{B_1}\right),{T}_{AC_2}-\min \left({T}_{AC_2},1-{T}_{B_2}\right)\right)\hfill \\ {}\hfill =\left(0.4-\min \left(0.4,0.7\right),0.4-\min \left(0.4,0.3\right)\right)\hfill \\ {}\hfill =\left(0.0,0.1\right)\hfill \end{array}} $$

• 3 Case-3: k = 3, Ss ³( ABC) =BC, S(ABC) = A i.e. ${T}_{Ss^3\left(\ ABC\right)}\equiv {T}_{BC}$ and T _S( ABC) ≡ T _A

$$ {\displaystyle \begin{array}{l}\\ {}\begin{array}{cc}\hfill \overrightarrow{{\mathrm{T}}_{\mathrm{ABC}}^3}=\left({T}_{ABC_1}^3,{T}_{ABC_2}^3\right)\hfill & \hfill \hfill \\ {}\hfill =\left({T}_{BC_1}-\min \left({T}_{BC_1},1-{T}_{A_1}\right),{T}_{BC_2}-\min \left({T}_{BC_2},1-{T}_{A_2}\right)\right)\hfill & \hfill \hfill \\ {}\hfill =\left(0.3-\min \left(0.3,0.4\right),0.5-\min \left(0.5,0.6\right)\right)\hfill & \hfill \hfill \\ {}\hfill =\left(0.0,0.0\right)\hfill & \hfill \hfill \end{array}\end{array}} $$

$$ \overrightarrow{{T_{ABC}}^{min}}=\left({T}_{ABC_1}^{min},{T}_{ABC_2}^{min}\ \right)=\left(\mathit{\max}\left(0.1,0,0\right),\mathit{\max}\left(0.1,\mathrm{0.1,0}\right)\right)=\left(0.1,0.1\right) $$

So, $\overrightarrow{{T_{ABC}}^{min}}=\left({T}_{ABC_1}^{min},{T}_{ABC_2}^{min}\ \right)=$(0.1, 0.1)

Thus, the minimum and maximum possible support sequences of temporal association pattern, T_ABC are $\overrightarrow{{T_{ABC}}^{min}}$= (0.1, 0.1) and $\overrightarrow{{T_{ABC}}^{max}}$= (0.3, 0.3) while the true support sequence of temporal pattern, T_ABC is (0.3, 0.3).

3 SRIHASS – the proposed Z-score based dissimilarity measure

Let T_p and R_r be the temporal and reference pattern and their respective prevalence values at k^th time slot are denoted by ${T}_{p_k}$, ${R}_{r_k}$. The corresponding prevalence time sequences over ‘m’ time slots are represented using $\overrightarrow{T_P}$ = (${T}_{p_1}$, ${T}_{p_2}$, ${T}_{p_3}$, ………., ${T}_{p_m}$) and $\overrightarrow{R_r}$ = (${R}_{r_1}$, ${R}_{r_2}$, ${R}_{r_3}$, ………., ${R}_{r_m}$). The dissimilarity measure discussed in this section is motivated from the basic Gaussian membership function [23] and is extended using [8, 44,45,46,47, 56]. Discovering time profiled (or similarity profiled) temporal patterns using proposed approach requires transforming support time sequences of temporal patterns (association pattern) into their equivalent standard score (z-score) values. The idea is to obtain z-score sequences and their corresponding normal probability values using standard normal distribution table.

3.1 Z-score of temporal pattern

The z-score of a temporal pattern at a given time slot is defined as the standard score obtained by considering the support value of a temporal and reference pattern for a chosen deviation (σ ^z). The deviation value is a function of threshold value specified in euclidean space denoted using notation, ∆. Formally, the z-score value of a temporal pattern, T_p w.r.t reference, R_r at k^th time slot is denoted using $Z\left({T}_{p_k}\right)$ and is computed using Eq. (11),

$$ Z\left({T}_{p_k}\right)=\frac{\left({T}_{p_k}-{R}_{r_k}\right)}{\sigma^z} $$

(11)

where

$$ {\sigma}^z=\frac{\Delta }{\sqrt{\mathit{\ln}\left(\frac{1}{abs\left(1-{0.2212}^{\ast}\Delta \right)}\right)}} $$

(12)

3.2 Z-score and probability sequence of temporal pattern

Z-score sequence is the standard score sequence obtained by representing z-score values of a temporal pattern for all ‘m’ time slots as an m-tuple. Z-score sequence of a temporal pattern over ‘m’ time slots is denoted by $\overrightarrow{Z\left({T}_p\right)}$and is formally represented using Eq. (13)

$$ \overrightarrow{Z\left({T}_p\right)}=\left(Z\left({T}_{p_1}\right),Z\left({T}_{p_2}\right),Z\left({T}_{p_3}\right),\dots \dots .,Z\left({T}_{p_m}\right)\right) $$

(13)

The normal probability of z-score of a temporal pattern, T_p at k^th time slot is denoted using the notation, $\mathrm{P}\left(Z\left({T}_{p_k}\right)\right)$ and the corresponding probability sequence,$\overrightarrow{P\left(Z\left({T}_p\right)\right)}$ over ‘m’ time slots is represented using Eq. (14)

$$ \overrightarrow{P\left(Z\left({T}_p\right)\right)}=\left(P\left(Z\left({T}_{p_1}\right)\right),P\left(Z\left({T}_{p_2}\right)\right),P\left(Z\left({T}_{p_3}\right)\right),\dots \dots ..\dots, P\left(Z\left({T}_{p_m}\right)\right)\right) $$

(14)

3.3 Z-score based dissmilarity measure

Consider the probability sequence, $\overrightarrow{\mathrm{P}\left(Z\left({T}_p\right)\right)}$ represented by Eq. (14). The membership value of a temporal pattern, T _p  at k^th time slot w.r.t reference is given by Eq. (15)

$$ {\mathcal{M}}_{R_{r_k}}^{T_{p_k}}={e}^{-{\left(\frac{P\left(Z\left({T}_{p_k}\right)\right)}{\sigma^z}\right)}^2} $$

(15)

Extending Eq. (15) for ‘m’ time slots, the normalized similarity of temporal pattern w.r.t reference is given by Eq. (16),

$$ {\mathcal{M}}_{T_p,{R}_r}^{avg}=\frac{\sum_{k=1}^{k=m}{\mathcal{M}}_{R_{r_k}}^{T_{p_k}}}{m} $$

(16)

The true dissimilarity between temporal pattern and reference is denoted by ${D}_Z^{true}$ and is defined using Eq. (17)

$$ {D}_Z^{true}=\frac{1-{\mathcal{M}}_{T_p,{R}_r}^{avg}}{0.2212}=\frac{1-\frac{\sum_{k=1}^{k=m}{e}^{-{\left(\frac{P\left(Z\left({T}_{p_k}\right)\right)}{\sigma^z}\right)}^2}}{m}}{0.2212} $$

(17)

Statement: Given ^′∆^′, T _P , and T _q  , two temporal patterns T _P  , T _q  are considered to be similar, if the computed dissimilarity value denoted by ${D}_{T_P,{T}_q}^{true}$ does not exceed, ∆^z. i.e. ${D}_{T_P,{T}_q}^{true}\le {\Delta }^z$.

3.4 Threshold in Z-space

Let ^′∆^′ be the threshold specified in Euclidean space which represents the allowable dissimilarity limit between temporal pattern and reference pattern, then, the z-score of ∆ is obtained using,${z}_{\Delta }=\frac{\Delta }{\sigma^z}$. The probability of z _∆ that is obtained using normal distribution chart is denoted by P(z _∆) . The expression for threshold in (normalized space) transformed space is given by Eq. (18)

$$ {\Delta }^z=\frac{1-{e}^{-{\left(\frac{P\left({z}_{\Delta }\ \right)}{\sigma^z}\right)}^2}}{0.2212} $$

(18)

The value for σ ^z used in the Eq. (18) is obtained by applying Eq. (12).

3.5 Deviation

The derivation of expression for deviation is straight forward. We can derive the expression by equating the dissimilarity expression for single time slot using proposed measure and dissmilarity value provided by the user in Euclidean space as depicted in Eq. (19)

$$ \frac{1-{e}^{-{\left(\frac{P\left(Z\left({T}_{p_k}\right)\right)}{\sigma^z}\right)}^2}}{0.2212}=\Delta $$

(19)

This results in Eq. (20)

$$ {e}^{-{\left(\frac{P\left(Z\left({T}_{p_k}\right)\right)}{\sigma^z}\right)}^2}=1-{0.2212}^{\ast}\Delta $$

(20)

Solving Eq. (20), we get expression for deviation given by Eq. (21) as specified in Eq. (12)

$$ {\sigma}^z=\frac{\Delta }{\sqrt{\mathit{\ln}\left(\frac{1}{abs\left(1-{0.2212}^{\ast}\Delta \right)}\right)}} $$

(21)

3.6 Analysis

In this section, we analyze possible values for the similarity measure for different cases.

3.6.1 Best case

In the best case, the dissimilarity between temporal patterns is zero. i.e. the similarity between temporal pattern and the given reference pattern is unity.

For the best case, for k^th time slot,

$$ Z\left({T}_{P_k}\right)=\frac{\left({T}_{p_k}-{R}_{r_k}\right)}{\sigma^z}=0 $$

This is because ${T}_{p_k}\cong {R}_{r_k}$. This gives $\mathrm{P}\left(Z\left({T}_{P_k}\right)\right)$ = 0. Hence, ${\mathcal{M}}_{R_{r_k}}^{T_{p_k}}={e}^{-{\left(\frac{\mathrm{P}\left(Z\left({T}_{p_k}\right)\right)}{\sigma^z}\right)}^2}=1$

Extending this to ‘m’ number of time slots, we get the average value for similarity as

$$ {\mathcal{M}}_{T_p,{R}_r}^{avg}=\frac{\sum_{k=1}^{k=m}{\mathcal{M}}_{R_{r_k}}^{T_{p_k}}}{m}=\frac{1+1+1\dots \dots m}{m}=1 $$

Hence the dissimilarity value for the best case situation is

$$ {D}_Z^{true}=\frac{1-{\mathcal{M}}_{T_p,{R}_r}^{avg}}{0.2212}=\frac{1-1}{0.2212}=0 $$

(22)

In other words, similarity between temporal pattern and the reference is, $sim=1-{D}_Z^{true}$ = 1–0 = 1.

3.6.2 Worst case

In the worst case, the dissimilarity between temporal patterns is one (or unity). i.e. the similarity between temporal pattern and the given reference pattern is zero. Similar to the best case, we have in the worst case,

$$ {\mathcal{M}}_{T_p,{R}_r}^{avg}=\frac{\sum_{k=1}^{k=m}{\mathcal{M}}_{R_{r_k}}^{T_{p_k}}}{m}=\frac{0.7788+\dots m\ times}{m}=0.7788 $$

Hence, the dissimilarity value for the worst case situation is

$$ {D}_Z^{true}=\frac{1-{\mathcal{M}}_{T_p,{R}_r}^{avg}}{0.2212}=\frac{1-0.7788}{0.2212}=1 $$

(23)

In other words, similarity between temporal pattern and the reference is, $sim=1-{D}_Z^{true}$ = 1–1 = 0.

3.7 Distance bound computations

3.7.1 Max-min distance bound

Let, $\overrightarrow{T_p^{max}}$ = (${T}_{p_1}^{max}$, ${T}_{p_2}^{max}$, ${T}_{p_3}^{max},$……., ${T}_{p_m}^{max}$) be the maximum possible support time sequence of temporal pattern, T_p. To obtain maximum possible minimum dissimilarity value, z-score value at each time slot is to be computed by considering $\overrightarrow{{T_p}^{max}}$ and $\overrightarrow{R_r}$ . The Z-score of a temporal pattern at k^th time slot may be obtained by using Eq. (24)

$$ Z\left(\ {T}_{p_k}^{max}\right)=\left\{\begin{array}{c}\frac{\left({R}_{r_k}-{T}_{p_k}^{max}\right)}{\sigma^z};{R}_{r_k}>{T}_{P_k}^{max}\ \\ {}\kern-.5em 0\kern3.8em ;{R}_{r_k}\le {T}_{P_k}^{max}\ \end{array}\right. $$

(24)

All these z-score values obtained by applying Eq. (24) for ‘m’ time slots are represented as the z-score sequence denoted by Eq. (25),

$$ \overrightarrow{Z\left(\overrightarrow{T_p^{max}}\right)}=\left(Z\left({T}_{p_1}^{max}\right),Z\left({T}_{p_2}^{max}\right),Z\left({T}_{p_3}^{max}\right)\dots \dots \dots .,Z\left({T}_{p_m}^{max}\right)\right) $$

(25)

The probability sequence, $\overrightarrow{P\left(\overrightarrow{Z\left(\overrightarrow{T_p^{max}}\right)}\right)}$ obtained by computing probability value using normal distribution chart for each $Z\left({T_{P_k}}^{max}\right)$ is represented using Eq. (26)

$$ \overrightarrow{P\left(\overrightarrow{Z\left(\overrightarrow{T_p^{max}}\right)}\right)}=\left(P\left(Z\left({T}_{p_1}^{max}\right)\right),P\left(Z\left({T}_{p_2}^{max}\right)\right),\dots .,P\left(Z\left({T}_{p_k}^{max}\right)\right)\right) $$

(26)

The membership degree between temporal pattern, $\overrightarrow{{T_p}^{max}}$ and the reference at k^th time slot is represented using ${{\mathcal{M}}_R^{T_{p_k}}}^U$and is given by Eq. (27)

$$ {\mathcal{M}}_R^{T_{p_k}U}=\left\{\begin{array}{c}\hfill {e}^{-{\left(\frac{P\left(Z\left({T}_{p_k}^{max}\right)\right)}{\sigma^z}\right)}^2}\kern0.5em ;P\left(Z\left({T}_{p_k}^{max}\right)\right)\ne 0\hfill \\ {}\hfill \begin{array}{ccc}\hfill 1\hfill & \hfill \begin{array}{cc}\hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \kern0.6em \hfill \end{array}\kern0.5em ;P\left(Z\left({T}_{p_k}^{max}\right)\right)=0\hfill \end{array}\right. $$

(27)

Equation (28) gives the normalized similarity of temporal pattern w.r.t reference considering all, ‘m’ dis-joint time slots,

$$ {{\mathcal{M}}_{T_p}^{avg}}^U=\frac{\sum_{k=1}^{k=m}{{\mathcal{M}}_R^{T_{p_k}}}^U}{m} $$

(28)

The dissimilarity bound denoted by ${D}_Z^{\mathit{\max}-\mathit{\min}}$ is computed using Eq. (29),

$$ {D}_Z^{\max -\min }=\frac{1-\frac{\sum_{k=1}^{k=m}\left\{\begin{array}{c}\hfill {e}^{-{\left(\frac{P\left(Z\left({T}_{p_k}^{max}\right)\right)}{\sigma^z}\right)}^2}\kern0.5em ;P\left(Z\left({T}_{p_k}^{max}\right)\right)\ne 0\hfill \\ {}\hfill \begin{array}{cc}\hfill \begin{array}{ccc}\hfill 1\hfill & \hfill \begin{array}{cc}\hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \kern0.6em \hfill \end{array}\hfill & \hfill; P\left(Z\left({T}_{p_k}^{max}\right)\right)=0\hfill \end{array}\hfill \end{array}\right.}{m}}{0.2212} $$

(29)

3.7.2 Min-min distance bound

Similar to the computation of max-min distance bound, the distance bound, ${D}_Z^{\mathit{\min}-\mathit{\min}}$ is given by Eq. (30)

$$ {D}_Z^{\min -\min }=\frac{1-\frac{\sum_{k=1}^{k=m}\left\{\begin{array}{c}\hfill {e}^{-{\left(\frac{P\left(Z\left({T}_{p_k}^{min}\right)\right)}{\sigma^z}\right)}^2}\kern0.5em ;P\left(Z\left({T}_{p_k}^{min}\right)\right)\ne 0\hfill \\ {}\hfill \begin{array}{cc}\hfill \begin{array}{ccc}\hfill 1\hfill & \hfill \begin{array}{cc}\hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \kern0.6em \hfill \end{array}\hfill & \hfill; P\left(Z\left({T}_{p_k}^{min}\right)\right)=0\hfill \end{array}\hfill \end{array}\right.}{m}}{0.2212} $$

(30)

3.7.3 Minimum distance bound

The dissimilarity degree between temporal pattern (T_p) and reference (R_r) obtained by summing two dissimilarity bounds, ${\mathrm{D}}_{\mathrm{Z}}^{\max -\min }$ and ${\mathrm{D}}_{\mathrm{Z}}^{\min -\min }$ is termed as the minimum bound dissimilarity and is denoted by${\mathrm{D}}_{\mathrm{Z}}^{\mathrm{min}}$. Equation (31) gives the expression for ${D}_Z^{min}$,

$$ {D}_Z^{min}={D}_Z^{\mathit{\max}-\mathit{\min}}+{D}_Z^{\mathit{\min}-\mathit{\min}} $$

(31)

4 Algorithm design

In the naive approach for temporal association pattern mining, we must find true supports of all patterns to judge if a temporal pattern is similar or not. This makes the computational complexity class, NP. If these resulting number of true support scans can be reduced, the computational efficiency shall be improved. The proposed Z-Spamine algorithm (which uses proposed dissimilarity measure that is based on standard score named as SRIHAAS) is designed to reduce the overall computation cost. The improvement in the computation cost is addressed by

• Proposing approach for estimating temporal pattern prevalence time sequence bounds without examining the temporal dataset before computing true supports for early pruning (section-2)

• Reducing temporal pattern search space through defining temporal dissimilarity measure that hold monotonicity. (section-3)

The following subsections outlines the algorithm design.

4.1 Cover of prevalence time sequences

One of the severe data sensitive operations when discovering time profiled association patterns is generating true prevalence time sequences of temporal patterns (or temporal itemset). This is because in the worst case, this can generate prevalence sequences of all possible temporal pattern combinations. Approaches for estimating temporal pattern support values are proposed in the work of Calders [54], Jin Soung Yoo [59,60,61] and Vangipuram [49, 50]. The prevalence estimation approach addressed in section-2 is used in the proposed Z-Spamine algorithm. The dissimilarity measure used in Z-Spamine algorithm is introduced in section-3.

4.2 Minimum dissimilarity bound

The minimum bound dissimilarity of a temporal pattern to a given reference is equal to the sum of the maximum and minimum bounding dissimilarities of temporal pattern. The computation cost of temporal pattern mining process can be reduced if we can somehow prune all the invalid temporal association patterns (i.e those temporal patterns whose dissimilarity value for the reference exceeds user threshold) much ahead in the pattern mining process. This objective is achieved through computing the minimum dissimilarity bound value in Z-spamine pattern mining algorithm. The basic idea is to find the value of minimum dissimilarity bound for a given temporal pattern (w.r.t reference) and if this value exceeds the threshold limit, then the temporal pattern is pruned. This is because whenever the minimum bound dissimilarity value exceeds the dissimilarity threshold then, its true dissimilarity also exceeds the threshold limit.

4.2.1 Definition-1

Given a reference support sequence, $\overrightarrow{R}$ = (${R}_{r_1},{R}_{r_2},{R}_{r_3},\dots \dots \dots \dots, {R}_{r_m}$) and the maximum possible prevalence sequence of an item set, $\overrightarrow{T_I^{max}}=\Big(\ {T}_{I_1}^{max},{T}_{I_2}^{max}$,${T}_{I_3}^{max}$, ………………,${T}_{I_m}^{max}\ \Big)$. let $\overrightarrow{R^U}=$ (r ₁ , r ₂ , ……… , r _w  ) and $\overrightarrow{T_I^L}=\Big(\ {T}_{I_1}^{max},{T}_{I_2}^{max}$, ………………,${T}_w^{max}\ \Big)$ be the subsequences of $\overrightarrow{R}$ and $\overrightarrow{T_I^{max}}$ respectively, where r _t > ${T}_{I_t}^{max}$; 1 ≤ t ≤ w. The maximum possible minimum dissimilarity value between temporal patterns, $\overrightarrow{R}$ and $\overrightarrow{T_I^{max}}$, ${D}_Z^{\mathit{\max}-\mathit{\min}}\left(\overrightarrow{T_I^{max}},\overrightarrow{\ R}\ \right)$ is defined as $D\left(\overrightarrow{T_I^L},\overrightarrow{\ {R}^U}\right)$.

Explanation:

Let $D\left(\overrightarrow{T_I},\overrightarrow{\ R}\right)$ denote the distance between temporal itemset and the reference sequence. For example, when the proposed dissimilarity function introduced in section-3 is used then,

$$ {D}_Z^{\max -\min}\left(\overrightarrow{T_I^{max}},\overrightarrow{\ R}\ \right)=D\left(\overrightarrow{T_I^L},\overrightarrow{\ {R}^U}\right)=\frac{1-\frac{\sum_{t=1}^{t=m}\ {\mathcal{M}}_R^{{T_{I_t}}^{max}}}{m}}{0.2212} $$

(32)

where, ${\mathcal{M}}_R^{{T_{I_t}}^{max}}={e}^{-{\left(\frac{P\left(Z\left({T}_{I_t}^{max}\right)\right)}{\sigma^z}\right)}^2}$; if $\mathrm{P}\left(Z\left({T}_{I_t}^{max}\right)\right)\ne 0$ and is equal to 1; if $\mathrm{P}\left(Z\left({T}_{I_t}^{max}\right)\right)=0$.

Similarly, the maximum possible minimum dissimilarity between true support sequence of temporal itemset association and the reference is

$$ {D}_Z^{true}\left(\overrightarrow{T_I},\overrightarrow{R_r}\right)=D\left(\overrightarrow{T_I^L},\overrightarrow{R^U}\right)=\frac{1-{\mathcal{M}}_{T_I,{R}_r}^{avg}}{0.2212}=\frac{1-\frac{\sum_{k=1}^{k=m}\left\{\begin{array}{c}\hfill {e}^{-{\left(\frac{P\left(Z\left({T}_{I_k}\right)\right)}{\sigma^z}\right)}^2}\kern0.5em ;P\left(Z\left({T}_{I_k}\right)\right)\ne 0\hfill \\ {}\hfill \begin{array}{cc}\hfill \begin{array}{ccc}\hfill 1\hfill & \hfill \begin{array}{cc}\hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \kern0.6em \hfill \end{array}\hfill & \hfill; P\left(Z\left({T}_{I_k}\right)\right)=0\hfill \end{array}\hfill \end{array}\right.}{m}}{0.2212} $$

(33)

4.2.2 Definition-2

Given a reference support time sequence, $\overrightarrow{R}$ = (${R}_{r_1},{R}_{r_2},{R}_{r_3},\dots \dots \dots \dots, {R}_{r_m}$), the maximum possible prevalence sequence of an item set, $\overrightarrow{T_I^{max}}=\Big(\ {T}_{I_1}^{max},{T}_{I_2}^{max}$,${T}_{I_3}^{max}$, ………………,${T}_{I_m}^{max}\ \Big)$ and the minimum possible prevalence sequence of an item set, $\overrightarrow{T_I^{min}}=\Big(\ {T}_{I_1}^{min},{T}_{I_2}^{min}$,${T}_{I_3}^{min}$, ………………,${T}_{I_m}^{min}\ \Big)$. The minimum dissimilarity bound, ${D}_Z^{min}\left(\overrightarrow{T_I^{max}},\overrightarrow{\ {T}_I^{min}},\overrightarrow{R_r}\ \right)$is equal to the sum of maximum possible minimum dissimilarity bound,${D}_Z^{\mathit{\max}-\mathit{\min}}\left(\overrightarrow{T_I^{max}},\overrightarrow{R_r}\right)$ and minimum possible minimum dissimilarity bound, ${D}_Z^{\mathit{\min}-\mathit{\min}}\left(\overrightarrow{\ {T}_I^{min}},\overrightarrow{R_r}\right)$. This is formally denoted as

$$ {D}_Z^{min}\left(\overrightarrow{T_I^{max}},\overrightarrow{\ {T}_I^{min}},\overrightarrow{R_r}\ \right)={D}_Z^{\mathit{\max}-\mathit{\min}}\left(\overrightarrow{T_I^{max}},\overrightarrow{R_r}\right)+{D}_Z^{\mathit{\min}-\mathit{\min}}\left(\overrightarrow{\ {T}_I^{min}},\overrightarrow{R_r}\right) $$

(34)

Explanation:

The distance is computed considering ‘m’ time slots and applying proposed dissimilarity measure. If true distance is to be computed then we consider support values of temporal and reference pattern for all time slots. Alternatively, if lower bounding distance is to be computed then, for computing upper-lower bound distance, only those support values which satisfy ${R}_{r_m}$>${T}_{I_m}^{max}$ at ‘m^th’ time slot are considered. Similarly, for lower-lower bound computation only those pattern support values which satisfy ${R}_{r_m}$< ${T}_{I_m}^{min}$ are considered. This makes the above definition hold well.

4.2.3 Lemma-1

Given the maximum possible prevalence sequence, $\overrightarrow{T_I^{max}}=\Big(\ {T}_{I_1}^{max},{T}_{I_2}^{max}$,${T}_{I_3}^{max}$, ………………,${T}_{I_m}^{max}\ \Big)$, minimum possible prevalence sequence, $\overrightarrow{T_I^{min}}=\Big(\ {T}_{I_1}^{min},{T}_{I_2}^{min}$,${T}_{I_3}^{min}$, ………………,${T}_{I_m}^{min}\ \Big)$, true support sequence, $\overrightarrow{T_I}$ = (${T}_{I_1},{T}_{I_2},{T}_{I_3},\dots \dots \dots \dots, {T}_{I_m}$) of temporal pattern T _I and a reference temporal pattern, $\overrightarrow{R}$ = (${R}_{r_1},{R}_{r_2},{R}_{r_3},\dots \dots \dots \dots, {R}_{r_m}$). The lower bounding distance and the true distance holds the inequality, ${D}_Z^{min}\left(\overrightarrow{T_I^{max}},\overrightarrow{\ {T}_I^{min}},\overrightarrow{R_r}\ \right)\le {D}_Z^{true}\left(\overrightarrow{T_I},\overrightarrow{R_r}\right),$if the proposed measure of section-3 is used as a similarity function.

Proof:

According to definition of lower-bounding distance using proposed dissimilarity measure, it is known that ${D}_Z^{min}\left(\overrightarrow{T_I^{max}},\overrightarrow{\ {T}_I^{min}},\overrightarrow{R_r}\ \right)$ = ${D}_Z^{\mathit{\max}-\mathit{\min}}\left(\overrightarrow{T_I},\overrightarrow{R_r}\right)+{D}_Z^{\mathit{\min}-\mathit{\min}}\left(\overrightarrow{T_I},\overrightarrow{R_r}\right)$

i.e.

$$ {\displaystyle \begin{array}{l}{D}_Z^{min}\left(\overrightarrow{T_I^{max},}\overrightarrow{T_I^{min},}\overrightarrow{R_r}\right)=\frac{1-\frac{\sum_{k=1}^{k=m}\left\{\begin{array}{c}\hfill {e}^{-{\left(\frac{P\left(Z\left({T}_{I_k}^{max}\right)\right)}{\sigma^z}\right)}^2}\kern0.5em ;{R}_{r_k}>{T}_{I_k}^{max}\hfill \\ {}\hfill \begin{array}{cc}\hfill \begin{array}{ccc}\hfill 1\hfill & \hfill \begin{array}{cc}\hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \kern0.6em \hfill \end{array}\hfill & \hfill; else\hfill \end{array}\hfill \end{array}\right.}{m}}{0.2212}+\frac{1-\frac{\sum_{k=1}^{k=m}\left\{\begin{array}{c}\hfill \begin{array}{cc}\hfill {e}^{-{\left(\frac{P\left(Z\left({T}_{I_k}^{min}\right)\right)}{\sigma^z}\right)}^2}\hfill & \hfill; {R}_{r_k}<{T}_{I_k}^{min}\hfill \end{array}\hfill \\ {}\hfill \begin{array}{cc}\hfill \begin{array}{ccc}\hfill 1\hfill & \hfill \begin{array}{cc}\hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \kern0.6em \hfill \end{array}\hfill & \hfill; else\hfill \end{array}\hfill \end{array}\right.}{m}}{0.2212}\\ {}\le \\ {}\frac{1-\frac{\sum_{t=1}^{t=m}\left\{\begin{array}{c}\hfill \begin{array}{cc}\hfill {e}^{-{\left(\frac{P\left(Z\left({T}_{I_t}^{max}\right)\right)}{\sigma^z}\right)}^2}\hfill & \hfill; P\left(Z\left({T}_{I_t}^{max}\right)\right)\ne 0\hfill \end{array}\hfill \\ {}\hfill \begin{array}{cc}\hfill \begin{array}{ccc}\hfill \kern1.32em 1\kern1.56em \hfill & \hfill \begin{array}{cc}\hfill; P\left(Z\left({T}_{I_t}^{max}\right)\right)=0\hfill & \hfill \kern0.36em \hfill \end{array}\hfill & \hfill\;\hfill \end{array}\hfill & \hfill \hfill \end{array}\hfill \end{array}\right.}{m}}{0.2212}+\frac{1-\frac{\sum_{t=1}^{t=m}\left\{\begin{array}{c}\hfill \begin{array}{cc}\hfill {e}^{-{\left(\frac{P\left(Z\left({T}_{I_t}^{min}\right)\right)}{\sigma^z}\right)}^2}\hfill & \hfill; P\left(Z\left({T}_{I_t}^{max}\right)\right)\ne 0\hfill \end{array}\hfill \\ {}\hfill \begin{array}{cc}\hfill \begin{array}{ccc}\hfill \kern1.32em 1\kern1.56em \hfill & \hfill \begin{array}{cc}\hfill; P\left(Z\left({T}_{I_t}^{max}\right)\right)=0\hfill & \hfill \kern0.36em \hfill \end{array}\hfill & \hfill\;\hfill \end{array}\hfill & \hfill \hfill \end{array}\hfill \end{array}\right.}{m}}{0.2212}\\ {}\\ {}\equiv \frac{1-\frac{\sum_{t=1}^{t=m}{e}^{-{\left(\frac{P\left(Z\left({T}_{I_t}\right)\right)}{\sigma^z}\right)}^2}}{m}}{0.2212}={D}_Z^{true}\left(\overrightarrow{T_I},\overrightarrow{R_r}\right)\end{array}} $$

(35)

4.3 Non-decreasing property of maximum-minimum dissimilarity bound

This section explores pruning scheme which is used to reduce the temporal itemset (or pattern) search space. Monotonicity property of the support (or prevalence) measure is the most popular technique which is used to reduce the search space of itemset [2]. The prevalence values of all possible superset temporal itemset (or patterns) of a given itemset cannot be greater than item set’s prevalence values. Hence, according to the monotonicity property of support measure [2], if a temporal itemset does not satisfy support threshold, then all its superset temporal itemset can also be pruned. If we can come up with an interest measure (also called as dissimilarity measure) which has a property that is like monotonicity then, the search space can be reduced, thus achieving improved computational efficiency. The supporting argument or proof for this is discussed in the following subsection 4.3.1.

4.3.1 Lemma-2

The prevalence time sequence of temporal associations (or patterns) decreases with the size of the temporal pattern at each disjoint time slot. i.e. the prevalence value is monotonically non-increasing.

Proof:

The prevalence time sequence of a temporal pattern is obtained by considering prevalence values obtained from disjoint set of transactions for each time slot. As the size of temporal pattern increases, the prevalence value of a temporal pattern (or itemset) decreases w.r.t each time slot. Prevalence time sequences for all temporal patterns hold this property. For example, if T _I and T _J are two temporal patterns such that J⊆I, then prevalence (T _I ) ≤ prevalence (T _J ).

4.3.2 Lemma-3

The maximum possible minimum (upper-lower) dissimilarity bound between the true support time sequence of temporal pattern and reference sequence monotonically increases with respect to the size of the temporal itemset.

Proof:

Here, the generalized proof for monotonicity of maximum possible minimum bound dissimilarity value to true prevalence time sequences using proposed dissimilarity measure in the section-3 is outlined. Let, $\overrightarrow{R}$ = (${R}_{r_1},{R}_{r_2},{R}_{r_3},\dots \dots \dots \dots, {R}_{r_m}$) and $\overrightarrow{T_I}$ = (${T}_{I_1},{T}_{I_2},{T}_{I_3},\dots \dots \dots \dots, {T}_{I_m}$) be the reference and temporal pattern support time sequences of a size-k itemset, I then the maximum possible minimum dissimilarity value is given by

$$ {D}_Z^{\max -\min}\left(\overrightarrow{T_I},\overrightarrow{R_r}\right)=\frac{1-\frac{\sum_{k=1}^{k=m}\ \left\{\begin{array}{c}{e}^{-{\left(\frac{P\left(Z\left(\ {T}_{I_k}^{max}\right)\right)}{\sigma^z}\right)}^2};\kern0.5em P\left(Z\left(\ {T}_{I_k}^{\kern0.5em \max}\right)\right)\ne 0\\ {}1\kern11em ;P\left(Z\left(\ {T}_{I_k}^{\kern0.5em \max}\right)\right)=0\end{array}\right.}{m}}{0.2212} $$

(36)

Consider the size, (k + 1) item set, I ^’ = I ∪ { i ^’} where I ^’ ∉ I. The prevalence time sequence of this temporal pattern is denoted by $\overrightarrow{T_{I^{'}}}$ = (${T}_{{I^{'}}_1},{T}_{{I^{'}}_2},{T}_{{I^{'}}_3},\dots \dots \dots \dots, {T}_{{I^{'}}_m}$). From lemma-2, it is known that the prevalence value of a temporal pattern shows non-increasing behavior with the increase in pattern size i.e. (${T}_{{I^{'}}_t}$) ≤ (${T}_{I_t}$) for any t^th time slot. This holds true for all time slots in case of time stamped temporal database. So, for any time slot ‘t’, the prevalence value of superset temporal pattern is less than or equal to its subset temporal patterns.

So, if ${T}_{{I^{'}}_t}$ ≤ ${T}_{I_t}$, ${T}_{I_t}$ < ${R}_{r_t}$ and ${T}_{{I^{'}}_t}$ < ${R}_{r_t}$ then,${R}_{r_t}-{T}_{I_t}$ ≤ ${R}_{r_t}-{T}_{{I^{'}}_t}$. This means that

$$ \frac{1-\frac{\sum_{t=1}^{t=m}\ \left\{\begin{array}{c}{e}^{-{\left(\frac{P\left(Z\left({T}_{I_t}\right)\right)}{\sigma^z}\right)}^2};\kern0.5em P\left(Z\left({T}_{I_t}\right)\right)\ne 0\\ {}1\kern4em ; else\end{array}\right.}{m}}{0.2212}\le \frac{1-\frac{\sum_{t=1}^{t=m}\ \left\{\begin{array}{c}{e}^{-{\left(\frac{P\left(Z\left({T}_{{I^{'}}_t}\right)\right)}{\sigma^z}\right)}^2};\kern0.5em P\left(Z\left({T}_{{I^{'}}_t}\right)\right)\ne 0\\ {}1\kern4em ; else\end{array}\right.}{m}}{0.2212} $$

(37)

i.e., ${D}_Z^{\mathit{\max}-\mathit{\min}}\left(\overrightarrow{T_I},\overrightarrow{R_r}\right)$ $\le {D}_Z^{\mathit{\max}-\mathit{\min}}\left(\overrightarrow{T_{{I^{'}}_t}},\overrightarrow{R_r}\right)$. On similar lines, it can also be proved that the monotonicity of maximum possible minimum dissimilarity to maximum possible prevalence sequence also holds good, i.e. ${D}_Z^{\mathit{\max}-\mathit{\min}}\left(\overrightarrow{T_I^{max}},\overrightarrow{R_r}\right)$ $\le {D}_Z^{\mathit{\max}-\mathit{\min}}\left(\overrightarrow{{T_{{I^{'}}_t}}^{max}},\overrightarrow{R_r}\right)$.

4.4 Temporal pattern pruning

We follow pruning strategies discussed in [8, 44, 59,60,61] but apply the pruning strategy using the proposed dissimilarity measure. Computational cost of pattern mining process is reduced by performing the pattern pruning process using minimum dissimilarity bound (lower bounding distance) and monotonicity of maximum possible minimum dissimilarity bound. The pattern pruning scheme is explained below.

4.4.1 Pruning using subset checkup

The first strategy of pruning temporal patterns is through subset checkup. In this strategy, if the maximum possible minimum dissimilarity bound, ${D}_Z^{\mathit{\max}-\mathit{\min}}\left(\overrightarrow{T_I^{max}},\overrightarrow{R_r}\right)$of any subset of a candidate temporal pattern is computed and if this dissimilarity value does not satisfy the threshold constraint then, the candidate temporal pattern is pruned by using the principle of monotonicity.

4.4.2 Pruning based on minimum dissimilarity bound

The second strategy of pattern pruning is through computing minimum dissimilarity bound value of its maximum and minimum possible prevalence sequence. A candidate temporal pattern is pruned without the need for examining the true prevalence of temporal pattern, whenever its minimum dissimilarity bound, ${D}_Z^{min}$ exceeds the allowable dissimilarity limit.

4.4.3 Pruning using maximum possible minimum dissimilarity ${D}_Z^{\mathit{\max}-\mathit{\min}}\left(\overrightarrow{T_I^{max}},\overrightarrow{R_r}\right)$

This strategy of pattern pruning is applied mainly to reduce the total number of next size candidate temporal patterns which are otherwise possible during pattern mining process. A candidate temporal pattern is pruned whenever the maximum possible minimum dissimilarity bound,${D}_Z^{\mathit{\max}-\mathit{\min}}\left(\overrightarrow{T_I^{max}},\overrightarrow{R_r}\right)$ to true prevalence sequence of a temporal pattern exceeds the dissimilarity threshold value. In this case, the temporal pattern is not retained for generating higher size candidate temporal patterns.

5 Z-SPAMINE

In this section, we outline the algorithm for mining time profiled temporal associations, Z-Spamine. Z-Spamine algorithm uses the proposed dissimilarity measure, SRIHASS as the similarity function to find similarity between temporal pattern and reference. Z-Spamine is extended by considering spamine proposed by Yoo and Sashi Sekhar [59,60,61] that uses Euclidean distance measure as the similarity function. Our approach requires transforming the threshold value to a new space, say z-space.

5.1 Algorithm

The Z-Spamine approach is outlined as an algorithm in this subsection.

Explanation

• Steps 1–12: Finding patterns at first level

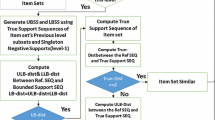
The computation process starts with obtaining true supports of first level temporal itemsets from the input dataset. These supports obtained at every time slot are tranformed to standard scores and probability scores using deviation given by Eq. (12). Compute ${D}_Z^{true}$ between reference and candidate pattern. If this satisfies the similarity condition, then the pattern is similar. Otherwise compute ${D}_Z^{\mathit{\max}-\mathit{\min}}$. If this distance satisfies similarity condition, then retain the pattern else kill the pattern. Record all retained and similar patterns at first level.

• Step 14–32: Finding patterns at level, L > 1

For each next level itemset, estimate the support bounds of itemsets at each time slot by considering the previous stage itemset true supports. Obtain ${D}_Z^{min}$using the computed support bounds. If ${D}_Z^{min}$ satisfies the similarity constraint, then find the true support of itemset. Now, compute ${D}_Z^{\mathit{\max}-\mathit{\min}}$ and ${D}_Z^{min}$. The pattern is similar if ${D}_Z^{min}$ satisfies similarity condition. If ${D}_Z^{min}$ exceeds the similarity condition, ${D}_Z^{\mathit{\max}-\mathit{\min}}$ is computed. If this value satisfies similarity constraint, then itemset is retained. Other wise, it is pruned. Record all retained and similar itemsets at each level.

• Step 33:

From the retained itemsets of previous levels, generate the combinations of itemsets for next level and repeat the steps from 14 to 32. Prune all itemset combinations that are supersets of subset itemset combinations that are not similar and not retained at the previous level. Continue the process in steps 14–32.

5.2 Working example

This section explains the working of Z-spamine algorithm using proposed dissimilarity measure. Consider the dataset shown in Fig. 1a and Lattice diagram depicted in Fig. 1b. The true distance and maximum-minimum dissimilarity values are shown in the lattice diagram. The true distance values of temporal itemset are as follows: ${D}_Z^{true}\left(\overrightarrow{T_A},\overrightarrow{R_r}\right)$ = 0.138, ${D}_Z^{true}\left(\overrightarrow{T_B},\overrightarrow{R_r}\right)$ = 0.035,$\kern0.50em {D}_Z^{true}\left(\overrightarrow{T_C},\overrightarrow{R_r}\right)$ = 0.312,$\kern0.50em {D}_Z^{true}\left(\overrightarrow{T_{AB}},\overrightarrow{R_r}\right)$ = 0.165,$\kern0.50em {D}_Z^{true}\left(\overrightarrow{T_{AC}},\overrightarrow{R_r}\right)$ = 0.069,$\kern0.50em {D}_Z^{true}\left(\overrightarrow{T_{BC}},\overrightarrow{R_r}\right)$ = 0.035,$\kern0.50em {D}_Z^{true}\left(\overrightarrow{T_{ABC}},\overrightarrow{R_r}\right)$ = 0.165. It is easy to verify that true distance does not satisfy monotonicity. For example, ${D}_Z^{true}\left(\overrightarrow{T_{AC}},\overrightarrow{R_r}\right)<{D}_Z^{true}\left(\overrightarrow{T_A},\overrightarrow{R_r}\right)$,$\kern0.50em {D}_Z^{true}\left(\overrightarrow{T_C},\overrightarrow{R_r}\right)$. Similarly, ${D}_Z^{true}\left(\overrightarrow{T_{BC}},\overrightarrow{R_r}\right)<{D}_Z^{true}\left(\overrightarrow{T_C},\overrightarrow{R_r}\right).$ i.e. the condition that the dissimilarity of superset temporal patterns must be greater than the distance of its subset temporal patterns fails in these cases. However, this property holds good w.r.t ${D}_Z^{\mathit{\max}-\mathit{\min}}$ of temporal pattern to the reference. For example, the maximum-minimum dissimilarity values for itemset associations AB, AC, BC, ABC are as follows: ${D}_Z^{\mathit{\max}-\mathit{\min}}\left(\overrightarrow{T_{AB C}},\overrightarrow{R_r}\right)=0.165,{D}_Z^{\mathit{\max}-\mathit{\min}}\left(\overrightarrow{T_{AB}},\overrightarrow{R_r}\right)=0.165,{D}_Z^{\mathit{\max}-\mathit{\min}}\left(\overrightarrow{T_{AC}},\overrightarrow{R_r}\right)=0.0692$. i.e. the distance values of all superset temporal patterns are greater than their subset temporal patterns. This also holds good for all superset temporal patterns w.r.t subset temporal patterns. It is to be noted that the values of max-min dissimilarity bound as indicated within parentheses while the true distance values are shown outside the parentheses in Fig. 1b.

6 Results and discussions

This section outlines results obtained by applying the prevalence estimation approach of section 2 and dissimilarity measure of section 3 in z-spamine algorithm. Test cases considered for the experiment are i) comparison of true support computations performed by naive using Euclidean and Z-Spamine using proposed dissimilarity measure ii) effect of threshold value iii) effect of the total number of transaction items, iv) effect of total number of time slots, v) effect of number of transactions per time slot. Subsections 6.1 to 6.5 outlines the results obtained from experiments performed by considering various test cases for scalability that includes

• i) comparison of true support computations

• ii) Effect of varying threshold value

• iii) Effect of varying number of transaction items

• iv) Effect of varying number of time slots

• v) Effect of varying number of transactions per time slot

6.1 Comparison of true support computations

This section outlines some of the results obtained by applying the proposed prevalence estimation approach in section 2.

Figure 3 depicts true support computations required for a randomly generated temporal database denoted as TD1000-T100-I20. TD indicates number of transactions per time slot, T is number of time slots, I is the total number of items in finite itemset. The temporal database generated from IBM data generator comprises of one lakh transactions. The total number of possible temporal association patterns possible is 2²⁰ which are 1 billion temporal patterns. For example, a database generated over 10 items has 1024 different possible pattern combinations. Figure 4 shows total number of true support computations required using proposed support bound estimation procedure for different thresholds 0.15, 0.25 and 0.35 applying dissimilarity measure in section 3 and Z-Spamine algorithm.

Fig. 3

True support computations – naïve approach

Fig. 4

True support computations – Z-Spamine

Figure 5 depicts the graph comparing the true support computations carried using naïve and proposed approaches for a threshold, δ = 0.35.

Fig. 5

Naïve vs. proposed - I20-T100-TD1000 and δ = 0.35

Figure 6 depicts the graph comparing retained association patterns to consider for similarity when adopting the naïve and proposed approaches for thresholds, δ equal to 0.15, 0.25 and 0.35.

Fig. 6

Retained patterns - naïve vs. proposed by level for, δ = 0.25

6.2 Varying threshold value

In the second experiment, we considered varying threshold values by maintaining constant values for transaction items, time slots and number of transactions per time slot. The experiment is conducted by considering a time stamped temporal dataset generated for 10 transaction items, 100 time slots and 1000 transactions per time slot. Threshold values are varied from 0.12 to 0.26 in steps of 0.02 and execution times for naïve, sequential, spamine and Z-Spamine approaches are plotted as a bar graph shown in the Fig. 7. It can be verified from the graph that Z-Spamine performs better to naïve and sequential approaches and has comparatively similar or better execution times w.r.t Spamine approach.

Fig. 7

Varying thresholds – 10 Items

Figure 8 shows the execution times of sequential and Z-Spamine approaches for various thresholds varied from 0.12 to 0.26 in steps of 0.02. The number of transaction items considered are 12. The total number of time slots is 100 and transactions in each time slot are 1000. From the graph depicted in Fig. 8, it can be verified that the sequential approach is very sensitive to variations in the threshold value.

Fig. 8

Varying thresholds – 12 Items

Figure 9 shows the effect of varying thresholds on naïve, sequential, spamine and z-spamine approaches on a time stamped temporal synthetic dataset generated consisting of 12 items, 100 time slots, and 1000 transactions per time slot. The execution time of naïve and sequential approaches are very high compared to spamine and z-spamine. Hence, we considered to plot the graph considering log value of execution time. Z-Spamine has better performance when compared to naïve and sequential approaches and has almost similar performance to spamine. The effect of varying thresholds on execution times of spamine and Z-Spamine algorithms can be viewed from the graph represented using Fig. 10 as this graph only compares spamine to Z-Spamine.

Fig. 9

Effect of varying thresholds on four approaches

Fig. 10

Spamine vs Z-Spamine – 12 Items

The performance of our algorithm w.r.t spamine is clearer from the bar graph in Fig. 10. It shows that the execution time of Z-Spamine is better to spamine.

6.3 Effect of varying total number of transaction per time slot

In the third experiment, the total number of transactions per time slot are varied with the fixed number of transaction items, number of time slots and threshold. For experimentation, the number of transaction items is 10, time slots are set to 100 and the threshold value chosen is 0.2. Figure 11 depicts the execution times of naïve, sequential and z-spamine approaches for varying transactions per time slot equal to 500, 750, 1000, 1250, 1300, 1350, 1400, 1450, 1500 and 2000. The dotted line graph indicates the exponential trend line of naïve approach. The total number of transactions are 1,00,000 defined over 100 time slots. It can be verified that the proposed approach (Z-Spamine) performs better to sequential and naïve approaches. Both sequential and naïve uses Euclidean distance measure. The reduce in time taken for Z-Spamine to output the result set is due to the reduced number of true support computations that are carried by Z-Spamine.

Fig. 11

Comparison of naïve, sequential and Z-Spamine

The comparison of execution times of Naive and Z-Spamine approaches for varying transactions per time slot equal to 500, 750, 1000, 1250, 1500 and 2000 is shown in Fig. 12. The dotted line graph indicates the linear trend line for naïve approach. The graph shows that Z-Spamine performs substantially better to naïve approach.

Fig. 12

Execution times - naïve and Z-Spamine

The performance of Sequential [61] and Z-Spamine approaches for varying transactions per time slot equal to 500, 1000, 1500 and 2000 are depicted in Fig. 13. The dotted line graph indicates the exponential trend for sequential approach and is denoted by the exponential function expression, y = 25.07e^0.9391x. The trend denoted by dotted exponential line shows that the execution time of sequential approach is sensitive to the total number of transactions per time slot and increases in an exponential manner. On the other hand, execution time of Z-Spamine is comparatively very much better to sequential approach and less sensitive to number of transactions per time slot.

Fig. 13

Sequential vs Z-Spamine for varying transactions per time slot

The performance of Spamine using Euclidean distance measure and proposed Z-Spamine approach using support bound estimation is recorded in the Fig. 14. Two dotted lines in the graph show the exponential trend line plotted w.r.t Spamine (top dotted line) and 2- point moving average (bottom dotted line). The execution times plotted in the graph of Fig. 14 proves that the execution time of Spamine has comparatively more exponential behavior than Z-Spamine approach. This is because the execution time of spamine meets the exponential trend line which is not true for Z-spamine as visible clearly for 2000 time slots. So, it can be deduced that, as the number of time slots increases, Z-Spamine is comparatively more scalable to Spamine approach.

Fig. 14

Spamine vs Z-Spamine for varying transactions per time slot

Figure 15 represents execution times of naïve, sequential and z-spamine approaches for varying transactions per time slot equal to 500, 750, 1000, 1250, 1300, 1350, 1400, 1450, 1500 and 2000 for a constant number of transaction items equal to 12. The two dotted line graphs indicate the exponential trend line of naïve and sequential approaches. The total number of transactions are 1,00,000 defined over 100 time slots. From the above graph, Z-Spamine has comparatively better performance to sequential and naïve approaches. Also, the two-dotted exponential trend in Fig. 15 proves that the execution time of Z-Spamine is less sensitive to the total number of transactions per time slot.

Fig. 15

Effect of varying transactions per time slot – 12 Items

The performance of Z-Spamine and Spamine approaches is recorded in Fig. 16 by varying transactions per time slot. The total number of transactions per time slot chosen are 500, 1000, 1500 and 2000 for a time-stamped temporal database defined over 100 time slots and the total number of transaction items equal to 12. Two trend lines are plotted corresponding to Spamine showing linear and exponential behaviors. The bar graph in Fig. 16 shows that the performance of Z-Spamine is almost same or better to Spamine. In general, Z-Spamine performance is comparatively better than Spamine.

Fig. 16

Effect of varying transactions per time slot on Spamine and Z-Spamine - 12 Items

6.4 Varying total number of time slots

In the fourth experiment, we consider varying the number of time slots for a constant number of transactions per time slot equal to 100, threshold equal to 0.2 and number of transaction items equal to 10. The minimum number of transactions is 50 k and maximum number of transactions is 200 k. Figure 17a compares the execution time of naïve, sequential and z-spamine approaches. The proposed approach performs better to naïve and sequential approaches. Execution times of Spamine and Z-Spamine are compared in Fig. 17b. The performance comparison of naïve, sequential, Spamine using Euclidean distance and Z-Spamine using proposed dissimilarity measure is depicted in Fig. 17c. The execution time of Z-Spamine is better compared to all other approaches. It can be concluded that execution time of z-spamine is less sensitive to change in time slots when compared to other approaches.

Fig. 17

a Comparison of naïve, sequential, Z-Spamine. b Comparison of Spamine, Z-Spamine for varying time slots for varying time slots. c Comparison of all approaches

The graph shown in Fig. 18 depicts the execution time comparison of spamine and z-spamine approaches for 12 items, 100 transactions per time slot and 0.2 threshold. The performance of z-spamine is better to Spamine approach that applies the Euclidean distance.

Fig. 18

Z-Spamine vs Spamine

6.5 Varying total number of transaction items

In the fifth experiment, the execution time and performance of naïve, sequential, spamine and Z-Spamine approaches are studied and recorded by varying the total number of transaction items. Figure 19 shows the line graph plotted depicting, the execution times of naïve, sequential and z-spamine approaches. The number of transaction items considered are 10, 11, 12, 13 and 14. The time stamped temporal database considered for this experiment has 100 time slots and each time slot has 1000 transactions which are constant. The threshold chosen is 0.2. The graph proves that Z-spamine is less sensitive to the increase in number of transaction items whereas the other two approaches i.e. naïve and sequential are more sensitive to number of transaction items and shows exponential increase in time.

Fig. 19

Effect of varying transaction items

The comparison of execution times of Spamine and Z-Spamine for variable transaction items (10, 11, 12, 13 and 14) is shown in Fig. 20 using a line graph. Similarly, Fig. 21 depicts execution times of Spamine and Z-Spamine for varying number of transaction items equal to 10,11,12,13,14,15,16,17,18,19 and 20. Both these graphs depict that Z-Spamine has nearly same or lesser execution time when compared to Spamine that applies the Euclidean distance. It is to be noted that Z-Spamine uses the proposed dissimilarity measure and support estimation technique.

Fig. 20

Effect of varying transaction items

Fig. 21

Effect of varying transaction items

The bar chart in Fig. 22 shows the execution time of two approaches (spamine and Z-Spamine) for number of transaction items equal to 10, 15, 20 and 25. In general, we can conclude that Z-Spamine has almost similar execution time or less execution time compared to Spamine approach. It is also seen that Z-Spamine is less sensitive to increase in transaction items compared to Spamine.

Fig. 22

Effect of varying transaction items

6.6 Visualization

To visualize the number of temporal associations for which true supports are computed, number of retained temporal associations and temporal trends, we have devoloped a visual tool for time profiled temporal association mining. Figure 23 shows the layout of the visual mining tool which has a provision to generate synthetic time stamped transcation database for a given set of specifications such as i)number of time slots ii) number of transactions per time slot iii) number of items iv) threshold v) reference sequence. A provision is also made available to choose any available and existing time stamped temporal dataset.

Fig. 23

Visualization – data selection screen

Figure 24 shows various algorithms that may be chosen for visualizing and understanding temporal trends of patterns to a given user reference sequence pattern.

Fig. 24

Visualization – algorithm selection screen

Figures 25 and 26 depicts the number of true support computations and number of retained itemsets over a time stamped temporal data having 100 time slots, 1000 transactions/timeslot, 14 items for a chosen threshold equal to 0.2.

Fig. 25

Visualization – true support computations

Fig. 26

Visualization – retained itemsets

Figures 27 and 28 depicts the number of true support computations and retained itemsets required on a time stamped temporal data consisting of 100 time slots, 500 transactions/timeslot, 12 items for a chosen threshold equal to 0.25 for naïve approach. It can be seen that both the number of true support computations and retained itemsets are equal for all levels for naïve approach and the graphs are bell-shape curve.

Fig. 27

visualization – retained itemsets

Fig. 28

visualization – retained itemsets

Figures 29 and 30 depicts the number of true support computations and retained itemsets required on a time stamped temporal data consisting of 100 time slots, 500 transactions/timeslot, 12 items for a chosen threshold equal to 0.25 with proposed z-spamine approach. It can be seen that, both the number of true support computations and retained itemsets are reduced compared to the naïve approach. It is also visually clear that the true supports and retained itemsets after level-4 for z-spamine is almost zero, whereas for naïve approach it keeps increasing till level-6 and then starts decreasing till level-12. Similarly, the seasonal pattern trends may also be visualized by selecting the trend visualization option. This provides the seasonal temporal trends that are hidden in the dataset w.r.t reference.

Fig. 29

Visualization – retained itemsets

Fig. 30

Visualization – retained itemsets

The following section gives details of the probability distribution chart used for design of similarity measure.

7 Normal distribution chart

Figure 31 shows the normal curve standard deviation graph and Fig. 32 shows the normal distribution probability chart using which the probailities for z-score value are obtained. To compute z-score value between temporal pattern and reference, we apply Eqs. (11) and (12). The probability value for this z-score is obtained using the distribution chart (http://www.westbrookstevens.com/continuous.htm), [35] in Fig. 32.

Fig. 31

Normal curve standard deviation

Fig. 32

Normal distribution probability chart

The probability sequence of temporal associations obtained from these z-score sequences are used to compute the dissimilarity between patterns. For example, the minimum value of z-score considered is 0 and the maximum possible value considered is 3.09 as shown in the distribution chart in Fig. 32. The normal probability for z = 0 is equal to 0 and for z = 3.09 it is equal to 0.5. The normal probability value, hence lies between 0 and 0.5. In this research, the similarity measure is designed by considering the probability distribution chart of Fig. 32. The following is the procedure to use the z-chart

• i) Find the z-value between temporal pattern support and reference support using standard normal value formula.

• ii) After finding the z-value, use the distribution chart to find the probability value.

• iii) Locate the z-value number from the left side of the chart by going vertically down. Once the first part of the number is found then locate the second part of the number by moving horizontally across the probability chart.

• iv) The value obtained by the defining cell is the probability of z-score.

8 Conclusions

Similarity-based temporal associating mining was initially coined by Yoo and Sashi Sekhar. Yoo and Sashi Sekhar applied the Euclidean distance and support estimation approaches to reduce computational complexity. Following the initial research of Yoo, subsequent works were restricted to the use of Euclidean distance. To the best of our knowledge, there are no known research studies, that have proposed novel dissimilarity measures, that apply standard score and probability distribution for time profiled temporal association mining and retain monotonicity property. Our research is pioneering work in this direction. In this research, we apply standard score and probability distribution concept to discover similarity-based time profiled temporal associations. This research introduces a novel dissimilarity measure, SRIHASS that is based on standard score computation for discovering time profiled temporal associations. Our similarity measure facilitates to understand hidden seasonal and emerging temporal trends among temporal patterns. We also proposed an approach for estimation of prevalence values of association patterns which helps to know the limits of support values and fits proposed measure. Estimating support limits helps to perform early pruning of invalid temporal associations by applying proposed dissimilarity measure. It is also analytically proved that the proposed measure holds closure property which can be used to prune temporal patterns. Several experiments have been carried under various test cases and the computational performance of Z-Spamine using proposed similarity measure is compared to the naïve, sequential and spamine approaches that apply the Euclidean distance. Experiment results and analysis prove that our approach is computationally more efficient and is substantially scalable compared to other approaches.