A new chaos based color image encryption algorithm using permutation substitution and Boolean operation

Abstract

A new color image encryption algorithm is proposed by using chaotic maps. Cipher image is constructed in three phases. In the first phase permutation of digital image is performed with the help of a chaotic map. The second phase uses chaotic substitution box for pixel substitution and finally in the third phase a Boolean operator XOR is used for mixing chaotic logistic based random sequence. Chaotic maps have main role in this encryption. Chaos theory, due to its randomness and unpredictable behaviors, is known as favorite for the purpose of image encryption. The RGB components of image scrambled by permutation-substitution and Boolean operation, show good results for security and performance analysis. Different tests of security analysis like key space, key sensitivity, correlation analysis, entropy, histogram analysis, number of pixel change rate (NPCR) and unified average changing intensity (UACI) tests are employed on the proposed scheme. On the basis of these tests, we believe that proposed scheme is well suited for practical applications.

1 Introduction

With the rapid growth in computer network technology, it becomes a trend to transmit a lot of sensitive information over a public network. Therefore information security has become very important in modern sciences. The rapid increase in image transmission grabs the attention of scientists towards making efficient and secure image encryption algorithms. The information carried by an image is quite different from plaintext. Images have bulk data, high redundancy and strong correlation between neighboring pixels. Therefore image encryption is far different from ordinary text encryption. Traditionally occurring encryption techniques DES, AES [8, 25] etc are not beneficial for the purpose of encryption of images.

Chaotic maps [14] have some very useful properties like sensitivity to initial conditions, non-periodicity and random like behavior. Chaotic maps have been highly appreciated for the generation of confusion and diffusion in image cryptography. As a result, it has endorsed a huge application in image coding, decoding, encryption, image hiding etc.

Image encryption algorithms have vast applications to benefit in many real life fields such as electronic medical record; such record is used to mange, transmit and even sometimes need to reproduce previous health history of patients securely. The use of chaotic maps in image encryption algorithms can enhance the security of such encryption schemes.

In 1989, Matthews [18] initiated the concept that, under certain conditions, easy non-linear iterative functions have tendency of producing chaotic sequences of random numbers. He derived a chaotic function and proposed that it is useful for cryptographic use. He produced a key stream based on a well known logistic chaotic map and used it for encryption of secret information. Later on 2004 Chen et al. [3] and Mao [19] used 3D chaotic Cat map and Baker map for generating permutations in image encryption scheme. Guan et al. [6] employed 2D Cat map and Chen’s map for permutation in pixel position and also for pixel value masking in 2005. Patidar et al. [21] in 2010 proposed “substitution-diffusion based image encryption scheme” using chaotic standard map and chaotic logistic maps. The proposed scheme was robust having confusion and diffusion properties. He also proposed a modified version of his scheme that was more secure for chosen plaintext attack and known plaintext attack. In 2011 Francois et al. [5] used coupling of chaotic functions and XOR operator in image encryption scheme. The main features of his scheme were the ability of producing large key space, possessing confusion and diffusion properties and encrypt images with any entropy structure. Zhang et al. [30] introduced an image encryption algorithm in 2014. In this article he employed spatiotemporal chaos of mixed linear non-linear coupled map lattices. In his proposed scheme he used the strategy of bit-level pixel permutation that enables lower-bit planes and higher-bit planes of pixels to permute mutually. A chaoticparametric switching system and its corresponding transforms for image encryption are presented in [32]. Recently, Liao et al. [10] presented a stenographic payload partition strategy for color images based on amplyfing channel model probabilities. It conceals equal amount of secret information in each color channel of RGB image. Liao et el. [9] proposed data hiding technique based on critical functions and pixel correlation function.

Many articles [11, 13, 20, 23] have been published about color image encryption algorithms. In most of color image encryption schemes during the encryption process three color components (red, green and blue) are dealt separately. Color images carry much more information as compare to ordinary text data. So there is a need of efficient image encryption scheme to handle this type of large amount of data.

In this paper we have introduced a chaotic color image encryption algorithm using permutation table, S-box and XOR Boolean operation. First, we split color image into three bit-level images each of 8 bit and overall three dimensional array of 24 bits. Then each entry of this array is permuted using permutation table generated by a chaotic map. An S-box is then generated using the same chaotic map and used to replace entries of permuted image by their corresponding values in the S-box. After this a chaotic random sequence of real numbers generated by logistic map is formed. The sequence is then converted to integers from 0 to 255 having the same size as of the image. Then bit wise XOR of sequence and image array is performed. Simulation results show that color image encryption scheme is effective and resists various typical cryptographic attacks.

The rest of the article is organized as: in Section 2 the new image encryption scheme is described. Section 3 contains decryption algorithm. Results and discussion with the help of examples and figures are in Section 4. The security analysis of the scheme and comparison with other schemes is discussed in Section 5. Finally the work is concluded in Section 6.

2 Description of proposed image encryption algorithm

In this section, we propose a new color image encryption algorithm containing three cryptogrphic phases and uses two chaotic systems to control the structure of the scheme for the obtaining high encryption performance. Firstly, in permutation phase, permutation is performed by a permutation table generated by a chaotic map. Then for substitution, a strong S-box generated by chaotic map is used. Finally, in diffusion phase an XOR function is used with another chaotic map to reinforce the statistical performance of the proposed scheme.

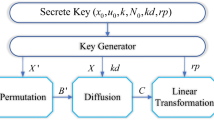
The flow diagram shown in Fig. 1 describes the step-wise working procedure of encryption scheme. In this flow diagram it can be seen that three keys (k₁,k₂,k₃) and the plain image are given as input, while the noise like scrambled cipher image is received as an output. A random chaotic sequence together with the sorted sequence are obtained by iterating piece-wise linear chaotic map (PWLCM) using k₁. The permutation sequence is formed by comparing position of numbers in the chaotic sequence and sorted sequence. Plain image is converted into 1-dimensional array and permuted using the permutation sequence. Then another chaotic sequence is generated by iterating PWLCM using k₂ and used for the S-box construction. The S-box is applied on the permuted 1-dimensional image sequence. Finally a chaotic sequence of real numbers is constructed by logistic map using k₃ and converted into integers sequence. This sequence is XORed with the substituted 1-dimensional image array sequence. The cipher image is received by converting this 1-dimensional array into image form. The summarized form of the procedure is depicted as block diagram and shown in Fig. 1.

Fig. 1

Flow chart of image encryption algorithm

2.1 Permutation phase

In this phase, the pixel positions of color image I are altered by using a suitable permutation. The permutation array is generated by using the piecewise linear chaotic map (PWLCM).

2.1.1 Piecewise linear chaotic map

PWLCM is a multi segmental map. Li et al. [12], described that PWLCM has fantastic dynamic properties like large positive Lyapunov exponent, uniform unvarying density function and random like behavior. These properties look highly useful and applicable for cryptographic purposes. For n = 0,1,2,3,...

$$ x_{n+1} = f(x_{n},y) = \left\{\begin{array}{lllll} {x_{n}}/{y} & \text{if\quad \quad } 0\leq x_{n} \leq y\\ ({x_{n}-y})/({0.5 - y}) & \text{if\quad\quad } y\ < x_{n} \leq 0.5\\ f(1-x_{n},y) & \text{if\quad\quad } 0.5 \ < x_{n} < 1 \end{array}\right. $$

(1)

Here x₀ is the initial condition of chaotic map, x₀ ∈ [0,1) and y ∈ (0,0.5) is the control parameter. The output of PWLCM has ergodicity, confusion and uniformly continuous distribution. The algorithm is based on an external secret key k₁ contains the parameters of used chaotic map (1), that is k₁ = (x₀,y), where x₀ ∈ (0,1) and y ∈ (0,0.5) are used as parameter of (1).

Algorithm 21

(Permutation algorithm) Input: Color image I, Secret key k₁ = (x₀,y), Chaotic map(1). Output: Scrambled image vector P.

• 1. Convert the image I in digital form M of size N, where M is a matrix with integer entries from 0 to 255 of order N = a × b × 3 and a, b are the numbers of rows and columns in M respectively.

• 2. Rewrite the matrix M as one dimensional array Z = {z₁,z₂,…,z_N}.

• 3. Obtain the sequence A = {a₁,a₂,...,a_N} by iterating the chaotic map (1) using the key k₁.

• 4. Sort sequence A in ascending order to form B = {b₁,b₂,…,b_N}.

• 5. Using the relationship of the sequences A and B, $b_{i}=a_{t_{i}}$, for i = 1,…,N, we compute permutation vector T = {t₁,t₂,…,t_N}.

• 6. Use T to permute the position of elements of vector Z.

• 7. After applying permutation on Z it becomes P = {p₁,p₂,p₃,...,p_N}.

2.2 Substitution phase

In this step permuted pixel vector P undergoes the substitution by using a substitution box as look up table. This technique is used to hide statistical properties of data and reduces correlation between neighboring data.

Substitution box, in short, S-box is used as the main non-linear component of algorithm. The purpose of using such S-box is to generate non-linearity in an encryption process and also to generate confusion and diffusion [24] in cipher image. The use of S-box enhances the protection of scheme against linear and differential cryptanalysis.

Here we have presented an algorithm comprising the generation of S-box with the help of chaotic map (1) and then its use as look up table for image encryption purpose. It is slightly modified algorithm presented in [2]. The secret key $k_{2}=(x^{\prime }_{o}, y^{\prime })$ is used for this phase, where $x^{\prime }_{n}\in (0, 1)$ and $y^{\prime } \in (0,0.5)$. The proposed algorithm is stated below:

Algorithm 22

(Substitution algorithm) Input: Secret key k₂, Chaotic map (1), Permuted image vector P = {p₁,p₂,...,p_N}. Output: Pre-encrypted image $S^{\prime }$. Given the chaotic map (1), we construct an S-box by executing the following steps.

• 1. Make 256 sub-interval regions of the interval $\left [ 0.1, 0.9 \right ]$ of fixed length △ h. That is,

  $$ \bigtriangleup h = (0.9-0.1)/{256}=0.003125 $$

  Label each sub-interval region as R₀,R₁,...,R₂₅₅.

• 2. Using the parameters $x^{\prime }_{0}$ and $y^{\prime }$ of the secret key $k_{2}=(x^{\prime }_{o}, y^{\prime })$ for chaotic map (1) to generate a sequence x_n of only those values that lies in [0.1, 0.9].

• 3. Initialize an empty array S.

• 4. Whenever a value x_n visit some particular sub-interval region R_i(i = 0,...,255), store that sub-interval region’s index i in S. Discard those values which does not fall in any sub-interval region or giving repeated sub-interval region’s index-value.

• 5. The array S contains all the distinct integers from 0-255 integers.

• 6. For each pixel p_i in the permuted image P = {p₁,p₂,…,p_N} replace p_i by S(p_i) where i ∈{1,…,256}. The resulting array is then denoted by $S^{\prime }=\{ s_{1}, s_{2},\ldots ,s_{N} \}$.

The output of this algorithm is the pre-encrypted image $S^{\prime }$. Note that in Step 2 the use of a slightly different value of $x^{\prime }_{0}$ or $y^{\prime }$ will result in an entirely different S-box. Thus, the above algorithm can be used to generate infinitely many S-boxes. One such S-box is constructed by setting parameter $x^{\prime }_{0}=0.7666$ and with fixed value of $y^{\prime } = 0.15$ in (1). The resulting array after step 5 is given in Table 1 as 16 × 16 matrix S-box is given in Table 1.

Table 1 S-Box

By using SET (S-box Evaluation Tool) [22], the properties of this S-box are examined. It is noted that S-box is balanced and exhibit reasonably strong cryptographic properties. The output is also validated by using a corresponding implementation on Matlab.

2.3 Diffusion phase

To scramble the internal structure of pixels, we use chaotic logistic map and a Boolean operation XOR. For this purpose first a random sequence is generated by using chaotic logistic map. This sequence is used to generates randomness in pre-encrypted image $S^{\prime }$.

2.3.1 Chaotic logistic map

Logistic map [17] is a type of chaotic system. It is one dimensional, discrete time and non-linear map with quadratic non-linearity. The state equation of logistic map with initial state w₀ is given by

$$ w_{n+1} = f(w_{n})= \mu w_{n} (1 - w_{n}), $$

(2)

where w₀ ∈ (0,1) is the state of the system at any time n and μ ∈ (0,4) is the control parameter also known as bifurcation parameter. Term w_n+ 1 expresses the next state and n shows the discrete time. For the values of μ between 3.567 and 4 the logistic map behaves chaotically with infinite period as shown in Fig. 2a.

Fig. 2

a Bifurcation diagram of chaotic logistic map, b Lyapunov exponent of chaotic logistic map

Lyapunov exponent [17] is the measure of sensitive dependence on initial condition. For μ = 3.57 to 4 the value of Lyapunov exponent is mostly positive as shown in Fig. 2b, which shows that in this interval logistic map exhibits chaotic behavior. A random sequence is constructed using logistic map and bitwise XOR is performed with substituted pixel values. The parameters of the chaotic map (2) are kept secret to constitute the secret key k₃ = (w₀,μ), where w₀ ∈ (0,1) and μ ∈ (3.57,4).

Algorithm 23

(Diffusion algorithm) Input: Pre-encrypted image $S^{\prime }$, Secret key k₃ = (w₀,μ), Chaotic map (2). Output: Final encrypted image C.

• 1. Input the secret key k₃ = (w₀,μ) in logistic map (2) and iterate it N times to obtain a sequence R of N real numbers R = {r₁,r₂,...,r_N}.

• 2. The real number sequence r_k where k = 1,2,...,N is changed into integer sequence using the relation,

  $$ \begin{array}{@{}rcl@{}} P_{k} = int(254 \times (r_{k} - \min(r_{k}))/d)+1, \end{array} $$

  (3)

  where $d = \max \limits (r_{k})- \min \limits (r_{k})$.

• 3. Encrypt each element of array $S^{\prime }$ by mixing with the corresponding element of R, using bitwise XOR i.e c_i↦s_i ⊕ r_i ⊕ s_i− 1;i = 1,…,N.

• 4. By converting resulting matrix into image form, a cipher image C is obtained.

Example 24

The above explained encryption process can be illustrated by a simple example. Let us take a block I as the original image image

$$ \text{I} =\left[\begin{array}{lllll} 10 & 13 & 6 & 14\\ 15 & 7 & 9 & 2\\ 8 & 1 & 4 & 11\\ 3 & 12 & 5 & 16 \end{array}\right]$$

By using Algorithm (21) we convert it into one dimensional array Z as:

$$Z=\{ 10,15,8,3,13,7,1,12,6,9,4,5,14,2,11,16 \}$$

Let the control parameter of Chaotic map (1) be x₀ = 0.766,y = 0.3432 as k₁, $x^{\prime }_{0} = 0.7666, y^{\prime } =0.15$ as k₂ and that of Chaotic map (2) be w₀ = 0.7666,μ = 0.3432 as k₃. Iterate the Chaotic map (1) with the given parameters the following sequence and its sorted sequence are obtained By using Algorithm (21)

$$ \begin{array}{@{}rcl@{}} A=\{& 0.7660,0.2340,0.6818,0.3182, 0.9217, 0.0729, 0.2129, 0.6189, 0.3811, 0.2418,\\ & 0.7045, 0.2955, 0.8611, 0.1389, 0.4046, 0.3915\} \end{array} $$

$$ \begin{array}{@{}rcl@{}} B=\{& 0.0729, 0.1389, 0.2124, 0.2340, 0.2418, 0.2955, 0.3182, 0.3811, 0.3915, 0.4046,\\ & 0.6189, 0.6818, 0.7045, 0.7660, 0.8611, 0.9271\} \end{array} $$

Sequence T is obtained from comparing A and B. It is applied on Z to get permuted image array P. That is:

$$T=\{ 6, 14, 7, 2, 10, 12, 4, 9, 16, 15, 8, 3, 11, 1, 13, 5 \}$$

$$P=\{ 7, 2, 1, 15, 9, 5, 3, 6, 16, 11, 12, 8, 4, 10, 14, 13 \}$$

The S-box given in Table 1 is applied on the array P to get $S^{\prime }$ as;

$$S^{\prime}=\{ 253, 61, 48, 213, 92, 76, 97, 139, 49, 120, 113, 196, 202, 186, 251, 245 \}$$

After this for diffusion purpose chaotic map (2) is used for the generation of random sequence R, the integer sequence P_k from R is obtained by using (3):

$$ \begin{array}{@{}rcl@{}} R=\{& 0.7666, 0.7157, 0.8139, 0.6058, 0.9552, 0.1713, 0.5677, 0.9816, 0.0721, 0.2675,\\ & 0.7838, 0.6778, 0.8735, 0.4420, 0.9865, 0.0531\} \end{array} $$

$$P_{k}=\{ 195, 181, 208, 151, 246, 33, 141, 254, 6, 59, 200, 171, 224, 107, 255, 1 \}$$

Finally, by using P_k, the cipher image C is obtained by following Step (3, 4) of Algorithm (23).

$$ C= \left[\begin{array}{lllll} 62 & 190 & 125 & 194\\ 182 & 211 & 62 & 19\\ 86 & 63 & 135 & 23\\ 20 & 74 & 232 & 227 \end{array}\right]$$

3 Decryption algorithm

The ciphered image C can be converted back to its original color image by using the following decryption algorithm. Decryption process is also a combination of three stages used in encryption scheme. In decryption first we eradicate the effects made by XOR operation on pre-encrypted image array. For this purpose a random sequence R of real number is generated using k₃. The sequence is converted into integers P_k and bitwise XOR is performed with the cipher image array including the preceding value.

In order to wipe out the effects generated by substitution using S-box, we use Algorithm (22) for the construction of an S-box and then generate its inverse S-box. The use of inverse S-box on the pre-encrypted image demolish all the effects generated by the use of S-box. In this way the permuted image array is retrieved. Finally a random sequence together with sorted sequence and the inverse permutation sequence is determined using Algorithm (21). The permutation effects are reversed by applying inverse permutation sequence. After converting the resulting array into image form, we get the original plain image.

Algorithm 31

(Image decryption algorithm) Input: Color cipher image C, Secret keys k₁,k₂,k₃, Algorithm (21, 22, 23), Chaotic map (1), Chaotic map (2). Output: Original image I.

• 1. Convert the cipher image C in digital form of size N, where C is a matrix with integer entries from 0 to 255 of order N = a × b × 3, a and b are the numbers of rows and columns in it respectively.

• 2. Rewrite matrix C as one dimensional array C = {c₁,c₂,…,c_N}.

• 3. As in step 1 and 2 of Algorithm (23) , the receiver by using common secret key k₃ generate the sequence R = {r₁,…,r_N} of size N.

• 4. Each element c_i of C (in step 2) is pre-decrypted as s_i↦c_i ⊕ r_i ⊕ c_i− 1;i = 1,…,N.

• 5. Again using common secret key $k_{2} = (x^{\prime }_{0}, y^{\prime })$, generate S-box S as in step 5 of Algorithm 2.2.

• 6. Find the inverse S-box S^− 1 of S.

• 7. Using S^− 1 as lookup table each element of pre-decrypted image $S^{\prime }$ is replaced by corresponding element in S^− 1 that is $p_{i} =S^{-1}(S^{\prime }_{i})$, i = 1…,N. The resulting array is stored in P = {p₁,p₂,…,p_N}.

• 8. Now using common secret key k₁, iterate the chaotic map (1) for k₁ to get the sequence A = {a₁,a₂,…,a_N}.

• 9. Sort sequence A in ascending order to form B = {b₁,b₂,…,b_N}.

• 10. The permutation array is computed as in step 5 of Algorithm (21), then the inverse permutation vector T^− 1 is calculated.

• 11. Use T^− 1 to permute the position of elements of image array P of step 7 to get pre-permuted array Z = {z₁,z₂,…,z_N}.

• 12. Store Z_i in a matrix to form image I.

Example 32

The above stated decryption algorithm wipes out all the effects of encryption on the original image. For the illustration of working procedure we take a cipher image block C and apply decryption Algorithm (31) on it.

$$ C =\left[\begin{array}{lllll} 62 & 190 & 125 & 194\\ 182 & 211 & 62 & 19\\ 86 & 63 & 135 & 23\\ 20 & 74 & 232 & 227 \end{array}\right]$$

The one dimensional array of C is:

$$C=\{ 62, 182, 86, 20, 190, 211, 63, 74, 125, 62, 135, 232, 194, 19, 23, 227 \}$$

Let the control parameter of Chaotic map (1) be x₀ = 0.766,y = 0.3432 as k₁, $x^{\prime }_{0} = 0.7666, y^{\prime } =0.15$ as k₂ and that of Chaotic map (2) be w₀ = 0.7666,μ = 0.3432 as k₃. Iterate the Chaotic map (2) with the given parameters in k₃ for a real sequence that is converted into an integer sequence P_k using (3) as:

$$P_{k}=\{ 195, 181, 208, 151, 246, 33, 141, 254, 6, 59, 200, 171, 224, 107, 255, 1 \}$$

Bitwise XOR of P_k, C and its preceding elements are performed as described in Step 4 of the Algorithm (31) to get $S^{\prime }$ as:

$$S^{\prime}=\{ 253, 61, 48, 213, 92, 76, 97, 139, 49, 120, 113, 196, 202, 186, 251, 245 \}$$

By using k₂ in chaotic map (1) and following Algorithm (22), we form an S-box and its inverse S-box. To get the permted array P we apply inverse S-box on $S^{\prime }$, that is:

$$P=\{ 7, 2, 1, 15, 9, 5, 3, 6, 16, 11, 12, 8, 4, 10, 14, 13 \}$$

Finally, we iterate chaotic map (1) with the given parameters in k₁ to make a random sequence, it is sorted and the inverse permutation sequence is determined using Algorithm (21), that is,

$$T^{-1}=\{ 14, 4, 12, 7, 16, 1, 3, 11, 8, 5, 13, 6, 15, 2, 10, 9 \}$$

This inverse permutation sequence T^− 1 is applied on P to get Z, as:

$$Z=\{ 10,15,8,3,13,7,1,12,6,9,4,5,14,2,11,16 \}$$

By converting it into a matrix form the original image I can be obtained as:

$$I= \left[\begin{array}{lllll} 10 & 13 & 6 & 14\\ 15 & 7 & 9 & 2\\ 8 & 1 & 4 & 11\\ 3 & 12 & 5 & 16 \end{array}\right]$$

4 Results and discussions

For the demonstration of the proposed scheme, we executed Algorithm (21, 22, 23) and Algorithm (31) on Matlab R2016b and applied it on two images as shown in the figures below. In the first example Fig. 3a, the standard color image of Lena (256 × 256) is selected for the demonstration of our proposed image encryption scheme and also for the comparison of the results with many other existing schemes. After applying the proposed image encryption scheme, the resulting cipher image is shown in Fig. 3b. Finally Fig. 3c is the results of decryption algorithm to get back the original image from the cipher image.

Fig. 3

Performance results of encryption an decryption algorithm: a plain image, b encrypted image, c recovered Image

It is evident that the decryption results are same as the original image having no distortion, noise or data loss effects. To see the further security aspects of encryption results, the cipher image is split into red, green and blue channels. The distribution of pixels around the image can be observed by using the histogram. Figure 4a, b, c shows the uniform distribution of cipher image component’s pixels. This shows that the cipher image does not provide any information about the distribution of pixel in the plain image. It is also important to see the correlation in the neighboring pixels of cipher image. From Fig. 5, it is evident that the neighboring pixels in RGB components of plain image are highly correlated. Figure 6a, b, c shows that the RGB components of the cipher image’s pixels have almost no correlation with each other. This shows that the neighboring pixel’s information of the original image is properly concealed in the RGB components of the cipher image.

Fig. 4

Histogram of cipher image’s color components: a red Component, b green Component, c blue Component

Fig. 5

Row-wise correlation of plain image’s color components: a red component, b green component, c blue component

Fig. 6

Row-wise correlation of cipher image’s color components: a red component, b green component, c blue component

Similarly, the proposed encryption and decryption algorithm are applied on the second color image of Baboon (256 × 256) depicted as Fig. 7a. The resulting cipher image is shown in Fig. 7b and c is the decrypted image. The distribution of the pixels in the RGB components of the cipher image (Fig. 7b) can be seen in the Fig. 8a, b, c. Moreover the correlation among the neighboring pixels of the plain image and cipher image can be seen in Figs. 9a, b, c and 10a, b, c. It can be seen that the cipher image’s pixels have almost no correlation with each other, thus they are helpful in concealing the information about neighboring pixels in the original image.

Fig. 7

Performance results of encryption an decryption algorithm: a plain image, b encrypted image, c recovered Image

Fig. 8

Histogram of cipher image’s color components: a red Component, b green Component, c blue Component

Fig. 9

Row-wise correlation of plain image’s color components: a red component, b green component, c blue component

Fig. 10

Row-wise correlation of cipher image’s color components: a red component, b green component, c blue component

5 Security analysis

This section is devoted to address the security properties of the proposed scheme.

5.1 Key space

Key space is considered an important feature in any cryptosystem. It should be large enough to have the ability to resist against brute force attacks. In the proposed encryption algorithm, secret key is a tuple of k = (k₁, k₂, k₃ ) comprising of 3 secret keys, each for the different phase of scheme. These secret keys contain parameters of associated chaotic maps that is $x_{0}, y, x^{\prime }_{0}, y^{\prime }, w_{0}, \mu$. If the precision of these parameters is taken as 10^− 15, the key space size will be (10¹⁵)³ × (10¹⁵)³ = 10⁹⁰ ≈ 2²⁹⁹. Alvarez et al. [1] identified that the adequate key space for image encryption scheme should be larger than 2¹⁰⁰ to oppose brute force attacks. Therefore the key space of our proposed scheme is large enough to resist against brute force attack. Table 2 shows the key space comparison of our proposed image encryption scheme with other existing image encryption schemes. For the recovery of the original image the adversary needs to correctly guess all these six components of shared secret key.

Table 2 Key space size comparison

5.2 Key sensitivity

An image encryption scheme should be highly conscious for its secret key and a change of single-bit in its secret key should crop an entirely different encrypted result. In the sensitivity analysis for secret key, a highly sensitive key is demanded. Cipher image should not be decrypted accurately even if there is a very small change in encryption key. Note that in our proposed scheme, the output of decrypted Algorithm 31 completely changed even if we make a very minor change in any of the component of Key k = (k₁, k₂, k₃). For example, by making a change in one parameter of k₁ that is, x₀ by adding 0.0000000000000001, a new value of x₀ will become 0.7660000000000001. Using this for decryption will not produce the original image. Here the encrypted image is shown in Fig. 11a, decrypted image in Fig. 11b and the decryption results obtained by using slightly different key is shown in Fig. 11c. Similar effects can be seen for a slight change in any parameter of used chaotic maps. From the decrypted image with the changed key, we observe that, no clue or gesture about the original image is found. Hence it is evident that proposed scheme is highly sensitive to secret keys.

Fig. 11

Key sensitivity performance with: a encrypted image, b decrypted image, c decrypted by slightly changed key

5.3 Distribution of pixels in cipher image

Image histogram displays the dispersion of pixels in an image. This can be observed as number of pixels are plotted in histogram. In the above examples RGB component-wise histograms of the cipher images are shown in Figs. 4a, b, c and 8a, b, c. It is clear that, there does not exist any clue to mount a statistical attack on the encrypted image.

5.4 Correlation analysis of two adjacent pixels

The property of having high confusion and diffusion can be checked by a test of correlation among neighboring pixels in the plain image and their corresponding cipher image. We have analyzed correlation in the adjacent pixels of the cipher image through Figs. 5a, b, c, 6a, b, c and 9a, b, c, Fig. 10a, b, c. For the calculation of correlation coefficients among the neighboring pixels in horizontal, vertical and diagonal directions. The following relation has been used,

$$ \begin{array}{@{}rcl@{}} C_{r} = \frac{(n{\sum}_{t=1}^{n}x_{t}y_{t} - {\sum}_{t=1}^{n}x_{t} {\sum}_{t=1}^{n}y_{t})}{(n{\sum}_{t=1}^{n}(x_{t})^{2} - ({\sum}_{t=1}^{n}x_{t})^{2})((n{\sum}_{t=1}^{n}(y_{t})^{2} - ({\sum}_{t=1}^{n}y_{t})^{2})}. \end{array} $$

(4)

Here x_t and y_t are values of neighboring pixels in the image and n is the total number of pixels taken for calculation of correlation.

The values in resulting Table 3 obtained from (4) are closer to zero for the cipher image. Hence neighboring pixels in encrypted image are almost uncorrelated.

Table 3 Correlation coefficient of two neighboring pixels in Plain and Cipher image

5.5 Information entropy

This feature of analysis measures the randomness in a cipher image. It also tells us the average amount of information carried by ciphered image. Let g be a ciphered image then entropy value of image g can be calculated by the formula (5) given below:

$$ \begin{array}{@{}rcl@{}} \ H(g) =\sum\limits_{i=o}^{{2^{N}}-1} P(g_{i}) log_{2} \frac{1}{P(g_{i})} \end{array} $$

(5)

Here P(g_i) shows the probability of appearing of symbol g_i in cipher image g. For exact random source having 256 different symbols, the ideal value of entropy H(g) is 8. If value of entropy is less than 8 in cipher image then it means that there is a possibility of predictability of plain image, which is dangerous for security of image encryption algorithm. In this scheme entropy for ciphered image g, that is H(g) is checked. The calculated value of entropy of ciphered image g is shown below

$$ \ H(g) = \sum\limits_{i=o}^{255}\ P(g_{i}) log_{2} \frac{1}{P(g_{i})} $$

In our example of proposed scheme , the entropy of cipher image C (Fig. 3b) with 2^N as 255, using Matlab R2016b, the entropy value for cipher image turns out to be 7.9984. A comparison of information entropy values of different image encryption schemes is given in Table 4.

Table 4 Entropy values comparison

The result shows that entropy value of our encryption result is very near to the ideal entropy value 8. It ensures that amount of information lost in proposed image encryption scheme is zero.

5.6 Differential analysis

An essential property of a good performance image encryption algorithm is that, images encrypted with that algorithm should be totally different from plain images. To check the difference in an encrypted image and making one pixel change in original image then encrypted image, we use number of pixel change rate (NPCR) and unified average changing intensity (UACI). The values of NPCR and UACI can be calculated by;

$$ \text{NPCR} = \frac{ {\sum}_{i, j} K (i, j)}{w\times h} \times 100 $$

(6)

$$ \text{UACI} = \frac{1}{w\times h}\left[ \sum\limits_{i, j} \frac{|X (i, j) - X^{\prime}(i, j)|}{255} \right] \times 100 $$

(7)

Here w and h show the width and height of the encrypted image respectively. X and $X^{\prime }$ are cipher images generated by plain image and one pixel difference in plane image respectively. If X = $X^{\prime }$ then K_i,j = 0 otherwise 1. To resist differential attacks, NPCR and UACI values should large and approach to their ideal values. It can be seen from the experimental results from (6) and (7), shown in Table 5, that the proposed scheme gets high performance for NPCR and UACI. Therefore it will give well resistance against “known plain text attacks” and “chosen plain text attacks”.

Table 5 NPCR and UACI values comparison

5.7 Noise and data loss attacks

A perfect encryption scheme ought to diminish the noise effects caused by differences in pixels in the dectypted image. For checking the capability of our proposed scheme in opposing noise and data loss attacks, we take Lena image of size 256 × 256 as test case. In the encryption result of test image we add 1%, 5% and 10% salt and pepper noise as shown in the Fig. 12a, c, e. The decryption results of noised cipher images are also shown in Fig. 12b, d, f. From the Fig. 12 it is clear that when the cipher image endure salt and pepper noise or data loss attacks, the decrypted image obtained by using our encryption scheme maintain vast majority of original image information having only a small portion of uniformally distributed noise. The peak signal to noise ratio (PSNR) provides a quantitative measure for the distinction between the original plain image I_P and its decryption result I_D. The cumulative squared error between the decrypted image and the original image can be measured by using mean square error (MSE). For an image of size MN the PSNR and MSE values can be calculated using the following relations,

$$ \text{PSNR} = 10. \log \frac{255^{2}}{\text{MSE}} (db), $$

(8)

$$ \text{MSE} = \frac{1}{M\times N} \sum\limits_{i=0}^{M-1} \sum\limits_{i=0}^{N-1} ({\text{I}_{P} (i, j) - \text{I}_{D} (i, j)})^{2}. $$

(9)

The least value of MSE (9) shows the minimum error by using the encryption scheme. While the PSNR measure (8) is usually employed to calculate the ability of rehabilitation.

Fig. 12

Experimental results for the performance evaluation of data loss attacks: a, c, e cipher images with 1%, 5% and 10% salt and pepper noise, b, d, f decryption results of corresponding images using our scheme

The greater value of PNSR indicates the higher fidelity of decrypted image towards its original plain image. If I_D and I_P are similar then the calculated value of PSNR approaches to infinity. The value above 30 db shows that I_D and I_P are not sensible for PSNR. For the values above 35 db, it is difficult to differentiate between the original image and decrypted image. For checking the cipher image’s robustness against noise attacks, 1%, 5% and 10% noise is added in the cipher image, as shown in Fig. 12a, c, e. The calculated values of PSNR for these modified cipher images are shown in Table 6. By observing the test results it can be seen that the encryption technique gives good performance for anti data loss and noise attacks.

Table 6 Performance of MSE and PSNR about salt and pepper noise

5.8 Analysis of speed

For any algorithm, security considerations are important but a good encryption algorithm should also robust and efficient. The running speed of encryption algorithm depends upon the internal structure of algorithm. The internal structure of proposed scheme is designed in such a way that it is efficient by computation. In permutation phase only single round is adopted, that gives efficiency in computation. In second phase S-box is used as lookup table then XOR is used for generation of randomness. All these stages are computationally efficient and make the whole algorithm dynamic and economic for use on real time encryption machines.

5.9 Performance for different type images

The proposed image encryption scheme can be used for the encryption of different type images like gray-scale, RGB or color (multi channel) images etc. Also we can encrypt different size images by using the proposed image encryption scheme for example 256 × 256, 512 × 512, 768 × 768 etc. Some results regarding the encryption and decryption of different type and sizes are illustrated in the figures below.

For the performance evaluation, we take Lena gray image of size 256 × 256 as shown in the Fig. 13a, encrypt it by using proposed image encryption scheme. The encryption results are shown in Fig. 13b, then apply the decryption scheme to get the original image as shown in Fig. 13c. The proposed encryption scheme is also implemented on RGB or color (multi-channel) images of 256 × 256 size and encryption/decryption results are depicted in Figs. 3 and 7. Here we implement it on different size images, for this purpose we take Lena RGB 512 × 512 size image as shown in Fig. 14a. The encryption and decryption are performed under the proposed encryption scheme and results are displayed in Fig. 14b, c. Another multi-channel 768 × 768 size image is taken. It is encrypted and decrypted by using the proposed scheme and results are depicted in Fig. 15. From these results it can be seen that the proposed scheme is implementable for various image types of different sizes.

Fig. 13

Encryption and decryption results of gray scale 256 × 256 size Lena: a plain image, b encrypted image, c decrypted image

Fig. 14

Encryption and decryption results of RGB (color) 512 × 512 size Lena: a plain image, b encrypted image, c decrypted image

Fig. 15

Encryption and decryption results of RGB (color) 768 × 768 size: a plain image, b encrypted image, c decrypted image

6 Comparison

Overall comparison of proposed image encryption scheme with some other image encryption schemes is given below in Table 7:

Table 7 Properties comparison of cipher generated by taking Lena as test image

7 Conclusion

In this paper a new color image encryption scheme is presented. This scheme firstly used a chaotic map to generate permutation vector. Plain image pixels are permuted using this vector. Then an S-box is generated using chaotic map and used for substitution purpose. The properties of confusion and diffusion can be observed after the use of S-box. Finally a random sequence is generated by using chaotic map and bitwise XOR is performed to each pixel value with the generated sequence. By mixing of pixels in this way, has shown a significant change in relationship of nearby pixels horizontally, vertically and diagonally. The proposed algorithm has also offered resistance to different types of cryptographic attacks as known plain text attack, brute force attack etc. Security analysis is done by using statistical analysis, differential analysis, key space analysis, key sensitivity analysis, entropy analysis and speed analysis. The calculated value of proposed scheme for key space is 2²⁹⁹, average correlation in cipher image is 0.0020, while NPCR, UACI and entropy values are 99.609, 33.46, 7.9984 respectively. From the security analysis, it seems that the perfect original image cannot be recovered by applying the known cryptographic attacks. Hence it is secure and implementable on real time image encryption transmission applications.