1 Introduction

Histogram equalization (HE) is one of the most typical techniques for image enhancement, unlike other complex algorithms such as methods based on fractional-order [2, 7, 17] or wavelet theory [8, 14]. Although these algorithms may get a better performance than HE but more time will be required when they are implemented so that these methods are unsuitable to the fields of consumer electronics and medical image processing. However, HE is a technique which is famous for its simplicity and validity, and it can produce an image that subjectively looks better than the original one by changing its pixel intensities. Global histogram equalization (GHE) [20] is one of the most commonly used methods based on histogram equalization. The GHE is basically using the intensity distribution of the whole image, and this will result in undesirable artifacts in the processed images, so the GHE is rarely introduced in consumer electronics such as TV, digital cameras etc.

In recent years, to overcome the flaws of the GHE mentioned above, many researchers have proposed plenty of effective algorithms. These methods can be broadly categorized by the number of sub-histogram for equalization, which are two-segments or multi-segments (the amount of sub-histograms are more than three) based. Methods based on two-segments include Brightness preserving Bi-Histogram Equalization (BBHE) [10], which separates the whole histogram into two parts with input mean brightness. Minimum Mean Brightness Error Bi-Histogram Equalization in Contrast Enhancement (MMBEBHE) [3] is an extension of BBHE, which is separated by the threshold level obtained through the minimum Absolute Mean Brightness Error (AMBE). Equal Area Dualistic Sub-Image Histogram Equalization (DSIHE) [21] is also similar to BBHE except that the histogram creating of the DSIHE is based on the median value. Range Limited Bi-Histogram Equalization for image contrast enhancement (RLBHE) [23] is another algorithm of this category, its threshold for histogram separation is calculated by Otsu’s method [15]. Threshold calculated by this method can separate the objects from the background effectively. There are still many algorithms based on two-segments [5, 16, 19]. However, there are also many kinds of algorithms based on multi-segments. Recursive Sub-Image Histogram Equalization (RMSHE) [4] is a recursive algorithm of the BBHE. Brightness Preserving Dynamic Fuzzy Histogram Equalization (BPDFHE) [18] also divides its histogram into multi-histograms, where the thresholds are obtained at the peaks of the crisp histogram. To tackle the vagueness of gray level values effectively, the BPDFHE uses fuzzy statistics of digital images for their representation and processing. Image Contrast Enhancement for Preserving Mean Brightness without losing image features [9] yields its thresholds by calculating its mean brightness and standard deviation for each recursion level, which leads to an optimum PSNR. And there are also many other algorithms can be classified as multi-segments [1, 6, 11–13, 22].

These approaches can improve the performance of histogram equalization, but they are not so effective in some situations. The BBHE and the DSIHE cannot preserve the mean image-brightness well when the middle gray level is differing from the mean or average gray level. The RMSHE produced better results over the BBHE in mean image-brightness preservation, while if the recursion level is large, the effect of contrast enhancement will be reduced rapidly. The BPDFHE uses fuzzy-histograms to handle the inexactness of gray level values, but this method will also face the same problem as the RMSHE in crisp histogram if it has too many peaks. The RLBHE uses a threshold calculated by Otsu’s method to separate the histogram into two parts, then a range limited method is employed to preserve the mean brightness of each part. Good results can be achieved with this approach, but in some conditions Otsu’s method cannot separates the objects from the background strictly, the results are un-stabilized.

In this paper, a novel contrast enhancement method called Range Limited Peak- Separate Fuzzy Histogram Equalization (RLPSFHE) is proposed to enhance the contrast of an image with a good preservation of mean image-brightness and a natural contrast enhancement. This method is a comprehensive and extension of the RLBHE and the BPDFHE. To achieve better contrast enhancement and avoid over enhancement, thresholds taken from peaks of the crisp fuzzy histogram, for remapping the peaks will lead to perceivable changes in mean image-brightness [18]. But this method may reduce the equalization effect if there are too many peaks. So we will restrict the number of thresholds by giving a threshold of region-size for each sub-histogram; then an intensity factor is applied to control the intension of contrast enhancement when a limited range method [23] for contrast enhancement is employed for each sub-histogram. Experimental results show that the proposed method can give a better performance than other state-of-the-art algorithms in the case of a wide range of natural digital images. The performance of the proposed method will be evaluated through qualitative and quantitative evaluations.

The rest of this paper is organized as follows; the GHE and the RLBHE for digital images are reviewed in Sections 2. The proposed method is presented in Section 3. Section 4 lists a comparison of the RLPSFHE with some other existing methods, and presents some mathematical analysis. Section 5 concludes this paper.

2 Rudimentary knowledge

This section covers the details regarding the GHE and the RLBHE as well as their mathematical analysis in mean image-brightness preservation. This is basically a restatement of [20] and [23].

2.1 Global histogram equalization

Let’s suppose that X = {X(i, j)} denotes a digital image, where X(i, j) denotes the gray level of the pixel at (i, j). The total number of the image pixels is N, and the image intensity is digitized into L levels that are {X 0, X 1, …, X L − 1}. Suppose n k denotes the total number of pixels with gray level of X k in the image, then the probability density of X k will be

$$ p\left({X}_k\right)={n}_k/N,\kern1em k=0,1,\dots, L-1. $$
(1)

The relationship between p(X k ) and X k is defined as the probability density function (PDF), and the graphical appearance of PDF is known as the histogram. Based on the image’s PDF, its cumulative distribution function (CDF) is defined as

$$ c\left({X}_k\right)={\displaystyle \sum_{i=0}^kp\left({X}_k\right)}, $$
(2)

where, k = 0, 1, …, L − 1. It is obvious that c(X L − 1) = 1. Thus the transform function of histogram equalization can be defined as

$$ f\left({X}_k\right)={X}_0+\left({X}_{L-1}-{X}_0\right)c\left({X}_k\right),\kern1em k=0,1,\dots, L-1. $$
(3)

Suppose Y = {Y(i, j)} is a equalized image of X, then

$$ Y=f(X)=\left\{f\left(X\left(i,j\right)\right)\left|\forall X\left(i,j\right)\right.\in X\right\}. $$
(4)

2.2 Range Limited Bi-Histogram Equalization

The RLBHE is an extension of the BBHE, it is defined in the following steps:

  1. 1)

    Choosing a proper threshold for histogram equalization.

  2. 2)

    Determine the upper and the lower bounds for histogram equalization.

  3. 3)

    Equalize each partition independently.

2.2.1 Choosing a proper threshold for histogram equalization

As we have described above, the RLBHE is a two-segment based method. In the RLBHE, Otsu’s method is used to get the threshold.

$$ {\sigma}^2\left({X}_T\right)={W}_L{\left(E\left({X}_L\right)-E(X)\right)}^2+{W}_U{\left(E\left({X}_U\right)-E(X)\right)}^2. $$
(5)

where X T is the threshold for histogram separation, X L and X U are the sub-images partitioned by X T ; E(X L ) and E(X U ) stand for the average brightness of the two sub-images respectively; W L and W U stand for the probability of each sub-images, which calculated by \( {W}_L=\frac{n_L}{N} \) and \( {W}_U=\frac{n_U}{N} \), respectively.

Thus the threshold X O can be calculated through the procedure of seeking the maximum of the inter-classes:

$$ {X}_O=\underset{X_T}{ \arg \kern0.3em \max}\left\{{\sigma}^2\left({X}_T\right),T=0,1,2,\dots, L-1\right\}. $$
(6)

2.2.2 Determine the upper and the lower bounds for histogram equalization

Although the threshold taken by Otsu’s method can effectively separate the objects from the background, the mean brightness may not be strictly constrained. So the RLBHE proposed a novel method to constrain the mean image-brightness, the mean image-brightness of the output image of bi-histogram equalization using X O is obtained by Eq. (7).

$$ E(Y)=E\left(Y\left|X\le {X}_O\right.\right)p\left(X\le {X}_O\right)+E\left(Y\left|X>{X}_O\right.\right)p\left(X>{X}_O\right). $$
(7)

Formula (7) can be decomposed to be

$$ E(Y)=\frac{1}{2}\left[\left({X}_l+{X}_O\right)\left({\displaystyle \sum_{i=l}^Op\left({X}_i\right)}\right)+\left({X}_u+{X}_O+1\right)\left(1-{\displaystyle \sum_{i=l}^Op\left({X}_i\right)}\right)\right], $$
(8)

where, X l and X u are the lower and the upper bound of the input histogram. The minimum Absolute Mean Brightness Error (AMBE) is applied to preserve the mean-brightness:

$$ AMBE\left({X}_u^{\prime },{X}_l^{\prime}\right)=\underset{X_u^{\prime },{X}_l^{\prime }}{ \arg \kern0.3em \min}\left\{\left|E(Y)-E(X)\right|\right\}, $$
(9)

where, E(X) denotes the original mean image-brightness, which can be defined as

$$ E(X)={X}_m={\displaystyle \sum_{j=l}^u{X}_jp\left({X}_j\right)}. $$
(10)

Then the formula (9) can be simplified to be

$$ AMBE\left({X}_u^{\prime },{X}_l^{\prime}\right)=\underset{X_u^{\prime },{X}_l^{\prime }}{ \arg \kern0.3em \min}\left\{{\left(a{X}_l^{\prime }+\left(1-a\right){X}_u^{\prime }-b\right)}^2\right\}, $$
(11)

where, \( a={\displaystyle \sum_{i=l}^Op\left({X}_i\right)} \), \( b=2{X}_m-{X}_O-\left(1-{\displaystyle \sum_{i=l}^Op\left({X}_i\right)}\right) \). Besides, some constraints should be applied to X ′ l and X ′ u :

$$ \left\{\begin{array}{c}\hfill {X}_l\le {X}_l^{\prime}\le {X}_O\hfill \\ {}\hfill {X}_O<{X}_u^{\prime}\le {X}_u\hfill \end{array}\right.. $$
(12)

Then problem in Eq. (11), a unique global optimum can be guaranteed with these two constraints in Eq. (12). The optimal X ′ l and X ′ u respectively minimize AMBE between the equalized image and the original image.

2.2.3 Equalize each partition independently

The next step in the RLBHE is to equalize each sub-histogram independently; this is same with all bi-histogram equalization methods except for the mapping range, so we will not represent here, one can refer to [10].

3 The proposed algorithm

The RLPSFHE can be defined as follows:

  1. 1)

    Fuzzy histogram computation

  2. 2)

    Choosing proper thresholds for histogram separation

  3. 3)

    Determine the upper and the lower bounds of each sub-histogram for equalization under the control of intensity factor

  4. 4)

    Equalize each sub-histogram independently

Details of each step will be provided in the following Subsections.

3.1 Fuzzy histogram computation

Since the values of digital image’s gray level are inexactly, using fuzzy statistics of digital images for their representation and processing can enable the technique to handle this drawback in a better way, which will improve its performance.

Let us suppose that h(l)(l ∈ {0, 1, …, L − 1}) denotes the statistic numbers of each gray level in a histogram, and a fuzzy histogram is a sequence of real numbers h(l). Considering X(i, j) as a fuzzy number \( \tilde{X}\left(i,j\right) \), the fuzzy histogram can be calculated as:

$$ h(l)\leftarrow h(l)+{\displaystyle \sum_i{\displaystyle \sum_j{\mu}_{\tilde{X}\left(i,j\right)l},k\in \left[a,b\right]}}, $$
(13)

where, k is the support domain of the membership function, and \( {\mu}_{\tilde{X}\left(i,j\right)l} \) is the triangular fuzzy membership function defined as

$$ {\mu}_{\tilde{X}\left(i,j\right)l}= \max \left(0,1-\frac{\left|X\left(i,j\right)-l\right|}{4}\right). $$
(14)

3.2 Choosing proper thresholds for histogram separation

The separation of histogram is based on the peaks of crisp fuzzy histogram.

The local maxima in the fuzzy histogram are located by using the first and second derivative of the fuzzy histogram [18]. Since the histogram is a discrete data sequence, the discrete derivative can be defined as follow:

$$ \tilde{h}(l)=\frac{ dh(l)}{ dl}\kern0.3em \triangleq \kern0.3em \frac{h\left(l+1\right)-h\left(l-1\right)}{2}, $$
(15)

where, \( \tilde{h}(l) \) represents the first order derivative of the fuzzy histogram h(l), and the second derivative can be computed through the first derivative as Eq. (16).

$$ \tilde{\tilde{h}}(l)=\frac{d\tilde{h}(l)}{ dl}=\frac{\left(h\left(l+1\right)-h(l)\right)-\left(h(l)-h\left(l-1\right)\right)}{1}=h\left(l+1\right)-2h(l)+h\left(l-1\right), $$
(16)

where, \( \tilde{\tilde{h}}(l) \) represents the second order derivative of the fuzzy histogram h(l).

From Eqs. (13)–(16), the peaks of a histogram can be obtained as (17) for those values of each gray level where it is zero crossing of the first order derivative along with a negative value of the second order derivative.

$$ {l}_{\max }=\left\{\left.l\right|l\in \left\{\tilde{h}\left(l+1\right)\cdot \tilde{h}\left(l-1\right)<0,\tilde{\tilde{h}}(l)<0\right\}\right\}. $$
(17)

However, if there are too many peaks in a fuzzy histogram, the number of sub-histograms will be large, which will reduce the equalization effect rapidly; such a problem has been mentioned at the first section [4]. So we must restrict the number of sub-histograms. There is a paradox that is preserving the mean image-brightness along with increasing the effect of equalization. The larger the number of sub-histogram is, the better preservation of mean image-brightness will be, but the less effect of equalization will be too. However, the smaller the number of sub-histogram is, the more effect of equalization will be, but simultaneously the worse preservation of mean image-brightness will be.

This paper reduces the numbers of sub-histograms to limit the size of each sub-histogram. Through Eq. (17), we can get a set of peaks:

$$ p=\left\{{p}_1,{p}_2,\dots, {p}_n\right\}, $$
(18)

where, p i , i = 1, 2, …, n, are the gray levels of each peak. And p can be regarded as a set of points for separation.

And the size of each sub-histogram is as:

$$ \varDelta =\left\{{\varDelta}_1,{\varDelta}_{2,\dots \dots, }{\varDelta}_n\right\}, $$
(19)

where, Δ i , i = 1, 2, …, n, are the sizes each of sub-histogram.

The maximum of set Δ max = max{Δ} is chosen as a threshold of restricting the number of sub-histogram, the chosen procedure steps are as follows:

  1. 1)

    Calculate the size of each sub-histogram Δ = {Δ 1, Δ 2,…, Δ n }.

  2. 2)

    Chose the maximum of Δ, named as Δ max.

  3. 3)

    Compare with the first element of Δ, if Δ 1 < Δ max, then kick p 2 out of p, and calculate Δ1 by p 1 with p 3. This procedure would not stop until Δ 1 ≥ Δ max, suppose the matched peak is p 5.

  4. 4)

    Put p 1, p 5, … p n into a new set p ′, and then compare the rest interval Δ i of sub-histograms with Δ max by the way of step 3.

  5. 5)

    Repeat step 3 and 4, until a limited number of thresholds p ′ is formed.

Remapping the peaks will lead to perceivable changes in mean image-brightness, but this method will reduce the equalization effect if there are too many peaks. So kicking some peaks out of p will break the preservation of mean image-brightness to some extent, and that will lead to more enhancement of image contrast.

3.3 Determine the upper and the lower bounds of each sub-histogram for equalization under the control of intensity factor

Since, a limited number of sub-histograms can be calculated by section of 3.2. But if we only apply p ′ to equalize the sub-histogram independently without any further modification, it will change the brightness of the input image significantly and cause undesirable artifacts. So each sub-histogram needs to be modified further to preserve the mean image-brightness. Range limited equalization for each sub-histogram is proposed to keep the mean brightness [23]. But unlike [23], in this paper, the mean brightness of each sub-histogram is used as a threshold to divide the input histogram into two independent sub-histograms. Furthermore, in order to achieve a good balance between mean-brightness preservation and contrast enhancement an intensity factor λ is employed to control the intension of brightness preservation.

$$ \lambda E\left({Y}_i\right)=E\left({X}_i\right), $$
(20)

The intensity factor λ is determined by mean-brightness of sub-histograms X mi and the input-image mean-brightness X m . Suppose Y i is the output mean, X i is the ith sub-histogram, and X mi is the mean of X i , then ΔE i (ΔE i  = E(Y i ) − E(X i )) represents the amount of changes between the output mean and input mean.

So the factor λ has following properties:

  1. 1.

    When X mi is near to X m , that is, to keep the mean-brightness of the original image, then λ will be close to 1, and \( \underset{X_{mi}\to {X}_m}{ \lim}\left(\varDelta {E}_i\right)=0 \).

  2. 2.

    When X mi is away from X m , that is, to increase the contrast enhancement, then λ will be away from 1, and \( \underset{X_{mi}\to {X}_L,{X}_U}{ \lim}\left(\varDelta {E}_i\right)=A \), here A is a non-zero const.

The cure of ΔE i can be described as in Fig. 1.

Fig. 1
figure 1

Curve of ΔE

Full size image

The algorithm assumes that the pixels of an image can be thresholded into two classes; one is bright part and another dark part. More specifically, gray levels above the mean-brightness X m are bright part, and the others are dark part. To easily identify the images, intra-class variance of bright part and dark part should be minimized [23]. So we try to achieve that the bright part becomes brighter, and the dark part darker.

Now, let’s back to the attributes of intensity factor λ, it can be more specific:

  1. 1.

    When \( \underset{X_{mi}\to {X}_m}{ \lim}\lambda =1 \), then E(Y i ) = E(X i ), and the algorithm can keep the mean-brightness of the ith sub-histogram mostly.

  2. 2.

    When \( \underset{X_{mi}\to {X}_L}{ \lim}\lambda ={A}_1 \), and A 1 ∈ (1, 2); then E(Y i ) < E(X i ), and the algorithm makes the dark part darker.

  3. 3.

    When \( \underset{X_{mi}\to {X}_U}{ \lim}\lambda ={A}_2 \), and A 2 ∈ (0, 1); then E(Y i ) > E(X i ), and the algorithm makes the bright part brighter.

In addition, these attributes must satisfy the equation Eq. (20). A 1 ∈ (1, 2), because if factor λ is too large, the algorithm can’t keep the mean-brightness well. So the size of A 1 is suitable, and it’s the same with A 2.

The cure of λ can be described as in Fig. 2.

Fig. 2
figure 2

Intensity factor curve

Full size image

According to the definition and properties of intensity factor λ, it can be chosen as λ = g(X mi  − X m ), here g(⋅) is a nonnegative monotonically decreasing function with g(0) = 1, g(−∞) = 2 and g(+∞) = 0. And to achieve the goal of the RLPSFHE, which is acquiring a good trade-off between brightness preservation and contrast enhancement, the intensity factor function should be an S-function within the scope of (1, 2) (Fig. 2). So g(⋅) can be a Sigmoid-type function with adjusting some parameters as (21).

$$ g(x)=\frac{2}{1+{e}^x}, $$
(21)

where x = (X mi  − X m )/a, a is normalization constant, and we take a = 50 in our experiment.

Now applying the intensity factor λ to the process of searching the upper and the lower bounds of each sub-histogram, we have

$$ \begin{array}{c}\hfill \lambda E\left({Y}_i\right)=E\left({Y}_i\left|{X}_{0i}\le {X}_i\le {X}_{mi}\right.\right) \Pr \left({X}_{0i}\le {X}_i\le {X}_{mi}\right)\hfill \\ {}\hfill +E\left({Y}_i\left|{X}_{mi}\le {X}_i\le {X}_{\left(L-1\right)i}\right.\right) \Pr \left({X}_{mi}\le {X}_i\le {X}_{\left(L-1\right)i}\right)\hfill \end{array}. $$
(22)

To maintain the mean brightness, we suppose:

$$ \lambda E\left({Y}_i\right)\kern0.3em \approx \kern0.3em E\left({X}_i\right)={X}_{mi}. $$
(23)

Then,

$$ \frac{1}{2}\lambda \left[\left({X}_{0i}+{X}_{mi}\right){\displaystyle \sum_{i=0i}^{mi}p\left({X}_i\right)}+\left({X}_{mi}+1+{X}_{L-1}\right)\left(1-{\displaystyle \sum_{i=0i}^{mi}p\left({X}_i\right)}\right)\right]\approx \kern0.3em {X}_{mi}. $$
(24)

From Eq. (22), we can see that X mi and p(X i ) are determined by the input image and λ is calculated by function g(⋅). To satisfy Eq. (24), we must modify the range of equalized image, which will find a new bound of this sub-histogram. We replace the upper bound X (L − 1)i and the lower bound X 0i with two variables X ′ (L − 1)i and X ′0i , which are chosen to yield minimum Absolute Mean Brightness Error (AMBE) between the equalized image and the original image:

$$ \begin{array}{l}\left({X}_{\left(L-1\right)i}^{\prime },{X}_{0i}^{\prime}\right)=\underset{X_{\left(L-1\right)i}^{\prime },{X}_{0i}^{\prime }}{ \arg \kern0.3em \min}\left|\left[\left({X}_{0i}+{X}_{mi}\right){\displaystyle \sum_{i=0i}^{mi}p\left({X}_i\right)}+\left({X}_{mi}+1+{X}_{\left(L-1\right)i}\right)\left(1-{\displaystyle \sum_{i=0i}^{mi}p\left({X}_i\right)}\right)\right]\right.\hfill \\ {}\begin{array}{llllllll}\hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & -\kern0.3em \frac{2{X}_{mi}}{\lambda}\hfill \end{array}\hfill \end{array}. $$
(25)

Equation (23) can be simplified as:

$$ \left({X}_{\left(L-1\right)i}^{\prime },{X}_{0i}^{\prime}\right)=\underset{X_{\left(L-1\right)i}^{\prime },{X}_{0i}^{\prime }}{ \arg \kern0.3em \min}\left\{{\left(a{X}_{0i}^{\prime }+\left(1-a\right){X}_{\left(L-1\right)i}^{\prime }-b\right)}^2\right\}, $$
(26)

where, \( a={\displaystyle \sum_{i=0i}^{mi}p\left({X}_i\right)},b=\left(\frac{2}{\lambda }-1\right){X}_{mi}-\left(1-a\right) \). Besides, there are some other constraints can be applied to X ′0i and X ′(L − 1)i [23]:

$$ \left\{\begin{array}{c}\hfill {p}_i\le {X}_{0i}^{\prime}\le {X}_{mi}\hfill \\ {}\hfill {X}_{mi}<{X}_{\left(L-1\right)i}^{\prime}\le {p}_{i+1}\hfill \end{array}\right., $$
(27)

where, p i and p i + 1 are the ith and (i + 1)th element of set of the peaks. These two constraints are obvious and the problem of Eq. (26) becomes to be an optimization problem and has a unique global optimum. And the Optimal X ′0i and X ′(L − 1)i minimize AMBE of the ith sub-histogram so that guarantee best brightness preservation.

3.4 Equalize each sub-histogram independently

After all sub-histograms go through the procedure of 3.3, the next step is to equalize each sub-histogram independently. This is similar to the RLBHE except that the threshold of each sub-histogram is the mean brightness. The final modulation function of ith sub-histogram is as follows:

$$ {f}_{Li}={X}_{0i}^{\prime }+\left({X}_{mi}\kern0.3em -\kern0.3em {X}_{0i}^{\prime}\right){c}_{Li}\left({X}_k\right),k=0i,0i+1,\dots mi, $$
(28)

and

$$ {f}_{Ui}={X}_{mi}+1+\left({X}_{{}_{\left(L-1\right)i}}^{\prime }-\left({X}_{mi}+1\right)\right){c}_{Ui}\left({X}_k\right),k= mi+1, mi+2,\dots \left(L-1\right)i. $$
(29)

Note that Eqs. (26) and (27) are remapped to the ranges of [X ′0i , X mi ] and [X m  + 1, X ′(L − 1)i ].

Suppose Y is the final output image, and n is the numbers of the thresholds, then Y can be expressed as

$$ Y=\left\{Y\left(i,j\right)\right\}={\left\{{Y}_{Li}\cup {Y}_{Ui}\right\}}_i={\left\{{f}_{Li}\left({X}_{Li}\right)\cup {f}_{Ui}\left({X}_{Ui}\right)\right\}}_i,i=1,2,\dots n, $$
(30)

where,

$$ {Y}_{Li}={f}_{Li}(X)=\left\{f\left(X\left(i,j\right)\left|\forall X\left(i,j\right)\kern0.3em \in \kern0.3em {X}_{Li}\right.\right)\right\}, $$
(31)
$$ {Y}_{Ui}={f}_{Ui}(X)=\left\{f\left(X\left(i,j\right)\left|\forall \right.X\left(i,j\right)\kern0.3em \in \kern0.3em {X}_{Ui}\right)\right\}. $$
(32)

Based on the description of the ith sub-histogram above, the decomposed sub-image (i = 1, 2, …, n) can be equalized independently and the compositions of the resulting equalized sub-images constitute the output of the RLPSFHE.

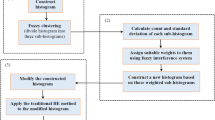
The flowchart of the proposed method can be summarized as shown in Fig. 3.

Fig. 3
figure 3

Flowchart of RLPSFHE

Full size image

4 Experiments and analysis

In this section, the results from previous algorithms and the proposed algorithms are simulated on various images, and will be compared by qualitative and quantitative evaluation methods.

4.1 Analysis for the brightness preservation of the proposed algorithm

For each single sub-histogram, to keep the mean-brightness mostly, we have:

$$ \lambda E\left({Y}_i\right)=E\left({X}_i\right), $$
(33)

where λ is determined by the distance of mean of the sub-histograms and the original histogram (Eq. 21).

Without loss of generality, we suppose there are two peaks in the input histogram p = {p 1, p 2}, and the input-image mean-brightness is located between p 1 and p 2. We make the mean-brightness as a pseudo-peak in practice (p m ), then the set of peaks turns out to be p = {p 1, p m , p 2}. So the formulation of the output mean-brightness is as follows:

$$ \begin{array}{c}\hfill \lambda E(Y)={\lambda}_0E\left(Y\left|{X}_0\le X\le {X}_{p1}\right.\right) \Pr \left({X}_0\le X\le {X}_{p1}\right)\hfill \\ {}\hfill +{\lambda}_1E\left(Y\left|{X}_{p1}\le X\le {X}_{pm}\right.\right) \Pr \left({X}_{p1}\le X\le {X}_{pm}\right)\hfill \\ {}\hfill +{\lambda}_2E\left(Y\left|{X}_{pm}\le X\le {X}_{p2}\right.\right) \Pr \left({X}_{pm}\le X\le {X}_{p2}\right)\hfill \\ {}\hfill +{\lambda}_3E\left(Y\left|{X}_{p2}\le X\le {X}_{L-1}\right.\right) \Pr \left({X}_{p2}\le X\le {X}_{L-1}\right)\hfill \end{array}, $$
(34)

where,

$$ \left\{\begin{array}{c}\hfill {\lambda}_0=\frac{2}{1+{e}^{\left({X}_{m1}-{X}_m\right)/a}}\hfill \\ {}\hfill {\lambda}_1=\frac{2}{1+{e}^{\left({X}_{m2}-{X}_m\right)/a}}\hfill \\ {}\hfill {\lambda}_2=\frac{2}{1+{e}^{\left({X}_{m3}-{X}_m\right)/a}}\hfill \\ {}\hfill {\lambda}_3=\frac{2}{1+{e}^{\left({X}_{m4}-{X}_m\right)/a}}\hfill \end{array}\right.. $$
(35)

According to our assumptions, we have non-equality: X m1 < X m2 < X m  < X m3 < X m4, then 1 < λ 1 < λ 0 < 2, 0 < λ 3 < λ 2 < 1.

There will be some corollaries can be got according to Eqs. (33), (32) and (34).

  1. 1.

    For sub-histogram of [X 0, X p1], we get E(Y 1) < E(X 1) and ΔE 1 < 0, which means the algorithm makes the dark part darker.

  2. 2.

    For sub-histogram of (X p1, X pm ], we get E(Y 2) < E(X 2) and ΔE 2 < 0, which means the algorithm makes the dark part darker.

  3. 3.

    For sub-histogram of (X pm , X p2], we get E(Y 3) > E(X 3) and ΔE 3 > 0, which means the algorithm makes the bright part brighter.

  4. 4.

    For sub-histogram of (X p2, X L − 1], we get E(Y 4) > E(X 4) and ΔE 4 > 0, which means the algorithm makes the bright part brighter.

  5. 5.

    For the whole histogram, we get ΔE 1 < ΔE 2 < 0 and 0 < ΔE 3 < ΔE 4, which means the changes of mean-brightness (ΔE = ΔE 1 + ΔE 2 + ΔE 3 + ΔE 4) would not big, but the contrast enhancement still be increased.

Based on the analysis on 4 cases of the sub-histograms shown above, we can see that the RLPSFHE wants to get a balance between mean-brightness preservation and contrast enhancement. To be more precise, the algorithm aims to enhance contrast along with a natural look in the equalized image. And it is not difficult to generalize the algorithm when the number of peaks is n.

While the RLPSFHE sometimes can’t preserve the mean-brightness well, for the result of AMBE is depended on the location of the input mean-brightness. When X m is very large or small, the changes of ΔE will increase, but the contrast enhancement will be also increased. In most case, the RLPSFHE can be implemented effectively.

4.2 Measurement tools to assess image quality

In this subsection, we will apply some quantitative evaluation methods to assess the after-enhancement image quality.

4.2.1 Absolute mean brightness error

The absolute mean brightness error, as we have discussed above, is the absolute of mean brightness between the input image and the equalized image. This of the AMBE is as:

$$ AMBE=\left|{\mu}_{input}-{\mu}_{equalized}\right|, $$
(36)

where, μ input is the mean of the input-image, μ equalized is the mean of the equalized-image.

4.2.2 Mean structural similarity index

The mean structural similarity index (SSIM) is as bellow:

$$ SSI\left(x,y\right)=\frac{\left(2{\mu}_x{\mu}_y+{C}_1\right)\left(2{\sigma}_{xy}+{C}_2\right)}{\left({\mu}_x^2+{\mu}_y^2+{C}_1\right)\left({\sigma}_x^2+{\sigma}_y^2+{C}_2\right)}, $$
(37)

where, μ x is the mean of image x, μ y is the mean of image y, σ x is the standard deviation of image x, σ y is the standard deviation of image y, σ xy is the square root of covariance of image x and y, and C 1 and C 2 are constants. The mean SSI is

$$ MSSI\left(X,Y\right)=\frac{1}{M}{\displaystyle \sum_{i=1}^M SSI\left({x}_i,{y}_i\right)}, $$
(38)

where, X and Y are the reference and the reconstructed images, respectively; x i and y i are the image contents at the ith local window; and M is the number of local windows of the image.

4.3 Experiment and discussion

In order to demonstrate the performance of the proposed method in the preserving and improving the quality of input-images, we compare its performance with that of other art-to-date methods HE, BBHE, MMBEBHE, RMSHE, RLBHE and BPDFHE on some various images. We choose 5 groups of them shown as in Figs. 4, 5, 6, 7, and 8. And in order to assess the quality of the equalized images, we use criteria based on AMBE and MSSI. Moreover, and the results are given as in Tables 1 and 2.

Fig. 4
figure 4

Experimental results for a peppers image

Full size image
Fig. 5
figure 5

Experimental results for a dollar image

Full size image
Fig. 6
figure 6

Experimental results for an aerial image

Full size image
Fig. 7
figure 7

Experimental results for an airplaneU2 image

Full size image
Fig. 8
figure 8

Experimental results for a baboon image

Full size image
Table 1 Results of AMBE for methods of HE, BBHE, MMBEBHE, RMSHE, RLBHE, BPDFHE and RLPSFHE
Full size table
Table 2 Results of MSSI for methods of HE, BBHE, MMBEBHE, RMSHE, RLBHE, BPDFHE and RLPSFHE
Full size table

In Fig. 4, we can easily observe that the proposed method (RLPSFHE) not only gets a good preservation of the overall brightness of the image, but also makes the equalized image looks better. From Fig. 4-(h) we can see that glosses on peppers look better than others. Moreover, the RLPSFHE can gain one of the best results in AMBE and MSSI shown as in Tables 1 and 2. Although the MMBEBHE and the RLBHE have the best result of AMBE, but the RLPSFHE has a good performance both in AMBE and MSSI. A good result in MSSI means a good structure protection during the processing of contrast enhancement.

In Figs. 5 and 6, the images of dollar and aerial are applied to process through HE, BBHE, MMBEBHE, RMSHE, RLBHE, BPDFHE and the proposed method. It seems the MMBEBHE (Fig. 5-(d)) get the best result in Fig. 5, but the equalized image looks much darker than the original one, which is unsuitable to consumer electronics. But if we enlarge the image of Figs. 5 and 6, we can see that the RLPSFHE obtains a more natural enhancement on images than others. The RLPSFHE manage to protect the main information of the original image along with increase the contrast enhancement. What’s more, the RLPSFHE also gains one of the best results in AMBE and MSSI.

In Fig. 7, we can see that results of the RLPSFHE and the MMBEBHE show better quality and more details than others, and from Table 1, the RLPSFHE has the best preservation of mean brightness which gains the minimum AMBE of 4.4341. But it is still not small enough comparing with other experiments; the equalized image is much brighter than the original one. From result of the experiment, we can see that the original set of peaks is p = {1, 23, 256}, mean-brightness of the original image X m  = 34, and after taking the procedure of limiting the number of sub-histogram in Section 4, the modified set of thresholds is p ′ = {1, 34, 256}. There are two sub-histograms, one is [1, 34], the dark part, intensity factor λ 0 = 1.1096; and another is (34, 256], the bright part, intensity factor λ 1 = 0.7087. |λ 0 − 1| < |λ 1 − 1| and area of bright part is bigger than dark part. So |ΔE 1| < |ΔE 2|, that makes the equalized image brighter than others and AMBE isn’t small. Moreover, we can see that location of X m is near to X 0, X m is so small that the RLPSFHE can’t preservation the mean-brightness, but will increase the contrast enhancement, that verified we have mentioned above in Section 4.1.

In Fig. 8, a simple image of baboon is applied to the contrast enhancement methods. From the results (a)-(h) presented as in Fig. 8, we can see that results of HE, the BBHE and the MMBEBHE are much darker than others, which means the whole visuals have changed; results of the RMSHE and the RLBHE are almost the same, the enhancement is not enough; it seems that the BPDFHE and the RLPSFHE show the best result, while the RLPSFHE are better than the BPDFHE, since that face of (h) is brighter than (g), and (h) shows more glosses on baboon’s nose than (g). With Tables 1 and 2, we can tell that the RLPSFHE gains one of the best results in AMBE, and the best result of MSSI.

The RLPSFHE is quite differ from the MMBEBHE and the RLBHE, in which the algorithms are aiming to achieve the minimum changes between the original and the equalized image, those methods can get the best result in AMBE, but the equalized image may looks unnatural. The RLPSFHE tries to enlarge the inter-class variance between the foreground and background, while keep the mean-brightness by controlling of the intensity factor λ. At the same time, the RLPSFHE is also differ from the RMSHE and the BPDFHE, in which the algorithms face the same problem if the recursion level is large, the equalization effect will be reduced rapidly. In the RLPSFHE, the recursion level has been modified.

5 Conclusions

In this paper, a new contrast enhancement algorithm referred as the Range Limited Peak-Separate Fuzzy Histogram Equalization (RLPSFHE) is proposed. The RLPSFHE is a generalization of the RLBHE and the BPDFHE in term of brightness preservation and contrast enhancement. The main idea of the RLPSFHE is to separate the fuzzy histogram by the peaks of the histogram, then to modify the set of peaks to break the preservation of brightness in some terms, which helps to increase the effect of equalization. After that an intensity factor is employed to control the intension of brightness preservation during the process of contrast enhancement for each sub-histogram. The crucial features that led to the success of the RLPSFHE are good preservation of mean-brightness and structural information, and better contrast with low AMBE, high MSSI.