A robust texture feature extraction using the localized angular phase

Abstract

This paper proposes a novel descriptor, referred to as the localized angular phase (LAP), which is robust to illumination, scaling, and image blurring. LAP utilizes the phase information from the Fourier transform of the pixels in localized polar space with a fixed radius. The application examples of LAP are presented in terms of content-based image retrieval, classification, and feature extraction of real-world degraded images and computer-aided diagnosis using medical images. The experimental results show that the classification performance of LAP in terms of the latter application examples are better than those of local phase quantization (LPQ), local binary patterns (LBP), and local Fourier histogram (LFH). Specially, the capability of LAP to analyze degraded images and classify abnormal regions in medical images are superior to those of other methods since the best overall classification accuracy of LAP, LPQ, LBP, and LFH using degraded textures are 91.26, 61.23, 35.79, and 33.47%, respectively, while the sensitivity of LAP, LBP, and spatial gray level dependent method (SGLDM) in classifying abnormal lung regions in CT images are 100, 95.5, and 93.75%, respectively.

1 Introduction

Texture represents the coarseness and statistical characteristics of the local variation of brightness between neighboring pixels, and plays an important role in image analysis and pattern recognition [46]. Texture analysis is indispensable for important applications, such as in medical image analysis, document analysis, target detection, industrial surface detection, and remote sensing [41].

The texture model involves basic texture primitives that form texture elements, called textons [14] or texels [11] and there are four major issues in texture analysis [21], namely texture feature, texture discrimination, texture classification, and shape from texture. This paper focuses on texture feature and texture discrimination. There is a wide range of image recognition methods using various texture feature approaches; basically, these can be divided into four approaches [18]; statistical (histogram, co-occurrence and autocorrelation), structural (Voronoi tessellation), model based (Markov random field), and spectral (Gabor filter, wavelet). These approaches can be carried out in the spatial domain (local binary patterns (LBP), Markov random field) or frequency domain (local Fourier histogram (LFH), Gabor filter, phase) depending on the required applications and the various domains.

There are two main classes of descriptors, namely, the sparse and dense descriptors [6]. The sparse descriptor detects the interest points in a given image, samples a local patch, and describes its invariant features [22, 23], whereas the dense descriptor extracts the local features pixel by pixel over the input image [26, 27, 37]. One well known sparse descriptor is the scale-invariant feature transform (SIFT), and the most popular dense descriptors are the Gabor filter [20] and LBP [26, 29]. In texture analysis, the dense descriptor shows better performance than the sparse descriptor since it describes the textons of the texture.

Textures often vary due to variations in illumination, scaling changes, blurring effects, or other visual appearance perturbations. One of the texture descriptors that are robust against illumination changes is LBP because it applies the difference values between pixels. Another simple approach of achieving illumination invariance is to use the phase of the image, which is invariant to pixel value shifts [25, 31]. Some methods achieve invariance against scaling and rotational changes by using the polar space, where the image scaling and rotations are converted into image translations [5, 36]. Approaches using the Zernike moment and Fourier magnitude are also shown to be invariant to the translations and rotations of the images [43]. For achieving invariance against blurring, the most famous approach is the image moment method [7, 19], and another approach is to exploit the phase of the image, which has proven to be insensitive to Gaussian blurring [30, 33].

However, most methods proposed for overcoming these texture visual appearance problems have high computational complexities [37]. Moreover, texture descriptor methods that have good overall integrated invariance with respect to illumination, scale and blurring have yet to be proposed; therefore, a versatile texture descriptor that has low computational complexity and is invariant to illumination and scaling changes as well as blurring is highly desirable.

This paper proposes a new versatile dense texture descriptor that is called the localized angular phase (LAP); it applies local analysis over the input image because of the superiority of the dense descriptor method in terms of classifying texture. The spectral-based texture feature is applied using the phase of the image in order to achieve invariance against illumination and scaling changes and blurring. LAP is based on the localized Fourier transform that provides information in both the time (position) and frequency domains [39]. In contrast with the 2D short term Fourier transform (STFT), the LAP applies the 1D Fourier transform locally over a 1D signal of image pixels that have been converted into the polar space with a fixed radius. The phase sign is analyzed to form 8-bit codewords where the distribution of their decimal values is used to describe textures.

In contrast with LPQ, the LAP applies the 1D Fourier transform locally over a 1D signal of image pixels that have been converted into the polar space with a fixed radius which increases the performance of the descriptor even on a very small image, e.g., a 3 × 3 image. LAP is the generic version of a previous descriptor [25] where the redundant information is discarded and includes multiple radii versions of the descriptor. Compared to the texture descriptor [24], LAP utilizes phase information instead of magnitude information which increases the discrimination power and robustness of the descriptor.

The remainder of this paper is organized as follows: in Section 2, related works of the current research are presented; in Section 3, detailed construction of the LAP method and its properties are presented; experimental studies and evaluations are described in Section 4; in Section 5, the application of the descriptor is presented and finally conclusions are given in Section 6.

2 Related works

2.1 Local binary patterns

Ojala et al. [26] proposed a robust way for describing pure local binary patterns (LBP) of texture in an image. In the original version, there are only 2⁸ = 256 possible texture units. The original 3 × 3 neighborhood, as shown in Fig. 1a, is thresholded by the value of the center pixel. If the neighboring pixel values are larger or equal to the center pixel, then the values are set to 1; otherwise, they are set to 0. The values of the pixels in the thresholded neighborhood, as shown in Fig. 1b, are then multiplied by the weights given to the corresponding pixels, as is shown in Fig. 1c; the results of this example are shown in Fig. 1d. Finally, the values of the eight pixels are summed to obtain the texture unit value for the 3 × 3 neighborhood.

Fig. 1

The basic LBP texture method

The LBP method is invariant to gray scales and the enhanced version of LBP [29] implements circular neighborhoods and uniform patterns. An image can be converted to its texture spectrum image by replacing the pixels’ gray level values with the values of the corresponding texture units. It is shown that the texture spectrum image takes on the visual character of the original image, and the image texture can be represented by the 256-bin LBP histogram for the frequency of the value of the texture units.

The extremely simple computations for constructing the the LBP make it very fast in classifying textures. However, a primary disadvantage of this is that the LBP method is sensitive to image degradation under blurring situations and it is sensitive to image rescaling because any interpolation applied in the image scaling changes the pixel values resulting in image quality degradation.

2.2 Local Fourier histogram

Zhou et al. [46] proposed a texture descriptor by using the magnitude of the 1D local Fourier transform with a 3 × 3 local window, as is shown in Fig. 2 and Ashan et al. compared this performance with others [1] as well as proposed the extended version of the method [2]. For each local window, a Fourier transform is obtained over the neighborhood from x(0) to x(7), as is shown in Fig. 2 which can be calculated by using the following formula:

$$ X(k)=\frac{1}{8}\displaystyle\sum\limits_{n=0}^7 x(n)e^{-\frac{{\pi}i}{4}kn} $$

(1)

where x(n) and X(k) are the coefficients in the spatial and frequency domains, respectively.

Fig. 2

A 3 × 3 window

From the Fourier transform, the magnitudes of the first five coefficients, |X(0)|, |X(1)|, ..., |X(4)| are used for the texture description and the computed coefficients are then normalized to take values from 0 to 255. Next, |X(0)| is linearly quantized into eight bins, and |X(1)| through |X(4)| are linearly quantized into sixteen bins. For describing the texture, all the eight bins of |X(0)| and the first eight bins of the remaining coefficients are used as the feature descriptor. As mentioned in [33], the magnitude contains less information about the image compared to the phase. Therefore, LFH only possesses less discrimination power than those methods using the phase of the image.

2.3 Local phase quantization

Ojansivu et al. [31] noticed that each coefficient of the Fourier transform with centrally symmetric 2D signals is always real-valued, and its phase is only a two valued function. Based on this property, a blur insensitive descriptor, named LPQ can be constructed using simple steps with 5 × 5 neighborhoods, as illustrated in Fig. 3. The coefficients are computed in the 5 × 5 neighborhood of the pixel for the lowest horizontal, vertical, and diagonal frequencies (a, 0); (0, a); (a, a); and (a, − a), respectively. For this case, the value of parameter a is set to 1. The imaginary and real parts of these four frequency coefficients are binary quantized, based on their sign, resulting in an 8-bit binary number, which is a decimal number between 0 and 255. The quantization can be made more efficient by decorrelating the frequency coefficients using the whitening transform before quantization. It is because information will be maximally preserved in scalar quantization if the coefficients are statistically independent. The one with the decorrelation is called the whitened LPQ whereas the one without the decorrelation is called the non-whitened LPQ. The extended version of the LPQ shows that it is also invariant to rotations [32].

Fig. 3

The LPQ method: the image illustrates the computation of the LPQ code for the gray pixel using a 5 × 5 neighborhood. The codes for every pixel are added to a histogram

LPQ is a good method for classifying blurred texture images, but it has some disadvantages such as its sensitivity to geometrical changes and its dependability on the vertical and horizontal information in each window. Because it is based on the short term Fourier transform (STFT), large samples are needed to produce relevant information of the input samples. With a small 3 × 3 window, its invariance to blurred images becomes less insensitive and its description capability also decreases. In addition, it takes a long time for LPQ to extract the texture feature because it needs to perform the Fourier transform for every row and column, and thus the computational time needed increases rapidly as the local window size grows.

3 The proposed method

3.1 Localized angular phase

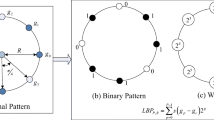
This section presents the proposed localized angular phase algorithm. As shown in Fig. 4, let the window be the subimage s(x, y) in the Cartesian coordinate where s(0, 0) pixel is at the center of the subimage. This 3 × 3 subimage is then converted into the fixed-radius polar space p(r, θ) using the following formula:

$$ p(r,\theta ) = s(x,y),r = 1,\theta = 0^\circ ,40^\circ ,\ldots,320^\circ, x = r\cos \theta ,y = r\sin \theta $$

(2)

Some s(x, y) points do not fall on the rectangular grid. These values need to be interpolated using bilinear interpolation given by [10]:

$$ s(x',y') = ax' + by' + cx'y' + d $$

(3)

where a, b, c and d are the four nearest neighbors of point s(x′, y′). Because r is fixed to 1, p(r, θ) can be seen as a 1D discrete signal with nine samples. We denote this discrete signal by p(n), n = 0,1,..., 8. The Fourier transform and inverse transform of p(n) are given by

$$ P(k) = \sum\limits_{n = 0}^{N - 1} {p(n){e^{ - \frac{{2\pi i}}{N}kn}}} $$

(4)

$$ p(n) = \frac{1}{N}\sum\limits_{k = 0}^{N - 1} {P(k){e^{ - \frac{{2\pi i}}{N}kn}}} $$

(5)

where N is the number of samples in p(n), and for 3 × 3 subimage, N is 9. Using (4), the discrete signals p(n) are converted to the Fourier coefficients P(k).

Fig. 4

The LAP algorithm

The reason to transform the image into polar space is to achieve invariance against image scaling, and blurring and to significantly reduce the number of elements to be transformed into the Fourier domain. By reducing the number of elements, the computational speed of LAP can be increased significantly. Moreover, by applying the Fourier transform in the polar space with fixed radius, invariance against blurring can be achieved.

After the Fourier transform, the values of nine complex coefficients P(0), P(1), ..., P(8) are obtained. The next step is to select some complex coefficients to extract the phase information. The P(0) is the DC value of the Fourier transform and contains no phase information; thus it is excluded from the selected coefficients. Because the image contains only real values, its Fourier transform becomes centrally symmetric where half of the coefficients are redundant.

The reason for using an angle interval of 40° is to obtain the appropriate odd number of samples. In previous research [25], eight circular neighbors were used as input for the Fourier transform. If the number of samples is even, e.g., eight samples, then the resulting complex coefficients will have another DC value. This extra DC value will reduce the number of useful non redundant complex coefficients; so, to avoid information loss, the LAP method uses nine samples, instead. This will result in only one DC value. Then, four non redundant complex coefficients are selected, whereby half of the complex coefficients are either P(1), P(2), P(3), P(4) or P(5), P(6), P(7), P(8), as is shown in the box in Fig. 4. The phase information can be extracted from these four complex coefficients by observing the signs of each real and imaginary part of the four complex coefficients, as is shown in Fig. 4. Let the C matrix contain the information of these four complex coefficients given by

$$\begin{array}{rll} C &=& \left[{\rm{Re}}\{X(4)\} {\rm{Im}}\{X(4)\} {\rm{Re}}\{X(3)\} {\rm{Im}}\{X(3)\} {\rm{Re}}\{X(2)\} {\rm{Im}}\{X(2)\}\right. \\ &&\left.{\rm{Re}}\{X(1)\} {\rm{Im}}\{X(1)\} \right] \end{array}$$

(6)

where matrix C is then quantized into 8-bit binary code by using the following formula:

$$ \arraycolsep=3pt b(k) = \left\{ \begin{array}{@{} cccc @{} } 1,{}{\rm{if}}{} C_k \ge 0 \\ 0,{\rm{otherwise}} \\ \end{array} \right. $$

(7)

where b(k) is the sign of each coefficient. By arranging b(1), b(2),...,b(7), the 8 bit binary code can be formulated, and a binomial factor is assigned as 2 for each b(k); hence, it is possible to transform (7) into a unique LAP number, given by

$$ LAP = \sum\limits_{k = 1}^8 {b(k)2^{k - 1} } $$

(8)

Based on (8), this LAP is a decimal value between 0 and 255 resulting from the 8-bit binary code. Next, a histogram is constructed with 256 dimensions using the LAP codes, and the histogram denotes the distribution. Finally, the texture descriptor is obtained from the histogram. A statistical approach using the distribution of the feature values is known to work well for micro-textures [11, 26].

The LAP is also a dense descriptor that analyzes the textons of the texture by locally extracting the texture feature on a moving window of a small size. Another advantage of using the polar space with a fixed radius is that the number of samples will not change much even when different radii are used. For example, 12 samples (angle interval 30°) are used for a LAP with radius 2 (window size 5 × 5), while 18 samples (angle interval 20°) are used for a LAP with radius 3 (window size 7 × 7). Similar to LAP with radius 1, complex coefficients from the second to the fifth of the 12 or 18 samples are used to create the binary code. With this characteristic, the LAP method does not significantly require more computation effort for a larger window. Note that an odd number of samples is not needed for the LAP with larger windows, such as 3 × 3 and 5 × 5, because the number of useful non redundant complex coefficients is sufficient.

Although both LPQ and LAP are using the phase, there are distinctive differences in the construction, and theoretical background between LAP and LPQ. LAP is based on the robustness of phase in polar space whereas LPQ is based on the phase in image space. LPQ uses discrete 2D Fourier transform on the local window whereas LAP uses polar Fourier transform with fixed radius on the local window. This polar Fourier transform with fixed radius can be simplified by performing 1D Fourier transform to the interpolated elements in the polar space with a fixed radius [3]. The Fourier transform elements of LPQ are depending on the number of pixels whereas the Fourier transform elements of LAP are not. It is because LAP utilizes polar transform that can interpolate unrestricted number of elements from any given pixels in a local window. This is the main reason of the effectiveness of LAP in robust texture classification even with small local window, e.g., 3 × 3 window. And lastly, the construction of LAP is based on invariance against image blurring, scaling, and illumination whereas LPQ is only based on invariance against image blurring. Due to the differences in theoretical background, one cannot assume that LAP is a variation of LPQ.

3.2 The properties of LAP

As mentioned in section 1, the LAP method is robust with respect to illumination variations, scaling changes and image blurring. This section explains each of these properties. Basically,the properties are obtained by exploiting two main elements: the phase and polar spaces.

3.2.1 The significance of LAP information

Images can be presented in the spatial domain or frequency domain; the spatial domain represents the normal image space, whereas the frequency domain represents the variation of brightness across the image. The frequency domain analysis can be performed by applying the Fourier transform to an image. A 2D Fourier transform and inverse Fourier transform of an image f(x, y) can be calculated using the following formula [10]:

$$ F(m,n)=\sum\limits_{x=0}^{M-1}\sum\limits_{y=0}^{N-1}{f(x,y)e^{-j\big(\frac{{2\pi xm}}{M}+{\frac{{2\pi yn}}{N}\big)}}} $$

(9)

$$ f(x,y)=\frac{{1}}{MN}\sum\limits_{m=0}^{M-1}\sum\limits_{n=0}^{N-1}{F(m,n)e^{j\big(\frac{{2\pi xm}}{M}+{\frac{{2\pi yn}}{N}\big)}}} $$

(10)

where f(x, y) is an image with size M × N. The magnitude and phase are calculated using the following formula:

$$ \mid F(m,n)\mid=\sqrt{{\rm{Re}}\{F(m,n)\}^{2}+{\rm{Im}}\{F(m,n)\}^{2}} $$

(11)

$$ \phi(m,n)=\tan^{-1}\left(\frac{{{\rm{Im}}\{F(m,n)\}}}{{\rm{Re}}\{F(m,n)\}}\right) $$

(12)

In order to transform the magnitude and phase back to the spatial domain, their values need to be combined by converting them into complex numbers. The formula to do this conversion is as follows:

$$ C(m,n)=|F(m,n)|e^{j\theta(m,n)} $$

(13)

where C(m, n) are 2D values containing complex numbers that have the same size as that of the original image f(x, y). By applying formula (10) to C(m, n), the original image f(x, y) is retained.

There has been much research on phase-only image analysis [13, 33], and these studies show that the information saved in the phase is more significant than that in the magnitude. The next example demonstrates the significance of information contained in the phase. The Fourier transform is applied to an image, as shown in Fig. 5a, and its magnitude values are obtained using (11). Next, the Fourier transform is applied to an image as shown in Fig. 5b, and its phase values are then obtained using (12). Using (13), the magnitude values of the image in Fig. 5a are combined with the phase values of the image in Fig. 5b and converted into complex values C(m, n). Using (10), these complex values C(m, n) are then converted back to the spatial space, and the resultant image c(x, y) is shown in Fig. 5c.

Fig. 5

a Barbara image used to generate magnitude. b Clown image used to generate the phase. c The resulting image by combining the magnitude from the Barbara image and phase from the Clown image

As can be seen in Fig. 5c, the reconstructed image closely resembles the image in Fig. 5b yet it has no visible similarity to the image in Fig. 5a even though the magnitude of the reconstructed image is obtained from the image in Fig. 5a. This shows how significant the phase information is compared to that from the magnitude.

3.2.2 Robustness against illumination change

An image can be seen as a 2D discrete signal, and the gray values correspond to the samples of the signal. As mentioned before, the phase is also invariant to illumination change [30, 31] because the phase does not change even if the samples of a signal are changed uniformly. For example, let the signal in Fig. 6a have nine samples, and Fig. 6b shows their phase values. The signal in Fig. 6c is uniformly modified from the original signal in Fig. 6a and d shows the phase values of the signal in Fig. 6c. As seen in Fig. 6d, the phase values of the uniformly modified signal produce the same values of the phase of the unmodified signal in Fig. 6b.

Fig. 6

An example of signals and their phases

For a gray image where the samples of the signal range from 0 to 255, an illumination change shifts the gray values in the image. Because the phase is invariant to shifts in the gray values, invariance can be easily obtained in the illumination changes. The LAP phase contains the overall information of the images because it is generated in the Fourier domain. Even if the gray value shift is nonlinear or random as is in natural illumination change, the phase is still able to extract sufficient information from the images. Another phase-based image feature also proved that the phase is invariant to illumination and contrast [16].

3.2.3 Robustness against blurring

Image blurring can be modeled as a linear shift invariant system in which the relation between an image f(x, y) and its observed image g(x, y) is given by

$$ g(x,y)=f(x,y)*h(x,y)+n(x,y) $$

(14)

where h(x, y) is the point spread function (PSF) of the system that causes the blurring, n(x, y) is the additive noise, and * denotes the 2D convolution operation [30]. If the noise is excluded, then formula (14) can be expressed in the frequency domain given by

$$ G(m,n)=F(m,n)\bullet H(m,n) $$

(15)

where G(u, v), F(u, v), and H(u, v) are the Fourier transforms of g(x, y), f(x, y), and h(x, y), respectively. The values are complex numbers and can be expressed in polar form given by

$$ \left| {G(m,n)} \right|\phi _g (m,n) = \left| {F(m,n)} \right|\phi _f (m,n) \bullet \left| {H(m,n)} \right|\phi _h (m,n) $$

(16)

where | ∘ |denotes the magnitude of the complex coefficient, and ϕ denotes the phase angle of the complex coefficient. It is understood that a signal convolved with any zero-phase signal such as the Gaussian blur, will produce another signal with the same phase as that of the original signal [33]. With this property, it is easy to achieve the blur invariant property just by using only the phase of a signal. Some other research [7] found that if a point spread function (PSF) h(x, y) is centrally symmetric, namely h(x, y) = h( − x, − y), then its Fourier transform H(m, n) is always real-valued, and as a consequence its phase is only a two-valued function, given by

$$ \arraycolsep=3pt {\phi _h}(m,n) = \left\{ \begin{array}{@{} cccc @{} } 0,{}{\rm{if}}{} H(m,n) \ge 0 \\ \pi,{}{\rm{if}}{} H(m,n) < 0 \\ \end{array} \right. $$

(17)

And because of the periodicity of the tangent

$$ tan\left[\phi _g (m,n)\right]=tan\left[\phi _g (m,n)+\phi _h (m,n)\right]=tan\left[\phi _f (m,n)\right] $$

(18)

where ϕ _f and ϕ _g are the phase of the original image and the blurred image, respectively. Thus, tan[ϕ _g (m,n)] is invariant to the convolution of the original image with any centrally symmetric PSF. The phase is the arctangent of the division between imaginary and real coefficients. Thus, the tangent of the phase will result in

$$ \tan[\phi _g (m,n)]=\tan \left[\tan^{-1}\left(\frac{{\rm{Im}}\{G(m,n)\}}{{\rm{Re}}\{G(m,n)\}}\right) \right]=\frac{{\rm{Im}}\{G(m,n)\}}{{\rm{Re}}\{G(m,n)\}} $$

(19)

where G(m, n) is the Fourier transform of the blurred image. By using the imaginary and real coefficients, we can also achieve the blur insensitive property, as applied by LAP. In the case of LAP, the Fourier transform is done in the Polar space, not in Cartesian space. However, robustness against blurring is still achievable. A blurred image g(x, y) is the result of a convolution operation between the original image f(x, y) and a PSF h(x, y) in the Cartesian space as shown in (14). This convolution can be modeled in the polar space using the following formula [3]:

$$ g(r,\theta)=f(r,\theta)*h(r,\theta)=\int^{\infty}_{0}\int^{2\pi}_{0}h(r,\theta)f(r-r_{0},\theta-\theta_{0})drd\theta $$

(20)

For a fixed-radius polar transformation, the convolution in the polar space becomes an angular convolution where the convolution is only carried out over the angular variable with a fixed value of r. This angular convolution is defined as:

$$ f(r,\theta)*_{\theta}h(r,\theta)=\frac{1}{2\pi}\int^{2\pi}_{0}f(r,\theta_{0})f(r,\theta-\theta_{0})d\theta $$

(21)

where the notation of * _θ is used to denote the angular convolution. This equation is proven to be a multiplication between the original image and PSF in the polar space [3] such that:

$${\rm{if}}{}\; g(r,\theta)=f(r,\theta)*_{\theta}h(r,\theta), \;{\rm{then}}{}\; G(\rho,\varphi)=F(\rho,\varphi)\bullet H(\rho,\varphi), $$

(22)

This is the same result obtained from the Fourier series of the 1D periodic function [3], which means that the values of the polar frequency vector (ρ, φ) can be seen as a 1D discrete signal. G(ρ, φ) can be expressed in polar form given by

$$ \left| {G\left(\overrightarrow w \right)} \right| = \left| {F\left(\overrightarrow w \right)} \right| \bullet \left| {H\left(\overrightarrow w \right)} \right| \;\rm{and}\; \phi _g \left(\overrightarrow w \right) = \phi _f \left(\overrightarrow w \right) + \phi _h\left(\overrightarrow w \right) $$

(23)

where $\left| \circ \right|$ denotes the magnitude of the complex coefficient, ϕ denotes the phase angle of the complex coefficients, and $(\overrightarrow w )$ denotes the polar frequency vector (ρ, φ).

If PSF in the spatial space h(x, y) is centrally symmetric, then the polar transform of PSF with fixed radius h(r, θ) will produce a uniform or symmetrical 1D discrete signal. Let x _h (n) be a 1D discrete signal that contains the uniform or symmetrical values of h(r, θ). The Fourier transform X _h (n) is always real-valued, and as a result its phase $\angle X_h$ is equal to zero. In the following Lemmas, 1 and 2, this property is verified.

Lemma 1

The Fourier Transform of a symmetrical signal results in a zero phase value.

Proof

Let x _h (n) be a symmetrical sequence, i.e., x _h ( − n) = x _h (n), n = 0,...,N − 1, and k = 0,...N − 1,

$$\begin{array}{rll} X_h (k) &=& \frac{1}{N}\sum\limits_{n = 0}^{N - 1} x_h (n)e^{\frac{{ - i2\pi nk}}{N}}\\ &=& \frac{1}{N}\sum\limits_{n = 0}^{N - 1} {x_h (n)\left( {\cos (\frac{{2\pi nk}}{N}) - i\sin \left(\frac{{2\pi nk}}{N}\right)} \right)}\\ &=& \frac{1}{N}\left[ \sum\limits_{n = 0}^{N - 1} {x_h (n)\cos \left(\frac{{2\pi nk}}{N}\right)} \right] \end{array}$$

Lemma 2

The Fourier Transform of a uniform signal results in a zero phase value.

Proof

Let x _h (n) be a uniform discrete signal of equal-strength impulses where

$$\begin{array}{rll} x_h (n) &=& \sum\limits_{n = 0}^{N - 1} {\delta (n)} ,n = 0,1,\ldots N - 1 \\ X_h (k) &=& \frac{1}{N}\sum\limits_{n = 0}^{N - 1} {x_h (n)e^{\frac{{ - i2\pi nk}}{N}} } \\ &=& \frac{1}{N}\sum\limits_{n = 0}^{N - 1} {x_h (n)e^{\frac{{ - i2\pi nk}}{N}} }\\ &=& \frac{1}{N}\sum\limits_{n = 0}^{N - 1} {e^{\frac{{ - i2\pi nk}}{N}} }\\ &=& \delta (n) \end{array}$$

□

From Lemma 1, it can be seen that the result is real valued because there is no imaginary part in the formula. The phase of this 1D signal is given by

$$ \angle X_h = \frac{{{\rm{Im}}\{ X_h (n)\} }}{{{\rm{Re}}\{ X_h (n)\} }} $$

(24)

So, if ${\mathop{\rm Im}\nolimits} \{ X_h (n)\}$ is equal to zero, then $\angle X_h$ is also equal to zero. Therefore, the phase of the symmetrical sequenced signal is zero. From Lemma 2, the Fourier transform of a uniform signal will only result in a single real value, so the phase $\angle X_h$ is also equal to zero. As seen, $\angle X_h$ is the phase of a PSF in polar phase, and it is equal to $\phi _h (\overrightarrow w )$. Because $\phi _h (\overrightarrow w )$ becomes zero with a centrally symmetric PSF h(x, y), (23) can be converted into

$$ \phi _g \left(\overrightarrow w \right) = \phi _f \left(\overrightarrow w \right)\;\,{}{\rm{if}}\; {}h(x,y)\; {}{\rm{is}}\; {}{\rm{centrally}}\; {}{\rm{symmetric}} $$

(25)

It is clearly seen that the phase of the blurred image in polar space is equal to the phase of the original image in polar space. In other words, the phase of the image in the polar space is invariant to blurring with a centrally symmetric PSF.

For example, consider a centrally symmetric PSF, such as the PSF of Gaussian blur, defined by

$$ h_G (x,y) = \frac{1}{{2\pi \sigma ^2 }}e^{ - \frac{{x^2 + y^2 }}{{2\sigma ^2 }}} $$

(26)

where σ is the standard deviation of the Gaussian distribution [38]. By replacing x, y with rsinθ and rcosθ, formula (26) can be converted into polar space, given by

$$ h_G (r,\theta ) = \frac{1}{{2\pi \sigma ^2 }}e^{ - \frac{{r^2 }}{{2\sigma ^2 }}} $$

(27)

As can be seen, θ is excluded in the right side of (27). This means that θ is uniform for each radius r. With a fixed radius polar transform, h _G (r, θ) has uniform values and its Fourier transform will result in a single real value so that its phase $\phi _h (\overrightarrow w )$ is equal to zero. By referring to (25), it is seen that the phase of the image in the polar space $\phi _h (\overrightarrow w )$ is invariant to blurring with a centrally symmetric PSF, such as the Gaussian blur PSF, average PSF, or disk PSF.

3.2.4 Robustness against scale change

A polar transform maps the circle Fig. 7a into the vertical lines shown in Fig. 7b and the lines at any angle through the center of the image shown in Fig. 7c into horizontal lines as shown in Fig. 7d, with rotation and scale invariance when the origin of the polar plane does not change [17]. In other words, rotating an image results in a vertical displacement (with modulo 2π) and a changing the image size results in a horizontal displacement. The distribution of LAP codes is robust to image translation, and this will affect LAP in achieving robustness against scale change.

Fig. 7

Concentric circles and radial lines in Cartesian space and Polar space

The scale-space theory is a framework for multi-scale signal representation with complementary motivations from physics and biological vision. It is a formal theory for handling image structures at different scales, by representing an image as a one-parameter family of blurred or smoothed or blurred images [45]. As our proposed LAP is robust to these smoothed images, theoretically, it also can be robust to the scale change.

As explained in this section, the phase is significant and robust to illumination, scaling, and blurring. We also showed that the phase is invariant to image blurring with centrally symmetric PSF by applying the polar transform with fixed radius that is implemented in the LAP algorithm. Because of these great advantages of phase, it is applied as the main feature in the LAP method in order to generate a robust and high discriminative texture descriptor. As we can see, the construction of LAP is based on a local analysis of the image. Because it is not based on global image analysis, it could not achieve 100% of the properties explained in this section, especially invariance against scaling, and blurring properties. However, LAP is still robust to illumination, scaling and blurring to a certain level where application utilizing the robust texture feature is pertinent.

4 Experimental studies and evaluations

4.1 Experimental environment and dataset

In the experimental studies, the consistency and classification accuracy of LAP are measured in terms of various conditions, such as normal, blurred, scaled, and gray shifted cases. Three other local-based texture descriptors, such as LPQ, LBP and LFH have been compared with the new proposed LAP method. A non-whitened LPQ is applied with window size 3 × 3 and a frequency parameter of a = 1, while the enhanced LBP [14] and LFH [1] methods use a neighborhood with a radius of one. The non-whitened LPQ is used to measure its raw performance without decorrelation because the proposed method is seen to perform well even without decorrelation. The experiment is conducted on computer with an Intel Core2Duo 2.33 GHz quad core processor and 2GB of main memory. All of the codes are written in MATLAB environment with Window XP operating system. The fft MATLAB function is used to generate LAP and LFH methods, while the fft2 MATLAB function is used to generate the LPQ method.

Three texture datasets are implemented in the experiment. The first one gives 40 different texture classes from Brodatz texture (http://www.ux.uis.no/~tranden/brodatz.html), and a set of Emphysema subregion images from Inha University Hospital, which have been used in previous works [24, 25]. For each texture, 16 sample images of size 50 × 50 are extracted. To imitate the diverse conditions of natural textures, each texture image is blurred using a Gaussian blur operation with a standard deviation of 0.5, which mimics the atmospheric turbulence [4], and blur radii of 1 and 2 pixels. Each class of texture contains 48 images. So, the total texture images used in these experiments is 1,968 images, including normal as well as two levels of blurred images. The second texture dataset is the KTH-TIPS [8] texture database where KTH-TIPS contains the planar samples of each of ten materials under varying illumination, pose and scale cases. The KTH-TIPS texture dataset contains ten texture classes with 810 images and the images are 200 × 200 pixels in size. The database contains images at nine scales spanning two octaves, under three different illumination directions, and three different poses. The last texture dataset implemented in the experiments is the Outex_TC_00000 test suite [28], which contains 24 texture classes with 480 images of size 128 × 128. Sample of images from the three dataset are shown in Fig. 8.

Fig. 8

The sample images from Brodatz, KTH-TIPS and Outex_TC_00000

4.2 Experiment set-up and results

This section describes the performance measure and the results of consistency and classification accuracy in terms of various conditions such as normal, blurred, scaled, and gray shifted cases. For texture classification, the k nearest neighbor (k-NN) is used, which has also been successfully utilized in texture classification [6, 31]. In these experiments, the k values used are 1, 3, 7, and 15. The classifier is trained and tested using appropriate sets of images to classify each query image. The Manhattan distance has been used to measure the distance between LAP, LBP, LPQ, and LFH equalized histograms. Herein, the classification accuracy can be calculated using the following formula:

$${\mbox{accuracy}}({\textrm \%} ) = \frac{{{\mbox{no}}{\mbox{. of correctly classif\/ications}}}}{{{\mbox{no}}{\mbox{. of total images}}}} $$

(28)

In the Brodatz texture image database, each texture class is randomly divided into four groups. Each group contains 12 images for each texture class. The same process is carried out for the KTH-TIPS database, where three groups contain 20 images for each texture class and one group contains 21 images for each texture class. As for the Outex_TC_00000 test suite, each group contains five images for each texture class. The classification is executed using the 4-fold cross-validation scheme. Classifications are performed four times, where on each time, one group of the dataset is used for testing and the remaining groups are used for training. The average accuracy of the classifications is recorded as the final accuracy. For the invariant texture classification experiments, the blurred, scaled, and gray shifted images are generated from images in the testing group of Outex_TC_00000 test suite.

4.2.1 Evaluation of invariance

This experiment evaluates the histogram consistency of each method, namely LAP, LPQ, LBP, and LFH with respect to various illuminations, scaling and blurring. For this test, 44 images from the USC-SIPI image database (http://sipi.usc.edu/database/database.cgi?volume=misc&image=12) are used. The images are rescaled into 128 × 128 and converted into 8-bit gray image for achieving feature extraction efficiency, as is shown in Fig. 9. Ten images are randomly selected from the image database and labeled as the original group. These images are then degraded in terms of changed illumination, blurring, and scale changed, and labeled as the modified group. For illumination changed images, the gray values of the images are shifted by adding and subtracting 10, 20, 30, and 50 gray values. For scale changed images, the images are rescaled using bilinear interpolation [10] with the scales of 0.5, 0.6, 0.7, 0.8, 0.9, 1.2, 1.4, 1.6, 1.8, and 2.0. And for blurred images, the images are blurred using Gaussian blurring with a 3 × 3 kernel. The standard deviations used for the Gaussian blurring are 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 1.1, 1.2, 1.3, and 1.4.

Fig. 9

The sample of images used in the consistency test

Standard deviation (SD) of the histogram is used to represent the normalized histogram of each method with a single feature value. These SD values are extracted from each image in both original and modified groups. The consistency of SD values between original and modified groups is measured by scrutinizing the p-value of the t-test. The significance level used in the t-test is 0.05. p-value that is lower than 0.05 validates significant difference between the original and modified groups, and thus proving the inconsistency of SD values between the original and modified groups. If the descriptor is robust to degraded images, then it will generate similar SD values for both original and modified images and will result in high p-value. The result of the t-test with respect to various illuminations, scaling, and blurring are shown in Table 1. The distributions of SD values for each method are normalized into the range between 0 and 1 by dividing them with the maximum SD values of each method and the box plots of the normalized distributions are shown in Fig. 10.

Table 1 t-test result of the illumination, blurring, and scale invariance test

Fig. 10

The box plot of SD values from both original and modified groups for each method in three categories (illumination, scaling, and blurring)

As we can see from the p-value of each test, LAP achieved a high p-value that is larger than the 0.05 significance level. This proves the consistency of the texture feature extracted using LAP. This also supports the proofs and related studies on the properties of LAP presented in previous section. In the scale invariance test, LPQ and LBP are not consistent since their p-values are lower than 0.05. In the blur invariance test, only LBP shows inconsistent SD values between original and blurred images. In the illumination invariance test, all of the descriptors show consistent SD values since all of them achieve high p-values. Each method uses the same input images. By comparing the variances of SD values for each method, one also can measure the consistency performance. As we can see, LAP achieves the lowest variance in all of the tests. The variance of LAP is about four times smaller than that of LPQ for each test. This shows that the SD values of LAP are consistent compared to that of LPQ. As shown in Fig. 10, the box plot shows that LAP is consistent because the distribution of the SD values generated by LAP is very narrow in each test whereas the LBP is not consistent because the distribution of SD values generated by LBP shows wide range.

4.2.2 Texture classification using the original datasets

Previous experiments only measure the consistency of the feature generated by LAP, LPQ, LBP, and LFH methods. In order to evaluate the discrimination power of the descriptor, texture classification experiment must to be conducted. In this subsection, the classification accuracies of the LAP, LPQ, LBP, and LFH methods are calculated and compared using the measures discussed in Section 4.1. The result of the texture classification using the Brodatz, KTH-TIPS, and Outex_TC_00000 datasets are shown in Table 2. For Brodatz textures, LAP performs the best with an average accuracy of 97.21% using 7-NN, while LFH performs the worst with 80.54% using 15-NN. For the KTH-TIPS textures, LAP still achieves the highest accuracy with 88.79% using 1-NN, and it can be seen that LBP performs the worst with 55.75% using 15-NN even though it is invariant to illumination changes. This is because LBP is very sensitive to pose, and scale changes. The KTH-TIPS dataset contains images with different illumination, pose and scales that make the classification of these images more difficult than those in the Brodatz and the Outex_TC_00000 textures. For the Outex_TC_00000 textures, the classification accuracy of the LAP and LPQ are the highest with 99.79% using 1-NN. On the other hand, LFH performs the worst because it only applies the magnitude. It can be seen that magnitude contains less information than the phase even though the combined approach of structural and statistics is implemented. Generally, the classification accuracies decrease as the number of nearest neighbor of the k-NN increases. However, the number of nearest neighbor of the k-NN does not significantly affects the classification accuracy for Brodatz and KTH-TIPS databases (p > 0.05) but only significantly affects the classification accuracy for Outex database (p < 0.05). This may be caused by the fine quality and the detailed structure of textures in Outex database where the images are captured using three CCD sensors [28].

Table 2 Average classification accuracy using Brodatz, KTH-TIPS, and Outex_TC_0000 databases

As for the overall performance, LAP and LPQ obtain high classification accuracy because of the significant information extracted from the phase information of the images. From this classification experiment, it can be seen that LAP does not just extract consistent features, but also extracts highly discriminating features that can be classified even with using a simple classifier. Even though LFH also extracts consistent feature, its feature is not highly discriminating. This means that LFH extracts a similar feature from different images that result in low classification accuracy.

4.2.3 Texture classification using modified datasets

To evaluate the discrimination power and consistency in terms of various illuminations, scaling, and blurring, texture classification using degraded textures is performed using the measures discussed in Section 4.1. This experiment uses Outex_TC_00000 because of its high classification accuracy shown in previous experiments. For this experiment, only the images in the testing group will be modified, and the images in the training group are the same as the original images. The 4-fold cross-validation scheme is conducted in this classification experiment, and the average accuracy of the 4-fold classification is recorded.

The image illumination is changed by adding and subtracting the amounts of gray values, which are 50 and 80. It is observed that the contrast is changed as the gray values are added and subtracted. As the values of the pixels grow beyond the gray value range, the values will be cut-off into the gray value range and change the contrast of the image. In other words, this experiment also evaluates the robustness of each descriptor when the contrast is changed. The image is rescaled using bilinear interpolation with scaling factors of 0.5, 0.75, 1.5, and 2. Finally, the image is blurred using Gaussian blur with standard deviation of 1. The blurring kernel sizes used in this experiment are 3 × 3, 5 × 5, and 7 × 7 sized kernels. Some samples images of modified textures are shown in Fig. 11.

Fig. 11

Sample of illumination changed, rescaled and blurred images of Outex_TC_00000

The average classification accuracies are shown in Table 3. Overall, the classification accuracies using 3-NN are the highest and the classification accuracies using 15-NN are the lowest. The result shows that LAP, LPQ, and LBP achieve persistent accuracies in classifying the textures with different illumination and contrast. Although LFH is proven to be invariant to gray displacement and linear transform [46], the LFH performance decreases for large values of gray value addition and subtraction. This is because the contrast changes and the transforms are no longer linear. By down-scaling the image, some information is distorted and mixed due to the aliasing effects. For the up-scaled images, it is seen that the image is blurred because, in up-scaling, the image signals are stretched far from their original signals and bilinear interpolation cannot perfectly estimate these stretched signal values. The average classification accuracy of LAP in classifying rescaled images is only decreased by 15% from the classification accuracy using the original image whereas the average classification accuracy of other methods is decreased by more than 50%. LBP performs the worst in the rescaled classification experiment due to its dependency on window size. The larger or smaller the scaling factor that is applied, the lower the classification accuracy is.

Table 3 Classification accuracy with illumination changed, rescaled, and blurred images

The peak signal-to-noise ratios (PSNR) have been calculated to measure the degradation of the blurred images. The PSNR of the blurred images with kernels 3 × 3, 5 × 5, and 7 × 7 are 23.6, 22.5, and 22.3 dB, respectively. Typical values for the PSNR in lossy image compressions are between 30 and 50 dB, so it can be seen that the blurred images are about 40% more degraded than the lossy compressed images by scrutinizing the PSNR values. The results show that the classification accuracy of LAP decreases slowly compared to the three other texture descriptors. With the blurring kernels of size 3 × 3, the LAP method achieves 92.3% of the classification accuracy, which is 6% less than the classification accuracy using the original texture image, whereas the classification accuracy of the LPQ, LBP, and LFH methods decreases by more than 30% of its original accuracy. One can see that LAP manages to get accuracy above 84% even with Gaussian blurring with 7 × 7 kernel size (blurring radius 3). It is because the polar transform in LAP is able to interpolate sufficient number of elements to achieve invariance against blurring. From the result, we can also see that LAP is applicable in classifying blurred images with various radii. Although LPQ is a blur invariant descriptor, the classification accuracy of LPQ is significantly lower than that of LAP because it uses 2D STFT that needs larger windows to increase its performance; in fact, a suitable window size for the LPQ method to perform blurring invariant effect is 7 × 7 [30]. The best overall classification using degraded textures from the Outex_TC_00000 databases for LAP, LPQ, LBP, and LFH are 91.26, 61.23, 35.79, and 33.47%, respectively. This high accuracy shows that LAP is able to produce a robust and high discrimination feature.

4.2.4 The efficiency evaluation

In this section, the efficiency of LAP, LPQ, LBP, and LFH is evaluated in terms of texture feature extraction by using 400 randomly selected texture images from Outex_TC_0000 (128 × 128 size images), Outex_TC_0001 (64 × 64 size images), and Outex_TC_0002 (32 × 32 size images) databases. Three windows of size 3 × 3, 5 × 5, and 7 × 7 are applied in the experiment, respectively. The feature extraction is repeated 100 times, and two ANOVA tests are conducted to see the significance of time difference in terms of different image sizes and different window sizes for each method, respectively.

The average computational time with respect to various image sizes of LAP, LPQ, LBP, and LFH are shown in Fig. 12 and the descriptive statistics is shown in Table 4. From the figure, it can be seen that the computational time increases as the window size increases. However the increase of computational time for LAP, LBP, and LFH are so small and almost not visible in Fig. 12. On the other hand, we can clearly see that the increase of computational time for LPQ is large, especially for the texture extraction of 128 × 128 size images. LBP consumes the shortest time to extract the texture feature. It is because LBP does not utilize the complex image transform and only uses addition and multiplication operations in its construction. This simple construction result in fast computation but high sensitivity against scaling, and blurring.

Fig. 12

The computational time of LAP, LPQ, LBP, and LFH with various images sizes and three different window sizes (left 3 × 3, center 5 × 5, right 7 × 7)

Table 4 Descriptive statistics of the computational time performance

Among the method that utilize Fourier transform, LAP achieves the fastest feature extraction time with overall average of 4.43 s. LFH consumes second shortest time because it needs to construct five histograms before generating the feature vector, whereas LAP only needs to generate one histogram. LPQ consumes the longest time because it requires a long computational time to calculate the 2D Fourier transform. It also can be perceived that the computational time increases as the size of the image increases. The computational time of LPQ increases quadratically compared to that of the other method due to the steeper incline of its line. From the both ANOVA tests, it can be concluded that the image size significantly affects the efficiency of each method for all 3 × 3, 5 × 5, and 7 × 7 windows (p < 0.01) and the window size significantly affects the efficiency of each method for all image sizes (p < 0.01). From this efficiency experiment, it can be observed that LAP is not only a robust and high discriminating descriptor, but it is also fast in extracting the texture feature.

5 Application examples

Image blurring frequently occurs when capturing real-world images due to the movement of the camera and object, and out-of-focus views. The illuminations in real-world images often change, and they depend on the weather. Finally, objects in the real-world are diverse in sizes. The range between the object and camera will also affect the size of the images that will be taken. To analyze images of different sizes, a multi-scale image analysis approach is needed. The scope of applications, such as plate number detection and recognition, content-based image retrieval (CBIR) of real-world images, computer-aided diagnosis (CAD) in the medical field, face detection and recognition, etc. demands integrated invariance against those degradations such as blurring, illumination, and scaling.

In this section, the applications of LAP in the field of pattern recognition and classification using real-world images are presented. The performance of LAP in terms of image retrieval, detection and classification is evaluated by using real-world blurred images, images in three different illuminations, and medical images with different resolutions and types. All the experiment set-ups used in this section are based on the measures discussed in Section 4.1.

5.1 Evaluation with real-world degraded images

5.1.1 Evaluation with real-world blurred images

To evaluate the performance of LAP using images with various real-world blurring effects, CBIR is conducted as presented in [42]. For this experiment, a set of 20 pairs of images (http://sipi.usc.edu/database/database.cgi?volume=misc&image=12) is used as the image database. Each pair has the same scene but different image blurring. The blur is caused by changing the acquisition parameters such as shutter time, aperture, and relative movement between the camera and object. The sample images are shown in Fig. 13. In order to extract the features from the images, each image is equally divided into 16 × 16 subimages. The texture feature is then extracted from each subimage. Finally, the texture features from each subimage are combined continuously into one long histogram. The retrieval is based on the Manhattan distance between the histograms of the query image and the images in the database.

Fig. 13

Example of images with real-world blurring effect: a, b motion blur, c change in focus from foreground to background, and d out-of-focus blur

The retrieval performance is assessed by using the ranked results of correct matches and the normalized average rank (NAR), which can be calculated using the following formula:

$$ NAR = \frac{1}{{N{N_R}}} \left( \displaystyle\sum\limits_{i = 1}^{N_R}{R_i} - \frac{{N_R}\left({N_R} + 1\right)}{2} \right) $$

(29)

where N is the number of images in the database, N _R the number of relevant images to the query, R _i is the rank at which the ith relevant image is retrieved. A NAR of zero indicates perfect results, and a NAR of 0.5 is equal to random retrieval. The average NAR over all queries is recorded as the average performance and indicated by ANAR, and the result is shown in Table 5. As shown in Table 5, LAP achieves the lowest ANAR indicating high retrieval performance. Most of the images are retrieved with rank 1, and the others are retrieved with more than rank 2. The low ANAR value of LAP shows that the retrieval rank is not large compared to that of other methods. From this test, it can be seen that LAP is robust to various blurring effects.

Table 5 Rank and ANAR of four methods using real-world blurred images

5.1.2 Evaluation with real-world illumination changed images

A texture classification test is conducted to evaluate the performance of LAP in analyzing images that are changed by the real-world illumination. The impact of illumination changes on the computed features of LAP are compared with that of other methods. For this purpose, the Outex_TC_00014 test suit is used as the dataset. This database contains images with different illuminations that were captured using three simulated illuminating sources: incandescent, horizon sunlight, and fluorescent tl84. Each illumination group contains 68 texture classes with 1,360 images of size 128 × 128. The sample images are shown in Fig. 14.

Fig. 14

Sample images in different illuminations: left incandescent, middle horizon and right tl84

3-fold cross-validation scheme is applied using three groups with different illuminations in the classification and the average classification accuracy is recorded as overall performance. The classification result is shown in Table 6. As it can be seen, the accuracy of LAP outperforms other methods with an average of 82.52%. Even though LBP and LFH are invariant to linear illumination change, they are not robust to nonlinear or random illumination change. Compared to LBP and LFH, the phase-based descriptors (LAP and LPQ) achieve high classification accuracies. This shows that phase-based descriptors are not also robust to constant illumination change, but also robust to nonlinear and random illumination change. This also supports the theoretical assertion discussed in Section 3.2.2.

Table 6 Classification accuracy with images in different illuminations

5.1.3 Evaluation with real-world scale changed images

In this section, the consistency of LAP in terms of texture feature extraction is evaluated by using the Emphysema regions with different image types and resolutions. A chest Computed tomography (CT) image can appear in different conditions depending on its type and dose. A high Resolution CT (HRCT) image has more details and contains more texture information of the lung. A standard CT image of the lung contains more homogeneous region than the textured region, and the image is blurrier than the HRCT image. Generally, a high radiation dose results in high-resolution images, while a lower dose leads to increased image noise and results in unsharp images [15]. The CT images can also appear in different resolution or scale depending on the machine and the physical attribute of the patient. Because of the various conditions of CT images, the texture information of the Emphysema subregion may vary. Therefore, a texture descriptor that robust to those variations is needed to extract consistent texture features from various types of CT images.

In this experiment, standard CT and HRCT images, which are gathered from Inha University Hospital, are applied. These standard CT and HRCT images are saved from the CT machine software in three different sizes which are 100%, 200%, and 400% of the original size, respectively. For each size, 30 Emphysema subregions, with a size of 30 × 30 pixels are randomly selected from the standard CT and HRCT images. There are now a total of 180 images of Emphysema subregions, and a sample of these images can be viewed in Fig. 15.

Fig. 15

Sample images of Emphysema subregion with respect to various CT image types and sizes

The SD values of histograms for LAP, LPQ, LBP, and LFH are calculated and shown in Fig. 16, and the descriptive statistics of SD values for these methods are shown in Table 7. As it can be seen, the SD values of LAP histogram are more uniform than those of LPQ, LBP and LFH. This means that the LAP histogram for each Emphysema subregion is consistent. Even though the distribution of SD values of LAP and LPQ are similar, but they are significantly different (t = −6.21, p < 0.01). From the table, it can be seen that LAP shows the lowest variance among all methods. The robustness of LAP in extracting texture feature from degraded textures enables LAP to extract a consistent texture feature from different types and sizes of CT images.

Fig. 16

The SD values of histogram for LAP, LPQ, LBP, and LFH with respect to various Emphysema subregions

Table 7 Descriptive statistics of various feature extraction methods

5.2 Application example in medical image analysis

LAP can be utilized in a lot of applications due to its robustness against blurring, illumination, and scaling. In this paper, one of the applications in the field of pattern recognition is presented. Recently, a number of computer-aided diagnosis (CAD) systems have been developed to help the radiologists to diagnose diseases. Using CAD systems to detect lung diseases such as emphysema, lung cancer, etc., is one of the important fields of medical image processing nowadays [34]. Feature extraction is one of the most important steps for recognizing abnormal regions in medical images. In the past decades, texture features such as the gray level difference method (GLDM) [44], the gray level run-length method (GLRLM) [9], the spatial gray level dependent method (SGLDM) [12], and the LBP have been widely used for medical image analysis. The combination of LBP and gray level generates a powerful texture descriptor in classifying three types of Emphysema and lung regions [35, 40].

With the characteristics of CT images, the pathological change of tissues in CT image is usually characterized with some local texture and brightness characteristics. The emphysema region is darker than the normal region and, its surface is smooth. Therefore, the combination of texture and brightness information will increase the classification of abnormal region. As shown in Fig. 17, a new Emphysema subregion representation is presented based on LAP. First, the histogram of LAP and gray value is constructed and combined into one long histogram. This feature dimension is too high, and implementing high dimensional feature vector will result in low efficiency in detecting and categorizing the abnormal region in CT images. In order to reduce the feature dimension, principle component analysis (PCA) is implemented. Ten significance principle components are selected as the final feature of the emphysema region or normal region.

Fig. 17

The algorithm to implement LAP for Emphysema region feature extraction

288 CT images are taken from Inha University Hospital, including 108 normal images and 180 emphysema ones. The size of the images is 1,024 × 1,024 and the gray value depth is 8-bit. Lung regions without vessels are first located and subregions are then obtained. The texture features are then extracted from the subregions covering more than 70% of the lung. 1,500 subregions, which are separated into two classes-1000 normal subregions and 500 emphysema subregions, are randomly selected for the following experiments. Fig. 18 shows some normal and emphysema subregions.

Fig. 18

First row, samples of Emphysema subregions, and second row, samples of normal subregions

To evaluate the performance of LAP, classification is performed between the Emphysema and normal subregions. We compared the classification performance of LAP with LBP and SGLDM. The algorithm used in extracting subregions feature for LBP and SGLDM is the same as the one implemented in literature [35]. The support Vector Machine (SVM) is used to classify the Emphysema and normal subregions. LAP and LBP are applied with a neighborhood radius of one while three directions of 0, 45, and 90° are applied to SGLDM. 100 normal subregions and 100 emphysema subregions are used to train the SVM. The remainder subregions (900 normal ones and 400 emphysema ones) are used for testing.

Table 8 shows the true positive (TP), true negative (TN), false positive (FP), false negative (FN), sensitivity, and specificity of the LAP, LBP, and SGLDM, respectively. As we can see, the performance of correctly classifying the emphysema regions of SGLDM depends on the feature extraction directions. The texture features extracted by LBP include multiple directions. Hence, LBP’s performance is the best compared with that of SGLDM from any direction. Since LAP extracts more information and is more robust than LBP, it achieves the best sensitivity and specificity performances compared to LBP and SGLDM. This shows that LAP demonstrates the technical viability for implementation in texture analysis applications, especially for computer-aided diagnosis.

Table 8 The classification performance of Emphysema and normal region

6 Conclusions and future work

In this paper, a versatile texture descriptor LAP based on the 1D local Fourier transform in the polar space has been presented. The phases of the four selected complex coefficients are uniformly quantized into 8-bit binary code which is then transformed into decimal numbers to generate a unique number between 0 and 255. The decimal values that are calculated locally for each local neighborhood are collected and transformed into a histogram, which describes the texture used for the classification.

Although LAP could not achieve perfect invariance due to the local approach, it is still robust to image blurring and scale changes, and it achieves high classification accuracy for those modified textures. By comparing the LAP, LPQ, LBP, and LFH methods, it is possible to see that LAP is reliable for classifying degraded textures. The application of LAP in image retrieval, classification, and CAD system also shows good results, and hence exhibits technical feasibility to be employed in real world applications or industries.

Real-world textures can occur at arbitrary spatial rotations, and this has inspired many studies regarding rotation invariance. Many methods apply the polar transform in order to get invariance to rotations by converting image rotation into image translation. The LAP method also utilizes the polar transform, but the phase is still variant to translations and future work in LAP intends to enhance the performance of the proposed method by extending it to be a rotation invariant texture descriptor.