An Approximate Solution to the Plastic Response of Clamped Sandwich Beams Under Concentrated Loading

In the present study, the bending behavior of a clamped sandwich beam subjected to a concentrated loading is investigated. An analytical model is developed considering the influence of localized deformation of the beam under the loading point on its overall bending. An approximate relationship for the load and local indention vs. global displacement is derived. The numerical results found by FEA models are in good agreement with theoretical solutions.

1. Introduction

Sandwich beams are usually made by bonding two thin face sheets to a lightweight core. The separation of face sheets by a core increases the bending rigidity of the structure with a minor increase in weight, producing an efficient structure for resisting bending and buckling loads [1]. The lightweight cores usually fall into two categories: incompressible and compressible ones. Fundamental analyses of sandwich beams with an incompressible core are presented by Allen [2] and Plantema [3]. For sandwich beams with a compressible core, the situation is more complicated, because their overall bending deformation is usually accompanied by a local indentation, especially when the sandwich beam is subjected to a concentrated load. The local indentation decreases the height of the core layer and reduces the load-carrying capacity of the whole structure. The coupling of local indentation and overall bending makes the analytical models of such beams much more complicated.

Some studies were focused on the effects of localized indentation on the bending responses of sandwich structures [4–9]. Frostig and Baruch [4] employed a high-order theory to model the bending behavior of a sandwich panel, in which the classical theory of thin plates was used for the face sheets and the three-dimensional elasticity theory for the core. Petras and Sutcliffe [5, 6] modeled the local deformation behavior of sandwich beams under three-point bending in a way similar to that employed in [4]. Steeves and Fleck [7] developed a model for the indentation response of sandwich structures with elastic faces and an elastic–plastic core in order to reveal the collapse mechanisms of sandwich beams loaded in three-point bending.

In the previous investigations, mainly an elastic behavior of the face sheet material was assumed. However, the plastic response of sandwich structures should also be taken into consideration, especially for the structures whose main design objective is energy absorption. To analyze the resistance of sandwich beams to a concentrated load, first the laws of local indentation and overall bending should be known. Xie et al. [10, 11] derived solutions for indentation forces and the shape functions of deformation based on the principle of virtual velocities. Both flat and cylindrical indenters were considered. Qin and Wang [12] also obtained a unified yield criterion for sandwich beams considering combinations of axial forces and bending moments. In this paper, the structural responses of sandwich beams are further studied considering the interaction of local indentation with their overall bending.

2. Statement of the Problem

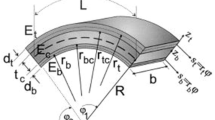
A clamped sandwich beam loaded at its midspan by a rigid cylindrical indenter with a radius R is considered, as shown in Fig. 1. The sandwich beam with a span 2L is composed of two face sheets of identical thickness h and a core of thickness c. The contact force between the indenter and face sheet is denoted by P.

Fig. 1

Schematic of a clamped sandwich beam loaded by a cylindrical line load: 1 — face sheets and 2 — core.

Under the action of the force P, a local indentation δ and an overall deflection ∆ occur in the sandwich beam, and the indenter displacement D is their sum, i.e.,

$$ D=\delta +\varDelta . $$

(1)

3. Contact Force due to Local Indentation

Approximate solutions to the local indentation responses of sandwich beams were derived by using the principle of virtual velocities [10]. In the analysis, sandwich beams were assumed continuously supported by a rigid plate to eliminate their global bending, and a perfectly plastic model was adopted for modeling the local indentation. A flat and a cylindrical line load were considered; the latter case is sketched in Fig. 2. The diameter of the contact region between the indenter and the upper face sheet is 2a, and the diameter of the deformation region of the top face sheet is 2ξ . Both of them vary with indentation depth δ. The final solutions for a, ξ and the indenter force P as functions of indentation depth δ are presented by the formulas

Fig. 2

Schematic of the indentation model.

$$ \begin{array}{l}a={\left[2{\sigma}_{\mathrm{p}}{R}^2\delta /\left({\sigma}_0h+{\sigma}_{\mathrm{p}}R\right)\right]}^{1/2},\hfill \\ {}\upxi ={\left[2\left({\sigma}_0h+{\sigma}_{\mathrm{p}}R\right)/{\sigma}_{\mathrm{p}}\right]}^{1/2}.\hfill \\ {}P=2b{\left[2\left({\sigma}_0h+{\sigma}_{\mathrm{p}}R\right){\sigma}_{\mathrm{p}}\delta \right]}^{1/2},\hfill \end{array} $$

(2)

where b is the width of the beam; σ ₀ and σ _p denote the flow stress of the face sheet material and the plateau stress of the foam core, respectively.

4. Yield Criterion for Overall Bending of Clamped Sandwich Beams

For large deflections of sandwich structures, the interaction between the bending moment and the axial force should be considered. Qin and Wang [11] presented a unified yield criterion for sandwich beams carrying an axial force and a bending moment:

$$ \begin{array}{c}\hfill \begin{array}{cc}\hfill \left|m\right|+\frac{{\left(\overline{\sigma}+2\overline{h}\right)}^2}{2\overline{\sigma}\overline{h}\left(1+\overline{h}\right)+{\overline{\sigma}}^2}{n}^2=1,\hfill & \hfill 0\le \left|n\right|\le \frac{\overline{\sigma}}{\overline{\sigma}+2\overline{h}},\hfill \end{array}\hfill \\ {}\hfill \left|m\right|+\frac{\left(\overline{\sigma}+2\overline{h}\right)\left[\left(\overline{\sigma}+2\overline{h}\right)\left|n\right|+2\overline{h}-\overline{\sigma}+2\right]\left(\left|n\right|-1\right)}{4\overline{h}\left(1+\overline{h}\right)+\overline{\sigma}}=0,\frac{\overline{\sigma}}{\overline{\sigma}+2\overline{h}}\le \left|n\right|\le 1,\hfill \end{array} $$

(3)

where $\overline{\sigma}$ =σ _p /σ ₀ , $\overline{h}$ = h / c , m = M / M _p , and n = N / N _p , with M and N being the plastic bending moment and the axial force, respectively. The fully plastic axial force and moment are

$$ \begin{array}{cc}\hfill {N}_{\mathrm{p}}=2{\sigma}_0bh+{\sigma}_{\mathrm{p}}bc,\hfill & \hfill {M}_{\mathrm{p}}={\sigma}_0bh\left(c+h\right)+\frac{1}{4}{\sigma}_{\mathrm{p}}b{c}^2.\hfill \end{array} $$

(4)

In particular, when the core strength is very low, i.e., $\overline{\sigma}\ll 2\overline{h}$ , the yield criterion, Eq.(3), is reduced to

$$ \begin{array}{cc}\hfill \left|m\right|+\left(\left|n\right|-1\right)\left(\frac{h}{c+h}\left|n\right|+1\right)=0,\hfill & \hfill \left|n\right|\le 1,\hfill \end{array} $$

(5)

and the fully plastic axial force and moment, Eq.(4), can be approximated by

$$ \begin{array}{cc}\hfill {N}_{\mathrm{p}}=2{\sigma}_0bh,\hfill & \hfill {M}_{\mathrm{p}}\hfill \end{array}={\sigma}_0bh\left(c+h\right). $$

When clamped beams are loaded by a concentrated force, the indentation occurs together with global bending, and the height of the core layer decreases. The height of the core layer at the midspan cross section becomes c – δ, and the yield criterion, Eq. (5), takes the form

$$ \begin{array}{cc}\hfill \left|m^{\prime}\right|+\left(\left|n\right|-1\right)\left(\frac{h}{c-\delta +h}\left|n\right|+1\right)=0,\hfill & \hfill \left|n\right|\le 1,\hfill \end{array} $$

(6)

where m ′ = M ′/M ^′_p , with M′ and M ^′_p the plastic and full bending moments at the midspan. The plastic moment at the midspan can be calculated by the formula M ^′_p  = σ ₀ bh(c − δ + h).

5. Analysis of the Bending Response Considering the Local Indentation

5.1. Deformation characteristic of the sandwich beam

In analyzing the overall deformation of clamped sandwich beam loaded at the midspan, only half of the structure is considered due to symmetry. Two plastic hinges with extensions e ₁ and e ₂ arise at the two ends of the one-half model, and the total extension e is the their sum of them,

$$ e={e}_1+{e}_2 $$

as shown in Fig. 3(a).

Fig. 3

Overall deformation of neutral axis of the clamped beam: transverse displacements (a) and cross-sectional forces and moments (b).

Based on the orthotropic plastic flow rule and the yield criterion given by Eq. (5), Qin and Wang [11] obtained the following relationship between the rates of extension $\overset{.}{\varepsilon }$ and curvature $\overset{.}{\kappa }$ of neutral surface of the sandwich beam:

$$ \begin{array}{cc}\hfill \frac{\overset{.}{\varepsilon }}{\overset{.}{\kappa }}=h\left|n\right|+\frac{1}{2}c,\hfill & \hfill \left|n\right|\le 1.\hfill \end{array} $$

So, the ratio of the extension rate at the supported ends to the rotational angular velocity can be written as

$$ \begin{array}{cc}\hfill \frac{{\overset{.}{e}}_1}{\overset{.}{\phi }}=\frac{{\overset{.}{\varepsilon}}_1}{\overset{.}{\kappa }}=h\left|n\right|+\frac{c}{2},\hfill & \hfill \left|n\right|\le 1.\hfill \end{array} $$

(7)

At the midspan, the height of core varies from c to c–δ, and the ratio of the extension rate ${\overset{.}{\varepsilon}}^{\prime }$ to that of curvature ${\overset{.}{\kappa}}^{\prime }$ can be expressed in the same way:

$$ \begin{array}{cc}\hfill \frac{{\overset{.}{\varepsilon}}^{\prime }}{{\overset{.}{\kappa}}^{\prime }}=h\left|n\right|+\frac{1}{2}\left(c-\delta \right),\hfill & \hfill \left|n\right|\le 1.\hfill \end{array} $$

Thus, the ratio of extension rate at the midspan to the rotational angular velocity becomes

$$ \begin{array}{cc}\hfill \frac{{\overset{.}{e}}_2}{\overset{.}{\phi }}=\frac{{\overset{.}{\varepsilon}}_2}{\overset{.}{\kappa }}h\left|n\right|+\frac{1}{2}\left(c-\delta \right),\hfill & \hfill \left|n\right|\le 1.\hfill \end{array} $$

(8)

Now, adding up the counterparts of both sides of Eqs. (7) and (8), we get the ratio of the rate of total extension $\overset{.}{e}$ to the rotational angular velocity $\overset{.}{\phi }$ in the form

$$ \frac{\overset{.}{e}}{\overset{.}{\phi }}=2h\left|n\right|+c-\frac{1}{2}\delta . $$

(9)

On the other hand, based on the geometric relationship between the axial extension and the transverse deflection, the total extension can be approximated as

$$ e\cong \frac{\varDelta^2}{2L}, $$

(10)

and the rotation angle of the neutral axis is

$$ \phi =\frac{\varDelta }{L}. $$

(11)

According to Eqs. (10) and (11), another formula for the ratio of the rate of the total extension $\overset{.}{e}$ to the rotational angular velocity $\overset{.}{\phi }$ of plastic hinge of the one-half construction can be obtained:

$$ \frac{\overset{.}{e}}{\overset{.}{\phi }}=\varDelta . $$

(12)

Comparing Eq. (9) with Eq. (12), we arrive at the relation for the dimensionless axial force n as a function of the overall deflection ∆ and the local indentation δ

$$ \left|n\right|=\frac{1}{2h}\left(\varDelta -c+\frac{1}{2}\delta \right). $$

(13)

5.2. Contact force due to global bending

Now, considering the internal forces on the neutral axis of the one-half structure, as shown in Fig. 3(b), we derive the moment equilibrium equation

$$ 2\left(M+{M}^{\prime}\right)- PL+2F\varDelta =0, $$

where F ≅ N for moderate deflections and the local indentation δ, which is assumed to be much smaller than the overall deflection ∆, is neglected. From this equation, the contact load due to global bending is expressed as

$$ P=2\left(M+{M}^{\prime }+N\varDelta \right)/L, $$

(14)

where, the influence of local indentation on the overall bending is neglected. Obviously, this is the same force which leads to the local indentation and global bending deformation of the sandwich beam under a concentrated load, which should satisfy Eqs. (2) and (14) simultaneously.

5.3. The two extreme boundary of yield condition

5.3.1. The dimensionless axial force equals zero. In the initial loading stage, the axial force is small, and the beam undergoes mainly flexural deformations. Thus, according to the yield criterion(Eqs. (5) and (6)), when the condition

$$ \begin{array}{cc}\hfill \left|n\right|=0,\hfill & \hfill \left|m\right|=\left|{m}^{\prime}\right|\hfill \end{array}=1 $$

(15)

is satisfied, the axial force and bending moment are reduced to

$$ N-0,M={M}_{\mathrm{p}},{M}^{\prime }={M}_{\mathrm{p}}^{\prime } $$

Inserting these values into Eq. (14), we obtain the critical load corresponding to the conditions of Eq. (15)

$$ {P}_0=2\left({M}_{\mathrm{p}}+{M}_{\mathrm{p}}^{\prime}\right)/L={P}_c\left[1-\frac{\delta_0}{2\left(c+h\right)}\right], $$

(16)

where the subscript 0 labels the values corresponding to Eqs. (15), and P _c is defined as

$$ {P}_c=4{M}_{\mathrm{p}}/L. $$

From Eqs. (1), (2), (13), and (16), the local indentation, indenter displacement, and contact force under the condition expressed by Eq. (15) are derived in the dimensionless form

$$ {\widehat{\delta}}_0=1+\frac{1}{2}{\alpha}^2-\frac{1}{2}\sqrt{4{\alpha}^2+{\alpha}^4}, $$

where

$$ \begin{array}{ccc}\hfill \alpha =\frac{4b}{P_c}{\left[c+h\left({\sigma}_0h+{\sigma}_{\mathrm{p}}R\right){\sigma}_{\mathrm{p}}\right]}^{1/2},\hfill & \hfill {\widehat{D}}_0=\frac{1}{2\left(1+\overline{h}\right)}+\frac{1}{2}{\widehat{\delta}}_0,\hfill & \hfill {P}_0={P}_c\left(1-{\widehat{\delta}}_0\right),\hfill \end{array} $$

and $\widehat{\delta}$ , and $\widehat{D}$ are the dimensionless local indentation and indenter displacement, respectively:

$$ \begin{array}{cc}\hfill \widehat{\delta}=\frac{\delta }{2\left(c+h\right)},\hfill & \hfill \widehat{D}=\frac{D}{2\left(c+h\right)}.\hfill \end{array} $$

5.3.2. The dimensionless axial force equals one. When the load increases and approaches another critical value, deformation of the structure is dominated by axial extension rather than bending. Now, the yield criterion is reduced to

$$ \begin{array}{cc}\hfill \left|n\right|=1,\hfill & \hfill \left|m\right|=\left|{m}^{\prime}\right|=0,\hfill \end{array} $$

and the corresponding contact force is

$$ {P}_1=2{N}_{\mathrm{p}}{\varDelta}_1/L. $$

(17)

Similarly, by combining Eqs. (1), (2), (13), and (17), the following relations for the local indentation δ ₁ and indenter displacement D ₁ are found:

$$ \begin{array}{cc}\hfill {\delta}_1=\frac{L}{\beta^2}{\left(-1+\sqrt{\omega}\right)}^2,\hfill & \hfill {D}_1=\frac{L}{\beta^2}\left(\omega -\sqrt{\omega}\right),\hfill \end{array} $$

where

$$ \begin{array}{cc}\hfill \beta =\frac{N_{\mathrm{p}}}{b{\left[2\left({\sigma}_0h+{\sigma}_{\mathrm{p}}L\right)\right]}^{1/2}},\hfill & \hfill \omega =1+2{\beta}^2\left(c+2h\right)/L.\hfill \end{array} $$

5.4. Three stages of structural response

5.4.1. Stage I: complicated elastic–plastic response. When δ < δ ₀ , i.e., D < D ₀ , the response of the sandwich beam is elastic–plastic. In terms of finite-element simulation results, the local indentation could be roughly assumed to increase linearly with indenter displacement,

$$ \delta =\frac{\delta_0}{D_0}D. $$

The local indentation and overall deformation arise from the same load. Inserting the previous relationship into Eq. (2), the contact force, with regard to the indenter displacement, is expressed as

$$ \begin{array}{cc}\hfill P=\alpha {P}_{\mathrm{c}}\sqrt{\frac{\delta_0}{D_0}\frac{D}{2\left(c+h\right)},}\hfill & \hfill D\le {D}_0.\hfill \end{array} $$

5.4.2. Stage II: full yielding under the action of bending moment and axial force. When δ ₀ < δ < δ ₁, i.e., D ₀ < D < D ₁, the sandwich beam yields under the combined effect of axial force and moment, controlled by Eqs. (5) and (6). The contact force can be deduced from Eqs. (5), (6), and (14) in the form

$$ \begin{array}{cc}\hfill P={P}_{\mathrm{c}}\left[1-\frac{\delta }{2\left(c+h\right)}+\frac{{\left(\varDelta -c+\delta /2\right)}^2}{4h\left(c+h\right)}\right],\hfill & \hfill {D}_0\le D\le {D}_1.\hfill \end{array} $$

(18)

The load causing the local indentation is the same leading to the overall deformation, hence the right sides of Eqs. (1) and (18) must be equal. In addition to Eq. (2), we finally obtain a relationship between the local indentation, the contact force, and the indenter displacement in the implicit form

$$ \begin{array}{c}\hfill \begin{array}{cc}\hfill \widehat{D}=\frac{1}{2\left(1+\overline{h}\right)}+\frac{1}{2}\widehat{\delta}+\sqrt{\frac{\overline{h}}{1+\overline{h}}\left(-1\alpha {\widehat{\delta}}^{1/2}+\widehat{\delta}\right)},\hfill & \hfill {\widehat{D}}_0\le \widehat{D}\le {\widehat{D}}_1,\hfill \end{array}\hfill \\ {}\hfill \begin{array}{cc}\hfill P=\alpha {P}_{\mathrm{c}}{\widehat{\delta}}^{1/2},\hfill & \hfill {\widehat{D}}_0\le \widehat{D}\le {\widehat{D}}_1.\hfill \end{array}\hfill \end{array} $$

With account of Eq. (13), we easily obtain that

$$ {D}_1-{D}_0=2h+\frac{1}{2}\left({\delta}_1-{\delta}_0\right). $$

Generally, the thickness of face sheets and the local indentation are both small compared with indenter displacement, so the difference D ₁–D ₀ is small too. Thus, the curve of the contact force between D ₀ and D ₁ can be well approximated by a straight line.

5.4.3. Stage III: postyielding dominated by the membrane force. When δ > δ ₁, i.e., D > D ₁ , the sandwich beam is dominated by the membrane force. The contact force, Eq. (14), can be reduced to

$$ \begin{array}{cc}\hfill P=2{N}_{\mathrm{p}}\varDelta /L,\hfill & \hfill D\ge {D}_1.\hfill \end{array} $$

(19)

Substituting Eq. (19) into Eq. (2), the local indentation δ and the contact force P are expressed as function of indenter displacement D in the form

$$ \begin{array}{c}\hfill \begin{array}{cc}\hfill \delta =D-\frac{L}{2{\beta}^2}\left(-1+\sqrt{1+4{\beta}^2\frac{D}{L}}\right),\hfill & \hfill D\ge {D}_1,\hfill \end{array}\hfill \\ {}\hfill \begin{array}{cc}\hfill P=\frac{N_{\mathrm{P}}}{\beta^2}\left(-1+\sqrt{1+4{\beta}^2\frac{D}{L}}\right)\hfill & \hfill D\ge {D}_1.\hfill \end{array}\hfill \end{array} $$

6. Results and Discussions

To verify the validity and applicability of the approximate solution, a finite-element analysis (FEA) of overall bending with local indentation of the clamped sandwich beam was performed using the FE code ABAQUS. Two sandwich configuration were considered, and results of the two cases are displayed in Figs. 4 and 6, respectively. The details of material properties used in the FEA model are given in [10].

Fig. 4

Predicted (1) and calculatrd (2) local indentation δ vs. indenter displacement D in cases 1 (a) and 2 (b). σ ₀ = 602.5 MPa, h = 1 mm, b = 15 mm, L = 100 mm, and R = 5 mm.

6.1. Deformation characteristics

From the analytical model, it can be found that the relationship between the local indentation and indenter displacement is the key to derive the contact force. According to the analytical solutions, the response process of the structure comprises three stages. The development of a local indentation δ with growing indenter displacement D is demonstrated in Fig. 4. It can be seen that the local indentation increases approximately linearly with indenter displacement when D < D ₀. The difference between the indenter displacements D ₁ and D ₀ is small, so the process in this stage can be approximated by a straight line. In the stage D > D ₀ , the predicted indentation is greater than the numerical result.

In the analytical model, we assumed the displacement field of overall deformation is distributed linearly, see Fig. 3. According to this assumption, the local indentation depth δ is equal to the change in magnitude of the midspan section. The indentation δ given by the FE model in Fig. 4 is actually the latter one. In fact, the displacement of neutral surface in the midspan is ∆ +δ/2 rather than ∆ due to the local indentation. Considering the fact that ∆ is greater than δ , we neglected the term δ/2 . On the other hand, we assumed that, as in a solid beam, a typical plastic hinge also comes into being in the sandwich beam. The FEA results shows us the difference between the foam sandwich construction and a solid beam, see Fig. 5. When a typical plastic hinge appears, a break angle arises in the midspan section, and the bottom edge stays at the point A. For the foam sandwich construction, this typical phenomenon did not take place, and the bottom edge ‘rose’ from the point A to B. In the case of local indentation, the rise of the bottom face may be equivalent to a descent of the upper face sheet. The indentation load depends on the relative indentation depth, so we can ‘drag’ the section from the point B to A keeping the section height unchanged. This ‘drag’ process has no effect on the local indentation response, but it increases the overall deflection ∆. On the whole, the main deviation of the analytical model stems from the overall deflection, but it is difficult to make any revision due to the uncertainty of position of the bottom face. To do this, further investigations are needed..

Fig. 5

Typical deformation pattern of a compressible core layer.

6.2. Load-carrying capacity

In the first stage, the materials of various parts undergo different elastic–plastic deformations. For a sandwich structure with thin face sheets and a weak core, a plastic indentation is apt to arise. According to the indentation response law presented above, the contact force can be determined from the relationship between the indentation depth and indenter displacement without considering the complicated elastic–plastic response of other parts. In the analytical model, this relationship was approximated as linear by the results of finite-element analysis. The contact load is better evaluated by this means, see Fig. 6. In the second stage, the response process is transitional and can be well approximated by a straight line. In the last stage, the response is dominated by the membrane force. The analytical solution overestimates the numerical result a bit.

Fig. 6

Predicted (1) and calculated (2) contact force P vs. indenter displacement D in cases 1 (a) and 2 (b). Initial data the same as in Fig. 5.

7. Conclusions

A clamped sandwich beam subjected to a concentrated load was analyzed including the effect of coupling of the local indentation with the overall bending. The local indentation decreases the load-carrying capacity of the construction and raises the difficulty of modeling the response of the structure.

Based on previous works and FEA results, the deformation characteristics and load resistance were derived. The structural response can be divided into three stages, and the second one is short. With the aid of FE simulation, it is found that the plastic hinge of sandwich beams have some difference from that of monolithic beams. This difference still further complicates the analysis of behavior of such structures and necessitates further investigations.