1 Introduction

Light-weight sandwich structures are of great interest for the design and manufacture of spacecraft, aircraft and marine vehicles, because of their high specific strength and stiffness. Furthermore, sandwich structures offer excellent damage tolerance in addition to low life cycle costs, see Lönnö [1]. In the development towards further weight savings modern sandwich structures are made with thin laminated composite face sheets and light-weight compliant cores such as polymeric foams or aramid nomex honeycomb. The use of a foam or low-strength honeycomb core rather than a metallic honeycomb is advantageous in terms of weight and manufacturing processes and resources. The major difference between a metallic honeycomb and a soft core is its flexibility in the vertical direction. This flexibility significantly affects behavior, especially under localized loads, and yields quite different behaviors as compared to other structures that have a stiff honeycomb core. The general approach assumes that the global buckling of the beam and the local buckling of the skins are uncoupled. The global buckling is defined by the solution of an equivalent beam, which incorporates the shear stiffness of the core in the flexural rigidity of the beam. Local buckling is determined by considering the isolated skins as a beam resting on elastic foundation provided by the core in the vertical direction. When a structure is subjected to compressive in-plane loads, the buckling phenomenon may occur and is distinguished via a rapid change in displacements due to an increment in loading process. Buckling resistance is an important factor which should be taken into consideration for design purposes. For the cases when loads are below the yield limit, buckling phenomenon is of high importance and have to be studied in elastic range.

Many researchers studied sandwich beams with honeycombed antiplane cores. Their basic assumption was that the longitudinal displacement is linear, i.e., that the section plane remains linear after deformation and that the vertical displacement is uniform through the depth of the core. Ogorkiewicz and Sayigh [2] described the behavior of the sandwich beam with a foam core as an ordinary beam with equivalent properties. A similar approach, which assumes that no interaction between the skins exists in the local buckling mode, was used by Bulson [3] and by Brush and Almroth [4]. This approach is satisfactory as long as the core is incompressible in the vertical direction. However, when a compressible type of core is considered, an interaction between the global and the local buckling mode exists, as well as collaboration between the two skins. Hence, the critical mode can be shifted from the global mode to the local one and vice versa. They replaced the sandwich structure with a high-order shear deformable beam but were unable to determine the local buckling modes as well as the imperfection effect on overall behavior. Hunt and Da Silva [5] used a different approach, based on energy methods and superposition of symmetrical and nonsymmetrical buckling modes. This approach is limited to specific configurations and to specific boundary conditions. Frostig and Baruch [6] and Frostig et al. [7], analyzed the sandwich beams with soft core with the aid of a superposition approach. Frostig and Baruch [8] presented the high-order buckling analysis of sandwich beams with transversely flexible core. Closed-form solutions are presented for simply supported beams with identical skins and only numerical results for other cases. Smith [9] yielded a unified analysis method based on two-dimensional elasticity theory for evaluation of bending, buckling and vibration of multilayer orthotropic sandwich beams and panels. Cheng et al. [10]. presented a method of continuous analysis for predicting the local delamination buckling load of the face sheet of sandwich beams. In a research by Bozhevolnaya and Kildegaard [11], a sandwich curved beam subjected to a uniform loading is experimentally investigated. Wang and Shenoi [12] performed an elasticity theory-based approach for delamination and flexural strength of curved layered composite laminates and sandwich beams. They also performed the analysis of curved sandwich beams with a focus on debonding and buckling/wrinkling of the faces [13]. Lyckegaard and Thomsen [14] formulated the buckling behavior of straight sandwich beams joined with curved sandwich beams loaded in pure bending using two different models. A two-dimensional mechanical model is developed by Ji and Waas [15] to predict the global and local buckling of a sandwich beam, using classical elasticity. Various methods of theoretical modeling of curved sandwich structures were recently reviewed [16, 17]. Thomsen and Vinson [18, 19], Lyckegaard and Thomsen [20, 21] and Skvortsov et al. [22] made analytical and numerical studies based on higher order sandwich beam theory of the junction between a curved and a straight sandwich beam incorporating other loading conditions.

In this paper, the governing equilibrium equations of a three layered sandwich curved beam in the von Karman sense are obtained. Two skins are formulated in the Euler–Bernoulli sense whereas the host layer is formulated by the two-dimensional elasticity equations. The pre-buckling deformations of the arch are obtained under the linear membrane pre-buckling deformations. Adjacent equilibrium criterion is used to establish the stability equations. A closed-form solution suitable for curved beams with both edges simply supported is developed which results in closed-form expression for the critical buckling pressures. Some numerical results are provided to study the effect of various involved parameters.

2 Geometry of problem and kinematic relations

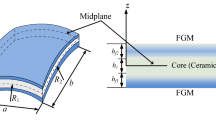
A cylindrically curved sandwich curved beam of the width b is considered. Geometry of the model with the system coordinates is shown in Fig. 1 [23].

Fig. 1
figure 1

Geometry of the mathematical model [23]

Full size image

In the following, indices t, b refer to the upper (top) and lower (bottom) faces of the beam, respectively. Each face has its own curvilinear coordinate system (zi, si), where

$$s_{i} = r_{i} \omega\quad \left( { i = t ,b } \right)$$
(1)

The local coordinate system (r,φ) for the core is polar and has its origin in the center of the beam curvature. The following assumptions form the basis of the presented model:

  1. 1.

    The length of the beam is of the order of its characteristic radii of curvature L ≤ R.

  2. 2.

    The faces may have a different thickness dt and db that are small in comparison with the length of the beam and radii of curvature. The faces are treated as thin elastic panels that follow Bernoulli assumptions.

  3. 3.

    The core of thickness tc is fully bonded with the faces. The core is considered to be a 2-D elastic medium with resistance to shear and radial stresses. In-plane (circumferential) stress in the core is neglected.

  4. 4.

    The kinematic relations of the core are those of small deformations and, therefore, they are linear. Note, that no a priori assumptions on the deformation fields through the thickness of the core are made.

  5. 5.

    Different kinds of the boundary conditions may be implemented for the various faces at the same section.

The radial w t, w b and circumferential u 0t, u 0b displacements of the centroids of the face elements are shown in Fig. 2a. In the polar coordinated system the kinematic relations for the faces read:

$$u_{i} = u_{0i} + z_{i} \beta_{i}$$
(2)
$$\varepsilon_{i} = \varepsilon_{0i} + z_{i} \kappa_{i} + \frac{1}{2}\beta_{i}^{ 2} \quad(i = t,b)$$
(3)
Fig. 2
figure 2

Displacement in the element of the sandwich beam (a); internal resultants in the differential elements of the faces, stresses at the interfaces and stresses in the differential element of the core (b) [23]

Full size image

In Eqs. (2) and (3) circumferential displacement u i and circumferential strain ɛ i are, respectively, in the skins that can be measured upwardly from the center of each skin and β i is equal to:

$$\beta_{i} = \frac{{u_{{ 0 {{i}}}} - w_{i}^{'} }}{{r_{i} }}$$
(4)

In the Eq. (3) ɛ 0i and κ i are the value of strain in the center of each skin and the curvature of each skins, respectively, and are equal to:

$$\varepsilon_{{ 0 {\text{i}}}} = \frac{{u_{{0i}}^{\prime } + w_{i} }}{{r_{i} }}$$
(5)
$$\kappa_{i} = \frac{{u_{\text{oi}}^{\prime } - w_{i}^{\prime \prime } }}{{r_{i}^{2} }}$$
(6)

In the mentioned relation, all derivations are considered based on ω angle. The appropriate kinematic relations for the core are

$$\varepsilon_{\text{rr}} = \frac{{\partial w_{c} }}{{\partial {\text{r}}}}$$
(7)
$$\gamma_{r\omega } = \gamma_{\text{sr}} = \frac{{\partial u_{c} }}{{\partial {\text{r}}}} - \frac{{u_{c} }}{r} + \frac{1}{r}\frac{{\partial w_{c} }}{\partial {\omega}}$$
(8)

Compatibility conditions emerge from the conditions of the fully bonded faces and core.

Upper interface:

$$\left. {w_{c} } \right|_{{{\text{r = }}r_{\text{tc}} }} = \left. {w_{\text{t }} } \right|_{{{\text{z = }}\frac{{ - d_{t} }}{2}}} \Rightarrow \left. {w_{c} } \right|_{{{\text{r = }}r_{\text{tc}} }} = w_{\text{t }}$$
(9)
$$\left. {u_{c} } \right|_{{{\text{r = }}r_{\text{tc}} }} = \left. {u_{\text{t }} } \right|_{{{\text{z = }}\frac{{ - d_{t} }}{2}}} \Rightarrow \left. {u_{c} } \right|_{{{\text{r = }}r_{\text{tc}} }} = u_{{ 0 {\text{t}}}} - \frac{{d_{t} }}{2}\beta_{t} \Rightarrow$$
$$\left. {u_{c} } \right|_{{{\text{r = }}r_{\text{tc}} }} = u_{{ 0 {{t}}}} - \frac{{d_{t} }}{{2r_{t} }}\left( {u_{{ 0 {{t}}}} - w_{t}^{\prime } } \right) \Rightarrow \left. {u_{c} } \right|_{{{\text{r = }}r_{\text{tc}} }} = u_{{ 0 {\text{t}}}} \left( { 1 { - }k_{t} } \right) + w_{t}^{\prime } k_{t}$$
(10)

In the recent relation k t is defined as follows:

$$k_{t} = \frac{{d_{t} }}{{2r_{t} }}$$
(11)

Lower interface:

$$\left. {w_{c} } \right|_{{{{r = }}r_{\text{bc}} }} = \left. {w_{b} } \right|_{{{\text{z = }}\frac{{d_{b} }}{2}}} \Rightarrow \left. {w_{c} } \right|_{{{\text{r = }}r_{\text{bc}} }} = w_{b}$$
(12)
$$\left. {u_{c} } \right|_{{{{r = }}r_{\text{bc}} }} = \left. {u_{\text{b }} } \right|_{{{\text{z = }}\frac{{d_{b} }}{2}}} \Rightarrow \left. {u_{c} } \right|_{{{\text{r = }}r_{\text{bc}} }} = u_{{ 0 {\text{b}}}} + \frac{{d_{b} }}{2}\beta_{b} \Rightarrow$$
$$\left. {u_{c} } \right|_{{{\text{r = }}r_{\text{bc}} }} = u_{{ 0 {\text{b}}}} + \frac{{d_{b} }}{{2r_{b} }}\left( {u_{{ 0 {\text{b}}}} - w_{b}^{\prime } } \right) \Rightarrow \left. {u_{c} } \right|_{{{\text{r = }}r_{\text{bc}} }} = u_{{ 0 {\text{b}}}} \left( { 1 { + }k_{b} } \right) - w_{b}^{\prime } k_{b}$$
(13)

In the recent relation k b is defined as follows:

$$k_{b} = \frac{{d_{b} }}{{2r_{b} }}$$
(14)

Stress resultants of the face sheets and stress field of the core are shown in Fig. 2b. The constitutive relations for the faces and for the core are

$$\sigma_{t}^{\left( k \right)} = Q_{{ 1 1 {\text{t}}}}^{\left( k \right)} \varepsilon_{t} ,\quad \sigma_{b}^{\left( k \right)} = Q_{{ 1 1 {\text{b}}}}^{\left( k \right)} \varepsilon_{b} ,\quad \sigma_{c} = E_{c} \varepsilon_{c} , \tau_{c} = G_{c} \gamma_{r \omega}$$
(15a–d)

We know

$$A_{ 1 1} {\text{ = b}}\mathop \sum \limits_{\text{k = 1}}^{N} \mathop \int \limits_{{z_{{k - 1}} }}^{{z_{k} }} Q_{ 1 1}^{\left( k \right)} {\text{dz}}$$
$$D_{ 1 1} {\text{ = b}}\mathop \sum \limits_{\text{k = 1}}^{N} \mathop \int \limits_{{z_{{k - 1}} }}^{{z_{k} }} Q_{ 1 1}^{\left( k \right)} z^{2} {\text{dz}}$$
(16a–b)

In the relation (16a–b), A 11 and D 11 are laminate membrane stiffness and flexural stiffness, respectively. \(Q_{{_{ 1 1} }}^{{({\text{k}})}}\) is the stiffness of each layer based on laminate angle such that

$$Q_{ 1 1}^{\left( k \right)} = Q_{ 1 1} { \cos }^{4} \theta { + }Q_{ 2 2} { \sin }^{4} \theta { + 2}\left( {Q_{ 1 2} + 2 {\text{Q}}_{ 6 6} } \right){ \sin }^{2} \theta {\text{cos}}^{2} \theta$$
(17)

that in the above relation we have

$$\begin{aligned} Q_{ 1 1} = \frac{{E_{ 1 1} }}{{ 1 { - }\nu_{ 1 2} \nu_{ 2 1} }} ,\quad Q_{ 2 2} = \frac{{E_{ 2 2} }}{{ 1 { - }\nu_{ 1 2} \nu_{ 2 1} }} \hfill \\ Q_{ 1 2} = \nu_{ 2 1} Q_{ 1 1} ,\quad Q_{ 6 6} = G_{ 1 2} \hfill \\ \end{aligned}$$
(18a–d)

N i and M i, respectively, are axial force and bending moment for each skins that are defined as follows:

$$N_{i} = \mathop \int \limits_{{\frac-{{d_{i} }}{2}}}^{{\frac{{d_{i} }}{2}}} {{b}}\sigma_{i} {\text{dz ,}}\;M_{i} = \mathop \int \limits_{{\frac{{ - d_{i} }}{2}}}^{{\frac{{d_{i} }}{2}}} b\sigma_{i} z{\text{dz}}\quad\left( {{i = t,b}} \right)$$
(19)

Now if we use kinematic relations (2), (3), (7), (8) and (16a–b)–(18a–d) with the simultaneous aid of constitutive relations (15a–d), Eq. (19) reaches one to

$$N_{i} = A_{ 1 1} \left[ {\frac{{u_{{0i}}^{\prime } + w_{i} }}{{r_{i} }} + \frac{1}{2}\left( {\frac{{u_{{ 0 {{i}}}} - w_{i}^{\prime } }}{{r_{i} }}} \right)^{2} } \right]$$
$$M_{i} = D_{ 1 1} \left( {\frac{{u_{{0i}}^{\prime } - w_{i}^{\prime \prime } }}{{r_{i}^{2} }}} \right)\quad\left( {i= t ,b} \right)$$
(20a–b)

2.1 The governing equations

The mathematical formulation starts with the derivation of the field equations and the appropriate boundary and continuity conditions. After that, the solution of the stress and the core’s deformation fields are obtained. Finally, governing equations expressed in terms of the displacement components are presented and solved analytically. The governing equations, the continuity requirements and the boundary conditions are derived via the variational principles, which minimize the total potential energy, as follows:

$$\delta \left( {U +V} \right) = 0$$
(21)

where in the Eq. (21) U, V and δ, respectively, are internal and external energies and the variation operator. The internal energy reads

$$\delta {\text{U = }}\mathop \int \limits_{{v_{\text{top}} }}^{ } \sigma_{t} \delta \varepsilon_{t} {\text{d}}v_{t} + \mathop \int \limits_{{v_{\text{bot}} }}^{ } \sigma_{b} \delta \varepsilon_{b} {\text{d}}v_{b} + \mathop \int \limits_{{v_{\text{core}} }}^{ } \left( {\tau_{c} \delta \gamma_{r} + \sigma_{c} \delta \varepsilon_{c} } \right) {\text{d}}v_{c}$$
(22)

where in the Eq. (22) σ t and ɛ t are the longitudinal normal stresses and strains in the upper skins and σb and ɛ b are the longitudinal normal stresses and strains in the lower skins; τ c and γ r are the shear stresses and strains in the core; σ c and ɛ c are the vertical normal stresses and strains in the core; v top, v bot, and v core are the volume of the upper and lower skins and the core, respectively; dv t , dv b and dv c are the volume of differential of the upper and lower skins and the core, respectively.

To obtain δU, the value of strains should be set from Eqs. (3), (7), (8) in (22).

$$\begin{aligned} \delta U{ = }\mathop \int \limits_{{v_{\text{top}} }}^{ } \sigma_{t} \delta \left( {\varepsilon_{{ 0 {\text{t}}}} + z_{t} \kappa_{t} + \frac{1}{2}\beta_{t}^{ 2} } \right) {\text{d}}v_{t} + \mathop \int \limits_{{v_{\text{bot}} }}^{ } \sigma_{b} \delta \left( {\varepsilon_{{ 0 {\text{b}}}} + z_{b} \kappa_{b} + \frac{1}{2}\beta_{b}^{ 2} } \right) {\text{d}}v_{b} + \hfill \\ \;\mathop \int \limits_{{v_{\text{core}} }}^{ } \left[ {\left( {\tau_{c} \delta \left( {\frac{{\partial u_{c} }}{{\partial {\text{r}}}} - \frac{{u_{c} }}{r} + \frac{1}{r}\frac{{\partial w_{c} }}{\partial }} \right)} \right) + \sigma_{c} \delta \left( {\frac{{\partial w_{c} }}{{\partial {\text{r}}}}} \right)} \right]{\text{d}}v_{c} \hfill \\ \end{aligned}$$
(23)

The value of differential of volume is equal to

$${\text{d}}v_{i} {\text{ = d}}A_{i} {\text{dx = bd}}z_{i} {\text{dx}}$$
(24)

where in the Eq. (24)

$${\text{dx = }}r_{i} {\text{d}}\varphi$$
(25)

The external energy reads

$$\delta V{ = - }\left[ {\mathop \int \limits_{\text{s = 0}}^{l} \left( {{\text{n}}_{t} \delta {\text{u}}_{{ 0 {\text{t}}}} + {\text{q}}_{t} \delta {\text{w}}_{t} - {\text{m}}_{t} \delta \beta_{t} } \right){\text{ds}}_{t} - } \right.\left. {\mathop \int \limits_{\text{s = 0}}^{l} \left( {{\text{n}}_{b} \delta {\text{u}}_{{ 0 {\text{b}}}} + {\text{q}}_{b} \delta {\text{w}}_{b} - {\text{m}}_{b} \delta \beta_{b} } \right){\text{ds}}_{b} } \right]$$
(26)

where in the Eq. (26) q i, n i, m i (i = t, b) are the external distributed vertical, horizontal, and bending moments, at upper and lower skins, u i, w i, β i (i = t, b) are the horizontal and vertical displacements and the rotation at upper and lower skins, respectively. The case of buckling in the curved beam would be set for the various status of loading. It is widely known that buckling may happen for the case of a beam subjected to uniformly distributed lateral load. In this regard also in this paper the buckling of curved beam in the presence of uniformly distributed load is analyzed. To this end other external loads that are introduced in relation (26) are considered equal to zero and consequently the work relation derived from external forces will be simplified as follows:

$$\delta {\text{V = }} - \mathop \int \nolimits q_{t} \delta w_{t} {\text{d}}A_{t} { = } - \mathop \int \limits_{0}^{{\alpha_{0} }} q_{t} \delta w_{t} {\text{br}}_{t} {\text{d}}\omega$$
(27)

In the relation (27), dA = brdφ is the area of a beam element. Substituting Eqs. (23) and (27) into (21) leads to

$$\begin{aligned} \delta \left( {U + V} \right) = 0 \Rightarrow \mathop \int \limits_{{v_{top} }}^{ } \sigma_{t} \delta \left( {\varepsilon_{0t} + z_{t} \kappa_{t} + \frac{1}{2}\chi_{t}^{ 2} } \right) {\text{d}}v_{t} + \mathop \int \limits_{{v_{bot} }}^{ } \sigma_{b} \delta \left( {\varepsilon_{0b} + z_{b} \kappa_{b} + \frac{1}{2}\beta_{b}^{ 2} } \right){\text{d}}v_{b} + \hfill \\ \mathop \int \limits_{{v_{\text{core}} }}^{ } \left[ {\left( {\tau_{c} \delta \left( {\frac{{\partial u_{c} }}{{\partial {\text{r}}}} - \frac{{u_{c} }}{r} + \frac{1}{r}\frac{{\partial w_{c} }}{\partial }} \right)} \right) + \sigma_{c} \delta \left( {\frac{{\partial w_{c} }}{{\partial {\text{r}}}}} \right)} \right]{\text{d}}v_{c} - \mathop \int \limits_{0}^{{\alpha_{0} }} q_{t} \delta w_{t} {\text{br}}_{t} {\text{d}}\omega = 0 \hfill \\ \end{aligned}$$
(28)

or

$$\mathop \int \limits_{0}^{{\alpha_{0} }} - N_{t}^{\prime } u_{{ 0 {\text{t}}}} {\text{d}}\omega + \left. {N_{t} u_{{ 0 {\text{t}}}} } \right|_{0}^{{\alpha_{0} }} + \mathop \int \limits_{0}^{{\alpha_{0} }} N_{t} w_{t} {\text{d}}\omega + \mathop \int \limits_{0}^{{\alpha_{0} }} \frac{{N_{t} }}{{r_{t} }}\left( {u_{{ 0 {\text{t}}}} - w_{t} } \right)u_{{ 0 {\text{t}}}} {\text{d}}\omega + \mathop \int \limits_{0}^{{\alpha_{0} }} \left( {\frac{{N_{t} }}{{r_{t} }}\left( {u_{{ 0 {\text{t}}}} - w_{t} } \right)^{\prime } } \right)^{\prime } w_{t} {\text{d}}\omega$$
$$- \left. {\frac{{N_{t} }}{{r_{t} }}\left( {u_{{ 0 {\text{t}}}} - w_{t} } \right)^{\prime } w_{t} } \right|_{0}^{{\alpha_{0} }} - \mathop \int \limits_{0}^{{\alpha_{0} }} \frac{{M_{t}^{\prime } }}{{r_{t} }}u_{{ 0 {\text{t}}}} {\text{d}}\omega + \left. {\frac{{M_{t} }}{{r_{t} }}u_{{ 0 {\text{t}}}} } \right|_{0}^{{\alpha_{0} }} - \mathop \int \limits_{0}^{{\alpha_{0} }} \frac{{M_{t}^{\prime \prime } }}{{r_{t} }}w_{t} {\text{d}}\omega + \left. {\frac{{M_{t}^{\prime } }}{{r_{t} }}w_{t} } \right|_{0}^{{\alpha_{0} }} - \left. {\frac{{M_{t} }}{{r_{t} }}w_{t}^{\prime } } \right|_{0}^{{\alpha_{0} }} +$$
$$\mathop \int \limits_{0}^{{\alpha_{0} }} - N_{b}^{\prime \,} u_{{ 0 {\text{b}}}} {\text{d}}\omega + \left. {N_{b} u_{{ 0 {\text{b}}}} } \right|_{0}^{{\alpha_{0} }} + \mathop \int \limits_{0}^{{\alpha_{0} }} N_{b} \delta w_{b} {\text{d}}\omega + \mathop \int \limits_{0}^{{\alpha_{0} }} \frac{{N_{b} }}{{r_{b} }}\left( {u_{{ 0 {\text{b}}}} - w_{b} } \right)\delta u_{{ 0 {\text{b}}}} {\text{d}}\omega + \mathop \int \limits_{0}^{{\alpha_{0} }} \left( {\frac{{N_{b} }}{{r_{b} }}\left( {u_{{ 0 {\text{b}}}} - w_{b} } \right)^{\prime } } \right)^{\prime } \delta w_{b} {\text{d}}\omega$$
$$+ \mathop \int \limits_{0}^{{\alpha_{0} }} \left( {\frac{{N_{b} }}{{r_{b} }}\left( {u_{{ 0 {\text{b}}}} - w_{b} } \right)^{\prime } } \right)^{\prime } \delta w_{b} {\text{d}}\omega - \left. {\frac{{N_{b} }}{{r_{b} }}\left( {u_{{ 0 {\text{b}}}} - w_{b} } \right)^{\prime } \delta w_{b} } \right|_{0}^{{\alpha_{0} }} - \mathop \int \limits_{0}^{{\alpha_{0} }} \frac{{M_{b}^{\prime } }}{{r_{b} }}\delta u_{{ 0 {\text{b}}}} {\text{d}}\omega + \left. {\frac{{M_{b} }}{{r_{b} }}u_{{ 0 {\text{b}}}} } \right|_{0}^{{\alpha_{0} }} - \mathop \int \limits_{0}^{{\alpha_{0} }} \frac{{M_{b}^{\prime \prime } }}{{r_{b} }}w_{b} {\text{d}}\omega$$
$$+ \left. {\frac{{M_{b}^{\prime } }}{{r_{b} }}\delta w_{b} } \right|_{0}^{{\alpha_{0} }} - \left. {\frac{{M_{b} }}{{r_{b} }}\delta w_{b}^{\prime } } \right|_{0}^{{\alpha_{0} }} + \mathop \int \limits_{0}^{{\alpha_{0} }} br_{\text{tc}} \left( { 1 { - }k_{t} } \right)\left. {\tau_{c} } \right|_{{r_{\text{tc}} }}^{ } \delta u_{{ 0 {\text{t}}}} {\text{d}}\omega - \mathop \int \limits_{0}^{{\alpha_{0} }} br_{\text{tc}} k_{t} \left. {\tau_{c}^{\prime } } \right|_{{r_{\text{tc}} }}^{ } \delta w_{t} {\text{d}}\omega + br_{\text{tc}} k_{t} \left. {\tau_{c} } \right|_{{r_{\text{tc}} }}^{{}} \delta \left. {w_{t} } \right|_{0}^{{\alpha_{0} }}$$
$$- \mathop \int \limits_{0}^{{\alpha_{0} }} br_{\text{bc}} \left( { 1 { + }k_{b} } \right)\left. {\tau_{c} } \right|_{{r_{\text{bc}} }}^{ } \delta u_{{ 0 {\text{b}}}} {\text{d}}\omega - \mathop \int \limits_{0}^{{\alpha_{0} }} br_{\text{bc}} k_{b} \left. {\tau_{c}^{\prime } } \right|_{{r_{\text{bc}} }}^{ } \delta w_{b} {\text{d}}\omega {\text{ + b}}r_{\text{bc}} k_{b} \left. {\tau_{c} } \right|_{{r_{\text{bc}} }}^{ } \delta \left. {w_{b} } \right|_{0}^{{\alpha_{0} }}$$
$$- \frac{\partial }{\partial r}\mathop \int \limits_{\omega }^{ } \mathop \int \limits_{r}^{ } \frac{\partial }{\partial r}\left( {{\text{br}}\tau_{c} } \right)u_{c} {\text{drd}}\omega - \mathop \int \limits_{\omega }^{ } \mathop \int \limits_{r}^{ } b\tau_{c} \delta u_{c} {\text{drd}}\omega + \mathop \int \limits_{r}^{ } \mathop \int \limits_{\omega }^{ } - {{ b}}\frac{{\partial \delta \tau_{c} }}{\partial }\partial w_{c} {\text{drd}}\omega + \mathop \int \limits_{r}^{ } b\tau_{c} \left. {\partial \delta w_{c} } \right|_{0}^{{\alpha_{0} }} {{dr}}$$
$$+ \mathop \int \limits_{0}^{{\alpha_{0} }} br_{\text{tc}} \left. {\sigma_{c} } \right|_{{r_{\text{tc}} }}^{ } \delta w_{t} {\text{d}}\omega - \mathop \int \limits_{0}^{{\alpha_{0} }} br_{\text{bc}} \left. {\sigma_{c} } \right|_{{r_{\text{bc}} }}^{ } \delta w_{b} {\text{d}}\omega - {\text{b}}\mathop \int \limits_{{}}^{ } \mathop \int \limits_{r}^{ } \frac{\partial }{{\partial {\text{r}}}}\left( {r\sigma_{c} } \right)\delta w_{c} {\text{drd}}\omega - \mathop \int \limits_{0}^{{\alpha_{0} }} q_{t} \delta w_{t} {\text{r}}_{t} {\text{d}}\omega { = 0}$$
(29)

To obtain the equilibrium equations, the coefficients of the nonzero parameters \(\delta u_{{ 0 {\text{t}}}} , \delta u_{{ 0 {\text{b}}}} , \delta {\text{w}}_{t} , \delta {\text{w}}_{b}\), \(\delta w_{c} ,\delta u_{c}\) are set equal to zero. By equaling the coefficients of \(\delta u_{{ 0 {\text{t}}}} , \delta u_{{ 0 {\text{b}}}} , \delta {\text{w}}_{t} , \delta {\text{w}}_{b}\), \(\delta w_{c} ,\delta u_{c}\) to zero, the following equilibrium equations are extracted.

$$\delta u_{{ 0 {\text{t}}}} : { - }N_{t}^{\prime } - \frac{{M_{t}^{\prime } }}{{r_{t} }} + \frac{{N_{t} }}{{r_{t} }}\left( {u_{{ 0 {\text{t}}}} - w_{t}^{\prime } } \right){{+ b}}r_{\text{tc}} \left( { 1 { - }k_{t} } \right)\left. {\tau_{c} } \right|_{{r_{\text{tc}} }}^{ } { = 0}$$
$$\delta u_{{ 0 {\text{b}}}} : { - }N_{b}^{\prime } - \frac{{M_{b}^{\prime } }}{{r_{b} }} + \frac{{N_{b} }}{{r_{b} }}\left( {u_{{ 0 {\text{b}}}} - w_{b}^{\prime } } \right) - {\text{b}}r_{\text{bc}} \left( { 1 { + }k_{b} } \right)\left. {\tau_{c} } \right|_{{r_{\text{bc}} }}^{ } { = 0}$$
$$\delta w_{t} :N_{t}^{ } - \frac{{M_{t}^{\prime \prime } }}{{r_{t} }} + \frac{1}{{r_{t} }}\left[ {N_{t}^{ } \left( {u_{{ 0 {\text{t}}}} - w_{t}^{\prime } } \right)} \right]^{\prime }+ {{b}}r_{\text{tc}} \left. {\sigma_{c} } \right|_{{r_{\text{tc}} }}^{ } - {{b}}r_{\text{tc}} \left. {k_{t} \tau_{c}^{\prime } } \right|_{{r_{\text{tc}} }}^{ } - {{b}}r_{t} q_{t} { = 0}$$
$$\delta w_{b} : N_{b}^{ } - \frac{{M_{b}^{\prime \prime } }}{{r_{b} }} + \frac{1}{{r_{b} }}\left[ {N_{b}^{ } \left( {u_{{ 0 {\text{b}}}} - w_{b}^{\prime } } \right)} \right]^{\prime }- {\text{ b}}r_{\text{bc}} \left. {\sigma_{c} } \right|_{{r_{\text{bc}} }}^{ } -{{ b}}r_{\text{bc}} k_{b} \left. {\tau_{c}^{\prime } } \right|_{{r_{\text{bc}} }}^{ } { = 0}$$
$$\delta u_{c} : - \frac{\partial }{\partial r}\left( {r\tau_{c} } \right) - \tau_{c} = 0 \Rightarrow r\frac{{\partial \tau_{c} }}{\partial r} + 2\tau_{c} = 0$$
$$\delta w_{c} : - \frac{{\partial \tau_{c} }}{\partial \varphi } - \frac{\partial }{\partial r}\left( {r\sigma_{c} } \right) = 0 \Rightarrow \frac{{\partial \sigma_{c} }}{\partial r} + \sigma_{c} + \frac{{\partial \tau_{c} }}{\partial \varphi } = 0$$
(30a–f)

According to Eq. (29), the boundary conditions in each end are as follows:

$$\delta u_{{ 0 {\text{b}}}} = 0 \quad {\text{or}}\quad N_{b}^{ } - \frac{1}{{r_{b} }}M_{b} { = 0}$$
$$\delta u_{{ 0 {\text{t}}}}= 0\quad {\text{or}}\quad N_{t}^{ } - \frac{1}{{r_{t} }}M_{t} { = 0}$$
$$\delta w_{b} = 0 \quad {\text{or}}\quad\frac{{M_{b}^{\prime } }}{{r_{b} }} - \frac{{N_{b} }}{{r_{b} }}\left( {u_{{ 0 {{b}}}} - w_{b}^{\prime } } \right){{ + b}}r_{\text{bc}} k_{b} \left. {\tau_{c} } \right|_{{r_{\text{bc}} }}^{ } { = 0}$$
$$\delta w_{t} = 0 \quad {\text{or}}\quad\frac{{M_{t}^{\prime } }}{{r_{t} }} - \frac{{N_{t} }}{{r_{t} }}\left( {u_{{ 0 {\text{t}}}} - w_{t}^{\prime } } \right) + {{b}}r_{\text{tc}} k_{t} \left. {\tau_{c} } \right|_{{r_{\text{tc}} }}^{ } { = 0}$$
$$\delta w_{b}^{{\prime}} = 0 \quad {\text{or}} \quad M_{b} = 0$$
$$\delta w_{b}^{{\prime}} = 0 \quad{\text{ or}} \quad M_{t} = 0$$
$$\delta w_{c}^{ } = 0\quad {\text{ or}}\quad \tau_{c} { = 0}$$
(31a–g)

We can compute the displacement field in the core precisely. The last two governing equations in the relation of (30a–f) is related to equilibrium equations of the core. Of the first equation we have

$$r\frac{{\partial \tau_{c} }}{{\partial {\text{r}}}} + 2\tau_{c} = 0 \Rightarrow 2\tau_{c} {\text{r + }}r^{2} \frac{{\partial \tau_{c} }}{{\partial {\text{r}}}}{ = 0 } \Rightarrow$$
$$\frac{\partial }{{\partial {\text{r}}}}\left( {r^{2} \tau_{c} } \right) = 0 \Rightarrow r^{2} \tau_{c} { = }\tau \left( \varphi \right) \Rightarrow \tau_{c} = \frac{\tau }{{r^{2} }}$$
(32)

That in the recent relation τ is only function of φ. By substituting τc from the last equation into Eq. (30a–f) we have

$$\frac{\partial }{{\partial {\text{r}}}}\left( {r\sigma_{c} } \right) + \frac{{\partial \tau_{c} }}{\partial \varphi }{ = 0 } \Rightarrow \frac{\partial }{{\partial {\text{r}}}}\left( {r\sigma_{c} } \right) + \frac{1}{{r^{2} }}\tau^{\prime } { = 0 } \Rightarrow {\text{r}}\sigma_{c} - \frac{{\tau^{\prime } }}{r} = C_{1}$$
(33)

In Eq. (33), C1 is the constant value of integration. Using the core constitutive relations (15a–d) we can write

$$rE_{c} \frac{{\partial w_{c} }}{{\partial {\text{r}}}} - \frac{{\tau^{\prime } }}{r} = C_{1} \Rightarrow \frac{{\partial w_{c} }}{{\partial {\text{r}}}} = \frac{1}{{E_{c} }}\left( {\frac{{C_{1} }}{r} + \frac{{\tau^{\prime } }}{{r^{2} }}} \right) \Rightarrow w_{c} = \frac{1}{{E_{c} }}\left( {C_{2} + C_{1} {\text{lnr}} - \frac{{\tau^{\prime } }}{r}} \right)$$
(34)

To obtain constant values C 1 and C 2 we use the boundary conditions in the upper and lower points of core. According to the compatibility condition in these two points we can write, at r = r tc:

$$w_{c} = w_{t} \Rightarrow w_{t} = \frac{1}{{E_{c} }}\left( {C_{2} + C_{1} { \ln }r_{\text{tc}} - \frac{{\tau^{\prime } }}{{r_{\text{tc}} }}} \right)$$
(35)

at r = rbc:

$$w_{c} = w_{b} \Rightarrow w_{b} = \frac{1}{{E_{c} }}\left( {C_{2} + C_{1} { \ln }r_{\text{bc}} - \frac{{\tau^{\prime } }}{{r_{\text{bc}} }}} \right)$$
(36)

By accomplishing the two equations simultaneously, the constants of C 1 and C 2 will be achieved as follows:

$$C_{1} = \frac{{E_{c} \left( {w_{b} - w_{t} } \right) + \tau^{\prime } \left( {\frac{1}{{r_{\text{bc}} }} - \frac{1}{{r_{\text{tc}} }}} \right)}}{{{ \ln }\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}}$$
$$C_{2} = E_{c} w_{b} + \frac{{\tau^{\prime } }}{{r_{\text{bc}} }} - \frac{{{ \ln }r_{\text{bc}} }}{{{ \ln }\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}}\left[ {E_{c} \left( {w_{b} - w_{t} } \right) + \tau^{\prime } \left( {\frac{1}{{r_{\text{bc}} }} - \frac{1}{{r_{\text{tc}} }}} \right)} \right]$$
(37a–b)

Defining the auxiliary parameter \(k_{0} = \frac{{r_{\text{tc}} - r_{\text{bc}} }}{{r_{\text{bc}} r_{\text{tc}} }}\) and inserting the constants C 1 and C 2 into Eq. (36), the normal deformation function of the core, w c, is obtained as

$$w_{c} = w_{b} + \frac{{\tau^{\prime } }}{{E_{c} }}\left( {\frac{1}{{r_{\text{bc}} }} - \frac{1}{r} + \frac{{{ \ln }\frac{r}{{r_{\text{bc}} }}}}{{{ \ln }\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}} {\text{k}}_{0} } \right) + \frac{{{ \ln }\frac{r}{{r_{\text{bc}} }}}}{{{ \ln }\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}}\left( {w_{b} - w_{t} } \right)$$
(38)

Recalling the definition of shear stress of the core from Eq. (15a–d) the tangential displacement of the beam may be written as

$$\tau_{c} = G_{c} \gamma_{r} \Rightarrow \gamma_{r} = \frac{{\tau_{c} }}{{G_{c} }} = \frac{1}{{r^{2} }}\frac{{\tau_{ } }}{{G_{c} }} \Rightarrow$$
$$\frac{{\partial u_{c} }}{{\partial {\text{r}}}} - \frac{{u_{c} }}{r} + \frac{1}{r}\frac{{\partial w_{c} }}{\partial \varphi } = \frac{1}{{r^{2} }}\frac{{\tau_{ } }}{{G_{c} }} \Rightarrow r\frac{\partial }{{\partial {\text{r}}}}\left( {\frac{{u_{c} }}{r}} \right) + \frac{1}{r}\frac{{\partial w_{c} }}{\partial \varphi } = \frac{1}{{r^{2} }}\frac{{\tau_{ } }}{{G_{c} }}$$
(39)

Upon substitution of Eq. (38) into Eq. (39) one may reach to

$$\frac{\partial }{{\partial {\text{r}}}}\left( {\frac{{u_{c} }}{r}} \right) = \frac{1}{{r^{3} }}\frac{{\tau_{ } }}{{G_{c} }} - \left\{ {\frac{{w_{b}^{\prime } }}{{r^{2} }} + \frac{\tau^{\prime \prime} }{{E_{c} }}\left[ {\left( {\frac{1}{{r^{2} r_{\text{bc}} }} - \frac{1}{{r^{3} }}} \right) + k_{0} \frac{{{\text{lnr} - {\text ln}}r_{\text{bc}} }}{{r^{2} { \ln }\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}}} \right] + \left( {w_{b}^{\prime } - w_{t}^{\prime } } \right)\left( {\frac{{{\text{lnr} - {\text ln}}r_{\text{bc}} }}{{r^{2} { \ln }\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}}} \right)} \right\}$$
(40)

Integrating Eq. (40) with respect to r in the interval [r, r tc] we will have

$$\frac{{u_{\text{tc}} }}{{r_{\text{tc}} }} - \frac{{u_{c} }}{r} = \frac{{{ - }\tau }}{{ 2 {\text{G}}_{c} }}\left( {\frac{1}{{r_{\text{tc}}^{2} }} - \frac{1}{{r^{2} }}} \right) + w_{b}^{\prime } \left( {\frac{1}{{r_{\text{tc}}^{ } }} - \frac{1}{{r^{ } }}} \right) + \frac{{\tau^{\prime \prime } }}{{r_{\text{bc}} E_{c} }}\left( {\frac{1}{{r_{\text{tc}}^{ } }} - \frac{1}{{r^{ } }}} \right)\frac{{\tau^{\prime \prime } }}{{ 2 {\text{E}}_{c} }}\left( {\frac{1}{{r_{\text{tc}}^{2} }} - \frac{1}{{r^{2} }}} \right) + \frac{{k_{0} }}{{E_{c} }}\tau^{\prime \prime } - \frac{1}{{{ \ln }\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}}$$
$$\left( {\frac{{{ \ln }r_{\text{tc}} }}{{r_{\text{tc}} }} - \frac{{{ \ln }r}}{r} + \frac{1}{{r_{\text{tc}} }} - \frac{1}{r}} \right) - \frac{{\tau^{''} }}{{E_{c} }}\frac{{{ \ln }r_{\text{bc}} }}{{r_{\text{bc}} }}\left( {\frac{1}{{r_{\text{tc}}^{ } }} - \frac{1}{{r^{ } }}} \right) + \frac{{\left( {w_{b}^{'} - w_{t}^{'} } \right)}}{{{ \ln }\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}}\left( {\frac{{{ \ln }r_{\text{tc}} }}{{r_{\text{tc}} }}} \right. - \left. {\frac{{{ \ln }r}}{r} + \frac{1}{{r_{\text{tc}} }} - \frac{1}{r}} \right) - \frac{{\left( {w_{b}^{'} - w_{t}^{'} } \right)}}{{{ \ln }\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}}\left( {\frac{1}{{r_{\text{tc}}^{ } }} - \frac{1}{{r^{ } }}} \right)$$
(41)

By solving the Eq. (41) in relation to u c, its distribution in the core will be as follows:

$$u_{c} = \frac{r}{{r_{\text{tc}}^{ } }}\left( { 1 { - }k_{t} } \right)u_{{ 0 {\text{t}}}} + \frac{r}{{r_{\text{tc}}^{ } }}w_{t}^{'} + \left( { 1 { - }\frac{r}{{r_{\text{tc}}^{ } }}} \right)w_{b}^{'} + \left( {w_{b}^{'} - w_{t}^{'} } \right)\left( {\frac{{r_{\text{tc}} {\text{ - r}}}}{{r_{\text{tc}} { \ln }\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}} + \frac{{{ \ln }\frac{r}{{r_{\text{bc}} }}}}{{{ \ln }\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}} + \frac{r}{{r_{\text{tc}}^{ } }}} \right) + \frac{{\tau^{''} }}{{E_{c} }}$$
$$\left[ {\left( {\frac{{r_{\text{tc}} {\text{ - r}}}}{{r_{\text{tc}} { \ln }\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}} + \frac{{{ \ln }\frac{r}{{r_{\text{bc}} }}}}{{{ \ln }\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}} + \frac{r}{{r_{\text{tc}}^{ } }}} \right)k_{0} \frac{{r_{\text{tc}} {\text{ - r}}}}{{r_{\text{tc}} r_{\text{bc}} }} - \frac{1}{2}\left( {\frac{{r_{\text{tc}}^{2} - r^{2} }}{{{\text{r }}r_{\text{tc}}^{2} }}} \right)} \right] - \frac{{\tau_{ } }}{{ 2 {\text{G}}_{c} }}\left( {\frac{{r_{\text{tc}}^{2} - r^{2} }}{{{\text{r }}r_{\text{tc}}^{2} }}} \right)$$
(42)

It should be considered that by solving the related equations to the core all parameters have been related to variable τ(φ). Therefore, a new equation should be replaced by two equations of core that have been written based on τ(φ). To obtain this equation we use the compatibility condition of (36) that in r = r bc we have

$$\left. {u_{c} } \right|_{{{\text{r = }}r_{\text{bc}} }} = u_{{ 0 {\text{b}}}} \left( { 1 { + }k_{b} } \right) - k_{b} w_{b}^{'}$$
(43)

By equaling Eqs. (42) and (43) we have

$$\begin{aligned} u_{{ 0 {\text{b}}}} \left( { 1 { + }k_{b} } \right) - k_{b} w_{b}^{\prime } = \frac{{r_{\text{bc}}^{ } }}{{r_{\text{tc}}^{ } }}\left( { 1 { - }k_{t} } \right)u_{{ 0 {\text{t}}}} + \frac{{r_{\text{bc}}^{ } }}{{r_{\text{tc}}^{ } }}w_{t}^{\prime } + \left( { 1 { - }\frac{{r_{\text{bc}}^{ } }}{{r_{\text{tc}}^{ } }}} \right)w_{b}^{\prime } + \left( {w_{b}^{\prime } - w_{t}^{\prime } } \right)\left( {\frac{{r_{\text{tc}} - r_{\text{bc}}^{ } }}{{r_{\text{tc}} { \ln }\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}}} \right. + \left. {\frac{{r_{\text{bc}}^{ } }}{{r_{\text{tc}}^{ } }}} \right) \hfill \\ + \frac{{\tau^{\prime \prime } }}{{E_{c} }}\left[ {\left( {\frac{{r_{\text{tc}} - r_{\text{bc}}^{ } }}{{r_{\text{tc}} { \ln }\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}} + \frac{{r_{\text{bc}}^{ } }}{{r_{\text{tc}}^{ } }}} \right)k_{0} + \frac{1}{{r_{\text{bc}}^{ } }} - \frac{1}{{r_{\text{tc}}^{ } }} - \frac{1}{{2r_{\text{bc}}^{ } }} + \frac{{r_{\text{bc}}^{ } }}{{2r_{\text{tc}}^{2} }} - \frac{{\tau_{ } }}{{ 2 {\text{G}}_{c} }}\left( {\frac{{r_{\text{tc}}^{2} - r_{\text{bc}}^{2} }}{{r_{\text{bc}}^{ } r_{\text{tc}}^{2} }}} \right){ = 0}} \right] \hfill \\ \end{aligned}$$
(44)

And after ordering relation (44) we will have

$$\begin{aligned} \left( { 1 { - }k_{t} } \right)u_{{ 0 {\text{t}}}} - \frac{{r_{\text{tc}}^{ } }}{{r_{\text{bc}}^{ } }}\left( { 1 { + }k_{b} } \right)u_{{ 0 {\text{b}}}} - \left[ {\left( { 1 { - }k_{t} } \right) + \frac{{k_{0} r_{\text{tc}}^{ } }}{{{ \ln }\frac{{r_{\text{bc}}^{ } }}{{r_{\text{tc}}^{ } }}}}} \right]w_{t}^{\prime } + \frac{{r_{\text{tc}}^{ } }}{{r_{\text{bc}}^{ } }}\left[ { 1 { + }k_{b} + \frac{{k_{0} r_{\text{bc}}^{ } }}{{{ \ln }\frac{{r_{\text{bc}}^{ } }}{{r_{\text{tc}}^{ } }}}}} \right]w_{b}^{\prime } - \frac{{k_{0} }}{{ 2 {\text{G}}_{c} }}\tau \left( {\frac{{r_{\text{tc}}^{ } + r_{\text{bc}}^{ } }}{{r_{\text{bc}}^{ } }}} \right) + \frac{{k_{0} }}{{ 2 {\text{E}}_{c} }}\tau^{\prime \prime } \hfill \\ \left( {2k_{0} \frac{{r_{\text{tc}}^{ } }}{{{ \ln }\frac{{r_{\text{bc}}^{ } }}{{r_{\text{tc}}^{ } }}}} + \frac{{r_{\text{tc}}^{ } + r_{\text{bc}}^{ } }}{{r_{\text{bc}}^{ } }}} \right){ = 0} \hfill \\ \end{aligned}$$
(45)

Equation (45) along with the four first equilibrium equations, will be the governing equations.

3 Pre-buckling analysis

This study analyzes the buckling of sandwich curved beam with flexible core in which its upper skin is subjected to uniform load of intensity q t. In the pre-buckling analysis of curved beam von Karman nonlinear terms can be disregarded. Because the raising of beam is not so great and consequently rotations of β t and β b are not so great and, therefore, the values of \(\beta_{t}^{ 2}\) and \(\beta_{b}^{ 2}\) may be ignored. In other words in the case of pre-buckling only linear analysis is sufficient, also in this case it is supposed that the beam contracts uniformly and, therefore, the components of displacement u 0t, u 0b and u c in the pre-buckling case can be disregarded (Figs. 3, 4).

Fig. 3
figure 3

Curved sandwich beam with simply supported boundary condition subjected to uniform load [24]

Full size image
Fig. 4
figure 4

Schematic of pre-buckling path and buckled form. A homogeneous curved beam with simply supported type of the boundary condition subjected to uniform load [24]

Full size image

According to the assumptions and using superscript of zero for pre-buckling case, the stability equations in this case would be as follows (it should be considered that because of uniform contract of beam all of derivations would be deleted) [24].

$$\delta {\text{u}}_{{0{\text{t}}}} :- {\text{b}}r_{\text{tc}} \left( { 1 { + }k_{t} } \right)\left. {\tau_{c}^{0} } \right|_{{r_{\text{tc}} }}^{ } { = 0}$$
$$\delta {\text{u}}_{{0{\text{b}}}} :- {\text{ b}}r_{\text{bc}} \left( { 1 { + }k_{b} } \right)\left. {\tau_{c}^{0} } \right|_{{r_{\text{bc}} }}^{ } { = 0}$$
$$\delta {\text{w}}_{\text{t}} :N_{t}^{0} + {\text{b}}r_{\text{tc}} \left. {\sigma_{c}^{0} } \right|_{{r_{\text{tc}} }}^{ } - {\text{b}}r_{\text{tc}} \left. {k_{t} \tau_{c}^{ ' 0} } \right|_{{r_{\text{tc}} }}^{ } - {\text{ b}}r_{t} q_{t} { = 0}$$
$$\delta {\text{w}}_{\text{b}} :N_{b}^{0} - {\text{b}}r_{\text{bc}} \left. {\sigma_{c}^{0} } \right|_{{r_{\text{bc}} }}^{ } - {\text{b}}r_{\text{bc}} \left. {k_{b} \tau_{c}^{ ' 0} } \right|_{{r_{\text{bc}} }}^{ } { = 0}$$
$$\delta \tau : \, \tau^{0 } = 0$$
(46)

Based on the last relation (46), we conclude that distribution of shear in the pre-buckling case will be equal to zero, by the way the two first equations would be satisfied and third and fourth equation would be simplified as follows:

$$N_{t}^{0} {\text{ + b}}r_{\text{tc}} \left. {\sigma_{c}^{0} } \right|_{{r_{\text{tc}} }}^{ } {\text{ = b}}r_{t} q_{t}$$
$$N_{b}^{0} - {\text{b}}r_{\text{bc}} \left. {\sigma_{c}^{0} } \right|_{{r_{\text{bc}} }}^{ } { = 0}$$
(47a–b)

To estimate the value of stress of \(\sigma_{\text{c}}^{0}\) we use the relation \(\sigma_{\text{c}}^{0} \; = \;E_{\text{c}} \varepsilon_{\text{rr}}^{ 0}\). According to the resulted distribution for \(w_{c}^{ }\) we can write

$$w_{c}^{0} = w_{b} + \frac{{{ \ln }\frac{r}{{r_{\text{bc}} }}}}{{{ \ln }\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}}\left( {w_{b}^{0} - w_{t}^{0} } \right) \Rightarrow \varepsilon_{\text{rr}}^{0} = \frac{1}{{r{ \ln }\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}}\left( {w_{b}^{0} - w_{t}^{0} } \right) \Rightarrow \sigma_{c}^{0} = \frac{{E_{c} }}{{r{ \ln }\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}}\left( {w_{b}^{0} - w_{t}^{0} } \right)$$
(48)

And consequently pre-buckling equations will be as follows:

$$N_{b}^{0} = \frac{{bE_{c} }}{{{ \ln }\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}}\left( {w_{b}^{0} - w_{t}^{0} } \right)$$
$$N_{t}^{0} = \frac {{-{\text{ b}}E_{c} }}{{{ \ln }\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}}\left( {w_{b}^{0} - w_{t}^{0} } \right){\text{ + b}}r_{t} q_{t}$$
(49a–b)

On the one hand, according to the stress results and regardless of β t and β b in the pre-buckling case we will have

$$N_{b}^{0} = A_{{ 1 1 {\text{b}}}} \frac{{w_{b}^{0} }}{{r_{b} }}$$
$$N_{t}^{0} = A_{{ 1 1 {\text{t}}}} \frac{{w_{t}^{0} }}{{r_{t} }}$$
(50a–b)

By equaling relations of (49a–b) and (50a–b), the following equations for \({\text{w}}_{t}^{0}\) and \({\text{w}}_{b}^{0}\) will be achieved.

$$A_{{ 1 1 {\text{b}}}} \frac{{w_{b}^{0} }}{{r_{b} }} = \frac{{bE_{c} }}{{{ \ln }\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}}\left( {w_{b}^{0} - w_{t}^{0} } \right)$$
$$A_{{ 1 1 {\text{t}}}} \frac{{w_{t}^{0} }}{{r_{t} }} = \frac{{- {\text{ b}}E_{c} }}{{{ \ln }\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}}\left( {w_{b}^{0} - w_{t}^{0} } \right){\text{ + b}}r_{t} q_{t}$$
(51a–b)

By solving two equations and two unknowns in the relation (51a–b) for \({\text{w}}_{t}^{0}\) and \({\text{w}}_{b}^{0}\) we will have

$$w_{b}^{0} = \frac{{br_{t} q_{t} }}{{\frac{{A_{{ 1 1 {\text{t}}}} }}{{r_{t} }}\left( { 1 { - }\frac{{A_{{ 1 1 {\text{b}}}} }}{{E_{c} br_{b} }} {\text{ln}}\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}} \right) + \frac{{A_{{ 1 1 {\text{b}}}} }}{{r_{b} }}}}$$
$$w_{t}^{0} = \frac{{br_{t} q_{t} \left( { 1 { - }\frac{{A_{{ 1 1 {\text{b}}}} }}{{E_{c} br_{b} }} {\text{ln}}\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}} \right)}}{{\frac{{A_{{ 1 1 {\text{t}}}} }}{{r_{t} }}\left( { 1 { - }\frac{{A_{{ 1 1 {\text{b}}}} }}{{E_{c} br_{b} }} {\text{ln}}\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}} \right) + \frac{{A_{{ 1 1 {\text{b}}}} }}{{r_{b} }}}}$$
(52a–b)

and pre-buckling forces are equal to,

$${{N}}_{t}^{0} = \frac{{br_{t} q_{t} \left( { 1 { - }\frac{{A_{{ 1 1 {\text{b}}}} }}{{E_{c} br_{b} }} {\text{ln}}\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}} \right)}}{{ 1 { - }\frac{{A_{{ 1 1 {\text{b}}}} }}{{E_{c} br_{b} }} {\text{ln}}\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }} + \frac{{r_{t} }}{{r_{b} }}\frac{{A_{{ 1 1 {\text{b}}}} }}{{A_{t} E_{t} }}}} = q_{t} n_{t}^{0}$$
$$N_{b}^{0} = \frac{{br_{t} q_{t} }}{{ 1 { + }\frac{{A_{{ 1 1 {\text{t}}}} }}{{A_{{ 1 1 {\text{b}}}} }}\frac{{r_{b} }}{{r_{t} }}\left( { 1 { - }\frac{{A_{{ 1 1 {\text{b}}}} }}{{E_{c} br_{b} }} {\text{ln}}\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}} \right)}} = q_{t} n_{b}^{0}$$
(53a–b)

4 Stability equations

For derivation of stability equations from the primary path the concept of adjacent equilibrium criterion is used. According to this criterion components of displacement field on primary equilibrium path are perturbed to establish a secondary equilibrium path. The amount of perturbations are nonzero zero. Otherwise, the structure will remain on its initial path. Denoting the amount of perturbations by superscript one, we will have a new stability path that its components will be as follows [24]:

$${\text{u}}_{0b} = {\text{u}}_{ 0b}^{ 0} + {\text{u}}_{ 0b}^{ 1}$$
$${\text{u}}_{0t} = {\text{u}}_{ 0t}^{ 0} + {\text{u}}_{ 0t}^{ 0}$$
$${\text{w}}_{b } = {\text{w}}_{b}^{0} + {\text{w}}_{b}^{1}$$
$$w_{t} = w_{t}^{0} + w_{t}^{1}$$
$$\tau = \tau^{0} + \tau^{1}$$
(54a–e)

Due to the increment in the displacement components, the stress resultants will perturb too. It should be considered that the values with superscripts one are very small and the second degrees will be disregarded. By the way stability equations for curved sandwich beam will be as follows:

$$- N_{b}^{{1^{'} }} - \frac{1}{{r_{b} }}M_{b}^{{1^{'} }} + \frac{{N_{b}^{0} }}{{r_{b} }}\left( {u_{{ 0 {{b}}}}^{1} - w_{b}^{{1^{'} }} } \right)- {{ b}}r_{\text{bc}} \left( { 1 { + }k_{b} } \right)\left. {\tau_{c}^{1} } \right|_{{r_{\text{bc}} }} { = 0}$$
$$- N_{t}^{{1^{'} }} - \frac{1}{{r_{t} }}M_{t}^{{1^{'} }} + \frac{{N_{t}^{0} }}{{r_{t} }}\left( {u_{{ 0 {\text{t}}}}^{1} - w_{t}^{{1^{'} }} } \right){{+b}}r_{\text{tc}} \left( { 1 { - }k_{t} } \right)\left. {\tau_{c}^{1} } \right|_{{r_{\text{tc}} }} { = 0}$$
$$N_{b}^{{1^{ } }} - \frac{1}{{r_{b} }}M_{b}^{1\prime \prime } + \frac{{N_{b}^{0} }}{{r_{b} }}\left( {u_{0b}^{1\prime } - w_{b}^{1\prime \prime } } \right) - {{b}}r_{\text{bc}} \left. {\sigma_{c}^{1} } \right|_{{r_{\text{bc}} }} - {{b}}r_{\text{bc}} \left. {k_{b} \tau_{c}^{1\prime } } \right|_{{r_{\text{bc}} }} { = 0}$$
$$\begin{aligned} \left( { 1 { - }k_{t} } \right)u_{{ 0 {\text{t}}}}^{1} - \frac{{r_{\text{tc}} }}{{r_{\text{bc}} }}\left( { 1 { + }k_{b} } \right)u_{{ 0 {\text{b}}}}^{1} - \left[ {\left( { 1 { - }k_{t} } \right) + \frac{{k_{0} r_{\text{tc}} }}{{{ \ln }\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}}} \right]w_{t}^{1\prime } + \frac{{r_{\text{tc}} }}{{r_{\text{bc}} }}\left[ { 1 { + }k_{b} + \frac{{k_{0} r_{\text{tc}} }}{{{ \ln }\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}}} \right]w_{b}^{1\prime } - \frac{{k_{0} }}{{2G_{c} }}\tau^{1} \left( {\frac{{r_{\text{tc}} + r_{\text{bc}} }}{{r_{\text{bc}} }}} \right) \hfill \\ + \frac{{k_{0} }}{{2E_{c} }}\tau^{1\prime \prime } \left( {2k_{0} \frac{{r_{\text{tc}} }}{{ {\text{ln}}\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}} + \frac{{r_{\text{tc}} + r_{\text{bc}} }}{{r_{\text{bc}} }}} \right){ = 0} \hfill \\ \end{aligned}$$
(55a–e)

The existent equations in the relation (55a–e) should be like an eigenvalue system with unknown coefficients \(N_{t}^{0}\) and \(N_{b}^{0}\). It should be stated that \(N_{t}^{1}\), \(M_{t}^{1}\), \(N_{b}^{1}\) and \(M_{b}^{1}\) are the value of perturbations of stress results that are calculated as follows:

$$N_{b}^{1} = A_{{ 1 1 {\text{b}}}} \left( {\frac{{u_{{ 0 {\text{b}}}}^{{1^{'} }} + w_{b}^{1} }}{{r_{b} }}} \right)$$
$$N_{t}^{1} = A_{{ 1 1 {\text{t}}}} \left( {\frac{{u_{{ 0 {\text{t}}}}^{{1^{'} }} + w_{t}^{1} }}{{r_{t} }}} \right)$$
$$M_{b}^{1} = D_{{ 1 1 {\text{b}}}} \left( {\frac{{u_{{ 0 {\text{b}}}}^{1\prime } - w_{b}^{1\prime \prime } }}{{r_{b}^{2} }}} \right)$$
$$N_{t}^{1} = D_{{ 1 1 {\text{t}}}} \left( {\frac{{u_{{ 0 {\text{t}}}}^{{1^{'} }} + w_{t}^{1} }}{{r_{t}^{2} }}} \right)$$
$$\sigma_{c}^{1} = \frac{1}{{r^{2} }}\tau^{{1^{'} }} + \frac{1}{r}\left( {\frac{{E_{c} }}{{ \ln \frac{{r_{bc} }}{{r_{tc} }}}}\left( {w_{b}^{1} - w_{t}^{1} } \right) + \frac{{\tau^{{1^{'} }} k_{0} }}{{ \ln \frac{{r_{bc} }}{{r_{tc} }}}}} \right)$$
(56a–e)

Boundary conditions in this analysis are considered to be simply supported on two ends. For two edges of \(\omega = {0, }\alpha_{0}\) these conditions are as

$$N_{b}^{1} + \frac{1}{r}M_{b}^{1} = 0$$
$$N_{t}^{1} + \frac{1}{r}M_{t}^{1} = 0$$
$$w_{b}^{1} = 0$$
$$w_{t}^{1} = 0$$
$$M_{b}^{1} = 0$$
$$M_{t}^{1} = 0$$
$${\text{w}}_{\text{c}}^{1} = 0$$
(57a–g)

According to what was obtained for \(w_{c}^{ }\) and according to the fact that \(w_{b}^{ }\) and \(w_{t}^{ }\) are equal to zero in two edges, the boundary conditions will be simplified as follows:

$$N_{b}^{1} { = 0}$$
$$N_{t}^{1} = 0$$
$$w_{b}^{1} = 0$$
$$w_{t}^{1} = 0$$
$$M_{b}^{1} = 0$$
$$M_{t}^{1} = 0$$
$$\tau^{{1^{'} }} { = 0}$$
(58a–g)

According to the definitions of \(N_{i}^{1}\) and \(M_{i}^{1}\) that are offered in the relation (56a–e), the above boundary conditions can be offered as follows:

$$u_{ 0b}^{{1^{'} }} = 0$$
$$u_{ 0t}^{{1^{'} }} = 0$$
$$w_{b}^{1} = 0$$
$$w_{t}^{1} = 0$$
$$w_{b}^{{1^{\prime \prime } }} = 0$$
$$w_{t}^{{1^{\prime \prime } }} = 0$$
$$\tau^{{1^{{9}} }} { = 0}$$
(59a–g)

To satisfy the boundary conditions (59a–g), functions \(u_{{ 0 {\text{b}}}}^{1}\), \(u_{{ 0 {\text{t}}}}^{1}\), \(w_{\text{b}}^{1}\), \(w_{\text{t}}^{1}\) and τ 1 will be considered as follows:

$$u_{0b}^{1} = U_{b} \cos \frac{n\pi \varphi }{{\alpha_{0} }}$$
$$u_{0t}^{1} = U_{t} \cos \frac{n\pi \varphi }{{\alpha_{0} }}$$
$$w_{b}^{1} = W_{b} \sin \frac{n\pi \varphi }{{\alpha_{0} }}$$
$$w_{t}^{1} = W_{t} \sin \frac{n\pi \varphi }{{\alpha_{0} }}$$
$$\tau_{ }^{1} = T_{t} \cos \frac{n\pi \varphi }{{\alpha_{0} }}$$
(60a–e)

Functions of relation (60a–e) are set in the stability equations. It is to mention that stability equations based on displacement components will be written as follows that for easy usage the superscript one is deleted.

$$- \frac{{A_{11b} }}{{r_{b} }}\left( {u_{0b}^{\prime \prime } + w_{b}^{\prime } } \right) - \frac{{D_{11b} }}{{r_{b}^{3} }}\left( {u_{0b}^{\prime \prime } - w_{b}^{\prime \prime \prime } } \right) + \frac{{N_{b}^{0} }}{{r_{b} }}\left( {u_{0b}^{ } - w_{b}^{\prime } } \right) - b\tau \frac{{\left( {1 + k_{b} } \right)}}{{r_{bc} }} = 0$$
$$- \frac{{A_{11t} }}{{r_{t} }}\left( {u_{0t}^{\prime \prime } + w_{t}^{\prime } } \right) - \frac{{D_{11t} }}{{r_{t}^{3} }}\left( {u_{0t}^{\prime \prime } - w_{t}^{\prime \prime \prime } } \right) + \frac{{N_{t}^{0} }}{{r_{t} }}\left( {u_{0t}^{ } - w_{t}^{\prime } } \right) + b\tau \frac{{\left( {1 - k_{t} } \right)}}{{r_{tc} }} = 0$$
$$\frac{{A_{11b} }}{{r_{b} }}\left( {u_{0b}^{\prime } + w_{b}^{ } } \right) - \frac{{D_{11b} }}{{r_{b}^{3} }}\left( {u_{0b}^{\prime \prime \prime } - w_{b}^{\prime \prime \prime \prime } } \right) + \frac{{N_{b}^{0} }}{{r_{b} }}\left( {u_{0b}^{ } - w_{b}^{\prime \prime } } \right) - br_{bc} \left\{ {\frac{{\tau^{\prime } }}{{r_{bc}^{2} }} + \frac{{E_{c} }}{{r_{bc} \ln \frac{{r_{bc} }}{{r_{tc} }}}}\left( {w_{b}^{ } - w_{t}^{ } } \right) + \frac{{\tau^{\prime } k_{0} }}{{ \ln \frac{{r_{bc} }}{{r_{tc} }}}}} \right\} - \frac{{bk_{b} }}{{r_{bc} }}\tau^{\prime } = 0$$
$$\frac{{A_{{ 1 1 {\text{t}}}} }}{{r_{t} }}\left( {u_{{ 0 {\text{t}}}}^{\prime } + w_{t}^{ } } \right) - \frac{{D_{{ 1 1 {\text{t}}}} }}{{r_{t}^{3} }}\left( {u_{{ 0 {\text{t}}}}^{\prime \prime \prime } - w_{t}^{\prime \prime \prime \prime } } \right) + \frac{{N_{t}^{0} }}{{r_{t} }}\left( {u_{{ 0 {\text{t}}}}^{ } - w_{t}^{\prime \prime } } \right)- {{b}}r_{\text{tc}} \left\{ {\frac{{\tau^{\prime } }}{{r_{\text{tc}}^{2} }} + \frac{{E_{c} }}{{r_{\text{tc}} { \ln }\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}}\left( {w_{b}^{ } - w_{t}^{ } } \right) + \frac{{\tau^{\prime } k_{0} }}{{ {\text{ln}}\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}}} \right\} - \frac{{bk_{t} }}{{r_{\text{tc}} }}\tau^{\prime } { = 0}$$
$$\begin{aligned} \left( {1 - k_{t} } \right)u_{0t}^{ } - \frac{{r_{tc} }}{{r_{bc} }}\left( {1 + k_{b} } \right)u_{0b}^{ } - \left[ {\left( {1 - k_{t} } \right) + \frac{{k_{0} }}{{ \ln \frac{{r_{bc} }}{{r_{tc} }}}}} \right]w_{t}^{'} + \frac{{r_{tc} }}{{r_{bc} }}\left[ {1 + k_{b} + \frac{{k_{0} r_{bc} }}{{ \ln \frac{{r_{bc} }}{{r_{tc} }}}}} \right]w_{b}^{' } - \frac{{k_{0} }}{{2G_{c} }}\left( {1 + \frac{{r_{tc} }}{{r_{bc} }}} \right)\tau + \frac{{k_{0} }}{{2E_{c} }}\tau^{''} \hfill \\ \times \left( {2k_{0} \frac{{r_{tc} }}{{ \ln \frac{{r_{bc} }}{{r_{tc} }}}} + 1 + \frac{{r_{tc} }}{{r_{bc} }}} \right) = 0 \hfill \\ \end{aligned}$$
(61a–e)

Therefore, if we set the solutions that have been used for functions of \(u_{ 0b}^{ } , u_{ 0t}^{ } , {\text{w}}_{b}^{ }\) and \(w_{t}^{ }\) in the relation (61a–e), the problem will be written as follows:

$$\left( {\left[ K \right]_{e} - {\text{q}}\left[ K \right]_{g} } \right)\left\{ {\begin{array}{*{20}c} {W_{t}^{ } } \\ {W_{b}^{ } } \\ {\begin{array}{*{20}c} {U_{t}^{ } } \\ {U_{b}^{ } } \\ T \\ \end{array} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \\ \end{array} } \right\}$$
(62)

That in relation (62), [K]e and [K]g respectively, show elastic and geometry stiffnesses. By definitions of \(\alpha_{n} = \frac{n\pi }{{\alpha_{0} }}\) elements of each of these two matrices can be written as follows:

$$K_{e}^{ 1 1} = \frac{{D_{{ 1 1 {\text{t}}}} }}{{r_{t}^{3} }}\alpha_{n}^{4} + \frac{{A_{{ 1 1 {\text{t}}}} }}{{r_{t} }} - \frac{{bE_{c} }}{{ {\text{ln}}\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}},\quad K_{e}^{ 1 2} = \frac{{bE_{c} }}{{ {\text{ln}}\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}}$$
$$K_{e}^{ 1 3} { = - }\frac{{D_{{ 1 1 {\text{t}}}} }}{{r_{t}^{3} }}\alpha_{n}^{3} - \frac{{A_{{ 1 1 {\text{t}}}} }}{{r_{t} }}\alpha_{n} ,\quad K_{e}^{ 1 4} { = 0} ,\quad K_{e}^{ 1 5} = \frac- {\text{ b}}{{r_{\text{tc}} }}\left[ {\left( { 1 { - }k_{t} } \right) + \frac{{k_{0} r_{\text{tc}} }}{{ {\text{ln}}\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}}} \right]\alpha_{n}$$
$$K_{e}^{ 2 1} = \frac{{bE_{c} }}{{ {\text{ln}}\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}},\quad K_{e}^{ 2 2} = \frac{{D_{{ 1 1 {\text{b}}}} }}{{r_{b}^{3} }}\alpha_{n}^{4} + \frac{{A_{{ 1 1 {\text{b}}}} }}{{r_{b} }} - \frac{{bE_{c} }}{{ {\text{ln}}\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}}$$
$$K_{e}^{ 2 3} { = 0} , K_{e}^{ 2 4} { = - }\frac{{D_{{ 1 1 {\text{b}}}} }}{{r_{b}^{3} }}\alpha_{n}^{3} - \frac{{A_{{ 1 1 {\text{b}}}} }}{{r_{b} }}\alpha_{n} , K_{e}^{ 2 5} = \frac{b}{{r_{\text{bc}} }}\left[ {\left( { 1 { + }k_{b} } \right) + \frac{{k_{0} r_{\text{bc}} }}{{ {\text{ln}}\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}}} \right]\alpha_{n}$$
$$K_{e}^{ 3 1} { = - }\frac{{D_{{ 1 1 {\text{t}}}} }}{{r_{t}^{3} }}\alpha_{n}^{3} - \frac{{A_{{ 1 1 {\text{t}}}} }}{{r_{t} }}\alpha_{n} ,\quad K_{e}^{ 3 2} { = 0}$$
$$K_{e}^{ 3 3} = \left( {\frac{{D_{{ 1 1 {\text{t}}}} }}{{r_{t}^{3} }} + \frac{{A_{{ 1 1 {\text{t}}}} }}{{r_{t} }}} \right)\alpha_{n}^{2} ,\quad K_{e}^{ 3 4} { = 0} ,\quad K_{e}^{ 3 5} = \frac{b}{{r_{\text{tc}} }}\left( { 1 { - }k_{t} } \right)$$
$$K_{e}^{ 4 1} { = 0}, K_{e}^{ 4 2} { = - }\frac{{D_{{ 1 1 {\text{b}}}} }}{{r_{b}^{3} }}\alpha_{n}^{3} - \frac{{A_{{ 1 1 {\text{b}}}} }}{{r_{b} }}\alpha_{n}$$
$$K_{e}^{ 4 3} { = 0}, K_{e}^{ 4 4} = \left( {\frac{{D_{{ 1 1 {\text{b}}}} }}{{r_{b}^{3} }} + \frac{{A_{{ 1 1 {\text{b}}}} }}{{r_{b} }}} \right)\alpha_{n}^{2} ,\quad K_{e}^{ 4 5} = \frac {- {b}}{{r_{\text{bc}} }}\left( { 1 { + }k_{b} } \right)$$
$$K_{e}^{ 5 1} = \frac{ -{ b}}{{r_{\text{tc}} }}\left[ {\left( { 1 { - }k_{t} } \right) + \frac{{k_{0} r_{\text{tc}} }}{{ {\text{ln}}\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}}} \right]\alpha_{n} , K_{e}^{ 5 2} = \frac{b}{{r_{\text{bc}} }}\left[ {\left( { 1 { + }k_{b} } \right) + \frac{{k_{0} r_{\text{bc}} }}{{ {\text{ln}}\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}}} \right]\alpha_{n}$$
$$K_{e}^{ 5 3} = \frac{b}{{r_{\text{tc}} }}\left( { 1 { - }k_{t} } \right) ,\quad K_{e}^{ 5 4} = \frac {-{ b}}{{r_{\text{bc}} }}\left( { 1 { + }k_{b} } \right)$$
$$K_{e}^{ 5 5} = \frac{{ - b}}{{2G_{c} }}\left( {\frac{{r_{\text{bc}} + r_{\text{tc}} }}{{r_{\text{bc}} r_{\text{tc}} }}} \right) - \frac{{bk_{0} }}{{2E_{c} }}\left( {\frac{{r_{\text{bc}} + r_{\text{tc}} }}{{r_{\text{bc}} r_{\text{tc}} }} + \frac{{2k_{0} }}{{ {\text{ln}}\frac{{r_{\text{bc}} }}{{r_{\text{tc}} }}}}} \right)\alpha_{n}^{2}$$
(63a–y)

that in derivation, the existent relations in the Eq. (63a–y), the last stability equation is multiplied in \(\frac{b}{{r_{\text{bc}} }}\) to set the members of the elastic matrix symmetric. Accordingly members of \(K_{g}^{ }\) are

$$K_{g}^{ 1 1} { = - }\frac{{n_{t}^{0} }}{{r_{t} }}\alpha_{n}^{2} ,\quad K_{g}^{ 1 2} { = 0}$$
$$K_{g}^{ 1 3} { = - }\frac{{n_{t}^{0} }}{{r_{t} }}\alpha_{n}^{ } ,\quad K_{g}^{ 1 4} = K_{g}^{ 1 5} { = 0}$$
$$K_{g}^{ 2 1} { = 0},\quad K_{g}^{ 2 2} { = - }\frac{{n_{b}^{0} }}{{r_{b} }}\alpha_{n}^{2}$$
$$K_{g}^{ 2 3} { = 0},\quad K_{g}^{ 2 4} = \frac{{n_{b}^{0} }}{{r_{b} }}\alpha_{n}^{ } ,\quad K_{g}^{ 2 5} = 0$$
$$K_{g}^{ 3 1} = \frac{{n_{t}^{0} }}{{r_{t} }}\alpha_{n}^{ } ,\quad K_{g}^{ 3 2} = 0$$
$$K_{g}^{ 3 3} { = - }\frac{{n_{t}^{0} }}{{r_{t} }},\quad K_{g}^{ 3 4} = K_{g}^{ 3 5} = 0$$
$$K_{g}^{ 4 1} = 0,\quad K_{g}^{ 4 2} = \frac{{n_{b}^{0} }}{{r_{b} }}\alpha_{n}^{ }$$
$$K_{g}^{ 4 3} { = 0},\quad K_{g}^{ 4 4} { = - }\frac{{n_{b}^{0} }}{{r_{b} }},\quad K_{g}^{ 4 5} = 0$$
$$K_{g}^{ 5 1} = K_{g}^{ 5 2} = K_{g}^{ 5 3} = K_{g}^{ 5 4} = K_{g}^{ 5 5} { = 0}$$
(64a–y)

By equaling determinant of the coefficient matrix of the problem there would be an eigen problem in which critical pressure by an eigenvalue and the buckle shape of beam will be like an eigenvector. As in the analysis of eigenvalue the eigenvector is not specified uniquely, the values of lateral rising and longitudinal displacement in the moment of buckling is not determined uniquely. For this reason the buckling shapes only show the schematic in the moment of buckling and lateral rising is in the moment show a schematic.

5 Results

In this section, using Matlab software and the theory offered in the previous sections, buckling of curved sandwich beam with simply supported boundary conditions is analyzed. The result of this method with accurate results from the theory of elasticity and Abaqus software are validated.

5.1 Numerical example

In this example, critical load of curved composite beam with a transversely flexible core and composite skins is estimated. The core is flexible and skins follow the classic theory. The type of skins is of graphite-epoxy A54/3501 that has the following mechanical and geometrical properties. The numerical results are shown in Figs. 5 and 6.

$$E_{ 1 1} { = 144} . 8 {\text{Gpa}} ,\quad E_{ 2 2} = E_{ 3 3} = 9. 6 5 {\text{Gpa}} ,\quad G_{ 1 2} = {\text{G}}_{ 1 3} { = 4} . 1 4 {\text{Gpa}} ,\quad G_{ 2 3} { = 3} . 4 5\;{\text{Gpa}}$$
$$\rho = 1389 . 2 3 {\text{kg/m}}^{ 3} ,\quad \nu_{ 1 2} = \nu_{ 1 3} { = 0} . 3 ,\quad \nu_{ 2 3} { = 0} . 4 8 ,\quad R = 0 . 8 {\text{m }}$$
$$r_{\text{bc}} = 0 . 7 {\text{m}} ,\quad r_{\text{tc}} = 0 . 9 {\text{m}} ,\quad r_{t} { = 0} . 9 { + 0} . 5 {\text{h}} , \quad r_{b} = 0 . 7 { - 0} . 5 {\text{h}} ,\quad b= 0 . 1 {\text{m}} ,\quad E_{c} = 100{\text{Mpa}}$$

where “h” is the thickness of the top and bottom skin. Numerical results for two values of thickness, i.e., one millimeter and two millimeters are offered.

Fig. 5
figure 5

Variation of critical buckling pressure versus curved beam angle

Full size image
Fig. 6
figure 6

Variation of critical buckling pressure versus curved beam angle

Full size image

The critical load values for different angles and skins thickness are calculated. The numerical values are shown in Tables 1 and 2 and depict excellent accuracy with those obtained from Abaqus software. In Figs. 5 and 6, the critical pressure for different layups and two different skin thicknesses is offered against the curved beam angles. The type of skins is of graphite-epoxy type. In the Fig. 5, results are for the skin thickness 1 mm and Fig. 6 for thickness 2 mm are shown. In both cases the values of core elasticity module and the Poisson ratio are, respectively, 100 Mpa and 0.3.

Table 1 The critical buckling load P cr (MN/m) of curved symmetric sandwich beam subjected to uniform load
Full size table
Table 2 The critical load buckling of curved sandwich beam symmetric subjected to uniform load P cr (MN/m)
Full size table

The radius of upper curve of core is equal to \(r_{\text{tc}} { = 0} . 9\, {\text{m}}\) and the radius of lower curve of core is equal to \(r_{\text{bc}} { = 0} . 7\, {\text{m}}.\)As can be seen, in each state of layup the load value in Fig. 6 is more than of Fig. 5. This is due to the increase in the thickness of skins which results in higher stiffness. As seen from the studied cases, layup of face sheets affects greatly on the critical buckling load and buckled shape.

Changes in the value of the critical load for angles higher than 90 degrees to the angles less than 90 degrees are not sensible.

6 Conclusions

In this study, the stability behavior of a sandwich arch with flexible core and composite-laminated face sheets is studied analytically. Displacement field in the core is solved via the compatible elasticity equations, while for the two skins classical laminate theory is adopted. Various layups and types of laminations are used for the faces. The resulted governing equations are established in general form via the virtual displacements principle. The case of an arch under uniform lateral pressure is analyzed. The pre-buckling solution is accomplished with proper linearizations and the stability equations are obtained via the adjacent equilibrium criterion. An exact solution is obtained for the case of a beam with both edges simply supported. Analytical closed-form phrase is presented to deduce the critical buckling load of the arch. As concluded the stiffness of the core, thickness of the core, curved beam angle, and face sheets lamination have influential effects on critical buckling loads and buckled shapes of the arch.