Introduction. In 1805, A. Legendre used the least squares method (LS) in his work “A new method for determining the orbits of comets.” Later, in 1808, R. Adrein in his work “Studies concerning the probabilities of errors that appear during measurements” gave a rough “proof” that, under some conditions, these errors obey the so-called “normal law” [1]. And in 1809, K. Gauss in his work “Theory of the motion of celestial bodies” also gave a substantiation of this law and stated that he had developed the LS back in 1795 while studying at the University of Göttingen. In 1900, in order to test simple hypotheses, K. Pearson proposed a χ2 goodness-of-fit test generalized by R. Fisher in 1928 for testing complex hypotheses in the maximum likelihood method. However, in 1929, for the construction of a cosmological distance scale in terms of the Hubble law for the radial velocity of galaxies under the Doppler interpretation of the z redshift, the LS was sufficient:

$$ cz={H}_0D, $$

where c is the velocity of light; H0 is the Hubble constant; and D is the distance [2].

In the case of unequal measurements, the modern version of the weighted least squares method was developed by A. Aitken in 1935 followed by the presentation of a proof for the goodness-of-fit theorem by G. Kramer in 1946. In 1957, the corresponding method for estimating the parameters in the works of K. Rao was called the “chi-square minimum method.” The specific feature of this method – the variance of the weighted average is lower than the smallest variance among the elements of the population – can create the illusion of a high accuracy of the results if not carefully applied. In 1998, the method referred to as the “Riess χ2 minimum method” was used to detect the “accelerating expansion of the Universe” [3].

It came as a surprise that, along with a growing accuracy of astrophysical measurements and the emergence of improved cosmological models, a situation called a dead end by V. Friedman – the leader of the Hubble Space Telescope (HST) project – arose in cosmology [4]. The causa proxima for this statement and the discussion about the crisis in cosmology was the discrepancy of more than “sacramental 3σ of normal law” (5–6 km·s–1·Mpc–1) in the estimates of the H0 parameter according to “distance ladder” cepheids [5] and measurements of microwave background radiation in the framework of the ΛCDM model [6]. However, since 1929, the estimates of the Hubble parameter have decreased from 530 to almost 50 km·s–1·Mpc–1 [7]. As a result, the transition from the Friedman–Robertson–Walker model with the curvature parameter to its representation according to the third-order Taylor formula is described in [8] with the assumption of an unknown “new physics outside the ΛCDM model” described in [9]. W. Friedman demanded to “increase the accuracy of the scale assessment to one percent” for the resolution of the crisis [4].

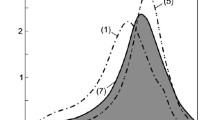
The root cause of the “dead end” in cosmology, which has been obvious since 1929, is presented in a figure in [2]. However, the preference was given to the actual redshift as the main scale.

“Dead end” metrology. Statistical methods, including the most popular of them, primarily require verification of the applicability conditions. The problem of calibrating the cosmological distance scale represents a typical measuring problem, which can be solved by the method of compatible measurements. The diverse mathematical apparatus of this method includes interpolation theory, statistical verification of structural (nonparametric) and parametric hypotheses, variance, regression, and confluent types of analysis [10,11,12]. Against the background of the generality in the statement of problems, the latter method of mathematical statistics is still the most problematic one for practical application, with the corresponding literature being very scarce [13,14,15,16,17].

In [3, 18,19,20], regression analysis algorithms were used to estimate the parameters of the Friedman–Robertson–Walker model as a general model of cosmological distance scales based on the redshift in the emission spectra of extragalactic sources. As a result, the “accelerating expansion of the Universe” was detected and confirmed.

It should be noted that, in the considered situation, regression analysis implies a set of statistical methods for analyzing relationships between quantitatively precisely specified Xi input variables and a mathematical model of an object with a statistical scatter of the Y output variable. In this case, the input and output variables represent the data of their compatible measurements or determinations.

Mathematical conditions for the applicability of classical linear regression analysis for the models of the form

$$ y={\sum}_{{{}_m}_{=0}}^M{\uptheta}_m{\upvarphi}_m(x)+\upvarepsilon, $$
(1)

where θm are the parameters, φm(x) are the given functions (xm, etc.), ε is a random variable (remainder), are determined by the following assumptions [16]:

  1. A1.

    εn remainders, where n = 1, 2, ..., N, are stochastic random variables according to Kolmogorov [21];

  2. A2.

    Mεn = 0 are their expected values;

  3. A3.

    Their covariances and variances are cov{εk, εl} = 0, k ≠ l, and Dεn = cov{εk, εk} = σ2, k ≤ N, respectively;

  4. A4.

    The εn random variables are Gaussian;

  5. A5.

    The φm(x) given functions are not random;

  6. A6.

    No restrictions are imposed on the values of the θm model parameters, i.e., nothing is known about their values in advance;

  7. A7.

    Number of compatible measurements is N ≥ M + 1;

  8. A8.

    Model (1) is neither redundant nor insufficient.

The main methods for parametric identification of models in regression analysis include LS, methods of least absolute deviation methods (LAD) and maximum likelihood, etc.

When the A.1–A.8 assumptions are fulfilled, the regression analysis estimates have a number of important properties: unbiasedness, efficiency and independence (taking into account the number of model parameters) of the mean square of the model remainders on the type of distribution [1]. If there is a possibility of additional verification or active planning of experiments, then the above assumptions are justified in some cases.

However, the Universe is a specific measurement object. Therefore, let us note violations of those applicability conditions of regression analysis [1, 14,15,16,17, 10, 22] that can elucidate the discrepancy between the parametric estimates of the Friedman–Robertson–Walker model, including the Hubble parameter, obtained from different sources.

A.1 is the condition of stochasticity, i.e., statistical homogeneity of the remainders. In this respect, an example of detecting a “disorder” of the mean for 36 SN Ia at z ≤ 0.1 [23], when the H0 = 72 ± 7 km·s–1·Mpc–1 estimate was obtained at distances less than 467 Mpc. The estimate with the “disorder” turned out to be more accurate: H0 = 71.66 ± 3.68 km·s–1·Mpc–1 (less than 309.5 Mpc) and further – the H0 = 65.95 ± 3.68 km·s–1·Mpc–1 estimate [24], which eliminated the discrepancy in estimates at the same time as indicating a violation of the A.2 assumption.

A.3 is the condition of uncorrelatedness and homoscedasticity. Violation of the homoscedasticity condition is associated with a decrease in the efficiency of parametric estimates of the regression model and a significant underestimation of the parametric variances and covariances. In this situation, the method of weighted least squares – the Riess χ2 minimum method with weights of the 1/σn2 form was used in [3]. However, in this case, the standard deviation (SD) of the weighted mean is less than the smallest SD among the remainders [25], which can create an illusion of a high accuracy of the averaged result.

Violation of the uncorrelated condition leads to the phenomenon of autocorrelation with the consequences similar to those of the homoscedasticity condition violation:

  • parametric estimates, although not biased, are already ineffective;

  • the variances of parametric estimates become biased, therefore leading to the recognition of input variables as statistically significant, which may not be so in reality;

  • the variance of the regression model estimate is underestimated;

  • Student and Fisher criteria lose their meaning.

Violation of A.4 condition leads to the LS estimates losing important properties.

Violation of A.5 non-confluence condition leads to a bias, an underestimation of the variance estimates, and a loss of consistency of the parametric estimates. Confluent analysis solves the same problem as regression analysis provided that the accuracy condition of the input variables is violated.

Violation of the A.6 unboundedness condition causes the phenomenon of stochastic multicollinearity known in cosmology as “degeneration of the ΛCDM model” [26, 27]:

  • the addition or exclusion of even one sample can lead to a strong change in the parametric estimates of the regression model and a sharp decrease in the accuracy of prediction according to the model;

  • a numerical instability of the estimation procedure resulting from rounding errors and their accumulation appears;

  • the parameters of the regression model turn out to be highly correlated, thus making interpretation meaningless;

  • the variances of model parametric estimates increase sharply;

  • the application of significance criteria becomes unreliable, since the SD values are included in the formulas of the significance criteria.

An explicit violation of the unboundedness condition is given directly in the tables of the final results [3, 18]: independent parametric estimates for the ΩM “dark mass” and the ΩΛ “dark energy,” having not yet received a satisfactory physical interpretation, diverged significantly until they were limited by the Ωk + ΩΛ = 1 condition. This condition was adopted in order to agree with the so-called “flat Universe” concept, which followed, in turn, from the interpretation within the framework of the ΛCDM model for the angular power spectrum of the microwave background radiation [28].

A.8 adequacy condition is related to the fact that, in regression analysis, the optimality of the data approximation by a model with an increase in its order or complexity in terms of the number of parameters or representation members depends not only on the accepted significance level of the difference between the remainders from zero [1], but also on the statistical criterion used.

At the same time, in regression analysis, the concept of “adequacy” in connection with “ordinary” remainders was transformed into two concepts – “pure error” and “lack-of-fit” [22]: if the parameters of the model are determined, then the value of the Yi* output variable calculated by the model given the value of the Xi input variables is called the “predicted value.” Then, introducing the ηi = MYi expected value of the “true” model, the remainder is divided into the Bi bias error and the qi random variable with zero mean, equal to

$$ {B}_i={\upeta}_i\hbox{--} \mathbf{M}{Y_i}^{\ast };\kern0.5em {q}_i=\left({Y}_i\hbox{--} {Y_i}^{\ast}\right)\hbox{--} \left({\upeta}_i\hbox{--} \mathbf{M}{Y_i}^{\ast}\right). $$

And if the model is correct (in fact, this is the result of averaging or smoothing), then [22]

$$ {\displaystyle \begin{array}{cc}\mathbf{M}{Y_i}^{\ast }={\upeta}_i;& {B}_i=0,\end{array}} $$

otherwise

$$ {\displaystyle \begin{array}{cc}\mathbf{M}{Y_i}^{\ast}\ne {\upeta}_i;& {B}_i\ne 0,\end{array}} $$

In other words, the “predicted value” in regression analysis has lost its direct meaning, while in the theory of measurement problems the lack-of-fit error of the model for the measured object is really defined as the error of model prediction in the crossover observation scheme – the extrapolation error [10,11,12].

The incompleteness of a model leads to a shift in remainders, while its redundancy results in overestimating the variances of parametric estimates [6, 15].

It seems that the A.8 goodness-of-fit condition is always violated.

The seven-year report of the WMAP experiment [24] noted that the introduction of one or two additional parameters of the ΛCDM model increases its accuracy by 90–300% with the SD of the H0 estimates increased by 1.28–6 times.

The special requirements for the model of cosmological distance scales, based on the redshift as an argument to the photometric distance function, include the absence of a zero point and monotonicity. At the same time, the transition from “decelerating to accelerating expansion of the Universe” should be accompanied, at least, by a change in the parameters of the scale model, the so-called “disorder” [29] called the “cosmic push” [30]. However, in [3, 18] for Λk = 0, the estimates of the Hubble parameter for the Friedman–Robertson–Walker model

$$ {D}_L(z)=\left(c/{H}_0\right)\left(1+z\right){+_0}^z{\int}_0^z{\left[{\left(1+x\right)}^2\left(1+{\Omega}_M\right)\hbox{--} {\Omega}_{\Lambda}x\left(2+x\right)\right]}^{\hbox{--} 1/2} dx $$
(2)

were below the Planck Collaboration estimates and did not cause problems. The corresponding initial data are presented in Table 1, where the μ distance moduli are replaced by DL = 100.2μ–5 photometric distances [3]; SN Ia supernovae with the same rank numbers of redshifts and photometric distances are shown in bold. The characteristics of the remaining supernovae do not form a monotonically increasing sequence, i.e., a rank inversion of the photometric distance estimates relative to the redshift estimates takes place.

TABLE 1. SN Ia Supernovae Rank Table According to [3, 18,19,20]
Full size table

The physical interpretation of rank inversion is associated with the properties of a random function with a space-time trend and significant errors in estimates of the relationship between redshift and photometric distance having a multiplicative nature [7, 24]. Therefore, it makes sense to consider the problem of calibration of the Friedman–Robertson–Walker model not as a regression problem, but as a confluent analysis problem with all the ensuing consequences. The most negative of them involve bias, underestimation of variance estimates, and loss of consistency of model parameter estimates.

These consequences are indicated in the discussion [4, 5, 9, 31]. The latter of the mentioned consequences of the non-confluence condition violation corresponds not only to the discrepancy between the estimates of the Hubble parameter in the Friedman–Robertson Walker model and the ΛCDM model, but also their total scattering from (61.4 ± 1.3) to (91.8 ± 5.3) km·s–1·Mpc–1 [7].

The problem of rank inversion in confluent analysis is referred to as an important “case, when, performing single observations, either there is a rule for dividing the measurement results of the input quantities into groups, regardless of the measurement errors, or the order of increasing true values of the input quantities is known” [32]. A more definite general conclusion was made in [33]: “an LS estimate exists if the data and approximating functions have similar qualitative characteristics (positivity, monotonicity, convexity, etc.).” However, these limitations do not solve the problem of applicability of statistical methods in non-confluence conditions [34].

Cross-sectional observation scheme. Until the shortest proof of the theorem on the expected value of the modulus of the difference of a random variable and its position parameter (the theorem on the modular criterion) had been obtained, as well as the lemma on the kappa-criterion for the reproducibility of the probability distribution density [35, 36], two facts were out of sight of metrologists:

– the Kolmogorov distance between distribution functions is the basis of the only goodness-of-fit criterion that has a strict probabilistic meaning – the area of intersection of the probability distribution densities at a single point of their intersection; this meaning is preserved when the criterion is generalized to the case of a finite number of intersections;

– the distance in the Feller variation [37] is reduced by a linear transformation to the goodness-of-fit probability and the kappa-criterion [35].

The identification of mathematical models of dependencies between physical and calculated quantities as a mapping of the function and arguments of the cause-and-effect relationship between them differs from the approximation of the relationship between the series of named numbers, even those having a physical meaning. The fundamental difference is that the properties of the parametric estimates and the models themselves should be preserved not only for intermediate values of the arguments, but also in a certain area outside the observation interval, when the model is extrapolated.

This distinguishes prediction (in the full sense of the word) from statistical averaging (smoothing), the results of which are called “predicted values.” Therefore, the errors of extrapolation are determined not only by the statistical dispersion of the output variable of the model, but also by the errors of the input variables. In this sense, it is the extrapolation errors that are a more complete characteristic of the model’s lack-of-fit rather than its remainders or approximation errors. Thus, algorithms for parametric identification of regression analysis in the scheme of lack-of-fit error cross-sectional observation serve for solving confluent analysis problems. The resulting additional component of the model error naturally takes into account the unobservable component of the input variable error.

It is crucial that, in the calibration problem, the difference between the mean modulus of the lack-of-fit error (MMLFE) and the mean absolute deviation (MAD) of the remainders characterizes errors due to the discrepancy between the measurement plan and the extrema of the systematic component of the model – the lack-of-fit error of the measurement plan. In the case of a cosmological distance scale based on the redshift attributed to SN Ia supernovae according to the redshift of the “parent” galaxies, the role of the measurement plan is played by the order of sampling, which, of course, is not balanced by chance. And this component of the model error in the calibration problem without a cross-over observation scheme remains unobservable.

The conducted analysis [7, 24, 38] of data samples on SN Ia supernovae [3, 18,19,20, 39] for model (2) and its representations by Taylor’s formula or power polynomial (1) showed the following.

1. All samples are compositionally inhomogeneous and each sample separately forms a nonzero zero-point, which can be excluded by combining data samples as a result of increasing the MMLFE.

2. In the absence of a zero-point, the best combination according to the criterion of the minimum MMLFE is formed by data [3, 18] in the

$$ {\tilde{D}}_L\left(l,b,z\right)=\left(c/{H}_0\right)\left[\left(1+{a}_bb\right)z+0.5\left(1\hbox{--} {q}_0\right)\left(1+{a}_ll\right){z}^2\right], $$
(3)

where ai = 2.568655129·10–3, ab = 2.027311498·10–3 are the anisotropy coefficients in galactic coordinates (l, b); H0 = 60.80404234 km·s–1·Mpc–1, q0 = –0.14378664 deceleration parameter [38].

The model is insensitive to the SN Ia 1997ck outlier at z = 0.97 (see Table 1) and is structurally similar to the Heckman representation [40]:

$$ {D}_L=\left(c/{H}_0\right)\left[z+0.5\left(1\hbox{--} {q}_0\right){z}^2\right]. $$
(4)

For all the data in Table 1, the model of optimal complexity in the class of three-dimensional polynomials not higher than the 3rd degree at MMLFE = 519.40485 Mpc is the anisotropic MCLS model (MC – maximum compactness method) (Fig.1):

Fig. 1.
figure 1

Anisotropic MСLS-model (Y – DL, X1 – z, X2 – b) for data [3, 18,19,20] built in the program “MMK- stat M ”[39]; the blue circle shows the moment of the redshift “cosmic push” according to [18], red arrows denote the most significant inversions.

Full size image
$$ {D}_L=\left(c/{H}_0\right)\left[\left(1+{a}_b\right)z+0.5\left(1\hbox{--} {q}_0\right){z}^2\right], $$

where H0 = 53.7096422 km·s–1·Mpc–1; ab = –7.408153677·10–4 is the coefficient of anisotropy in galactic latitude (corresponding to the polar dipole in galactic transparency windows); q0 = 0.9993918367.

3. The remainders of model (2) according to the data [3, 18] at the ΩM = 0.24, ΩΛ = 0.76 values of the parameters reach the minimum MMLFE = 113.4913127 Mpc with the estimate H0 = 65.2 km·s–1·Mpc–1 [42]. But at ΩM = 0.28, ΩΛ = 0.72 with the estimate H 0 = 63.0 km s–1·Mpc–1 its MAD = 460.3806527 Mpc, and with the estimate H 0 = 70.0 km s–1Mpc–1 – MAD = 1759.828986 Mpc, which confirms the suspicions [3].

4. The transition to a model with the push parameter j0 [5]:

$$ {D}_L(z)=\left(c/{H}_0\right)\left[z+\left(1\hbox{--} {q}_0\right){z}^2/2\hbox{--} \left(1\hbox{--} {q}_0\hbox{--} 3{q_0}^2+{j}_0\right){z}^3/6\right] $$
(5)

led to an estimate of H0 = 73.24 km s–1·Mpc–1, which became the reason for discussions about the crisis in cosmology at the same time as denying the results of 1998–1999. However, model (3) with MMLFE = 247.72842 Mpc and MAD = 226.03539 Mpc showed that model (5) is redundant [41, 42].

5. The parametric identification by the least absolute deviation method (LAD) of the interpolation model with the shape parameter α [43]:

$$ {D}_L(z)=\upalpha \left(c/{H}_0\right)\left[{\left(1+z\right)}^{1/\upalpha}\hbox{--} 1\right] $$
(6)

gave an unexpected result: at α = 0.499160639 ≈ 1/2, H0 = 77.2924661 km s–1·Mpc–1 the MAD of the model remainders was 278.32 Mpc. But for α = 1/2, the photometric distance is defined as

$$ {D}_L(z)=\upalpha \left(c/{H}_0\right){\left[{\left(1+z\right)}^{1/\upalpha}\hbox{--} 1\right]}_{\upalpha =1/2}\equiv \left(c/{H}_0\right)\left[z+{z}^2/2\right], $$
(7)

and there is a strict coincidence with model (4) at q0 = 0.

6. The verification of the structural-parametric identification of model (7) by the algorithms without taking into account the “disorder” gave the following estimates:

H 0 = 74.01766727 km·s–1·Mpc–1; MMLFE = 2252.901035 Mpc; MAD = 276.4261897 Mpc for MCLS;

H 0 = 73.48214569 km·s–1·Mpc–1; MMLFE = 466.1801294 Mpc; MAD = 276.3335578 Mpc for MCLS.

7. Only the random (observed) component of the error or the residuals of the considered variants of the Friedman–Robertson–Walker model as a function of the photometric distance is of a multiplicative nature, which on average is more than 10% [24], that is, as a percentage, an order of magnitude more than is accepted in works of the discussion groups. And the reason for this state of affairs is in the properties of the weighted average.

8. The “disorders” of the models, although they are expressed by changes in the parameters and structure of the characteristics of the position of the models, are accompanied by the rank inversion of the data on the redshift and photometric distance, which makes the most significant contribution to the MMLFE model.

Otherwise, it should be recognized that the photometric distances to supernovae SN Ia were determined with large errors, since, for this, the problem of reconstructing their luminosity curves from discrete data was solved to find the luminosity maximum, and this is another problem of the same confluent analysis. As a result, photometric distances are determined by the method of indirect measurement, and a reasonable question arises about the lack-of-fit errors of the models and formulas for distance modules used for this.

Conclusions. The discrepancy between the estimates of the Hubble parameter within the framework of the so-called “normal law” is, most likely, a purely external manifestation of the real reasons for the “dead end” in cosmology. However, the rank inversion of the data on the redshift and distance to extragalactic objects should have been qualitatively evident at least since 1929. Nevertheless, the fundamental result of works on the “accelerating expansion of the Universe” [3, 18] and “extraordinary proofs” of its existence [19, 20] – rank inversion – takes place in the data on redshift and photometric distances. This is a direct illustration of the fact that the redshift scale in cosmology has no status of either a metric or an ordinal scale.

In other words, at the maximum luminosity, brighter SN Ia supernovae, which are attributed to a larger redshift of the host galaxies, may actually be closer than those supernovae with a lower redshift. Therefore, due to the importance of rank inversions as “extraordinary evidence,” the data for 2004–2007 appears to be doubtful.

Most likely, there will be no “dead ends” in cosmology. However, it makes sense to pay attention to the problems concerning applicability of mathematical statistics and metrology in the problem of calibrating the cosmological distance scale, as well as to the lack-of-fit problem of mathematical models.