1 Introduction

This study is related to modeling and control of artificial locomotion systems that can move through a resistive environment without special propelling devices (wheels, legs, water screws, etc.) due to change in their configuration. During the motion, these systems do not change the sets of their points of contact with the environment. Such systems are designed as multibody linkages the bodies of which are connected by cylindrical (revolute) or prismatic (translational) joints. The joints are equipped with drives that control the relative motion of adjacent bodies. The forces and torques generated by the drives are internal with respect to the entire locomotion system. The control forces and torques cause the motion of the system’s components relative to one another and relative to the environment. The environment acts on the bodies of the system with the resistance forces that are external with respect to the locomotor and depend on the motion of the respective bodies. Therefore, control of the internal forces and torques generated by the drives enables one to control the external forces and torques applied to the system by the environment, thus controlling the motion of the system as a whole. This principle of motion has been borrowed from living nature, it imitates the motion of some terrestrial and aquatic limbless animals, such as snakes, worms, eels, etc. The investigations in the dynamics and control of limbless artificial locomotion systems are rapidly developing in the context of biomechanics and mobile robotics.

Two basic kinds of limbless motion can be distinguished: snake-like motion and worm-like motion. The snake-like locomotors are designed usually as multi-link systems the links of which are connected by cylindrical (revolute) joints, and the configuration of the locomotor changes by means of lateral bending. The worm-like systems are designed, as a rule, as multi-body systems the bodies of which are connected by prismatic (translational) joints, and the configuration changes due to relative longitudinal displacement of the bodies. The motion of worm-like systems resembles a peristaltic motion. For mathematical modeling of snake-like and worm-like locomotion, both lumped-mass and distributed mass systems can be used.

In our paper, a crawling system that consists of two bodies connected by a prismatic joint is studied. It can be regarded as the simplest model of a worm-like locomotion system. The bodies interact with one another by a force acting along the line that connects the bodies. This force is generated by a drive and plays the role of a control force.

The general issues of worm-like locomotion are addressed in [1,2,3,4]. Biological and biomechanical aspects are discussed in [1, 2], while the books [3, 4] deal with mathematical modeling of worm-like locomotion systems. Various aspects of dynamics, control, and optimization of worm-like locomotors on the basis of lumped-mass models are considered in [5,6,7,8]. In [9,10,11,12,13,14,15], the locomotion of the worm-like systems (both natural and artificial) is studied on the basis of distributed-mass models. In some of the cited papers, lumped-mass models are used along with distributed-mass models, these kinds of models are compared, and the relationship between them is discussed. The advantage of worm-like locomotors in comparison with snake-like ones is that the gaits of worm-like locomotors do not involve lateral bending, owing to which the worm-like locomotors are more prospective for the motion in narrow tubes and slots. Artificial worm-like locomotion systems are presented, e.g., in [16,17,18,19,20].

The rectilinear motion of a two-body locomotion system on a rough horizonal plane was investigated in a number of studies, see, e.g., [21,22,23,24,25,26,27]. The cited papers mostly deal with periodic motions, in which the distance between the bodies and their velocities relative to the environment change periodically with the same period. Various control strategies are proposed and analyzed. Special attention is given to the optimization of the motions with respect to the average velocity of the locomotor (to be maximized) or the energy consumption per unit path (to be minimized). The constraints on the parameters, subject to which a two-body system can move in such a way that neither of the bodies change the direction of their motions, are identified.

A two-body crawling system is uncontrollable on a horizontal plane in that sense that it cannot be driven from any initial state of rest on the plane to any terminal state of rest. The uncontrollability is explained by the fact that all forces that act in the system are directed along the line that connects the bodies in the initial state. The situation changes for an inclined plane. In this case, if both bodies do not lie on the common line of maximal slope, the projections of the gravity forces applied to the bodies onto the underlying plane are not directed along the line that connects the bodies. The aim of our paper is to investigate the controllability of a two-body crawler on a rough (Coulomb’s friction) inclined plane. It will be shown that if the tangent of the plane inclination angle is less that the coefficient of friction between the bodies and the plane multiplied by the ratio of the difference of the masses of the bodies to the total mass of the system and if no constraints are imposed on the control force, the system can be moved from any initial state of rest, except for the case where both bodies lie on the common line of maximum slope, into an arbitrarily small neighborhood of any prescribed terminal state of rest. A control strategy that alternates infinitely slow (quasistatic) motions and infinitely fast motions will be presented. Thereby it will be shown that on an inclined plane the crawler is controllable from any state of rest, apart from the singular case where both bodies lie on the common line of maximum slope.

The motion of a two-body system on an inclined plane along a line of maximal slope is dealt with in [28, 29]. If at an initial time instant both bodies of a two-body crawler lie on the common line of maximum slope, the system, as was the case for the motion on a horizontal plane, cannot quit this line, since all forces that act in the system act along this line.

The ability of two-body artificial limbless locomotors to crawl along a rough plane has been confirmed experimentally. In [24], an electrically driven experimental prototype of a two-body crawling locomotor is described. It was established theoretically and experimentally that this prototype could move along a straight line on a horizontal rough plane. It can be used also for the motion on an inclined rough plane along a line of maximal slope, which has been justified theoretically in [28, 29].

Two-body crawlers may have practical applications. For example, they can be used as mobile robotic systems for the motion inside straight narrow pipes. In [30, 31], a two-module push-pull in-pipe robot is described. The robot consists of two modules (rigid bodies) that interact with one another by means of an electromagnetic drive. The drive contains a coil that is rigidly fixed to one of the modules (active module) and a ferromagnetic core that is rigidly attached to the other (passive) module by means of a rod and can move inside the coil. The modules are connected by a spring. Each module has a bristly coating that provides an anisotropy for the friction between the modules and the walls of the pipe. The bristles are oriented in such a way that the friction resisting the forward motion is much lower than the friction resisting the backward motion. The locomotion of the robot occurs due to the alternation of active and passive phases. In the active phases, a voltage is applied across the coil, the core is pulled into the coil, and the passive module moves forward, while the active module is virtually kept at rest by the forces of friction. In the passive phases, the voltage is switched off and the active module is pushed forward by the spring, while the passive module is virtually kept at rest.

So far, two-body limbless artificial locomotors were used mostly for rectilinear motions along a guide, in particular, inside pipes. We study the locomotion of a two-body crawler on an inclined plane in order to answer the question, whether such a simple system is suitable for more complicated motions, rather than only for the motions along a guide, along a straight line on a horizontal plane, or along a straight line of maximal slope on an inclined plane. It will be shown that a two-body crawling system is in principle controllable on an inclined plane. This fact extends the area of potential applications of such systems.

2 Mechanical model and the aim of the study

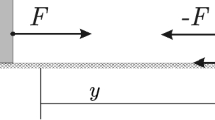
We consider a model of a two-body limbless crawling system on an inclined plane \(\Pi\) shown in Fig. 1. The bodies of the system are treated as mass points. The bodies interact with one another and with the plane. The forces of interaction between the bodies obey Newton’s third law and play the role of control forces. Dry friction forces due to interaction of the bodies with the underlying plane are acting on each of the bodies. The coefficient of friction against the plane is the same for both bodies. The control forces are internal forces, while the friction forces are external forces for the crawler.

Let M and m be the masses of the bodies; in what follows, we will refer to the body of mass M and the body of mass m as body M and body m, respectively. Let \(\mathbf{f}\) denote the interaction force applied by body M to body m; \(\gamma\) \((0< \gamma < \pi /2)\) the inclination angle of the plane; g the magnitude of the acceleration due to gravity; k the coefficient of Coulomb’s friction between the underlying plane and the bodies of the system. According to Newton’s third law, the force \(\mathbf{f}\) acts along the line that connects the bodies of the system.

Fig. 1
figure 1

Two-body crawling system on an inclined plane. Oxyz is the inertial reference frame, \(\mathbf{f}\) is the control force, \(\mathbf{g}\) is the vector of the acceleration due to gravity, \(\mathbf{n}\) is the vector normal to the plane

Full size image

We will be interested in the controllability of this system. By controllability we understand the ability of the crawler to move from an arbitrary initial state of rest to an arbitrary terminal state of rest. On a horizontal plane, a two-body crawler is uncontrollable; in this case, the crawler can move only along the line that connects the bodies in the initial state, since the interaction forces of the bodies and the forces of friction are acting along this line. The situation changes for an inclined plane, because in this case the projections of the gravity forces that act on the bodies onto the plane do not lie on the line that connects the current positions of the bodies, apart from the case where the bodies lie on the common line of maximum slope. If in the initial state the bodies lie on the common line of maximum slope on an inclined plane, the crawler cannot leave this line, as is the case for a horizontal plane.

We will be interested in the controllability in principle. For this reason, we do not impose any quantitative constraints on the control forces and on the distance between the bodies. In particular, we admit impulsive forces that change instantaneously the velocities of the bodies and even the forces that change instantaneously the distance between the bodies of the crawler. Moreover, we will assume that the bodies may “penetrate” one another.

We will construct a control by means of which the crawler could move between two prescribed states of rest on the plane. We will show that if at the initial instant the bodies of the crawler do not lie on the common line of maximum slope, then the system can be driven into an arbitrarily small neighborhood of the prescribed terminal state. The motion of the crawler will alternate slow (quasistatic) phases and fast phases. In the slow phases, one of the bodies moves, while the other body is kept fixed on the plane due to friction force. The velocity and acceleration of the moving body in the slow phase are so small that this motion can be regarded as a continuous sequence of equilibria governed by the static relations. The fact that the body is moving is reflected in the assumption that the magnitude of the force of friction acting on this body is equal to the magnitude of the sliding friction force. The direction opposite to that of the force of friction will be identified with the instantaneous direction of motion of the body in the slow phase. During the slow motions the position of the center of mass of the crawler and the orientation of the crawler on the plane are changing. In the fast modes, the distance between the bodies changes instantaneously, the position of the center of mass and the orientation of the crawler remaining unchanged. The fast motions are an idealization of very quick motions induced by large control forces of small duration. These forces must be much larger than the gravity forces and friction forces acting on the bodies of the system but the duration of their action must be so small that the change in the linear and angular momenta of the system during the fast motion be negligible. The motion that alternates slow and fast phases was considered in [32, 33] for multi-link snake-like limbless locomotors that consist of rigid links connected by revolute joints and perform bending motions on a horizontal rough plane.

The Coulomb’s dry friction force \(\mathbf{R}\) for a point mass on the plane \(\Pi\) is given by

$$\begin{aligned} \mathbf{R } = \left\{ \begin{array}{ll} -kN\frac{\mathbf {v}}{|{\mathbf {v}}|}, &{} {\mathbf {v}} \ne 0, \\ -{\varvec{\Phi }}_{\Pi }, &{} {\mathbf {v}} = 0, \quad |{\varvec{\Phi }}_{\Pi }| \le kN, \\ -kN\frac{{\varvec{\Phi }}_{\Pi }}{|{\varvec{\Phi }}_{\Pi }|}, &{} {\mathbf {v}} = 0, \quad |{\varvec{\Phi }}_{\Pi }| > kN, \end{array} \right. \end{aligned}$$
(1)

where \({\varvec{\Phi }}_{\Pi }\) is the projection of the resultant impressed force \({\varvec{\Phi }}\) applied to the mass point onto the plane \(\Pi\), \(\mathbf{v}\) is the velocity of the mass point relative to the plane, N is the magnitude of the normal reaction force applied to the mass point by the plane. The force \({\varvec{\Phi }}_{\Pi }\) in Eq. (1) is defined by

$$\begin{aligned} {\varvec{\Phi }}_{\Pi } = {\varvec{\Phi }} - ({\varvec{\Phi }} \cdot \mathbf{n} )\mathbf{n} , \end{aligned}$$
(2)

where \(\mathbf{n}\) is the unit vector of the normal to the plane and the dot stands for the scalar product of the respective vectors. Since the mass point is constrained to move along the plane without separation, the normal force N in Eq. (1) is given by

$$\begin{aligned} N = -({\varvec{\Phi }} \cdot \mathbf{n} ). \end{aligned}$$
(3)

For the bodies of the system under consideration, the impressed forces are the gravity forces and the control forces; we have

$$\begin{aligned} {\varvec{\Phi }}^M = M\mathbf{g} - \mathbf{f} , \quad {\varvec{\Phi }}^m = m\mathbf{g} + \mathbf{f} , \end{aligned}$$
(4)

where \(\mathbf{g}\) is the vector of the acceleration due to gravity; the superscript M or m indicates the body to which the respective expression is related.

Introduce a normal \(\mathbf{n}\) in such a way that the ends of the vectors \(\mathbf{n}\) and \(\mathbf{g}\) belong to different half-spaces with respect to the plane \(\Pi\), provided that the origins of these vectors belong to the plane \(\Pi\), so that \(\mathbf{n} \cdot \mathbf{g} < 0\). The vectors \(\mathbf{g}\), \(\mathbf{f}\), and \(\mathbf{n}\) satisfy the following relations:

$$\begin{aligned} \mathbf{g} \cdot \mathbf{n} = -g\cos \gamma , \quad \mathbf{f} \cdot \mathbf{n} = 0. \end{aligned}$$
(5)

These relations reflect the fact that the plane \(\Pi\) is inclined by an angle of \(\gamma\) and the control force \(\mathbf{f}\) is parallel to this plane.

Use Eqs. (2)–(5) to obtain

$$\begin{aligned} \begin{array}{l} {\varvec{\Phi }}_{\Pi }^M = M\mathbf{g} - \mathbf{f} + Mg\cos \gamma \,\mathbf{n} , \\ {\varvec{\Phi }}_{\Pi }^m = m\mathbf{g} + \mathbf{f} + mg\cos \gamma \,\mathbf{n} , \\ N^M = Mg\cos \gamma , \quad N^m = mg\cos \gamma . \end{array} \end{aligned}$$
(6)

We will construct a motion that alternates slow and fast phases. In the slow phases body m quasistatically moves, while body M remains at rest. To start a slow phase body m must be able to start moving from a state of rest so that body M remains fixed. It is important to identify the conditions subject to which such motions are allowed and the properties of the motions. For body m to be able to start moving from a state of rest while body M is not moving, the Coulomb’s friction law (1) and the relations of (6) imply the inequalities

$$\begin{aligned} |M\mathbf{g} - \mathbf{f} + Mg\cos \gamma \,\mathbf{n} | \le kMg\cos \gamma . \end{aligned}$$
(7)
$$\begin{aligned} |m\mathbf{g} + \mathbf{f} + mg\cos \gamma \,\mathbf{n} | > kmg\cos \gamma . \end{aligned}$$
(8)

Introduce in the plane \(\Pi\) a right-handed Cartesian coordinate system Oxyz, in which O is an arbitrary fixed point on the plane \(\Pi\), the z-axis is directed along the normal vector \(\mathbf{n}\); the y-axis lies on the line of intersection of the plane \(\Pi\) with the plane formed by the vectors \(\mathbf{g}\) and \(\mathbf{n}\) and is directed “upward” along this line; the x - axis completes the axes y and z to a right-handed orthogonal triple. In this coordinate system, the vectors \(\mathbf{n}\), \(\mathbf{g}\), and \(\mathbf{f}\) are represented as follows:

$$\begin{aligned} \mathbf{n} = \left[ \begin{array}{l} 0 \\ 0 \\ 1 \end{array} \right] , \quad \mathbf{g} = \left[ \begin{array}{l} 0 \\ -g\sin \gamma \\ -g\cos \gamma \end{array} \right] , \quad \mathbf{f} = \left[ \begin{array}{l} f_x \\ f_y \\ 0 \end{array} \right] . \end{aligned}$$
(9)

Then the inequalities (7) and (8) can be rewritten as

$$\begin{aligned}&f_x^2 + (f_y + Mg\sin \gamma )^2 \le (kMg\cos \gamma )^2, \end{aligned}$$
(10)
$$\begin{aligned}&\quad f_x^2 + (f_y - mg\sin \gamma )^2 > (kmg\cos \gamma )^2. \end{aligned}$$
(11)

These inequalities have a graphic geometrical interpretation. Introduce in the plane \(f_xf_y\) two circles \(C_M\) and \(C_m\) defined by

$$\begin{aligned} \begin{array}{l} C_M = \left\{ f_x, f_y: \; f_x^2 + (f_y + Mg\sin \gamma )^2 \right. \\ \left. \qquad \quad \le (kMg\cos \gamma )^2\right\} , \\ C_m = \left\{ f_x, f_y: \; f_x^2 + (f_y - mg\sin \gamma )^2 \right. \\ \left. \qquad \quad \le (kmg\cos \gamma )^2\right\} . \end{array} \end{aligned}$$
(12)

Relations (10) and (11) imply that the end-point of the vector \(\mathbf{f}\) drawn from the origin belongs to the circle \(C_M\) and does not belong to the circle \(C_m\), i.e., \(\mathbf{f} \in C_M \setminus C_m\). The circles \(C_M\) and \(C_m\) are shown in Fig. 2. The area shaded in light grey depicts the region \(C_M \setminus C_m\).

Fig. 2
figure 2

Circles \(C_M\) and \(C_m\). Relationship between the forces \({{\varvec{\Phi }}}^m_{\Pi }\) and \(\mathbf{f}\)

Full size image

Since body m starts moving from a state of rest in the direction of the force \({\varvec{\Phi }}^m_{\Pi }\) defined in Eq. (6), the diagram with circles \(C_M\) and \(C_m\) allows determining the directions in which body m can start moving from a state of rest, provided that body M does not move. In accordance with (6) and (9) we have

$$\begin{aligned} {\varvec{\Phi }}^m_{\Pi } = \left[ \begin{array}{l} f_x \\ f_y \\ 0 \end{array} \right] + \left[ \begin{array}{l} 0 \\ -mg\sin \gamma \\ 0 \end{array} \right] . \end{aligned}$$
(13)

This implies that the force \({\varvec{\Phi }}^m_{\Pi }\) can be represented geometrically as a vector drawn from the center of the circle \(C_m\) (the point \((0,\,mg\sin \gamma )\) on the plane \(\Pi\)) to the end point of the vector \(\mathbf{f}\) drawn from the origin of the coordinate system Oxyz. Therefore, an admissible direction of motion of body m is defined by any ray on the plane \(\Pi\) that is drawn from the center of the circle \(C_m\) and intersects the set \(C_M \setminus C_m\). Any point of intersection defines the control force \(\mathbf{f}\) that provides the motion of body m in the respective direction. One should remember that the control force \(\mathbf{f}\) lies on the line that connects bodies M and m. Therefore, different control forces that allow moving body m in the same direction correspond to different orientations of the two-body system on the plane \(\Pi\).

Consider three cases of mutual positions of the circles \(C_M\) and \(C_m\) in the plane \(f_xf_y\).

  • Case 1: the circles do not intersect. In this case, the circle \(C_M\) lies in the half-plane \(f_y < 0\) and the circle \(C_m\) lies in the half-plane \(f_y > 0\), which corresponds to the inequality

    $$\begin{aligned} \tan \gamma > k. \end{aligned}$$
    (14)

    Therefore, the bodies cannot remain at rest on the plane for \(\mathbf{f} = 0\). Moreover, both bodies cannot stay at rest for any force \(\mathbf{f}\). Any value of the control force than keeps body M at rest does not allow body m to remain at rest.

  • Case 2: the circles intersect but the circle \(C_m\) is not contained in the circle \(C_M\). This case is characterized by the inequalities

    $$\begin{aligned} \frac{M-m}{M+m}\,k \le \tan \gamma \le k. \end{aligned}$$
    (15)

    In this case, both bodies will remain fixed while \(\mathbf{f} = 0\), however, not all directions of motion are allowed for body m. In particular, body m cannot start moving upward if bodies M and m lie on the common line of maximal slope.

  • Case 3: the circle \(C_M\) contains the circle \(C_m\). For this case,

    $$\begin{aligned} \tan \gamma < \frac{M-m}{M+m}\,k. \end{aligned}$$
    (16)

    This inequality allows body m to be moved in any direction, provided that the line Mm has an appropriate orientation on the plane \(\Pi\). In particular, from the state in which both bodies lie on the common line of maximum slope and do not move, body m can be moved by an appropriate force \(\mathbf{f}\) upward along this line, provided that body M remains at rest. In what follows, we assume inequality (16) to hold.

For \(0< \gamma < \pi /2\), the inequality of (16) implies that \(M > m\), i.e., the mass of the body that can move quasistatically must be less than the mass of the other body.

Figure 2 illustrates the the mutual position of the circles \(C_M\) and \(C_m\) for Case 2 and the relationship between the vectors of the forces \({{\varvec{\Phi }}}^m_{\Pi }\) and \(\mathbf{f}\). The vector of an admissible (allowing body m to start moving when body M is at rest) force \({{\varvec{\Phi }}}^m_{\Pi }\) is drawn from the center of the circle \(C_m\) to a point A that belongs to the circle \(C_M\) and does not belong to the circle \(C_m\). The corresponding vector of the control force \(\mathbf{f}\) is drawn from the origin of the coordinate plane \(f_x\,f_y\) to the same point A. The directions of the admissible forces \({{\varvec{\Phi }}}^m_{\Pi }\) define the directions of feasible velocities of body m at the starting instant of the motion. The case where the vectors \({{\varvec{\Phi }}}^m_{\Pi }\) and \(\mathbf{f}\) end at a point B that lies on the boundary of the circle \(C_m\) and belongs to the circle \(C_M\) is the critical case and corresponds to the pending motion of body m. For this case, body m is in equilibrium but the friction force applied to this body is equal to the sliding friction force, and any, however small, increase in the magnitude of the control force \(\mathbf{f}\) will make this body moving. The critical equilibria of body m will play a key role in the following section where quasistatic motions of body m are studied.

3 Quasistatic motions of body m

In this section, the slow phase of the motion of the crawler is studied. Recall that in the slow phase, body M is kept fixed on the plane \(\Pi\), while body m moves with so small velocity and acceleration that the resultant of all forces applied to body m is zero. The trajectory of such a motion can be regarded as a “continuous sequence” of equilibrium positions. The fact that body m is actually moving is reflected in the assumption that the friction force applied to this body is equal in magnitude to the sliding friction force \(kmg\cos \gamma\). The direction opposite to that of the friction force is assumed as the positive direction of the tangent to the trajectory of the motion at the current position of the body.

Introduce in the plane \(\Pi\) a fixed right-handed coordinate system Mxy, with origin at the point M and y-axis directed upward along the line of maximum slope (Fig. 3).

Fig. 3
figure 3

Coordinate system Mxy, polar radius r and polar angle \(\varphi\) of body m relative to body M

Full size image

Denote: \(\mathbf{r}\) is the position vector of body m relative to body M; f the projection of the force \(\mathbf{f}\), applied by body M to body m, onto the direction of the vector \(\mathbf{r}\) (\(\mathbf{f} = f\mathbf{r} /|\mathbf{r} |\)); \(\mathbf{g} _{\Pi }\) the projection of the gravity acceleration vector \(\mathbf{g}\) onto the plane \(\Pi\). The introduced vectors are represented in the coordinate system Mxy as follows:

$$\begin{aligned} \mathbf{r} = \left[ \begin{array}{l} x \\ y \end{array} \right] , \; \mathbf{f} = \frac{f}{\sqrt{x^2+y^2}}\left[ \begin{array}{l} x \\ y \end{array} \right] , \; \mathbf{g} _{\Pi } = \left[ \begin{array}{c} 0 \\ -g\sin \gamma \end{array} \right] . \end{aligned}$$
(17)

The equation of balance of the forces applied to body m (equilibrium equation for body m) is given by

$$\begin{aligned} (kmg\cos \gamma ) \mathbf{t } = m\mathbf{g _{\Pi }} + \mathbf{f }, \end{aligned}$$
(18)

where \(\mathbf{t }\) is a unit vector directed against the friction force that acts on body m (the unit vector of the tangent to the trajectory of the quasistatic motion of this body). Raise both sides of Eq. (18) to a scalar square taking into account the relations \(|\mathbf{t }| =1\) and (17) to obtain the quadratic equation for the quantity f:

$$\begin{aligned} \begin{array}{l} f^2-2mg\sin \gamma \frac{y}{\sqrt{x^2+y^2}}f \\ + m^2g^2(\sin ^2\gamma - k^2\cos ^2\gamma ) = 0. \end{array} \end{aligned}$$
(19)

Solving this equation yields

$$\begin{aligned} \frac{f}{mg} = \sin \gamma \frac{y}{\sqrt{x^2+y^2}} \pm \sqrt{k^2\cos ^2\gamma - \sin ^2\gamma \frac{x^2}{x^2+y^2}}. \end{aligned}$$
(20)

The assumption of (16) implies that \(k > \tan \gamma\). Using this inequality we obtain

$$\begin{aligned} \sqrt{k^2\cos ^2\gamma - \sin ^2\gamma \frac{x^2}{x^2+y^2}} > |\sin \gamma |\frac{|y|}{\sqrt{x^2+y^2}}. \end{aligned}$$

Therefore, the quadratic Eq. (20) has two real roots, one of which is positive and the other is negative.

Parameterize the trajectory of the qusistatic motion by its natural parameter s (the length of the curve that connects the initial point of the trajectory with the current point), i.e., represent the position vector of body m by the vector-valued function \(\mathbf{r} = \mathbf{r} (s)\). Differential geometry yields the relation

$$\begin{aligned} \frac{d\mathbf{r} }{ds} = \mathbf{t} . \end{aligned}$$
(21)

From (18) and (21) we obtain

$$\begin{aligned} \frac{d\mathbf{r} }{ds} = \frac{1}{kg\cos \gamma }\left( \mathbf{g} _{\Pi } + \frac{1}{m}\mathbf{f }\right) . \end{aligned}$$
(22)

If the force \(\mathbf{f}\) is defined as a function of the variables \(\mathbf{r}\) and s, then the relation of (22) is a differential equation for the trajectory of the quasistatic motion. To find the function \(\mathbf{r} (s)\) one should solve this differential equation subject to the initial condition \(\mathbf{r} (0) = \mathbf{r} _0\), where \(\mathbf{r} _0\) is the initial position vector of body m.

In the coordinate form, Eq. (22) is represented by a system of two differential equations

$$\begin{aligned} \begin{array}{l} \frac{dx}{ds} = \frac{fx}{kmg\cos \gamma \sqrt{x^2+y^2}}, \\ \frac{dy}{ds} = -\frac{\tan\,\gamma }{k}+\frac{fy}{kmg\cos \gamma \sqrt{x^2+y^2}}, \end{array} \end{aligned}$$
(23)

where f is defined by one of the expressions of (20).

For solving the equations of (23), it is convenient to proceed from the Cartesian coordinates \((x,\,y)\) to the polar coordinates \((r,\,\varphi )\). The polar and Cartesian coordinates are related by

$$\begin{aligned} x = r\cos \varphi , \quad y = r\sin \varphi , \end{aligned}$$
(24)

where r and \(\varphi\) are treated as functions of the variable s. Substitute the expressions of (24) into the equations of (23) to obtain

$$\begin{aligned} \begin{array}{l} \frac{dr}{ds}\cos \varphi - \frac{d\varphi }{ds}r\sin \varphi = \frac{f}{kmg\cos \gamma }\cos \varphi \\ \frac{dr}{ds}\sin \varphi + \frac{d\varphi }{ds}r\cos \varphi = -\frac{\tan \gamma }{k} + \frac{f}{kmg\cos \gamma }\sin \varphi , \end{array} \end{aligned}$$
(25)

where

$$\begin{aligned} f = mg\left( \sin \gamma \sin \varphi \pm \sqrt{k^2\cos ^2\gamma - \sin ^2\gamma \cos ^2\varphi }\right) . \end{aligned}$$
(26)

The relation of (26) follows from those of (20) and (24).

Solve the equations of (25) for the derivatives dr/ds and \(d\varphi /ds\) and use the expression of (26) to represent these equations in the normal form

$$\begin{aligned} \begin{array}{l} \frac{dr}{ds} = \pm \sqrt{1 - q^2\cos ^2\varphi }, \quad \frac{d\varphi }{ds} = -\frac{q}{r}\cos \varphi , \\ q = \frac{\tan \gamma }{k}, \quad 0< q < 1. \end{array} \end{aligned}$$
(27)

The second equation of (27) implies that in the domain where \(\cos \varphi > 0\) (\(\cos \varphi < 0\)), the polar angle \(\varphi\) monotonically decreases (increases) as the parameter s increases. The inequality \(\cos \varphi > 0\) (\(\cos \varphi < 0\)) means that body m is in the half-plane \(x > 0\) (\(x < 0\)). This implies that for the quasistatic motion, the position vector \(\mathbf{r}\) of body m rotates clockwise in the half-plane \(x > 0\) and counterclockwise in the half-plane \(x < 0\). The equations of (27) are invariant to the change of variables \(\varphi = \pi - \widetilde{\varphi }\). Therefore, without loss of generality, we will assume that \(-\pi /2< \varphi < \pi /2\). In this domain, the quasistatic motion occurs with a decrease of the the angle \(\varphi\).

Proceed in the equations of (27) to the new independent variable \(\varphi\) to obtain a differential equation for the polar radius r as a function of the polar angle \(\varphi\) of body m:

$$\begin{aligned} \frac{dr}{d\varphi } = {\mp }\frac{r}{q\cos \varphi }\sqrt{1-q^2\cos ^2\varphi }. \end{aligned}$$
(28)

The double sign \({\mp }\) in Eq. (28) is consistent with the double sign ± in the expression of (26). The general solution of Eq. (28) is given by

$$\begin{aligned} \begin{array}{l} \ln {r} = {\mp }\frac{1}{q}\int \frac{\Delta (\varphi )}{\cos \varphi }{d\varphi } + \ln {C}, \\ \Delta (\varphi ) = \sqrt{1-q^2\cos ^2\varphi }, \end{array} \end{aligned}$$
(29)

where C is a positive constant. The integral in the relation of (29) can be expressed in terms of elementary functions:

$$\begin{aligned} \begin{array}{l} \int \frac{\Delta (\varphi )}{\cos \varphi }{d\varphi } \\ = \frac{1}{2}\ln \frac{\Delta (\varphi ) + \sin \varphi }{\Delta (\varphi ) - \sin \varphi } - q\ln \left( q\left( \Delta (\varphi ) + q\sin \varphi \right) \right) . \end{array} \end{aligned}$$
(30)

By substituting (30) into (29) and taking an exponential of both sides of the resultant relation we obtain finally

$$\begin{aligned} \begin{array}{l} r= r_{\pm }(\varphi ) \\ = C\left( \frac{\Delta (\varphi ) {\mp } \sin \varphi }{\Delta (\varphi ) \pm \sin \varphi }\right) ^{\frac{1}{2q}} \left( q(\Delta (\varphi ) + q\sin \varphi )\right) ^{\pm 1}. \end{array} \end{aligned}$$
(31)

The expressions of (31) allow identifying important qualitative features in the behavior of the quasistatic trajectories. By passing in these expressions to the limit as \(\varphi \rightarrow -\pi /2 + 0\) and \(\varphi \rightarrow \pi /2 - 0\) we obtain

$$\begin{aligned} \begin{array}{l} \lim \limits _{\varphi \rightarrow -\frac{\pi }{2}+0}r_+(\varphi )= \infty , \quad \lim \limits _{\varphi \rightarrow \frac{\pi }{2} - 0}r_+(\varphi ) = 0, \\ \lim \limits _{\varphi \rightarrow -\frac{\pi }{2}+0}r_-(\varphi ) = 0, \quad \lim \limits _{\varphi \rightarrow \frac{\pi }{2} - 0}r_-(\varphi ) = \infty . \end{array} \end{aligned}$$
(32)

Investigate the behavior of the coordinates \(x = r\cos \varphi\) and \(y = r\sin \varphi\) of body m in the qusiatatic motion. The derivative of the coordinate x with respect to \(\varphi\) is given by

$$\begin{aligned} \frac{dx}{d\varphi } = \frac{dr}{d\varphi } \cos \varphi - r\sin \varphi . \end{aligned}$$
(33)

Substitute the expression of (28) into that of (33) to obtain

$$\begin{aligned} \frac{dx_{\pm }}{d\varphi } = {\mp }\frac{r}{q}\left( \sqrt{1-q^2\cos ^2\varphi } -q\sin \varphi \right) . \end{aligned}$$
(34)

The expression in the parentheses is positive and, hence, \(dx_+/d\varphi < 0\) and \(dx_-/d\varphi > 0\) for \(\varphi \in (-\pi /2,\;\pi /2)\). This implies that the coordinate x monotonically decreases, if the interaction force \(\mathbf{f}\) is directed from body M to m, and monotonically increases, if this force is directed from body m to body M. From the second equation of (27) it follows that for any direction of the interaction force, the angle \(\varphi\) decreases in the process of the quasistatic motion. Therefore, the variables r and x increase for the motion under the force directed from body M to body m and decrease for the motion under the force directed from body m to body M.

The variable \(x_+\) increases without limit as \(\varphi \rightarrow -\pi /2 + 0\), while the variable \(x_-\) increases without limit as \(\varphi \rightarrow \pi /2 - 0\). We will prove this proposition for the variable \(x_+\); for the variable \(x_-\), the proof is similar. In the neighborhood of the value \(\varphi = -\pi /2\), the relation \(\sin \varphi = -\sqrt{1-\cos ^2\varphi }\) holds. Denote \(z = \cos \varphi\) and, using the relation of (31), represent the expression for \(x_+\) as follows:

$$\begin{aligned}\begin{array}{l} {x_ + } = C{\left( {\frac{{\sqrt {1 - {q^2}{z^2}} + \sqrt {1 - {z^2}} }}{{\sqrt {1 - {q^2}{z^2}} - \sqrt {1 - {z^2}} }}} \right)^{\frac{1}{{2q}}}}\\ \times \, zq\left( {\sqrt {1 - {q^2}{z^2}} - q\sqrt {1 - {z^2}} } \right) \end{array}\end{aligned}$$
(35)

Replace the expressions that occur in the relation of (35) by their Taylor expansions as \(z \rightarrow 0\) (\(\cos \varphi \rightarrow 0\) as \(\varphi \rightarrow \pi /2\)) to represent this relation as follows:

$$\begin{aligned} \begin{array}{l} x_+ = C\left( \frac{2z^{2q}(1 + O(z^2))}{(1-q^2)z^2 + O(z^4)}\right) ^{\frac{1}{2q}} \\ \times \, q\left( 1-q^2 + O(z^2)\right) \\ = C\left( 1-q^2\right) ^{\frac{2q-1}{2q}}z^{\frac{q-1}{q}}\left( q+O(z^2)\right) . \end{array} \end{aligned}$$
(36)

Since \(q < 1\), the quantity \(x_+\) goes to infinity as \(z \rightarrow 0\).

Investigate now the behavior of the coordinate \(y = r\sin \varphi\). Passing in this expression to the limit as \(\varphi \rightarrow \pm \pi /2\), with reference to (32), we obtain

$$\begin{aligned} \lim \limits _{\varphi \rightarrow -\frac{\pi }{2}+0}y_+(\varphi )= -\infty , \quad \lim \limits _{\varphi \rightarrow \frac{\pi }{2}-0}y_-(\varphi )= +\infty . \end{aligned}$$
(37)

Differentiating the expression \(y = r\sin \varphi\) with respect to \(\varphi\), taking into account the expression of (28), yields

$$\begin{aligned} \frac{dy_{\pm }}{d\varphi } = {\mp }\frac{r}{q\cos \varphi }\left( \sin \varphi \sqrt{1-q^2\cos ^2\varphi } {\mp } q\cos ^2\varphi \right) . \end{aligned}$$
(38)

The analysis of this expression shows that

$$\begin{aligned} \begin{array}{l} \frac{dy_{+}}{d\varphi } > 0, \;\; -\frac{\pi }{2}< \varphi< \text{ arctan }\,q; \\ \frac{dy_{+}}{d\varphi } = 0, \;\; \varphi = \text{ arctan }\,q; \\ \frac{dy_{+}}{d\varphi }< 0, \;\; \text{ arctan }\,q< \varphi < \frac{\pi }{2}. \end{array} \end{aligned}$$
(39)
$$\begin{aligned} \begin{array}{l} \frac{dy_{-}}{d\varphi }< 0, \;\; -\frac{\pi }{2}< \varphi< -\text{ arctan }\,q; \\ \frac{dy_{-}}{d\varphi } = 0, \;\; \varphi = -\text{ arctan }\,q; \\ \frac{dy_{-}}{d\varphi } > 0, \;\; -\text{ arctan }\,q< \varphi < \frac{\pi }{2}. \end{array} \end{aligned}$$
(40)

Therefore, the function \(y_+(\varphi )\) has a maximum for \(\varphi = \text{ arctan }\,q\), while \(y_-(\varphi )\) has a minimum for \(\varphi = -\text{ arctan }\,q\). The extreme values of these functions are defined by

$$\begin{aligned} \begin{array}{l} y_{+}^{\max } = Cq\left( \frac{1-q}{1+q}\right) ^{\frac{1}{2q}}, \\ y_{-}^{\min } = -C\left( \frac{1-q}{1+q}\right) ^{\frac{1}{2q}}\frac{1}{1-q^2}. \end{array} \end{aligned}$$
(41)

The change of variable \(\varphi \rightarrow -\varphi\) leads to the change in the sign on the right-hand side of Eq. (28). Therefore, the sets of quasistatic trajectories corresponding to signs \(+\) and − are symmetric to one another with respect to the x-axis of the coordinate system Mxy.

The trajectories constructed above are the basic quasistatic trajectories. In what follows, we will call the trajectories labelled by sign \(+\) the repulsive trajectories and the trajectories labeled by sign − the attractive trajectories. For the repulsive trajectories, the force acted by body M onto body m is directed toward body m (repels body m from body M), while for the attractive trajectories, this force is directed toward body M (attracts body m to body M). According to (27), the distance r between bodies M and m increases along the repulsive trajectories and decreases along the attractive trajectories.

According to the analysis presented above, the basic quasistatic trajectories possess the following properties.

  1. 1.

    All repulsive trajectories emerge from body M and are tangent at this point to the upward ray of the line of maximum slope. Similarly, all attractive trajectories enter body M and are tangent at this point to the downward ray of the line of maximum slope.

  2. 2.

    The motion of body m relative to body M along both repulsive and attractive quasistatic trajectories occurs clockwise in the right-hand half-plane relative to the line of maximum slope passing through body M and counterclockwise in the left-hand half-plane.

  3. 3.

    Through each point on the xy-plane, apart from the points of the line of maximum slope passing through body M, there pass one and only one basic repulsive trajectory and one and only one basic attractive trajectory.

  4. 4.

    The sets of repulsive and attractive trajectories are symmetric to one another with respect to the x-axis of the coordinate system Mxy.

  5. 5.

    Repulsive and attractive trajectories do not intersect the line of maximum slope passing trough body M.

The basic quasistatic trajectories form a network in the plane \(\Pi\) shown in Fig. 4.

Fig. 4
figure 4

Basic quasistatic trajectories

Full size image

In this figure, only the trajectories of the right-hand half-plane are depicted. The trajectories of the left-hand half-plane are symmetric about the y-axis to the trajectories of the right-hand half-plane.

When moving quasistatically, it is unnecessary to remain on a single basic trajectory. The general quasistatic motion allows switchings between the repulsive and attractive trajectories. Using these switchings one can implement a complex quasistatic trajectory that can approximate a curvilinear trajectory from a wide class of curves. In particular, from any point P of the plane, body m can move around body M along a curve arbitrarily close to the semi-circumference that is centered at body M and lies in the open half-plane to which the point P belongs. In view of the importance of such a motion for what follows, we formulate its properties as a separate proposition.

Proposition 1

From any point P of the plane, body m can move around body M along a curve arbitrarily close to the semi-circumference that is centered at body M and lies in the open half-plane with respect to the line of maximum slope passing through body M to which the point P belongs. This motion occurs clockwise in the right-hand half-plane and counterclockwise in the left-hand half-plane. It requires multiple switchings (in the limit, infinitely many switchings) between the repulsive and attractive trajectories.

For brevity, we will call the motions described in Proposition 1 circumferential motions or motions along a circumference. Such motions will be used in what follows as a part of the motion that drives the system under consideration between the initial and terminal positions.

Since neither of the basic quasilinear trajectories intersects the line of maximum slope passing through body M, neither complex curvilinear trajectory can intersect this line.

We defined the basic quasistatic trajectories as the curves governed by the equations of (28). These equations were derived under the assumption that \(\varphi \in (-\pi /2,\,\pi /2)\); the cases of \(\varphi = \pm \pi /2\) were excluded. Consider now these cases separately using the equations of (27). These equations have the solutions

$$\begin{aligned} r(s) = r_0 \pm s, \quad \varphi (s) = \pm \frac{\pi }{2}, \quad r_0> 0, \quad s > 0, \end{aligned}$$
(42)

where \(r_0\) is the polar radius of a point from which the length s of the trajectory of body m is measured. These solutions correspond to the quasistatic motions of body m along the line of maximum slope passing through body M. Sign plus (minus) in the expression for r(s) corresponds to the motion away from (toward) body M. For \(\varphi = \pi /2\) (\(\varphi = -\pi /2\)), body m moves along the positive (negative) semi-axis My. Thus, body m can move quasistatically upward and downward along both semi-axes of the axis My, if the inequality of (16) is valid.

We will not consider the trajectories defined by the relations of (42), since we have excluded the cases where bodies M and m lie on the common line of maximal slope at the initial time instant. From any other positions, it is impossible to bring body m onto the line of maximum slope passing through body M by combining the quasistatic motions and the fast motions that are considered in the next section.

Thus, we have described all possible quasistatic motions of the system. These motions will be used as components of the combined motion that alternates the quasistatic and fast motions and drives the crawler into the desired terminal state.

4 Fast motions

This section deals with the fast motions of the system. The fast motions are produced by an impulsive control force \(\mathbf{f} = \psi \dot{\delta }(t-t_0)\mathbf{e}\), where \(\delta (t-t_0)\) is Dirac’s delta function concentrated at a time instant \(t_0\), \(\mathbf{e}\) is the unit vector that defines the line of action of the impulsive force, and \(\psi\) is a scalar parameter that characterizes the intensity of the impulsive force. This force changes the positions of bodies m and M in an infinitesimal time. As a result, the bodies shift along the line that connected the bodies at the time instant immediately preceding the fast motion. The fast motion does not change the position of the center of mass of the system on the underlying plane \(\Pi\). Let \(\mathbf{r} _m(t)\) and \(\mathbf{r} _M(t)\) be the position vectors of the respective bodies on the plane \(\Pi\) defined as functions of time, and let \(t_0\) be the instant of the fast motion. Denote

$$\begin{aligned} \begin{array}{l} \mathbf{r }_{m}^-=\mathbf{r }_m(t_0-0), \quad \mathbf{r }_{M}^-=\mathbf{r }_M(t_0-0), \\ \mathbf{r }_m^+=\mathbf{r }_m(t_0+0), \quad \mathbf{r }_M^+=\mathbf{r }_M(t_0+0), \\ \mathbf{e} = \frac{\mathbf{r }_m^- - \mathbf{r }_{M}^-}{|\mathbf{r }_{m}^- - \mathbf{r }_{M}^{-}|}, \end{array} \end{aligned}$$
(43)

where \(t_0-0\) and \(t_0+0\) are the time instants that immediately precedes and immediately follows the fast motion. The changes in the positions of the bodies resulting from the fast motion are given by

$$\begin{aligned} \mathbf{r} _m^+ = \mathbf{r} _m^- + \frac{\psi }{m}\,\mathbf{e} , \quad \mathbf{r} _M^+ = \mathbf{r} _M^- - \frac{\psi }{M}\,\mathbf{e} . \end{aligned}$$
(44)

where \(\psi\) characterises the action of the control force for the fast motion and can be chosen arbitrarily. These relations, in particular imply that the fast motion does not change the position of the system’s center of mass:

$$\begin{aligned} \mathbf{r} _C^+ = \frac{m\mathbf{r} _m^+ + M\mathbf{r} _M^+}{M+m} = \frac{m\mathbf{r} _m^- + M\mathbf{r} _M^-}{M+m} = \mathbf{r} _C^-. \end{aligned}$$
(45)

The fast motion allows bringing one of the bodies m or M to any position on the line \(\mathbf{e}\) by choosing an appropriate parameter \(\psi\) of the impulsive control force \(\mathbf{f}\). The position of the other body is then defined uniquely.

Fig. 5
figure 5

Fast motion: The positions of bodies m and M change instantaneously along the line that connects these bodies, the position of the center of mass does not change

Full size image

The fast motion of the system is illustrated in Fig. 5. Black and grey circles depict the positions of the bodies immediately before and straight after the fast motion, respectively.

The fast motion can be regarded as a limiting case of a motion produced by a piecewise constant control force that has a small duration. The motion of bodies m and M on an inclined plane \(\Pi\) is governed by the equations

$$\begin{aligned} m\ddot{\mathbf{r }}_m=\, \mathbf{f } + m\mathbf{g } + mg\cos \gamma \,\mathbf{n } + \mathbf{R }_m, \end{aligned}$$
(46)
$$\begin{aligned} M\ddot{\mathbf{r }}_M= & {} -\mathbf{f } + M\mathbf{g } + Mg\cos \gamma \,\mathbf{n } + \mathbf{R }_M, \end{aligned}$$
(47)

where \(\mathbf{R} _m\) and \(\mathbf{R} _M\) are the forces of friction applied by the plane to the respective bodies.

Proceed in these equations from the variables \(\mathbf{r} _m\) and \(\mathbf{r} _M\) to the variables \(\mathbf{r} _C\) and \(\varvec{\rho }\) introduced as follows:

$$\begin{aligned} \mathbf{r} _C = \frac{m\mathbf{r} _m + M\mathbf{r} _M}{M+m}, \quad {\varvec{\rho }} = \mathbf{r} _m - \mathbf{r} _M. \end{aligned}$$
(48)

The vector \(\mathbf{r} _C\) is the position vector of the system’s center of mass and the vector \(\varvec{\rho }\) is drawn from body M to body m. In the new variables, the equations of (46) and (47) become

$$\begin{aligned} \ddot{\mathbf{r }}_{C}= \, \mathbf{G }_{1}, \quad \mathbf{G }_{1} = \mathbf{g } + g\cos \gamma \,\mathbf{n } + \frac{\mathbf{R }_{m}+\mathbf{R }_{M}}{M+m}, \end{aligned}$$
(49)
$$\begin{aligned} \ddot{\varvec{\rho }}= & {} \frac{M+m}{Mm}\left( \frac{{\varvec{\rho }}}{\rho }\right) f + \mathbf{G }_{2}, \; \mathbf{G }_{2} = \frac{M\mathbf{R }_{m} - m\mathbf{R }_{M}}{Mm}. \end{aligned}$$
(50)

where \(\rho = |{\varvec{\rho }}|\) and \(f = ({\varvec{\rho }} \cdot \ \mathbf{f} )/\rho\). The quantities \(\mathbf{G} _1\) and \(\mathbf{G} _2\) are bounded. The equations of (49) and (50) can be represented in the integral form

$$\begin{aligned} \mathbf{r} _C= & {} \mathbf{r} _C(t_0) + \dot{\mathbf{r }}_C(t_0)(t-t_0) + \int \limits _{t_0}^t(t-\xi )\mathbf{G} _1d\xi , \end{aligned}$$
(51)
$$\begin{aligned}&\quad \begin{array}{l} {\varvec{\rho }} = {\varvec{\rho }}(t_0) + {\dot{\varvec{\rho }}}(t_0)(t-t_0) \\+\frac{M+m}{Mm}\int \limits _{t_0}^t(t-\xi )\left( \frac{{\varvec{\rho }}}{\rho }\right) fd\xi + \int \limits _{t_0}^t(t-\xi )\mathbf{G} _2d\xi , \end{array} \end{aligned}$$
(52)

where \(t_0\) is an arbitrary fixed time instant.

Define the quantity f as follows:

$$\begin{aligned} f = \left\{ \begin{array}{rl} 0, &{} \, t \notin [t_0 - \varepsilon ,\;t_0 + \varepsilon ], \\ a, &{} \, t \in [t_0 - \varepsilon ,\;t_0 - \varepsilon + \tau ), \\ 0, &{} \, t \in [t_0 - \varepsilon + \tau ,\;t_0 + \varepsilon - \tau ), \\ -a, &{} \, t \in [t_0 + \varepsilon - \tau ,\;t_0 + \varepsilon ], \end{array} \right. \end{aligned}$$
(53)

where \(0< \tau < \varepsilon\). Using Eqs. (51) and (52) we obtain

$$\begin{aligned}&\begin{array}{l} \mathbf{r} _C(t_0+\varepsilon ) - \mathbf{r} _C(t_0-\varepsilon ) \\ =2\varepsilon \dot{\mathbf{r }}_C(t_0-\varepsilon ) + \int \limits _{t_0-\varepsilon }^{t_0+\varepsilon }(t_0 + \varepsilon -\xi )\mathbf{G} _1d\xi , \end{array} \end{aligned}$$
(54)
$$\begin{aligned}&\quad \begin{array}{l} {\varvec{\rho }}(t_0+\varepsilon ) - {\varvec{\rho }}(t_0-\varepsilon ) = 2\varepsilon {\dot{\varvec{\rho }}}(t_0-\varepsilon ) \\ +\frac{M+m}{Mm}\int \limits _{t_0-\varepsilon }^{t_0+\varepsilon }(t_0+\varepsilon -\xi )\left( \frac{{\varvec{\rho }}}{\rho }\right) fd\xi \\ +\int \limits _{t_0-\varepsilon }^{t_0+\varepsilon }(t_0+\varepsilon -\xi )\mathbf{G} _2d\xi , \end{array} \end{aligned}$$
(55)

Since \(\mathbf{G} _1\) and \(\mathbf{G} _2\) are bounded, in the limit as \(\varepsilon \rightarrow +0\) we have

$$\begin{aligned}&\mathbf{r} _C(t_0+0) - \mathbf{r} _C(t_0-0) = 0, \end{aligned}$$
(56)
$$\begin{aligned}&\quad \begin{array}{l} {\varvec{\rho }}(t_0+0) - {\varvec{\rho }}(t_0-0) \\ =\frac{M+m}{Mm}\left( \lim \limits _{\varepsilon \rightarrow +0}\int \limits _{t_0-\varepsilon }^{t_0+\varepsilon }(t_0+\varepsilon -\xi )\left( \frac{{\varvec{\rho }}}{\rho }\right) fd\xi \right) . \end{array} \end{aligned}$$
(57)

It can be shown that

$$\begin{aligned} \begin{array}{l} \lim \limits _{\varepsilon \rightarrow +0}\int \limits _{t_0-\varepsilon }^{t_0+\varepsilon }(t_0+\varepsilon -\xi )\left( \frac{{\varvec{\rho }}}{\rho }\right) fd\xi \\ = \left( \lim \limits _{\varepsilon \rightarrow +0}\int \limits _{t_0-\varepsilon }^{t_0+\varepsilon }(t_0+\varepsilon -\xi )f(\xi )d\xi \right) \mathbf{e} , \quad \mathbf{e} = \frac{{\varvec{\rho }}(t_0-0)}{\rho (t_0-0)}. \end{array} \end{aligned}$$
(58)

For f defined by Eq. (53), we have

$$\begin{aligned} \int \limits _{t_0-\varepsilon }^{t_0+\varepsilon }(t_0+\varepsilon -\xi )f(\xi )d\xi = 2a\tau \varepsilon \left( 1-\frac{\tau }{2\varepsilon }\right) . \end{aligned}$$
(59)

Choose the parameters \(\tau\) and a in (53) so that

$$\begin{aligned} \lim \limits _{\varepsilon \rightarrow +0}2a\tau \varepsilon \left( 1-\frac{\tau }{2\varepsilon }\right) = \psi , \end{aligned}$$

for example, as follows:

$$\begin{aligned} \tau = \varepsilon ^2, \quad a = \frac{\psi }{2\varepsilon ^3}. \end{aligned}$$

Then Eqs. (57) and (58) imply

$$\begin{aligned} {\varvec{\rho }}(t_0+0) - {\varvec{\rho }}(t_0-0) = \frac{M+m}{Mm}\psi \mathbf{e} . \end{aligned}$$
(60)

By proceeding in the last relation from the variables \(\varvec{\rho }\) and \(\mathbf{r} _C\) to the variables \(\mathbf{r} _m\) and \(\mathbf{r} _M\), using Eq. (48) and taking into account Eq. (56), we arrive at the relations of (44).

5 Algorithm for driving the system to the terminal state

The algorithm that is presented in this section alternates the fast and slow (quasistatic) motions and drives the system into an arbitrarily small neighborhood of the desired terminal state. This algorithm involves an operation that drives body m from an initial position in the plane \(\Pi\) into a prescribed terminal position in this plane in such a way that the resulted position of body M is arbitrarily close to its initial position. For brevity, this operation will be referred to as Motion \(\mathfrak {R}\). Motion \(\mathfrak {R}\) is possible only if in the state preceding this operation, bodies M and m do not lie on the common line of maximum slope.

5.1 Motion \(\mathfrak {R}\)

The feasibility of Motion \(\mathfrak {R}\) is justified by the following proposition.

Proposition 2

From any state of rest in which bodies M and m do not lie on the common line of maximum slope, the system can be driven to a state of rest in which body m occupies any prescribed position on the plane \(\Pi\) and the position of body M is arbitrarily close to its initial position.

Proof

Let A and B be the initial and terminal positions of body m on the plane \(\Pi\). The position of body m relative to body M is characterized by the Cartesian coordinates \((x,\,y)\) or the polar coordinates \((r,\,\varphi )\) in the reference frame Mxy, the origin of which is located at body M. Denote by \(\Pi _l\) and \(\Pi _r\) the left-hand and right-hand half-planes relative to the coordinate axis My:

$$\begin{aligned} \Pi _l = \left\{ x,\,y:\; x < 0\right\} , \quad \Pi _r = \left\{ x,\,y:\; x > 0\right\} . \end{aligned}$$
(61)

In terms of the polar coordinates the sets \(\Pi _l\) and \(\Pi _r\) are defined by

$$\begin{aligned} \begin{array}{l} \Pi _l = \left\{ r,\,\varphi :\; r> 0, \, \varphi \in \left( \frac{\pi }{2},\,\frac{3\pi }{2}\right) \right\} , \\ \Pi _r = \left\{ r,\,\varphi :\; r > 0, \, \varphi \in \left( -\frac{\pi }{2},\,\frac{\pi }{2}\right) \right\} . \end{array} \end{aligned}$$
(62)

Assume without loss of generality that \(A \in \Pi _l\); the case of \(A \in \Pi _r\) can be considered in a similar way.

Let \(B \in \Pi _r\). Then the strategy for driving body m to the point B involves several steps.

  • Step 1 Body m is driven quasistatically toward body M along the attractive trajectory that passes through the point A. Body m moves to a point C the distance \(\varepsilon\) from which to body M is small enough. The properties of the quasistatic trajectories imply that the angle between the line CM and the axis My tends to zero as \(\varepsilon \rightarrow +0\).

  • Step 2 By fast motion the system is transferred into the configuration symmetric to the configuration resulted from Step 1 about the center of mass of the system. Body M shifts (in jump) from its initial position but remains close to it for \(\varepsilon\) small enough. Body m jumps from the position C to a position D in the half-plane \(\Pi _r\). More precisely, the point D belongs to the right-hand half-plane with respect to the line of maximum slope passing through the new position of body M, however, this half-plane virtually coincides with \(\Pi _r\) for small \(\varepsilon\).

  • Step 3 Body m moves quasistatically clockwise along a circumference of radius \(\varepsilon\) about body M from the point D into a point E. The point E is defined as the point of intersection of the circumference with the repulsive quasistatic trajectory passing through the point B.

  • Step 4 Body m moves quasistatically from the point E into the point B along a repulsive trajectory.

Thus, we have proved the proposition for the case where the initial and terminal positions of body m lie in different half-planes. If \(A \in \Pi _l\) and \(B \in \Pi _l\), one should perform steps 1 and 2 and then regard the point D as the new initial position for body m.

In the case where the point B lies on the axis My, one should perform Steps 1 and 2. As a result of Step 2 body M jumps to a new position and the point B will appear in the right-hand half-plane relative to the line of maximum slope passing through the new position of body M. Then one can perform Steps 3 and 4.

Motion \(\mathfrak {R}\) is illustrated in Fig. 6. In this figure, as well as in Figs. 7 and 8, larger and smaller circles depict the successive positions of bodies M and m, respectively. The shading density of the circles decreases as the later positions are depicted.

Fig. 6
figure 6

Motion \(\mathfrak {R}\): Driving body m from the point A to the point B, with body M staying close to its initial position

Full size image

We will describe now the entire algorithm. Denote by \(P_M^i\) and \(P_M^t\) the initial and terminal positions of body M, respectively, by \(P_m^i\) and \(P_m^t\) the respective positions of body m. Let \(\Gamma\) be the line that connects the points \(P_M^i\) and \(P_M^t\). We assume that this line is not a line of maximum slope on the plane \(\Pi\). If the line \(\Gamma\) is a line of maximum slope, one can proceed as follows. At the initial time instant, shift by means of fast motion body M from its initial position and then consider the resulting positions of bodies M and m as new initial positions for these bodies. The new initial position of body M will not lie on the line of maximum slope passing through the point \(P_M^t\), since at the initial positions bodies M and m do not lie of the common line of maximum slope. The line \(\Gamma\) divides the plane \(\Pi\) into two half-planes, \(\Pi _+\) and \(\Pi _-\). The half-plane \(\Pi _+\) is the upper half-plane, in which the positive semi-axis My lies. (Recall that the axis My is directed upward along the line of maximum slope.) The half-plane \(\Pi _-\) is the lower half-plane. Consider separately two cases, Case 1 and Case 2. Case 1 implies that \(P_m^i \in \Pi _+ \cup \Gamma\), i.e., the initial position of body m lies above or on the line \(\Gamma\). For Case 2, the inclusion \(P_m^i \in \Pi _-\) holds.

5.2 Algorithm: Case 1

If the point \(P_m^i\) lies above or on the line \(\Gamma\), i.e., \(P_m^i \in \Pi _+ \cup \Gamma\), then the following steps should be performed to transfer the system from the initial state to the terminal state.

  • Step 1. By quasistatic motion along a circumference that is centered at the point \(P_M^i\) and has a radius of \(|P_M^iP_m^i|\) move body m onto the line \(\Gamma\). As a result of this step, body M remains in its initial position \(P_M^i\) and body m appears in a new position \(P_m^1\). If \(P_m^i \in \Gamma\), this step should be skipped.

  • Step 2. By fast motion move body M into the terminal position \(P_M^t\). Body m will shift along the line \(\Gamma\) into a position \(P_m^2\).

    Steps 1 and 2 of the algorithm for Case 1 are illustrated in Fig. 7.

    Fig. 7
    figure 7

    Steps 1 and 2 of the algorithm in Case 1. Step 1: Body m moves quasistatically between positions \(P_m^i\) and \(P_m^1\), body M does not move. Step 2: Body M jumps between positions \(P_M^i\) and \(P_M^t\), body m jumps between positions \(P_m^1\) and \(P_m^2\)

    Full size image

  • Step 3. Perform Motion \(\mathfrak {R}\) to drive body m from the position \(P_m^2\) into the terminal position \(P_m^t\). This motion shifts body M from the prescribed position \(P_M^t\) but this shift can be made arbitrarily small by choosing \(\varepsilon\) small enough.

5.3 Algorithm: Case 2

If \(P_m^i \in \Pi _-\), the algorithm implies the following strategy.

  • Step 1. Move body m quasistatically along an attractive trajectory from the position \(P_m^i\) to a point \(P_m^1\) close to the point \(P_M^i\).

  • Step 2. By fast motion transfer the two-body system into the configuration symmetric to the configuration resulted from Step 1 about the center of mass of the system. After this step, body M jumps into a position \(P_M^1\) that is close to the position \(P_M^i\) and body m jumps into a position \(P_m^2\). If we draw the line \(\Gamma ^1\) through the points \(P_M^t\) and \(P_M^1\), the point \(P_m^2\) will lie in the upper half-plane with respect to the line \(\Gamma ^1\).

  • Step 3. Perform steps 1 to 3 of the algorithm of Case 1 using the point \(P_M^1\) as \(P_M^i\), the point \(P_m^2\) as \(P_m^i\), and the line \(\Gamma ^1\) as \(\Gamma\).

    Steps 1 and 2 of the algorithm for Case 2 are illustrated in Fig. 8.

    Fig. 8
    figure 8

    Steps 1 and 2 of the algorithm in Case 2. Step 1: Body m moves quasistatically between positions \(P_m^i\) and \(P_m^1\), body M does not move. Step 2: Body M jumps between positions \(P_M^i\) and \(P_M^1\), body M jumps between positions \(P_m^1\) and \(P_m^2\)

    Full size image

6 Conclusions

A two-body limbless crawler on a rough (Coulomb’s friction) plane inclined to the horizon under a nonzero angle can in principle be moved from an arbitrary initial state of rest to an arbitrarily small neighborhood of any prescribed terminal state of rest, provided that both bodies do not lie on the common line of maximal slope at the initial instant and the tangent of the plane inclination angle is less than the coefficient of friction multiplied by the ratio of the difference between the masses of the bodies to the total mass of the crawler. A control strategy is presented for the case where no constraints are imposed on the force of interaction between the bodies that plays the role of a control force and on the distance between the bodies. This strategy combines infinitely slow (quasistatic) motions and infinitely fast (jumping) motions. It can be said that the two-body crawler on an inclined plane is controllable from almost all initial states of rest to any terminal state of rest. The controllability fails if at the initial time instant both bodies of the crawler lie on the common line of maximal slope, as well as if the plane is horizontal. In both these cases the crawler remains on the line that connected the bodies at the initial time instant. Thus, on a plane inclined under a nonzero angle, the feasible motions are not confined to rectilinear motions, which considerably expands the potential application area of two-body crawlers in robotics and may give new explanations to locomotion of some limbless animals.