Analysis of a double layer porous hybrid journal bearing considering the combined influence of wear and non-Newtonian behaviour of lubricant

Abstract

Use of porous materials in fluid film is well established so as to make more uniform distribution of pressure along the journal surface. The work presented in this paper deals with theoretical examination into the effect of worn bearing surface on the behaviour of a hybrid double layer porous journal bearing system (DLPJB_S) operating with power-law lubricants. The governing equation for the flow of non-Newtonian lubricant in the bearing porous clearance space is solved by using the FEM. The effects of non-Newtonian lubricant on the bearing characteristics of a worn bearing have been studied. Findings of this study indicates that the hybrid DLPJB_S operating under non-Newtonian lubricant offers enhanced values of ${\bar{h}}_{min}$, ${\bar{\omega}}_{th}$ and rotor dynamic coefficients (stiffness and damping coefficients).

1 Introduction

Porous fluid film bearings systems rely on the fact that lubricant is able to flow through a large number of pores in order to ensure uniform distribution of pressure on journal surface. This feature makes them more preferable vis-à-vis recessed bearings. Besides this porous bearing do not require an external supply of lubricant oil over a prolonged period of time. In recent years, many researchers have presented both theoretical as well as experimental studies concerning porous journal bearing systems. A study by Cameron and Morgan [1, 2] proposed a theoretical model to analyze the porous journal bearing lubrication under hydrodynamic conditions. Rhodes and Rouleau [3] studied the effect of permeability parameter $\left(\Psi \right)$ on the performance of a narrow porous journal bearing with sealed ends using the Darcy equation. They numerically simulated the results for the values of permeability parameter $\left(\Psi \right)$ in the range of 0.001 to 0.1. Mokhtar et al. [4] carried out an experimental and numerical study on the performance behaviour of porous journal bearing in terms of eccentricity ratio, friction coefficient and angle of attitude for different value of permeability parameters. Howarth [5] carried out numerical and experimental study of porous journal bearing for circular thrust bearing. Chattopadhyay and Majumdar [6] investigated the performance characteristics behavior of porous hydrostatic circular journal bearings considering the Beavers–Joseph model on the porous surface. Guha [7] theoretically analyzed the stability performance parameter of externally pressurized porous bearing system by considering the slip effect on the porous surface, operating with a Newtonian lubricant.

Single layer porous journal bearing system (SLPJB_S) have less load carrying capacity due to lubricant seepage through the bearing wall. This problem may be overcome by restricting seepage of lubricant into the wall of bearing. Bearing designers tempted to overcome this limitation by using DLPJB_S with a thin layer of surface backed by a thick layer substrate that was highly permeable. Many researchers [8,9,10,11,12,13] have discussed the characteristics behaviour of porous hydrostatic journal bearing configurations. A theoretical study reported by Cusano [8, 9] made use of short and long approximations for the solution of a double layer porous bearing in hydrodynamic lubrication condition. The results were presented for the values of permeability parameter $\left(\Psi =0.0001\,\text{to}\,0.1\right)$, permeability ratio $\left(\frac{{k}_{2}}{{k}_{1}}=20\right)$ and porous layer thickness ratio $\left(\gamma =0.02, 0.05\right)$. Saha and Majumdar [10] theoretically analyzed the steady-state and stability performance parameter of externally pressurized DLPJB_S and their findings revealed that DLPJB_S have better performance characteristics than that of a SLPJB_S. A study by Okano [11] reported that stability performance parameter of DLPJB_S get enhanced as compared to SLPJB_S. Rao et al. [12] theoretically analyzed the DLPJB_S by using the Brinkman’s model for modelling the non-Newtonian lubricant flow in the porous. Srinivasan [13] studied the performance behaviour of double layer porous slider bearings and presented the results for the commonly used non-dimensional parameters i.e. permeability parameter $\Psi =0.0001\,\text{to}\,1.0$, permeability ratio $\left(\frac{{k}_{2}}{{k}_{1}}=20\right)$ and porous layer thickness ratio $\left(\frac{{H}_{2}}{{H}_{1}}=0.9\right)$. They reported that the double layer porous slider bearings provide better performance than the conventional porous slider bearings.

Due to prolonged usage of bearing systems, the wear of bearing surfaces is rather inevitable and affects the bearing clearance space. Thus, the bearing performance gets affected. Therefore, the influence of wear must be considered in the analysis for accurately predicting the performance of bearing. Several researchers [14,15,16,17,18,19,20,21] have analyzed the effect of wear on bearing performance, both qualitatively and quantitatively. Hashimoto et al. [14] studied the influence of wear on the behaviour of hydrodynamic journal bearing running under turbulent and laminar flow conditions. The values of wear depth parameter $\left({\bar{\delta}}_{w}\right)$ were varied in the range of 0 to 0.5. Dufrane et al. [15] analytically and experimentally evaluated the influence of wear on the behaviour of journal bearing in hydrodynamic condition and reported that worn zone occurs at bottom surface. In their analysis they reported that the maximum wear footprint is around 50% of the radial clearance. Therefore, the values of wear depth parameter $\left({\bar{\delta}}_{w}\right)$ was varied from 0 to 0.5. Laurant and Childs [16] analyzed the influence of wear on the recess journal bearing under hybrid operating mode used for application of turbo-pumps in liquid rocket engine. Tokar and Alexandrov [17] used a FEM model to evaluate effect of wear on the behaviour of hydrostatic journal bearing. Kumar and Mishra [18, 19] carried out a numerical study on the behaviour of hydrodynamic bearings in terms of Sommerfeld number, flow rate, friction and stability parameters for various values of wear depth parameters. Awasthi et al. [20] studied the static and dynamic performance of non-recessed hole-entry hybrid journal bearings considering the influence of wear in the analysis using a Dufrane model. They presented the results for the non-dimensional values of wear depth parameter $\left({\bar{\delta}}_{w}\right)$ in the range of 0 to 0.5. Vaidyanathan and Keith [21] analyzed the non-circular journal bearing considering effect of wear depth parameter including the cavitation effects.

Further, it may be noted that mixing of different types of additive packages is essential in order to obtain favourable lubricating performance from a chosen lubricant. Adding these additive makes the behaviour of lubricant non-Newtonian. There are different models of non-Newtonian fluid like cubic law, micropolar fluid, power law, couple stress fluid etc. to describe the non-Newtonian behaviour. Many researchers [22,23,24,25,26,27] claims that power-law model is the most practical and is generally used model to define the shear thickening and shear thinning behaviour of lubricant. Safar [23] numerically studied the hydrodynamic journal bearing system for considering the behaviour of non-Newtonian lubricant (power-law model). Results were presented for the values of power law index $n=0.9, 1.0, 1.1$. Tayal et al. [24, 25] theoretically evaluated the characteristics of an elliptical journal bearing and circular journal bearing in hydrodynamic condition considering the influence of non-Newtonian behaviour using the power-law and cubic-law. The non-dimensional values of power law index $\left(n\right)$ were chosen in the range of 0.5–1.5. Prashad [26] developed a method for analysing performance of hydrodynamic bearings on the basis of maximum fluid temperature in fluid film incorporating the variation of clearance ratio and viscosity. Further, Wu and Dareing [27] used the power-law rheological model for calculating the pressure in squeeze film under hydrostatic conditions. Sinhasan et al. [28] carried out a theoretical study concerning the hydrostatic flexible journal bearing compensated with orifice restrictors operating with non-Newtonian lubricants for the various values of power law index $\left(n=0.5, 0.7, 1.0\right)$.

The review of the literature as shown in earlier sections indicates that the design of fluid film bearings is affected by a number of parameters such as aspect ratio $\left(\lambda =\frac{L}{D}\right)$, speed parameter $\left(\Omega \right)$, radial clearance $\left(c\right)$, viscosity of lubricant $\left(\mu \right)$, supply pressure $\left({p}_{s}\right)$, permeability parameter $\left(\Psi \right)$, flow behaviour index $\left(n\right)$, wear depth parameter $\left({\bar{\delta}}_{w}\right)$, etc. and their individual/interactive effects. It may be noticed that majority of the published studies have been carried out using the commonly used representative values of non-dimensional parameters such as permeability parameter $\left(\Psi =0.001\,\text{to}\,0.1\right)$, permeability ratio $\left(\frac{{k}_{2}}{{k}_{1}}=20\right)$ and porous layer thickness ratio $\left(\gamma =0.02, 0.05\right)$, wear depth parameter $\left({\bar{\delta}}_{w}=0\,\text{to}\,0.5\right)$ and power law index $\left(n=0.5\,\text{to}\,1.5\right)$. Further, the choice of lubricant affects the performance of the bearings significantly. From the previous studies it has been observed that the use of shear thinning (pseudoplastic) lubricant [23,24,25, 28, 29]. reduces the fluid film pressure, load capacity and improves the stability of bearing, whereas the use of shear thickening (dilatant) lubricant [23,24,25, 28, 29] improves the fluid film pressure, load capacity and reduces the stability of bearing, so that a designer has to trade off the various requirements during the design process.

Due to continuous operation of bearings, wear of tribo-pairs is inevitable and this greatly affects the bearing performance. The wear ultimately results into premature failure of bearing. So it becomes imperative that the effect of wear on the bearing performance must be predicted accurately so that the designer can make appropriate changes in the design process [14, 15, 20, 21]. As the DLPJBs are also bearing elements which gets worn out due to continuous operation of machines. Thus, the bearing performance gets affected and consequently the performance of machine i.e. loss of accuracy, productivity, repeatability etc. Besides this the stability of the bearing is an important issue from the dynamics point of view. If the stability of DLPJBs can be improved further, it would be desirable not only from the design point of view but also from industry point of view. As mentioned in the reported literature [23,24,25, 28, 29] the use of shear thinning (pseudoplastic) lubricant, the stability of bearing further can be improved. Unstable operation of the journal bearing system is detrimental to the performance of machine, as the system would be subjected to very high vibrations. Thus, for the smooth operation of bearings it is desirable to have an improved stability threshold speed margin $\left({\bar{\omega}}_{th}\right)$ for the given geometric and operating conditions. Therefore, the author(s) gets motivated to explore the combined influence of non-Newtonian behaviour of lubricant and influence of wear on the performance of hybrid DLPJBs. In this article, the performance of hybrid DLPJBs considering the effects of shear thinning/shear thickening and influence of wear has been studied. The results presented in this paper are expected to be quite useful to the bearing designers.

2 Double layer porous journal bearing model description

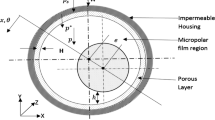
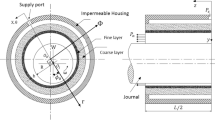
Figure 1a, b illustrates the schematic of hybrid DLPJB_S configuration. In this study, the material of porous bearing is assumed to be isotropic and homogeneous. The modified Reynolds equation governing the flow of non-Newtonian lubricant in clearance space of a hybrid DLPJB_S considering steady state, incompressible, and laminar flow is given as [8, 10, 13, 30, 31]:

Fig. 1

a Schematic of porous journal bearing system. b Another view of porous journal bearing system

$$\frac{\partial }{\partial x}\left(\frac{{h}^{3}}{12\mu }\frac{\partial p}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{{h}^{3}}{12\mu }\frac{\partial p}{\partial y}\right)=\frac{U}{2}\frac{\partial h}{\partial x}+\frac{\partial h}{\partial t}+\frac{{k}_{1}}{\mu }{\left(\frac{\partial {p}_{1}}{\partial z}\right)}_{Z=0}$$

(1)

where $z=0$ indicates the porous surface and fluid film region interface.

The pressure distribution $\left({p}_{1}\right)$ and $\left({p}_{2}\right)$ in the inner and outer layer of porous surface (Fig. 1a, b) is represented by the Laplace equation of the form [8, 10, 13]:

$$\frac{{\partial }^{2}{p}_{1}}{{\partial x}^{2}}+\frac{{\partial }^{2}{p}_{1}}{{\partial y}^{2}}+\frac{{\partial }^{2}{p}_{1}}{{\partial z}^{2}}=0$$

(2a)

$$\frac{{\partial }^{2}{p}_{2}}{{\partial x}^{2}}+\frac{{\partial }^{2}{p}_{2}}{{\partial y}^{2}}+\frac{{\partial }^{2}{p}_{2}}{{\partial z}^{2}}=0$$

(2b)

Integrating Eq. (2a) with respect to ‘$z$’ within the limits ${-H}_{1}$ to 0, yields

$${\left(\frac{\partial {p}_{1}}{\partial z}\right)}_{Z=0}=-\underset{{-H}_{1}}{\overset{0}{\int }}\left(\frac{{\partial }^{2}{p}_{1}}{{\partial x}^{2}}+\frac{{\partial }^{2}{p}_{1}}{{\partial y}^{2}}\right)dz+{\left(\frac{\partial {p}_{1}}{\partial z}\right)}_{Z={-H}_{1}}$$

(3)

Since, the normal flow between the boundary of two porous layer is equal, i.e.

$${{k}_{1}\left(\frac{\partial {p}_{1}}{\partial z}\right)}_{Z={-H}_{1}}={{k}_{2}\left(\frac{\partial {p}_{2}}{\partial z}\right)}_{Z={-H}_{1}}$$

(4)

Therefore,

$$ \left( {\frac{{\partial p_{1} }}{\partial z}} \right)_{Z = 0} = - \mathop \int \nolimits_{{ - H_{1} }}^{0} \left( {\frac{{\partial^{2} p_{1} }}{{\partial x^{2} }} + \frac{{\partial^{2} p_{1} }}{{\partial y^{2} }}} \right)dz + \frac{{k_{2} }}{{k_{1} }}\left( {\frac{{\partial p_{2} }}{\partial z}} \right)_{{Z = - H_{1} }} . $$

(5)

Further Integrating Eq. (2b) with reect to ‘$z$’ within limits $-H$ to ${-H}_{1}$

$$ \left( {\frac{{\partial p_{2} }}{\partial z}} \right)_{{Z = - H_{1} }} = - \mathop \int \nolimits_{ - H}^{{ - H_{1} }} \left( {\frac{{\partial^{2} p_{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} p_{2} }}{{\partial y^{2} }}} \right)dz\,\,\,{\text{since}},\,\, \left( {\frac{{\partial p_{2} }}{\partial z}} \right)_{Z = - H} = 0 $$

(6)

From Eqs. (5) and (6), gives

$${\left(\frac{\partial {p}_{1}}{\partial z}\right)}_{Z=0}=-\underset{{-H}_{1}}{\overset{0}{\int }}\left(\frac{{\partial }^{2}{p}_{1}}{{\partial x}^{2}}+\frac{{\partial }^{2}{p}_{1}}{{\partial y}^{2}}\right)dz-\frac{{k}_{2}}{{k}_{1}}\underset{-H}{\overset{{-H}_{1}}{\int }}\left(\frac{{\partial }^{2}{p}_{2}}{{\partial x}^{2}}+\frac{{\partial }^{2}{p}_{2}}{{\partial y}^{2}}\right)dz$$

(7)

Now, for bearing film interface;

$${p}_{1}\left(x,y,0\right)=p\left(x,y\right)$$

(8)

and for an interface between the porous layer

$${p}_{1}\left(x,y,{-H}_{1}\right)={p}_{2}\left(x,y,{-H}_{1}\right)$$

(9)

Therefore,

$$ \left( {\frac{{\partial p_{1} }}{\partial z}} \right)_{Z = 0} = - H\left[ {\frac{{k_{2} }}{{k_{1} }}\left( {1 - \frac{{H_{1} }}{H}} \right) + \frac{{H_{1} }}{H}} \right]\left( {\frac{{\partial^{2} p}}{{\partial x^{2} }} + \frac{{\partial^{2} p}}{{\partial y^{2} }}} \right) $$

(10)

$${\left(\frac{\partial {p}_{1}}{\partial z}\right)}_{Z=0}=-H\left[{K}_{r}\left(1-\upgamma \right)+\upgamma \right]\left(\frac{{\partial }^{2}p}{{\partial x}^{2}}+\frac{{\partial }^{2}p}{{\partial y}^{2}}\right)$$

(11)

where ${K}_{r}=\frac{{k}_{2}}{{k}_{1}}$, and $\upgamma =\frac{{H}_{1}}{H}$.

Now substituting the value ${\left(\frac{\partial {p}_{1}}{\partial z}\right)}_{Z=0}$ from Eq. (11) in Eq. (1), the modified Reynolds equation becomes:

$$\frac{\partial }{\partial x}\left[\left\{\frac{{h}^{3}}{12\mu }+\frac{{k}_{1}H}{\mu }\left({K}_{r}\left(1-\upgamma \right)+\gamma \right)\right\}\frac{\partial p}{\partial x}\right]+\frac{\partial }{\partial y}\left[\left\{\frac{{h}^{3}}{12\mu }+\frac{{k}_{1}H}{\mu }\left({\bar{p}}_{r}\left(1-\gamma \right)+\gamma \right)\right\}\frac{\partial p}{\partial y}\right]=\frac{U}{2}\frac{\partial h}{\partial x}+\frac{\partial h}{\partial t}$$

(12)

The Eq. (12) can also be expressed for non-Newtonian fluid which is given as:

$$\frac{\partial }{\partial x}\left[\left\{{F}_{2}+\frac{{F}_{0}{k}_{1}\text{H}}{h}\left({K}_{r}\left(1-\upgamma \right)+\gamma \right)\right\}\frac{\partial p}{\partial x}\right]+\frac{\partial }{\partial y}\left[\left\{{F}_{2}+\frac{{F}_{0}{k}_{1}\text{H}}{h}\left({\bar{p}}_{r}\left(1-\gamma \right)+\gamma \right)\right\}\frac{\partial p}{\partial y}\right]={\omega }_{J}{R}_{J}\left\{\frac{\partial }{\partial x}\left(h-\frac{{F}_{1}}{{F}_{0}}\right)\right\}+\frac{\partial h}{\partial t}$$

(13)

where ${F}_{0}={\int }_{0}^{h}\frac{1}{\mu }dz$ ; ${F}_{1}={\int }_{0}^{h}\frac{z}{\mu }dz$ ; ${F}_{2}={\int }_{0}^{h}\left(\frac{{z}^{2}}{\mu }-\frac{z}{\mu } \frac{{F}_{1}}{{F}_{0}}\right)dz$.

After making use of following non-dimensional parameters, the Eq. (13) reduces to the following form:

$$\begin{aligned}&\alpha =\frac{x}{{R}_{j}}; \quad \beta =\frac{y}{{R}_{j}}; \quad \bar{p}=\frac{p}{{p}_{s}}; \quad \Omega ={\omega }_{J}\left(\frac{{\upmu }_{r}{R}_{j}^{2}}{{c}^{2}{P}_{s}}\right); \quad U={\omega }_{j}{R}_{j}; \quad \bar{h}=\left(\frac{h}{c}\right); \quad \bar{t}=t\left(\frac{{c}^{2}{P}_{s}}{{\upmu }_{r}{R}_{j}^{2}}\right);\\ & \bar{\upmu }=\left(\frac{\upmu }{{\upmu }_{r}}\right); \quad \Psi =\frac{{k}_{1}H}{{c}^{3}}; \quad {\bar{F}}_{0}={F}_{0}\left(\frac{{\upmu }_{r}}{h}\right); \quad {\bar{F}_{1}} ={F}_{1}\left(\frac{{\upmu }_{r}}{{h}^{2}}\right); \quad {\bar{F}}_{2}={F}_{2}\left(\frac{{\upmu }_{r}}{{h}^{3}}\right)\\&\frac{\partial }{\partial \alpha }\left[\left\{{\bar{F}}_{2}{ \bar{h}}^{3}+{\bar{F}}_{0}\Psi \left({K}_{r}\left(1-\gamma \right)+\gamma \right)\right\} \frac{\partial \bar{p}}{\partial \alpha } \right]+\frac{\partial }{\partial \beta }\left[\left\{{\bar{F}}_{2}{ \bar{h}}^{3}+{\bar{F}}_{0}\Psi \left({K}_{r}\left(1-\gamma \right)+\gamma \right)\right\} \frac{\partial \bar{p}}{\partial \beta } \right]=\Omega \left[\frac{\partial }{\partial \alpha }\left\{\left(1-\frac{{\bar{F}}_{1}}{{\bar{F}}_{0}}\right) \bar{h}\right\}\right]+ \frac{\partial \bar{h}}{\partial \bar{t}}\end{aligned}$$

(14)

where ${\bar{F}}_{0} ; {\bar{F}}_{1}and {\bar{F}}_{2}$ are known as cross-film viscosity integrals and is given as:

$${\bar{F}}_{0}={\int }_{0}^{1}\frac{1}{\bar{\mu }}d\bar{z}; \quad {\bar{F}_{1}}={\int }_{0}^{1}\frac{\bar{z}}{\bar{\mu}}d\bar{z}\quad\,\text{and}\quad\,{\bar{F}}_{2}={\int }_{0}^{1}\left(\frac{{\bar{z}}^{2}}{\bar{\mu}}-\frac{\bar{z}}{\bar{\mu}} \frac{{\bar{F}}_{1}}{{\bar{F}}_{0}}\right)d\bar{z}.$$

2.1 Fluid film thickness

Figure 1a shows the worn out bearing geometry. Dufrane et al. [15] based on their study of worn out bearings in industries, found that the footprint created by the shaft is almost exactly symmetrical at the bottom of the bearing. The model given by Dufrane et al. [15] for the change in bush geometry ($\Delta \bar{h}$) due to wear defect is expressed as [14, 20, 21]:

$$\Delta \bar{h}={\bar{\delta}}_{w}-1-\text{sin}\alpha ;\quad \text{for}\,\, {\alpha }_{b}\le \alpha \le {\alpha }_{e}$$

(15a)

$$\Delta \bar{h}=0;\quad \text{for}\,\, \alpha <{\alpha }_{b}\quad \text{or}\quad \alpha >{\alpha }_{e}$$

(15b)

The ${\alpha }_{b}$ and ${\alpha }_{e}$ (as shown in Fig. 1a) angles indicate the start and end of footprint for the bearing, respectively.

Where ${\bar{\delta}}_{w}$ is wear depth parameter of worn zone.

The start angle ${\alpha }_{b}$ and end angle ${\alpha }_{e}$ of the worn zone are calculated by considering $\Delta \bar{h}=0$ at that location and is obtained as;

$$\begin{aligned}&\text{sin}\alpha ={\bar{\delta}}_{w}-1;\\&\alpha ={\text{sin}}^{-1}\left({\bar{\delta}}_{w}-1\right)\end{aligned}$$

(15c)

For a given value of ${\bar{\delta}}_{w}$, Eq. (15c) provides a negative value of $\text{sin}\alpha$, which may be considered to occur in both the 3rd and 4th quadrants as represented by ${\alpha }_{b}$ and ${\alpha }_{e}$, respectively.

The expression for film thickness ($\bar{h}$) in hybrid DLPJBS including the change in bush geometry ($\Delta \bar{h}$) due to wear defect, in dimensionless form is given as [14, 20]:

$$\bar{h}=1-{\bar{X}}_{j}\text{cos}\alpha -{\bar{Z}}_{j}\text{sin}\alpha +\Delta \bar{h}$$

(15d)

2.2 Model formulation using FEM technique

The modified Reynolds Eq. (14) is solved by FEM using Galerkin’s technique. The fluid film domain is discretized using four-noded quadrilateral isoparametric elements. The fluid film pressure interpolation is expressed as:

$$\bar{p}=\sum_{j=1}^{{n}^{e}}{N}_{j}{\bar{p}}_{j}$$

where ${N}_{j}=$ nodal shape function, ${n}^{e}=$ elemental number of nodes.

Applying the orthogonality condition of Galerkin’s on Eq. (14), the global system equation is given as [32]:

$${\left[{\bar{F}}_{ij}\right]}^{e}{\left\{{\bar{p}}_{j}\right\}}^{e} ={\left\{{\bar{Q}}_{j}\right\}}^{e}+{\Omega \left\{{\bar{R}}_{Hj}\right\}}^{e}+{\bar{\dot{X}}}_{j}{\left\{{\bar{R}}_{Xj}\right\}}^{e}+{\bar{\dot{Z}}}_{j}{\left\{{\bar{R}}_{Zj}\right\}}^{e}$$

(16)

where

$${\left[{\bar{F}}_{ij}\right]}^{e}={\iint }_{{\Omega }^{e}}\left[\left\{{\bar{F}}_{2}{ \bar{h}}^{3}+{\bar{F}}_{0}\Psi \left({K}_{r}\left(1-\gamma \right)+\gamma \right)\right\}\left(\frac{\partial {N}_{i}}{\partial \alpha } \frac{\partial {N}_{j}}{\partial \alpha }+\frac{\partial {N}_{i}}{\partial \beta } \frac{\partial {N}_{j}}{\partial \beta }\right)\right]d\alpha d\beta $$

(16a)

$${\left\{{\bar{Q}}_{j}\right\}}^{e}={\oint }_{{\Gamma }^{e}}\left\{{\bar{F}}_{2}{ \bar{h}}^{3}+{\bar{F}}_{0}\Psi \left({K}_{r}\left(1-\gamma \right)+\gamma \right)\right\}\left(\frac{\partial \bar{p}}{\partial \alpha } {n}_{\alpha }+\frac{\partial \bar{p}}{\partial \beta } {n}_{\beta }\right){N}_{i}d\Gamma -\Omega {\oint }_{{\Gamma }^{e}}{N}_{i}\left\{\left(1-\frac{{\bar{F}}_{1}}{{\bar{F}}_{0}}\right) \bar{h}\right\} {n}_{\alpha }d\Gamma $$

(16b)

$${\left\{{\bar{R}}_{Hj}\right\}}^{e}={\iint }_{{\Omega }^{e}}\frac{\partial {N}_{i}}{\partial \alpha }\left\{\left(1-\frac{{\bar{F}}_{1}}{{\bar{F}}_{0}}\right) \bar{h}\right\}d\alpha d\beta $$

(16c)

$${\left\{{\bar{R}}_{Xj}\right\}}^{e}={\iint }_{{\Omega }^{e}}{N}_{i}\text{cos}\alpha d\alpha d\beta $$

(16d)

$${\left\{{\bar{R}}_{Zj}\right\}}^{e}={\iint }_{{\Omega }^{e}}{N}_{i}\text{sin}\alpha d\alpha d\beta $$

(16e)

Here $\left(\text{i},\text{j }=\text{ 1,2},\text{3,4}\right)$ and ${n}_{\alpha }$, ${n}_{\beta }$ are direction of cosines.

2.3 Power-law model

The relation between the shear stress $\left(\tau \right)$ and shear strain rate $\left(\bar{\dot{\gamma }}\right)$ for the power-law model can be described as [22, 25]:

$$\bar{\tau }=\bar{m}{\left(\bar{\dot{\gamma }}\right)}^{n}$$

(17)

where $\bar{m}$ and $n$ are respectively the index of consistency and flow behaviour.

The apparent viscosity of a power-law model is written as:

$$\bar{\mu}=\tau /\bar{\dot{\gamma }}$$

(18a)

where $\bar{\dot{\gamma }}$ is known as shear strain rate and is given as [28]:

$$\bar{\dot{\gamma }}={\left[{\left\{\frac{\bar{h}}{\bar{\mu}}\frac{\partial \bar{p}}{\partial \alpha }\left(\bar{z}-\frac{{\bar{F}}_{1}}{{\bar{F}}_{0}}\right)+\frac{\Omega }{\bar{\mu}\bar{h}{\bar{F}}_{O}}\right\}}^{2}+{\left\{\frac{\bar{h}}{\bar{\mu}}\frac{\partial \bar{p}}{\partial \beta }\left(\bar{z}-\frac{{\bar{F}}_{1}}{{\bar{F}}_{0}}\right)\right\}}^{2}\right]}^{1/2}$$

(18b)

2.4 Performance characteristics parameters

The performance behaviour of a hybrid DLPJB_S is studied in terms of flow rate ($\bar{Q}$), frictional torque$\left({\bar{T}}_{f}\right)$, stiffness coefficients (${\bar{S}}_{xx},{\bar{S}}_{zz}$), minimum film thickness (${\bar{h}}_{min}$), damping coefficients (${C}_{xx},{\bar{C}}_{zz}$), and stability threshold speed parameter (${\bar{\omega}}_{th}$) are computed.

2.4.1 Resultant fluid film reaction $\left({\bar{F}}_{o}\right)$

The expression for the dimensionless resultant fluid film reaction of the porous bearing system is expressed as [33]:

$${\bar{F}}_{o}=\sqrt{{\bar{F}}_{xo}^{2}+{\bar{F}}_{zo}^{2}}$$

(19)

Here

$${\bar{F}}_{xo}={\iint }_{{\Omega }^{e}}\bar{p} \text{cos}\alpha d\alpha d\beta $$

$${\bar{F}}_{zo}={\iint }_{{\Omega }^{e}}\bar{p} \text{sin}\alpha d\alpha d\beta $$

2.4.2 Lubricant flow rate $\left(\bar{Q}\right)$

The flow rate of lubricant through the bearing clearance space may be given as [6, 10, 34]:

$${\bar{Q}}_{c}=-\frac{1}{6}\underset{0}{\overset{2\pi }{\int }}{\bar{h}}^{3}\left(\frac{\partial \bar{p}}{\partial \beta }\right)d\alpha $$

(20a)

2.4.3 Friction torque $\left({\bar{T}}_{f}\right)$

The non-dimensional expression for the frictional torque for the porous journal bearing is expressed as [10, 32]:

$$ \left. {\begin{array}{*{20}l} {\overline{T}_{f} = \mathop{\iint }\nolimits_{{{\Omega }^{e} }} \overline{\tau }d\alpha d\beta } \hfill \\ {\overline{T}_{f} = \mathop{\iint }\nolimits_{{{\Omega }^{e} }} \left[ {\frac{{\overline{h}}}{{\overline{\mu }}}\frac{{\partial \overline{p}}}{\partial \alpha }\left( {\overline{z} - \frac{{\overline{F}_{1} }}{{\overline{F}_{0} }}} \right) + \frac{{\Omega }}{{\overline{\mu }\overline{h}\overline{F}_{O} }}} \right]d\alpha d\beta } \hfill \\ \end{array} } \right\} $$

(21)

2.4.4 Rotor dynamic coefficients $\left({\bar{S}}_{ij} \quad \text{and}\quad {\bar{C}}_{ij}\right)$

Derivatives of fluid film reaction force component $\left({\bar{F}}_{o}\right)$ with respect to journal centre displacement and velocity components gives the stiffness and damping coefficient are expressed as [28]:

$$ \overline{S}_{ij} = - \frac{{\partial \overline{F}_{i} }}{{\partial \overline{q}}},\quad {\text{and}}\quad \overline{C}_{ij} = - \frac{{\partial \overline{F}_{i} }}{{\partial \overline{{\dot{q}}} }}\quad (i = x,z; j = x,z; \overline{q} = \overline{X}_{j,} \overline{Z}_{j} ; \overline{{\dot{q}}} = \overline{{\dot{X}}}_{j,} \overline{{\dot{Z}}}_{j} ). $$

(22)

The dynamic coefficients (${\bar{S}}_{ij} , {\bar{C}}_{ij}$) are represented in matrix form as:

$$\left[\begin{array}{cc}{\bar{S}}_{xx}& {\bar{S}}_{xz}\\ {\bar{S}}_{zx}& {\bar{S}}_{zz}\end{array}\right]=\left[\begin{array}{cc}-\frac{\partial }{\partial {\bar{X}}_{j}}{\iint }_{{\Omega }^{e}}\bar{p} \text{cos}\alpha d\alpha d\beta & -\frac{\partial }{\partial {\bar{Z}}_{j}}{\iint }_{{\Omega }^{e}}\bar{p} \text{cos}\alpha d\alpha d\beta \\ -\frac{\partial }{\partial {\bar{X}}_{j}}{\iint }_{{\Omega }^{e}}\bar{p} \text{sin}\alpha d\alpha d\beta & -\frac{\partial }{\partial {\bar{Z}}_{j}}{\iint }_{{\Omega }^{e}}\bar{p} \text{sin}\alpha d\alpha d\beta \end{array}\right]$$

$$\left[\begin{array}{cc}{\bar{C}}_{xx}& {\bar{C}}_{xz}\\ {\bar{C}}_{zx}& {\bar{C}}_{zz}\end{array}\right]=\left[\begin{array}{cc}-\frac{\partial }{\partial {{\bar{\dot{X}}}}_{j}}{\iint }_{{\Omega }^{e}}\bar{p} \text{cos}\alpha d\alpha d\beta & -\frac{\partial }{\partial {{\bar{\dot{Z}}}}_{j}}{\iint }_{{\Omega }^{e}}\bar{p} \text{cos}\alpha d\alpha d\beta \\ -\frac{\partial }{\partial {{\bar{\dot{X}}}}_{j}}{\iint }_{{\Omega }^{e}}\bar{p} \text{sin}\alpha d\alpha d\beta & -\frac{\partial }{\partial {{\bar{\dot{Z}}}}_{j}}{\iint }_{{\Omega }^{e}}\bar{p} \text{sin}\alpha d\alpha d\beta \end{array}\right]$$

2.4.5 Stability threshold speed margin $\left({\bar{\omega}}_{th}\right)$

The non-dimensional ${\bar{M}}_{c}$ is expressed as:

$${\bar{M}}_{c}=\frac{{\bar{G}}_{1}}{{\bar{G}}_{2}-{\bar{G}}_{3}}$$

where

$${\bar{G}}_{1}=\left[{\bar{C}}_{xx}{\bar{C}}_{zz}-{\bar{C}}_{zx}{\bar{C}}_{xz}\right];$$

$${\bar{G}}_{2}=\frac{\left[{\bar{S}}_{xx}{\bar{S}}_{zz}-{\bar{S}}_{zx}{\bar{S}}_{xz}\right]\left[{\bar{C}}_{xx+}{\bar{C}}_{zz}\right]}{\left[{\bar{S}}_{xx}{\bar{C}}_{zz}+{\bar{S}}_{zz}{\bar{C}}_{xx}-{\bar{S}}_{xz}{\bar{C}}_{zx}-{\bar{S}}_{zx}{\bar{C}}_{xz}\right]};$$

$${\bar{G}}_{3}=\frac{\left[{\bar{S}}_{xx}{\bar{C}}_{xx}+{\bar{S}}_{xz}{\bar{C}}_{xz}+{\bar{S}}_{zx}{\bar{C}}_{xz}+{\bar{S}}_{zz}{\bar{C}}_{zz}\right]}{\left[{\bar{C}}_{xx}+{\bar{C}}_{zz}\right]}$$

Thus, ${\bar{\omega}}_{th}$ can be obtained in terms of ${\bar{M}}_{c}$ is expressed as [35, 36]:

$${\bar{\omega}}_{th}={\left[\bar{M}_{c}\bigg/ \bar{F}_{o}\right]}^{1/2}$$

(23)

where ${\bar{F}}_{o}$ is the resulting force of fluid film $\left(\frac{\partial \bar{h}}{\partial \bar{t} }=0\right)$.

2.5 Boundary conditions [8, 10, 13, 37, 38]

• 1. The value of pressure for the film region and porous matrix region at open ends is equal to zero, i.e. $\bar{p} \left(\alpha ,\pm 1\right)={\bar{p}}_{1}\left(\alpha ,\pm 1,\bar{z}\right)={\bar{p}}_{2}\left(\alpha ,\pm 1,\bar{z}\right)=0$.

• 2. The pressure value at inner porous surface and fluid film region interface is equal, i.e. ${\bar{p}}_{1}\left(\alpha ,\beta ,0\right)=\bar{p} \left(\alpha ,\beta \right)$.

• 3. The value of pressure at two porous layer interface is equal, i.e. ${\bar{p}}_{1}\left(\alpha ,\beta ,-{\bar{h}}_{1}\right)={\bar{p}}_{2}\left(\alpha ,\beta ,-{\bar{h}}_{1}\right)$.

• 4. The pressure at the outside surface of outer layer of porous bearing is equal to the supply pressure, i.e. ${p}_{2}\left(\alpha ,\beta ,-\bar{h}\right)={p}_{s}$.

  $${\bar{p}}_{2}\left(\alpha ,\beta ,-\bar{h}\right)=\frac{{p}_{2}}{{p}_{s}}=1$$

• 5. There is press-fitting between porous facing and solid housing; therefore, ${\left(\frac{\partial {\bar{p}}_{2}}{\partial \bar{z}}\right)}_{\bar{z}=-\bar{h}}=0$.

• 6. The pressure gradient in the circumferential direction is zero, i.e. $\bar{p}=\frac{\partial \bar{p}}{\partial \alpha }=0$. It is Reynolds Boundary Condition (RBC), i.e. the fluid film pressures are assigned zero value in the cavitating region.

3 Flow chart for numerical algorithm

Figure 2 shows the solution scheme flow chart for the numerical simulation of influence of wear and nonlinear behaviour of lubricants. A MATLAB based source code has been generated on the basis of FEM solution technique to compute performance characteristics of bearings system. Due to its flexibility and diversity, the FEM is used to achieve the required solution of governing global system Eq. (16). The steps involved to compute the numerically simulated results are as follows:

• 1. Initially, the specified value of the journal centre coordinate (${\bar{X}}_{j}$, ${\bar{Z}}_{j}$) and the input data (two-dimensional mesh, ${\bar{W}}_{o}$, $\Omega$) is fed to the program.

• 2. For the solution of non-Newtonian lubricant, the value of ${\bar{F}}_{0}$, ${\bar{F}}_{1}$ and ${\bar{F}}_{2}$ are calculated by using Simpson’s method and the value of $\bar{\dot{\gamma }}$ is evaluated using the Eq. (18b).

• 3. At each node point, the value of fluid film thickness is computed by the Eq. (15d) with using a specified value of the wear depth by Eq. (15a).

• 4. Further, a MATLAB code is developed based on Gauss–Seidel iteration simulation procedure for computing the value of fluid film pressure values by solving the global system Eq. (16) in the lubricant field at every nodal points by using boundary conditions as reported in Sect. 2.5.

• 5. For a particular value of ${\bar{W}}_{o}$, the journal centre equilibrium position is obtained using the following equations

  $$ \overline{F}_{X} = 0\quad {\text{and}} \quad \overline{F}_{Z} - \overline{W}_{o} = 0 $$

  (24)

  where ${\bar{F}}_{X}$ and ${\bar{F}}_{Z}$ are the fluid film reactions components in the $X$ and $Z$ directions.

  Thus, journal center equilibrium position is achieved by using the Newton–Raphson iterative method as follows:

  $${\left({\bar{F}}_{X}\right)}_{i+1}={\left({\bar{F}}_{X}\right)}_{i}+\frac{\partial {\left({\bar{F}}_{X}\right)}_{i}}{\partial {\bar{X}}_{j}}\Delta {\bar{X}}_{j}+\frac{\partial {\left({\bar{F}}_{X}\right)}_{i}}{\partial {\bar{Z}}_{j}}\Delta {\bar{Z}}_{j}=0$$

  (24a)
  $${\left({\bar{F}}_{Z}\right)}_{i+1}-{\bar{W}}_{o}={\left({\bar{F}}_{Z}\right)}_{i}+\frac{\partial {\left({\bar{F}}_{Z}\right)}_{i}}{\partial {\bar{X}}_{j}}\Delta {\bar{X}}_{j}+\frac{\partial {\left({\bar{F}}_{Z}\right)}_{i}}{\partial {\bar{Z}}_{j}}\Delta {\bar{Z}}_{j}-{\bar{W}}_{o}=0$$

  (24b)

  Now above equations are linear in $\Delta {\bar{X}}_{j}$ and $\Delta {\bar{Z}}_{j}$. Therefore, the above Eqs. (24a) and (24b) are presented in matrix form as [28, 32, 39, 40]:

  $$\begin{aligned}&\left[\begin{array}{c}-{\left({\bar{F}}_{X}\right)}_{i}=\frac{\partial {\left({\bar{F}}_{X}\right)}_{i}}{\partial {\bar{X}}_{j}}\Delta {\bar{X}}_{j}+\frac{\partial {\left({\bar{F}}_{X}\right)}_{i}}{\partial {\bar{Z}}_{j}}\Delta {\bar{Z}}_{j}\\ -\left({\left({\bar{F}}_{Z}\right)}_{i}-{\bar{W}}_{o}\right)=\frac{\partial {\left({\bar{F}}_{Z}\right)}_{i}}{\partial {\bar{X}}_{j}}\Delta {\bar{X}}_{j}+\frac{\partial {\left({\bar{F}}_{Z}\right)}_{i}}{\partial {\bar{Z}}_{j}}\Delta {\bar{Z}}_{j}\end{array}\right]\\&\quad\Rightarrow\left[\begin{array}{c}\frac{\partial {\left({\bar{F}}_{X}\right)}_{i}}{\partial {\bar{X}}_{j}}\Delta {\bar{X}}_{j}+\frac{\partial {\left({\bar{F}}_{X}\right)}_{i}}{\partial {\bar{Z}}_{j}}\Delta {\bar{Z}}_{j}\\ \frac{\partial {\left({\bar{F}}_{Z}\right)}_{i}}{\partial {\bar{X}}_{j}}\Delta {\bar{X}}_{j}+\frac{\partial {\left({\bar{F}}_{Z}\right)}_{i}}{\partial {\bar{Z}}_{j}}\Delta {\bar{Z}}_{j}\end{array}\right] =\left[\begin{array}{c}{-\left({\bar{F}}_{X}\right)}_{i}\\ -\left({\left({\bar{F}}_{Z}\right)}_{i}-{\bar{W}}_{o}\right)\end{array}\right]\end{aligned}$$

  (24c)
  $$\left[\begin{array}{c}\frac{\partial {\bar{F}}_{X}}{\partial {\bar{X}}_{j}} \frac{\partial {\bar{F}}_{X}}{\partial {\bar{Z}}_{j}}\\ \frac{\partial {\bar{F}}_{Z}}{\partial {\bar{X}}_{j}} \frac{\partial {\bar{F}}_{Z}}{\partial {\bar{Z}}_{j}}\end{array}\right]\left[\begin{array}{c}\Delta {\bar{X}}_{j}\\ \Delta {\bar{Z}}_{j}\end{array}\right] =-\left[\begin{array}{c}{\left({\bar{F}}_{X}\right)}_{i}\\ \left({\left({\bar{F}}_{Z}\right)}_{i}-{\bar{W}}_{o}\right)\end{array}\right]$$

  (24d)
  $$ \left[ {\overline{D}_{j} } \right]\left[ {\begin{array}{*{20}c} {\Delta \overline{X}_{j} } \\ {\Delta \overline{Z}_{j} } \\ \end{array} } \right] = - \left[ {\begin{array}{*{20}c} {\left( {\overline{F}_{X} } \right)_{i} } \\ {\left( {\left( {\overline{F}_{Z} } \right)_{i} - \overline{W}_{o} } \right)} \\ \end{array} } \right]; \, \quad {\text{where}},\quad \left[ {\overline{D}_{j} } \right] = \left[ {\begin{array}{*{20}c} {\frac{{\partial \overline{F}_{X} }}{{\partial \overline{X}_{j} }} \frac{{\partial \overline{F}_{X} }}{{\partial \overline{Z}_{j} }}} \\ {\frac{{\partial \overline{F}_{Z} }}{{\partial \overline{X}_{j} }} \frac{{\partial \overline{F}_{Z} }}{{\partial \overline{Z}_{j} }}} \\ \end{array} } \right] $$

  (24e)

  Taking inverse of $\left[{\bar{D}}_{j}\right]$,

  $$\left[\begin{array}{c}\Delta {\bar{X}}_{j}\\ \Delta {\bar{Z}}_{j}\end{array}\right] =-{\left[{\bar{D}}_{j}\right]}^{-1}\left[\begin{array}{c}{\bar{F}}_{X}\\ {\bar{F}}_{Z}-{\bar{W}}_{o}\end{array}\right]$$

  (24f)

  The new journal center coordinate $\left({\bar{X}}_{j}^{i+1},{\bar{Z}}_{j}^{i+1}\right)$ are computed by using the following relation:

  $${\bar{X}}_{j}^{i+1} ={\bar{X}}_{j}^{i}+\Delta {\bar{X}}_{j}^{i} and {\bar{Z}}_{j}^{i+1} ={\bar{Z}}_{j}^{i}+\Delta {\bar{Z}}_{j}^{i}$$

  (24g)

  where, ${\bar{X}}_{j}^{i}$ and ${\bar{Z}}_{j}^{i}$ are the coordinates of ${i}^{th}$ iteration of journal center equilibrium position.

• 6. Further, ${i\text{th}}$ iteration is continued until equilibrium position of journal center is attained by applying following convergence criteria [32]:

  $${\left[\frac{{\left(\Delta {\bar{X}}_{j}^{i}\right)}^{2}+{\left(\Delta {\bar{Z}}_{j}^{i}\right)}^{2}}{{\left({\bar{X}}_{j}^{i}\right)}^{2}+{\left({\bar{Z}}_{j}^{i}\right)}^{2}}\right]}^{1/2}\times 100\le {10}^{-3}$$

  (25)

  If the above convergence criteria are not satisfied, then go to step (3) otherwise go to step (7).

• 7. After establishing the above convergence criteria, the static and dynamic characteristics behaviour of bearing system are evaluated.

Fig. 2

Solution scheme flow chart

4 Model validation

In order to ascertain the accuracy of developed MATLAB source code, results obtained in the present study has been compared with results of previously published works [4, 8, 14, 41]. In this work, the numerically evaluated values are compared with published values of Cusano [8] for similar operational and geometrical conditions of bearing. Figure 3a presents the variation in load number $\left(1/{s}_{o}{\left(\frac{L}{D}\right)}^{2}\right)$ with eccentricity ratio $\left(\varepsilon \right)$ for a DLPJB_S. As shown from Fig. 3a, the theoretically simulated results shows a good agreement with available results of Cusano [8] and 4% deviation is observed at maximum. Further, Fig. 3b presents experimental validation of SLPJB_S with available results of Mokhtar et al. [4]. Figure 3b shows a comparison of load parameter of the present results with the experimental results of reference studies Mokhtar et al. [4]. The results presented between two studies shows a reasonably good agreement and 8% deviation is observed at maximum Fig. 3c presents the validation of SLPJB_S with the results of Sharma et al. [41] operating under non-Newtonian fluid conditions. From Fig. 3c, it can be noted that simulated results are in well agreement with published results of Sharma et al. [41] and 5% deviation is observed at maximum. The wear effect has been validated for non-porous journal bearing by comparing a plot of Sommerfeld number (${S}_{o}$) versus eccentricity ratio $\left(\varepsilon \right)$ obtained from the present study to that of Hashimoto et al. [14] (as shown in Fig. 3d). As no study is available for porous bearing by taking wear effect into consideration. Based on the available literature [2, 8, 10, 14, 15, 22, 23, 26] in the present study, the operational and geometrical parameters used in numerical simulation of hybrid DLPJB_S are taken from the open literature as shown in Table 1.

Fig. 3

a Eccentricity ratio $\left(\varepsilon \right)$ versus load number $\left(1/{s}_{o}{\left(\frac{L}{D}\right)}^{2}\right)$. b Eccentricity ratio $\left(\varepsilon \right)$ versus load parameter $\left(1/{\text{S}}_{\text{o}}\right)$. c Fluid film reaction $\left({\bar{F}}_{O}\right)$ versus permeability parameter $\left(\Psi \right)$. d Eccentricity ratio $\left(\varepsilon \right)$ versus Sommerfeld number $\left({S}_{0}\right)$

Table 1 Geometric and Operating parameters of hybrid double layer porous journal bearing

5 Convergence and discretization

In the current study, a grid convergence test has been performed, and the optimal size of mesh, i.e. 149 $\times$ 47 has been chosen as shown in Fig. 4a. Here, ‘149’ denotes number of nodes in a circumferential direction, and ‘47’ denotes number of nodes in an axial direction as presented in Fig. 4b. On the basis of convergence criteria, the characteristics parameters of hybrid DLPJB_S have been obtained.

Fig. 4

a Mesh sensitivity analysis. b Mesh and Boundary for fluid film domain

6 Results and discussions

The static and dynamic characteristics of the hybrid DLPJB_S have been obtained considering the effect of wear and non-Newtonian lubricant behaviour. Bearing characteristics parameters are compared for both single layer and double layer porous journal bearings operating in wear and non-Newtonian lubricant condition with a permeability parameter $\left(\Psi =0.005\right)$. The hybrid SLPJB_S operating under unworn and Newtonian lubricant condition is assumed as a base bearing for comparison purpose. Also, for conciseness and brevity of the paper, the cross-coupled damping and stiffness coefficient are not presented in this paper. The numerically computed results are discussed below.

6.1 Circumferential fluid film pressure $(\bar{p})$ distributions

Figure 5 a–c presents the variation of circumferential fluid film pressure $\left(\bar{p}\right)$ considering combined influence of non-Newtonian lubricant under worn and unworn conditions for hybrid SLPJBS and DLPJBS. Circumferential fluid film pressure $\left(\bar{p}\right)$ has been plotted for a constant value of ${S}_{o}=0.55$. It is noticed that for the case of worn porous journal bearing operating under non-Newtonian and Newtonian lubricants, the value of $\bar{p}$ gets enhanced compared to unworn porous journal bearing, because the bearing operating under worn condition operates at higher eccentricity ratio. Thus, higher value of $\bar{p}$ is noticed. From Fig. 5c, it can be seen that porous bearing operating under dilatant $\left(n=1.3\right)$ lubricant condition provides a higher value of $\bar{p}$, whereas pseudoplastic $\left(n=0.7\right)$ lubricant gives the lower value of $\bar{p}$. Further, From Fig. 5d, it may be observed that no significant variation in the value of $\bar{p}$ occurs for the hybrid DLPJBS as compared to SLPJBS operating for the same value of permeability parameter $\left(\Psi =0.005\right)$. The percentage variation of ${\bar{p}}_{max}$ at a constant value of ${S}_{o}=0.55$ has been presented in Fig. 5d. From Fig. 5d, it may be observed that for the worn porous bearing, The value of ${\bar{p}}_{max}$ gets increased by an order of magnitude 7.11%, 4.52% and 2.75% respectively for dilatant lubricant $\left(n=1.3\right)$, Newtonian lubricant $\left(n=1\right)$ and pseudoplastic lubricant $\left(n=0.7\right)$ as compared to the base bearing. The pressure $\left(\bar{p}\right)$ plot for a constant value of operating eccentricity ratio $\left(\varepsilon =0.45\right)$ for the single and double layer porous journal bearing has been shown in Fig. 5e. It may be observed from Fig. 5e that the fluid film pressure $\left(\bar{p}\right)$ profile gets altered slightly for single layer and double layer porous journal bearings. Further, it may also be seen that the value of ${\bar{p}}_{max}$ is higher for double layer porous journal bearing as compared to single layer porous journal bearing.

Fig. 5

a Fluid film pressure $\left(\bar{p}\right)$ distribution at the axial mid-plane along circumferential direction for single layer porous hybrid journal bearing. b Fluid film pressure $\left(\bar{p}\right)$ distribution at the axial mid-plane along circumferential direction for double layer porous hybrid journal bearing. c Fluid film pressure distribution at the axial mid-plane along circumferential direction. d % difference of maximum fluid film pressure $\left({\bar{p}}_{max}\right)$ due to combine effect of worn and power-law lubricant at ${S}_{o}=0.55$. e Fluid film pressure distribution at the axial mid-plane along circumferential direction

6.2 Minimum fluid film thickness $\left({\bar{{h}}}_{{{m}}{{i}}{{n}}}\right)$

Figure 6a depicts the variation of ${\bar{h}}_{min}$ with ${S}_{o}$ for the influence of non-Newtonian behaviour of lubricant under the worn and unworn condition for hybrid SLPJB_S and DLPJB_S. Noticing in this figure, the value of ${\bar{h}}_{min}$ gets enhanced with an increment in value of Sommerfeld number. From Fig. 6a, it may be seen that SLPJB_S and DLPJB_S operating under worn condition gives lower value of ${\bar{h}}_{min}$ as compared to unworn condition. This is because of the fact that bearing operating under worn condition gives larger value of eccentricity ratio and journal tends to fall into the damaged footprint, thus reducing the value of ${\bar{h}}_{min}$ [42, 44]. Further, it can be observed that the double layer porous bearing provides a higher value of ${\bar{h}}_{min}$ than single layer porous bearing running under unworn condition. This behaviour is due to the fact that for a low value of permeability parameter $\left(\Psi \right)$ i.e. the porous matrix is less permeable. As a result, the seepage of lubricant in the porous media is less. Thus, more lubricant is available in the bearing clearance space and the value of ${\bar{h}}_{min}$ becomes more [43]. Furthermore, From Fig. 6a, the double layer porous journal bearing operating under dilatant $\left(n=1.3\right)$ lubricant provides the higher value of ${\bar{h}}_{min}$, while pseudoplastic $\left(n=0.7\right)$ lubricant gives the lesser value of ${\bar{h}}_{min}$. Figure 6b, c shows the 3-D contours plots for the fluid film thickness in bearing clearance space of hybrid SLPJB_S and DLPJB_S for the worn and unworn condition at a constant value of ${S}_{o}=0.55$ both for Newtonian and non-Newtonian lubricant. As shown in Fig. 6b, c, the hybrid SLPJB_S and DLPJB_S operating under dilatant $\left(n=1.3\right)$ lubricant provides the higher value of ${\bar{h}}_{min}$, whereas pseudoplastic $\left(n=0.7\right)$ lubricant gives the lower value of ${\bar{h}}_{min}$. Further, from Fig. 6b, c, it is observed that the SLPJB_S and DLPJB_S operating under worn condition gives lower value of ${\bar{h}}_{min}$ as compared to unworn condition [42, 44]. The percentage variation in the value of ${\bar{h}}_{min}$ at a constant value of ${S}_{o}=0.55$ has been presented in Fig. 6d. As apparent from Fig. 6d, unworn DLPJB_S operating with dilatant $\left(n=1.3\right)$ lubricant condition, increases the value of ${\bar{h}}_{min}$ of the magnitude of 4.72% as compared to base bearing. However, the following trends are observed from the simulated results for the value of ${\bar{h}}_{min}$:

Fig. 6

a Minimum fluid film thickness $\left({\bar{h}}_{min}\right)$ versus Sommerfeld number $\left({S}_{0}\right)$. b Contour plots of fluid film thickness for the single layer porous hybrid journal bearing at ${S}_{o}=0.55$. c Contour plots of fluid film thickness for the double layer porous hybrid journal bearing at ${S}_{o}=0.55$. d % difference of ${\bar{h}}_{min}$ due to combine effect of worn and power-law lubricant at ${S}_{o}=0.55$

$${\left[{\left.{\bar{h}}_{min}\right|}_{Double\,Layer}>{\left.{\bar{h}}_{min}\right|}_{Single\,Layer}\right]}_{\left(n=\text{0.7,1.0,1.3}\right) \left[\text{for both unworn and worn condition}\right]}$$

6.3 Lubricant flow rate $\left({\bar{{Q}}}\right)$

The variation of lubricant flow rate $\left(\bar{Q}\right)$ with respect to Sommerfeld number $\left({S}_{o}\right)$ due to the influence of non-Newtonian lubricant under the worn and unworn condition of a hybrid SLPJB_S and DLPJB_S is presented in Fig. 7a. The value of $\bar{Q}$ gets reduced with increase in Sommerfeld number. From Fig. 7a, it may be noticed that the value of $\bar{Q}$ gets reduce for hybrid DLPJB_S than the hybrid SLPJB_S for both non-Newtonian and Newtonian lubricant under worn and unworn condition. The reason for the lower value of $\bar{Q}$ may be due to reduced seepage into the wall for the double layer porous journal bearing. The value of lubricant flow rate $\left(\bar{Q}\right)$ for worn-out porous journal bearing is more than that of the unworn porous journal bearing for a range of values of Sommerfeld number $\left({S}_{o}\right)$ taken in the present study. This is due to the reason that bearing operating under worn condition, runs at higher value of eccentricity ratio. Therefore, to support a constant value of external applied load, more lubricant flow is needed [42, 44, 45]. As shown in Fig. 7a, the porous journal bearing operating under dilatant $\left(n=1.3\right)$ lubricant provides the lower value of $\bar{Q}$, while pseudoplastic $\left(n=0.7\right)$ lubricant gives the higher value of $\bar{Q}$. Further, the double layer porous bearings operating with dilatant $\left(n=1.3\right)$ lubricant at a constant value of ${S}_{o}=0.55$ under unworn condition reduces the value of $\bar{Q}$ by the magnitude of 6.09% vis-à-vis the base bearing, as presented in Fig. 7b. Following trends for the value of $\bar{Q}$ for porous bearing system have been observed based on the simulated results:

Fig. 7

a Lubricant flow $\left(\bar{Q}\right)$ versus Sommerfeld number $\left({S}_{0}\right)$. b % difference of $\bar{Q}$ due to combine effect of worn and power-law lubricant at ${S}_{o}=0.55$

$${\left[{\left.\bar{Q}\right|}_{Double\,Layer}<{\left.\bar{Q}\right|}_{Single\,Layer}\right]}_{\left(n=\text{0.7,1.0,1.3}\right) \left[\text{for both unworn and worn condition}\right]}$$

6.4 Friction torque $\left({\bar{{{T}}}}_{{{f}}}\right)$

Figure 8a presents the variation of ${\bar{T}}_{f}$ under combined effect of non-Newtonian lubricant and for worn and unworn conditions of the hybrid SLPJB_S and DLPJB_S. It can be noted that the value of ${\bar{T}}_{f}$ reduces with increase in the value of Sommerfeld number $\left({S}_{o}\right)$. From Fig. 8a, it may be observed that the value of ${\bar{T}}_{f}$ for a worn-out porous journal bearing gets reduced as compared to unworn porous journal bearing. The reason for this behaviour is that due to lack of viscous drag in the worn zone, the eccentricity ratio increases leading to reduction in ${\bar{h}}_{min}$ which subsequently reduces ${\bar{T}}_{f}$ [42, 44, 45]. Also, the value of ${\bar{T}}_{f}$ further reduces for DLPJB_S as compared to the SLPJB_S operating under worn condition. Further, Fig. 8a shows that ${\bar{T}}_{f}$ reduces with increment in power-law index $\left(n\right)$ for the porous bearing operating under worn and unworn condition. The reason for reduced value of ${\bar{T}}_{f}$ is that the bearing operating under higher value of power-law index $\left(n\right)$ gives lesser lubricant viscosity. The difference in terms of percentage for ${\bar{T}}_{f}$ at a constant value of ${S}_{o}=0.55$ has been shown in Fig. 8b. Further, as apparent from Fig. 8b, for worn porous journal bearing operating under dilatant $\left(n=1.3\right)$ lubricant condition, the value of ${\bar{T}}_{f}$ decreases by an order of 19.55% for single layer condition and 20.05% for double layer conditions with reference to the base bearing. However, the following trends for the value of ${\bar{T}}_{f}$ for porous bearing system have been observed based on the simulated results:

Fig. 8

a Frictional torque $\left({\bar{T}}_{f}\right)$ versus Sommerfeld number $\left({S}_{0}\right)$. b % difference of ${\bar{T}}_{f}$ due to combine effect of worn and power-law lubricant at ${S}_{o}=0.55$

$${\left[{\left.{\bar{T}}_{f}\right|}_{Double\,Layer}<{\left.{\bar{T}}_{f}\right|}_{Single\,Layer}\right]}_{\left(n=\text{0.7,1.0,1.3}\right) \left[{\text{for both unworn and worn condition}}\right]}$$

6.5 Fluid film stiffness coefficients $\left({{{\bar{S}}}}_{{{x}}{{x}}} \,\,\text{and} \,\,{{{\bar{S}}}}_{{{z}}{{z}}}\right)$

Figure 9a, b presents the variation of fluid film direct stiffness coefficient (${\bar{S}}_{xx}$ and ${\bar{S}}_{zz}$) for both single and double layer system considering the effect of non-Newtonian and Newtonian lubricant operating under unworn and worn conditions. It can be seen that the value of ${\bar{S}}_{xx}$ gets reduced by considering the wear effect along with SLPJB_S with respect to that of unworn condition. While, there is an increment in the value of ${\bar{S}}_{zz}$ when SLPJB_S is considered with the wear effect. In addition to this, it may be observed that DLPJB_S operating under unworn condition gives a higher value of ${\bar{S}}_{xx}$. Whereas DLPJB_S operating under worn condition, gives a higher value of ${\bar{S}}_{zz}$ for both non-Newtonian and ideal lubricant. Further from Fig. 9a, the DLPJB_S operating under pseudoplastic $\left(n=0.7\right)$ lubricant provides lower value of ${\bar{S}}_{xx}$, while dilatant $\left(n=1.3\right)$ lubricant gives higher value of ${\bar{S}}_{xx}$. Figure 9c, d represents percentage (%) difference of ${\bar{S}}_{xx}$ and ${\bar{S}}_{zz}$ in a SLPJB_S and DLPJB_S considering the influence of non-Newtonian lubricant under worn and unworn condition. From Fig. 9c, it can be noted that, for an unworn porous bearing operating at a constant value of ${S}_{o}=0.55$, dilatant $\left(n=1.3\right)$ lubricant gives higher value of ${\bar{S}}_{xx}$ by a factor of 5.45% for double layer condition and 2.68% of single layer vis-à-vis the base bearing. Further, From Fig. 9d, it may be noticed that for a worn porous bearing operating under pseudoplastic $\left(n=0.7\right)$ lubricant gives larger value of ${\bar{S}}_{zz}$ by a factor of 33.13% for double layer condition and 30.51% of single layer conditions respectively with reference to the base bearings. From the numerically computed results for the value of ${\bar{S}}_{xx}$ and ${\bar{S}}_{zz}$ the following general trends are observed:

Fig. 9

a Stiffness coefficient $\left({\bar{S}}_{xx}\right)$ versus Sommerfeld number $\left({S}_{0}\right)$. b Stiffness coefficient $\left({\bar{S}}_{zz}\right)$ versus Sommerfeld number $\left({S}_{0}\right)$. c % difference of ${\bar{S}}_{xx}$ due to combine effect of worn and power-law lubricant at ${S}_{o}=0.55$. d % difference of ${\bar{S}}_{zz}$ due to combine effect of worn and power-law lubricant at ${S}_{o}=0.55$

$${\left[{\left.{\bar{S}}_{xx}/{\bar{S}}_{zz}\right|}_{Double\,layer}>{\left.{\bar{S}}_{xx}/{\bar{S}}_{zz}\right|}_{Single\,layer}\right]}_{\left(n=\text{0.7,1.0,1.3}\right) \left[{\text{for both unworn and worn condition}}\right]}$$

6.6 Fluid film damping coefficients $\left({{{\bar{C}}}}_{{{x}}{{x}}} \,\,\text{and}\,\,{{{\bar{C}}}}_{{{z}}{{z}}}\right)$

The variation of ${\bar{C}}_{xx}\text{ and }{\bar{C}}_{zz}$ with ${S}_{o}$ for considering the combined effect of non-Newtonian lubricant and worn and unworn conditions is presented in Fig. 10a, b. From Fig. 10a, b, it can be seen that for the SLPJB_S operating under worn condition, the value of ${\bar{C}}_{xx}\text{and }{\bar{C}}_{zz}$ get reduces with respect to unworn condition for both Newtonian and non-Newtonian lubricants. In addition to this, it may be observed that DLPJB_S operating with unworn condition gives a higher value of ${\bar{C}}_{xx}\text{and }{\bar{C}}_{zz}$ as compare to SLPJB_S for both non-Newtonian and ideal lubricant. Further, from Fig. 10a, the DLPJB_S operating under pseudoplastic $\left(n=0.7\right)$ lubricant provides the higher value of ${\bar{C}}_{xx}$, while dilatant $\left(n=1.3\right)$ lubricant gives the lower value of ${\bar{C}}_{xx}$. But from Fig. 10b, it may be noticed that DLPJB_S operating under dilatant $\left(n=1.3\right)$ lubricant provides higher value of ${\bar{C}}_{zz}$, while pseudoplastic $\left(n=0.7\right)$ lubricant gives lower value of ${\bar{C}}_{zz}$. The percentage difference of ${\bar{C}}_{xx}\text{and }{\bar{C}}_{zz}$ at ${S}_{o}=0.55$ has been presented in Fig. 10c, d. From Fig. 10c, it can be seen that the unworn porous bearing operating under pseudoplastic $\left(n=0.7\right)$ lubricant increases the value of ${\bar{C}}_{xx}$ by a factor of 1.03% and 4.16% for single and double layer condition than the base bearing. Whereas, the value of ${\bar{C}}_{zz}$ from Fig. 10d, dilatant $\left(n=1.3\right)$ lubricant provided higher value by a factor of 3.55% for single layer and 6.16% for double layer case with respect to base bearings. Additionally, from the numerically computed results for the value of ${\bar{C}}_{xx}\text{and }{\bar{C}}_{zz}$ the following general trends are noticed:

Fig. 10

a Damping coefficient $\left({\bar{C}}_{xx}\right)$ versus Sommerfeld number $\left({S}_{0}\right)$. b Damping coefficient $\left({\bar{C}}_{zz}\right)$ versus Sommerfeld number $\left({S}_{0}\right)$. c % difference of ${\bar{C}}_{xx}$ due to combine effect of worn and power-law lubricant at ${S}_{o}=0.55$. d % difference of ${\bar{C}}_{zz}$ due to combine effect of worn and power-law lubricant at ${S}_{o}=0.55$

$${\left[{\left.{\bar{C}}_{xx}/{\bar{C}}_{zz}\right|}_{Double\,layer}>{\left.{\bar{C}}_{xx}/{\bar{C}}_{zz}\right|}_{Single \,layer}\right]}_{\left(n=\text{0.7,1.0,1.3}\right) \left[\text{for both unworn and worn condition}\right]}$$

6.7 Stability threshold speed margin $\left({\bar{\omega}}_{th}\right)$

The stability threshold speed margin $\left({\bar{\omega}}_{th}\right)$ is an essential parameter to assess the stability of journal bearing. The value of ${\bar{\omega}}_{th}$ depends on rotor dynamic coefficients (${\bar{S}}_{xx}, {\bar{S}}_{zz}, {\bar{C}}_{xx}, and {\bar{C}}_{zz}$). Figure 11a shows the variation of ${\bar{\omega}}_{th}$ with ${S}_{o}$ for both single and double layer porous bearing including the combined effect of non-Newtonian lubricant operating under unworn and worn conditions. Further, it can be noticed that SLPJBS operating under worn condition gives lower value of ${\bar{\omega}}_{th}$ as compared to unworn condition. Additionally, it has been observed that DLPJBS operating under unworn condition gives higher value of ${\bar{\omega}}_{th}$ than SLPJBS. Furthermore, it may also be noticed that, for unworn condition, the DLPJBS operating under pseudoplastic $\left(n=0.7\right)$ lubricant provides a higher value of ${\bar{\omega}}_{th}$, while dilatant $\left(n=1.3\right)$ lubricant gives the lower value of ${\bar{\omega}}_{th}$. The variation in terms of percentage for ${\bar{\omega}}_{th}$ than base bearing at ${S}_{o}=0.55$ for different configurations of bearing is shown in Fig. 11b. It can be noted from Fig. 11b that unworn porous bearing operating under pseudoplastic $\left(n=0.7\right)$ lubricant gives a higher value of ${\bar{\omega}}_{th}$ by a factor of 3.07% for double layer condition and 1.74% of single layer conditions respectively vis-à-vis the base bearing.

Fig. 11

a Stability threshold speed $\left({\bar{\omega}}_{th}\right)$ versus Sommerfeld number $\left({S}_{0}\right)$. b % difference of ${\bar{\omega}}_{th}$ due to combine effect of worn and power-law lubricant at ${S}_{o}=0.55$

$${\left[{\left.{\bar{\omega}}_{th}\right|}_{Double\,Layer}>{\left.{\bar{\omega}}_{th}\right|}_{Single\,Layer}\right]}_{\left(n=\text{0.7,1.0,1.3}\right)\left[\text{for both unworn and worn condition}\right]}$$

7 Conclusion

The presents work describes the influence of wear and non-Newtonian lubricant on the performance behaviour of a hybrid DLPJB_S is numerically analyzed. It may be concluded that:

• The value of ${\bar{h}}_{min}$ for hybrid SLPJB_S operating under worn condition is reduced than the unworn condition for both Newtonian and non-Newtonian lubricant. Additionally, DLPJB_S gives higher value of ${\bar{h}}_{min}$ as compared to SLPJB_S operating under unworn condition. This value of ${\bar{h}}_{min}$ gets further enhanced with the use of dilatant $\left(n=1.3\right)$ lubricant.

• The hybrid DLPJB_S operating under worn condition gives lower value of ${\bar{T}}_{f}$ as compared to the unworn condition, while hybrid SLPJB_S operating under worn condition gives higher value of ${\bar{T}}_{f}$. In addition to this, the hybrid DLPJB_S with the dilatant fluid $\left(n=1.3\right)$ provides the lowest value of ${\bar{T}}_{f}$ operating under worn condition.

• For the hybrid DLPJB_S operating under unworn condition, the values of fluid film stiffness and damping coefficients get enhanced with respect to hybrid SLPJB_S, but opposite trends is observed for DLPJB_S operating under worn condition. Further, it may be noticed that, for hybrid SLPJB_S and DLPJB_S conditions, the dilatant $\left(n=1.3\right)$ lubricant provides larger values of ${\bar{S}}_{xx}$ and pseudoplastic $\left(n=0.7\right)$ lubricant provides larger values of ${\bar{S}}_{zz}$ than the base journal bearing system. Whereas, pseudoplastic (n = 0.7) offers higher values of ${\bar{C}}_{xx}$ and dilatant $\left(n=1.3\right)$ offers higher values of ${\bar{C}}_{zz}$ than the base journal bearing.

• The hybrid DLPJB_S operating in unworn condition provides enhance stability threshold speed margin $\left({\bar{\omega}}_{th}\right)$ than the hybrid SLPJB_S for Newtonian and non-Newtonian lubricant. Whereas value of ${\bar{\omega}}_{th}$ for hybrid DLPJB_S operating under worn condition gets reduced as compared to that of hybrid SLPJB_S for Newtonian and non-Newtonian lubricant.