1 Introduction

Energy harvesting, known also as energy scavenging, covers a great body of technologies and devices that transform low grade energy sources such as solar energy, environmental vibrations, thermal energy, and human motion into usable electrical energy. Thanks to the recent technology progress recorded in the electronic domain, the electrical energy consumption by the electronics components has dramatically decreased, incited the proliferation of the wireless devices. Thus, the energy harvesting technology has become a very attractive solution for a wide variety of applications such as consumer electronics, outpatient medical electronics (hearing aids, pacemakers, smart implants) or imaging (camera inside the human body).

It is know in the literature that, there are three mechanisms allow to transduce vibration energy to electricity namely electrostatic [1], electromagnetic [2] and piezoelectric [3]. Many authors namely Elvin et al. [4], Inman [5], reviewing the state of the art on the energy harvesting. Most works on energy harvesting took the deterministic approach by considering the nonlinearity what can exhibit transduction materials and study its impact on the system performance. Mann [6] designed a nonlinear electromagnetic energy harvester that uses magnetic interactions to create a bistable potential well and validated the potential well escape phenomenon can be used to broaden the frequency response by theory and experiments. Spector et al. [7] proposed a theoretical model by using a beam element and performed experiment to harvest power from PZT material. They showed that a simple beam bending can provide the self-power source of the strain energy sensor. Kim et al. [8] reported that piezoelectric energy harvesting showed a promising results under pre-stress cyclic conditions and validated the experimental results with finite element analysis.

Let us notice that, the main objective in this research field is to enhance harvested energy by the devices. For this, build the hybrid system combining two mechanisms of transduction is essential. Bin et al. [9] built a hybrid energy harvester combined piezoelectric with electromagnetic mechanism to scavenge energy from external vibration. They studied the effect of the relative position of the coils and magnets on the PZT cantilever end and the poling direction of magnets on the output voltage of the harvested energy. Wang et al. [10] built a hybrid device for powering wireless sensor nodes in smart grid. It emerges from the results obtained that, from current-carrying conductor of 2.5 A at 50 Hz , the proposed harvester combining piezoelectric components and electromagnetic elements can generate up to 295.3 \(\mu W\). Madinei et al. [11] developed a hybrid cantilever beam harvester and by using an applied DC voltage as a control parameter to change the resonant frequency of the harvester to ensure resonance as the excitation frequency varies. These hybrid models mentioned above functioning in the surrounding where the vibration source can be modeled by the coherence excitation. However, in the most situations, the vibrations are random and time-varying. Cottone et al. [12] found numerically and experimentally that the nonlinear oscillators can outperform the linear ones under stochastic excitation. Fokou et al. [13] used a probabilistic approach to analytically predict the system’s response, the stability and the estimation of system’s reliability. Mokem et al. [14] proposed a hybrid device combining piezoelectric and electromagnetic transduction and subjected to the colored noise. The authors shows that, the system performance can be improve for the small value of the relaxation time. Foupouapouognigni et al. [15] built the hybrid model and studied the stochastic resonance phenomenon, which is characterized by the large amplitude of vibration and increase the system performance. Let us remind that, when the nonlinear system is subjected to the combination of the harmonic excitation and the random force, many phenomena can be observed such as the stochastic resonance and the ghost-stochastic resonance. These two phenomena are characterized by the large amplitude of vibration. Indeed, the stochastic resonance occurs when the frequency of system’s vibration is present in the frequency bandwidth of the harmonic excitation. However, when the maximum amplitude of the system is reached for a frequency of vibration absent in the frequency bandwidth of the harmonic force, this phenomenon is called a ghost-stochastic resonance.

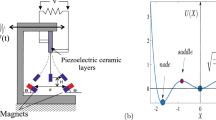
While one observes in the literature, a growing interest in the theoretical investigation of the ghost-stochastic resonance phenomenon in the nonlinear systems [16,17,18,19,20,21,22], in our knowledge, the study of this phenomenon on the performance of the energy harvesting devices is not made. The main objective of this manuscript is to investigated the performance of the hybrid system when the ghost-stochastic resonance occurs (Fig. 1).

Fig. 1
figure 1

Schematic of the hybrid energy harvester

Full size image

The rest of paper is organized as follows: In Sect. 2, we describe the system with model equation, followed by the assessment of the statistic response of the system. We draw the probability density function in order to search for the probable amplitude of the mechanical and electrical response in Sect. 3. In Sect. 4, numerical simulations are made, from which we study the ghost-stochastic resonance. We conclude the Work in Sect. 5

2 Description of the system with the model equation

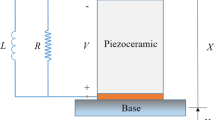
The design of hybrid energy harvester combining two mechanisms of transduction of ambient energy is composed of two parts namely the mechanical and the electrical part. We used the energy scavenger build by Lefeuvre in Ref. [23] with some modifications, by changing the rigid mass by a permanent magnet rod, and by adding a coil, in oder to enhance the output power and enlarge its application field. It is worth noting that, in the schematic model, the mechanical part is composed of a nonlinear spring with the linear stiffness coefficient \(k_{1}\) and nonlinear stiffness coefficient \(k_{3}\) while the electrical part presents two subsystems namely the piezoelectric circuit and the electromagnetic circuit. The piezoelectric circuit is composed of the piezoelectric element and the load resistance \(R_{p}\). The electromagnetic circuit has a permanent magnet of mass M, that produces a magnetic field \(B_{z}\), the coil, connected to the rigid housing representing the stator is characterized by an inductance \(L_{e}\). The load resistance of magnetic circuit is \(R_{L}\). When the harvester is subjected to the external excitation Z(t), the displacement of the magnetic mass M induces in the piezoelectric circuit, the deformation of piezoelectric element giving rise to the electrical field across the piezoelectric element. However, in the magnetic circuit, the displacement of the magnetic mass M induces a fluctuation of the magnetic flux in the surface of the coil, and consequently, a generation of electromotive force \( f_{m}(i)=B_{z}iL_{coil}\) in the mechanical part, while in the magnetic circuit, we can note the Lenz electromotive voltage \(f_{e}(\dot{z})=-B_{z}L_{coil}\dot{z}\) with z, \(L_{coil}\), and i, the displacement, the length of the coil and the current that flows in the coil respectively, \(B_{z}\) being the magnetic field generated by the permanent magnet. A summary of equations is provided here [23] giving a full derivation of the mechanical and piezoelectric circuit equations. Using the Kirchhoff’s law in the electromagnetic circuit by letting \( \mathbf {B}_z = B\mathbf {u}_z\), we obtained motion equations given by:

$$\begin{aligned} \begin{array}{ll} M \ddot{z}+ d \dot{z}+k_{{1}}z +k_{{3}}z^{3}+Bil_{coil} - \theta _2\,v=Z \left( t \right) \\ &{}\\ C_{{p}}\dot{v}+{\frac{v \left( t \right) }{R_{{p}}}}+\theta _{{2}}\dot{z} =0\\ &{}\\ L_{{e}}\dot{i}+R_{l}i-Bl_{coil}\dot{z}=0 \end{array} \end{aligned}$$
(1)

where d is the damping coefficient, \(C_{p}\), the capacity of the capacitor and \(\theta _2\) the electromechanical coupling coefficient. The physical parameters used in this manuscript are given in Table 1.

Table 1 Physical parameters of hybrid model
Full size table

By using the time-transformation( \(t={\ \displaystyle \frac{\tau }{\omega }}\)), Eq. (1) gives rise to the following non-dimensional system:

$$\begin{aligned} \begin{array}{ll} x^{\prime \prime } +\mu a\,x^{\prime } +{\omega _{0}}\,x -{ \beta _{2}}\,y +\sigma \,x^{3}+{\beta 1}\,r =N \left( \tau \right) (a)\\ &{}\\ y^{\prime } +\alpha _{{2}}y -\beta _{{22}}x^{\prime } =0 (b)\\ &{}\\ r^{\prime } +{\alpha _{3}}\,r -{\beta _{11}}\,x^{\prime } =0 (c) \end{array} \end{aligned}$$
(2)

with \(N(\tau )=\sum \limits _{i = 1}^m {f_{0}\cos \left( {\omega _i \tau } \right) }+\xi \left( \tau \right) \) where \(\sum \limits _{i = 1}^m {f_{0}\cos \left( {\omega _i \tau } \right) }\) is a harmonic excitation, with \(f_{0}\) the amplitude of coherence force, \(\omega _i = \left( {k+i-1} \right) \omega _0\) is the frequency of the coherence force with k a constant took here equal to 2. \( \omega _{0} \) is the fundamental frequency. The variable \(\xi \left( \tau \right) \), is the Gaussian white noise verifying the statistics properties: \(<\xi \left( \tau \right) >=0\), \(<\xi \left( \tau \right) \xi \left( s\right) >=2D \delta ({\tau })\). The dimensionless parameters are given as follow:

$$\begin{aligned} \begin{array}{ll} \mu _{{a}}=-{\frac{\omega \,d}{k_{{1}}}};\sigma =-{\frac{{l}^{2}k_{{3}}}{k_{{1}}}};\beta _{{2}}=-{\frac{\theta _{{2}}{ v_{o}}}{lk_{{1}}}}; \beta _{{1}}=-{\frac{BL_{{coil}}i_{{o}}}{lk_{{1}}}} \\ &{}\\ \alpha _{{2}}={\frac{1}{\omega \,C_{{p}}R_{{p}}}}; \beta _{{22}}=-{\frac{\theta _{{2}}l}{v_{{o}}C_{{p}}}}; \beta _{{11}}={\frac{lBL_{coil}}{Li_{{o}}}};\alpha _{{3}}={\frac{R_{{L}}}{\omega \,L_{{e}}}} ;\\ &{}\\ z=lx \left( t\omega \right) ;v={ vo}\,y \left( t\omega \right) ;i={ io}\,r \left( t\omega \right) ;\\ &{}\\ N \left( \tau \right) =-Z \left( {\frac{\tau }{\omega }} \right) {l}^{- 1}{k_{{1}}}^{-1} \end{array} \end{aligned}$$
(3)

3 Stochastic averaging method

In this heading, we assume that, \(f_{0}=0\). We use the stochastic averaging method to provide the statistic response of the harvester. In the quasi-harmonic regime, the solution of the mechanical system (2) is of the form:

$$\begin{aligned} \begin{array}{ll} x\left( \tau \right) =a(\tau )\left( \tau \right) \cos \left( \theta \right) ; &{} x^{\prime }(\tau )=-\omega a(\tau )\left( \tau \right) \sin \left( \theta \right) \\ \end{array} \end{aligned}$$
(4)

where \(\theta =\omega \tau +\psi (\tau )\) with \(\psi \), the phase angle and \(a(\tau )\) the amplitude. Substituting Eq. (4) into Eq. (2) (b)–(c), the solution of obtained equation can be written as follow:

$$\begin{aligned} \begin{array}{ll} y \left( \tau \right) =C_{{1}}{\mathrm{e}^{-{ \alpha 2}\,\tau }}+{\frac{ { \beta _{22}}\,a \left( \tau \right) \omega \, \left( \omega \,\cos \left( \theta \right) -{ \alpha _{2}}\,\sin \left( \theta \right) \right) }{{\omega }^{2}+{{ \alpha _{2}}^{2}}}}\\ &{}\\ r \left( \tau \right) =C_{{2}}{\mathrm{e}^{-{ \alpha _{3}}\,\tau }}+{\frac{ a \left( \tau \right) \beta _{{11}}\omega \, \left( \omega \,\cos \left( \theta \right) -\alpha _{{3}}\sin \left( \theta \right) \right) }{{ \omega }^{2}+{{ \alpha _{3}}}^{2}}}\\ \end{array} \end{aligned}$$
(5)

In the steady state, Eqs. (5 a)–(b) can be rewritten as:

$$\begin{aligned} \begin{array}{ll} y \left( \tau \right) ={\frac{ {\beta _{22}}\,a \left( \tau \right) \omega \, \left( \omega \,\cos \left( \theta \right) -{ \alpha _{2}}\,\sin \left( \theta \right) \right) }{{\omega }^{2}+{{\alpha _{2}}^{2}}}}\\ &{}\\ r \left( \tau \right) ={\frac{ a \left( \tau \right) \beta _{{11}}\omega \, \left( \omega \,\cos \left( \theta \right) -\alpha _{{3}}\sin \left( \theta \right) \right) }{{ \omega }^{2}+{{ \alpha _{3}}}^{2}}} \\ \end{array} \end{aligned}$$
(6)

where

$$\begin{aligned} \begin{array}{ll} \omega \,\cos \left( \theta \right) -\alpha _{{2}}\sin \left( \theta \right) =\sqrt{{\omega }^{2}+{\alpha _{{2}}}^{2}}\cos \left( \theta + \arctan \left( {\frac{\alpha _{{2}}}{\omega }} \right) \right) \\ &{}\\ \omega \,\cos \left( \theta \right) -\alpha _{{3}}\sin \left( \theta \right) =\sqrt{{\omega }^{2}+{\alpha _{{3}}}^{2}}\cos \left( \theta + \arctan \left( {\frac{\alpha _{{3}}}{\omega }} \right) \right) \end{array} \end{aligned}$$
(7)

Thus, the amplitudes of steady-state current and charge are given by:

$$\begin{aligned} \begin{array}{ll} Y={\frac{{\beta _{22}}\,a\omega }{\sqrt{{\omega }^{2}+{{ \alpha _{2}}}^{2 }}}}; R={\frac{a{\beta _{11}}\,\omega }{\sqrt{{\omega }^{2}+{{\alpha _{3}}}^{2 }}}} \end{array} \end{aligned}$$
(8)

Substituting Eqs. (4) and (6) into Eq. (2), and applying the determinist averaging method in the determinist part of the obtained system, we have:

$$\begin{aligned} \begin{array}{ll} a^{\prime } =-\,{\frac{\gamma _{{22}}N \left( \tau \right) \sin \left( \theta \right) }{2\omega \,\gamma _{{55} }}}-\,{\frac{\gamma _{{11}}a}{2\omega \,\gamma _{{55}}}}\\ &{}\\ \varphi ^{\prime }={\frac{\gamma _{{33}}N \left( \tau \right) \cos \left( \theta \right) }{\gamma _{{44}}a}}+{ \frac{{a}^{2}\gamma _{{12}}}{\gamma _{{44}}}}+{\frac{\gamma _{{13}}}{ \gamma _{{44}}a}} \end{array} \end{aligned}$$
(9)

where

$$\begin{aligned} \begin{array}{ll} \gamma _{{11}}={{\beta _{1}}}^{2}{\omega }^{3}{ \alpha _{3}}-{{\beta _{2}}}^ {2}{\omega }^{3}{\alpha _{2}}+\mu a\,{\omega }^{3}{{\alpha _{3}}}^{2}+\mu a\,{\omega }^{5}\\ &{}\\ \quad +\mu a\,\omega \,{{\alpha _{2}}}^{2}{{\alpha _{3}}}^{2}+ \mu a\,{\omega }^{3}{{\alpha _{2}}}^{2}-{{ \beta _{2}}}^{2}\omega \,{\alpha _{2}}\,{{ \alpha _{3}}}^{2}+{{\beta _{1}}}^{2}\omega \,{\alpha _{3}}\,{{ \alpha _{2}}}^{2}\\ &{}\\ \gamma _{22}=2\,{{\alpha _{2}}}^{2}{\omega }^{2}+2\,{{ \alpha _{2}}}^{2}{ {\alpha _{3}}}^{2}+2\,{\omega }^{2}{{\alpha _{3}}}^{2}+2\,{\omega }^{4}\\ &{}\\ \gamma _{{33}}=-8\,{{\alpha _{2}}}^{2}{{ \alpha _{3}}}^{2}-8\,{\omega }^{4} -8\,{\omega }^{2}{{\alpha _{3}}}^{2}-8\,{{\alpha _{2}}}^{2}{\omega }^{2}\\ &{}\\ \gamma _{{44}}=8\,{\omega }^{5}+8\,{\omega }^{3}{\alpha _{{3}}}^{2}+8\,{ \omega }^{3}{\alpha _{{2}}}^{2}+8\,\omega \,{\alpha _{{2}}}^{2}{\alpha _{{3 }}}^{2}\\ &{}\\ \gamma _{{55}}={\omega }^{4}+{\omega }^{2}{\alpha _{{3}}}^{2}+{\alpha _{{2} }}^{2}{\omega }^{2}+{\alpha _{{2}}}^{2}{\alpha _{{3}}}^{2}\\ &{}\\ \gamma _{{12}}=3\,\sigma \,{\omega }^{2}{\alpha _{{3}}}^{2}+3\,\sigma \,{ \alpha _{{2}}}^{2}{\omega }^{2}+3\,\sigma \,{\omega }^{4}+3\,\sigma \,{ \alpha _{{2}}}^{2}{\alpha _{{3}}}^{2} \\ &{}\\ \gamma _{{13}}=-4\,{\omega }^{2}{\alpha _{{2}}}^{2}{{ \alpha _{3}}}^{2}+4\, {\beta _{{1}}}^{2}{\omega }^{4}-4\,{\omega }^{4}{\alpha _{{2}}}^{2}-4\,{ \omega }^{6}-4\,{\beta _{{2}}}^{2}{\omega }^{4}\\ &{}\\ \quad -4\,{\omega }^{4}{\alpha _{{ 3}}}^{2}+4\,{\beta _{{1}}}^{2}{\omega }^{2}{{ \alpha _{2}}}^{2}-4\,{\beta _ {{2}}}^{2}{\omega }^{2}{\alpha _{{3}}}^{2}\\ &{}\\ \quad +4\,\omega _{{0}}{\alpha _{{2}}} ^{2}{\alpha _{{3}}}^{2}+4\,\omega _{{0}}{\alpha _{{2}}}^{2}{\omega }^{2}+4 \,\omega _{{0}}{\omega }^{2}{\alpha _{{3}}}^{2}+4\,\omega _{{0}}{\omega }^{ 4} \end{array} \end{aligned}$$
(10)

Finally, applying the stochastic averaging method, in Eq. (9) , we obtain the Ito equation defined as:

$$\begin{aligned} \begin{array}{ll} { da}= \left( -\,{\frac{2\gamma _{{11}}a}{\omega \,\gamma _{{55}}}} +\,{\frac{D}{2a{\omega }^{2}}} \right) { dt}+\sqrt{{\frac{D}{{ \omega }^{2}}}}{} { dB_{1}}\\ &{}\\ d\theta ={\frac{ \left( \gamma _{{12}}{a}^{2}+\gamma _{{13}} \right) { dt}}{\gamma _{{44}}}}+\sqrt{{\frac{D}{{\omega }^{2}{a}^{2}}}}{} { dB_{2}} \end{array} \end{aligned}$$
(11)

where \(B_{1}\) and \(B_{2}\) are the normalized wiener process. We observe in Eq. (11) that a and \(\theta \) are independent. Thus, we can provided the probability density for the amplitudes( a), rather than a joint probability density for \(\theta \). The probability density \(P(a,\tau )\) of the instantaneous amplitude a satisfies the Fokker–Planck–Kolmogorov equation:

$$\begin{aligned} \begin{array}{ll} {\frac{\partial }{\partial \tau }}p \left( a,\tau \right) =- \left( - \,{\frac{\gamma _{{11}}}{2\omega \,\gamma _{{55}}}}-\,{\frac{D}{{ \omega }^{2}2{a}^{2}}} \right) p \left( a,\tau \right) \\ &{}\\ \quad - \left( -\,{ \frac{\gamma _{{11}}a}{2\omega \,\gamma _{{55}}}}+\,{\frac{D}{2a{ \omega }^{2}}} \right) {\frac{\partial }{\partial a}}p \left( a,\tau \right) +\,{\frac{ \left( D \right) {\frac{\partial ^{2}}{ \partial {a}^{2}}}p \left( a,\tau \right) }{{2\omega }^{2}}} \end{array} \end{aligned}$$
(12)

In the stationary state, the solutions of Eq. (12) is given by:

$$\begin{aligned} \begin{array}{ll} p \left( a \right) =Na{\mathrm{e}^{-\,{\frac{\gamma _{{11}}{a}^{2} \omega }{ \left( 2D \right) \left( {\omega }^{2}+{\alpha _{{3}}}^{2} \right) \left( {\omega }^{2}+{\alpha _{{2}}}^{2} \right) }}}} \end{array} \end{aligned}$$
(13)

where N is the normalization constant which can be assessed numerically using Simpson’s method. Through a transformation from variable \(( a,\theta )\), to the original variables \((x, x^{\prime })\), an expression for the stationary densities function of x and \(x^{\prime }\) can be derived as:

$$\begin{aligned} P_{{n}} \left( x,x^{\prime } \right)= & {} \,{\frac{P \left( a,\theta \right) }{ 2\pi \,a}} \end{aligned}$$
(14)
$$\begin{aligned} p\left( a \right)= & {} \frac{N}{{2\pi }}\exp \left( { - \frac{{\gamma _{11} \omega \left( {x^2 + \frac{{x^{'2} }}{{\omega ^2 }}} \right) }}{{2D\left( {\omega ^2 + \alpha _3^2 } \right) \left( {\omega ^2 + \alpha _2^2 } \right) }}} \right) \end{aligned}$$
(15)

Thus, the expected value of the mean square electric current and charge can be calculated following this formula (Fig. 3):

$$\begin{aligned} \begin{array}{ll} \langle y^2 \left( \tau \right) \rangle = \langle Y^2 \rangle = \left( {\frac{{\beta _{22} \omega }}{{\sqrt{\omega ^2 + \alpha _2^2 } }}} \right) ^2 \times \langle a^2 \rangle \\ &{}\\ \quad = \left( {\frac{{\beta _{22} \omega }}{{\sqrt{\omega ^2 + \alpha _2^2 } }}} \right) ^2 \int \limits _0^{ + \infty } {a^2 p\left( a \right) da}\\ &{}\\ \langle Y^2 \rangle = \frac{{2\beta _{22}^2 \omega D\left( {\omega ^4 + \omega ^2 \left( {\alpha _3^2 + \alpha _2^2 } \right) + \alpha _2^2 \alpha _3^2 } \right) }}{{\gamma _{11} \left( {\omega ^2 + \alpha _2^2 } \right) }} \end{array} \end{aligned}$$
(16)

and

$$\begin{aligned} \begin{array}{ll} \langle r^2 \left( \tau \right) \rangle = \langle R^2 \rangle = \left( {\frac{{\beta _{11} \omega }}{{\sqrt{\omega ^2 + \alpha _2^2 } }}} \right) ^2 \times \langle a^2 \rangle \\ &{}\\ \quad = \left( {\frac{{\beta _{11} \omega }}{{\sqrt{\omega ^2 + \alpha _3^2 } }}} \right) ^2 \int \limits _0^{ + \infty } {a^2 p\left( a \right) da}\\ &{}\\ \langle R^2 \rangle = \frac{{2\beta _{11}^2 \omega D\left( {\omega ^4 + \omega ^2 \left( {\alpha _3^2 + \alpha _2^2 } \right) + \alpha _2^2 \alpha _3^2 } \right) }}{{\gamma _{11} \left( {\omega ^2 + \alpha _3^2 } \right) }} \end{array} \end{aligned}$$
(17)
Fig. 2
figure 2

Stationary probability density of the system in 3D representation for: for \(\mu _{a}=0.3\), \(\beta _{2}=0.005\), \(\beta _{1}=0.003\), \(\alpha _{2}=0.000001\), \(\beta _{22}=-0.005\), \(\beta _{11}=0.003\), \(\alpha _{3}=0.0003\), \(\sigma =0.05\), \(\omega _{0}=1\)

Full size image
Fig. 3
figure 3

a Evolution of mean square voltage of piezoelectric circuit versus coefficient \(\beta _{11}\),b Evolution of mean square current of magnetic circuit versus coefficient \(\beta _{22}\) for \(\mu _{a}=0.3\), \(\beta _{2}=0.005\), \(\beta _{1}=0.003\), \(\alpha _{2}=0.000001\), \(\beta _{22}=-0.005\), \(\beta _{11}=0.003\), \(\alpha _{3}=0.0003\), \(\sigma =0.05\), \(D=0.1\), \(\omega _{0}=1\)

Full size image

4 Numerical simulation

4.1 Algorithm of numerical simulation

The numerical scheme used in this manuscript is based on the Euler version algorithm. By letting \(\dot{x} = u\), Eq. (2) can be rewritten as follow:

$$\begin{aligned} x^{\prime }= & {} u \nonumber \\ u^{\prime }= & {} - \mu _a u - \omega _0 x + \beta _2 y - \sigma x^3 - \beta _1 r + N\left( \tau \right) \nonumber \\ y^{\prime }= & {} - \alpha _2 y + \beta _{22} u \nonumber \\ r^{\prime }= & {} - \alpha _3 y + \beta _{11} u \end{aligned}$$
(18)

The discrete equations can be written as:

$$\begin{aligned} x_{i + 1}= & {} x_i + u_i h \nonumber \\ u_{i + 1}= & {} u_i + \left[ { - \mu _a u_i - \omega _0 x_i + \beta _2 y_i - \sigma x_i ^3 - \beta _1 r_i } \right] h + \zeta _k \left( \tau \right) \nonumber \\ y_{i + 1}= & {} y_i + \left[ { - \alpha _2 y_i + \beta _{22} u_i } \right] h \nonumber \\ r_{i + 1}= & {} r_i + \left[ { - \alpha _3 y_i + \beta _{11} u_i } \right] h \end{aligned}$$
(19)

In the purpose to compare the analytical results obtained via the stochastic averaging method, the numerical simulation is made for the harvester. Figure 4 , shows the good agreement between the numerical results and those obtained analytically. We also draw in Fig. 2, the 3D representation of probability density of harvester. It emerges from these results that, the probability distribution is unimodal.

Fig. 4
figure 4

Stationary probability density for different values of noise intensity for \(\mu _{a}=0.3\), \(\beta _{2}=0.005\), \(\beta _{1}=0.003\), \(\alpha _{2}=0.000001\), \(\beta _{22}=-0.005\), \(\beta _{11}=0.003\), \(\alpha _{3}=0.0003\), \(\sigma =0.05\), \(\omega _{0}=1\)

Full size image
Fig. 5
figure 5

a Mean amplitude response \(x_{m}(\omega )\) versus noise intensity D , b Mean residence time versus noise intensity D, c–d Efficiency versus noise intensity D for \(\alpha _{3}=0.0003\),\(\alpha _{2}=0.000001\), e–f Output voltage versus noise intensity for \(\mu _{a}=0.3\), \(\beta _{2}=0.005\), \(\beta _{1}=0.003\), \(\beta _{22}=-0.005\), \(\beta _{11}=0.003\), \(\sigma =0.05\), \(f_{0}=0.39\), \(\omega _{0}=1\)

Full size image
Fig. 6
figure 6

a Output power versus noise intensity D, b 3D- representation of the Output power of hybrid model versus noise intensity D and piezoelectric coupling coefficient for \(\alpha _{3}=0.0003\),\(\alpha _{2}=0.000001\), \(\mu _{a}=0.3\), \(\beta _{2}=0.005\), \(\beta _{1}=0.003\), \(\beta _{22}=-0.005\), \(\beta _{11}=0.003\), \(\sigma =0.05\), \(f_{0}=0.39\), \(\omega _{0}=1\)

Full size image
Fig. 7
figure 7

a, c, Time series of the mechanical subsystem, b, d, Probability distribution of the mechanical subsystem for for \(\mu _{a}=0.3\), \(\beta _{2}=0.005\), \(\beta _{1}=0.003\), \(\alpha _{2}=0.000001\), \(\beta _{22}=-0.005\), \(\beta _{11}=0.003\), \(\alpha _{3}=0.0003\), \(\sigma =0.05\), \(f_{0}=0.39\), \(\omega _{0}=1\)

Full size image

4.2 Mean residence time and ghost-stochastic resonance phenomenon

In this heading, we assume that, \( f_0 \ne 0 \). Thus, the harvester is subjected to the combination of the coherence excitation \(\sum \nolimits _{i = 1}^m {f_{0}\cos \left( {\omega _i \tau } \right) }\) and the random force \(\zeta _k \left( \tau \right) \). In the purpose to get a deep understanding of the observed dynamics and the influence of noise, we can assess the mean residence time and mean amplitude response.

Let us remind that equation(Eq.(2)) is nonlinear and should exhibit many frequency components. For the large value of time(\(\tau \rightarrow \infty \)), the asymptotic solution of Eq.(2) can be given as follows:

$$\begin{aligned} \begin{array}{ll} <x(\tau )>_{as} = \sum \limits _j^{} {x_m (j\omega _{i} )} \cos \left[ { j\omega _{i} \tau - \psi _{m} (j\omega _{i} )} \right]&\end{array} \end{aligned}$$
(20)

where j is a non-negative constant which may be in integer or fractional form, \(x_{m}(j\omega _{i})\) and \(\psi _{m}(j\omega _{i})\) are the mean response amplitude and phase lag respectively at the frequency \(j\omega _{i}\). The mean amplitude response is defined as in Ref. [13]:

$$\begin{aligned} \begin{array}{ll} x_m = \sqrt{A_s^2 + A_c^2 }&\end{array} \end{aligned}$$
(21)

where \(A_{s}\) and \(A_{c}\) are the ith sine and cosine components of the Fourier coefficients defined as follows:

$$\begin{aligned} \begin{array}{ll} A_S = \frac{2}{{nT}}\int \limits _0^{nT} {x(\tau )\sin (\omega _{i} \tau )d\tau } &{} \\ A_c = \frac{2}{{nT}}\int \limits _0^{nT} {x(\tau )\cos (\omega _{i} \tau )d\tau } &{} \end{array} \end{aligned}$$
(22)

where \(n=500\), while \(T= \frac{{2\pi }}{\omega _{i} }\) is the period harmonic excitation.

Figure 5a shows the evolution of the numerically computed \(x_{m}(\omega )\) for \(\omega =\omega _{0}\), \(\omega =\omega _{1}=2\omega _{0}\) and \(\omega =\omega _{2}=3\omega _{0}\) as a function of the noise intensity D. A typical noise-induced resonance is realized with theses frequencies. \(\omega _{1}\) and \(\omega _{2}\) are present in the input signal. The resonance observed with these frequencies is the usual stochastic resonance [24, 25]. The resonance associated with the missing frequency \(\omega _{0}\) is ghost-stochastic resonance. The ghost-stochastic resonance occurs at \(D=D_{max}=0.3\). This can be corroborated in Fig. 5b by plotting the mean residence time. Indeed, in Fig. 5b, when the noise intensity D is equal to \(D=0.05\), the size of the orbit increases when the value of D increases. However, the orbit remains in the right well. For \(D \ge 0.05\), the orbit visits the left well and gives rise to the ghost-stochastic resonance phenomenon when the noise intensity takes the value \(D=D_{max}=0.3\).

In Fig. 6a, we compare the output power generated by the hybrid model and those obtained by the piezoelectric and electromagnetic model respectively. We notice that the energy harvested by the hybrid model is higher than the one harvested by the piezoelectric or electromagnetic circuit. We provide in Fig. 6b, the 3D-representation of the output power of the hybrid model versus noise intensity and electrical impedance of piezoelectric circuit \(\alpha _2\). We observe that, for a fixed value of noise intensity D, the maximum of output power decreases when \(\alpha _2\) increases.

4.3 Efficiency in power conversion of the harvester

The efficiency conversion of energies dispersed in the environment by the electricity’s generator is the one of the fundamental elements for evaluating the system’s performance. Thus, the efficiency of the hybrid model is assessed by using this formula:

$$\begin{aligned} \begin{array}{ll} \eta = \frac{{P_e }}{{P_m }} \times 100&\end{array} \end{aligned}$$
(23)

with \(P_{e}\) and \(P_{m}\), are respectively, the electrical and the mechanical power effective value. It is well known in the literature that the power effective value is defined as:

$$\begin{aligned} \begin{array}{ll} p_{t} = \sqrt{\frac{1}{\tau }\int \limits _0^\tau {\left( {p_{t}^{ins} } \right) ^2 d\tau } }&\end{array} \end{aligned}$$
(24)

where \({p_{t}^{ins} }\) is the instantaneous power and \(\tau \) is the time.

In Fig. 5c, d, we drawn the efficiency conversion of the piezoelectric and electromagnetic subsystem versus noise intensity D. It emerges from these figures that, when \(\omega =\omega _{0}\), the efficiency increases for \(D<D_{max}\), reaches a maximum for \(D=D_max=0.3\) when the ghost-stochastic resonance occurs, and decreases for \(D>D_{max}\). We also provided in Fig. 5e, f, the output power for \(\omega =\omega _{0}\), for different values of electrical impedance of the piezoelectric \(\alpha _{2}\) and magnetic circuit \(\alpha _{3}\). We observe in these figures that, while the fundamental frequency is absent in the input signal, the harvester can generated a significative energy. In addition, we also notice in these figures Fig. 5e, f that, an enhancing the \(\alpha _{2}\) and \(\alpha _{3}\) lead to decrease the output power.

We plotted in Fig. 7, the time series of the harvester, with the corresponding probability distribution. In Fig. 7a, b, we observe that the system vibrates in the right-well and presents a lot of maximum and minimum. No any transition is observed in this condition. However, in Fig. 7c, the transition phenomenon is observed. The system vibrates around the position X = 0 between the positions X = −4.29 and X = 4.359. This is corroborated by Fig. 7d. We plot in Fig. 8a–d, the voltage of the piezoelectric subsystem and the magnetic current of the magnetic circuit versus the time, corresponding to the probability density function plotted in Fig. 7b, d. We notice in Fig. 8, the amplitude of the voltage of the piezoelectric circuit and magnetic current of the magnetic circuit is higher when the ghost-stochastic resonance occurs. Thus, when the ghost-stochastic resonance occurs, the piezoelectric output power and the magnetic output power will be maximized, and consequently, improves the amount of energy harvested by the scavenger. This shows the correlation between the peaks location in the probability density function and the output power.

Fig. 8
figure 8

Time series of the piezoelectric voltage and magnetic current, a Voltage of piezoelectric circuit before the ghost-stochastic resonance, b Magnetic current of the magnetic circuit before the ghost-stochastic resonance,c Voltage of piezoelectric circuit when the ghost-stochastic resonance occurs, d Magnetic current of the magnetic circuit when the ghost-stochastic resonance, for for \(\mu _{a}=0.3\), \(\beta _{2}=0.005\), \(\beta _{1}=0.003\), \(\alpha _{2}=0.000001\), \(\beta _{22}=-0.005\), \(\beta _{11}=0.003\), \(\alpha _{3}=0.0003\), \(\sigma =0.05\), \(f_{0}=0.39\), \(\omega _{0}=1\)

Full size image

5 Discussion

In a broad sense and as we show in this work, kinetic energy harvesters can convert any mechanical motion (like fluid flows, pressure variations and ambient vibrations) into electrical energy to power systems located in its environs [26]. In this purpose, it is necessary to take account of the presence of nonlinearity, both desired and undesired. Nonlinearities appear through nonlinearity in the spring force [27] and others component’s nonlinearities. A number of recent contributions seek to use nonlinearity in a novel way to improve the harvesters performances (see [28,29,30]), thus justifying the consideration of nonlinearity in this work.

This work shows that for our device, the maximum power of the hybrid model is greater than that of the piezoelectric and electromagnetic models independently (Fig.6). As pointed in [31], hybridization of two conversion mechanisms in a single system improved the functionality of the harvester in the low frequency range (such as vehicle motion, human motion, and wave heave motion, which usually occur at low frequencies (\(<20Hz\)) [32,33,34]). It is seen that the results are qualitatively in rather good agreement with those from [35], that noticed that the total synergistically extracted power from the hybrid harvester is more than the power obtained from each independently. Many authors [36,37,38] have pointed that, hybridization could be deliberately exploited within a mechanical system for optimized energy harvesting. Experimental results from [35] confirms that the extracted power at various loading conditions for available ambient excitations is greater.

In this manuscript, the harmonic excitation is combined with Gaussian white noise. As we mentioned in the preceding sections, the type of energy harvester system under study, could be subjected to noise, coming from many sources (such as physical structure-generated noise [39], environmental and transportation noise [40,41,42,43] and pneumatic noise [44,45,46].

The results obtained in this work, shows an improvement of the system performance when the noise intensity is around \(D\approx 0.3\) (See Fig. 5c, d) for a frequency of vibration absent in the frequency bandwidth of the harmonic force. It is known in the literature that, when the nonlinear system is subjected to the combination of the harmonic excitation and the random force, many phenomena can be observed such as the stochastic resonance and the ghost-stochastic resonance. These two phenomena are characterized by the large amplitude of vibration [47,48,49]. Zheng at al. [50, 51] in their work, have indicated that the available power generated under stochastic resonance is noticeably higher than the power that can be collected under other harvesting conditions. As in this study this resonance occurs and the maximum amplitude of the system is reached for a frequency of vibration absent in the frequency bandwidth of the harmonic force, this phenomenon is called a ghost-stochastic resonance [52,53,54,55].

6 Conclusion

In summary, the hybrid energy scavenging device subjected to the Gaussian White noise is investigated. Using the stochastic averaging method, we constructed the \(Fokker -Plank-Kolmogorov\) equation whose the solution in the stationary state is the probability density. From this statistic response, we assessed the output power of the piezoelectric and electromagnetic circuit under the form of mean square voltage and current. The impact of electrical impedance of piezoelectric and electromagnetic subsystem is presented with detail. It emerges from these results that, the output power of the two electrical circuit enhance when the coupling parameters increase while a enhancing of the electrical impedances lead to the reduction of the output power. In addition, combining the coherence force with random excitation, the ghost-stochastic resonance occur and improved the system performance. The agreement between the analytical and numerical results validated the efficiency of the analytical method proposed. The results obtained in this manuscript reveal that, while the natural frequency is absent in the coherent excitation, the system performance can be improved for certain value of the noise intensity.