Abstract
In this paper a three-dimensional isotropic fractional viscoelastic model is examined. It is shown that if different time scales for the volumetric and deviatoric components are assumed, the Poisson ratio is time varying function; in particular viscoelastic Poisson ratio may be obtained both increasing and decreasing with time. Moreover, it is shown that, from a theoretical point of view, one-dimensional fractional constitutive laws for normal stress and strain components are not correct to fit uniaxial experimental test, unless the time scale of deviatoric and volumetric are equal. Finally, the model is proved to satisfy correspondence principles also for the viscoelastic Poisson’s ratio and some issues about thermodynamic consistency of the model are addressed.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Real viscoelastic materials, such as polymers [1, 2], biological tissues [3–5], asphalt mixtures, soils [6] and many more exhibit power-law creep and relaxation behaviour. This means that during a creep/relaxation test the stress/strain response is characterized by a power law with respect to time. The main issue is then how to model this behaviour in a robust and efficient way. In the classical modeling approach, relaxation and creep functions have been modeled, mainly, by means of single and/or linear combinations of exponential functions in an attempt to capture the contribution of both solid and fluid phases. This approach does not allow for a correct fit of experimental results. It has been demonstrated that a power-law in the creep and relaxation responses leads to fractional viscoelastic constitutive models that are characterized by the presence of so-called fractional derivatives and integrals, namely derivatives and integrals of non-integer order (see [7, 8]); when the order of derivation (or integration) is integer, the fractional operators reduce to the classical differential operators. The most interesting aspect of fractional operators is that they have a long “fading” memory. In this context the term “hereditariness” is usually used in the sense that the actual response in terms of stress/displacement depends on the previous stress/strain history. If a relaxation or creep test is well fitted by a power-law decay, then the fractional constitutive law is directly derived by simply applying Boltzmann’s superposition principle [9, 10]. Such a constitutive law is defined by a small number of parameters and avoids the need to combine a number of simple models which depend on several parameters to capture both the creep and relaxation behaviour. Although some aspects remain unclear, for example how to distinguish between elastic and inelastic strain, the use of this kind of model is attractive for many researchers because of its ability to capture both creep and relaxation behaviour and the effects of “fading” memory observed experimentally. In the last decades, a lot of effort has been devoted to theoretical aspects of 1D fractional constitutive laws [2, 11–13] as well as experimental aspects and parameters characterization [3, 14–16] of the constitutive behavior and to numerical implementation in finite element codes [5]; fractional viscoelastic beams have been also studied, both from a deterministic and stochastic point of view [17–19]. However it is very important to properly define multi-axial constitutive relationship in order to simulate the viscoelastic behavior of complex shaped engineering components. Some authors (see for example [4, 20–22]) have proposed 3D formulations of fractional viscoelastic models with both small strain and large strain formulations, but to the best of authors’ knowledge only in one case [22] the three-dimensional behavior of these models is investigated; in particular in [22] the behaviour of the three-dimensional fractional viscoelastic model is investigated in terms of storage and loss moduli in the frequency domain and in terms of Poisson’s ratio in the time domain; a generalized three-dimensional fractional viscoelastic model is adopted in order to reproduce the experimental behaviour of some polymers in frequency domain.
For this reason, in this paper, some theoretical aspects about three-dimensional fractional viscoelasticity are discussed. First of all, a linear isotropic fractional viscoelastic model is defined in terms of deviatoric and volumetric contributions; it is shown that as soon as different time scales are assumed for the two contributions, the interpretation of uniaxial test (creep and relaxation) should be performed by means of two power law and not only one as usual researchers of the field do. Moreover, it is shown that time varying Poisson’s ratio can be easily obtained by choosing different time scales for the deviatoric and volumetric components; in particular increasing, decreasing or constant viscoelastic Poisson’s ratios are determined by the order of the power law in the deviatoric and volumetric contributions. This is a desirable feature, since viscoelastic materials exhibit increasing and decreasing viscoelastic Poisson’s ratio [23]. The influence of the Poisson’s ratio behavior is also shown by monitoring strain and stresses in creep and relaxation tests.
Finally, it is shown that the model satisfies correspondence principles [24] hence can be accepted by the general theory of viscoelasticity; moreover, by means of correspondence principles it is proved that for fractional viscoelasticity that the equivalent of the elastic Poisson’s ratio is the viscoelastic Poisson’s ratio in relaxation conditions and not in creep. This is an important result that confirms results by other authors [25, 26] that have not referred to fractional viscoelasticity. Some concepts about thermodynamic consistency of the model are also discussed.
2 Preliminary concepts
In this section we introduce some preliminary concepts on fractional viscoelasticity and fractional differentiation and integration.
It is well known that a viscoelastic material can be characterized, for one dimensional problems, by its Relaxation and Creep functions \(G_R(t)\) and \(G_C(t)\) respectively. These functions describe the behavior of the material when a constant strain and a constant stress are applied, respectively. Classical models are characterized by exponential functions. This happens when viscoelastic materials are modeled by different combinations of elastic elements (springs) and viscous elements (dashpots); the simplest models of this kind are Maxwell and Kelvin-Voigt models in which a spring and a dashpot are combined in series and in parallel, respectively. Although these models are able to describe a kind of time-dependent behavior of viscoelastic materials, they fail to capture both the relaxation and the creep behavior of real materials; for this reason more complicated models with combinations of springs and dashpots are used (Zener models), but this leads to complicated creep and relaxation functions and governing equations; furthermore these classical models are not able to describe the long-time memory of real viscoelastic materials. Creep and relaxation tests on real viscoelastic materials, such as polymers, asphalt mixtures, biological tissues, have shown that creep and relaxation tests are well fitted by power laws of real order rather than exponential functions. These functions can be written as follows [1, 27]:
where \(\Gamma (\cdot )\) is the Euler gamma function, \(\rho \) is a real number \(0\le \rho \le 1\) and \(C_\rho \) is a material parameter evaluated by fitting creep or relaxation experimental curves; the subscripts R and C stand for relaxation and creep, respectively. It is to be noted that the coefficient \(C_\rho \) has an anomalous dimension; indeed it depends on the value of \(\rho \); if mega-Pascal and minute seconds are used for the stress and the time, respectively, then the coefficient \(C_\rho \) has dimension \(\left[ {\text {MPa}}\;s^\rho \right] \). As a consequence \(G_R(t)\) and \(G_C(t)\) have dimension (MPa) and (MPa\(^{-1}\)), respectively.
It is well known that, in the frame of linear viscoelasticity, the Boltzmann superposition principle is valid; this principle allows us to obtain the response of a material when the imposed stress or strain history is not constant and can be expressed in two forms:
where \(\tau (t)\) and \(\gamma (t)\) are tangential stress and the corresponding strain, respectively. These integrals are often labeled as “hereditary” integrals, because the actual value of \(\tau (t)\) (or \(\gamma (t)\)) depends on all previous history of \(\gamma (t)\) (or \(\tau (t)\)). By taking Laplace transforms of Eq. (2) an interesting relationship between the relaxation and creep functions in the Laplace domain is obtained:
where the superimposed hat means Laplace transform and \(s\in {\mathbb {C}}\) is the variable in the Laplace domain. This implies that it is sufficient to perform a creep or relaxation test to determine all the relevant parameters of the viscoelastic model.
Substitution of Eq. (1) in Eq. (2) leads to constitutive laws that involve fractional operators, namely derivatives and integrals of real order [7, 8]:
where \(\gamma (0)=0\) and \(\tau (0)=0\) has been assumed, respectively. In Eq. (4a) \(\left( _0^C D_t^\rho \cdot \right) \) is the so called Caputo fractional derivative [7] of order \(\rho \). In Eq. (4b) \(\left( _0 I_t^\rho \cdot \right) \) is the Riemann-Liouville fractional integral of order \(\rho \). For brevity sake’s in the remainder part of the paper we will refer to these as \(D^\rho \) and \(I^\rho \). Both the Caputo and the Riemann-Liouville operator are convolution integrals with power law kernel [7].
These constitutive laws represent the response of a springpot element, introduced in [28]. It has been shown in [11, 29, 30] that the behaviour of the springpot can be reproduced in a classical viscoelasticity framework by an infinite sequence of springs and dashpots linked in a hierarchical way. These results are a confirmaton of the fact that fractional models can reproduce the viscoelastic behavior of real materials with much less mechanical parameters than those needed in classical viscoelasticity.
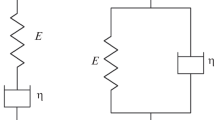
Caputo’s fractional derivative and the Riemann-Liouville fractional integral are considered integro-differential operators because all rules for derivatives and integrals of integer order are still valid (Fourier and Laplace transforms of a derivative or an integral, Leibniz rule, semi group rule, for more informations see [7]). Moreover, when \(\rho \) reaches limit values of 0 and 1, derivatives of order 0 and 1 are obtained. This underlines a very important characteristic: when \(\rho \rightarrow 0\) the fractional viscoelastic constitutive law of Eq. (4) reduces to the purely elastic (one-dimensional) Hooke law, while for \(\rho \rightarrow 1\) the fractional constitutive law becomes the constitutive law of a dashpot. For this reason, as the fractional operators are generalizations of integro-differential operators of integer order, the constitutive law of the springpot can be seen as a generalization of the constitutive laws of springs and dashpots. This concept is summarized in Fig. 1.
The main advantages of fractional viscoelastic models in comparison with classical models are:
-
The fitting of experimental tests is straightforward with a power law type relaxation and creep functions and it leads to very good results, both for the short and long time behaviour; this is not true for classical viscoelastic models that need a number of mechanical elements (springs and dashpots) thus requiring many fitting parameters to capture the long time behaviour.
-
Constitutive equations are derived consistently with the Boltzmann superposition principle.
-
Fractional viscoelastic models are characterized by long fading memory because of the power law kernel and this is in agreement with the time dependent behaviour of real viscoelastic materials.
-
When the order of derivation reaches integer values, the springpot reduces to one of the classical elements, spring or dashpot; it can therefore be considered as an element with intermediate behaviour between the two classical elements.
-
Viscoelastic models with fractional derivatives are linked to molecular theories that describe the macroscopic behaviour of viscoelastic materials [31, 32].
-
Fractional order viscoelasticity has proved to satisfy the second law of thermodynamics and to predict elliptical stress-strain hysteresis loop [31, 32].
Equations of this section are intentionally written referring to shear stress and strain; usually the same form of creep functions, relaxation functions and governing equations are assumed also for normal stresses and strains. However, in the next section it will be shown that the form of Eqs. (1), (2) and (4) is not correct for the normal stresses and strains.
3 Three-dimensional fractional constitutive law
In this section we introduce the isotropic 3D fractional model of the springpot; the model is intended to be isotropic throughout the deformation, hence it is assumed that the effects due to memory do not alter the material symmetries.
The constitutive model is obtained by means of a generalization of the elastic constitutive law (Hooke’s Law); in that case only two parameters are required to define the whole stiffness (or compliance) matrix of the material and these two parameters can be chosen as Young’s modulus and Poisson’s ratio, or Young and shear modulus, or Bulk and shear modulus, or Lamé constants. Hereinafter, we choose to write the relaxation matrix in terms of the shear and Bulk (volumetric) contributions, for two main reasons: (1) the terms of the relaxation (or creep) matrix can be expressed as a simple summation of the relaxation (or creep) volumetric and deviatoric functions, leading to simple and easy manageable governing equations as it is shown later in this section; (2) the volumetric and deviatoric contributions have clear physical meanings and the relative relaxation (or creep) functions have to be measured experimentally. The relaxation matrix can be easily obtained by substituting in the stiffness matrix the shear modulus \(G=\frac{E}{2(1+\nu )}\) and the Bulk modulus \(K=\frac{E}{3(1-2\nu )}\), where E is the Young modulus and \(\nu \) is the Poisson’s ratio, with the deviatoric relaxation function G(t) and the volumetric relaxation function K(t), respectively; in this way the relaxation matrix is written as follows:
where \(\delta _{ij}\) is the Kronecker symbol and \(R_{ijkh}\) has dimension (MPa). For both deviatoric and volumetric relaxations functions power law functions, analogous to the one dimensional relaxation law of the springpot [27, 28], are selected:
where \(G_\alpha \), \(\alpha \) and \(K_\beta \), \(\beta \) are parameters of the deviatoric and volumetric relaxation functions, respectively.
By assuming relaxation functions with the form of Eq. (6), a four parameters mechanical model is obtained. The strain-stress relationship can be obtained simply by applying the Boltzmann superposition principle:
where \({\varvec{\sigma }}(t)=\left[ \sigma _{11}\,\sigma _{22}\,\sigma _{33}\,\tau _{12}\,\tau _{13}\,\tau _{23}\right] \) and \({\varvec{\varepsilon }}(t)=\left[ \varepsilon _{11}\,\varepsilon _{22}\,\varepsilon _{33}\right. \left. \gamma _{12}\,\gamma _{13}\,\gamma _{23}\right] \) are the stress and strain vectors, respectively, and \({\varvec{R}}(t)\) is the relaxation matrix (5). Since \({\varvec{R}}(t)\) contains power law functions, the components of the stress vector \({\varvec{\sigma }}(t)\) depends on the fractional derivatives of the components of the strain vector \({\varvec{\varepsilon }}(t)\):
The inverse relationship of Eq. (7) is obtained by applying the dual form of Boltzmann’s superposition principle:
In order to use Eq. (9) we need to obtain the creep matrix \({\varvec{C}}(t)\) by using Eq. (3) (adapted for the 3D case). \({\varvec{C}}(t)\) is evaluated by performing a Laplace transformation of the relaxation matrix and evaluating its inverse in the Laplace domain:
By taking the inverse Laplace transform of \(\hat{\varvec{C}}(s)\) in Eq. (10) the creep matrix can be written as:
where \(C_{ijkh}\) has dimension (MPa\(^{-1}\)), \(K_C(t)\) and \(G_C(t)\) are creep functions of the volumetric and deviatoric parts, respectively, and are analogous to Eq. (1):
Note that in both Eqs. (5) and (11) the shear strain is considered as the engineering shear strain, e.g. \(\gamma _{12}=2\varepsilon _{12}\). By substituting Eq. (12) in Eq. (9), the components of the strain vector \({\varvec{\varepsilon }}(t)\) depend on the fractional integrals of the components of the stress vector \({\varvec{\sigma }}(t)\):
Governing equations can be also obtained simply by writing separately the volumetric and deviatoric contribution and then summing them.
It is to be emphasized that as in the pure torsion case there is a perfect duality between the direct and the inverse constitutive laws [see Eq. (4)], such a duality is preserved in the three dimensional direct and inverse constitutive laws [see Eqs. (8a) and (13a)].
In some applications it could be necessary to define anisotropic viscoelastic models; this is for example the case of fiber reinforced composites with polymeric matrices, especially when the fiber have a prevalent orientation (pultruded bars); for this reason the mechanical properties are different between the direction along the fibers and the directions orthogonal to fibers hence anisotropic constitutive model are required. As in elasticity the number of mechanical constant increases with the increasing level of anisotropy, in viscoelasticity for anisotropic models more than two relaxation (or creep) tests have to be performed in order to define more than one viscoelastic Poisson’s ratio, however concepts discussed in this paper remain valid with the correct adaptation for the level of anisotropicity at hand. At this stage some remarks are important for understanding the physics of the problem at hand.
Remark 1
It is worth noticing that the three-dimensional fractional viscoelastic constitutive law of Eq. (7) can be obtained also by using correspondence principles, also know as comparable elasticity relations [24]. Based on these principles, constitutive equations and relationships between different moduli for a viscoelastic model can be found simply by substituting in the correspondent elasticity relationship the s-multiplied Laplace transform to the elastic quantity. For example since in elasticity:
in viscoelasticity the following relation holds:
Using the correspondence principles, the three-dimensional fractional viscoelastic model in the Laplace domain is written as:
or
Now since in Laplace domain multiplication for s corresponds to derivation in time domain and the product between two functions corresponds to convolution product in time domain, inversion of Eq. (17) yields directly Eq. (7).
This means that the three-dimensional fractional viscoelastic mechanical model satisfies correspondence principles and then it may be included in the general framework of the theory of viscoelasticity.
Remark 2
It is to be remarked that the choice of deviatoric and volumetric relaxation or creep leads to the most simple and correct choice for the direct derivaton of the three-dimensional governing law. As soon as Eq. (6) are assumed then in the tensile creep test, in which a constant unitary stress is applied to the specimen, we obtain:
leading to the constitutive equations:
where \(\sigma _L(t)\) and \(\varepsilon _L(t)\) are the longitudinal stress and strain, respectively, while \(\varepsilon _T(t)\) is the transverse strain. From these relations it is evident that, from a theoretical pint of view, the constitutive laws expressed with the unique parameter \(\rho \) defined in Eq. (4) is not correct for the normal components of stress and strain. The reason is that the summation of two power laws [see Eqs. (18) and (19)] cannot be expressed as an unique power law, except if the two power laws are of the same order. People working in experimental fractional viscoelasticity may be disconcerted for the previous statement because the experimental tests (creep or relaxation) are usually performed with a uniaxial test; the best fitting procedure of the data appears to be good and absolutely acceptable. The same concept holds for the relaxation; however, in uniaxial relaxation, while the superimposed longitudinal strain is constant, the transverse strain is not constant and must be evaluated in Laplace domain in order to obtain its contribution to the longitudinal stress; this implies a number of manipulations that for the sake of simplicity are not reported here.
On the other hand, the use of the three-dimensional fractional constitutive law confirms that the single power law function and governing equation of Sect. 2 are correct for the interpretation of pure shear or torsion tests. This may explains the reason that, in the uniaxial test, the parameter \(\rho \) that fits very well the creep phase do not fits the recovery phase. In conclusion the ideal tests in order to characterize a viscoelastic material are shear and volumetric tests, since only one component of stress and corresponding strain are present (shear and hydrostatic). On the other hand the volumetric test (creep or relaxation) is not easy to perform since the experimental machines are manufactured only for uniaxial and torsion creep or relaxation test. It follows that, in order to define the 3D constitutive laws, it may be performed the torsion test and uniaxial test and by using Eqs. (18) and (19) both deviatoric and volumetric components may be easily separated.
The concepts outlined in this remark may be readily applied to the interpretation of experimental data. The one dimensional creep of some polymers is well fitted, both in creep and recovery phase, by a fractional Maxwell model constituted by a spring and a springpot connected in series; a practical example is the Ultra High Molecular Weight PolyEthylene (UHMWPE) [16] commonly used for human joint replacements. The creep function in one dimensional conditions \(E_C(t)\) of the fractional Maxwell model reads as follows:
where E is the Young modulus of the spring and \(\rho \) and \(C_\rho \) are the mechanical parameters of the springpot. The same creep function can be obtained from Eq. (18a) if \(\alpha =\rho \), \(3G_\alpha =C_\rho \), \(\beta =0\) and \(9K_\beta =E\) is assumed. This means that theoretically the three dimensional viscoelastic features of the UHMWPE may be captured with the three-dimensional fractional viscoelastic model discussed in this paper with \(\beta =0\). Such a model is similar to elastically compressible fractional viscoelastic model described in [22]; the difference is that the deviatoric behaviour here is described by a spingpot model, while in [22] it is a fractional Kelvin-Voigt model. This possibility cannot be completely verified only by means of a uniaxial test, but it is necessary to perform at least a uniaxial and a torsion test as explained above.
Remark 3
It is to be remarked that the volumetric component assumed as in Eq. (12b) has an undesired physical inconsistence: as \(t\rightarrow \infty \) a finite specimen will be collapsed in a single point. In order to avoid this undesired feature some authors propose a modification on \(K_C(t)\) (and as consequence on \(K_R(t)\)) by simply adding a purely elastic contribution [4]. However this way to enforce a constant contribution in Eq. (12b) is meaningless. In the authors opinion the correct way is to follow the path in large displacement theory. When the specimen reduces in size the repulsive effects between adjacent particles (coming from the Lennard-Jones potential) modify the original constitutive law in a sensible manner since the repulsive force between adjacent particles are strongly non linear when their distance becomes smaller.
On the other hand the example of the UHMWPE described at the end of Remark 2 reveals that potentially a special case (\(\beta =0\)) of the three-dimensional springpot model could be already acceptable in order to reproduce the behaviour of some materials. However the authors do not exclude that some applications requires necessarily the adoption of models not simple as the springpot, as for example it has been found in [22], at least for the interpretation of tests in frequency domain.
4 The fractional viscoelastic Poisson’s ratio
One of the most important aspects of 3D viscoelastic models is the behavior of the ratio between the lateral contraction and the elongation, i.e. the viscoelastic Poisson ratio. It is well known that during the infinitesimal deformation of any real viscoelastic material, the lateral contraction is a time-dependent (or equivalently frequency-dependent) function. Among all studies devoted to the viscoelastic Poisson’s ratio, the works of Lakes and Tschoegl [23, 25, 26] are of particular interest. In the paper [25] some concepts about viscoelastic Poisson’s ratio are clarified: firstly, it is shown that the viscoelastic Poisson’s ratio depends on the test performed, then viscoelastic Poissson’s ratio is different in creep and in relaxation test; secondly it is shown, by means of correspondence principles [24], that the viscoelastic counterpart of the elastic Poisson’s ratio is the viscoelastic Poisson’s ratio in relaxation and not in creep; finally, it is shown how to switch between Poisson’s ratio in creep and in relaxation. In the paper [26] the same results are achieved. Moreover, in the papers [23, 26] it is shown that the viscoelastic Poisson’s ratio can increase or decrease with time; indeed, most polymers for example exhibit an increasing Poisson ratio because of the fact that the volumetric part of stress relaxes much less than the deviatoric part, but materials with a particular microstructure can behave in the opposite way. Furthermore, in the paper [26] it is demonstrated that the viscoelastic Poisson’s ratio do not need to be monotonic with time.
However in the aforementioned papers the authors do not refer to Poisson’s ratio for fractional viscoelasticity. For this reason in the following section results of papers [23, 25, 26] are confirmed for fractional viscoelasticity. It will be shown that the fractional viscoelastic Poisson’s ratio can be constant, decreasing or decreasing depending only on the parameters \(\alpha \) and \(\beta \), demonstrating the great flexibility of the 3D fractional viscoelastic constitutive law.
4.1 Poisson’s ratio in creep
The Poisson ratio is evaluated in an ideal creep test on a viscoelastic cube; only one face of the cube is fixed only in the normal direction and in the opposite face the cube is loaded by a constant normal stress \(\sigma _0\); using the springpot model of Fig. 1 considering the creep functions specified in Eq. (12) the Poisson ratio in creep, denoted as \(\nu _C(t)\), is given as:
where \(\varepsilon _L(t)=\left( \frac{K_C(t)}{9}+\frac{G_C(t)}{3}\right) U(t)\) and \(\varepsilon _T(t)=\left( \frac{K_C(t)}{9}+\right. -\left. \frac{G_C(t)}{6}\right) U(t) \) are the longitudinal and transverse strain, respectively, U(t) is the unit step function and \(a=\frac{K_\beta \Gamma (1+\beta )}{G_\alpha \Gamma (1+\alpha )}>0\). If \(\alpha =\beta \), the Poisson ratio is constant over time:
Note that Eq. (21) can be written in this form because, since in creep all the components of the stress vector are unit step functions (the longitudinal one is a unit step function, while the others are zero), the convolution (9) reduces to a product between \({\varvec{C}}(t)\) and \({\varvec{\sigma }}(t)\). Both \(\varepsilon _L(t)\) and \(\varepsilon _T(t)\) can then be simply written in terms of volumetric and deviatoric creep functions.
If \(\alpha \ne \beta \), the Poisson ratio varies in time and it has limit values at \(t=0\) and \(t=\infty \), as summarized in the Table 1.
Note that both the values have to be evaluated as a limit. The main consequences of these results are:
-
If \(\alpha >\beta \), the material exhibits a Poisson ratio of −1 at \(t=0\), then its behavior gradually changes until it becomes incompressible for large values of t. The anomalous behaviour at \(t=0\) has been already found for the elastically compressible fractional viscoelastic material described in [22].
-
If \(\beta >\alpha \), the material is incompressible at \(t=0\), then its behavior gradually changes until it exhibits a negative Poisson ratio for large values of t.
It is to be emphasized, that although the coefficient \(G_\alpha \) and \(K_\beta \) are dimensionally anomalous, the viscoelastic Poisson’s ratio is non-dimensional as expected. Indeed, since the coefficients \(G_\alpha \) and \(K_\beta \) have dimension \({\text {MPa\;s}}^\alpha \) and \({\text {MPa\;s}}^\beta \), the term a of Eq. (21) has dimension \(s^{\beta -\alpha }\); since the term a is multiplied for \(t^{\alpha -\beta }\) in Eq. (21) and the other terms of the same equation are pure numbers, the viscoelastic Poisson’s ratio in creep \(\nu _C(t)\) is a non-dimensional quantity.
4.2 Poisson’s ratio in relaxation
The Poisson ratio can also be evaluated for an ideal relaxation test on a cube with the same boundary conditions of the creep test; on the face opposite the fixed one, a normal constant displacement is applied. In this case the longitudinal strain is imposed while the transverse strain is unknown; in order to obtain it we simply need to write Eq. (7) and assume that the transverse components of the stress are both zero. Since \(\varepsilon _T(t)\) is not constant as \(\varepsilon _L(t)=\varepsilon _0 U(t)\), relationship (7) does not simplify in a simple product between \({\varvec{R}}(t)\) and \({\varvec{\varepsilon }}(t)\), then an expression of the Poisson ratio in relaxation in terms of the relaxation functions is not straightforward. In [33] a relationship between the two ratios has been found:
where \(C_{11}(t)\) is the term that gives \(\sigma _{11}(t)\) for an applied \(\varepsilon _{11}(t)\), that is \(C_{11}(t)=\frac{\bar{K}(t)}{9}+\frac{\bar{G}(t)}{3}\). In order to find \(\nu _R(t)\) Laplace transform can be used, but inversion of the Laplace transform of \(\nu _R(t)\) to the time domain is very difficult. Only in the case when \(\alpha =\beta \) the transverse strain \(\varepsilon _T(t)\) is constant during the relaxation test and is equal to:
where \(\varepsilon _0\) is the amplitude of the superimposed strain. Since \(\varepsilon _L(t)=\varepsilon _0 U(t)\) the Poisson ratio is
The Poisson ratio in relaxation when \(\alpha \ne \beta \) can be found in another way. The longitudinal stress \(\sigma _L(t)\) can be decomposed into its deviatoric and volumetric components, labeled as \(\sigma _L^{d}(t)\) and \(\sigma _L^{v}(t)\), respectively; the volumetric component of the longitudinal stress is
being \(I_1\) the first invariant of stress; the deviatoric component of the stress is instead
On the other hand, by considering the constitutive law (7), \(\sigma _L^{(v)}(t)\) and \(\sigma _L^{(d)}(t)\) are written as:
where ε V is the volumetric strain.
Since from Eqs. (26) and (27) descends that \(\sigma _L^{(d)}(t)=2\sigma _L^{(v)}(t)\), by considering Eq. (28) the following equation is obtained:
This equation can be solved in the Laplace domain and gives the following results for the Poisson’s ratio:
where \(E_\lambda \left( \cdot \right) \), with \(\lambda >0\), is the one parameter Mittag-Leffler function defined as:
As expected, the expression for \(\nu (t)\) is not the same as for the creep test; however since, for \(c>0\), \(E_\lambda (-c t^\lambda )\rightarrow 1\) for \(t\rightarrow 0\) and \(E_\lambda (-c t^\lambda )\rightarrow 0\) for \(t\rightarrow \infty \), the general trend and limiting values still hold, hence observations made above for the creep test are still valid. In particular for \(\alpha =\beta \) the Poisson ratio assumes the same constant value \(\bar{\nu }\) of Eq. (22). As noted for \(\nu _C(t)\), the viscoelastic Poisso’s ratio in relaxation \(\nu _R(t)\) is non dimensional since the term \(\frac{3K_\beta }{G_\alpha }t^{\alpha -\beta }\) is non dimensional.
It is to be emphasized that Eq. (30) can be obtained directly by using the three-dimensional constitutive law (7) particularized for the case in which a uniaxial relaxation test is performed.
In Fig. 2 it is shown the viscoelastic Poisson ratio in a relaxation test for fixed \(\alpha =0.5\) and different values of \(\beta \); from this Figure it is possible to appreciate that the proposed 3D model is able to produce different trends in the behavior of the viscoelastic Poisson ratio; in creep conditions the viscoelastic Poisson’s ratio is only slight different from the behaviour described in Fig. 2 and is not reported for brevity. In Fig. 3 the influence of the parameters \(G_\alpha \) and \(K_\beta \) on the Poisson’s ratio is shown; Fig. 3a shows an increasing Poisson’s ratio (\(\alpha >\beta \)) for fixed \(G_\alpha \) and different values of \(K_\beta \); the same is shown in Fig. 3b for a decreasing Poisson’s ratio (\(\alpha <\beta \)). From this figures it is possible to appreciate that the greater is \(K_\beta \) than the faster the Poisson’s ratio approaches the limit value of \(\nu =0.5\) for increasing Poisson’s ratio, while for decreasing Poisson’s ratio the greater is \(K_\beta \) than the slower the Poisson’s ratio reaches the limit value of \(\nu =-1\). The parameters \(G_\alpha \) affects the Poisson’s ratio in the opposite way of the coefficient \(K_\beta \): for increasing Poisson’s ratio, a greater \(G_\alpha \) determines a slower increasing Poisson’s ratio, while for decreasing Poisson’s ratio a greater \(G_\alpha \) determines a faster decreasing one.
It is theoretically possible to further manipulate the behavior of the Poisson’s ratio; this can be done by using more complex fractional viscoelastic models, as for example fractional Kelvin-Voigt model, fractional Maxwell model or fractional Standard Linear Solid model (see for example [3, 22]); in particular the value in \(t=0\) and at \(t=\infty \) can be modified by the use of the aforementioned multi-element fractional models. However these fractional models are not investigated here for brevity.
4.3 Poisson’s ratio from correspondence principles
The Poisson’s ratio can be evaluated also by means of correspondence principles. In elasticity the Poisson’s ratio can be evaluated from elastic constants as
It follows from correspondence principles that
or from the equivalences \(s\hat{G}_R(s)=1/s\hat{G}_C(s)\) and \(s\hat{K}_R(s)=1/s\hat{K}_C(s)\) (see Eqs. (3) and (10))
Equation (34) can be obtained by means of correspondence principle. To this purpose, let us consider a relaxation test as in Sect. 4.1; the correspondence principles allow to write the Poisson ratio in Laplace domain as
Substitution of the relaxation or creep functions in Eq. (33) or in Eq. (34), respectively, gives the following:
Application of the inverse Laplace transform operator yields exactly Eq. (30), that is the Poisson’s ratio in time domain for the relaxation test and not for the creep test. This is an important result because reveals that also for fractional viscoelastic models the Poisson’s ratio in relaxation is the equivalent of the Poisson’s ratio in elasticity, confirming results of other authors [25, 26] that were not devoted specifically to fractional viscoelasticity.
5 Influence of Poisson’s ratio on stress and strain time evolution
The influence of the Poisson ratio, and then of the relative values of \(\alpha \) and \(\beta \), can be analyzed also by monitoring the normal components of stress and strain in ideal creep and relaxation tests in 3D conditions.
To this purpose, two ideal tests, one in creep with recovery and one in relaxation, are considered.
In the creep test, the boundary conditions are the same of those considered for the evaluation of the Poisson’s ratio; in this case the final value of the applied stress \(\sigma _0= 1\;\)MPa is reached with a linear ramp of duration \(t_0\); after a time \(t_1\) the loading is removed with a linear ramp of duration \(t_2-t_1=t_0\). The applied stress history \(\sigma (t)\) for the creep/recovery test depicted in Fig. 4a can be written as following:
The value of \(\alpha \) is fixed, while different \(\beta \) values are considered. The evolution of the longitudinal and transverse strain is monitored and reported in Fig. 5. From these figures it is clear that while the behavior of the longitudinal strain is affected only in the amplitude, the transverse strain can even radically change its behavior depending on the relative values of \(\alpha \) and \(\beta \); indeed, if \(\beta >\alpha \) the amplitude of the transverse strain decrease even if the longitudinal one increase.
The values of \(\alpha \) and \(\beta \) affect also the stresses; in order to analyze this influence, a relaxation behavior on a cube is considered. The cube has all faces but one fixed in the normal direction and in the free face a normal displacement is applied; with these boundary conditions the transverse strain is zero, but the transverse stress is not zero. The free face is strained reaching the final value of the strain \(\varepsilon _0= 1 \%\) by a linear ramp, as depicted in Fig. 4b and written as follows:
While the behavior of the longitudinal stress is slightly affected by the relative values \(\alpha \) and \(\beta \) and it is always decreasing with time, the transverse stress can increase or decrease with time, in particular if \(\beta <\alpha \) the transverse stress increases instead of decreasing as one expects.
The results of Figs. 5 and 6 have shown the flexibility of the three-dimensional springpot model in which the order of the power law for creep (and relaxation) volumetric and deviatoric functions can have different values. However these are only theoretical behaviors and in some cases they can be not so intuitive, as for example when \(\beta >\alpha \) in creep and for \(\beta <\alpha \) in relaxation. In this light, it would be necessary to apply the second principle of thermodynamics to see if some restrictions apply to the mechanical parameters of the mechanical model, especially regard the value of \(\alpha \) and \(\beta \). Thermodynamic consistency of material with memory have been widely investigated and demonstrated (see e.g. [34, 35]). Some studies on the thermodynamics of viscoelastic materials have been devoted to fractional viscoelasticity only. In particular, in [31] thermodynamics restrictions on the parameters of a one-dimensional fractional Standard Linear Solid (FSLS) viscoelastic model have been found; the model holds the second principle of thermodynamics if all multiplicative mechanical parameters are positive and if the order of the power law is in the range 0–1. In [32], thermodynamic consistency of a one-dimensional springpot model has been proved to be satisfied if the relaxation spectrum is positive, and this happens if the multiplicative coefficient is positive and if the order of power law lays in the range 0–1. Although the works [31, 32] refer to one-dimensional models, i.e. with only one relaxation/creep function, their results can be extended to the three-dimensional model studied in this paper. Indeed, for the deviatoric and volumetric relaxations functions considered separately, results of [32] are valid. When both deviatoric and volumetric components are “activated” during a loading process, in linear viscoelasticity their contributions can be analyzed separately and then summed. For the single relaxation function the thermodynamic restrictions on parameters are known, the same restrictions apply to both components, deviatoric and volumetric. The fact that the deviatoric and volumetric parts are both present does not imply that the second principle of thermodynamics imposes more restriction on the parameters \(\alpha \) and \(\beta \). Then we must conclude that all the behaviors described in this and in the previous section are thermodynamically consistent, the mechanical model of the three-dimensional springpot satisfies the second principle of thermodynamics whatever are the order of power laws \(\alpha \) and \(\beta \) in the range 0–1. A further confirmation of the last statement is reported in the “Appendix”.
6 Conclusions and discussion
In this paper the 3D fractional constitutive model has been presented for linear isotropic material. It has been shown that as soon as the deviatoric and volumetric components of the stress tensor are well fitted by [1] power law for the creep (and/or relaxation) the constitutive laws are ruled by fractional operators.
The Nutting experience was made on many materials like rubber, steel and many others and at that time the test was made in pure tension or compression. Many other experimentalists in the last half century confirmed the Nutting experiments. However usually the test is limited to the creep phase. People working on this subject confirm the Nutting results in the creep phase (by means of best fitting procedure); the parameters obtained in such a phase do not fit the recovery phase very well. Moreover the parameters obtained by experimental data (by using the results in a short time) have to be re-adapted when the duration of the test increases. Another unsatisfactory result is that the parameters obtained by a test with a sinusoidal input do not coincide with those obtained by the creep test. These inconsistencies are not explicitly claimed by the scientists working in this field but it is in contrast with the linear theory of viscoelasticity. In order to cover this lack of consistency many other models have been proposed in the past by adding an elastic or a viscous element to fractional one.
In the authors opinion all these modifications are artificious and do not present a clear physical meaning. In this paper we assume that the 3D costitutive law may be expressed as a summation of two contributions: the first one is the volumetric and the second one is the deviatoric contribution. For isotropic material the deviatoric and volumetric parts are totally separated (as in elasticity) and involve only one stress and corresponding strain. As soon as it is assumed that the creep law for the volumetric component is ruled by a power law (say \(t^\beta \)) and the deviatoric one is ruled by a power law (say \(t^\alpha \)) then in the tensile test the creep law is ruled by a linear combination of \(t^\alpha \) and \(t^\beta \). A summation of two distinct fractional operators are present. Now since \(\alpha \ne \beta \) an unique power law of the kind \(t^\rho \) may not fit in a perfect way creep or relaxation. This cause a dramatic withdraw from the experimental result in the recovery phase. Once this aspect is clarified it maybe stated that in order to fully characterize the 3D constitutive law two tests have to be performed: a creep test in pure torsion and a creep test in hydrostatic regime. Since the test machine in hydrostatic regime is not at the moment available, a pure tension may be performed. The 3D equations can be then written for the pure tension (or compression) in terms of both deviatoric and hydrostatic parameters.
In this paper a wide discussion on the role played by the Poisson ratio in creep and relaxation is presented. It has been shown that if the exponent of the hydrostatic component is greater than that of the deviatoric one then the model exhibits a decreasing Poisson’s ratio both in creep and in relaxation. If the exponent of the hydrostatic component is smaller than that of the deviatoric one then the Poisson ratio is increasing with time both in creep and in relaxation. If the two exponent are equal the Poisson ratio is constant over time. Moreover, it has been found that the equivalent of elastic Poisson’s ratio is the fractional viscoelastic Poisson’s ratio in relaxation and not in creep; this result was already found in other works that however were not devoted to fractional viscoelasticity. The influence of the Poisson ratio on stress and strain components has also been analyzed and the thermodynamic admissibility of the model has been discussed.
References
Nutting PG (1921) A new general law of deformation. J Frankl Inst 191:679–685
Bagley RL, Torvik PJ (1984) On the appearance of the fractional derivative in the behavior of real materials. J Appl Mech 51:294–298
Demirci N, Tonuk E (2014) Non-integer viscoelastic constitutive law to model soft biological tissues to in-vivo indentation. Acta Bioeng Biomech 16(4):13–21
Freed AD, Diethelm K (2006) Fractional calculus in biomechanics: a 3D viscoelastic model using regularized fractional derivative kernels with application to the human calcaneal fat pad. Biomech Model Mechanobiol 5:203–215
Kobayashi Y, Kato A, Watanabe H, Hoshi T, Kawamura K, Fujie MG (2012) Modeling of viscoelastic and nonlinear material properties of liver tissue using fractional calculations. J Biomech Sci Eng 7(2):117–187
Alotta G, Di Paola M, Pirrotta A (2014) Fractional Tajimi–Kanai model for simulating earthquake ground motion. Bull Earthq Eng 12(6):2495–2506
Podlubny I (1999) Fractional differential equation. Academic Press, San Diego
Samko GS, Kilbas AA, Marichev OI (1993) Fractional integrals and derivatives. Gordon and Breach Science, Amsterdam
Flugge W (1967) Viscoelasticity. Blaisdell Publishing Company, Waltham
Mainardi F (2010) Fractional calculus and waves in linear viscoelasticity. Imperial College, London
Di Paola M, Pinnola FP, Zingales M (2013) A discrete mechanical model of fractional hereditary materials. Meccanica 48(7):1573–1586
Rossikhin YA, Shitikova MV (1997) Application of fractional derivatives to the analysis of damped vibrations of viscoelastic single mass systems. Acta Mech 120:109–125
Rossikhin YA, Shitikova MV (2016) Dynamic response of a viscoelastic plate impacted by an elastic rod. J Vib Control 22(8):2019–2031
Craiem DO, Rojo FJ, Atienza JM, Guinea GV, Armentano RL (2008) Fractional calculus applied to model arterial viscoelasticity. Lat Am Appl Res 38:141–145
Di Paola M, Fiore V, Pinnola FP, Valenza A (2014) On the influence of the initial ramp for a correct definition of the parameters of fractional viscoelastic materials. Mech Mater 69(1):63–70
Guedes RM (2011) A viscoelastic model for a biomedical ultra-high molecular weight polyethylene using the time–temperature superposition principle. Polym Test 30:294–302
Di Paola M, Heuer R, Pirrotta A (2013) Fractional visco-elastic Euler–Bernoulli beam. Int J Solids Struct 50(22–23):3505–3510
Di Paola M, Failla G, Pirrotta A (2012) Stationary and non-stationary stochastic response of linear fractional viscoelastic systems. Probab Eng Mech 28:8590
Di Lorenzo S, Di Paola M, Pinnola FP, Pirrotta A (2014) Stochastic response of fractionally damped beams. Probab Eng Mech 35:37–43
Fukunaga M, Shimizu N (2015) Fractional derivative constitutive models for finite deformation of viscoelastic materials. J Comput Nonlinear Dyn 10:061002
Hilton HH (2012) Generalized fractional derivative anisotropic viscoelastic characterization. Materials 5:169–191
Makris N (1997) Three-dimensional constitutive viscoelastic laws with fractional order time derivatives. J Rheol 41:1007–1020
Lakes RS (1992) The time-dependent Poisson’s ratio of viscoelastic materials can increase or decrease. Cell Polym 11:466–469
Christensen RM (1982) Theory of viscoelasticity: an introduction. Academic Press, New York
Tschoegl NW, Knauss WG, Emri I (2002) Poisson’s ratio in linear viscoelasticity—a critical review. Mech Time Depend Mater 6:3–51
Lakes RS, Wineman A (2006) On Poisson’s ratio in linearly viscoelastic solids. J Elast 85:45–63
Gemant A (1936) A method of analyzing experimental results obtained from elasto-viscous bodies. Physics 7:311–317
Scott Blair GW, Caffyn JE (1949) An application of the theory of quasi-properties to the treatment of anomalous strain–stress relations. Philos Mag 40(300):80–94
Heymans N, Bauwens JC (1994) Fractal rheological models and fractional differential equations for viscoelastic behavior. Rheol Acta 33:210–219
Schiessel H, Blumen A (1993) Hierarchical analogues to fractional relaxation equations. J Phys A Math Gen 26:5057–5069
Bagley RL, Torvik PJ (1986) On the fractional calculus model of viscoelastic behaviour. J Rheol 30(1):133–155
Adolfsson K, Enelund M, Olsson P (2005) On the fractional order model of viscoelasticity. Mech Time Depend Mater 9:15–34
Van der Varst PGThn, Kortsmit WGE (1992) Notes on the lateral contraction of linear isotropic visco-elastic materials. Arch Appl Mech 62:338–346
Day WA (1970) Restrictions on relaxation functions in linear viscoelasticity. Q J Mech Appl Math 23:1–15
Coleman BD (1964) Thermodynamics of materials with memory. Arch Ration Mech Anal 17:1–46
Deseri L, Di Paola M, Zingales M (2014) Free energy and states of fractional-order hereditariness. Int J Solids Struct 51:3156–3167
Staverman A, Schwarzl T (1952) Thermodynamics of viscoelastic behavior. Ver Akad Can Wet Amst B55:474–485
Acknowledgments
GA wish to acknowledge support from the University of Palermo to visit the University of Oxford during which period this research was conducted. OB would like to acknowledge the Engineering and Physical Sciences Research Council [Programme Grant Number EP/L014742/1].
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare that they have no conflict of interest.
Appendix
Appendix
The thermodynamic consistency of fractional viscoelastic model has been widely investigated and demonstrated by several authors (see e.g. [31, 32, 34, 35]). In this “Appendix” two cases are studied in order to further confirm the results of other authors, a relaxation test and a dynamic test.
The thermodynamic consistency is usually investigated by imposing non-negative internal work (elastic energy stored in the solid) and non-negative rate of energy dissipation and if these hold what restrictions apply to its parameters in order to respect the conditions. In classical models the internal work is related to the stored energy in the solid, then to the elastic part of strain; the dissipated energy is related to the viscous part of the strain. However in fractional viscoelasticity is not possible to distinguish between elastic and inelastic strain; this is due to the the fact that the springpot model contains in itself the features of both spring and dashpot, as shown by the hierarchical or selfsimilar models that are able to reproduce power law viscoelasticity [11, 29, 30]. To overcome this problem, it is possible to work with state functions and in particular with the concept of free energy (corresponding to the elastic energy) and dissipation rates; indeed, in the paper [36] it has been found what is the right definition of the free energy for the springpot model shown in the following. In this way the free energy itself and the dissipation rate can be evaluated.
The specific Helmotz free energy \(\psi \) is a thermodynamic state function whose gradient with respect to the actual value of strain \(\varepsilon \) gives the measured stress; it represents the energy stored in the solid, that is what in elasticity is defined as elastic energy. The rate of free energy can be expressed as follows:
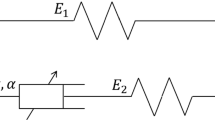
Applied strain histories for the evaluation of free energy and dissipation rate with Eq. (43): sinusoidal (a) and constant with initial linear ramp (b)
where \(\dot{u}\) is the rate of specific internal energy, T is the the absolute temperature and \(\dot{s}\) is the entropy production. The second principle of thermodynamics states that \(\dot{s}\ge \dot{q}/T\), being \(\dot{q}\) the rate of change of specific thermal energy, or simply the rate of thermal energy exchange. It is to be emphasized that:
-
The rate of change of specific internal energy is related to the rate of the specific mechanical work done on the system and on the thermal energy exchange, then \(\dot{u}=\dot{w}_{ext}+\dot{q}\).
-
Introducing the entropy production rate due to irreversible transformations labeled as \(\dot{s}^{(i)}\ge 0\), that is related to the dissipated energy, the second principle of thermodynamics can be written as \(\dot{s}=\dot{q}/T+\dot{s}^{(i)}\).
By performing these two substitutions in Eq. (39) we get:
where \(D(t)=T\dot{s}\) denotes the dissipation rate. When we apply a strain or stress history to the viscoelastic solid, in Eq. (40) the external work rate is known and can be evaluated as \(\dot{w}_{ext}=\sigma (t) \dot{\varepsilon }(t)\). If it is possible to define also the free energy rate then also the dissipation rate can be evaluated from Eq. (40). Unfortunately the free energy is not uniquely defined unless a rheological model with well defined and distinct elastic and viscous phases is available, as it is in classical viscoelasticity. In fractional viscoelasticity the only possibility to distinguish between elastic and viscous phases is to make use of hierarchical models [11, 29, 30] but the number of elements to be taken into account is significant and depends also on the observation time and on the input on the system; for these reasons this strategy is not applicable. However, in the paper [36] the mechanical models of fractional viscoelasticity have been used to prove that the correct form of the free energy function for the fractional viscoelastic material is the one proposed by Stavermann and Schwartzl [37] and defined as:
where \(R(\cdot )\) is the relaxation function as usual and the pedex SS stands for Stavermann and Schwartzl. By using Eq. (41) in Eq. (40), the following expression for the dissipation rate is obtained:
For the particular case of the springpot Eqs. (41) and (42) read as follow:
Equations (43) should be firstly applied to the one-dimensional springpot model and then to the three-dimensional springpot model; however from a one-dimensional point of view the thermodynamic consistency of the springpot has been already proved. In this case in order to evaluate the free energy and the dissipation rate it is needed to take all the components of stress and strain into account from both the volumetric and deviatoric contributions. Limitations on the relationship between \(\alpha \) and \(\beta \) can be found by enforcing the condition that \(\psi (t)\ge 0\;\;\forall t\) and \(D(t)\ge 0\;\;\forall t\). However the analytical solution of the double integrals in Eqs. (43) is not straightforward hence numerical integration has been performed. The analysis is performed for two cases: i) a sinusoidal hystory of strain is applied, but differently from the paper [31], also transient conditions are examined; ii) a constant strain, reached with a linear ramp, is applied.
Equations (43) have been evaluated by considering a large range of values of \(\alpha \) and \(\beta \); the other mechanical parameters (\(G_\alpha \) and \(K_\beta \)) are chosen positive, because negative value of multiplicative parameters violate thermodynamic restrictions also in one-dimensional conditions. For simplicity here we show only results with the following values: (1) \(\alpha =\beta =0.5\); (2) \(\alpha =0.5\), \(\beta =0.25\); (3) \(\alpha =0.5\), \(\beta =0.75\). Figure 8 shows the specific dissipation rate (dissipation rate per unit volume), while Fig. 9 show s the specific free energy function for the two applied strain histories of Fig. 7.
Figures 8 and 9 show that the dissipation rate and the free energy function are non-negative whatever the relationship between the values of \(\alpha \) and \(\beta \) is. From this evidence it has to be concluded that the 3D fractional viscoelastic models are thermodynamically consistent independently of the relationship between \(\alpha \) and \(\beta \); this means that both an increasing and a decreasing viscoelastic Poisson’s ratio are possible for 3D fractional constitutive models that hence are suitable to represent both behaviors.
Rights and permissions
About this article
Cite this article
Alotta, G., Barrera, O., Cocks, A.C.F. et al. On the behavior of a three-dimensional fractional viscoelastic constitutive model. Meccanica 52, 2127–2142 (2017). https://doi.org/10.1007/s11012-016-0550-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11012-016-0550-8