Cosserat elastic lattices

Abstract

Lattices composed of cubic and triangular prismatic unit cells with polymeric Sarrus linkage rib elements are designed, fabricated via 3D printing and studied experimentally. Size effects in these lattices are observed experimentally; slender specimens appear more rigid in torsion and in bending than expected via classical elasticity. Effects are analyzed via Cosserat elasticity. The magnitude of size effects is sensitive to geometry of the lattices; triangular cells with short ribs revealed the most extreme effects, also the largest characteristic length in relation to cell size. The torsion coupling number is 1, its upper bound, for all lattices. A path to the attainment of arbitrarily large nonclassical effects is delineated.

1 Introduction

Continuum theories are commonly used to model materials with microstructure, including the lattices presented here, as continuous media. Many different continuum theories of elasticity with varying degrees of freedom exist. One of the earliest theories, the uniconstant theory, was developed by Navier [1]. The uniconstant theory allows only one isotropic elastic constant, a modulus. This theory was governed by the assumption that forces acted along the lines joining pairs of atoms and were proportional to changes in the distance between them. This uniconstant theory predicted a Poisson’s ratio of 1/4 for all isotropic materials and was proven obsolete when experimentation disclosed a range of Poisson’s ratios. The currently accepted classical theory of elasticity is a step up in complexity and descriptive capability from Navier’s uniconstant theory because it incorporates two independent isotropic elastic constants. The classical theory of elasticity predicts Poisson’s ratio to range from $-\,1$ to 1/2 for isotropic materials.

Classical elasticity suffices for objects in which the structure size is many orders of magnitude smaller than the experimental size scale. Generalized continuum theories such as Cosserat elasticity entail more freedom than classical elasticity. Such theories are intended to deal with solids in which the structural length scale is non-negligible. To experimentally determine what kind of theory applies, one may do size effect measurements or study concentration of strain or stress. Experimental tests for Cosserat elasticity at the macroscopic scale in aluminum disclosed classical behavior [2]. However, classical elasticity can break down when the experimental length scale approaches the structural length scale of the material or structure being tested as reviewed later in the introduction. Additionally, neither classical elasticity nor the uniconstant theory incorporate a length scale in their definitions which is important when considering material properties such as toughness which has a length scale in its units, MPa$\sqrt{\mathrm {m}}$. The lack of a length scale prohibits either of these theories from being used to describe materials that are sensitive to strain gradients.

The Cosserat theory of elasticity [3] (with inertia terms called micropolar [4]) has even more freedom than the classical theory; Cosserat elasticity incorporates a local rotation of points and a couple stress (torque per unit area) in addition to the translation of points and force stress (force per unit area) present in classical elasticity. The physical origin of the Cosserat couple stress is the summation of bending and twisting moments transmitted by the structural elements in materials. The Cosserat local rotation corresponds to the rotation of structural elements. Forces and moments were considered in the classic analyses of foam by Gibson and Ashby [5] in which classic elastic moduli were determined; effects of rotation gradients were not considered.

The additional freedom in Cosserat elasticity is represented by its six isotropic elastic constants, $\alpha , \beta , \gamma , \kappa , \lambda ,$ and G. The constitutive equations for a linear isotropic elastic Cosserat solid [4] are as follows.

$$\begin{aligned} \sigma _{ij}&= 2G \epsilon _{ij} +\lambda \epsilon _{kk}\delta _{ij} + \kappa e_{ijk} (r_{k}- \phi _{k}) \end{aligned}$$

(1)

$$\begin{aligned} m_{ij}&= \alpha \phi _{k,k} \delta _{ij}+ \beta \phi _{i,j}+ \gamma \phi _{j,i} \end{aligned}$$

(2)

In Cosserat elasticity the stress, ${\sigma }_{ij}$, can be asymmetric. The moment that results is balanced by a couple stress, $m_{ij}$. The antisymmetric part of the stress is related to local rotations: ${\sigma }_{jk}^{antisym} = {\kappa }{e}_{jkm}(r_{m}-{\phi }_{m})$ in which $\phi _{m}$ is the rotation of points, called micro-rotation, $e_{jkm}$ is the permutation symbol, and $r_{k} = \frac{1}{2}e_{klm}u_{m,l}$ is the macro-rotation based on the antisymmetric part of gradient displacement $u_{i}$.

On their own, the six elastic constants do not provide sufficient physical insight. To do so, the following technical constants have been derived from them:

$$\begin{aligned} Young's \ \ modulus \quad \quad E&= \frac{G(3{\lambda } + 2G)}{{\lambda } + G} \end{aligned}$$

(3)

$$\begin{aligned} Shear \ \ modulus \quad \quad \quad G&\quad \quad \quad \quad \quad \quad \end{aligned}$$

(4)

$$\begin{aligned} Poisson's \ \ ratio \quad \quad {\nu }&= \frac{{\lambda }}{2({\lambda } + G)} \end{aligned}$$

(5)

$$\begin{aligned} Characteristic \ \ length, \ \ torsion \quad \quad {\ell }_{t}&= \sqrt{\frac{{\beta } + {\gamma }}{2G}} \end{aligned}$$

(6)

$$\begin{aligned} Characteristic \ \ length, \ \ bending \quad \quad {\ell }_{b}&= \sqrt{\frac{{\gamma }}{4G}} \end{aligned}$$

(7)

$$\begin{aligned} Coupling \ \ number \quad \quad N&= \sqrt{\frac{{\kappa }}{2G + {\kappa }}} \end{aligned}$$

(8)

$$\begin{aligned} Polar \ \ ratio \quad \quad {\Psi }&= \frac{{\beta } + {\gamma }}{{\alpha } + {\beta } + {\gamma }} . \end{aligned}$$

(9)

Extension of this analysis to include viscoelasticity can be done by invoking the correspondence principle as is done in the classical case. Elastic constants then become dependent upon time or frequency. Extensions to nonlinear behavior are also known.

The range for Poisson’s ratio is the same as in classical elasticity, from $-\,1$ to 1/2. Cosserat solids differ from classical solids as follows. Circular and elliptic holes demonstrate lower stress concentration than expected classically. Small holes impose less stress concentration than larger ones [6]. Pertinent to the work presented here, Cosserat elasticity predicts size effects in the torsion [7] and bending [8] of circular cylinders of Cosserat elastic materials. A size effect in this context is the nonclassical dependence of specimen rigidity on one or more of its dimensions. Size effects are manifested as slender cylinders appearing stiffer than predicted classically. In contrast to classical elasticity, Cosserat elasticity incorporates a length scale, manifested as characteristic lengths of bending and torsion, Eqs. 6 and 7. Both the characteristic lengths of bending and torsion and size effects in the same modes will be explored in this work.

Cosserat elastic effects have been observed in several materials with structure on the $\mu$m and mm scales. Cosserat elastic size effects in bending and torsion have been observed and measured in closed cell foams [9, 10], open cell foams [11, 12], and negative Poisson’s ratio tetragonal lattices [13]. In each of these studies, the apparent moduli increased as specimen diameter decreased in contrast to classical predictions in which modulus is independent of diameter. Cosserat characteristic lengths were found to be on the order of the size scale of the cells in the materials. Cosserat elastic constants on the scale of spacing between atoms have been inferred from wave dispersion in diamond crystals [14].

The Cosserat characteristic length has been determined experimentally in a two-dimensional polymer honeycomb [15] and via theoretical homogenization in straight elastic ribbed lattices [16,17,18]. In the latter case, the characteristic lengths were much smaller than the cell size of the lattices and the lattices behaved nearly classically. This is because these structures were stretch dominated, meaning the effects of rib extension dominate the effects of rib bending and torsion. Cosserat elastic effects depend on bending and twisting of the ribs to transmit the moments corresponding to the Cosserat couple stress. The characteristic lengths of the two-dimensional polymer honeycomb were similar to the average cell size of the material. The honeycomb material was determined to be bend dominated, meaning rib deformation occurred primarily in bending rather than compression or axial stretch. Consequently, the size effects measured were much greater than those observed in the lattice with straight elastic ribs.

Recent experimental study of cellular materials (foams) has demonstrated dramatic Cosserat characteristics [11, 12]. Additionally, truss lattice materials with cubic symmetry have been analytically and numerically modeled as classical media in the elastic regime and in the plastic regime via continuum mechanics [19]. Nonclassical plastic effects have been observed in the bending of epoxy microcantilevers [20]. However, experimental studies in generalized continua are few compared with the number of theoretical studies. The work detailed here seeks to improve the balance of experiment in relation to theory. The primary purpose of this study is to compare the nonclassical phenomena of lattices with similarly designed rib structures but different unit cell shapes within the framework of linear Cosserat elasticity. Experiments on lattices are comparatively new compared with studies on other materials, and comparisons of lattices in the literature mostly deal with classical behavior.

2 Methods

2.1 Materials and experiment

The lattices detailed in each section were printed using a 3D Systems sPro 60 HS-HD selective laser sintering printer. This printer provided the best resolution available at the time. The parent material was a polyamide considered equivalent to nylon 12. Progressively larger lattices of each type were made. Each lattice was cemented to metal end pieces to provide appropriate end conditions. Cell sizes were chosen as a compromise between desired smoothness of ribs and to prevent specimens from becoming too large. Roughness of ribs was not a problem because there were so many of them in even the smallest specimens.

In an attempt to incorporate unique structural effects into these lattices, the ribs of each unit cell for all structure types were constructed with Sarrus linkages as shown in Fig. 1. A Sarrus linkage is a mechanical linkage which achieves limited but exact straight line motion from a combination of flexure joints [21]. The idealized linkage contains frictionless hinge joints; the compressive rigidity is exactly zero. An all flexible linkage, or corrugation as it will be called, is characterized by high bending and torsional rigidity as compared to compressive rigidity [22]. The moduli in bending, torsion, and compression are detailed further in Sect. 2.2.1. The rationale for such a rib shape is to enhance the resistance to gradient of rotation of the rib, hence enhance the Cosserat effects of the lattice considered as a continuum. A related concept, corrugated fibers, was used to design unidirectional composites incorporating segments of corrugated tubing [23]. In these composites, experimental results disclosed large sensitivity to gradients and large Cosserat elastic constants. Based on these observations, lattices incorporating strain gradient sensitive structural elements in different configurations offer potential for similar nonclassical size effects.

Fig. 1

Four-sided Sarrus linkage. Left, drawing; right, detail of SLS 3D printed segment

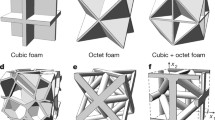
The lattice structures studied here are (a) cubic with orientation in the [100] direction; (b) cubic with orientation in the [111] direction; (c) triangular cells with long ribs corresponding to a relatively open structure; (d) triangular cells with shorter ribs corresponding to a more compact structure. Optical images of the lattice structures are shown in shown in Fig. 2. Corresponding drawings are shown in shown in Fig. 3.

Fig. 2

Lattice structure images: a cubic, [100]; b cubic, [111]; c triangular open (long rib); d triangular compact (short rib). Scale bar is 10 mm for all

Fig. 3

Lattice structure drawings: a cubic, [100]; b cubic, [111]; c triangular open (long rib); d triangular compact (short rib)

Torsional and bending rigidities for each specimen were measured using a broadband viscoelastic spectrometer (BVS). The BVS device uses a pair of orthogonal Helmholtz coils to generate a torque, either in bending or torsion, upon a magnet attached to the specimen’s end piece via a ceramic stalk (Fig. 4). The ceramic stalk was necessary because the specimens are too large to fit in the Helmholtz coils. The magnet is centered in the Helmholtz coils. Deformation of the lattices was measured by reflecting a laser beam from a mirror cemented to the top surface of the bottom end piece of each specimen onto a silicon light detector. Mounting mirrors on the specimens this way was necessary to eliminate possible error from compliance of the ceramic stalk. The silicon light detector measures either horizontal or vertical displacement of the laser beam, depending on its setting, as a change in voltage. The light detector was calibrated prior to bending and torsion tests. Calibration was done by measuring the change in output voltage over the linear measurement regime of the detector using a precision micrometer driven calibration stage. The change in output per change in position was used as the beam calibration constant $({\mathrm{V}}/\upmu {\mathrm{m}})$.

Fig. 4

Instrument diagram

Each specimen was tested using a sinusoidal signal with a frequency of 1 Hz from an SRS Model DS345 function generator. A frequency of 1 Hz was used because it is well below any resonant frequencies. By using the same frequency for all tests across all specimens, viscoelastic effects are decoupled from the size effects being probed. Even if one does not probe viscoelastic effects, the input has a time history; the protocol chosen will decouple viscoelastic effects from the size effects of interest. Torque was inferred from the voltage across a $1\,\Omega$ resistor in series with the coils. The torque channel was calibrated via measurements on the well characterized 6061 aluminum alloy. The torque signal vs. angular displacement signal was displayed as a Lissajous figure on a Tektronix TDS3014B oscilloscope using DC coupling. Data points from the Lissajous figures along with dimensional measurements of the specimens were used to calculate the moduli of the specimens. Maximum strain during testing was $5 \,\times \,10^{-5}$, well within linearity for these specimens. Linearity was verified from the shape of the Lissajous figures.

Compression tests were conducted to ascertain the moduli of the specimens in the absence of macroscopic gradients of strain and rotation. This was accomplished using an Instron screw driven load frame at constant strain rate. Poisson’s ratio was also calculated using compression testing by measuring transverse deformation via digital photography and a micrometer.

2.2 Lattice structures

2.2.1 Rib properties

The Sarrus linkage rib element incorporated in these lattices were tested individually. The measured effective bending modulus of an individual rib was 281 MPa while the Young’s modulus in compression was 14 MPa. The torsional modulus was measured to be 387 MPa. The ribs, therefore, resist torsion and bending to a much greater extent than compression. In such flexible structures, the compressive Young’s modulus is not exactly zero as it would be in a hinged structure. Ideal hinges cannot be made via 3D printing.

2.2.2 Cubic unit cell lattices

Analytical and numerical studies have been performed on a variety of lattices containing straight ribs as classical media [19] in and beyond the elastic regime. The strengthened diagonal unit cells in the present study were essentially face centered cubic (FCC) unit cells where the bonds between atoms were replaced with elastic ribs. The cells are referred to as cubic in the sequel. If the ribs are straight the elastic properties do not differ much from isotropy. The lattices presented in this section use a similar unit cell but incorporate a fourfold Sarrus linkage rib element rather than a straight rib.

Lattices with ribs 14 mm long containing all flexible Sarrus linkage and with cubic unit cells are explored, Fig. 2. A first set of lattices was created that had the cubic unit cells oriented with their $\langle 111\rangle$ axes parallel to the longitudinal axes of the specimens. A second set of lattices was then made wherein the unit cells were oriented such that their $\langle 100\rangle$ axes were parallel to the longitudinal axes of the specimens. Both sets of lattices use identical cubic unit cells.

As for structures with $\langle 100\rangle$ cell axes parallel to longitudinal axis, four progressively larger specimens were created for this orientation. Because of the orientation of the unit cells, it was possible to create a specimen of only one unit cell in cross section. The largest specimen size was dictated by the dimensions of the BVS chamber. The average density of this set of lattices was 0.201 g/cc. Since these specimens have square cross sections, Eqs. 12 and 14 were used to analyze experimental data gathered from bending and torsion, respectively.

2.2.3 Triangular unit cell lattices

As for triangular unit cell structures, two sets were made, one with longer ribs and one with shorter ribs. The rationale was that for a structure without $45^\circ$ cross ribs, larger gradient effects were hypothesized. The first set of lattices was made with rib elements the same length, 14 mm, as those in the cubic unit cells. The smallest specimen was limited to one unit cell in cross section while the largest specimen was governed by the height of the BVS chamber. The cross section of the larger specimens were hexagonal while the cross section of the smallest specimen was triangular. All specimens were approximated as circular so that the exact solution for Cosserat torsion and bending of elastic materials with circular cross section, Eqs. 10 and 11, could be used. The average density for these lattices was 0.093 g/cc.

The design of short rib triangular cell lattices was driven by the observation of deformation induced tilt of the ribs in torsion and bending of the long rib triangular prismatic unit cell structures. By shortening the rib portions of the structural elements and keeping the corrugation region constant, the effects of the corrugations were expected to govern the behavior of the lattices to a greater degree. The new structural elements here were 8 mm long compared to 14 mm long in the previous set of lattices. Including hexagonal nodes, the cells were approximately 10.5 mm long on each side of the triangular base and 9.0 mm tall.

2.3 Analysis and interpretation

Size effects were interpreted within the framework of Cosserat elasticity. Specimens with hexagonal cross sections were approximated as circular and corresponding results were interpreted using exact analytical solutions for the torsion and bending of Cosserat elastic solids with circular cross sections. Exact solutions for bending and torsion of Cosserat elastic solids with square cross sections do not exist so approximate solutions were used. The analysis of materials with square cross sections entails warp in torsion. This is in contrast to materials with a circular cross section for which warping does not occur. In both cases, isotropic solutions are used because no anisotropic solutions are available. Therefore, elastic constants obtained are technical constants. This is similar to classical elastic constants obtained from quasistatic tests such as standard tensile or compression tests in principal directions. Size effects do not occur in classical anisotropic elasticity [24], effective modulus is independent of specimen size just as in isotropic elasticity. Therefore, size effects are a distinct nonclassical behavior and anisotropy is not a confounding factor.

Considering elastic solids with circular cross sections of radius r, the classical torsional rigidity is $\frac{M}{\theta } = G[ \frac{\pi }{2} r^{4}]$. Cosserat torsional rigidity if N = 1 or for large r is $\frac{M}{\theta } = G[ \frac{\pi }{2} r^{4}] (1 + 6(\ell _{t}/r)^{2})$. G is the true shear modulus in the absence of gradients; M is applied moment and ${\theta }$ is angular displacement per unit length. This expression is exact when N = 1. For all other N the exact solution involves Bessel functions and is as follows [7]:

$$\begin{aligned} {\Omega } = (1 + 6(\ell _{t}/r)^{2}) \left[ \frac{(1 - 4{\Psi }{\chi }/3)}{1 - {\Psi }{\chi }}\right] , \end{aligned}$$

(10)

Here, ${\chi } = I_{1}(pr)/pr I_{0}(pr)$, $p^{2} = 2{\kappa }/({\alpha } + {\beta } + {\gamma })$ and $I_{0}$ and $I_{1}$ are modified Bessel functions of the first kind. The constant ${\Psi }$ only has an appreciable influence for small radius specimens and was determined based on behavior of the data near the origin. The shear modulus, G, characteristic length of torsion, $\ell _{t}$, and the coupling number N were found by fitting Eq. 10 to the full set of experimental data using MATLAB.

For bending of a Cosserat elastic rod with radius r, the relative rigidity ratio involving Bessel functions is:

$$\begin{aligned} {\Omega } = 1 + 8(\ell _{b}/r)^{2} \frac{(1 - ({\beta }/{\gamma })^{2})}{(1+{\nu })} + \frac{8N^{2}}{(1+\nu )} \left[ \frac{(\beta /\gamma + \nu )^{2} }{ {\zeta }(\delta a) + 8N^{2}(1-\nu )}\right] \end{aligned}$$

(11)

with $\delta = N/\ell _{b}$ and ${\zeta }(\delta r) = (\delta r)^{2} [((\delta r) I_{0}((\delta r)) - I_{1}((\delta r))) / ((\delta r)I_{0}(\delta r) - 2I_{1}(\delta r))]$. Classical bending rigidity follows $\frac{M}{\theta }= E[ \frac{\pi }{4} r^{4}]$. Both Young’s modulus, E, and the Poisson’s ratio $\nu$ were calculated from compression testing. The coupling number, N, ${\beta }/{\gamma }$, and the characteristic length of bending, $\ell _{b}$, were determined by fitting the full set of experimental data with Eq. 11.

Cubic lattices with $\langle 111\rangle$ orientation and lattices with triangular prism cells were not circular in cross section but hexagonal. Such specimens were treated as circular with equivalent area so that the solutions for Cosserat torsion and bending, Eqs. 10 and 11, could be used.

The procedure for analyzing and interpreting data from specimens with square cross sections is similar; different analytical solutions are used as follows. Torsion of a square cross section Cosserat elastic bar of width 2a gives rise to the following relation between torque and angle. When $\kappa \rightarrow \infty$, corresponding to $N=1$, the total torque M [26] simplifies to

$$\begin{aligned} M=\frac{4}{21} G \left( \frac{a}{2}\right) ^4 \theta \frac{1796+126 \left( 449+2740 {\bar{\ell }}^2+3960 {\bar{\ell }}^4\right) {\bar{\ell }}^2+693 \left( 152+2280 {\bar{\ell }}^2+6615 {\bar{\ell }}^4\right) {\bar{\ell }}_b^2}{8 \left( 19+465 {\bar{\ell }}^2+990 {\bar{\ell }}^4\right) +1485 \left( 6+49 {\bar{\ell }}^2\right) {\bar{\ell }}_b^2}. \end{aligned}$$

(12)

in which ${\bar{\ell }}=2\ell _{t}/a$, ${\bar{\ell }}_b=2\ell _b/a$ and ${\theta }$ as the angular displacement per length. This solution is superior in the regime of strong coupling or for ${\beta }$/${\gamma } < 0$, to that of [27], which overestimates the effects for large N.

For bending of a rectangular bar of width 2a, the rigidity ratio depends on the characteristic length and the Poisson’s ratio [25]. If ${\beta }/{\gamma } = -{\nu }$, the rigidity ratio ${\Omega } = \frac{M}{1/R} \frac{1}{EI}$ is, with M as moment and R as radius of curvature,

$$\begin{aligned} {\Omega } = [1+24(\ell _{b}/2a)^{2}(1-{\nu })]. \end{aligned}$$

(13)

For other values of Poisson’s ratio, the rigidity ratio is, (to fourth order in $\ell _{b}/2a)$,

$$\begin{aligned} {\Omega } = \Bigg [1+24 \frac{1+2 \frac{\beta }{\gamma } \nu +\nu ^2}{1+\nu }\left( \frac{\ell _b}{2a} \right) ^2-480\left( \frac{\beta }{\gamma }+\nu \right) ^2 \frac{44-38\nu +3N^2(1-\nu )(13-9\nu )}{N^2(1+\nu )(22-19\nu )}\left( \frac{\ell _b}{2a} \right) ^4\Bigg ]. \end{aligned}$$

(14)

3 Results and discussion

3.1 Cubic unit cell lattices

3.1.1 Lattices with $\langle 111\rangle$ cell axes parallel to longitudinal axis

Three progressively larger specimens were created in this orientation. The size of the smallest specimen was dictated by the minimum resolution of the SLS printer while the maximum specimen size was limited by the diameter of the BVS chamber. These specimens were hexagonal in cross section but approximated as circular so the exact solutions for torsion, Eq. 10, and bending, Eq. 11, of Cosserat elastic solids could be used to analyze experimental data. The average density of this set of lattices was 0.230 g/cc.

The results of torsion testing are shown below in Fig. 5. For analysis, N was allowed to vary between 0 and 1, ${\ell }_{t}$ was restricted by thermodynamic limitations to be greater than 0 mm, and the asymptotic shear modulus was restricted to values greater than 0 Pa. Since no roll off occurred for small sizes, the fit was insensitive to $\Psi$, although best fit occurred for $\Psi = 1.5$. The best fit yielded the following results: ${\ell }_{t} = 6.0\,{\mathrm{mm}}$, $G = 3.9$ MPa, $N = 1.0$, and $\Psi = 1.5$. The goodness of fit was $R^2 = 0.99$. The maximum size effect in torsion was $\Omega = 2.8$.

Fig. 5

Size effects in torsion for specimens composed of cubic unit cells with their $\langle 111\rangle$ axes parallel to specimen axes. Points are experimental. The solid curve is theoretical for ${\ell }_{t} = 6.0\,{\mathrm{mm}}$, $G = 3.9\,$MPa, $N = 1.0$, and $\Psi = 1.5$. Fit is insensitive to $\Psi$ because no roll off occurs at small sizes. Classical elasticity predicts $\Omega$ independent of diameter as illustrated by the red horizontal dashed line. Inset: lattice structure. (Color figure online)

Bending size effects and their interpretation are shown in Fig. 6.

Fig. 6

Size effects in bending for specimens composed of cubic unit cells with their $\langle 111\rangle$ axes parallel to specimen axes. Points are experimental. The solid curve is theoretical for ${\ell }_{b}$ = 8.2 mm, E = 6.0 MPa, N = 1.0, and $\beta /\gamma$ = 0. Classical elasticity predicts $\Omega$ independent of diameter as illustrated by the red horizontal dashed line. (Color figure online)

Fitting was accomplished using the asymptotic bending modulus, 6.0 MPa, determined from compression testing and the coupling number, $N = 1.0$ obtained from torsion; also the Poisson’s ratio $\nu = 0.3$ from compression tests and was found to be independent of transverse direction. In the analysis, $\beta /\gamma$ was free to vary from $-\,1$ to 1, the thermodynamic limits; ${\ell }_{b}$ was free to vary among values greater than 0. Best fit resulted in the following: $\beta /\gamma = 0$ and ${\ell }_{b} = 7.82\,{\mathrm{mm}}$. The goodness of this fit was $R^{2} = 0.995$. The maximum size effect in bending was $\Omega = 4.1$. The specimens are approximately hexagonal in cross section, but the material has cubic symmetry because it is composed of cubic unit cells. Due to this symmetry, they are elastically anisotropic. Therefore, the characteristic length of torsion is independent from the characteristic length of bending. Also due to anisotropy, the coupling number from torsion is not necessarily applicable to bending results. However, N calculated from torsion led to the best fit results for bending.

In summary, nonclassical size effects are observed in torsion and bending for lattices of cubic unit cells aligned in the $\langle 111\rangle$ direction. The maximum size effects of 2.8 and 4.1 for torsion and bending, respectively, are significant deviations from classical predictions. These size effects are consistent with Cosserat elasticity.

3.1.2 Lattices with $\langle 100\rangle$ cell axes parallel to longitudinal axis

Compression testing disclosed $E = 9.64$ MPa, essentially independent of specimen side length. Poisson’s ratio in this direction was $\nu = 0.03$. Bending test results are shown in Fig. 7, assuming the asymptotic bending modulus to be that found in the compression test of 9.64 MPa. Best fitment yielded: ${\ell }_{b} = 7.4\,{\mathrm{mm}}$, $\beta /\gamma = 0.028$ and $N = 0.23$. The goodness of fit was $R^2 = 0.88$. For comparison with the lattices from the previous section, a second fit was performed using $N = 1$. The resulting $R^2$ was 0.32. This suggests the anisotropy in N is real.

Fig. 7

Size effects in bending for specimens composed of cubic unit cells with their $\langle 100\rangle$ axes parallel to specimen axes. Points are experimental. The solid curve is theoretical for ${\ell }_{b} = 7.4$ mm, $E = 9.64$ MPa, $N = 0.23$, and $\beta /\gamma = 0.28$. The red horizontal dashed line illustrates the relationship of normalized rigidity to specimen diameter in classical elasticity. (Color figure online)

The roll off near the origin is due to the second term in the approximate solution, Eq. 14, dominating at small side length values when $\beta /\gamma \ne -\nu$, especially when N is small as it is in this case. After the roll off at the smallest point, the theoretical model predicts a sharp decrease in rigidity. This phenomenon is likely due to the approximate solution being a two-term approximation. If more terms were used, fidelity of analysis near the origin is expected to increase. However, prediction of rigidity at sizes smaller than the smallest structural element, which in this case is an individual unit cell, is non-physical and can be ignored. Additionally, the function, Eq. 11, does not vary much over the range of values considered. Consequently there is a range of values for the coupling number N, and $\beta /\gamma$, that achieve a very similar goodness of fit.

Results for torsion size effect studies are shown in Fig. 8. The solution for torsion of a square bar of Cosserat elastic material, Eq. 12, used here, is specifically for the case $N = 1$. For analysis, thermodynamic restrictions were placed on the bounds on the characteristic length of torsion, $\ell _t$, and bending, $\ell _{b}$ to be greater than 0 mm. The asymptotic shear modulus, G was limited to values greater than 0. Best fit results, assuming $N = 1$ in torsion, are as follows: $G = 4.3$ MPa, $\ell _{t} = 3.8$ mm, and $\ell _{b} = 3.3\,{\mathrm{mm}}$. The goodness of fit was $R^2 = 0.856$.

Fig. 8

Size effects in torsion for specimens composed of cubic unit cells with their $\langle 100\rangle$ axes parallel to specimen axes. Points are experimental. The solid curve is theoretical for $N = 1$, ${\ell }_{t} = 3.8$ mm, and $G = 4.3$ MPa. Classical elasticity predicts $\Omega$ independent of diameter as illustrated by the horizontal red dashed line. Inset: lattice structure. (Color figure online)

The curve fit in Fig. 8 is based on Eq. 12 in which rigidity is strongly dependent on $\ell _{t}$ but very weakly dependent on $\ell _{b}$. Therefore the value of $\ell _{b}$ obtained from the fit is not at all precise. Indeed $\ell _{b} = 3.3\,{\mathrm{mm}}$ from torsion is much less than $\ell _{b} = 7.4\,{\mathrm{mm}}$ from the bending experiment; the latter value is to be used. The difference in $R^2$ between the best fit with $\ell _{b} = 3.3\,{\mathrm{mm}}$ and with $\ell _{b} = 7.4\,{\mathrm{mm}}$, all other parameters held constant, is only 0.0003; this illustrates the weak dependence of Eq. 12 upon $\ell _{b}$. Also Eq. 12 applies for the limiting case $N = 1$; varying N entails considerable complexity for square sections.

The unit cell has cubic symmetry. Therefore, an individual unit cell has equal moduli in principal directions but is elastically anisotropic. The modulus in the $\langle 111\rangle$ direction does not need to equal the modulus in the $\langle 100\rangle$ direction. Indeed E from compression, in which there are no gradients, was 9.64 MPa for $\langle 100\rangle$ and 6.0 MPa for $\langle 111\rangle$, a ratio of a factor 1.6. The relationship between the asymptotic shear modulus and asymptotic bending modulus determined for the $\langle 100\rangle$ lattice differs little from the classical elastically isotropic, following $E = 2G(1+\nu )$ within 10%. Detailed comparisons of anisotropy of lattices is given in Table 1. For a structurally cubic material, there are three independent classical constants and the isotropic relationship does not need to hold.

In summary, nonclassical size effects are observed in torsion and bending of lattices composed of cubic unit cells oriented with their $\langle 100\rangle$ axes parallel to the specimens longitudinal axes. These size effects are consistent with Cosserat elasticity. The characteristic length of bending was 7.4 mm and the characteristic length of torsion was 3.8 mm. The largest size effects in torsion and bending were $\Omega = 2.2$ and 3.3, respectively.

3.2 Triangular prismatic unit cell lattices

3.2.1 Long rib triangular unit cell lattices

Results for the first set of lattices made using the triangular prismatic unit configuration are presented in this section. These unit cells were made of rib elements the same length, 14 mm, as those in the cubic unit cells of previous sections. The smallest specimen was limited to one unit cell in cross section while the largest specimen was governed by the height of the BVS chamber. The cross section of the larger specimens were hexagonal while the cross section of the smallest specimen was triangular. The average density for these lattices was 0.093 g/cc.

The results of torsion testing are shown below in Fig. 9. For the analysis, asymptotic G was allowed to vary between 0 and 0.53 MPa, the smallest shear modulus of the structures tested, N varied from 0 to 1, $\Psi$ was set to 1.5 owing to the lack of obvious dependence on $\Psi$, and ${\ell }_{t}$ was allowed to be any value greater than 0. The best fit resulted in $G = 0.34$ MPa, ${\ell }_{t} = 8.9\,{\mathrm{mm}}$, and $N = 1.0$. $R^2$ was 0.9988.

Fig. 9

Torsion size effect for long triangular unit cell structures. Points are experimental and the solid black curve is a theoretical best fit for $G = 0.34$ MPa, $\Psi = 1.5$, ${\ell }_{t} = 8.9\,{\mathrm{mm}}$ and $N = 1.0$. $R^2 = 0.9988$. The horizontal dashed red line illustrates the classical predicted relationship between normalized rigidity and specimen size. Inset: lattice structure. (Color figure online)

The results of bending size effect studies are shown in Fig. 10. The modulus determined from compression testing, $E = 2.3$ MPa, was used as the asymptotic bending modulus. Poisson’s ratio, determined by high resolution digital photography at 60 degree intervals about the longitudinal axis during compression testing, was $\nu = 0.05\pm {0.06}$. The variation in Poisson’s ratio with angle is consistent with the hexagonal structural symmetry because Poisson’s ratio can have a range exceeding the isotropic range in hexagonal materials. Limits on variables for fitting are as follows: N varied between 0 and 1, $\beta /\gamma$ was free to vary from -1 to 1, and $\ell _{b}$ was limited to values greater than 0. The best fit disclosed $N = 0.99$, $\beta /\gamma = 0$, and ${\ell }_{b} = 13.2\,{\mathrm{mm}}$, resulting in a goodness of fit $R^2 = 0.9719$.

Fig. 10

Bending size effects for long triangular unit cell structures. Points are experimental and the solid black curve is a theoretical best fit for $E = 2.3$ MPa, $\nu = 0.05$, $\ell _{b} = 13.2\,{\mathrm{mm}}$, $\beta /\gamma = 0$, and $N = 0.99$. The goodness of fit is $R^2 = 0.9719$. The horizontal red dashed line illustrates the classical independence of rigidity ratio to specimen diameter. The asymptotic Young’s modulus from compression provides an additional datum. (Color figure online)

As for comparisons with previous specimens and results, these lattices share more similarities with bend dominated 2D chiral honeycomb lattices [15] than stretch dominated straight rib lattices [16–18]. For torsion and bending, the coupling number approaches or attains the upper bound of 1, respectively. In torsion, the characteristic length was smaller than the average cell size but exceeded the relationship of characteristic length to cell size in stretch dominated straight rib lattices [18]. In bending, the characteristic length was approximately the same as the average cell size, just as in 2D chiral honeycomb lattices [15]. Due to the relationship of characteristic lengths to average cell size and the magnitude of the coupling number, these lattices are bend dominated.

Nonclassical size effects are clear in both torsion and bending of these structures. However, confidence in fitting parameters could be increased with additional specimens which would be possible if resolution of 3D printing were improved. The height of the BVS chamber coupled with the configuration of these specimens and the length of the ribs limited the number of specimens to three with complete cells. A fourth datum is provided by the asymptotic Young’s modulus derived from compression tests.

Visual analysis of the specimens in torsion and bending by hand revealed deformation induced tilt of the rib elements from the nodes connecting ribs rather than deformation in the corrugation. Recalling the relationship between torsional and bending moduli for an individual rib element were 387 MPa and 281 MPa, respectively, the opposite relationship is found in these lattices: the bending moduli are significantly larger than those in torsion. This phenomenon may be due to the reduced effect of the corrugations due to long rib length and the presence of deformation induced tilt of the ribs.

In summary, size effects are observed in the torsion and bending of lattices composed of triangular prismatic unit cells with 14 mm rib elements. The size effects are consistent with Cosserat elastic predictions and cannot be explained via classical elasticity. This lattice revealed characteristic lengths smaller than the cell size; for torsion, considerably smaller. The characteristic lengths were nonetheless considerably larger than would be expected from a fully stretch dominated lattice.

To achieve larger effects, a further lattice was designed with shorter ribs to maximize the influence of the Sarrus segment. Shorter ribs also permit a wider range of specimen sizes to be made and accommodated within the test instrument. Results for this lattice are presented in the following section.

3.2.2 Short rib triangular prismatic unit cell lattices

Further details on the behavior of these lattices were published in a companion paper [22]. Here they are presented for comparison with the other lattices.

By shortening the rib portions of the structural elements compared with the prior lattice, more specimens were able to be created that would fit inside the BVS for testing. The smallest specimen was one unit cell in cross section and four more incrementally larger specimens were created, all with approximately the same aspect ratio of 3:1. The average density of these lattices was 0.212 g/cc.

Results for torsion size effect studies are shown in Fig. 11. Points are experimental and the curves are theoretical fits. The black curve is the theoretical best fit while the other two curves illustrate the effects of changing characteristic length of torsion on the resulting fit. Since no roll off occurs for small specimens $\Psi < 1.5$. The best fit occurred when $\Psi = 1.0$, but the results were not sensitive to $\Psi$ in this regime. The remaining best fit parameters were $G = 1.1$ MPa, $\ell _{t} = 9.4\,{\mathrm{mm}}$, and $N = 0.999$. The mean absolute percent error (MAPE) between experimental results and Cosserat prediction was $12\%$; between experiment and classical, 3500%. Error bars were calculated from noise in the signal and uncertainty in specimen dimensions. Error bars shown are representative of those in all the experiments. The largest size effect in torsion was $\Omega = 36$. The goodness of fit was $R^{2}= 0.999$.

Fig. 11

Size effects for short rib triangular prismatic unit cells in torsion. The solid black curve is a theoretical best fit for $G = 1.1$  MPa, $\ell _{t} = 9.4\,{\mathrm{mm}}$, $N = 1$, and $\Psi = 1.0$. Blue and cyan curves are the theoretical models for $\ell _{t} = 5.0$ and 14 mm, respectively. The green horizontal dashed line is the classically predicted relationship between normalized rigidity and specimen size [22]. Inset: lattice structure in cross section. (Color figure online)

Results for bending size effect studies are shown in Fig. 12. The asymptotic bending modulus and Poisson’s ratio calculated from compression testing were $E = 3.14$ MPa and $\nu = 0.05$. Points are experimental and the curves are theoretical fits. The black curve is the theoretical best fit for the experimental data and corresponds to $E = 3.14$ MPa, $\nu = 0.05$, $\ell _{b} = 8.8\,{\mathrm{mm}}$, $\beta /\gamma = 0.5$, and $N = 0.99$. The MAPE between experimental data and Cosserat prediction was 14% ; between experiment and classical, 2843%. The largest size effect in bending was $\Omega = 29.4$. The goodness of fit was $R^{2} = 0.997$. Blue and cyan curves illustrate the effects of changing the characteristic length of bending on the resulting fits with all other parameters kept constant. The blue curve is for $\ell _{b} = 4.8\,{\mathrm{mm}}$ and the cyan curve is for $\ell _{b} = 13\,{\mathrm{mm}}$. The green horizontal dashed line is the classical relationship between normalized rigidity and specimen size. Error bars were again calculated from signal to noise ratio and specimen dimension uncertainty.

Fig. 12

Size effects for short rib triangular prismatic unit cells in bending. The solid black curve is a theoretical best fit for $E = 3.14$ MPa, $\nu = 0.05$, $\ell _{b} = 8.8$ mm, $\beta /\gamma = 0.5$, and $N = 0.99$. Blue and cyan curves are the theoretical models for $\ell _{b} = 4.8$ and 13 mm, respectively. The green horizontal dashed line is the classically predicted relationship between normalized rigidity and specimen size [22]. Inset: lattice structure in transverse view. (Color figure online)

These specimens exhibit characteristic lengths approximately the same as the average cell size. Also, the coupling number, N, in torsion and bending were 1.0 and 0.99, respectively. Large size effects occur.

Shortening the rib segments on the structural elements compared with the long rib lattices in the previous section has a profound effect on the size effects. Specifically, the magnitude of size-dependent stiffening is much greater—a factor of more than 35 in torsion here compared to a factor of 8.5 for the long rib lattices.

Currently, there is no known analysis available for any of the lattice structures studied here. However, as mentioned earlier, several cellular materials have been analyzed as Cosserat continua. Several lattices with straight ribs [16–18] have been theoretically homogenized and had their Cosserat elastic constants extracted. These lattices were stretch dominated and, consequently, the characteristic lengths were much smaller than the average cell size. The present lattices are considered bend dominated because the ratio of characteristic lengths to average cell size exceeds that of stretch dominated materials and the coupling number approaches the upper bound of 1.

In summary, large size effects were observed in torsion, $\Omega _T = 36$, and bending, $\Omega _B = 29.4$, of a lattice with small triangular prismatic unit cells. These results are inconsistent with classical elasticity but are predicted to occur in Cosserat elasticity. Incorporating strain gradient sensitive structural elements into 3D printed cellular lattices provides a path to the attainment of arbitrarily large size effects as advancements in 3D printing technology give rise to better resolution. Such resolution will allow reduction of the wall thickness of the hollow ribs.

3.2.3 Comparison of lattices

Size effects were observed in four series of 3D printed cellular lattices incorporating strain gradient sensitive structural elements. A comparison of elastic constants, density and cell size as well as maximum size effect is provided in Table 1. The cell size for cubic cells is the edge of the cube. For other cell shapes, the cell dimension in the longitudinal and transverse directions, (L, T) are provided. Also shown for comparison are results for negative Poisson’s ratio (denoted neg $\nu$) tetragonal lattices [13]. These size effects are inconsistent with classical elasticity for which $\Omega _T = \Omega _B = 1$ but can be modeled via Cosserat elasticity. The magnitude of the size effects depends sensitively on the geometry of the structures. The largest size effects occurred in the short rib triangular prismatic unit cell lattices. For these, the characteristic lengths were similar to the cell size; for the other lattices the characteristic lengths were smaller than the cell size.

The anisotropy may be quantified by the Zener ratio [28], $Z= 2\frac{C_{44}}{C_{11} - C_{12}}$, which applies for cubic materials; isotropy entails $Z=1$. The Zener ratio may be written in terms of technical elastic constants, $Z = \frac{2G(1 + \nu )}{E}$. By this measure, the negative Poisson’s ratio lattice exhibited the greatest degree of anisotropy. This is not surprising because the lattice was designed for high stiffness for compression in the longitudinal direction. The cubic lattice in the $\langle 100\rangle$ direction had a Zener ratio closest to 1 followed by the triangular short rib lattice. For that lattice, pulsed acoustic wave measurements revealed the lattice material to exhibit elastic transverse isotropy [13]. The longitudinal modulus was lower than the transverse by a factor 1.3. This value is close to the inverse of the Zener ratio. So the triangular short rib lattice does not deviate much from isotropy in comparison with the other lattices.

To obtain an elastically isotropic lattice, desirable for comparative simplicity of interpretation, one may titrate the length or wall thickness of ribs in different directions. In fully isotropic materials one can perform internal consistency tests such as independently measuring E, G, $\nu$ in the absence of gradients and checking if the isotropic relation between them is satisfied. One may also measure compressive moduli in different directions and check if they are equal. As for the Cosserat constants, $\ell _T$, $\ell _B$, and ${\beta }/{\gamma }$ are related by the definitions of characteristic length, enabling consistency checks based on a detailed comparison of size effects in torsion and in bending. Moreover in an isotropic material, N obtained from bending size effects must equal the value obtained from torsion size effects.

3.2.4 Physical interpretation

The Young’s modulus E represents a continuum average of force–displacement relations or effective spring constants of the structural elements in each solid. The Cosserat characteristic lengths $\ell _T$, $\ell _B$ (Eqs. 6 and 7) quantify the ratio of the average moments (via couple stress $m_{ij}$, Eq. 2) transmitted through the solid to the average forces (via stress $\sigma _{ij}$, Eq. 1). The ratio depends on both the size and the shape of the structural elements. For example experimental study of a particulate composite developed as a possible Cosserat solid [7] revealed no nonclassical effects, hence a characteristic length of zero. This is not intuitively obvious. Rigorous homogenization analysis disclosed such composites containing stiff spheres have characteristic lengths of zero [29]. The dimensionless coupling number N quantifies the coupling between local and global rotation fields, hence between forces and moments in the solid. For the solids studied, most N values obtained equal or approach its upper bound of 1, indicating strong coupling. By contrast, some solids such as dense foams, exhibit weak coupling [30].

As for limitations of the present study, it is recognized that Cosserat elasticity is not the only generalized continuum theory. Some theories have more freedom and some have different freedom. The difficulty in using such theories is that in most cases the requisite torsion and bending analyses are not available for interpreting experiments. As for experimental error, the nonclassical effects observed are so large that experimental errors do not obtrude. As stated, viscoelasticity was decoupled from size effects by conducting all the tests at one frequency. One could certainly probe dependence of the Cosserat parameters on frequency. Such dependence is known in bone [31] which has constituents with different frequency dependence. Frequency dependence of characteristic lengths is likely to be minimal in lattices which have only one solid constituent. Finer resolution in 3D printing would be helpful as that would allow smaller specimens and more of them. Solids with a smaller cell size could be made to compare with micro-cellular foams. Lattices with a greater range of scale in the rib dimensions could enable more extreme behavior. Future advances in 3D printing are expected to facilitate studies of this type.

Table 1 Summary of maximum size effect, rigidity ratio in torsion $\Omega _T$ and in bending $\Omega _B$; cell size, density $\rho$; elastic constants Young’s modulus E, shear modulus G, Poisson’s ratio $\nu$ of lattices

4 Conclusions

All lattices exhibited Cosserat elastic effects. The magnitude of the effects is sensitive to structure. The largest size effects and the largest ratio of characteristic length to cell size were observed in the triangular short rib lattice. Concepts such as those developed here provide a path to the attainment of arbitrarily large nonclassical effects via additive manufacturing.