1 Introduction

In this work, considering plane masonry structures in equilibrium under the action of known loads, we propose a method for predicting the effect, in terms of fractures, of given settlements.

Fractures and cracks in masonry are physiological, and rather than the result of over-loading, are most likely the direct product of small changes of the boundary conditions. However, geometry and loads play a role in the specific fracture pattern that actually nucleates into the structure. In other words, the specific way in which a certain fracture pattern opens up and evolves, even if usually not directly due to an excess of loading (and more likely the direct effect of settlements of the foundation or of internal distortions), is in a strong relation with the geometry of the structure and of the loads themselves.

A simple mathematical model allowing for the prediction of this peculiar behaviour is the unilateral masonry-like material of Heyman (see [1]); a very crude but genial model for masonry, for which the two theorems of limit analysis, created for analysing ductile structures, are still valid.

We refer to the works by Kooharian [2], Livesley [3], Como [4], Angelillo [5], Brandonisio et al. [6,7,8], Gesualdo et al. [9], Angelillo et al. [10] and Fortunato et al. [11, 12] for discussion and the application of limit analysis to masonry-like structures.

It is a fact that the key issue in the peculiar response of masonry structures, is represented by their essentially unilateral behaviour. While a standard structure under bilateral constraints, will usually respond to comparatively small settlements and eigenstrains with elastic deformations, and then with a substantial modification of the internal forces, a unilateral structure, even if heavily over-constrained, can exhibit zero energy modes, and then may compensate the effect of small settlements, without any increase of the internal forces, through mechanisms requiring essentially vanishing energy dissipation.

We call the search for a kinematically admissible displacement, that is for the solution of the boundary value problem (bvp) for the displacement u under Heyman’s restrictions: kinematical problem, as opposed to the equilibrium problem, that is the search of a statically admissible stress field under Heyman’s restrictions. For masonry-like materials these two problems are essentially independent, and can be dealt with separately.

When trying to solve the kinematical problem, the problem arises of selecting, among the possibly many kinematically admissible displacement fields responding to the given kinematical data (settlements and eigenstrains), the ones that guarantee also the equilibrium of the loads imposed on the structure.

For elastic, and even for some elastic-brittle materials, these states, that we can call solutions of the boundary value problem, can be found by searching for the minimum of some, suitably defined, form of energy. For elastic-brittle materials this energy is the sum of the potential energy of the loads, of the elastic energy and of the interface energy necessary to activate a crack on an internal surface (see [13,14,15]). For elastic materials is the sum of the potential energy of the loads and of the elastic energy. For Heyman’s materials is just the potential energy of the loads.

Then we may search a displacement field which is the solution of the boundary value problem, by minimizing the potential energy ℘ of the loads over a convenient function set \({\mathcal{K}}\) for the displacements. A possible simple choice for the set \({\mathcal{K}}^{*}\) approximating this set \({\mathcal{K}}\) for a continuum made of Heyman’s material is to consider that the strain is zero a.e. inside the domain, namely that \({\mathcal{K}}^{*}\) is the set of piecewise rigid displacements. This is actually the case if the structure is composed of monolithic blocks which are not likely to break at their inside (see De Serio et al. [16])

We must point out that piecewise rigid displacements, which are the most frequent and evident manifestation of masonry deformation in real masonry constructions, are not at all simple displacement fields for a continuum, and are usually ruled out in the standard numerical codes for fluids and solids which are employed to handle the complex boundary value problems of continuum mechanics. A usual setting for problems in which finite jumps of the displacement are admitted is the space SBV. The main difficulty with displacements that belong to the space SBV, besides, for deformable materials, the managing of the singularity of strain at the tip of the crack, is the fact that the location of the support of the singularity (that is of the jump set) is not known in advance, and that the shape and the topology of the parts over which the displacement is regular, can be, in principle, rather wild.

Actually, a recent piecewise rigidity result by Chambolle et al. (see [17]) generalizing the classical Liouville result for smooth functions now states that an SBV function y satisfying the constraint \(\nabla y \in SO\left( 2 \right)\) a.e., is a collection of an at most countable family of rigid deformations, i.e. the body may be divided into different components each of which is subject to a different rigid motion.

Some issues connected with the managing of rigid deformations with unknown interfaces is discussed, with the aid of some simple examples, in the forthcoming paper (by some of the present authors) [18].

Here we consider a numerical approximation of the minimum problem, based on a finite element subdivision of the structure (a Caccioppoli partition) into parts behaving as rigid blocks. The interfaces we are talking about, that is the potential fracture lines, are the common boundaries among the blocks. In the plane case, these interfaces must be made of straight pieces. To obtain an approximation of the minimizer (that is of the mechanism minimizing the energy) we can proceed into two ways: (1) Fix a mesh geometry and iterate the minimization with respect to the rigid body displacements, by refining the mesh until a satisfying picture of the interfaces is obtained. (2) Fix the topology of the mesh and minimize both with respect to the geometry of the mesh in the reference configuration and to the rigid body displacements.

The first method produces a sequence of linear programming problems, the second one a single constrained non-linear minimization problem.

The application of the second method is explored in [18], by applying it to some benchmark problems.

In the present paper we apply the first method, by considering piecewise rigid displacements over a partition of the structures that is fixed in advance and whose geometry is not a part of the sought solution. A minimal energy criterion, based on the described discretization of the structure into rigid blocks, is proposed to select the mechanism of the structure responding to given boundary displacements. For any given partition of the structure into rigid blocks, this simple criterion can easily detect, at least in principle, the position of the articulations of the blocks (hinges) and find the corresponding field of piecewise rigid displacement.

Two case studies, concerning two real ancient masonry structures, are analysed to illustrate the method.

2 The masonry-like material

A 2d masonry structure \(S\) is modelled as a continuum occupying a domain \(\varOmega\) of the 2d Euclidean space \({\mathcal{E}}^{2}\). The stress inside \(\varOmega\) is denoted \(\varvec{T}\) and the displacement of material points \(\varvec{x}\) belonging to \(\varOmega\) is denoted \(\varvec{u}\). We restrict to the case of small strains and displacements and adopt the infinitesimal strain \(\varvec{E}\) as the strain measure.

We call masonry-like material a continuum that is Normal Rigid No-Tension (see [5]) in the sense defined by the following restrictions

$$\varvec{T} \in Sym^{ - } ,\quad \varvec{E} \in Sym^{ + } ,\quad \varvec{T} \cdot \varvec{E} = 0,$$
(1)

\(Sym^{ - } ,\,\, Sym^{ + }\) being the convex cones of negative semidefinite and positive semidefinite symmetric tensors.

Under these restrictions, the material satisfies a law of normality with respect to the cone \(Sym^{ - }\) of the feasible stresses, in the sense that restrictions (1) are equivalent to the normality assumptions:

$$\varvec{T} \in Sym^{ - } ,\quad \left( {\varvec{T} - \varvec{T}^{\varvec{*}} } \right) \cdot \varvec{E} \ge 0,\quad \forall \,\,\, \varvec{T}^{\varvec{*}} \in Sym^{ - } ,$$
(2)

and to the dual normality assumptions

$$\user2{E} \in Sym^{ + } ,\quad \left( {\user2{E} - \user2{E}^{*} } \right) \cdot T \ge 0,\quad \forall {\mkern 1mu} {\mkern 1mu} \user2{E}^{*} \in Sym^{ + } .$$
(3)

In particular the normality assumptions represent the essential ingredients for proving the validity of the theorems of Limit Analysis (see [5, 10, 19]).

We observe that the restrictions (1) essentially translate into mathematical terms the Heyman’s assumptions on masonry behaviour (see [1]), namely:

  1. 1.

    Stone has no tensile strength;

  2. 2.

    The compressive strength of stone is effectively infinite;

  3. 3.

    Sliding of one stone upon another cannot occur.

Remark 1

Though Heyman analysis is not concerned with a continuum, condition (1)Footnote 1 appears as a natural extension of assumptions (1), (2). The presence of elastic deformations in compression, even if is not explicitly excluded, is never considered by Heyman. For what concerns the law of normality, Heyman formulates it for characteristics rather than for stresses. Consequently, the role of and the restrictions on the latent strain, that is the deformation associated to the unilateral constraint on stress, are not defined. In the context of the continuum model, assumption (3), that is the no-sliding assumption, is implied by normality, but the no-sliding assumption, by itself, is not sufficient to prove normality in this broader context.

3 Regularity of stress and strain: singular fields

3.1 Concentrated strain and stress

For NRNT materials, it is possible to admit that strain and stress are bounded measures. Bounded measures can be decomposed into the sum of two parts

$$\varvec{E} = \varvec{E}^{r} + \varvec{E}^{s} ,\quad \varvec{T} = \varvec{T}^{r} + \varvec{T}^{s} ,$$
(4)

where \((.)^{r}\) is the part that is absolutely continuous with respect to the area measure (that is \((.)^{r}\) is a density per unit area) and \((.)^{s}\) is the singular part.

On admitting singular strains and stresses, it is possible to admit that both the displacement \(\varvec{u}\) and the stress vector \(\varvec{s}\) be discontinuous. The stress vector is the contact force transmitted across a surface of unit normal \(\varvec{n}\), and, in Cauchy’s sense, is related to the regular part of the stress through the relation \(\varvec{s} = \varvec{T}^{r} \varvec{n}\).

3.2 Displacement jumps

If the displacement vector exhibits a jump discontinuity across a regular curve \({{\varGamma }}\), on such a curve the strain is concentrated, namely is a line Dirac delta whose amplitude coincides with the value of the jump of \(\varvec{u}\) across \(\varGamma\). Denoting \(\varvec{t}, \varvec{n}\) the unit tangent and the unit normal to \(\varGamma\), and calling \(\varOmega^{ - } ,\,\varOmega^{ + }\) the two parts on the two sides of \(\varGamma ,\varOmega^{ + }\) being the part toward which \(\varvec{n}\) points, the jump of \(\varvec{u}\) across \(\varGamma\) can be denoted as follows

$$\left[ \varvec{u} \right] = \varvec{u}^{ + } - \varvec{u}^{ - } ,$$
(5)

and decomposed into tangential and normal components:

$$\left[ \varvec{u} \right] = w \varvec{t} + v \varvec{n} ,\quad w = \left[ \varvec{u} \right] \cdot \varvec{t} ,\quad v = \left[ \varvec{u} \right] \cdot \varvec{n} .$$
(6)

Denoting \(\delta \left( \varGamma \right)\) the unit line Dirac delta with support on \(\varGamma\), the concentrated strain on \(\varGamma\), taking into account the relation defining the infinitesimal strain in terms of the displacement: \(\varvec{E} = \frac{1}{2}\left( {\nabla \varvec{u} + \nabla \varvec{u}^{T} } \right)\), and the material restrictions on strains for NRNT materials, takes the form

$$\varvec{E} = v \delta \left( \varGamma \right) \varvec{n} \otimes \varvec{n} ,\quad v \ge 0 ,$$
(7)

since, taking into account the restriction \(\varvec{E} \in Sym^{ + }\), it must be

$$w = 0 ,$$
(8)

That is, the two parts \(\varOmega^{ - } ,\,\varOmega^{ + }\) may separate but cannot penetrate each other, and the sliding \(w\) along \(\varGamma\) must be zero.

3.3 Stress vector jumps

If the stress vector exhibits a jump discontinuity across a regular curve \(\varGamma\), on such a curve the stress is concentrated, namely is a line Dirac delta whose amplitude P is related to the jump of \(\varvec{s}\) across \(\varGamma\). Recalling the definition introduced above for \(\varvec{t}, \varvec{n}\), on adopting the previous notation, the jump of \(\varvec{s}\) across \(\varGamma\) can be denoted as follows

$$\left[ \user2{s} \right] = \user2{s}^{ + } - \user2{s}^{ - } ,$$
(9)

and decomposed into normal and tangential components

$$\left[ \user2{s} \right] = p \user2{t} + q \user2{n},\quad p = \left[ \user2{s} \right] \cdot \user2{t},\quad q = \left[ \user2{s} \right] \cdot \user2{n}.$$
(10)

Denoting \(\delta \left( \varGamma \right)\) the unit line Dirac delta with support on \(\varGamma\), the stress concentrated on \(\varGamma\), taking into account the balance equations \(div\varvec{T} + \varvec{b} = 0\), and the material restrictions for NRNT materials, takes the form

$$\user2{T} = P \delta \left( \varGamma \right) t \otimes \user2{t},\quad P^{\prime } + p = 0,\quad P\rho + q = 0,\quad P \le 0,$$
(11)

where \(\rho\) is the curvature of the line \(\varGamma\) and \(P^{\prime}\) is the derivative of \(P\) with respect to its argument, namely the arc length along \(\varGamma\). The amplitude P of the concentrated stress represents a concentrated axial contact force acting along the 1d substructure \(\varGamma\). The last relation in (11) says that such a force must be compressive.

4 The boundary value problem for masonry like materials

We consider a masonry structure \({{\varOmega }}\), composed of NRNT masonry-like material in equilibrium under the action of body loads and given surface loads and surface settlements, prescribed on a fixed partition of its boundary \(\partial \varOmega_{N} \cup \partial \varOmega_{D} = \partial \varOmega\). The boundary value problem (bvp) for such a structure can be formulated as follows:

“Find a displacement field \(\varvec{u}\) and the allied strain \(\varvec{E}\) , and a stress field \(\varvec{T}\) such that

$$\varvec{E} = \frac{1}{2}\left( {\nabla \varvec{u} + \nabla \varvec{u}^{T} } \right),\quad \varvec{E} \in Sym^{ + } , \quad \varvec{u} = \bar{\varvec{u}}\, on\, \partial \varOmega_{D} ,$$
(12)
$$div\varvec{T} + \varvec{b} = 0,\quad \varvec{T} \in Sym^{ - } ,\quad \varvec{Tm} = \bar{\varvec{s}}\, on\, \partial \varOmega_{N} ,$$
(13)
$$\varvec{T} \cdot \varvec{E} = 0 ,$$
(14)

\(\varvec{m}\) being the unit outward normal to \(\partial \varOmega\)”.

We introduce the sets of kinematically admissible displacements \({\mathcal{K}}\), and of statically admissible stresses \({\mathcal{H}}\), defined as follows:

$${\mathcal{K}} = \left\{ {\varvec{u} \in S /\varvec{E} = \frac{1}{2}\left( {\nabla \varvec{u} + \nabla \varvec{u}^{T} } \right) \in Sym^{ + } \& \varvec{u} = \bar{\varvec{u}}\, on \,\partial {{\varOmega }}_{D} } \right\},$$
(15)
$${\mathcal{H}} = \left\{ {\varvec{T} \in S^{\prime } /div\varvec{T} + \varvec{b} = 0,\quad \varvec{T} \in Sym^{ - } ,\quad \varvec{Tm} = \bar{\varvec{s}} \,on\, \partial {{\varOmega }}_{N} } \right\},$$
(16)

\(S,\,S^{\prime }\) being two suitable function spaces. A solution of the bvp for masonry-like structures is a triplet \(\left( {\varvec{u}, \varvec{E}\left( \varvec{u} \right),\varvec{ T}} \right)\) such that \(\varvec{u} \in {\mathcal{K}},\) \(\varvec{T} \in {\mathcal{H}},\) and \(\varvec{T} \cdot \varvec{E}\left( \varvec{u} \right) = 0\).

Remark 2

On admitting discontinuous displacements and singular stresses, the differential equations in (12), (13) must be interpreted in a weak sense. Besides, the boundary condition in (12) makes sense only if we consider that the domain is closed on \(\partial {{\varOmega }}_{D}\), that is, that the displacement must actually take the given value on this part of the boundary, and considering the possible mismatch of the displacement between the outside and the inside of the domain as a strain concentrated along the boundary. Finally, in the boundary condition in (13), the trace of \(\varvec{T}\) at the boundary, that is the emerging stress vector \(\varvec{s}\left( \varvec{T} \right)\) on \(\partial {{\varOmega }}_{N}\), is not of the Cauchy form \(\varvec{s}\left( \varvec{T} \right) = \varvec{Tm}\), unless \(\varvec{T}\) is regular. If \(\varvec{T}\) is a line Dirac delta of the form \(\varvec{T} = P \delta \left( \varGamma \right) \varvec{t} \otimes \varvec{t}\) and \(\varGamma\) crosses the boundary at a point \(\varvec{X} \in \varGamma\) at an angle, that is \(\varvec{t} \cdot \varvec{m} \ne 0\), then \(\varvec{s}\left( \varvec{T} \right) = P \delta \left( {\text{X}} \right)\varvec{ t}\). The special case in which the line \(\varGamma\) is tangent to \(\partial \varOmega_{N}\), deserves a special attention. In such a case, there is not any stress vector \(\varvec{s}\left( \varvec{T} \right)\) emerging at the boundary due to the singular stress, but still the boundary condition \(\varvec{Tm} = \bar{\varvec{s}}\) must be modified, since the given tractions \(\bar{\varvec{s}}\) can be balanced, wholly or in part, by the singular stress concentrated on \(\varGamma\). Therefore, there is not any local restriction on the sign of the normal component of the tractions given along the boundary: purely tangential tractions and even tensile loads may be applied if the boundary is locally concave. In the particular case in which the interface is straight, equilibrium and material restrictions can be enforced if and only if \(\bar{\varvec{s}} \cdot \varvec{m} \le 0\), but still there is no restriction on \(\bar{\varvec{s}} \cdot \varvec{k}\text{,}\,\varvec{k}\) being the unit tangent vector to \(\partial \varOmega\).

5 The kinematical problem, the equilibrium problem and the coupling of stress and strain

The bvp for masonry-like materials can be split into two parts: the search of a displacement field belonging to \({\mathcal{K}}\), and the search for a stress field belonging to \({\mathcal{H}}\). We call the first problem “the Kinematical Problem (KP) for ML structures”, and the second problem “the Equilibrium Problem (EP) for ML structures”. These two problems are essentially uncoupled but for condition (14), and can be taken up separately.

First of all, we observe that either of the two problems can be incompatible, in the sense that the sets \({\mathcal{K}}\), \({\mathcal{H}}\) can both be void. In particular, the compatibility of the EP is the key issue of the two theorems of Limit Analysis, which deal with the possibility of collapse of the structure.

In what follows we will assume that both \({\mathcal{K}}\) and \({\mathcal{H}}\) are not empty, that is that the kinematical and the equilibrium problem are both compatible (that is, in particular, there is no possibility of collapse) and study the case in which both \({\mathcal{K}}\) and \({\mathcal{H}}\) have infinitely many elements.

Remark 3

A trivial case of compatibility occurs if the data are homogeneous. If the displacement data are zero, the KP is homogeneous and admits the solution \(\varvec{u} = 0\). If the load data are zero, the EP is homogeneous and admits the solution \(\varvec{T} = 0\).

In what follows we will study thoroughly the KP in the case in which the displacement data (the settlements) are not zero, and also the load applied on \(\varOmega\) are not zero.

6 The non-homogeneous KP: an energy criterion

When trying to solve the non-homogeneous kinematical problem, that is the boundary value problem for the displacement \(\varvec{u}\) under restrictions (1), the problem arises of selecting, among the possibly many kinematically admissible displacement fields, the ones that guarantee also the equilibrium of the loads imposed on the structure.

For elastic, and even for some elastic-brittle materials, these states, that we can call solutions of the boundary value problem, can be found by searching for the minimum of some, suitably defined, form of energy. For NRNT materials such an energy is just the potential energy of the loads.

Then a displacement field which is the solution of the boundary value problem, can be searched by minimizing the potential energy ℘ of the loads. Such minimum problem is formulated as follows:

“Find a displacement field \(\varvec{u}^\circ \in {\mathcal{K}}\) , such that

$$\wp \left( {\varvec{u}^\circ } \right) = \mathop {\hbox{min} }\limits_{{\varvec{u} \in {\mathcal{K}}}} \wp \left( \varvec{u} \right),$$
(17)

where

$$\wp \left( {\mathbf{u}} \right) = - \int_{{\partial {{\varOmega }}_{\text{N}} }} {\bar{\varvec{s}} \cdot {\mathbf{u}} ds} - \int_{{{\varOmega }}} {{\mathbf{b}} \cdot {\mathbf{u}} {\text{da}}} ,$$
(18)

is the potential energy of the given loads”.

7 Minimum of ℘ and equilibrium

The proof of the existence of the minimizer \(\varvec{u}^\circ\) of \(\wp \left( \varvec{u} \right)\) for \(\varvec{u} \in {\mathcal{K}}\), is a complex mathematical question and is beyond the scopes of the present paper. The interested reader can refer to the papers [20, 21], where the existence of the minimum is discussed, with the direct method of the calculus of variation, for the parent problem concerning Elastic Normal No-Tension materials. In those papers the existence of the minimizer \(\varvec{u}^\circ\) of the total potential energy, is proved under some restrictions on the given loads (among which the so-called safe load condition) for \(\varvec{u} \in BD\left( \varOmega \right)\), in the case either of pure traction problems or pure displacements problems: the case of mixed problem is not considered.

On assuming that the KP is compatible (that is \({\mathcal{K}} \ne \emptyset )\), what we can easily show is that:

  1. a.

    If the load is compatible (that is \({\mathcal{H}} \ne \emptyset\)) the linear functional \(\wp \left( u \right)\) is bounded from below.

  2. b.

    If the triplet \(\left( {\varvec{u}^\circ ,\varvec{ E}\left( {\varvec{u}^\circ } \right),\varvec{ T}^\circ } \right)\) is a solution of the bvp, it corresponds to a weak minimum of the functional \(\wp \left( \varvec{u} \right)\).

Proofs

  1. a.

    If the load is compatible then there exists a stress field \(\varvec{T} \in {\mathcal{H}}\), through which the functional \(\wp \left( \varvec{u} \right)\) defined on \({\mathcal{K}}\), for any \(\varvec{u} \in {\mathcal{K}}\), can be rewritten as follows

    $$\wp \left( \varvec{u} \right) = - \int_{{\partial {{\varOmega }}_{N} }} {\bar{\varvec{s}} \cdot \varvec{u} \,ds} - \int_{\varOmega } {\varvec{b} \cdot \varvec{u}\, da} = \int_{{\partial \varOmega_{D} }} {\varvec{s}\left( \varvec{T} \right) \cdot \bar{\varvec{u}}\,ds} - \int_{\varOmega } {\varvec{T} \cdot \varvec{E}\left( \varvec{u} \right)\,da} ,$$
    (19)

    \(\varvec{s}\left( \varvec{T} \right)\) being the trace of \(\varvec{T}\) at the boundary (see Remark 2). Assuming that the displacement data are sufficiently regular (say continuous), being \(\varvec{s}\left( \varvec{T} \right)\) a bounded measure (see Remark 2), the integral \(\int_{{\partial \varOmega_{D} }} {\varvec{s} (\varvec{T} )\bar{\varvec{u}}\,d\sigma }\) is finite; then, since \(\varvec{T} \in Sym^{ - }\) and \(\varvec{E} \in Sym^{ + }\), the volume integral is non negative, and \(\wp \left( \varvec{u} \right)\) is bounded from below.

  2. b.

    If \(\left( {\varvec{u}^\circ ,\varvec{ E}\left( {\varvec{u}^\circ } \right),\varvec{ T}^\circ } \right)\) is a solution of the bvp, then, for any \(\varvec{u} \in {\mathcal{K}}\), we can write

    $$\wp \left( \varvec{u} \right) - \wp \left( {\varvec{u}^\circ } \right) = - \int_{{\partial \varOmega_{N} }} {\bar{\varvec{s}} \cdot \varvec{u}\,ds} - \int_{\varOmega } {\varvec{b} \cdot \left( {\varvec{u} - \varvec{u}^\circ } \right)\,da} = - \mathop \smallint \limits_{\varOmega }^{{}} \varvec{T}^\circ \cdot \left( {\varvec{E}\left( \varvec{u} \right) - \varvec{E}\left( {\varvec{u}^\circ } \right)} \right) \,da .$$
    (20)

The result \(\wp \left( \varvec{u} \right) - \wp \left( {\varvec{u}^\circ } \right) \ge 0 , \forall \varvec{u} \in {\mathcal{K}}\), follows form dual normality [see (3)].

The physical interpretation of the above result is the following. Since the displacement field solving the bvp corresponds to a state of weal minimum for the energy, then it is a neutrally stable equilibrium state, in the sense that the transition to a different state requires a non-negative supply of energy.

Remark 4

Based on the minimum principle, if the EP is compatible and the KP is homogeneous, \(\varvec{u} = 0\) is a minimum solution. Indeed, in such a case

$$\wp \left( \varvec{u} \right) = - \int_{{\partial {{\varOmega }}_{N} }} {\bar{\varvec{s}} \cdot \varvec{u} ds} - \int_{{{\varOmega }}} {\varvec{b} \cdot \varvec{u} da} = - \int_{{{\varOmega }}} {\varvec{T} \cdot \varvec{E}\left( \varvec{u} \right)da } ,$$
(21)

\(\varvec{T}\) being any element of \({\mathcal{H}}\). Since the right hand side of (18) is non negative, \(\wp \left( 0 \right) = 0\) is the minimum of \(\wp\) and \(\varvec{u} = 0\) is a minimizer of the potential energy. Notice that, in this case, any \(\varvec{T} \in {\mathcal{H}}\) is a possible solution in terms of stress, since \(\varvec{T} \cdot \varvec{E}\left( 0 \right) = 0\) for any \(\varvec{T}\).

8 Approximation of the KP with piecewise rigid displacements: rigid blocks

We consider the approximate solution of the minimum problem (17) obtained by restricting the search of the minimum in the restricted class \({\mathcal{K}}_{pr}\) of piecewise rigid displacements. This infinite dimensional space is discretized by considering a finite partition

$$\left( {\varOmega_{i} } \right)_{{i \in \left\{ {1,2, \ldots ,M} \right\}}} ,$$
(22)

of \(\varOmega\) into a number \(M\) of rigid pieces, such that

$$\mathop \sum \limits_{i = 1}^{M} P\left( {\varOmega_{i} } \right) < \infty ,$$
(23)

\(P\left( {\varOmega_{i} } \right)\) being the perimeter of \(\varOmega_{i}\). In particular, restricting to convex polygonal elements, the boundary \(\partial \varOmega_{i}\) of the n-polygone \(\varOmega_{i}\), is composed of n segments \(\varGamma\), of length \(\ell\), whose extremities are denoted generically 0,1.

We call interfaces the segments \(\varGamma\) that are, either the common boundaries between adjacent elements, or part of the constrained boundary (that is those \(\varGamma\) representing interfaces with the soil).

We call the finite dimensional approximation of \({\mathcal{K}}_{pr}\) generated by this partition: \({\mathcal{K}}_{pr}^{M}\), and consider the minimum problem

$$\wp \left( {\hat{\varvec{u}}} \right) = \mathop {\hbox{min} }\limits_{{\varvec{u} \in {\mathcal{K}}_{pr}^{M} }} \wp \left( \varvec{u} \right).$$
(24)

To represent a generic piecewise rigid displacement \(\varvec{u} \in {\mathcal{K}}_{pr}^{M}\) we may use the vector \(\varvec{U}\) of \(3M\) components represented by the \(3M\) rigid body parameters of translation and rotation of the elements. These parameters are restricted by the assumption that the strain must be positive semidefinite. For piecewise rigid displacements the strain is concentrated along the interfaces among blocks (that is, in the present case, along the segments \(\varGamma\)), and recalling (11), takes the form:

$$\varvec{E} = v \delta \left( \varGamma \right) \varvec{n} \otimes \varvec{n},$$
(25)

where

$$v = \left[ \varvec{u} \right] \cdot \varvec{n} \ge 0.$$
(26)

Then, on each segment \(\varGamma\), besides the unilateral restriction (26), we also have the equation

$$w = \left[ \varvec{u} \right] \cdot \varvec{t} = 0.$$
(27)

Notice that conditions (26), (27), derived from the assumption of normality, represent a condition of unilateral contact with no-sliding among blocks.

The static counterpart of these constraints concerns the stress vector \(\varvec{s}\) applied along \(\varGamma\). Such a stress vector represents, along the interfaces (that is the internal interfaces and the external interfaces with the soil), the reaction associated to the constraints (26), (27). It coincides with the given applied tractions \(\bar{\varvec{s}}\) where the boundary of the blocks coincides with the loaded part of the boundary. By calling

$$\sigma = {\mathbf{s}} \cdot \varvec{n},\quad \tau = {\mathbf{s}} \cdot \varvec{t},$$
(28)

the normal and tangential stress along \(\varGamma\), the condition on \(\varvec{s}\) is

$$\sigma \le 0 .$$
(29)

Notice that the tangential component of \(\varvec{s}\) is not constrained and can be applied along the straight interface \(\varGamma\), even if \(\sigma = 0\) (see Remark 2).

By calling \(N\) the number of the interfaces \(\varGamma\), and \(v\left( 0 \right), v\left( 1 \right),w\left( 0 \right),w\left( 1 \right)\) the normal and tangential components of the relative displacements of the ends 0, 1 of the segment \(\varGamma\), the restrictions (26), (27) are equivalent to the \(2N\) inequalities

$$v\left( 0 \right) \ge 0 , v\left( 1 \right) \ge 0 ,$$
(30)

and the \(2N\) equalities

$$w\left( 0 \right) = 0 , w\left( 1 \right) = 0 .$$
(31)

The restrictions (30), (31) can be easily expressed in terms of \(\hat{\varvec{U}}\), rewriting them in the matrix forms

$$\varvec{A} \hat{\varvec{U}} \ge 0,$$
(32)
$$\varvec{B} \hat{\varvec{U}} = 0 .$$
(33)

Finally, the minimum problem (24) which approximates the minimum problem (17) can be transformed into

$$\wp \left( { \hat{\varvec{U}} ^{0} } \right) = \mathop {\hbox{min} }\limits_{{\hat{\varvec{U}} \in {\mathbb{K}}^{M} }} \wp \left( { \hat{\varvec{U}} } \right),$$
(34)

\({\mathbb{K}}^{M}\) being the set

$${\mathbb{K}}^{M} = \left\{ { \hat{\varvec{U}} \in {\mathcal{R}}^{3M} / \varvec{A} \hat{\varvec{U}} \ge 0 ,\quad \varvec{B} \hat{\varvec{U}} = 0} \right\}.$$
(35)

Remark 5

The minimization problem (34) that we propose for approximating the minimization problem (17), transforms the original minimization problem for a continuum, into a minimization problem for a structure composed of rigid parts, acted on by given loads and given settlements and subject to unilateral contact conditions along the interfaces. Problem (34) is a standard linear finite dimensional minimization problem, since the function \(\wp \left( { \hat{\varvec{U}} } \right)\) is a linear function of the 3 M-vector \(\hat{\varvec{U}}\) and the constraints are linear. The existence of the solution of this approximate problem is trivially guaranteed if the original problem is bounded from below (see Sect. 9). For a small number of variables it can be solved exactly with the simplex method (see [22]), and for large problems there exist a number of well-known, and efficient, approximate alternatives (see [23, 24]).

9 Some examples

The examples we present here are developed with the program Mathematica® [25]. The analysis proceeds into the following steps:

  1. 1.

    Definition of the structural geometry and of its discretization;

  2. 2.

    Discretization of the displacement field;

  3. 3.

    Definition of the potential energy as a linear functional of the rigid displacement parameters;

  4. 4.

    Definition of the internal and external boundary conditions;

  5. 5.

    Numerical solution of the problem with a linear programming routine;

  6. 6.

    Post-processing (evaluation of the displacement corresponding to the solution).

1. Let us denote \(\varOmega_{*}\) the domain representing the structural geometry in \({\mathcal{E}}^{2}\); consider the minimum rectangular domain \(\varOmega^{*}\) containing \(\varOmega_{*}\). The whole domain \(\varOmega^{*}\) is partitioned into N rectangular basic units \(\varOmega_{i}\), we call them subdomains. The set \(\pi^{*} = \left( {\varOmega_{i} } \right)_{{i \in \left\{ {1, \ldots ,N} \right\}}}\) constitutes a partition of \(\varOmega^{*}\), that is:

$$\mathop {\bigcup }\limits_{i = 1}^{N} \varOmega_{i} = \varOmega^{ *} \,{\text{and}}\,\varOmega_{i} \cap \varOmega_{j} = \emptyset , \quad \forall \;i,j \in \left\{ {1, \ldots ,N} \right\}/i \ne j.$$
(36)

To take into account the presence of voids in the domain \(\varOmega_{*}\) is necessary to perform an appropriate elimination of some elements belonging to \(\pi^{*}\). To this purpose, we consider the set

$$\pi_{M} = \left\{ {\varOmega_{i} \in \pi^{*} /\varOmega_{i} {\bigcap } \varOmega_{ *} \ne \emptyset } \right\}$$
(37)

where M is the cardinality of \(\pi_{M}\). Defining \(\varOmega = \mathop {\bigcup }\limits_{{{{\varOmega }}_{\text{j}} \in \pi_{M} }} \varOmega_{\text{j}}\) from (37) it follows:

$${{\varOmega}}{ } \supseteq {{\varOmega}}_{{*}} .$$
(38)

Therefore \(\pi_{M}\) is a particular cover of the real structural domain \(\varOmega_{*}\): it is the minimum cover of \(\varOmega_{*}\) (with respect to the cardinality) and at the same time it constitutes a finite partition of \(\varOmega\), which becomes our structural model domain. Finally, it is to be noticed that \(\pi_{M}\) is a countable set of subdomains having finite perimeter, therefore, is a Caccioppoli partition of \(\varOmega\) in the sense of Chambolle et al. [17].

2. The displacement field \(\varvec{u} = \varvec{u}\left( \varvec{x} \right)\), defined in \(\varOmega\), is approximated as piecewise rigid. We use \(\pi_{M}\) to introduce this approximation, namely:

$$\varvec{u}:\varvec{x} \in \varOmega \to \left\{ {\begin{array}{*{20}l} {\varvec{u}_{1} ,\quad if\; \user2{x} \in \varOmega_{1} ,} \hfill \\ \vdots \hfill \\ {\varvec{u}_{j} ,\quad if\;\user2{x} \in \varOmega_{j} ,} \hfill \\ \vdots \hfill \\ {\varvec{u}_{M} ,\quad if\;\user2{x} \in \varOmega_{M} ,} \hfill \\ \end{array} } \right.$$
(39)

where \(\varvec{u}_{j} = \left. \varvec{u} \right|_{{\varOmega_{j} }}\) \(\forall \varvec{ }j \in \left\{ {1, \ldots ,M} \right\}\) is an infinitesimal rigid displacement. In 2d problems, \(\varvec{u}_{j}\) is a function of three Lagrangian parameters assumed as the two translations of the centroid \(G_{j}\) of \(\varOmega_{j}\) and the rotation about \(G_{j}\):

$$\varvec{u}_{j} = \varvec{v}_{j} + {\varvec{\Phi}}_{\varvec{j}} \left( {\varvec{x} - \varvec{x}_{j}^{0} } \right) ,$$
(40)

where \(\varvec{x}_{j}^{0}\) is the position vector of \(G_{j}\), and

$${\varvec{\Phi}}_{\varvec{j}} \in Skw ,$$
(41)

and then

$${\text{Sym}}\nabla \varvec{u}_{j} = 0 ,$$
(42)

In (40) \(\varvec{v}_{j} = \left( {U_{j} ,V_{j} } \right)\) is a vector collecting the two translation components in a fixed global Cartesian reference, and:

$${\varvec{\Phi}}_{\varvec{j}} = \left( {\begin{array}{*{20}l} 0 \hfill & { - {{\varPhi }}_{j} } \hfill \\ {{{\varPhi }}_{j} } \hfill & 0 \hfill \\ \end{array} } \right)$$
(43)

is the infinitesimal rotation matrix in the same reference.

Therefore, the displacement field \(\varvec{u} = \varvec{u}\left( \varvec{x} \right)\) depends on \(3M\) unknown Lagrangian parameters:

$$(U_{j} ,V_{j} ,\varPhi_{j} )_{{j \in \{ 1, \ldots ,M\} }} .$$
(44)

The \(3M\) independent parameters can be collected in the single vector:

$$\hat{\varvec{U}} = \left( {U_{1} ,V_{1} ,{{\varPhi }}_{1} , \ldots ,U_{j} ,\quad V_{j} ,{{\varPhi }}_{j} , \ldots ,U_{M} ,V_{M} ,{{\varPhi }}_{M} } \right) ,\quad \hat{\varvec{U}} \in {\mathbb{R}}^{3M} .$$
(45)

3. Since in our theory, both fracture energy and elastic energy are neglected, the potential energy \(E\) coincides with the potential energy of the external forces only, and can be expressed in terms of the components of \(\hat{\varvec{U}}\). \(E\) is the opposite of the scalar product of the applied forces times the displacements of their points of application, and is a linear function of \(3M\) unknown Lagrangian parameters, that can be symbolically expressed as follows:

$$E = E\left( {\hat{\varvec{U}}} \right) ,\quad \hat{\varvec{U}} \in {\mathbb{R}}^{3M} .$$
(46)

The problem can be formulated [as already described in (34), see Sect. 10] as a linear programming one, in the form:

$$\mathop {\min }\limits_{{\user2{\hat{U}} \in \mathbb{K}^{M} }} E(\user2{\hat{U}}),$$
(47)

\({\mathbb{K}}^{M}\) being the subset of \({\mathbb{R}}^{3M}\) defined by the unilateral and bilateral constraints associated to the contact and fixing conditions. It remains to define explicitly the subset \({\mathbb{K}}^{M} \subseteq {\mathbb{R}}^{3M}\), taking into account Heyman’s masonry-like restrictions (1) defining NRNT materials. The kinematical consequence of Heyman’s assumptions are summarized in Sect. 4 and condensed in the conditions (9), (10). In the subsequent point such restrictions are rewritten as contact conditions along the element interfaces, in terms of relative displacements, taking into account the analysis presented in Sect. 10 [see conditions (26), (27) and (30), (31)].

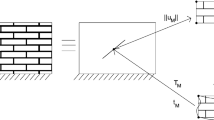
4. To fix ideas, let \(\varOmega_{i}\) and \(\varOmega_{j}\) be two contiguous subdomains, with the \(l\left( {A,B} \right)\varvec{ }\) side in common (see Fig. 1). Let \(\varvec{n}\) and \(\varvec{t}\) be the normal and tangential unit vectors to \(l\left( {A,B} \right)\) (see Fig. 1b), and \(\varvec{u}_{j} \left( P \right)\) the nodal displacement of a material point \(P\) belonging to the \({{\varOmega }}_{j}\) subdomain.

Fig. 1
figure 1

Example of the partition of the domain with a grid of squares (a). Close up of two adjacent elements \(\varOmega_{\text{i}}\) and \(\varOmega_{\text{j}}\) and showing the common interface \(l\left( {A,B} \right)\) (b)

Full size image

The kinematical conditions between \({{\varOmega }}_{i}\) and \(\varOmega_{j}\) along \(l\left( {A,B} \right)\varvec{ }\) can be expressed [recalling (26), (27)] as follows:

$$\left( {\varvec{u}_{j} \left( P \right) - \varvec{u}_{i} \left( P \right)} \right) \cdot \varvec{n} \ge 0 \quad \forall \;P \in l\left( {A,B} \right),$$
(48)
$$\left( {\varvec{u}_{j} \left( P \right) - \varvec{u}_{i} \left( P \right)} \right) \cdot \varvec{t} = 0 \quad \forall P \in l\left( {A,B} \right).$$
(49)

\({{\varOmega }}_{j}\) being the subdomain toward which the unit normal \(\varvec{n}\) points. Taking into account the linearity of \(\varvec{u}_{k}\) \(\forall \varvec{ }k \in \left\{ {1, \ldots ,M} \right\}\), the first of the previous conditions is equivalent to two inequalities [see (30)]:

$$\left( {\varvec{u}_{j} \left( A \right) - \varvec{u}_{i} \left( A \right)} \right) \cdot \varvec{n} \ge 0$$
(50)
$$\left( {\varvec{u}_{j} \left( B \right) - \varvec{u}_{i} \left( B \right)} \right) \cdot \varvec{n} \ge 0 .$$
(51)

Similarly, the no-sliding condition can be expressed (in a redundant way) through the two equations (see (31)):

$$\left( {\varvec{u}_{j} \left( A \right) - \varvec{u}_{i} \left( A \right)} \right) \cdot \varvec{t} = 0$$
(52)
$$\left( {\varvec{u}_{j} \left( B \right) - \varvec{u}_{i} \left( B \right)} \right) \cdot \varvec{t} = 0 ,$$
(53)

that, due to the rigidity, can be rewritten into one of the two equivalent forms:

$$\left( {\varvec{u}_{j} \left( A \right) - \varvec{u}_{i} \left( B \right)} \right) \cdot \varvec{t} = 0 \Leftrightarrow \left( {\varvec{u}_{j} \left( B \right) - \varvec{u}_{i} \left( A \right)} \right) \cdot \varvec{t} = 0 .$$
(54)

Finally, the Heyman conditions (9), (10) relative to \(l\left( {A,B} \right)\varvec{ }\) are synthesized into three relations:

$$\left( {\varvec{u}_{j} \left( A \right) - \varvec{u}_{i} \left( A \right)} \right) \cdot \varvec{n} \ge 0 ,$$
(55)
$$\left( {\varvec{u}_{j} \left( B \right) - \varvec{u}_{i} \left( B \right)} \right) \cdot \varvec{n} \ge 0 ,$$
(56)
$$\left( {\varvec{u}_{j} \left( A \right) - \varvec{u}_{i} \left( B \right)} \right) \cdot \varvec{t} = 0 ,$$
(57)

which can be easily expressed in terms of the 6 Lagrangian parameters \(\left( {U_{k} ,V_{k} ,{{\varPhi }}_{k} } \right)_{{k \in \left\{ {i,j} \right\}}} .\) If \(n\) denotes the number of internal sides, the internal boundary conditions consist of \(2n\) linear inequalities and \(n\) linear equalities; with some easy transformations, the external boundary conditions can be implemented as fictitious internal contact conditions. If the constraints are perfect, then the corresponding equalities and inequalities are homogeneous. The given settlements (or eigenstrains) are the known terms of the non-homogeneous conditions. All together the constraints define a domain \({\mathbb{K}}^{M} \subseteq {\mathbb{R}}^{3M}\), in which the optimal solution has to be found; such domain is a convex polytope of the \({\mathbb{R}}^{3M}\) space.

5. With the above approximation the structural problem is formulated as a minimum problem:

“find a piecewise rigid displacement \(\hat{\varvec{U}}^{0}\) which minimizes the potential energy \(E\) in \({\mathbb{K}}^{M}\)”:

$$E\left( {\hat{\varvec{U}}}^{\circ} \right) = \mathop {\hbox{min} }\limits_{{\hat{\varvec{U}} \in {\mathbb{K}}^{M} }} E\left( {\hat{\varvec{U}}} \right).$$
(58)

This linear programming problem is solved with the simplex method, or with the interior point method if the number of unknowns is large.

6. Once the minimizer \(\hat{\varvec{U}}^{0}\) has been obtained it is an easy task to construct the deformed shape of the structure. The moving part of the structure represents a one degree of freedom mechanism controlled by the form of the given settlements, i.e. it is statically determined. The relative displacements among the blocks play the part of fractures, and hopefully give an approximation of the real fracture pattern produced by known settlements.

Remark 6

Usually, the problem to be solved for real structures presents itself in a different way, since cracks are detectable and the settlements producing them are usually unknown. Therefore, to adopt our scheme in practical applications, a sort of inverse identification procedure must be implemented.

10 Numerical examples

As an illustration of the method two examples are carried out.

10.1 Example 1: XVIII century building in Torre Annunziata (Naples)

The first example we present concerns the analysis of the façade of a XVIII century historical buildings, made of local tuff stone, located in via Nazionale, Torre Annunziata. In Fig. 2 the front of the building with the drawing of the cracks (obtained through a photographic image reconstruction), and its second floor plan are shown.

Fig. 2
figure 2

Front view of a XVIII century building in Torre Annunziata (Naples) (a). In a the crack pattern, traced through digital image reconstruction from the photo, is also reported. Plan of the second floor of the building b some parts of the plan are not shown

Full size image

With reference to Fig. 3a, we observe that the parapet inside the dashed rectangle is a non-structural element and then is not considered in the analysis. The masonry structure in the dot-dashed rectangle is a semi-detached construction and therefore is not considered in the analysis either. In the model we construct (see Fig. 3b), we use 490 identical square elements of side 0.80 m, for which the corresponding number of unknowns of problem (56) is 1470. As external load we consider the self-weight only, on assuming a masonry density of 1600 kg/m3.

Fig. 3
figure 3

Front view of the building (a) and rigid block discretization (b). The zone of crushing is highlighted with two light grey strips. Notice that the drawing in a was obtained by photo reconstruction and that the two openings at the ground floor are not visible being covered by shop windows

Full size image

We consider as data of the problem both foundation settlements and given eigenstrains concentrated along the two light grey strips, located above two of the ground floor masonry panels. The eigenstrains simulate a widespread crushing of such wall panels, caused by the enlargement of the adjacent openings (see Fig. 3b). Both settlements and eigenstrains represent the known terms of some of the inequalities considered as constraints in the LP program. The total number of restrictions, both equalities and inequalities (including internal and external boundary conditions) is 5244.

Since the exact distribution and the relative amplitude of the set of settlements and distortions which caused the cracks were not known exactly, we considered simple forms of such settlements and performed some qualitative parametric analysis to identify the relative values giving the better description of the detected crack pattern. The foundation settlement and eigenstrains shape which better reflect the real crack pattern are shown in Fig. 4. We used the interior point routine implemented in the program Mathematica ® to solve the related LP problem; the solution, corresponding to the optimal choice of the parameters is shown, in term of displacement, in Fig. 4.

Fig. 4
figure 4

Two representations of the same solution \(\varvec{u}^{0}\) corresponding to the minimizer \(\hat{\varvec{U}}^{0}\) of the LP problem

Full size image

10.2 Example 2: XVII centuries Church (Naples)

The second example concerns the analysis of “Chiesa di Santa Maria Incoronatella della Pietà dei Turchini”, a XVII century church located in via Monteoliveto in Naples. In Fig. 5a, b, the plan and a lateral section view of the structure are reported. The typical structure of a Church of Latin plan is rather vulnerable to seismic effects and has been the object of several studies (among which we recall [8, 26], and references therein).

Fig. 5
figure 5

Plan (a) and section A–A′ (b) of the church and the rigid block discretization (c). The crack pattern, reconstructed from a photographic survey, is shown in a and b. The distributed tractions due to the secondary structures are reported in c

Full size image

In particular we study, as a plane case, the left wall of the central nave, the big arch of the transept and the left lateral wall of the apse. The discretized plane model we construct, is constituted by 3183 square blocks of side 0.52 m (see Fig. 5c). As external loads, in addition to the self-weight of the structure (\(\rho\) = 1800 kg/m3), uniformly distributed tractions (applied as shown in Fig. 5c) representing the action of the secondary structures, and whose values are also reported in Fig. 5c, are also considered. The total unknowns of the problem are 9549 and the number of restrictions, both equalities and inequalities, is 36,256.

In the lateral section view of Fig. 5b, the existing crack pattern, detected and drawn before the restoration works had taken place, is reported. The disarray that was visible consisted essentially in a rigid body mechanism of a number of macro-blocks of the structure, separated by manifest cracks, and presumably due to ground settlements. However the overall size of such rigid body displacements, and the size of the cracks, were everywhere small when compared to the overall size of the structure, and not such to compromise, in any way, the equilibrium of the structure.

The aim of the present analysis is to obtain a simulation of such crack pattern and macro-block mechanism as close as possible to the real one. Although the cause of the mechanism was pretty clear, since the exact distribution and the relative amplitude of the set of settlements which caused the cracks were not known exactly, we considered simple forms of such settlements and performed a number of qualitative parametric analyses to identify the relative values of such data giving the better description of the detected crack pattern. The foundation settlement profile shown in Fig. 6, was identified as that giving the best qualitative fit with the real crack pattern. The results in terms of rigid body displacements of the blocks are reported in Fig. 6.

Fig. 6
figure 6

Two representations of the same solution \(\varvec{u}^{0}\) corresponding to the vertical foundation settlements

Full size image

An even better fit of the real partition into blocks was obtained considering, besides the profile of vertical settlements represented in Fig. 6, also the set of horizontal displacements depicted in Fig. 7.

Fig. 7
figure 7

Silhouette of the deformed configuration, and of the macro-block partition and macro-block boundaries obtained numerically and corresponding to vertical and horizontal foundation settlements. In the central figure the colour map represents the value of the rotation: rigid macro-blocks are identified by uniform colour, meaning uniform rotation; the real crack pattern is also reported in transparency. In the bottom figure the contours of the blocks are reported, together with the real crack pattern, in transparency. (Color figure online)

Full size image

In Fig. 7, besides the silhouette of the deformed configuration obtained through energy minimization, also two comparisons between the real and simulated crack patterns and macro-block mechanisms, are also reported. In particular in the center picture, in order to identify the rigid blocks, a colour map of the intensity of the rotation is depicted. Macro-elements having the same rotation have a uniform colour and are separated among each other by cracks. In the bottom picture the boundaries of the simulated macro-blocks are drawn together with the real cracks.

We must say that, though a close correlation between the size, the number and the location of the blocks can be detected, the direction of real and simulated cracks differ markedly, especially in the case of slanted orientations.

11 Conclusions

In the present work, we propose and develop a computer code for the prediction of fracture patterns produced by a given set of kinematical data (settlements/distortions).

In practical applications to real structures, the main critical issue of a fracture survey is identifying the particular form of foundation settlements producing the detected crack pattern.

The computer program we develop here, represents a deterministic tool enabling to find the mechanism and the fracture pattern due to known kinematical data, in a structure composed of rigid pieces in mutual unilateral contact.

In this work, we apply the method to two real examples. Based on the results we obtain for these two examples of different complexity, we can say that the method is able to reproduce satisfactorily the size, the number and the location of the rigid macro-blocks in which the structure decomposes when a mechanism forms due to known settlements. A lesser degree of correlation is detected concerning the crack path, in particular when the orientations of the real cracks are sensibly different from those of the element interfaces.

In these two examples, since the exact settlements producing the mechanism are not known, we try to identify manually a specific combination of simplified settlements over a given set. A number of different runs of the program were performed, by varying the relative value of the settlements over a specified grid of individual values, choosing the combination which gave the “best fit”.

It goes without saying that a rational identification scheme, based on the code that we introduce in the present paper, should be implemented to make the method effective in practical applications. The development of such a task is outside the scopes of the present paper.