Supersonic flutter analysis of FGM shallow conical panel accounting for thermal effects

Abstract

Supersonic flutter behaviors of functionally graded material (FGM) shallow conical panel with steady thermal stress are investigated. It is assumed that temperature dependent material properties are graded along the radial direction following power law form. The shallow conical panel is formulated with the aid of first-order shear deformation theory and von-Karman geometrical nonlinearity. The aerodynamic loads are evaluated by using the first-order piston theory. The equations of motion in the form of nonlinear partial differential are derived by applying the Hamilton’s principle. In order to get a high dimensional dynamic discrete system, the Galerkin’s method is utilized and this system includes the effect of steady thermal stress due to considering the thermal stress. Newton–Raphson method and continuation method are applied to obtain the equilibrium points, and flutter boundaries are analyzed by solving the eigenvalue problem. The influences of damping, ratio of length to thickness and volume fraction index on the flutter characteristics of the simply supported FGM shallow conical shell panel are studied.

1 Introduction

Vibration of engineering structures due to interaction with flowing air is called flutter. It is well known that flutter is an unstable self-excited vibration and it may cause fatigue failure of these structures. Usually, engineering structures are subjected to aerodynamic pressure and aerodynamic heating which can weaken their material properties. As one kind of important structural components shallow conical shell are used in many fields such as turbine blades or aircraft fuselages. Functionally graded materials (FGMs) structures have aroused general interest and gained wide application recently because of their tailored thermo-mechanical ability. Because it is possible for them to be subjected to external forces such as mechanical loads, thermal loads and aerodynamic pressures and so on. So how to predict their mechanical behavior including aero-thermo-elasticity is essential for the safety and reliable design of them [1].

Recently, the flutter behaviors of FGM plates and shells in supersonic air flow have been studied. Applying finite element method, Prakash and Ganapathi [2] studied the supersonic flutter of rectangular plates which were made of functionally graded material. They got the critical aerodynamic loads for different parameters. Sohn and Kim [3, 4] researched the thermal buckling of functionally graded material panels which were subjected to both aerodynamic pressure and thermal forces. At the same time, they studied the flutter boundary and flutter characteristics of them. Jafarpour et al. [5] simulated the coupled thermo-aero-mechanical FGM rectangular plate model and its response under supersonic flow. Fazelzadeh et al. [6] examined the influences of main parameters on the thermal divergence boundaries and critical temperature of supersonic FGM plate by the standard eigenvalue algorithm. Mahmoudkhani et al. [7] predicted the flutter boundaries about the functionally graded truncated conical shell simply supported at two ends in supersonic flow with different semi-vertex cone angles, volume fraction indices and temperature distributions.

It is notable that all the aforementioned contributions are about the linear flutter researches for functionally graded material plates and shells. However, in most cases these structures are used in complex environment and the dynamical system is nonlinear. On the basis of finite element method, Ibrahim et al. [8, 9] researched nonlinear flutter of the functionally graded material panels which were subjected to aero-thermo-elastic loading and at the same time they also researched the thermal buckling characteristics. Navazi and Haddadpour [10, 11] studied the aero-thermo-elastic critical stable boundaries of functionally graded material panels in the supersonic speed airflow and the nonlinear aeroelastic response of them. Hesham et al. [12] analyzed thermal buckling behaviors and the problem of geometrical nonlinear flutter of functionally graded panel numerically by employing Newton–Raphson technique. Also the nonlinear finite element model was used to analyze the supersonic flutter behavior of FGM panels which were subjected to aerodynamic pressure, thermal loads and stationary white-Gaussian random acoustic exciting forces. Haddadpour et al. [13] studied the nonlinear aero-elastic behavior and post-flutter region of functionally graded plates under von-Karman assumptions. Prakash et al. [14] studied geometrical nonlinear flutter characteristics of FGM plates in supersonic flow based on flexible finite element method. Hosseini et al. [15] analyzed the nonlinear response of infinitely long simply supported FGM curved panels in high temperature supersonic air flows. By bifurcation analysis and Lyapunov’s exponents, the periodic and chaotic motions were determined. Yang et al. [16] analyzed the complex nonlinear dynamics of ceramic–metal functionally graded conical shell including the aerodynamic pressure and mechanical loads. This nonlinear system was studied by bifurcation analysis and solving the maximum Lyapunov exponents. The influences of the material properties, semi-vertex angle, external loads on the nonlinear dynamics were given. Hao et al. [17] investigated the bifurcation of functionally graded materials hypersonic plate which was subjected to the external excitation. The Mach number and longitudinal loading are used as bifurcation parameters.

As far as the authors know, studies on nonlinear flutters of functionally graded materials shallow conical shell appear to be very few in opening literatures. Fazelzadeh et al. [18] studied the vibration of FGM walled-blade in supersonic flow with high temperature by using the differential quadrature method. The dynamic system was obtained on the basis of the first-order shear theory. Shahverdi [19] presented the aero-thermo-elastic behavior of FGM curved panels which is in hypersonic airflow numerically and chaotic motions were found for the functionally graded curved panel. In the present research, the nonlinear flutter analysis of functionally graded material shallow conical panel under aerodynamic pressure and thermal stress is given. The high dimensional nonlinear flutter equations of functionally graded material shallow conical panel with steady thermal stress are obtained by Galerkin’s method. The steady thermal stress in nonlinear flutter equations can affect the position of equilibrium point. Newton–Raphson method and continuation method are applied to calculate the equilibrium point of the system and then by solving eigenvalue problem the flutter boundary can be obtained.

2 Theoretical formulation

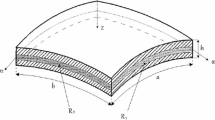
Consider a functionally grade material shallow conical panel with coordinate system along the meridional, circumferential and normal directions respectively. The origin is located at the corner of shallow conical panel on the mid-surface (see Fig. 1). The minor inner radius, semi-vertex angle, length of meridional and the total thickness of the shallow conical panel are R ₁, β, L and h, respectively. And radius of curvature any point along the meridional can be obtained by R(x) = R ₁ + x sin β. The material at the bottom side of the shallow conical panel is metal rich, however, the top side of it is ceramic rich. According to a simple power law of the volume fraction of ceramic, the effective Young’s modulus E, the density ρ and thermal expansion α can be written as [20],

$$\begin{aligned} E & = \left( {E_{c} - E_{m} } \right)\vartheta^{n} + E_{m} ,\quad \rho = \left( {\rho_{c} - \rho_{m} } \right)\vartheta^{n} + \rho_{m} , \\ \alpha & = \left( {\alpha_{c} - \alpha_{m} } \right)\vartheta^{n} + \alpha_{m} , \\ \end{aligned}$$

(1)

where n is the variable which represents volume fraction of ceramic, the subscripts m and c refers to metal and ceramic, respectively. And variable ϑ is as value of $\left( {\frac{z}{h} + \frac{1}{2}} \right)$. The value of the Poisson’s ratio ν is considered to be a constant in this paper. The material properties are the functions of temperature [21].

Fig. 1

Geometry of FGM shallow conical panel

The temperature due to the viscous aerodynamic heating can be calculated from [22]

$$T_{c} - T_{\infty } = M_{a}^{2} T_{\infty } \varsigma ,$$

(2-a)

$$\varsigma = R_{f} \frac{{\gamma_{a} - 1}}{2},$$

(2-b)

where T _∞ is the incoming flow temperature and T _c is the temperature on the top surface. Variables R _f and γ _a denote steady temperature recovery factor and specific heat ratio respectively. The temperature distribution along the radial direction of the shallow conical panel can be expressed by polynomial series [23]

$$T\left( z \right) = T_{m} + \left( {T_{c} - T_{m} } \right)\,\eta \left( z \right),$$

(3)

where

$$\begin{aligned} \eta \left( z \right) & = \frac{\vartheta }{C}\left[ {1 - \frac{{k_{cm} }}{{k_{m} \left( {n + 1} \right)}}\vartheta^{n} + \frac{{k_{cm}^{2} }}{{k_{m}^{2} \left( {2n + 1} \right)}}\vartheta^{2n} } \right. \\ & \quad { - \frac{{k_{cm}^{3} }}{{k_{m}^{3} \left( {3n + 1} \right)}}\vartheta^{3n} + \,\frac{{k_{cm}^{4} }}{{k_{m}^{4} \left( {4n + 1} \right)}}\vartheta^{4n}} \\ & \left. \quad -\,\frac{{k_{cm}^{5} }}{{k_{m}^{5} \left( {5n + 1} \right)}}\vartheta^{5n} \right], \\ \end{aligned}$$

(4)

with

$$k_{cm} = k_{c} - k_{m} ,$$

(5)

and

$$\begin{aligned} C & = 1 - \frac{{k_{cm} }}{{\left( {n + 1} \right)k_{m} }} + \frac{{k_{cm}^{2} }}{{\left( {2n + 1} \right)k_{m}^{2} }} - \frac{{k_{cm}^{3} }}{{\left( {3n + 1} \right)k_{m}^{3} }} \\ & \quad + \,\frac{{k_{cm}^{4} }}{{\left( {4n + 1} \right)k_{m}^{4} }} - \frac{{k_{cm}^{5} }}{{\left( {5n + 1} \right)k_{m}^{5} }}, \\ \end{aligned}$$

(6)

where k _m and k _c are heat conduction coefficients of metal and ceramic, respectively.

2.1 Aerodynamic pressure

For supersonic airflow paralleling to the meridian of the functionally graded shallow conical panel, the aerodynamic pressure caused by the interaction of vibration of shallow conical panel and airflow is obtained by the first order piston theory [24, 25]

$$\begin{aligned} P_{a} & = - \frac{{\gamma _{a} p_{\infty } M_{a}^{2} }}{{\sqrt {M_{a} ^{2} - 1} }}\,\left[ {\frac{{\partial w}}{{\partial x}} + \left( {\frac{{M_{a} ^{2} - 2}}{{M_{a} ^{2} - 1}}} \right)\frac{1}{{M_{a} a_{\infty } }}\frac{{\partial w}}{{\partial t}}} \right. \\ & \quad \left. { - \frac{w}{{2R\sqrt {M_{a} ^{2} - 1} }}} \right], \\ \end{aligned}$$

(7)

where M _a , a _∞, p _∞ and γ _a represent the Mach number, the free stream speed of sound, the free stream static pressure and the adiabatic exponent, respectively. In Eq. (7), the last term is the curvature correction term.

2.2 Governing equations of motion

The displacements which take the transverse shear deformations into account of the shallow conical panel are described as follows [26]

$$u\left( {x,\theta ,z,t} \right) = u_{0} \left( {x,\theta ,t} \right) + z\phi_{x} \left( {x,\theta ,t} \right),$$

(8a)

$$v\left( {x,\theta ,z,t} \right) = v_{0} \left( {x,\theta ,t} \right) + z\phi_{\theta } \left( {x,\theta ,t} \right),$$

(8b)

$$w\left( {x,\theta ,z,t} \right) = w_{0} \left( {x,\theta ,t} \right),$$

(8c)

where u and v are in-plane displacements and w represents the transverse displacement of an arbitrary point of the shallow conical panel. And u ₀, v ₀, and w ₀ are mid-plane displacements, ϕ _x and ϕ _θ are the rotations of transverse normal about the θ and x axes. Using Eq. (8) and by considering von-Karman strain–displacement relation the strain tensor elements including nonlinear terms can be written as

$$\begin{aligned} \left\{ \begin{aligned} \varepsilon_{x} \hfill \\ \varepsilon_{\theta } \hfill \\ \gamma_{x\theta } \hfill \\ \end{aligned} \right\} & = \left\{ \begin{aligned} \varepsilon_{x}^{\left( 0 \right)} \hfill \\ \varepsilon_{\theta }^{\left( 0 \right)} \hfill \\ \gamma_{x\theta }^{\left( 0 \right)} \hfill \\ \end{aligned} \right\} + z\left\{ \begin{aligned} \varepsilon_{x}^{\left( 1 \right)} \hfill \\ \varepsilon_{\theta }^{\left( 1 \right)} \hfill \\ \gamma_{x\theta }^{\left( 1 \right)} \hfill \\ \end{aligned} \right\}, \\ \left\{ \begin{aligned} \gamma_{\theta z} \hfill \\ \gamma_{xz} \hfill \\ \end{aligned} \right\} & = \left\{ \begin{array}{c} \phi_{\theta } + \frac{1}{R}\frac{{\partial w_{0} }}{\partial \theta } - \frac{1}{R}v_{0} \cos \beta \\ \frac{{\partial w_{0} }}{\partial x} + \phi_{x} \\ \end{array} \right\}, \\ \end{aligned}$$

(9)

where

$$\begin{aligned} \left\{ \begin{array}{c} \varepsilon_{x}^{\left( 0 \right)} \hfill \\ \varepsilon_{\theta }^{\left( 0 \right)} \hfill \\ \gamma_{x\theta }^{\left( 0 \right)} \hfill \\ \end{array} \right\} & = \left\{ \begin{array}{c} \frac{{\partial u_{0} }}{\partial x} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} \\ \frac{1}{R}\frac{{\partial v_{0} }}{\partial \theta } + \frac{1}{R}w_{0} \cos \beta + \frac{1}{R}u_{0} \sin \beta + \frac{1}{{2R^{2} }}\left( {\frac{{\partial w_{0} }}{\partial \theta }} \right)^{2} \\ \frac{1}{R}\frac{{\partial u_{0} }}{\partial \theta } - \frac{1}{R}v_{0} \sin \beta + \frac{{\partial v_{0} }}{\partial x} + \frac{1}{R}\frac{{\partial w_{0} }}{\partial x}\frac{{\partial w_{0} }}{\partial \theta } \\ \end{array} \right\}, \\ \left\{ \begin{array}{c} \varepsilon_{x}^{\left( 1 \right)} \hfill \\ \varepsilon_{\theta }^{\left( 1 \right)} \hfill \\ \gamma_{x\theta }^{\left( 1 \right)} \hfill \\ \end{array} \right\} & = \left\{ \begin{array}{c} \frac{{\partial \phi_{x} }}{\partial x} \\ \frac{1}{R}\frac{{\partial \phi_{\theta } }}{\partial \theta } + \frac{1}{R}\phi_{x} \sin \beta \\ \frac{1}{R}\frac{{\partial \phi_{x} }}{\partial \theta } - \frac{1}{R}\phi_{\theta } \sin \beta + \frac{{\partial \phi_{\theta } }}{\partial x} \\ \\ \end{array} \right\}. \\ \end{aligned}$$

(10)

The constitutive equations accounting for thermal effects are written as

$$\begin{aligned} \left\{ \begin{gathered} \sigma _{x} \hfill \\ \sigma _{\theta } \hfill \\ \sigma _{{x\theta }} \hfill \\ \sigma _{{\theta z}} \hfill \\ \sigma _{{xz}} \hfill \\ \end{gathered} \right\} & = \left[ {\begin{array}{*{20}c} {Q_{{11}} } & {Q_{{12}} } & {} & {} & {} \\ {Q_{{12}} } & {Q_{{22}} } & {} & {} & {} \\ {} & {} & {Q_{{66}} } & {} & {} \\ {} & {} & {} & {Q_{{44}} } & {} \\ {} & {} & {} & {} & {Q_{{55}} } \\ \end{array} } \right] \\ & \quad \times \,\left\{ {\left\{ \begin{gathered} \varepsilon _{x} \hfill \\ \varepsilon _{\theta } \hfill \\ \gamma _{{x\theta }} \hfill \\ \gamma _{{\theta z}} \hfill \\ \gamma _{{xz}} \hfill \\ \end{gathered} \right\} - \left\{ \begin{gathered} \alpha \\ \alpha \\ 0 \\ 0 \\ 0 \\ \end{gathered} \right\}\Delta T} \right\}, \\ \end{aligned}$$

(11)

where temperature elevation ΔT = T(z) − T ₀, T ₀ is the reference temperature. And the stiffness coefficients Q _ij are given by

$$\begin{aligned} Q_{ 1 1} & = Q_{ 2 2} = \frac{E}{{1 - \nu^{2} }},\quad Q_{ 1 2} = \frac{\nu E}{{1 - \nu^{2} }}, \\ Q_{ 4 4} & = Q_{ 5 5} = Q_{ 6 6} = \frac{E}{{2\left( {1 + \nu } \right)}}. \\ \end{aligned}$$

(12)

By the Hamilton’s principle, dynamical equations are established as

$$N_{xx,x} + \frac{1}{R}\left( {N_{x\theta ,\theta } + N_{xx} \sin \beta - N_{\theta \theta } \sin \beta } \right) = I_{0} \ddot{u}_{0} + I_{1} \ddot{\phi }_{x} ,$$

(13a)

$$N_{x\theta ,x} + \frac{1}{R}\left( {N_{\theta \theta ,\theta } + 2N_{x\theta } \sin \beta + Q_{\theta } \cos \beta } \right) = I_{0} \ddot{v}_{0} + I_{1} \ddot{\phi }_{\theta } ,$$

(13b)

$$\begin{aligned} & Q_{x,x} + N_{xx,x} \frac{{\partial w_{0} }}{\partial x} + N_{xx} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \frac{1}{R}\left( {Q_{\theta ,\theta } + Q_{x} \sin \beta - N_{\theta \theta } \cos \beta } \right. \\ & \quad \left. { + \,N_{xx} \frac{{\partial w_{0} }}{\partial x}\sin \beta + N_{x\theta ,\theta } \frac{{\partial w_{0} }}{\partial x} + 2N_{x\theta ,\theta } \frac{{\partial^{2} w_{0} }}{\partial x\partial \theta } + N_{x\theta ,x} \frac{{\partial w_{0} }}{\partial \theta }} \right) \\ & \quad + \,\frac{1}{{R^{2} }}\left( {N_{\theta \theta ,\theta } \frac{{\partial w_{0} }}{\partial \theta } + N_{\theta \theta } \frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}} \right) + P_{a} - \kappa \dot{w}_{0} = I_{0} \ddot{w}_{0} , \\ \end{aligned}$$

(13c)

$$M_{xx,x} + \frac{1}{R}\left( {M_{x\theta ,\theta } - Q_{x} + M_{xx} \sin \beta - M_{\theta \theta } \sin \beta } \right) = I_{1} \ddot{u}_{0} + I_{2} \ddot{\phi }_{x} ,$$

(13d)

$$M_{x\theta ,x} - Q_{\theta } + \frac{1}{R}\left( {M_{\theta \theta ,\theta } + 2M_{x\theta } \sin \beta } \right) = I_{1} \ddot{v}_{0} + I_{2} \ddot{\phi }_{\theta } .$$

(13e)

where double dots denote the second order derivative to time and the mass inertia terms are defined as

$$(I_{0} ,I_{1} ,I_{2} ) = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {(1,z^{1} ,z^{2} )\rho } dz,$$

(14)

The membrane resultants $\varvec{N} = \left[ {N_{xx} ,N_{\theta \theta } ,N_{x\theta } } \right]^{\prime }$, shear resultants $\varvec{Q} = \left[ {Q_{x} ,Q_{\theta } } \right]^{\prime }$ and moment resultants $\varvec{M} = \left[ {M_{xx} ,M_{\theta \theta } ,M_{x\theta } } \right]^{\prime }$ are expressed as

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} \varvec{N} \\ \varvec{M} \\ \end{array} } \right\} & = \left[ {\begin{array}{*{20}c} \varvec{A} & \varvec{B} \\ \varvec{B} & \varvec{D} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\left\{ {\varepsilon ^{{(0)}} } \right\}} \\ {\left\{ {\varepsilon ^{{(1)}} } \right\}} \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}c} {\varvec{N}^{\varvec{T}} } \\ {\varvec{M}^{\varvec{T}} } \\ \end{array} } \right\}, \\ \varvec{Q} & = K\left[ \varvec{A} \right]\left\{ {\begin{array}{*{20}c} {\gamma _{{xz}} } \\ {\gamma _{{\theta z}} } \\ \end{array} } \right\}, \\ \end{aligned}$$

(15)

where shear correction factor K is taken to 5/6, $\varvec{N}^{\varvec{T}}$ and $\varvec{M}^{\varvec{T}}$ are resultants of the thermal stresses which are defined by

$$\left[ {\begin{array}{ll} {N_{xx}^{T} } & {M_{xx}^{T} } \\ {N_{\theta \theta }^{T} } & {M_{\theta \theta }^{T} } \\ {N_{x\theta }^{T} } & {M_{x\theta }^{T} } \\ \end{array} } \right] = - \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left\{ {\begin{array}{ll} {Q_{11} + Q_{12} } \\ {Q_{21} + Q_{22} } \\ 0 \\ \end{array} } \right\}} \alpha (1,z)\Delta Tdz,$$

(16)

and

$$\begin{aligned} \left( {A_{ij} ,B_{ij} ,D_{ij} } \right) & = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {Q_{ij} \left( {1,z,z^{2} } \right)} dz,\quad \left( {i,j = 1,2,6} \right), \\ A_{ij} & = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {Q_{ij} } dz,\quad \left( {i,j = 4,5} \right). \\ \end{aligned}$$

(17)

Utilizing Eqs. (13a)–(17), nonlinear partial differential dynamical equations for the FGM shallow conical panel in terms of generalized displacements (u ₀, v ₀, w ₀, ϕ _x and ϕ _θ ) can be obtained. They can be seen in “Appendix”.

The moveable simply supported boundary conditions are considered and can be expressed as

$$\begin{aligned} v_{0} & = w_{0} = \varphi_{\theta } = N_{xx} = M_{xx} = 0\,\,{\text{at}}\,\,x = 0, \,x = L, \\ u_{0} & = w_{0} = \varphi_{x} = N_{\theta \theta } = M_{\theta \theta } = 0\,\,{\text{at}}\,\,\theta = 0,\, \theta = \gamma . \\ \end{aligned}$$

(18)

The simply supported boundary conditions are satisfied by the following double Fourier sine series

$$\begin{aligned} u_{0} & = \sum\limits_{m = 1}^{M} {} \sum\limits_{n = 1}^{N} {u_{mn} \left( t \right)} \cos \left( {\frac{m\pi x}{L}} \right)\sin \left( {\frac{n\pi \theta }{\gamma }} \right), \\ v_{0} & = \sum\limits_{m = 1}^{M} {} \sum\limits_{n = 1}^{N} {v_{mn} } \left( t \right)\sin \left( {\frac{m\pi x}{L}} \right)\cos \left( {\frac{n\pi \theta }{\gamma }} \right), \\ w_{0} & = \sum\limits_{n = 1}^{M} {} \sum\limits_{m = 1}^{N} {w_{mn} \left( t \right)} \sin \left( {\frac{m\pi x}{L}} \right)\sin \left( {\frac{n\pi \theta }{\gamma }} \right), \\ \varphi_{x} & = \sum\limits_{m = 1}^{M} {} \sum\limits_{n = 1}^{N} {\varphi_{xmn} \left( t \right)} \cos \left( {\frac{m\pi x}{L}} \right)\sin \left( {\frac{n\pi \theta }{\gamma }} \right), \\ \varphi_{\theta } & = \sum\limits_{m = 1}^{M} {} \sum\limits_{n = 1}^{N} {\varphi_{\theta mn} } \left( t \right)\sin \left( {\frac{m\pi x}{L}} \right)\cos \left( {\frac{n\pi \theta }{\gamma }} \right). \\ \end{aligned}$$

(19)

where m is axial half waves number and n is circumferential waves number. It is difficult for high order modes to be excited by aerodynamic pressure in the direction of coordinate axis θ [26], so M = 6 and N = 1 are used in numerical simulation. To supersonic flutter which the air flow parallels to the meridian line of the shallow conical panel, the transverse flutter is more important than others. The effects of inertia terms in in-plane and rotations are small and they can be neglected. Employing the Galerkin’s method, we can get four constant coefficients coupled algebraic equations and one dynamic ordinary differential equation in transverse direction under aerodynamic and aero-thermal load. Consequently, the nonlinear equations of motion in terms of ordinary differential can be expressed by transverse displacements and can be written as

$$\begin{aligned} & \ddot{w}_{m} + (\mu_{km} + \mu_{am} )\dot{w}_{m} + \sum\limits_{i = 1}^{6} {K_{mi} w_{i} } + \sum\limits_{i = 1}^{6} {\sum\limits_{j = 1}^{6} {K_{2mij} } } w_{i} w_{j} \\ & \quad + \,\sum\limits_{i = 1}^{6} {\sum\limits_{j = 1}^{6} {\sum\limits_{l = 1}^{6} {K_{3mijl} } } } w_{i} w_{j} w_{l} = C_{{\Delta Tm}} \,\,\,\left( {m = 1,2, \ldots ,6} \right) \\ \end{aligned}$$

(20)

where μ _km and μ _am represent the structural damping and the aerodynamic damping, K _mi is the linear stiffness term induced by structure and aerodynamic and aero-thermal, K _2mij and K _3mijl are quadratic and cubic nonlinear stiffness coefficients, stable constant C _ΔTm is thermal stress resultants and can make the equilibrium position be not origin but shift to a new equilibrium state by deformation.

3 Numerical simulations

The FGM shallow conical panel considered in the study is composited by steel (SUS304) and silicon nitride (Si₃N₄) and the material properties of them are presented in Table 1. The following geometric parameters and airflow characteristics are used as: slanted length L = 2 m, semi-vertex angle $\beta = 30^{^\circ }$, subtended angle $\gamma = 60^{^\circ }$, the radius at the top end R ₁ = 0.8 m, M _a  = 2, γ _a  = 1.4, a _∞ = 213.36 m s⁻¹ and $T_{\infty } = 223.26\,\,{\text{K}}$, respectively. The point (3L/4, π/6, 0) of the FGM shallow conical panel is considered to be the referential location.

Table 1 The temperature-dependent coefficients of SUS304 and SI₃N₄

3.1 Numerical algorithms for the equilibrium point

According to the flutter Eq. (20), the stable constant C _ΔTm can make the equilibrium position of the system deviate original location which should be computed.

The equilibrium points of Eq. (20) corresponding to parameter p _∞ can be computed as follows:

• 1. Give an initial point vector ${\text{x}}_{0}$ and parameter p _∞. Calculate the Jacobi matrix DF of Eq. (20) at the initial point ${\text{x}}_{0}$.

• 2. If the absolute value of the Jacobi matrix DF is not zero, solve the unique equilibrium point ${\text{x}}^{ *}$ of Eq. (20) by the Newton–Raphson method [29]. Otherwise, the equilibrium point ${\text{x}}^{ *}$ of the system may be a limit point or a bifurcation point. In these cases, we should track the solution path by pseudo arc-length continuation method [30].

• 3. Solve the real part of eigenvalue λ of the Jacobi matrix DF at ${\text{x}}^{ *}$, and then output ${\text{x}}^{ *}$.

• 4. ${\text{x}}_{ 0} = {\text{x}}^{*}$ is taken as the initial point at parameter p _∞ + dp _∞. Repeat steps (1) through (3) until p _∞ is less than the given value $p_{ \hbox{max} }$.

The critical free-stream static pressure p _cr for the system can be achieved by inspecting the maximum real part of the eigenvalue λ. Figure 2 shows the simulation flowchart on computation of the equilibrium point. As we all know, when the maximum real part of the eigenvalue λ of the Jacobi matrix DF changes from negative to positive, the flutter will occur and the system will turn to instability.

Fig. 2

Simulation flowchart on computation of the equilibrium point

3.2 Comparison and convergence studies

To validate the present approach, the dimensionless fundamental frequencies $\bar{\omega } = (\omega L^{2} /h)\sqrt {\rho_{{ 0 {\text{m}}}} /E_{{ 0 {\text{m}}}} }$ are compared with the results from Shen and Wang [27] and Jooybar [28] for cylindrical panel with the geometric parameters as h = 0.001 m, L/R = 1, L/h = 20 and γ = 180°/π, respectively. It is apparent from the Table 2 that the present results are good agreement with literatures listed in this Table and can validate the present approach.

Table 2 Comparisons of the natural frequencies $\bar{\omega } = (\omega L^{2} /h)\sqrt {\rho_{{0{\text{m}}}} /E_{{0{\text{m}}}} }$ of FGM shallow conical panel under thermal environment

Figure 3 illustrates the effect of the numbers of mode on the maximum real part of eigenvalues with the increases of the free-stream static pressure of FGM shallow conical shell with the n = 10. The moveable simply supported edges of the shell is considered. It can be seen that the response curves of the maximum real part of eigenvalues roughly the same when the number of mode M equals 6 and 8 respectively. A further increasing mode numbers will make no significant difference to critical point. Based on the above analysis, the six longitudinal modes can be applied in all calculations for the purpose of both accuracy of the solution.

Fig. 3

Maximum real part of eigenvalue versus the free-stream static pressure of FGM shallow conical panel when the mode numbers are 4, 6 and 8, respectively

3.3 Effect of damping on flutter boundary

In order to study the effect of aerodynamic damping on the flutter boundary of the FGM shallow conical panel, maximum real part of eigenvalue versus the free-stream static pressure of FGM shallow conical panel are presented in Fig. 4, where h = 0.001 m and n = 10. According to Fig. 4 that the critical free-stream static pressures are $4. 1 5\times 10^{ 6} \,{\text{Pa}}$ with aerodynamic damping compared to $2. 3 2\times 10^{ 6} \,{\text{Pa}}$ when we neglect the aerodynamic damping. It is found that the aerodynamic damping can stabilize the system by improving the free-stream static pressure. The stability boundaries of FGM conical panel are provide in Fig. 5. According to the numerical results in Fig. 5a for the system with movable simply supported boundary, it can be seen that there are three types of behaviors about shallow conical panel: static deflection, limit cycle oscillation (LCO) and periodic but not simple harmonic. Line AB is the flutter boundary of the shallow conical panel which the flutter motion begins. It is found that with the increase of structural damping μ _k , the flutter boundary is higher. By the phase portraits which can be gained by using the Runge–Kutta algorithm, one can obtain the periodic but not simple harmonic regions of the system. And line CD divides the LCO and the nonharmonic periodic regions. Numerical results reported in Fig. 5b shows that when the immovable simply supported boundary is assumed there are two types of behaviors: static deflection and limit cycle oscillation (LCO). The phase portraits are given in Fig. 6 for the system with movable boundary to illustrate the static deflection, the LCO and the nonharmonic periodic behavior. It may be inferred that the system with moveable simply supported boundary is more unstable. In the following, the FGM shallow conical panel with movable boundary is considered.

Fig. 4

Maximum real part of eigenvalue versus the free-stream static pressure of FGM shallow conical panel with/without aerodynamic damping

Fig. 5

Stability boundaries of FGM shallow conical panel. a simply supported FGM shallow conical panel with movable edges and b simply supported FGM shallow conical panel with immovable edges

Fig. 6

The phase portraits of simple supported FGM shallow conical panel with movable edges: a static deflection; b LCO and c nonharmonic periodic

3.4 Effect of the ratio of length to thickness

The influence of the ratio of length to thickness on the FGM shallow conical panel with movable simply supported boundary can be seen from Fig. 7, where Fig. 7b is the partial enlarged detail of Fig. 7a. It should be observed that when ratio of length to thickness is L/h = 2000, L/h = 1000 and L/h = 500 respectively, the corresponding critical free-stream static pressures are $4. 1 5\times 10^{ 6} ,\, 8. 2 8\times 10^{ 6}$ and $1. 5 5\times 10^{7} \,{\text{Pa}}$, respectively. One can deduce that decreasing the ratio of length to thickness makes the structure stiffer and the flutter point move backward gradually.

Fig. 7

Real part of eigenvalue versus the free-stream static pressure of FGM shallow conical panel with different length-thickness ratios

The 4th-order Runge–Kutta algorithm is applied to simulate the dynamic responses of the shallow conical panel. The time history record of the system can be shown in Fig. 8, where Fig. 8a, b are the attenuation vibration and the limit cycle oscillation, respectively. Figure 9 reveals the maximum and minimum displacement of FGM shallow conical panel with changing of length to thickness ratios. Here, the solid line indicates the maximum displacement, while the imaginary line indicates the minimum displacement. It can be drawn from Fig. 9 that the displacement of equilibrium position decreases with the reduction of the L/h because of the increasing of the stiffness of the system. And larger L/h can lead to easier vibration. A further study reveals that the change of amplitude become smaller for low ratios of length to thickness. It can be seen that for the length to thickness ratio of L/h ≥ 1200, transverse amplitude of vibration is not of the same order of magnitude as the thickness of the conical panel but a very lager vibration which means the conical panel has a larger deflection and rotation. The von-Karman nonlinearities is accurate for moderately larger vibration of the structure, see Ref. [24]. So in this case the nonlinear terms in nonlinear strain displacement relations should include the in-plane displacement in addition to the transverse displacement for more accurate expressions.

Fig. 8

The time history record of FGM shallow conical panel with different length-thickness ratios. a The attenuation vibration and b the limit cycle oscillation

Fig. 9

The maximum and minimum displacement of FGM shallow conical panel with different length-thickness ratios

3.5 Effect of volume fraction index

The influence of the ceramic content on the dynamical system can be seen from Fig. 10, where Fig. 10b is the partial enlarged detail of Fig. 10a. It is obviously that the critical free-stream static pressures are 1.07 × 10⁷, 2.95 × 10⁷ and 4.80 × 10⁷ Pa when n = 5, n = 1 and n = 0.5, respectively. And we can easily get conclusion that the critical free-stream static pressure will increase with the decrease of ceramic content. It is because that the increasing of the ceramic content can increase the stiffness of the system. Figure 11 exhibits the time history record of the system, where Fig. 11a, b are the attenuation vibration and the limit cycle oscillation, respectively. Figure 12 depicts the maximum and minimum displacement of FGM shallow conical panel with different volume fraction indexes. The “solid line” indicates the maximum displacement, while the “imaginary line” indicates the minimum displacement. It should be mentioned that the displacement of equilibrium position increases with the increasing of n, and larger n can result in easier vibration.

Fig. 10

Real part of eigenvalue versus the free-stream static pressure of FGM shallow conical panel with different indexes of volume fraction

Fig. 11

The time history record of FGM shallow conical panel with different indexes of volume fraction. a The attenuation vibration and b the limit cycle oscillation

Fig. 12

The maximum and minimum displacement of FGM shallow conical panel with different indexes of volume fraction

4 Conclusions

Supersonic flutter behaviors of FGM shallow conical panel with steady thermal stress are investigated in this study. The physical properties of this functionally graded material of the shallow conical panel are temperature-dependent and supposed to be gradient change in thickness direction taking the form of power law distribution. The aero dynamic pressure is evaluated by the first-order piston theory. First-order shear deformation theory, Hamilton’s principle and Galerkin’s method are utilized to obtain a high dimensional nonlinear dynamic system including thermal stress constants. The Newton–Raphson method and continuation method are applied to obtain the equilibrium point, and flutter characteristics are analyzed by solving the eigenvalue problem. The influences of damping, ratio of length to thickness and volume fraction index on the flutter characteristics of the simply supported FGM shallow conical panel are studied. It can be concluded that:

• 1. The aerodynamic damping can stabilize the system by consuming some energy and then improving the free-stream static pressure.

• 2. With the increase of structural damping, the flutter boundary is higher.

• 3. Decreasing the ratio of length to thickness may lead to increasing of the critical free-stream static pressure. And deflection of equilibrium position increases with the increase of L/h.

• 4. The decrease of the volume fraction index may result in enlargement of the critical free-stream static pressure. And the displacement of equilibrium position increases with the increasing of n.

Appendix

$$\begin{aligned} A_{11} \frac{{\partial^{2} u_{0} }}{{\partial x^{2} }} + \frac{1}{{R^{2} }}A_{66} \frac{{\partial^{2} u_{0} }}{{\partial \theta^{2} }} + \frac{1}{R}A_{11} \frac{{\partial u_{0} }}{\partial x}\sin \beta - \frac{1}{{R^{2} }}A_{22} u_{0} \cos^{2} \beta + \,\frac{1}{R}\left( {A_{12} + A_{66} } \right)\frac{{\partial^{2} v_{0} }}{\partial x\partial \theta } + \frac{1}{2R}\left( {A_{11} - A_{12} } \right)\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\sin \beta - \,\frac{1}{{2R^{3} }}\left( {A_{12} - A_{22} } \right)\frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}\sin \beta + \frac{1}{R}A_{12} \frac{{\partial w_{0} }}{\partial x}\cos \beta - \,\frac{1}{{R^{2} }}A_{22} w_{0} \sin \beta \cos \beta + B_{11} \frac{{\partial^{2} \varphi_{x} }}{{\partial x^{2} }} + \frac{1}{{R^{2} }}B_{66} \frac{{\partial^{2} \varphi_{x} }}{{\partial \theta^{2} }} + \,\frac{1}{R}B_{11} \frac{{\partial \varphi_{x} }}{\partial x}\sin \beta - \frac{1}{{R^{2} }}B_{22} \varphi_{x} \sin^{2} \beta + A_{11} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\frac{{\partial w_{0} }}{\partial x} + \,\frac{1}{R}\left( {B_{12} + B_{66} } \right)\frac{{\partial^{2} \varphi_{\theta } }}{\partial x\partial \theta } - \frac{1}{{R^{2} }}\left( {B_{22} + B_{66} } \right)\frac{{\partial \varphi_{\theta } }}{\partial \theta }\sin \beta + \,\frac{1}{R}N_{xx}^{T} \sin \beta - \frac{1}{R}N_{\theta \theta }^{T} \sin \beta = I_{0} \ddot{u}_{0} + I_{1} \ddot{\varphi }_{x} \end{aligned}$$

(21)

$$\begin{aligned} & \frac{1}{R}\left( {A_{12} + A_{66} } \right)\frac{{\partial^{2} u_{0} }}{\partial x\partial \theta } + \frac{1}{{R^{2} }}\left( {A_{22} + A_{66} } \right)\frac{{\partial u_{0} }}{\partial \theta }\sin \beta + A_{66} \frac{{\partial^{2} v_{0} }}{{\partial x^{2} }} + \,\frac{1}{{R^{2} }}A_{22} \frac{{\partial^{2} v_{0} }}{{\partial \theta^{2} }} + \frac{1}{{R^{2} }}KA_{44} \frac{{\partial w_{0} }}{\partial \theta }\cos \beta - \frac{1}{{R^{2} }}\left( {KA_{44} \cos^{2} \beta + A_{66} \sin^{2} \beta } \right)v_{0} + \,\frac{1}{R}A_{66} \frac{{\partial w_{0} }}{\partial \theta }\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \frac{1}{{R^{3} }}A_{22} \frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}\frac{{\partial w_{0} }}{\partial \theta } + \frac{1}{R}A_{66} \frac{{\partial v_{0} }}{\partial x}\sin \beta + \,\frac{1}{R}\left( {A_{12} + A_{66} } \right)\frac{{\partial^{2} w_{0} }}{\partial x\partial \theta }\frac{{\partial w_{0} }}{\partial x} + \frac{1}{{R^{2} }}A_{66} \frac{{\partial w_{0} }}{\partial \theta }\frac{{\partial w_{0} }}{\partial x}\sin \beta + \frac{1}{{R^{2} }}A_{22} \frac{{\partial w_{0} }}{\partial \theta }\cos \beta + \,\frac{1}{R}\left( {B_{12} + B_{66} } \right)\frac{{\partial^{2} \varphi_{x} }}{\partial x\partial \theta } + \frac{1}{{R^{2} }}\left( {B_{22} + B_{66} } \right)\frac{{\partial \varphi_{x} }}{\partial \theta }\sin \beta + \frac{1}{R}B_{66} \frac{{\partial \varphi_{\theta } }}{\partial x}\sin \beta + \,\frac{1}{{R^{2} }}B_{22} \frac{{\partial^{2} \varphi_{\theta } }}{{\partial \theta^{2} }} + \left( {\frac{1}{R}KA_{44} \cos \beta - \frac{1}{{R^{2} }}B_{66} \sin^{2} \beta } \right)\varphi_{\theta } = I_{0} \ddot{v}_{0} + I_{1} \ddot{\varphi }_{\theta } \end{aligned}$$

(22)

$$\begin{aligned} & \frac{2}{{R^{2} }}B_{66} \frac{{\partial^{2} w_{0} }}{\partial x\partial \theta }\frac{{\partial \varphi_{x} }}{\partial \theta } + \frac{1}{2R}A_{11} \left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{3} \sin \beta - \frac{1}{R}N_{\theta \theta }^{T} \cos \beta + \frac{1}{R}\left( {B_{11} + B_{22} } \right)\frac{{\partial \varphi_{x} }}{\partial x}\frac{{\partial w_{0} }}{\partial x} + \,A_{11} \frac{{\partial^{2} u_{0} }}{{\partial x^{2} }}\frac{{\partial w_{0} }}{\partial x} - \frac{1}{{R^{2} }}A_{66} \frac{{\partial v_{0} }}{\partial \theta }\frac{{\partial w_{0} }}{\partial x}\sin \beta - \frac{1}{{R^{3} }}\left( {A_{12} + A_{66} } \right)\frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}\frac{{\partial w_{0} }}{\partial x} + \,\frac{2}{{R^{2} }}\left( {A_{12} + 2A_{66} } \right)\frac{{\partial^{2} w_{0} }}{\partial x\partial \theta }\frac{{\partial w_{0} }}{\partial \theta }\frac{{\partial w_{0} }}{\partial x} + \frac{1}{R}\left( {B_{12} + B_{66} } \right)\frac{{\partial^{2} \varphi_{\theta } }}{\partial x\partial \theta }\frac{{\partial w_{0} }}{\partial x} + \frac{1}{{R^{2} }}A_{66} \frac{{\partial^{2} u_{0} }}{{\partial \theta^{2} }}\frac{{\partial w_{0} }}{\partial x} + \,\frac{1}{R}\left( {KA_{55} + N_{xx}^{T} } \right)\frac{{\partial w_{0} }}{\partial x}\sin \beta + \frac{3}{2}A_{11} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} + \frac{1}{{2R^{2} }}\left( {A_{12} + 2A_{66} } \right)\frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}\left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} + \,\frac{1}{2R}A_{12} \left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} \cos \beta + \frac{1}{R}\left( {A_{11} + A_{12} } \right)\frac{{\partial w_{0} }}{\partial x}\frac{{\partial u_{0} }}{\partial x}\sin \beta + \frac{1}{{R^{2} }}A_{12} \frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}\frac{{\partial u_{0} }}{\partial x} - A_{12} \frac{{\partial u_{0} }}{\partial x}\cos \beta + \,A_{11} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\frac{{\partial u_{0} }}{\partial x} + \frac{2}{R}A_{66} \frac{{\partial^{2} w_{0} }}{\partial x\partial \theta }\frac{{\partial v_{0} }}{\partial x} - \frac{1}{{R^{2} }}A_{66} \frac{{\partial w_{0} }}{\partial \theta }\frac{{\partial v_{0} }}{\partial x} + \frac{1}{R}A_{12} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}w_{0} \cos \beta + \,\frac{1}{{R^{3} }}A_{22} \frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}w_{0} \cos \beta - \frac{1}{{R^{2} }}A_{22} w_{0} \cos \beta + \frac{1}{R}B_{12} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\varphi_{x} \sin \beta + \frac{1}{{R^{3} }}B_{22} \frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}\varphi_{x} \sin \beta + \,\frac{1}{R}\left( {A_{12} + A_{66} } \right)\frac{{\partial^{2} v_{0} }}{\partial x\partial \theta }\frac{{\partial w_{0} }}{\partial x} + \left( {\frac{1}{R}KA_{55} - \frac{1}{{R^{2} }}B_{22} \cos \beta } \right)\varphi_{x} \sin \beta + \frac{1}{{R^{3} }}B_{66} \frac{{\partial w_{0} }}{\partial \theta }\varphi_{\theta } \sin^{2} \beta - \,\frac{2}{{R^{2} }}B_{66} \frac{{\partial^{2} w_{0} }}{\partial x\partial \theta }\varphi_{\theta } \sin \beta + \frac{1}{{R^{3} }}A_{22} \frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}u_{0} \sin \beta - \frac{1}{{R^{2} }}A_{22} u_{0} \sin \beta \cos \beta + \frac{1}{R}A_{12} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}u_{0} \sin \beta + \,B_{11} \frac{{\partial^{2} \varphi_{x} }}{{\partial x^{2} }}\frac{{\partial w_{0} }}{\partial x} - \frac{1}{{R^{2} }}B_{66} \frac{{\partial \varphi_{\theta } }}{\partial x}\frac{{\partial w_{0} }}{\partial x}\sin \beta + \frac{1}{{R^{3} }}\left( {B_{22} - B_{66} } \right)\frac{{\partial \varphi_{x} }}{\partial \theta }\frac{{\partial w_{0} }}{\partial \theta } + \frac{1}{{R^{3} }}A_{66} \frac{{\partial^{2} v_{0} }}{{\partial \theta^{2} }}\frac{{\partial w_{0} }}{\partial \theta } + \,\frac{1}{{R^{3} }}A_{66} \frac{{\partial w_{0} }}{\partial \theta }v_{0} \sin^{2} \beta - \frac{2}{{R^{2} }}A_{66} \frac{{\partial^{2} w_{0} }}{\partial x\partial \theta }v_{0} \sin \beta + \frac{1}{{R^{2} }}\left( {KA_{44} + N_{\theta \theta }^{T} } \right)\frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }} + \frac{1}{R}A_{66} \frac{{\partial^{2} v_{0} }}{{\partial x^{2} }}\frac{{\partial w_{0} }}{\partial \theta } + \,\left( {KA_{55} + N_{xx}^{T} } \right)\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \frac{1}{2R}\left( {A_{12} + 2A_{66} } \right)\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\left( {\frac{{\partial w_{0} }}{\partial \theta }} \right)^{2} + \frac{1}{R}B_{66} \frac{{\partial^{2} \varphi_{\theta } }}{{\partial x^{2} }}\frac{{\partial w_{0} }}{\partial \theta } + \,\frac{3}{2R4}A_{22} \frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}\left( {\frac{{\partial w_{0} }}{\partial \theta }} \right)^{2} + \frac{1}{R}A_{12} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\frac{{\partial v_{0} }}{\partial \theta } + \frac{1}{{R^{3} }}A_{22} \frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}\frac{{\partial v_{0} }}{\partial \theta } + KA_{55} \frac{{\partial \varphi_{x} }}{\partial x} - \,\frac{1}{{R^{2} }}\left( {KA_{44} + A_{22} } \right)\frac{{\partial v_{0} }}{\partial \theta }\cos \beta + B_{11} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\frac{{\partial \varphi_{x} }}{\partial x} - \frac{1}{R}B_{12} \frac{{\partial \varphi_{x} }}{\partial x}\cos \beta + \frac{1}{{R^{2} }}B_{12} \frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}\frac{{\partial \varphi_{x} }}{\partial x} + \,\frac{2}{R}B_{66} \frac{{\partial^{2} w_{0} }}{\partial x\partial \theta }\frac{{\partial \varphi_{\theta } }}{\partial x} - \frac{1}{{R^{2} }}B_{66} \frac{{\partial w_{0} }}{\partial \theta }\frac{{\partial \varphi_{\theta } }}{\partial x}\sin \beta + \frac{1}{{R^{3} }}\left( {A_{22} - A_{66} } \right)\frac{{\partial w_{0} }}{\partial \theta }\frac{{\partial u_{0} }}{\partial \theta }\sin \beta + \,\frac{1}{{R^{2} }}B_{66} \frac{{\partial^{2} \varphi_{x} }}{{\partial \theta^{2} }}\frac{{\partial w_{0} }}{\partial x} + \frac{1}{{R^{2} }}\left( {A_{12} + A_{66} } \right)\frac{{\partial^{2} u_{0} }}{\partial x\partial \theta }\frac{{\partial w_{0} }}{\partial \theta } + \frac{1}{{2R^{3} }}A_{22} \frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}\cos \beta + \frac{1}{{R^{3} }}B_{22} \frac{{\partial^{2} \varphi_{\theta } }}{{\partial \theta^{2} }}\frac{{\partial w_{0} }}{\partial \theta } + \,\frac{1}{{R^{2} }}\left( {B_{12} + B_{66} } \right)\frac{{\partial^{2} \varphi_{x} }}{\partial x\partial \theta }\frac{{\partial w_{0} }}{\partial \theta } + \frac{2}{{R^{2} }}A_{66} \frac{{\partial^{2} w_{0} }}{\partial x\partial \theta }\frac{{\partial u_{0} }}{\partial \theta } + P_{a} - \gamma \dot{w}_{0} = I_{0} \ddot{w}_{0} \end{aligned}$$

(23)

$$\begin{aligned} & B_{11} \frac{{\partial^{2} u_{0} }}{{\partial x^{2} }} + \frac{1}{{R^{2} }}B_{66} \frac{{\partial^{2} u_{0} }}{{\partial \theta^{2} }} + \frac{1}{R}B_{11} \frac{{\partial u_{0} }}{\partial x}\sin \beta - \frac{1}{{R^{2} }}B_{22} u_{0} \sin^{2} \beta + \frac{1}{R}\left( {B_{12} + B_{66} } \right)\frac{{\partial^{2} v_{0} }}{\partial x\partial \theta } - \,\frac{1}{{R^{2} }}\left( {B_{22} + B_{66} } \right)\frac{{\partial v_{0} }}{\partial \theta }\sin \beta + \frac{1}{2R}\left( {B_{11} - B_{12} } \right)\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\sin \beta - \frac{1}{{R^{2} }}B_{22} w_{0} \sin \beta \cos \beta + \,\frac{1}{R}B_{12} \frac{{\partial w_{0} }}{\partial x}\cos \beta + B_{11} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\frac{{\partial w_{0} }}{\partial x} + \frac{1}{{R^{2} }}B_{66} \frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}\frac{{\partial w_{0} }}{\partial x} - KA_{55} \frac{{\partial w_{0} }}{\partial x} + \frac{1}{{R^{2} }}D_{66} \frac{{\partial^{2} \varphi_{x} }}{{\partial \theta^{2} }} - \,\frac{1}{{2R^{2} }}\left( {B_{12} + B_{22} } \right)\frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}\sin \beta + \frac{1}{{R^{2} }}\left( {B_{12} + B_{66} } \right)\frac{{\partial^{2} w_{0} }}{\partial x\partial \theta }\frac{{\partial w_{0} }}{\partial \theta } - \left( {KA_{55} + \frac{1}{{R^{2} }}D_{22} } \right)\varphi_{x} + \,\frac{1}{R}\left( {D_{12} + D_{66} } \right)\frac{{\partial^{2} \varphi_{x} }}{\partial x\partial \theta } + \frac{1}{R}D_{11} \frac{{\partial \varphi_{x} }}{\partial x}\sin \beta + D_{11} \frac{{\partial^{2} \varphi_{x} }}{{\partial x^{2} }} - \frac{1}{R}M_{\theta \theta }^{T} \sin \beta - \,\frac{1}{{R^{2} }}\left( {D_{22} + D_{66} } \right)\frac{{\partial \varphi_{\theta } }}{\partial \theta }\sin \beta + \frac{1}{R}M_{xx}^{T} \sin \beta = I_{1} \ddot{u}_{0} + I_{2} \ddot{\varphi }_{x} \end{aligned}$$

(24)

$$\begin{aligned} & \frac{1}{R}\left( {B_{12} + B_{66} } \right)\frac{{\partial^{2} u_{0} }}{\partial x\partial \theta } + \frac{1}{{R^{2} }}\left( {B_{22} + B_{66} } \right)\frac{{\partial u_{0} }}{\partial \theta }\sin \beta + B_{66} \frac{{\partial^{2} v_{0} }}{{\partial x^{2} }} + \frac{1}{{R^{2} }}B_{22} \frac{{\partial^{2} v_{0} }}{{\partial \theta^{2} }} + \,\frac{1}{{R^{2} }}\left( {D_{22} + D_{66} } \right)\frac{{\partial \varphi_{\theta } }}{\partial \theta } + \left( {\frac{1}{R}KA_{44} \cos \beta - \frac{1}{{R^{2} }}B_{66} \sin^{2} \beta } \right)v_{0} + \,\frac{1}{{R^{2} }}B_{66} \frac{{\partial w_{0} }}{\partial x}\frac{{\partial w_{0} }}{\partial \theta }\sin \beta - \left( {KA_{44} + \frac{1}{{R^{2} }}D_{66} \sin^{2} \beta } \right)\varphi_{\theta } + \,\left( {\frac{1}{{R^{2} }}B_{22} \cos \beta - \frac{1}{R}KA_{44} } \right)\frac{{\partial w_{0} }}{\partial \theta } + \frac{1}{{R^{3} }}B_{22} \frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}\frac{{\partial w_{0} }}{\partial \theta } + \frac{1}{R}B_{66} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\frac{{\partial w_{0} }}{\partial \theta } + \,\frac{1}{{R^{2} }}D_{22} \frac{{\partial^{2} \varphi_{\theta } }}{{\partial \theta^{2} }} + \frac{1}{R}B_{66} \frac{{\partial v_{0} }}{\partial x}\sin \beta + \frac{1}{R}\left( {B_{12} + B_{66} } \right)\frac{{\partial^{2} w_{0} }}{\partial x\partial \theta }\frac{{\partial w_{0} }}{\partial x} + \,\frac{1}{R}\left( {D_{12} + D_{66} } \right)\frac{{\partial^{2} \varphi_{x} }}{\partial x\partial \theta } + D_{66} \frac{{\partial^{2} \varphi_{\theta } }}{{\partial x^{2} }} + \frac{1}{R}D_{66} \frac{{\partial \varphi_{\theta } }}{\partial x} = I_{1} \ddot{v}_{0} + I_{2} \ddot{\varphi }_{\theta } \end{aligned}$$

(25)