1 Introduction

Shallow shells are widely used as structural elements [1] in various fields of engineering, including aircraft and aerospace industries. Compared to plates, the membrane stresses, resulting from the curvature of the shell surface, contribute to better susceptibility to various types of static and dynamic loads including the case of a streamline flow of supersonic gas. Because of excessively high velocity, it can initiate the dynamic loss of stability in a thin-walled body known as panel flutter. The study of this hazardous phenomenon, leading to accumulation of fatigue damage with subsequent structural failure, has long been the focus of many researchers [2,3,4,5,6,7,8,9]. Using a variety of analytical, numerical-analytical, and numerical methods, they have studied the influence of various geometrical, physical and mechanical, structural, and force factors on the aeroelastic stability boundary of plates and shells made of isotropic, orthotropic, layered, composite, functional-gradient materials, as well as materials with piezoelectric properties. In particular, flutter of curvilinear panels in the framework of linear and nonlinear problem formulations has been studied in Refs. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64]. These studies use simple analytical expressions for the aerodynamic pressure, which are based on the law of plane sections [65,66,67]. Various modifications of formulas for linear and nonlinear formulations have been proposed as an effective tool both for direct determination of stability boundaries and for parametric analysis or solution of optimization problems for structures of different geometry. The validity of the quasi-steady piston theory, as well as the linearized potential flow theory used by most of the authors, has been demonstrated in a number of publications by way of comparison with the solutions obtained by computational fluid dynamic (CFD) methods. In Ref. [68], for Mach numbers greater than 1.6 the obtained results demonstrate close fit.

Following Ref. [2], we will distinguish between studies dealing with the supersonic gas flow along the curvature of the plate and across it. At the same time, it is to be noted that for a number of publications, in which the gas flow is considered at different angles of yaw, the proposed differentiation will be conditional. In view of the focus of our paper, such studies will not be cited. Some of them can be found in the review given in Ref. [69].

The problem of aeroelastic stability of an unbounded cylindrical panel, the curvature of which is perpendicular to the supersonic gas flow, is considered in Ref. [10]. Here, an analytical expression, determining the critical flow rate for a panel hinged along its generatrices, is obtained based on the Vlasov general linear theory of shallow shells and the formula for excess aerodynamic pressure proposed in 1947 by A.A. Il’yushin [66]. A similar problem for a panel of finite dimensions simply supported along all edges was solved in Refs. [11, 12]. Particularly in Ref. [11], the effect of panel curvature, structural and aerodynamic damping on the critical flutter velocities was evaluated using Reissner’s equations for shallow shells, quasi-steady piston theory, and Galerkin’s method. Similar theories and method of solution are used in paper [13], the purpose of which is to investigate the effect of boundary conditions on the natural frequencies and flutter characteristics of curvilinear panels. The obtained numerical results are used to make general recommendations for setting them at the edges of the plate to prevent the loss of stability. The integral equation technique is used in Ref. [14] to analyze isotropic and layered shallow shells described within the framework of Donnell thin shell theory. It has been demonstrated that the critical frequency and flow parameters increase as the shell rise increases. The Donnell shell theory is also used in Ref. [15] to study deformation of nonuniformly heated composite cylindrical panels in a supersonic gas flow. It has been demonstrated that nonuniform aerodynamic heating has incomparably greater effect on the static deformation than aerodynamic pressure. Several publications [16,17,18,19,20], in which the finite element method (FEM) was used to analyze shallow shells appeared in the literature practically at the same time. These works, in spite of different constitutive relations, aerodynamic theories and types of finite elements, have revealed the unique potentialities of this numerical method for the analysis of the influence of various factors on the flutter boundaries at different combinations of boundary conditions. A strict formulation of the aeroelasticity problem in the framework of the piston theory for a shallow shell arbitrarily oriented with respect to the flow velocity vector is given in Ref. [21]. Based on the concepts of the piston theory, a mathematical model of aeroelastic vibrations was constructed in Ref. [22], taking into account the shock wave. Using a shallow shell as an example, it has been shown that the piston theory is supplemented by a summand, which leads to a decrease in the critical flow velocity. The work [23] is devoted to computational aspects of a new method for solving the problem of panel flutter of curved panels, in which discretization of the biharmonic operator is based on the interpolation formula containing Chebyshev’s polynomials. The wave propagation method, combined with a FEM, is used in Ref. [24] to determine the flutter characteristics of multi-span long curved panels. Here, as in some other works [18, 19], aerodynamic damping is not taken into account. In Ref. [25], viscoelastic composite cylindrical panels are studied based on the zig-zag layer-wise shell theory using FEM. The aerodynamic pressure includes the Kumhar correction originally proposed in the analysis of shells of revolution. It has been show that for an accurate assessment of the aeroelastic characteristics, it is necessary to take into account structural damping even though it is insignificant. In the finite-element study  [26], the emphasis is placed on the effect of thermal stress, in-plane compressive and shear stresses on the critical aerodynamic pressure of laminated composite cylindrical panels under different boundary conditions. In Ref. [27], a commercial FE package is used to solve an optimization problem, the purpose of which is to provide the maximum value of the critical aerodynamic pressure for a set of design variables, which are the parameters of the laminated material. Numerical experiments revealed a number of differences in the response of flat and curved composite panels to aerodynamic loading.

The nonlinear formulation of the problem of flutter of a panel with a cross-stream curvature was first presented in Ref. [28], with the numerical results given only for a flat plate. The study of the influence of geometric nonlinearity on the amplitude-velocity relation in the case of cylindrical panel is presented in Ref. [29]. It has been shown that the dependence of the amplitude of nonlinear flutter oscillations on the value of the stream flow velocity can be of multivalued nature. Two-dimensional and three-dimensional simply supported and clamped curved panels are studied in Refs. [30, 31]. It has been found that plates with spanwise curvature are very sensitive to in-plane boundary support conditions. In this regard, it is recommended to investigate higher span-wise modes, in which the occurrence of instability is also possible. The finite difference method was used in Ref. [32] to obtain an improved solution to the problem of nonlinear vibrations of a cylindrical panel streamlined by a supersonic gas flow along the generatrix. The nonlinear flutter of shallow viscoelastic orthotropic shells was studied in Refs. [33, 34] using a numerical method, which is based on the quadrature formulas. The numerical study has revealed the destabilizing effect of viscoelastic properties of the panel material on the critical flutter velocity. The vibration characteristics and supersonic flutter of cylindrical laminated panels subjected to thermal loads are analyzed in Ref. [35] in the framework of a layer-wise theory using geometrically nonlinear finite elements. It is shown that dynamic properties are very sensitive to structural parameters (radius, shallowness angles, lamination type), so that at a certain combination of these parameters the supersonic flutter of panels can occur in very high circumferential modes. In Ref. [36], the nonlinear response of cross-stream curved two-bay panels is investigated. Based on this analysis, it has been inferred that the single panel modeling approach may not be appropriate safe for structural design and ensure fatigue-life estimation for supersonic flutter suppression.

From the analysis of publications devoted to the flutter of plates, for which the gas flow direction coincides only with their curvature, it is evident that studies carried out in the nonlinear formulation prevail. In some of them, including the pioneering works [37, 38], the solution is developed in a two-dimensional formulation, where the effect of curvature is modeled by an initial irregularity. Another peculiarity of this formulation is the consideration of static deflection due to static aerodynamic load. The corresponding refinement of the formula for aerodynamic pressure proposed by Dowel [30, 31] has been used in many studies. This mechanism significantly affects the flutter boundary due to pre-flutter deformation. A two-dimensional simply supported panel, modeled as a bent beam, is studied in Ref. [39]. The authors’ formulation is complicated by the fact that the supersonic gas flow is not considered as a continuous flow, but as a free-molecule flow, which affects the flutter boundary due to the effect of aerodynamic shear. The onset of flutter in two- and three-dimensional curved panels subjected simultaneously to aerodynamic and thermal loading is studied in Ref. [40]. It has been shown that the flutter dynamic behavior changes significantly when temperature effects are taken into account. In Ref. [41], the effect of thermal degradation of the elastic modulus and thermal expansion coefficient on the reduction of flutter boundary is evaluated for infinitely long two-dimensional curved panels. The modified local piston theory, the parameters of which are specified by applying the CFD technique, is used in Ref. [42]. A new computational model, which takes into account the span-wise variation of the plate deflection and a comparison of the obtained estimates with the experimental results for the clamped curved plate, is presented in Ref. [43]. It has been shown that there is an encouraging agreement between theory and experiment.

In a number of works [12, 44,45,46,47,48,49,50,51], the aeroelastic stability of double curvature panels has been studied in linear and nonlinear formulations. The influence of various parameters (temperature effects, variable thickness, radius-to-thickness ratio, reinforcement angles, etc.) on the flutter characteristics was considered. It has been shown that the critical flutter velocities for spherical and parabolic panels are exceeded by those of cylindrical ones (with cross-stream curvature) and depend on the ratio of stream-wise and cross-stream curvature.

With the advent of modern advanced materials [70,71,72,73,74] researchers received a strong impetus for incorporating them in structures interacting with supersonic gas flow with a view to improve their flutter characteristics. The finite element method for the analysis of cylindrical laminated panels made of shape memory alloy hybrid composite and subjected to aerodynamic-thermal loading was applied in Ref. [52]. The performed numerical simulation showed that such material is rather effective for increasing the stability boundaries under combined loading conditions. Supersonic panel flutter of piezolaminated cylindrical panels subject to thermal and piezoelectric loads is studied in Ref. [53] by the finite element method based on the multifield layer-wise theory. Numerical results demonstrate that active piezoelectric actuation can effectively increase the critical aerodynamic pressure of piezolaminated panels. The aeroelastic dynamic response of a composite cylindrical thin panel with piezoelectric patches perfectly bonded to its surfaces is studied in Ref. [54]. It is shown that significant increase of the aeroelastic stiffness in flutter can be achieved using of piezoelectric actuators. Eventually, this makes it possible to control the critical flow velocity, at which the flutter occurs. In Ref. [55], the study focuses on a three-layered sandwich curved panel with an adaptive electro-rheological fluid core layer, which is modeled by a first order isotropic Kelvin – Voigt viscoelastic material. Numerical examples demonstrate poor effectiveness of the applied control configuration in suppression of structural vibrations. In Ref. [56], the authors investigated the flutter characteristics of cylindrical sandwich panels made of a saturated functionally graded porous core and two homogeneous face sheets. The parameters associated with material porosity were analyzed. It has been shown that proper selection of these parameters allows increasing the critical velocities of stability loss. Vibration and flutter of the functionally graded porous cylindrical panels reinforced with graphene platelet under supersonic flow are studied in Ref. [57]. The parametric analysis performed in this work made it possible to establish a number of regularities determining the influence of pore and graphene platelets on the supersonic flutter characteristics. The nonlinear analysis of cylindrical panels made of functionally graded materials was carried out in Refs. [58,59,60]. Various parameters were analyzed including functionally graded material volume fraction index. Being properly selected, they can provide active control of the nonlinear flutter and critical velocity of FGM panels.

A number of publications have demonstrated that, apart from the use of modern materials, reinforcing the structure with ribs (stringers and/or stiffening rings) can also prevent the onset of flutter instability in the region of operational velocity range. In contrast to flat plates, the study of aeroelastic stability of stiffened shallow shells is extremely limited [61,62,63,64]. The pioneering finite-element work [61], which has long been a benchmark for other studies, is currently out of date and does not reflect the realities of modern computational technology. The number of three-dimensional degenerated shell elements used in this work does not ensure the asymptotic convergence of the solution. Nevertheless, in the course of calculations it was found that in order that stability should be increased, the stiffener must be located in the airflow direction. Its location perpendicular to the airflow leads to a decrease in the critical flutter velocity below the value obtained in the absence of stiffener. The opposite conclusion was obtained in Ref. [62]. Taking into account the stiffener’s base and setting a certain combination of the fiber orientation angle and stacking sequence, the authors achieved better stability indices compared to the case when the stiffener is located perpendicular to the airflow direction. A similar approach to stiffener modeling was used in Ref. [63], in which the aeroelastic stability of shape memory alloy hybrid composites cylindrical stiffened panel was analyzed. The analysis of heated to constant temperature shallow cylindrical shell with stringers is presented in Ref. [64]. In the above publications, the ribs are generally modeled as a one-dimensional beam. In the present work, we propose a more universal approach, in which both the elastic body itself and stiffening elements are considered within the framework of the linear theory of elasticity. This formulation makes it possible to abandon a number of assumptions used in various shell theories, simplifies the mating of ribs with the structure and eliminates restrictions on the thickness of the shallow shell. Moreover, the application of the finite element method for numerical implementation removes the restrictions on possible variants of kinematic boundary conditions imposed on the edges of the structure. All these refinements together with the mode-superposition technique and modern mathematical apparatus for determining eigenvalues make it possible to create an effective numerical tool. In this paper, it was used to perform a detailed study of the influence of stringers on the aeroelastic stability boundary of a cylindrical panel streamlined by a supersonic gas flow.

2 Governing equations

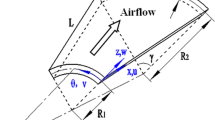
We consider a rectangular segment of a shallow cylindrical shell with length L, chord C and thickness h, which interacts with an external supersonic gas flow with velocity \(U_\infty \) along the generatrix (Fig. 1). The inner surface of the structure is stiffened with ribs, which are parallel to airflow (stringers). The convexity (rise) of the shell relative to the plane Oxy is characterized by the parameter H, which allows us to determine its radius R using expressions

Fig. 1
figure 1

Shallow shell stiffened with stringers

Full size image
$$\begin{aligned} R = \frac{H}{{1 - \cos \varphi }},\qquad 2\varphi = 4\arctan \left( {\frac{{2H}}{C}} \right) . \end{aligned}$$
(1)

The shallow shell together with the stiffening elements is a piecewise homogeneous body of volume V. Small strains \({\varvec{\varepsilon }}\) in this structure are determined using the relations of linear elasticity theory (2).

$$\begin{aligned}&{\varvec{\varepsilon }} = {\left\{ {{\varepsilon _x},{\varepsilon _y},{\varepsilon _z},2{\varepsilon _{xy}},2{\varepsilon _{yz}},2{\varepsilon _{xz}}} \right\} ^{\mathrm{{T}}}} \nonumber \\&\quad = {\left\{ {\frac{{\partial u}}{{\partial x}},\frac{{\partial v}}{{\partial y}},\frac{{\partial w}}{{\partial z}},\frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}},\frac{{\partial v}}{{\partial z}} + \frac{{\partial w}}{{\partial y}},\frac{{\partial u}}{{\partial z}} + \frac{{\partial w}}{{\partial x}}} \right\} ^{\mathrm{{T}}}}, \end{aligned}$$
(2)

where u, v and w are the components of displacement vector \({\mathbf{d}} = {\{ u,v,w\} ^{\mathrm{{T}}}}\) in the direction of x, y and z -axes of Cartesian coordinate system.

In practice, the shell and stringers are made of different materials, but in this study the entire structure is considered completely homogenous and, for simplicity, isotropic. In this case, the relationship between the stresses \({\varvec{\sigma }}\) and strains \({\varvec{\varepsilon }}\) is written in the matrix form as

$$\begin{aligned} {\varvec{\sigma }} = {\left\{ {{\sigma _x},{\sigma _y},{\sigma _z},{\sigma _{xy}},{\sigma _{yz}},{\sigma _{xz}}} \right\} ^{\mathrm{{T}}}} = {\mathbf{D}{\varvec{\varepsilon }}}, \end{aligned}$$
(3)

where \(\mathbf{D}\) is the matrix of elastic constants determined in a conventional manner.

The pressure exerted by the supersonic gas flow on the outer surface of the shell \(S_\sigma \) is calculated according to the quasi-steady first-order piston theory [30]

$$\begin{aligned} p= & {} - \left( {q\frac{{\partial w}}{{\partial x}} + {q_1}\frac{{\partial w}}{{\partial t}}} \right) , \\ q= & {} \frac{{{\rho _\infty }U_\infty ^2}}{\beta } = \frac{{\kappa {p_\infty }\mathrm{{\mathrm{M}}}_\infty ^2}}{\beta },\quad {q_1} = q\frac{{\mathrm{{M}}_\infty ^2 - 2}}{{{U_\infty }{\beta ^2}}},\quad \beta = \sqrt{\mathrm{{M}}_\infty ^2 - 1} .\nonumber \end{aligned}$$
(4)

Here: q is a modified dynamic pressure; \({\mathrm{{M}}_\infty } = {{{U_\infty }} \big / {{c_\infty }}}\) is the Mach number in gas; \(\rho _\infty \), \(p_\infty \) and \(c_\infty \) are density, static pressure and speed of sound in the unperturbed gas flow; \(\kappa \) is the adiabatic index; t is time.

A mathematical formulation of the problem on the dynamics of stiffened shallow shell is based on the variational principle of virtual displacements taking into account the work done by inertial forces and aerodynamic pressure of the external supersonic gas flow p. In the matrix form, it is written as follows

$$\begin{aligned} \int \limits _V {\delta {{\varvec{\varepsilon }} ^{\mathrm{{T}}}}{\mathbf{D}} {\varvec{\varepsilon }} dV} + \int \limits _V {\delta {{\mathbf{d}}^{\mathrm{{T}}}}\rho {\ddot{\mathbf{d}}}dV} - \int \limits _{{S_\sigma }} {\delta {{\mathbf{d}}^{\mathrm{{T}}}}{\mathbf{t}}dS} = 0, \end{aligned}$$
(5)

where \(\rho \) is density of the structure material, \({\mathbf{t}} = {\{ 0,0,p\} ^{\mathrm{{T}}}}\).

In this paper, we consider cylindrically curved panels with different variants of kinematic boundary conditions at the edges. The following abbreviations are used for their designation: F — free edge, S — simple support (\(u = w = 0\) or \(v = w = 0\)), C — rigid clamping (\(u = v = w = 0\)). All schemes are shown in Fig. 2.

Fig. 2
figure 2

Boundary conditions for shallow shell

Full size image

3 Numerical modeling

The problem is solved using the finite element method. The variational Eq. (5) taking into account relations (2), (3) and pressure representation (4) is transformed to a matrix form in a conventional manner

$$\begin{aligned}&{\mathbf{M} \ddot{\mathbf{d}}} + {\mathbf{C} \dot{\mathbf{d}}} + \left( {{\mathbf{K}} + {\mathbf{A}}} \right) {\mathbf{d}} = 0,\\&{\mathbf{M}} = \int \limits _V {{{\mathbf{N}}^{\mathrm{{T}}}}\rho {\mathbf{N}}dV}, \qquad {\mathbf{C}} = - \int \limits _{{S_\sigma }} {{q_1}{{{\bar{\mathbf{N}}}}^{\mathrm{{T}}}}{\bar{\mathbf{N}}}dS} ,\nonumber \\&{\mathbf{K}} = \int \limits _V {{{\mathbf{B}}^{\mathrm{{T}}}}{\mathbf{DB}}dV}, \qquad {\mathbf{A}} = - \int \limits _{{S_\sigma }} {q{{{{\bar{\mathbf{N}}}}}^{\mathrm{{T}}}}\frac{{\partial {\bar{\mathbf{N}}}}}{{\partial {\bar{x}}}}dS} .\nonumber \end{aligned}$$
(6)

Here: \(\mathbf{B}\) is the gradient matrix relating the strain vector to the vector of nodal displacements of the finite element; \(\mathbf{N}\) and \(\bar{\mathbf{N}}\) are the shape functions of the nodal displacement vector and its normal component. The typical matrices \(\mathbf{C}\) and \(\mathbf{A}\) of a separate finite element are calculated in the coordinates \(({\bar{x}},{\bar{y}},{\bar{z}})\) related to the lateral surface of the shallow shell \(S_\sigma \) and then converted to the global Cartesian coordinate system (x, y, z) using the matrix of direction cosines in a conventional manner [75].

Representing the perturbed motion of the structure as an exponent \({\mathbf{d}}({\mathbf{x}},t) = {\tilde{\mathbf{d}}}({\mathbf{x}})\exp (\mathrm{{i}}\lambda t)\), we obtain

$$\begin{aligned} \left( { - {\lambda ^2}{\mathbf{M}} + \mathrm{{i}}\lambda {\mathbf{C}} + {\mathbf{K}} + {\mathbf{A}}} \right) {\tilde{\mathbf{d}}} = 0, \end{aligned}$$
(7)

where \(\tilde{\mathbf{d}}\) is the coordinate functions, \(\lambda = \omega + \mathrm{{i}}\gamma \) is the characteristic index, \(\omega \) is the natural frequency of vibrations, \(\gamma \) is the value, characterizing damping of the system, \(\mathrm {i}\) is the imaginary unit.

The system of Eq. (7) is transformed to the generalized eigenvalue problem for asymmetric matrices of double size [76]

$$\begin{aligned} \left( {\left[ {\begin{array}{*{20}{c}} {{\mathbf {C}}}&{}{{\mathbf {K}} + {\mathbf {A}}}\\ { - {\mathbf {I}}}&{}0 \end{array}} \right] + {\mathrm {i}}\lambda \left[ {\begin{array}{*{20}{c}} { {\mathbf {M}}}&{}0\\ 0&{}{\mathbf {I}} \end{array}} \right] } \right) \left\{ {\begin{array}{*{20}{c}} {{\mathrm {i}}\lambda {\tilde{\mathbf {d}}}}\\ {{\tilde{\mathbf { d}}}} \end{array}} \right\} = 0, \end{aligned}$$
(8)

where \(\mathbf{I}\) is the unit matrix.

The computational efficiency of the algorithm is increased by performing expansion in terms of mode shapes of the structure in vacuum. For this purpose, from the solution of problem (9) in the absence of aerodynamic loading, we determine n natural frequencies \(\omega _j\) and vibration modes \(\varvec{\Phi }_j\), which satisfy the orthogonality condition (10)

$$\begin{aligned}&- {\omega ^2}{\mathbf{M}}{\varvec{\Phi }} + {\mathbf{K}}{\varvec{\Phi }} = {\mathbf{0}}, \end{aligned}$$
(9)
$$\begin{aligned}&\forall (i,j):\quad {\varvec{\Phi }}_i^{\mathrm{{T}}}{\mathbf{M}}{{\varvec{\Phi }}_j} = {\delta _{ij}},\quad {\varvec{\Phi }}_i^{\mathrm{{T}}}{\mathbf{K}}{{\varvec{\Phi }}_j} = \omega _i^2{\delta _{ij}}, \end{aligned}$$
(10)

where \(\delta _{ij}\) is the Kronecker symbol.

Using the representation \({\tilde{\mathbf{d}}} = {\varvec{\Phi }} \mathbf{u}\), where \(\varvec{\Phi }\) is a matrix containing n mode shapes (column-vectors), and \(\mathbf{u}\) is the modal coordinates, and condition (10), we obtain instead of Eq. (7) the following equation:

$$\begin{aligned} \left( { - {\lambda ^2}{\mathbf{I}} + \mathrm{{i}}\lambda {\tilde{\mathbf{C}}} + {\varvec{\Omega }} + {\tilde{\mathbf{A}}}} \right) {\mathbf{u}} = 0, \end{aligned}$$
(11)

where \({\tilde{\mathbf{C}}} = {{\varvec{\Phi }}^{\mathrm{{T}}}}{\mathbf{C}}{\varvec{\Phi }} \), \({\tilde{\mathbf{A}}} = {{\varvec{\Phi }}^{\mathrm{{T}}}}{\mathbf{A}}{\varvec{\Phi }} \), and \(\varvec{\Omega }\) is a diagonal matrix, whose elements satisfy the condition \({\Omega _{jj}} = \omega _j^2\).

Thus, instead of solving the generalized eigenvalue problem (8) containing full-size sparse matrices \(\mathbf{K}\), \(\mathbf{M}\), \(\mathbf{C}\), \(\mathbf{A}\) and \(\mathbf{I}\), we solve the system of Eq. (12) with matrices of dimension \(n \times n\)

$$\begin{aligned} \left( {\left[ {\begin{array}{*{20}{c}} {\tilde{\mathbf { C}}}&{}{{\mathbf {\Omega }} + {\tilde{\mathbf {A}}}}\\ { - {\mathbf {I}}}&{}0 \end{array}} \right] + {\mathrm {i}}\lambda \left[ {\begin{array}{*{20}{c}} {\mathbf {I}}&{}0\\ 0&{}{{\mathbf {I}}} \end{array}} \right] } \right) \left\{ {\begin{array}{*{20}{c}} {{\mathrm {i}}\lambda {\mathbf {u}}}\\ {\mathbf {u}} \end{array}} \right\} = 0. \end{aligned}$$
(12)

The numerical algorithm is implemented in MATLAB software using the ANSYS package capabilities for finite-element meshing. The global matrices including the integral of the aerodynamic pressure p over the surface \(S_\sigma \) (\(\mathbf{C}\), \(\mathbf{A}\) and \(\tilde{\mathbf{C}}\), \(\tilde{\mathbf{A}}\)) are calculated only once for \(q = 1\). In the course of solving the sequence of modal problems (8) or (12), they are multiplied by the value of the varying parameter q to find the critical flutter velocity. Complex eigenvalues are calculated with the algorithm, which is based on the implicitly restarted Arnoldi method [77].

4 Verification of the numerical algorithm

4.1 Aeroelastic stability of unstiffened flat plate

The obtained solution of the aeroelastic stability problem was verified through a comparison of the results with the known numerical [78,79,80,81] and analytical [3] solutions. The calculated values of the critical dynamic pressure and the related flutter frequencies are given in Table 1 for square plate with SSSS and CCCC boundary conditions (Fig. 2). Here and below, numerical calculations were performed with the following parameters, unless otherwise stated: \(C = L = 0.24\) m, \(L/h = 120\), elasticity modulus \(E = 69\) GPa, Poisson’s ratio \(\nu = 0.3\), \(\rho = 2700\) kg/m\(^3\). The air flow has the following characteristics: \({\mathrm{{M}}_\infty } = 3\), \(\kappa = 1.4\), \({c_\infty } = 299.5\) m/s. In this example, a comparison was made on the assumption that the aerodynamic damping is absent (the second term in (4) is equal to zero). The obtained results are represented in terms of the following dimensionless quantities: eigenvalue \(\Lambda \) and dynamic pressure Q

$$\begin{aligned} \Lambda = {\Lambda _{{\mathrm{Re}} }} + \mathrm{{i}}{\Lambda _{{\mathrm{Im}} }} = \lambda \frac{{\rho h{L^4}}}{D}, \qquad Q = q\frac{{{L^3}}}{D}, \qquad D = \frac{{E{h^3}}}{{12\left( {1 - {\nu ^2}} \right) }}. \end{aligned}$$
(13)
Table 1 Comparison of critical dynamic pressure \(Q_{\mathrm{{cr}}}\) and flutter frequencies \(\Lambda _{{\mathrm{Re}}}^2\)
Full size table

As it follows from the tabulated data, the results obtained using the developed finite-element algorithm agree well with the previously published data.

4.2 Aeroelastic stability of unstiffened shallow shell

Figure 3 shows the variation of the critical dynamic pressure \(Q_{\mathrm{{cr}}}\) of a shallow isotropic cylindrical shell depending on the curvature ratio H/h. The solid line is used for comparison with the finite-element solution [18] in the absence of aerodynamic damping (\(q_1 = 0\)). In this case, the critical flutter pressure can reduce to almost zero when the flutter frequency shifts to higher frequency range. The obtained curves duplicate data from [18], but also contain new “dips”. Their presence can be explained by the insufficient accuracy of the calculations made in [18]. When using large increments of pressure q, rise H, or a small number of required eigenvalues, these areas can be easily omitted.

Fig. 3
figure 3

Flutter dynamic pressure \(Q_{\mathrm{{cr}}}\) versus shell rise: a — CCCC, b — SSSS

Full size image

Taking into account the aerodynamic damping or the correction induced by panel curvature leads to finite values of \(Q_{\mathrm{{cr}}}\) and smoother dependencies. This is clearly demonstrated in Fig. 3 by a dashed line, which was constructed using expression (14) [61] instead of relation (4)

$$\begin{aligned} p = - \left( {q\frac{{\partial w}}{{\partial {\bar{x}}}} + g\frac{{\partial w}}{{\partial t}}} \right) , \quad g \approx \sqrt{\frac{\mu }{{{\mathrm{{M}}_\infty }}}} \sqrt{q\frac{{\rho h}}{L}} , \end{aligned}$$
(14)

where \(\mu = {{{\rho _\infty }L} \big / {(\rho h)}}\) is the mass density ratio of air to the shell (\({\mathrm{{M}}_\infty } = 3\), \({{\mu } \big / {{\mathrm{{M}}_\infty }}} = 0.005\)).

For comparison, we present the results obtained by calculating the aerodynamic pressure using Eq. (4). In this case, the values of critical dynamic pressure \(Q_{\mathrm{{cr}}}\) increase, and the dip in the vicinity of \(H/h = 5\) in Fig. 3a is absent.

4.3 Natural vibrations of rectangular stiffened plate

In the last group of examples, demonstrating the validity of the obtained solution, consideration is given to natural vibrations of a simply supported (SSSS) isotropic plate with a rectangular stiffener of thickness \(d_h\) and width \(d_c\), which is located in the center of the side C (\(C = 0.6096\) m, \(L = 0.4046\) m, \(C/h = 96\), \(E = 211\) GPa, \(\nu = 0.3\), \(\rho = 7842.72\) kg/m\(^3\), \(d_c = 12.7\times 10^{-3}\) m). A comparison with the results of other authors is given in Table 2. In Ref. [82], a fully conforming rectangular finite element with twelve degrees of freedom is used to model the plate, and the stringer is modeled in a simplified manner using a beam model. In Ref. [83], a three-dimensional degenerated shell element based on the basic concept of Ahmad [84] is used to model both the plate and the stringer. Bending of the stiffening rib in the plane tangent to the shell is ignored. In spite of the assumptions used for numerical modeling, all results mentioned above agree to an accuracy of 3%.

Table 2 Natural frequency \(\omega \) (Hz) of simply supported rectangular stiffened plate
Full size table

4.4 Reduced order model

The accuracy of the solution of problem (12), which was obtained using the reduced order model, essentially depends on the number of mode shapes of the structure in vacuum retained in the expansion. The convergence of the solution is demonstrated in Table 3 using, as an example, the unstiffened shallow shell (SSSS, \(H/h = 5\)) considered in Sect. 4.2. The critical flutter pressure \(Q_{\mathrm{{cr}}}\) and the real \(\Lambda _{\mathrm{{Re}}}\) and imaginary \(\Lambda _{\mathrm{{Im}}}\) parts of the complex eigenvalue \(\Lambda \), corresponding to the mode, in which the stability loss occurs, are compared with the results of calculations made by applying a full model (8). The dimensionless values are calculated by expressions (15).

$$\begin{aligned} \Lambda = {\Lambda _{{\mathrm{Re}} }} + \mathrm{{i}}{\Lambda _{{\mathrm{Im}}}} = \lambda {L^2}\sqrt{\frac{{\rho h}}{D}} , \quad Q = q\frac{{{L^3}}}{D}. \end{aligned}$$
(15)

From the data, presented, it is clearly seen that to determine the real part of the eigenvalue \(\Lambda _{\mathrm{{Re}}}\) (frequency of vibrations) with relative accuracy \(\bigtriangleup < 1\)%, one can use a much smaller number n of retained mode shapes than that used for its imaginary part \(\Lambda _{\mathrm{{Im}}}\). That is why, the critical pressure value \(Q_{\mathrm{{cr}}}\) depends to a greater extent on the accuracy of \(\Lambda _{\mathrm{{Im}}}\) calculation.

Table 3 Convergence of reduced order model for unstiffened shallow shell (SSSS, \(H/h~=~5\))
Full size table

The variation of eigenvalues as a function of the dynamic pressure of the supersonic gas flow Q is presented in Fig. 4. The results obtained with the reduced order model at \(n = 100\) are denoted by symbols. This number of mode shapes is quite sufficient to reliably describe the behavior of complex eigenvalues. Nevertheless, in the numerical examples that follow, their increased number (\(n = 150\)) will be used.

Figure 4 shows that the loss of stability is realized in the form of a coupled flutter. The imaginary parts of eigenvalues corresponding to modes \(\omega _6\) and \(\omega _7\), grow linearly with increasing dynamic pressure Q. In this case, the vibration modes undergo only a slight change, which is manifested as the movement of the region of maximal values of normal displacements w along the flow direction (Fig. 5). At \(Q \approx 1850\), the real parts of these modes merge and the imaginary ones split into two branches. The shapes of vibration modes \(\omega _6\) and \(\omega _7\) become similar. They are maintained until the onset of stability loss at \(Q \approx 2302\), when the imaginary part of one of the modes becomes negative and remains unchanged with a further increase in Q.

Fig. 4
figure 4

The dependence of the real and imaginary parts of eigenvalues \(\Lambda \) on the dynamic pressure Q (lines — reduced order model, symbols — full model): a — SSSS, \(H/h = 5\), without stringers; b — CCFF, \(H/h = 5\), five stringers

Full size image
Fig. 5
figure 5

Natural mode shapes (top view) of shallow shell (SSSS, \(H/h = 5\))

Full size image

5 Numerical results

In this section, we study the aeroelastic stability of shallow cylindrical shells with different curvature ratios with a focus on the influence of kinematic boundary conditions at the edges of the structure and its stiffening with stringers. The parameters specified in Sect. 4.1 were used in the calculations. The pressure of supersonic gas flow was calculated by formula (4). The dimensionless quantities were determined by expressions (15).

5.1 Influence of curvative ratio

It has been known (see, for example, Refs. [3, 30]) that stability of a shallow shell streamlined by a supersonic gas flow along the generatrix increases with increasing curvature ratio. Figure 6a shows the dependences, which supplement the known results with other combinations of boundary conditions and a wider range of variation of H/h. As is evident from the data presented, the monotonic increase in the critical flutter pressure \(Q_{\mathrm{{cr}}}\) is valid only for the SSSS and CCFF variants of support. In the other examined cases, there are regions of local reduction of the critical parameter caused by a change in the type of stability loss.

Another important characteristic of this class of problems is the flutter frequency \(\Lambda _F\). The corresponding dependences are shown in Fig. 6b. They all tend to grow monotonically with increasing curvature ratio. Some fluctuations around the straight trend line are observed in the case of CCCC and CFCC boundary conditions (Fig. 6b). For the other variants of support (SSSS and CCFF), the above dependences qualitatively duplicate the curves of stability loss given in Fig. 6a.

A change in the curvature ratio is accompanied by an increase in the volume of the shallow shell. In the examined cases, this value for \(H/h = 10\) is 1.8% with respect to a plate of similar dimensions. In this case, the stability of the structure increases many times. In particular, the value of critical pressure increases by a factor of 10.3, 5.9, 7.2, and 2.9 for the SSSS, CCCC, CFCC, and CCFF boundary conditions, respectively. The insignificant growth of pressure for the last combination of boundary conditions is obviously due to the absence of membrane stresses at the free edges of the panel.

Fig. 6
figure 6

Effect of curvature ratio H/h on the critical dynamic pressure \(Q_{\mathrm{{cr}}}\) (a) and flutter frequency \(\Lambda _{F}\) (b) for different boundary conditions

Full size image

5.2 Shallow shells with stringers

The aeroelastic stability boundary can be influenced not only by changing the curvature of a shallow shell. Another contributing factor is the stiffening of its inner surface with ribs. Taking into account the results of Ref. [61], we will restrict ourselves only to stiffening ribs located along the gas flow direction (stringers). In the examples considered below, we analyze three variants of a symmetrical arrangement of rectangular stringers with the following geometric dimensions: \(d_c = L/100\) and \(d_h = 1.5h\), (Fig. 7). Their efficiency is characterized by the ratio of \(\Psi = {{Q_{\mathrm{{cr}}}^{\mathrm{{str}}}} \big / {{Q_{\mathrm{{cr}}}}}}\), where \(Q_{\mathrm{{cr}}}^{\mathrm{{str}}}\) and \({Q_{\mathrm{{cr}}}}\) are the critical flutter pressures obtained in the presence and in the absence of stringers.

The presence of stringers affects the flutter vibration mode of the shallow shell. Here we are talking not about a change in the mode of the coupled flutter, but about small qualitative changes in the shape of vibration mode itself, which are caused by the presence of additional elastic elements on the inner surface of the structure. From Fig. 8, it is evident that the greatest effect occurs when a single stringer is used. With increase in their number the difference is practically unnoticeable, at least for given geometric parameters. Note that at the CCFF boundary conditions the flutter mode changes for variants of shell with three and five stringers.

Fig. 7
figure 7

Location of stringers

Full size image
Fig. 8
figure 8

Flutter mode shapes of shallow shells (top view) with various number of stringers (\(H/h = 5\))

Full size image

Figure 9 shows changes in the critical pressure depending on the H/h ratio for shallow shells with different variants of shell support at the edges. The number of symmetrically arranged stringers is shown in figures by numbers (Fig. 7). In most of the cases considered, increasing the stiffness of the structure by stringers leads to increase of stability. The results show that the use of one stringer has no desired effect. This is due to a slight increase in the critical pressure and the existence of curvature ratios, at which the stiffened shells with SSSS and CFCC boundary conditions are less stable than the unstiffened ones (\(\Psi < 1\)). A characteristic feature of the above dependences, except for the CCFF variant, is their non-monotonic character and the presence of a range of the H/h ratios, at which the number of stringers has no significant effect on the stability of the shallow shell: \(H/h \approx 4\) for CCCC, \(H/h \in (2; 3)\) for SSSS, and \(H/h \in (3; 4)\) for CFCC. The case that needs to be mentioned separately is the shallow shell, in which the edges parallel to the flow are not fixed (Fig. 2, CCFF). Two conclusions follow from the analysis of Fig. 9. First, at \(H/h > 2.5\) it is impossible to influence the flutter boundary by means of one stringer (\(\Psi \approx 1\)). When it is located at the center of the shell (Fig. 7), it falls on the nodal line (Fig. 8). Second, for some combinations of boundary conditions, the supported flat plates are more stable than the shallow shells (the curves only decrease with increasing curvature ratio). It is reasonable to assume that the stringer location cannot be universal for different H/h ratios and it should be selected from the condition of maximum value of \(\Psi \). The relevant discussion is given in the next section. The evolution of eigenvalues as a function of the dynamic pressure of the supersonic gas flow Q is presented at Fig. 4b for CCFF shallow shell with five stringers. The presented data demonstrate the complex postcritical behavior of the system caused by the interaction between the modes. In the region of a dense frequency spectrum (\(Q \approx 1600\)), the imaginary parts \(\gamma _1\) and \(\gamma _4\) are close to each other, but do not merge together. This feature is not unique to the considered case. It can be observed with other parameters of the system; therefore, it is presented here as an illustrative example.

Fig. 9
figure 9

Growth of flutter dynamic pressure of shallow shell \(\Psi \) with different number of stringers

Full size image

5.3 Optimal location of stringers

In the examples presented above, the stringer location was fixed and determined by the angle \(\alpha \), as shown in Fig. 7. In order to increase the stability boundary as much as possible, its choice should be based on the solution of the optimization problem

$$\begin{aligned} \Psi \left( \alpha \right) \rightarrow \max ,\quad \alpha \in [{\alpha _{\min }};{\alpha _{\max }}], \end{aligned}$$
(16)

where \({\alpha _{\min }} = {{2{d_c}} \big / R}\) and \({\alpha _{\max }} = \varphi - {\alpha _{\min }}\) define the shift from the center and the edge of the shell, which is equal to the stringer width in the circumferential direction.

A variation of the objective function with the ratio \(\alpha /\varphi \) is shown in Fig. 10 for a shallow shell with three stringers. The flat plate (\(H/h = 0.025\)) is compared with two curved panels (\(H/h = 5\) and \(H/h = 10\)) for different variants of support. The results presented show the nonmonotonic behavior of the function \(\Psi (\alpha /\varphi )\) obtained for flat plates, with a pronounced extremum on the interval \([\alpha _{\mathrm{{min}}}; \alpha _{\mathrm{{max}}}]\). The exception is the CCFF boundary conditions. In this case, the maximum increase in the critical flutter pressure is achieved when stringers are located along the unfixed edges of the structure. The analysis of the results leads to the conclusion that the previously used value \(\alpha /\varphi = 0.5\) (results shown in Fig. 9) is not optimal. The same conclusion is true for other variants of support. The optimal values of \(\alpha /\varphi \) calculated for \(H/h = 5\) and \(H/h = 10\) differ insignificantly and lie in the range 0.3–0.4 of the ratio \(\alpha /\varphi \).

Fig. 10
figure 10

Growth of flutter dynamic pressure of stiffened shallow shell \(\Psi \) with three stringers depend on the angle \(\alpha \): \(\bullet \) — \(H/h = 0.025\), — \(H/h = 5\), \(\circ \) — \(H/h = 10\)

Full size image

6 Conclusion

In this paper, the aeroelastic stability of a shallow cylindrical shell with cross-stream curvature flow stiffened with ribs oriented in the direction of the gas flow has been analyzed in the framework of a three-dimensional formulation, using the finite element method and mode-superposition technique. The series of calculations allowed us to formulate the following conclusions:

—:

An increase in the convexity (rise) of the shallow shell results in an increase in the critical flutter pressure. The character of its behavior depends on the boundary conditions at the edges of the structure and can be both monotonic (SSSS and CCFF) and involve areas of local decrease (SSSS and CFCC).

—:

The presence of stringers on the inner surface leads, in general, to increase of stability. However, there are curvature ratios, at which the stiffened shells with one stringer are less stable than unstiffened. For example, at \(H/h = \left[ 2.1; 2.2\right] \) for SSSS boundary conditions and \(H/h = \left[ 4.7; 6.1\right] \) for CFCC.

—:

There is a range of H/h ratios, in which the number of stringers has no significant effect on the stability of the shallow shell. Its specific values depend on the boundary conditions at the edges of the structure.

—:

Stringer location is not universal for different H/h ratios. Its selection based on the solution of optimization problem makes it possible to achieve more than double the critical flutter pressure.

The results presented in this article have clearly demonstrated that the boundary of aeroelastic stability of a shallow shell can be controlled over wide a range by selecting an appropriate curvature ratio and location of stiffened ribs (stringers).