1 Introduction

There are many challenges in the oil and gas industry; drilling is one of them. The drill string dynamics is complex, and depends on many elements, such as well trajectory, size and geometry of the well, properties of the rock formation being drilled, drilling mud, drilling rig equipment (mud pumps, hoisting system and top drive), drill bit, and bottom hole assembly (BHA) components. Another challenge is that industry is facing certain obstacles in improving the drilling efficiency in the pre-salt reservoirs offshore Brazil. These include, amongst others, limited or low-quality data measurements, and non-systematic practices for controlling the operating parameters. The end result is sub-optimal control of the operating parameters (rotary speed, weight-on-bit, and flow), which can directly affect the rate of penetration (ROP).

Vibration is a problem that is constantly present in the drilling operation. There are three important vibrations in a drill string system: (1) axial, (2) lateral and (3) torsional. One of the most recurrent and destructive forms of vibration is the torsional one, where, in its severe state, is known as stick-slip. It can expose the BHA components, rotary steerable systems, measure while drilling and logging while drilling equipments (MWD/LWD), drill collars and drill pipes to catastrophic failures that can lead to non-productive time (NPT), loss of equipment at the bottom of the bore hole (called LIH—lost in hole), sometimes even leading to the loss of an entire well section. Therefore, managing the dynamics of the drill string through analysis and modeling would be a valuable step in order to avoid the negative impacts on drilling performance.

During drilling, downhole vibration and loading can cause severe damage to drilling tools, including bits, drive systems, and logging/measurement while drilling (L/MWD) tools. In the oil and gas industry, tremendous efforts have been made to measure, evaluate, and mitigate downhole vibration. Traditionally, downhole vibration can be qualitatively and indirectively evaluated by tool wear, dull conditions, and shock and vibration on the rig floor. MWD tools provide real-time and recorded data and help understand some downhole dynamics. Another way to understand the downhole vibration is through drillstring modeling. Field dynamics recording and drilling system modeling can work hand in hand to understand downhole vibration [28].

There are several ways to model the nonlinear dynamics of a drill string. Christoforou and Yigit [1] use a one-mode approximation to analyze the problem. Huang [26] uses a Finite Element Model using beam elements coupled with a complex bit/rock interaction based on bit design and actual lab measurements of singular cutter/rock interaction to provide the dynamic response of a drilling system. Khulief and Al-Naser [2] and Ritto et al. [3] use a beam model with the finite element method. Pabon et al. proposes a finite rigid body (FRB) approach in order to understand transient dynamics of a drilling system. Aguiar et al. [4] use a lumped parameter system, Richard et al. (2007) [7] use a two degrees of freedom system, while Tucker and Wang [8] use the Cosserat theory. In all of these models there is coupling among the types of vibrations (axial, lateral, torsional).

The present paper is interested in torsional instabilities of a drill string in a vertical well. In its most drastic form, the bit comes to a standstill while the top end rotates with a constant rotary speed, increasing the torque in the drill string, until the bit suddenly comes loose again. There are some works that have investigated the torsional stability and stick-slip vibrations of a drill string [9–14]. Others, have been devoted to control stick-slip oscillations [15–18]. There are few works with a experimental setup [19, 21, 22].

In all of the above cited papers, no field data are taken into account. The present paper has two specific contributions. First, field data (with frequency rate of 50 Hz) are used to partially validate a numerical model (simple lumped parameter model for torsional vibration). For this purpose, the bit-rock interaction model must be identified. Secondly, the torsional stability is investigated through a stability map, with controlled variables: the top speed and the weight on bit. The results obtained with the proposed curve for the bit rock-interaction model (torque-on-bit vs. bit speed) is compared with the results obtained with a commonly used curve used in the literature [1, 23, 24].

The downhole information used in this paper was acquired using a downhole mechanics measurement unit capable of providing both real-time measurement through mud telemetry and continuously recorded high-frequency data throughout the run. The sub, installed at the BHA above the bit, contains a suite of 19 sensors sampled at 10,000 Hz and downsampled and filtered prior to recording at 50 Hz. Following is a list of 50 Hz data recorded in this sub: triaxial accelerations; gyro rpm; magnetometer rpm; axial loading (DWOB); torque (DTOR); bending moment [28].

In [4], the same modeling approach is used to model the lateral vibrations of the drill string. Experimental data based on laboratory tests (not field data) is used to validate the model. Lateral accelerations at the bit and at the BHA are measured during laboratory drilling tests. By comparing both time and frequency domain responses of the experimental data and the model it is shown that such approach (lumped parameters) is validated for the available data.

The organization of the present paper is the following. In Sect. 2 the numerical model is presented. In Sect. 3 the results are analyzed, including identification of the bit-rock interaction model, the validation of the lumped model, and torsional stability analysis. Finally, Sect. 4 draws the concluding remarks.

2 Drill string torsional dynamical model

This section discusses the development of the model, which includes the top drive, the drill string torsional dynamics and the bit/rock interaction. The aim is to find the appropriate scale and level of detail for the modeling, in order to strike a balance between fast execution (needed for real-time operation) and accurate system description. The idea is to create a map of the modules, with inputs/outputs, to make it modular, so that different models can be plugged in/out [4]. All models implemented in this Matlab/Simulink framework are dynamic, in order to capture the transient behavior of the system.

For the purposes of this article, the work will focus on vertical wells, drilled with PDC bits, using rotary drilling: with top drive rotation (no turbine/motor), and focus on the torsional dynamics of the drill string.

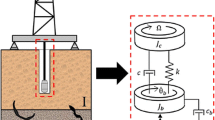
The drill string is modeled taking into consideration its torsional dynamics only. The drill string is discretized using lumped mass-spring-damper systems (each node has 1 degree-of-freedom) [20]. The model divides the BHA and drill pipes into lumped parameters system, see Fig. 1, leading to a second order differential equation system shown in Eq. (1):

$$\begin{aligned} {\mathbf {M}}\ddot{\mathbf {q}}(t)+{\mathbf {C}}\dot{\mathbf {q}}(t)+{\mathbf {K}}{\mathbf {q}}(t)={\mathbf {F}}({\mathbf {q}},\dot{\mathbf {q}},t) \end{aligned}$$
(1)
Fig. 1
figure 1

Drill string model scheme

Full size image

where \({\mathbf {M}}\), \({\mathbf {C}}\) and \({\mathbf {K}}\) are matrices (inertia, proportional damping and stiffness, respectively). The vector \({\mathbf {q}}\) represents the system variables (rotational angles) and the vector \({\mathbf {F}}\) represents the external generalized forces. The mass and stiffness are assemble as

$$\begin{aligned} {\mathbf {M}}=\left[ \begin{array}{ccc}J_{elem1} & 0 & \ldots \\ 0 & J_{elem2} & \ldots \\ \ldots & \ldots & \ldots \end{array}\right] \quad {\mathbf {K}}=\left[ \begin{array}{ccc}K_{elem1} & -K_{elem1} & \ldots \\ -K_{elem1} & (K_{elem1}+K_{elem2}) & \ldots \\ \ldots & \ldots & \ldots \end{array}\right] \end{aligned}$$
(2)

The dimension of matrices and vectors will depend on how many degrees of freedom the system is discretized (user input). The drill string torsional dynamics is coupled to the bit/rock interaction.

The system is discretized using inertia-spring elements. For the string parameters, the element mass is obtained through the BHA and drill pipe geometry and specific mass. The moment of inertia is defined as:

$$\begin{aligned} J_{elem} = \frac{\rho }{L}\frac{\pi }{32}(D_o^{4} - D_i^{4}) \end{aligned}$$
(3)

where \(\rho\) is the element specific mass, L is the element length, \(D_o\) and \(D_i\) are the element outer and inner diameters, respectively. The torsional stiffness of each element is defined as:

$$\begin{aligned} K_{elem} = \frac{G}{L}\frac{\pi }{32}(D_o^{4}-D_i^{4}) \end{aligned}$$
(4)

where G is the shear modulus. A computational routine, based on the user entry discretization (number of elements each BHA tool and drill pipe segments are discretized), was developed in order to automatically generated the mass, inertia and stiffness of each element and assemble the global mass and stiffness matrices, where the mass matrix is a diagonal matrix and the stiffness and damping matrices are tridiagonal [20].

3 Numerical results

The parameters of the system analyzed are the following: \(hole depth = 5200\) m, \(\rho =7800\,\hbox {kg/m}^3\), \(E=220\,\hbox {GPa}\), \(\nu =0.29\), \(G=E/(2(1+\nu ))\), \(J_{top drive}=1000\,\hbox {kg m}^2\). Other parameters are summarized in Table 1. The damping ratios related to the natural modes are about 2.5%. The first five natural frequencies of the system are [0.00, 0.17, 1.11, 3.13, 6.02] Hz. The first natural frequency is associated with the rigid body torsional mode. The equation of motion, Eq. (1), is integrated numerically using the Runge–Kutta scheme.

Table 1 Summary of drill string geometry
Full size table

3.1 Bit-rock interaction identification

Figure 2 shows the field data, which has a frequency rate of 50 Hz. It is very rare to have this type of data available due to the cost involved in obtaining them. We used a drilling mechanics module tool (DMM) for downhole measurements. The tool is located in the BHA, above the bit. Because the axial and lateral vibration during the run where we obtained the high frequency measurements present low operational risk (low RMS amplitude and peaks), the article is focused on the validation of the torsional dynamics model.

Two samples are going to be considered, sample 1 is the response without a full developed stick-slip, and sample 2 is the response with a full developed stick-slip. The nominal rotational speed for both data samples is 120 RPM (12.57 rad/s), and the mean weight-on-bit is about 191 kN (43 klbf) for data sample 1 and about 245 kN (55 klbf) for data sample 2.

Fig. 2
figure 2

Field data available (sample rate 50 Hz). a rotational speed of the bit, and b torque-on-bit (klbf.ft) versus rotational speed of the bit

Full size image

Sample 2 is used to identify the bit-rock interaction model, which is defined by a nonlinear map \(\dot{\theta }_{bit} \mapsto TOB(\dot{\theta }_{bit})\). For this purpose, first the mean value of the torque is obtained at \(DRPM=0\) RPM, which is 9.9 kN m. Then the mean value of the torque is obtained at \(DRPM=3.5\) RPM, which corresponds to the peak of the torque curve, 12.9 kN m. Then, from \(DRPM=8\) RPM on, a polynomial approximation is pursued. The best approximation is the cubic one; more terms of the polynomial do not improve the fitting. Figure 3 shows the linear, quadratic and cubic approximations for the torque curve, from \(DRPM=8\) RPM on.

Fig. 3
figure 3

Approximating of the bit-rock interaction curve. The blue points are me mean of the field data at several values of RPM. (Color figure online)

Full size image

Figure 4 shows the approximation of the torque curve, together with the field data (samples 1 and 2), from \(DRPM=0\) RPM up to \(DRPM=240\) RPM. Assuming the same formation, the only difference between the black and magenta curves is related to the value of the weight-on-bit, which is commonly assumed to multiply linearly the torque curve. Therefore, the mean value of the torque of sample 2 is used to define the ratio that must multiply the original identified curve (magenta), yielding \(r=WOB/WOB_{ref}=0.77\). For sample 2, WOB corresponds to 192.5 kN, and the reference weight-on-bit \(WOB_{ref}\) is equal to 244.2 kN, value at which the identification of the curve was performed. Thus, the measured torque and RPM relationship is given by (TOB given in kNm)

$$\begin{aligned} TOB=\left\{ \begin{array}{ll} r(a_0 + a_1 DRPM)1.36 & \text {for} \quad DRPM \in [0.0,3.5]\\ \ r(a_2 + a_3 DRPM)1.36 & \text {for} \quad DRPM\in [3.5,8.0]\\ \ r(a_4 + a_5 DRPM + a_6 DRPM^2 + a_7 DRPM^3)1.36 & \text {for} \quad DRPM\in [8.0,240]\\ \ \end{array} \right. \end{aligned}$$
(5)

where \(a_0=7.7\), \(a_1=0.63\), \(a_2=10.80\), \(a_3=-0.37\), \(a_4=8.39\), \(a_5=-6.8\times 10^{-2}\), \(a_6=4.5\times 10^{-4}\), \(a_6=-1.0\times 10^{-6}\), with the appropriate units.

Fig. 4
figure 4

Approximating of the bit-rock interaction curve. Torque is in (klbf.ft) units, where 10 klbf.ft equals to 13.6 kN m

Full size image

3.2 Model validation

Figure 5 shows a comparison of the response of the model prediction (simulation) and the samples available (field data). Figure 5a shows the dynamical response at the bit when there is no full developed stick-slip vibrations and Fig. 5b shows the response with full developed sitck-slip vibrations. One should have in mind that a 5200 meter column is been simulated assuming a constant formation and constant WOB, and neglecting lateral and axial vibrations (of the column and of the bit). Therefore, the results are quite satisfactory. First, both conditions (with and without stick-slip) were able to be reproduced. Secondly, the amplitude of the responses (simulation and field data) are very close to each other, for both conditions. Secondly, the frequency of stick-slip oscillations, of both simulation and field data, are also very similar to each other.

Figure 6 shows the power spectral density (PSD) for both samples available together with the simulated response. For the case without full developed stick-slip oscillations, Fig. 6a shows that the amplitude of the simulated response is of the same order of the magnitude of the PSD of sample 1, up to 0.6 Hz. However, a peak around 0.4 Hz was not predicted, and higher frequencies did not appear in the simulated data.

For the case with full developed stick-slip oscillations, Fig. 6b, the results are much better. The simulated PSD was able to well represent the overall amplitude in all the frequency band analyzed. The first peak is around 0.13 Hz, a little lower than the first natural frequency of the system. Also, multiples of this first fundamental frequency are well pronounced in the figure.

Fig. 5
figure 5

Dynamical response of the bit: field data together with the model prediction. a Without stick slip and b with stick-slip

Full size image
Fig. 6
figure 6

Power spectral density of the bit speed:field data together with the model prediction. a Without stick slip and b with stick-slip

Full size image

These are encouraging results. The simple torsional lumped-parameter model proposed in this work is able to reproduce the bit speed vibrations which are consistent with the ones measured in a 5200 m real drill-string system. It might be concluded that this simple model is partially validated, because it is able to reproduce both qualitatively and quantitatively the measured torsional vibrations (field data).

3.3 Stability map

In this section the results obtained in the last section are extrapolated for other values of weight-on-bit (WOB) and surface rotation speed (SRPM). Figure 7 shows the stability map for different pairs (WOB, SRPM). The torsional stability of the system is determined by the stick-slip factor

$$\begin{aligned} SS(\%) = \frac{max(DRPM)-min(DRPM)}{2SRPM} \times 100\,, \end{aligned}$$
(6)

where DRPM is the downhole RPM, and SRPM is the nominal surface RPM. The stability map is constructed by computing SS for each input (WOB,  SRPM). When \(SS=0\) there is no torsional oscillations and the rotational speed at the bottom coincides with the rotational speed at the top. When \(SS>0\) there is a persistent undesirable torsional oscillation at the bit, and the system is considered unstable.

As it can be seen in Fig. 7, the dark blue region is stable, while the other colors represent different degrees of instability. For reference, the red circle is at the location of the unstable experimental field data available (sample 1), and the black circle is at the location of the stable data field available (sample 2).

As SS increases, the instability also increases. Figure 7b shows a 3D plot, where a jump phenomenon can be observed in the frontier between stable and unstable regimes. It should be noted that the limit state function, which is the line that separated the stable (dark blue region) from the unstable region (other colors), presents an unusual shape. This has to do with the novel bit-rock interaction model, Eq. (5), that was proposed in this work.

Fig. 7
figure 7

Stability map and the 3D plot showing the jump phenomenon. The red circle is at the location of the unstable experimental field data available, and the black circle is at the location of the stable data field available. Force is in (klbf) units, where (5, 60) klbf equals to (22.2 266.4) kN. (Color figure online)

Full size image

For comparison, a very common model for the bit rock interaction [1, 23, 24], which is given bellow, will also be analyzed (TOB in kNm)

$$\begin{aligned} TOB = 1.36 \ b_0\left( \tanh (b_1 DRPM)+\frac{b_2 DRPM}{1+b_3DRPM^2}\right) \end{aligned}$$
(7)

where \(b_0\), \(b_1\) and \(b_2\) are the parameters of this model. Note that the parameter \(b_1\) is multiplying the rotational speed inside \(\tanh (\cdot )\). This is necessary because the hyperbolic tangent is not homogeneous, so there would be a problem of converting units if \(b_1\) is not inside \(\tanh (\cdot )\).

Let us call the previous model, Eq. (5), which is a combination of linear and cubic functions, model number 1. And let the model represented by Eq. (7), with hyperbolic tangent (\(\tanh\)), model number 2. Solving a nonlinear least squares problem to determine the parameters of model number 2, one gets \(b_0=4.17\), \(b_1=0.05\), \(b_2=0.92\) and \(b_3=0.05\), with the appropriate units. Figure 8 shows the field data together with the curves obtained by models number 1 and 2. It is clear that the previous model (model number 1) gives a better fit to the data available. Nevertheless, model number 2 also presents a good fit with the available field data.

Fig. 8
figure 8

Fitting both models

Full size image

Figure 9 shows the stability map using the model number 2 for the bit-rock interaction. One can observe that the stable region is much larger for model number 2, comparing to model number 1 (Fig. 7). Note that the limit state function, for model number 2, presents now the usual quadratic shape.

It is clear that, for the present system, and the available field data, model number 2 is not good enough to represent the system response. Note that the torsional response at SRPM = 120 PM and WOB = 55 klbf (244.2 kN) is stable for model number 2, and it should not be, since the field data at this point is unstable.

Fig. 9
figure 9

Stability map with bit-rock for model number 2. The red circle is at the location of the unstable experimental field data available, and the black circle is at the location of the stable data field available. Force is in (klbf) units, where (5, 60) klbf equals to (22.2 266.4) kN. (Color figure online)

Full size image

Although the presented bit-rock interaction model shows very good agreement with field data, the model has a limitation. The model is not capable of reproducing stick-slip levels in between the stable (\(SS = 0\)) and unstable conditions (\(SS {>}100\%\)). This is observed by the nonlinear jump in the stability map (Figure 7). Based on field experience, it is common to observe (\(0{<}SS{<}100\%\)). From the authors experience testing different bit-rock interaction models based on the torque-on-bit (TOB) as a function of the bit rotation speed (DRPM), it is not possible to generate stick-slip levels between the stable and unstable conditions (\(0{<}SS{<}100\%\)) when using such models coupled with the drill string torsional dynamics. Therefore, as a future work, it is intended to investigate improvements in the overall drilling model in a way that it is capable of reproducing stick-slip levels observed in the field. One possible way to do so is to couple the drill string torsional dynamics with the other vibration models (axial and/or lateral).

4 Conclusions

Field data with 50 Hz sampling rate is used to partially validate a torsional dynamical drill-string model. Data include a response without full developed stick-slip vibrations, and a response with full developed stick-slip. The \(TOB\times DRPM\) shows that the bit-rock interaction curve might be represented by a combination of linear and cubic functions, which is a new model, not found in the literature.

The dynamical response of the proposed model gave excellent results comparing to the field data, thus partially validating the numerical model. The response of the model could predict the available field data (with and without full developed stick-slip vibrations). The frequency content of the computational model response could very well represent the full developed stick-slip case, while the higher frequencies were not capture for the case without full developed stick-slip. A common curve used to model the bit-rock interaction model (\(\tanh\)) was tested. However, it was not sufficient to represent the available field data.

The model was extrapolated for different WOB and SRPM. The stability map \(SRPM \times WOB\) shows an unusual limit state function. Although the presented bit-rock interaction model shows very good agreement with field data, the model has the limitation of not reproducing stick-slip levels in between the stable (\(SS = 0\)) and unstable conditions (\(SS > 100\%\)). This should be the subject of further investigation.

As future works we intend to further validate the presented model, including the drill string model and the bit-rock interaction model. Also, the current model should be improved to consider other drill string dynamical instabilities. Furthermore, we are interested in the optimization of the drilling operating.