Design and analysis of a novel parallel manipulator for pick-and-place applications

Abstract

This paper presents a novel 4 degree-of-freedom Schönflies-motion parallel manipulator, which is an upgraded design of a 3 degree-of-freedom planar parallel manipulator. The manipulator consists of three identical ${{\mathcal {RRP}}}_{a}{{\mathcal {R}}}$ (${\mathcal {R}}$: a revolute joint, ${{\mathcal {P}}}_{a}$: a planar parallelogram) and one ${\mathcal {RRRRR}}$ subchain. The three actuated joints, the first revolute joints, of ${{\mathcal {RRP}}}_{a}{{\mathcal {R}}}$ subchains are designed to have a common rotation axis, and the actuated joint (the second ${\mathcal {R}}$ joint) axis of the ${\mathcal {RRRRR}}$ subchain is perpendicular to the common rotation axis. This architecture contributes large rotationally-symmetric workspace and unlimited rotational capability of the end-effector. The fundamental demerit of typical parallel manipulators, limited workspace, is completely removed. In this paper, the loop-closure equations are derived. The inverse and forward kinematics and singularity analysis are discussed. An algebraic derivation of the dextrous workspace is presented.

1 Introduction

To fulfill pick-and-place applications, the manipulators are required to undergo the Schönflies motion, a motion of three-translational and one-rotational degree of freedom. The Delta robot [1] and the Quattro robot [2, 3] families are the successful Schönflies-motion parallel manipulators in industry, which are able to perform such motion at high speed (more than 10 m/s) and high acceleration (10 g, g: the gravitational acceleration).

Most parallel manipulators (including the Delta robot and the Quattro robot), however, suffer from drawbacks of a large footprint, a limited workspace and, particularly, low rotation capability. In order to avoid the drawbacks, several 3–5 degree-of-freedom (DoF) parallel mechanisms whose actuated arms have a common axis of rotation were proposed [4–6]. Some of 4-DoF manipulator variants use redundant actuation to overcome singularities [7]. In the mechanisms, high-DoF joints (e.g., universal joints or ball joints) are used at both ends of passive links. Those manipulators’ workspaces and kinematic properties are rotationally symmetric [7] due to the common axis of rotational actuation. Because of the complicated structures, some manipulators have limited end-effector rotation capability. Specially designed amplification systems are proposed at the end-effector to increase the rotation range, which further complicates the mechanism. SCARA-Tau manipulator is the typical mechanism, which is investigated in detail to improve the performance [8–11].

The literatures [12, 13] have presented a class of actuated arms common-axis (or co-axis in short) parallel manipulators whose each subchain is ${\mathcal {RRR}}$ (${\mathcal {R}}$: revolute joint) kinematic chain. These parallel manipulators are planar 3-DoF manipulators. The manipulator (shown in Fig. 1), named the V3 robot, has three ${\mathcal {RRR}}$ subchains, which are respectively arranged in three parallel planes to avoid collision. With an innovative design of the end-effector, it possesses unlimited rotation capability. In [14], the kinematics and workspace have been briefly analyzed. The optimal design exhibits greatly improved performance in workspace and velocities for pick-and-place motion. Since the V3 robot is a 3-DoF planar manipulator, however, it is short of a vertical translation to the plane to fulfill the 4-DoF Schönflies motion. One approach to the problem is to serially add an air cylinder or other translation compensating system on the end-effector to provide the vertical motion. The resulting manipulator thus becomes a hybrid mechanism. Another approach is to introduce a fourth subchain to provide the vertical translation and, in the meantime, to keep the manipulator fully parallel-kinematics. Since the subchains of V3 robot are comparable to cantilever beam structures, their bending deformation may be significant due to heavy load. In this paper, an upgraded design is proposed and analyzed so that the new robot mechanism possesses 4-DoF Schönflies motion capability with single DoF joints.

This paper is organized as follows. In sect. 2, the upgraded design manipulator is introduced. The geometric model, inverse and forward kinematics, workspace and singularity are derived and analyzed in Sects. 3, 4  and 5. Finally, conclusions are drawn in Sect. 6.

Fig. 1

The V3 robot: a 3D model; b Side view

2 The upgraded design: the T4 robot

The V3 robot is a parallel manipulator capable of planar 2T1R motion. It is topologically a 3-${\mathcal {RRR}}$ parallel mechanism, whose motion type is exactly the same as that of each subchain. According to mechanism synthesis theory in [15], if we would like to design a fully parallel mechanism to undergo the Schönflies motion, the generated motion by its subchain should contain the Schönflies motion. That is, the subchains undergo 4-DoF Schönflies motion at least. By investigating subchains of the V3 robot, it is found that it lacks a vertical translation for Schönflies motion. For parallel manipulators with co-axis actuated joints, the advantages are large rotationally-symmetric workspace and small footprint. Especially, V3 has an end-effector that links to subchains with passive revolute joints, so that the end-effector possesses unlimited rotation capability. In design of the Schönflies-motion parallel mechanism, those advantages must be retained. That is, revolute joints are still used to link the base and the end-effector. A feasible scheme could be to add a 1-DoF joint that can offer a vertical translation motion between the first and the last revolute joints. In [16], the authors presented representative serial subchains generating the Schönflies motion. From those serial subchains, it is clear that this added joint can be ${\mathcal {P}}$ (prismatic joint), ${\mathcal {H}}$ (helical joint) or ${{\mathcal {P}}}_{a}$ (plane-hinged parallelogram). In Fig. 2a, the serial chain ${\mathcal {RRPR}}$ can generate motion if the prismatic join axis does not perpendicular to the revolute joint axis. The serial chain ${{\mathcal {RRP}}}_{a}{{\mathcal {R}}}$ (Fig. 2b) generates the Schönflies motion with the planar parallelogram not parallel to the original motion plane. In order to keep the large rotationally-symmetric workspace and the unlimited rotation capability of the end-effector, the first and the last revolute joints should be remained. Since ${\mathcal {P}}$ and ${\mathcal {H}}$ joints are usually taken as actuated ones, they will not be chosen to compose the subchain. Therefore, the ${{\mathcal {RRP}}}_{a}{{\mathcal {R}}}$ topology is used for serial subchains of the new Schönflies-motion parallel mechanism, whose plane-hinged parallelogram is vertical to the motion plane of the V3 robot, which is composed of three ${\mathcal {RRR}}$ subchains.

Fig. 2

Example subchains: a ${\mathcal {RRPR}}$; b ${{\mathcal {RRP}}}_{a}{{\mathcal {R}}}$

The new manipulator should consist of four subchains since it is desirable to have a single actuator in each subchain. However, a fully parallel mechanism consisting of four identical ${{\mathcal {RRP}}}_{a}{{\mathcal {R}}}$ subchains with a common axis of first rotation joints will lead to uncontrollable translation of the plane-hinged parallelograms due to gravity. Therefore, four identical ${{\mathcal {RRP}}}_{a}{{\mathcal {R}}}$ subchains described above seem infeasible to produce the Schönflies motion.

An immediate idea is to introduce a different subchain to constrain the ${{\mathcal {P}}}_{a}$ shape changing. This subchain may be a simple lifting mechanism similar to a crane, which provides vertical translation and makes the parallelograms controllable. We propose a subchain composed of five serially linked revolute joints, which is presented in the dashed zone in Fig. 3. In this subchain, the first revolute joint is passive with its axis identical to the common axis. The second ${\mathcal {R}}$ joint is actuated and perpendicular to the common axis. In [4–6], similar subchains are used, but not identical. The plane-hinged parallelograms constrain the end-effector vertically, so the rotation axis of the end-effector is vertical to the ground. Therefore, the last link l in the lifting subchain has fixed orientation.

Fig. 3

The lifting subchain design

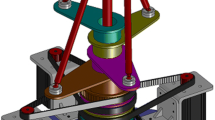
Therefore, we obtain a novel 4-DoF Schönflies-motion parallel manipulator consisting of three $\underline{\mathcal {R}}{\mathcal{RP}}_{a}{\mathcal {R}}$ subchains and one ${\mathcal {R}}\underline{\mathcal {R}}{\mathcal {RRR}}$ subchain, as shown in Fig. 4. Since the actuated axis in the $\mathcal {R\underline{R}RRR}$ subchain and the common actuated axis in the three $\underline{\mathcal {R}}{\mathcal{RP}}_{a}{\mathcal {R}}$ subchains are perpendicular and form the shape “T”, the manipulator is thus named the T4 robot, where the Fig. 4 denotes its degrees of freedom. The T4 robot retains not only advantages of the V3 robot, but also provides a fourth vertical translation. The lifting subchain greatly reduces the bending effect of the three ${{\mathcal {RRP}}}_{a}{{\mathcal {R}}}$ subchains since they are cantilever beam structures.

Fig. 4

The T4 robot: 3D illustration

Here, the motion type of the T4 robot is verified using the method in [15], whose notation convention is borrowed. The end-effector tangent space of the T4 robot configuration space can be spanned by the twists of the rigid body. And the end-effector tangent space is the intersection of that of each subchain. The notations and coordinate system of this robot are defined in Fig. 5. First, define ${\mathbf {x}}=(1,0,0)^T, {\mathbf {y}}=(0,1,0)^T$ and ${\mathbf {z}}=(0,0,1)^T$. At the home configuration e, the ${{\mathcal {RRP}}}_{a}{{\mathcal {R}}}$ subchain’s tangent space is

$$\begin{aligned} {{T}_{e}}C_i=\mathrm{span}\left\{ \left[ \begin{array}{l} {{\mathbf {0}}} \\ {{\mathbf {z}}} \\ \end{array} \right] ,\left[ \begin{array}{l} {{\mathbf {x}}} \\ {{\mathbf {0}}} \\ \end{array} \right] ,\left[ \begin{array}{l} {{\mathbf {y}}} \\ {{\mathbf {0}}} \\ \end{array} \right] ,\left[ \begin{array}{l} {{\mathbf {z}}} \\ {{\mathbf {0}}} \\ \end{array} \right] \right\} ,i=1,2,3. \end{aligned}$$

Since these three subchains layouts are the same, it is easy to know that the motions intersection of these three subchains can be obtained as

$$\begin{aligned} \bigcap \limits _{i=1}^{3}{{{T}_{e}}{{C}_{i}}}=\mathrm{span}\left\{ \left[ \begin{matrix} {\mathbf {0}} \\ {\mathbf {z}} \\ \end{matrix} \right] ,\left[ \begin{matrix} {\mathbf {x}} \\ {\mathbf {0}} \\ \end{matrix} \right] ,\left[ \begin{matrix} {\mathbf {y}} \\ {\mathbf {0}} \\ \end{matrix} \right] ,\left[ \begin{matrix} {\mathbf {z}} \\ {\mathbf {0}} \\ \end{matrix} \right] \right\} . \end{aligned}$$

Define a fixed body frame $A_4-X'Y'Z'$ on the lifting subchain, where the $Y'$ axis is coincident with the actuated axis, the $+X'$ axis passes through the point $D_4$. The tangent space of configuration space of the lifting subchain in this coordinate frame is

$$\begin{aligned} {{T}_{e}}{{C}_{4}}&= {} \mathrm{span}\left\{ \left[ \begin{matrix} {\mathbf {0}} \\ {\mathbf {z}} \\ \end{matrix} \right] \right. ,\left[ \begin{matrix} {\mathbf {0}} \\ {\mathbf {y}} \\ \end{matrix} \right] ,\left[ \begin{matrix} {{{\mathbf {A}}}_{{\mathbf {4}}}}{{{\mathbf {B}}}_{{\mathbf {4}}}}\times {\mathbf {y}} \\ {\mathbf {y}} \\ \end{matrix} \right] ,\left[ \begin{matrix} {{{\mathbf {A}}}_{{\mathbf {4}}}}{{{\mathbf {C}}}_{{\mathbf {4}}}} \times {\mathbf {y}} \\ {\mathbf {y}} \\ \end{matrix} \right] ,\\&\quad \left. \left[ \begin{matrix} {{{\mathbf {A}}}_{{\mathbf {4}}}}{{{\mathbf {D}}}_{{\mathbf {4}}}}\times {\mathbf {z}} \\ {\mathbf {z}} \\ \end{matrix} \right] \right\} \\&= {} \mathrm{span}\left\{ \left[ \begin{matrix} {\mathbf {0}} \\ {\mathbf {z}} \\ \end{matrix} \right] \right. ,\left[ \begin{matrix} {\mathbf {0}} \\ {\mathbf {y}} \\ \end{matrix} \right] ,\left[ \begin{matrix} {{{\mathbf {A}}}_{{\mathbf {4}}}}{{{\mathbf {B}}}_{{\mathbf {4}}}}\times {\mathbf {y}} \\ {\mathbf {0}} \\ \end{matrix} \right] ,\left[ \begin{matrix} {{{\mathbf {B}}}_{{\mathbf {4}}}}{{{\mathbf {C}}}_{{\mathbf {4}}}}\times {\mathbf {y}} \\ {\mathbf {0}} \\ \end{matrix} \right] ,\\&\quad \left. \left[ \begin{matrix} {{{\mathbf {A}}}_{{\mathbf {4}}}}{{{\mathbf {D}}}_{{\mathbf {4}}}}\times {\mathbf {z}} \\ {\mathbf {0}} \\ \end{matrix} \right] \right\} . \end{aligned}$$

Suppose ${{{\mathbf {A}}}_{{\mathbf {4}}}}{{{\mathbf {B}}}_{{\mathbf {4}}}}=a{\mathbf {x}}+b{\mathbf {z}}, {{{\mathbf {B}}}_{{\mathbf {4}}}}{{{\mathbf {C}}}_{{\mathbf {4}}}}=c{\mathbf {x}}+d{\mathbf {z}}, {{{\mathbf {B}}}_{{\mathbf {4}}}}{{{\mathbf {D}}}_{{\mathbf {4}}}}=e{\mathbf {x}}+f{\mathbf {z}}$, and $a,\ldots ,f$ are constants. Thus,

$$\begin{aligned} {{T}_{e}}{{C}_{4}}&= {} \mathrm{span}\left\{ \left[ \begin{matrix} {\mathbf {0}} \\ {\mathbf {y}} \\ \end{matrix} \right] ,\left[ \begin{matrix} {\mathbf {0}} \\ {\mathbf {z}} \\ \end{matrix} \right] ,\left[ \begin{matrix} a{\mathbf {z}}-b{\mathbf {x}} \\ {\mathbf {0}} \\ \end{matrix} \right] ,\left[ \begin{matrix} c{\mathbf {z}}-d{\mathbf {x}}\\ {\mathbf {0}} \\ \end{matrix} \right] ,\left[ \begin{matrix} -e{\mathbf {y}} \\ {\mathbf {0}} \\ \end{matrix}\right] \right\} \\&= {} \mathrm{span}\left\{ \left[ \begin{matrix} {\mathbf {0}} \\ {\mathbf {y}} \\ \end{matrix} \right] ,\left[ \begin{matrix} {\mathbf {0}} \\ {\mathbf {z}} \\ \end{matrix} \right] ,\left[ \begin{matrix} {\mathbf {x}} \\ {\mathbf {0}} \\ \end{matrix} \right] ,\left[ \begin{matrix} {\mathbf {y}} \\ {\mathbf {0}} \\ \end{matrix} \right] ,\left[ \begin{matrix} {\mathbf {z}} \\ {\mathbf {0}} \\ \end{matrix} \right] \right\} . \end{aligned}$$

After coordinate frames transformations, in the inertial frame, we know that the motions of the lifting subchain are 3-DoF translation and 2-DoF rotation where one rotation axis is Z axis and the other is parallel to the moving actuated axis. We obtain the tangent space of the motion of the T4 robot by taking intersection of tangent spaces of motions of all subchains,

$$\begin{aligned} \bigcap \limits _{i=1}^{4}{{{T}_{e}}{{C}_{i}}}=\mathrm{span}\left\{ \left[ \begin{matrix} {\mathbf {0}} \\ {\mathbf {z}} \\ \end{matrix} \right] ,\left[ \begin{matrix} {\mathbf {x}} \\ {\mathbf {0}} \\ \end{matrix} \right] ,\left[ \begin{matrix} {\mathbf {y}} \\ {\mathbf {0}} \\ \end{matrix} \right] ,\left[ \begin{matrix} {\mathbf {z}} \\ {\mathbf {0}} \\ \end{matrix} \right] \right\} , \end{aligned}$$

which is exactly the tangent space of Schönflies motion. Clearly, the rotation motion about the moving axis vanishes. By the theory in [15], thus, the T4 robot has 4-DoF Schönflies motion capability.

3 Kinematic analysis

3.1 Geometry description

Figure 5 shows a CAD implementation of the T4 robot. An inertial coordinate frame $O-XYZ$ is attached, with the lowest subchain $A_1B_1C_1D_1$ in the XOY plane and the origin O being coincident with point $A_1$, the first actuated revolute joint. At home configuration, suppose the plane-hinged parallelograms are rectangles (not changing shape), and the $+X$ axis passes through the point $D_1$. The joint variables and geometric parameters are defined in Figs. 5, 6 and 7 and Table 1. The workspace of the manipulator is described by the coordinate of point $D_1$ and the orientation angle $\phi$ of the end-effector.

Fig. 5

Notations and coordinate system

Fig. 6

The T4 robot: a An xy projection; b An xz projection

Fig. 7

a The end-effector crank design; b The plane-hinged parallelogram

Table 1 Nomenclature

To analyze kinematics of a parallel mechanism, the first step is to obtain its loop-closure equations. It is straightforward to obtain the position relation for the first subchain.

$$\begin{aligned} \left\{ \begin{array}{l} x={{l}_{11}}\cos {{\theta }_{1}}+({{l}_{12}}\cos {{\beta _1}+l_{13}})\cos ( {{\theta }_{1}}-{{\gamma }_{1}} )\\ y={{l}_{11}}\sin {{\theta }_{1}}+({{l}_{12}}\cos {\beta _1+l_{13}})\sin ( {{\theta }_{1}}-{{\gamma }_{1}} )\\ z=l_{12}\sin {\beta _1} \end{array}\right. \end{aligned}$$

(1)

The loop-closure equations for subchains 2–4 are readily obtained as follows.

$$\begin{aligned}&\left\{ \begin{array}{l} x_2\,=\,{{l}_{21}}\cos {{\theta }_{2}}+({{l}_{22}}\cos {{\beta _2}+l_{23}})\cos ( {{\theta }_{2}}+{{\gamma }_{2}} )\\ y_2\,=\,{{l}_{21}}\sin {{\theta }_{2}}+({{l}_{22}}\cos {\beta _2+l_{23}})\sin ( {{\theta }_{2}}+{{\gamma }_{2}} )\\ z_2\,=\,z+h_2=l_{22}\sin {\beta _2}+h_2 \end{array}\right. \end{aligned}$$

(2)

$$\begin{aligned}&\left\{ \begin{array}{l} x_3\,=\,{{l}_{31}}\cos {{\theta }_{3}}+({{l}_{32}}\cos {{\beta _3}+l_{33}})\cos ( {{\theta }_{3}}-{{\gamma }_{3}} )\\ y_3\,=\,{{l}_{31}}\sin {{\theta }_{3}}+({{l}_{32}}\cos {\beta _3+l_{33}})\sin ( {{\theta }_{3}}-{{\gamma }_{3}} )\\ z_3\,=\,z+h_2+h_3=l_{32}\sin {\beta _3}+h_2+h_3 \end{array}\right. \end{aligned}$$

(3)

$$\begin{aligned}&\left\{ \begin{array}{l} x_4=x_3\\ y_4=y_3\\ z_4=z_3+h_4 \end{array}\right. \end{aligned}$$

(4)

The coordinate $(x_2,y_2)$ and $(x_3,y_3)$ can be computed from the coordinate of (x, y), and the orientation of bars ${{H}_{1}}{{H}_{2}}$ (and ${{H}_{3}}{{H}_{4}}$), angle $\phi$, as follows.

$$\begin{aligned}&\left[ \begin{matrix} {{x}_{2}} \\ {{y}_{2}} \\ \end{matrix} \right] =\left[ \begin{matrix} x \\ y \\ \end{matrix} \right] +\left[ \begin{matrix} \cos \phi\quad -\sin \phi \\ \sin \phi\quad\cos \phi \\ \end{matrix} \right] \left[ \begin{matrix} {{b}_{1}} \\ 0 \\ \end{matrix} \right] \end{aligned}$$

(5)

$$\begin{aligned}&\left[ \begin{matrix} {{x}_{3}} \\ {{y}_{3}} \\ \end{matrix} \right] =\left[ \begin{matrix} x \\ y \\ \end{matrix} \right] +\left[ \begin{matrix} \cos \phi\quad -\sin \phi \\ \sin\phi\quad\cos \phi \\ \end{matrix} \right] \left[ \begin{matrix} {{b}_{1}}-{{b}_{2}} \\ 0 \\ \end{matrix} \right] \end{aligned}$$

(6)

3.2 Inverse kinematics

The actuated joint angles $\theta _i$ can be computed from the projection length of ${{{\mathbf {B}}}_{{\mathbf {i}}}}{{{\mathbf {D}}}_{{\mathbf {i}}}}$ in the XOY plane for $i=1,\ldots ,3$, with given the Cartesian coordinate of the end-effector (x, y,  $z,\phi )$. First, for the three suchains with plane-hinged parallelograms, it can be derived from Eqs. (1)–(3) by simple manipulations.

$$\begin{aligned} {{\left( {{x}_{i}}-{{l}_{i1}}\cos {{\theta }_{i}} \right) }^{2}}+{{\left( {{y}_{i}}-{{l}_{i1}}\sin {{\theta }_{i}} \right) }^{2}}-L_i^{2}=0 \end{aligned}$$

(7)

for $i=1,2,3$, where $x_1=x$ and $y_1=y, L_i=l_{i2}\cos {\beta _i}+l_{i3}$, where $\beta _i$ can be determined according to Fig. 7b given the coordinate z. This leads to three equations of $\cos \theta _i$ and $\sin \theta _i$ as follows. The only unknown is $\theta _i$ of the $ith$ equation.

$$\begin{aligned} {x_{i}^{2}+y_{i}^{2}-2{{l}_{i1}}{{x}_{i}}\cos {{\theta }_{i}}-2{{l}_{i1}}{{y}_{i}}\sin {{\theta }_{i}}+l_{i1}^{2}-L_i^{2}=0} \end{aligned}$$

(8)

Let $t_i=\tan (\theta _i/2)$ and by the universal substitution for trigonometric functions, the equations above become quadratic with respect to $t_i$,

$$\begin{aligned} {{D}_{i}}t_{i}^{2}+{{E}_{i}}{{t}_{i}}+{{F}_{i}}=0,\quad i=1,2,3 \end{aligned}$$

(9)

where

$$\begin{aligned} {{D}_{i}}\,=\,& {} x_{i}^{2}+y_{i}^{2}+l_{i1}^{2}-L_i^{2}+2{{l}_{i1}}{{x}_{i}}; \\ {{E}_{i}}\,=\,& {} -4{{l}_{i1}}{{y}_{i}}; \\ {{F}_{i}}\,=\,& {} x_{i}^{2}+y_{i}^{2}+l_{i1}^{2}-L_i^{2}-2{{l}_{i1}}{{x}_{i}}. \end{aligned}$$

For the ${\mathcal {RRRRR}}$ lifting subchain, its rotation axis of the actuated joint is not fixed. The length of the projection in the XOY plane is $R_4$ (${R_i}^2={x_i}^2+{y_i}^2$). So, using the height of the top point, the geometrical equation can be derived.

$$\begin{aligned} h_1+l_{41}\sin \theta _4=z_4+\left[ l_{42}^{2}-( R_4-l_{41}\cos {\theta _4}-l_{43} )^{2}\right] ^{0.5} \end{aligned}$$

(10)

This leads to an equation with respect to $\theta _4$ as follows.

$$\begin{aligned}&H^2+(R_4-l_{43})^2-2l_{41}(R_4-l_{43})\cos \theta _4 \nonumber \\&\quad \quad +2Hl_{41}\sin \theta _4+l_{41}^2-l_{42}^2=0 \end{aligned}$$

(11)

where $H=h_1-(z+h_2+h_3+h_4)$. Similarly, let $t_4=\tan (\theta _4/2)$, we have

$$\begin{aligned} {{D}_{4}}t_{4}^{2}+{{E}_{4}}{{t}_{4}}+{{F}_{4}}=0, \end{aligned}$$

(12)

where

$$\begin{aligned} {{D}_{4}}&=H^2+(R_4-l_{43})^2+l_{41}^2-l_{42}^2+2l_{41}(R_4-l_{43});\\ {{E}_{4}}&= 4Hl_{41}; \\ {{F}_{4}}&= H^2+(R_4-l_{43})^2+l_{41}^2-l_{42}^2-2l_{41}(R_4-l_{43}). \end{aligned}$$

The coordinate $(x_i,y_i,z_i), i=1,\ldots ,4$, can be computed from $(x,y,z,\phi )$. The coefficients $D_i, E_i, F_i, i=1,\ldots ,4$, are functions of Cartesian coordinate $(x,y,z,\phi )$ and link lengths. Readily $t_i, i=1,\ldots ,4$ can be solved from the Eqs. (9) and (12) and $\theta _i$ can thus be obtained by ${{\theta }_{i}}=2\arctan {{t}_{i}}$.

Clearly, there are at most sixteen inverse kinematic solutions for a single $(x,y,z,\phi )$. They correspond to sixteen different assembly modes. Once the mechanism is assembled, one branch of solutions is chosen. In usual applications, the mechanism always operates in the chosen mode since a transfer from one mode to another will lead to an occurrence of singularity, which may cause unexpected damages. It is not desirable in practice.

3.3 Forward kinematics

The forward kinematics problem is to find pose of the end-effector given a set of actuated joint angles. For the T4 robot, it is to find the Cartesian coordinate $(x,y,z,\phi )$, given actuated joint angles $\theta _i, i=1,\ldots ,4$.

From (8), for $i=1$, we can obtain a quadratic equation relating (x, y, z) and $\theta _1$.

$$\begin{aligned} x^2+y^2-2l_{11}x\cos \theta _1-2l_{11}y_1\sin \theta _1+l_{11}^2-L_1^2=0. \end{aligned}$$

(13)

While for $i=2,3$, the following equations present the relationship between $(x,y,z,\phi )$ and $\theta _i$.

$$\begin{aligned}&x^2+y^2+2(b_1\cos \phi -l_{21}\cos \theta _2)x\nonumber \\&\quad \quad +2(b_1\sin \phi -l_{21}\sin \theta _2)y-2b_1l_{21}\cos (\phi -\theta _2)\nonumber \\&\quad \quad +b_1^2+l_{21}^2-L_2^2=0 \end{aligned}$$

(14)

$$\begin{aligned}&x^2+y^2+2((b_1-b_2)\cos \phi -l_{31}\cos \theta _2)x\nonumber \\&\quad \quad +2((b_1-b_2)\sin \phi -l_{31}\sin \theta _2)y\nonumber \\&\quad \quad -2(b_1-b_2)l_{21}\cos (\phi -\theta _2)+(b_1-b_2)^2+l_{31}^2-L_3^2=0 \end{aligned}$$

(15)

where $L_i$ is functions of z. Subtracting Eq. (13) from (14) and (15), two linear algebraic equations with respect to x and y are obtained.

$$\begin{aligned}&P_1x+Q_1y+S_1=0 \end{aligned}$$

(16)

$$\begin{aligned}&P_2x+Q_2y+S_2=0 \end{aligned}$$

(17)

where $P_i, Q_i, S_i, i=1,2$, are functions of $z, \phi$ and $\theta _i, i=1,2,3$ and link lengths as follows.

$$\begin{aligned} {{P}_{1}}&= 2(b_1\cos \phi -l_{21}\cos \theta _2+l_{11}\cos \theta _1);\\ {{Q}_{1}}&= 2(b_1\sin \phi -l_{21}\sin \theta _2+l_{11}\sin \theta _1);\\ {{S}_{1}}&= -2b_1l_{21}\cos (\phi -\theta _2)+b_1^2+l_{21}^2-L_2^2-l_{11}^2+L_1^2;\\ {{P}_{2}}&= 2((b_1-b_2)\cos \phi -l_{31}\cos \theta _3+l_{11}\cos \theta _1);\\ {{Q}_{2}}&=2((b_1-b_2)\sin \phi -l_{31}\sin \theta _2+l_{11}\sin \theta _1);\\ {{S}_{2}}&=-2(b_1-b_2)l_{31}\cos (\phi -\theta _3)+(b_1-b_2)^2+l_{31}^2-L_3^2\\&\qquad \qquad \qquad -l_{11}^2+L_1^2. \end{aligned}$$

Readily x and y can be solved from (16) and (17) when $P_1Q_2-P_2Q_1\ne 0$.

$$\begin{aligned} x= & {} \frac{{{Q}_{1}}{{S}_{2}}-{{Q}_{2}}{{S}_{1}}}{{{P}_{1}}{{Q}_{2}}-{{P}_{2}}{{Q}_{1}}} \end{aligned}$$

(18)

$$\begin{aligned} y= & {} \frac{{{P}_{1}}{{S}_{2}}-{{P}_{2}}{{S}_{1}}}{{{P}_{1}}{{Q}_{2}}-{{P}_{2}}{{Q}_{1}}} \end{aligned}$$

(19)

Clearly x, y are expressed as functions of $(z,\phi )$.

Substituting (18) and (19) into (13) and (11), we can get two equations with respect to z and $\phi$. After eliminating z, there is a high order equation of $\cos \phi$ and $\sin \phi$. Using the universal substitution for trigonometric functions again, we obtain a solution of $\phi$. Then, z, x and y can be solved in order.

4 Dextrous workspace

The limited rotation capability is a major drawback of traditional parallel manipulators. The T4 robot retains the property of full $360^{\circ }$ rotation of the V3 robot. In this section, the dextrous workspace, or the position workspace with full $360^{\circ }$ rotation, is discussed for pick-and-place operations.

The T4 robot consists of 3 ${{\mathcal {RRP}}}_{a}{{\mathcal {R}}}$ subchains and one ${\mathcal {RRRRR}}$ subchain. The three ${\mathcal {R}}$ joints in the ${{\mathcal {RRP}}}_{a}{{\mathcal {R}}}$ subchain contribute a planar motion. By introducing a ${{\mathcal {P}}}_{a}$ joint (and the lifting subchain), the T4 robot is able to undergo planar motion in different operation plane depending on coordinate z. Therefore, it is applicable to analyze the dextrous workspace of the T4 robot by analyzing the dextrous workspace in different operation plane using the procedure in [14]. The inner radius $r'_d$ and the outer radius $R'_d$ of the dexterous workspace torus generated by the three ${{\mathcal {RRP}}}_{a}{{\mathcal {R}}}$ subchains can be obtained as follows:

$$\begin{aligned} r'_d\,=\, & {} \max \{ | l_{11}-L_{1}|, |l_{21}-L_{2}|+b_1, |l_{31}-L_{3}|+|b_1-b_2|\};\\ R'_d\,=\,& {} \min \{ l_{11}+L_{1},l_{21}+L_{2}-b_1,l_{31}+L_{3}-| b_1-b_2 |\}. \end{aligned}$$

The whole workspace is the intersection of all subchains’ workspaces. Let us derive the workspace of the lifting subchain. If inverse kinematic Eq. (12) has real solution, the corresponding configuration must be in the workspace. For a quadratic algebraic equation, the existence of real solutions is equivalent to that the following inequality holds.

$$\begin{aligned} {{\varDelta }_{4}}=E_{4}^{2}-4{{D}_{4}}{{F}_{4}}\ge 0. \end{aligned}$$

(20)

Applying ${{D}_{4}}, {{E}_{4}}$ and ${{F}_{4}}$ in (12) to the inequality (20), it becomes

$$\begin{aligned} \left[ H^2+(R_4-l_{43})^2-l_{41}^2-l_{42}^2\right] ^2\le 4l_{41}^2l_{42}^2. \end{aligned}$$

(21)

The inequality (21) can be further reduced to

$$\begin{aligned} (l_{41}-l_{42})^2-H^2\le (R_4-l_{43})^2\le (l_{41}+l_{42})^2-H^2. \end{aligned}$$

(22)

In practical design, since the base radius is nonzero, $R_4 \ge l_{43}$. The radius range of the lifting subchain workspace can be derived in a reasonable operation plane:

Case 1: $|l_{41}-l_{42}|\ge H$,

$$\begin{aligned} \left[ (l_{41}-l_{42})^2-H^2\right] ^{0.5}+l_{43}\le R_4 \le \left[ (l_{41}+l_{42})^2-H^2\right] ^{0.5}+l_{43}. \end{aligned}$$

Case 2: $|l_{41}-l_{42}|< H$ and $l_{41}+l_{42}\ge H$,

$$\begin{aligned} l_{43}\le R_4 \le \left[ (l_{41}+l_{42})^2-H^2\right] ^{0.5}+l_{43}. \end{aligned}$$

Case 3: $l_{41}+l_{42}< H$, no solution.

Notice $R_3=R_4$, so the relationship between manipulator workspace radius R ($R^2=x^2+y^2$) and $R_4$ can be determined like in [14]:

$$\begin{aligned}&\underset{\phi \in \left[ -\pi ,\pi \right] }{\mathop {\min }}\,R_{4}^{2}={{\left( R-\left| {{b}_{1}}-{{b}_{2}} \right| \right) }^{2}},\nonumber \\&\text {when}\qquad \cos \left( \phi -\gamma \right) =-sgn \left( {{b}_{1}}-{{b}_{2}} \right) ; \end{aligned}$$

(23)

$$\begin{aligned}&\underset{\phi \in \left[ -\pi ,\pi \right] }{\mathop {\max }}\,R_{4}^{2}={{\left( R+\left| {{b}_{1}}-{{b}_{2}} \right| \right) }^{2}},\nonumber \\&\text {when}\quad \cos \left( \phi -\gamma \right) =sgn \left( {{b}_{1}}-{{b}_{2}} \right) ; \end{aligned}$$

(24)

where $\cos \gamma =x/R, \sin \gamma =y/R$ and $sgn (\cdot )$ is the sign function defined as follows.

$$\begin{aligned} sgn \left( x \right) =\left\{ \begin{matrix} 1,\quad x>0 \\ 0,\quad x=0 \\ -1,\quad x<0 \\ \end{matrix} \right. \end{aligned}$$

Therefore, we determine the inner radius $r_d$ and the outer radius $R_d$ of the manipulator dexterous workspace torus in a designated operation plane (fixed z) as follows:

$$\begin{aligned} r_d=\max \{ r'_d, \min R_4+|b_1-b_2|\};\\ R_d=\min \{ R'_d, \max R_4-|b_1-b_2|\}. \end{aligned}$$

The minimal and maximal values of $R_4$ are dependent on the cases discussed above. It is easy to see that the whole manipulator workspace is made up of a series of torus with a common axis, like an ellipsoid with a vertical hole in the center. Let us investigate an example design with the following kinematic parameters, $l_{i1}=0.3, l_{i2}=0.5, l_{i3}=0.05, i=1,\ldots ,3, l_{41}=0.5, l_{42}=0.5, l_{43}=0.05, b_1=0.03, b_2=0.075, h_1=0.8, h_2=0.15, h_3=0.15, h_4=0.05$, all in m. Figure 8 shows the dexterous workspace projections.

Fig. 8

a Dexterous workspace in XOY plane; b Dexterous workspace in XOZ plane

5 Singularity analysis

Since the three ${{\mathcal {RRP}}}_{a}{{\mathcal {R}}}$ subchains have the same Schönflies motion type as the T4 robot, there is no chance that the parallel mechanism obtains additional DoFs at some specific configurations. Therefore, the T4 robot has no constraint singularity [17].

Due to different topologies of the lifting subchain and the three ${{\mathcal {RRP}}}_{a}{{\mathcal {R}}}$ subchains, they are separately treated to achieve the velocity equation of the robot.

For the three ${{\mathcal {RRP}}}_{a}{{\mathcal {R}}}$ subchains, ${{\mathbf {O}}}{{{\mathbf {D}}}_{{\mathbf {i}}}}- {{\mathbf {O}}}{{{\mathbf {B}}}_{{\mathbf {i}}}}= {{{\mathbf {B}}}_{{\mathbf {i}}}}{{{\mathbf {D}}}_{{\mathbf {i}}}}$. Differentiating the equation, it leads to the velocity relationship of the ith ($i=1,2,3$) subchain.

$$\begin{aligned} {{{\mathbf {V}}}_{{{{\mathbf {D}}}_{{\mathbf {i}}}}}} -{{{\mathbf {V}}}_{{{{\mathbf {B}}}_{{\mathbf {i}}}}}}= & {} \left[ \begin{matrix} {{{\dot{L}}}_{i}}\cos \left( {{\theta }_{i}}-sgn(i)\cdot {{\gamma }_{i}} \right) \\ {{{\dot{L}}}_{i}}\sin \left( {{\theta }_{i}}-sgn(i)\cdot {{\gamma }_{i}} \right) \\ {\dot{z}} \\ \end{matrix} \right] \nonumber \\&+\left( {{{\dot{\theta }}}_{i}}-sgn(i)\cdot {{{\dot{\gamma }}}_{i}} \right) {\mathbf {z}}\times {{{\mathbf {B}}}_{{\mathbf {i}}}}{{{\mathbf {D}}}_{{\mathbf {i}}}} \end{aligned}$$

(25)

where ${{{\mathbf {V}}}_{{{{\mathbf {D}}}_{{\mathbf {i}}}}}}$ and ${{{\mathbf {V}}}_{{{{\mathbf {B}}}_{{\mathbf {i}}}}}}$ are respectively the velocity of point $D_i$ and $B_i$ with respect to the inertial coordinate frame, ${\mathbf {z}}=(0,0,1)^T$. Here, $sgn(i)=1$, when $i=1,3$; $sgn(i)=-1$, when $i=2$.

Suppose that the translational velocity and the rotational velocity of end-effector are ${\mathbf {v}}=[\dot{x},\dot{y},\dot{z}]^T$ and ${\mathbf {w}}=[0,0,\dot{\phi }]^T$, respectively. That is, the point $D_1$ has the translational velocity ${\mathbf {v}}$. $\dot{{\mathbf {\theta }}_i}$ is the ith actuated velocity vector and $\dot{{\mathbf {\gamma }}_i}$ is the ith passive velocity vector. We can compute the velocities of $B_i$ and $D_i, i=1,2,3$ as follows:

$$\begin{aligned}&{{{\mathbf {V}}}_{{{{\mathbf {B}}}_{{\mathbf {i}}}}}}={\dot{\mathbf {\theta }}_{i}}\times {{{\mathbf {A}}}_{{\mathbf {i}}}}{{{\mathbf {B}}}_{{\mathbf {i}}}} \end{aligned}$$

(26)

$$\begin{aligned}&\left\{ \begin{array}{l} {{{\mathbf {V}}}_{{{{\mathbf {D}}}_{{\mathbf {1}}}}}} ={\mathbf {v}}= {\mathbf {v}}+{\mathbf {w}} \times {{{\mathbf {u }}}_{{\mathbf {1}}}} \\ {{{\mathbf {V}}}_{{{{\mathbf {D}}}_{{\mathbf {2}}}}}}={\mathbf {v}}+{\mathbf {w}} \times {{{\mathbf {H}}}_{{\mathbf {1}}}}{{{\mathbf {H}}}_{{\mathbf {2}}}}={\mathbf {v}}+{\mathbf {w}} \times {{{\mathbf {u}}}_{{\mathbf {2}}}} \\ {{{\mathbf {V}}}_{{{{\mathbf {D}}}_{{\mathbf {3}}}}}}={\mathbf {v}}+{\mathbf {w}} \times ({{{\mathbf {H}}}_{{\mathbf {1}}}}{{{\mathbf {H}}}_{{\mathbf {2}}}}+{{{\mathbf {H}}}_{{\mathbf {3}}}}{{{\mathbf {H}}}_{{\mathbf {4}}}})={\mathbf {v}}+{\mathbf {w}} \times {{{\mathbf {u}}}_{\mathbf {3}}} \\ \end{array} \right. \end{aligned}$$

(27)

where ${\mathbf {u}}_{\mathbf {1}}={\mathbf {0}}, {\mathbf {u_{2}}}={\mathbf {H_1H_2}}$ and ${\mathbf {u_{3}}}={\mathbf {H_1H_2}}+{\mathbf {H_3H_4}}$. By (25), we have

$$\begin{aligned} {\mathbf {v}}+{\mathbf {w}}\times {{{\mathbf {u}}}_{{\mathbf {i}}}}-{{\dot{{\mathbf {\theta }}}}_{{\mathbf {i}}}}\times {{{\mathbf {A}}}_{{\mathbf {i}}}}{{{\mathbf {B}}}_{{\mathbf {i}}}}= & {} \left[ \begin{array}{l} {{{\dot{L}}}_{i}}\cos \left( {{\theta }_{i}}-sgn(i)\cdot {{\gamma }_{i}} \right) \\ {{{\dot{L}}}_{i}}\sin \left( {{\theta }_{i}}-sgn(i)\cdot {{\gamma }_{i}} \right) \\ {\dot{z}} \\ \end{array} \right] \nonumber \\&+\left( {{\dot{{\mathbf {\theta }}}}_{{\mathbf {i}}}}-sgn(i)\cdot {{\dot{{\mathbf {\gamma }}}}_{{\mathbf {i}}}} \right) \times {{{\mathbf {B}}}_{{\mathbf {i}}}}{{{\mathbf {D}}}_{{\mathbf {i}}}}. \end{aligned}$$

(28)

Taking inner product to both sides by ${{{\mathbf {B}}}_{{\mathbf {i}}}}{{{\mathbf {D}}}_{{\mathbf {i}}}}$, we obtain

$$\begin{aligned}&{{{\mathbf {B}}}_{{\mathbf {i}}}}{{{\mathbf {D}}}_{{\mathbf {i}}}}^T {\mathbf {v}}+( {{l}_{i3}}z/{{( l_{i2}^{2}-{{z}^{2}})}^{0.5}})\dot{z}+( {{{\mathbf {u }}}_{{\mathbf {i}}}}\times {{{\mathbf {B}}}_{{\mathbf {i}}}}{{{\mathbf {D}}}_{{\mathbf {i}}}} )^T {\mathbf {w }}\nonumber \\&=({{{\mathbf {A}}}_{{\mathbf {i}}}}{{{\mathbf {B}}}_{{\mathbf {i}}}}\times {{{\mathbf {B}}}_{{\mathbf {i}}}}{{{\mathbf {D}}}_{{\mathbf {i}}}})^T{{\dot{\mathbf {\theta }}}_{{\mathbf {i}}}}. \end{aligned}$$

(29)

The velocity Eq. (29) can be expressed in the following matrix form

$$\begin{aligned} J_x^{\#}\dot{{\mathbf {X}}}=J_{\theta }^{\#}\dot{\varvec{\Theta }} \end{aligned}$$

(30)

where

$$\begin{aligned} J_{x}^{\#} &= \left[ \begin{array}{ll} {{{\mathbf {B}}}_{{\mathbf {1}}}}{{{\mathbf {D}}}_{{\mathbf {1}}}}^T+J_{x_1}{{{\mathbf {z}}}^{T}} & ( {\mathbf {u_1 }}\times {{{\mathbf {B}}}_{{\mathbf {1}}}}{{{\mathbf {D}}}_{{\mathbf {1}}}} )^T{\mathbf {z}}\\ {{{\mathbf {B}}}_{{\mathbf {2}}}}{{{\mathbf {D}}}_{{\mathbf {2}}}}^T+J_{x_2}{{{\mathbf {z}}}^{T}} &( {\mathbf {u_2}}\times {{{\mathbf {B}}}_{{\mathbf {2}}}}{{{\mathbf {D}}}_{{\mathbf {2}}}} )^T{\mathbf {z}} \\ {{{\mathbf {B}}}_{{\mathbf {3}}}}{{{\mathbf {D}}}_{{\mathbf {3}}}}^T+J_{x_3}{{{\mathbf {z}}}^{T}} & ( {\mathbf {u_3 }}\times {{{\mathbf {B}}}_{{\mathbf {3}}}}{{{\mathbf {D}}}_{{\mathbf {3}}}} )^T{\mathbf {z}} \\ \end{array} \right] , \\ J_{\theta }^{\#} & = {} \left[ \begin{array}{llll}{{J}_{{{\theta }_{1}}}} & 0 & 0 & 0 \\ 0 & {{J}_{{{\theta }_{2}}}} & 0 & 0 \\ 0 & 0 & {{J}_{{{\theta }_{3}}}} & 0 \\ \end{array} \right] , \end{aligned}$$

and $\dot{{\mathbf {X}}}=(\dot{x},\dot{y},\dot{z},\dot{\phi })^T$ is the velocity vector of the end-effector in Cartesian space, $\dot{\varvec{\Theta }}=(\dot{\theta _1}, \dot{\theta _2},\dot{\theta _3},\dot{\theta _4})^T$ is the velocity vector of the actuated joint variables in the joint space, and $J_{x_i}={{{l}_{i3}}z}/{{{\left( l_{i2}^{2}-{{z}^{2}} \right) }^{0.5}}}, {{J}_{{{\theta }_{i}}}}=\left( {{{\mathbf {A}}}_{{\mathbf {i}}}}{{{\mathbf {B}}}_{{\mathbf {i}}}}\times {{{\mathbf {B}}}_{{\mathbf {i}}}}{{{\mathbf {D}}}_{{\mathbf {i}}}} \right) ^T {\mathbf {z}}, i=1,2,3, {\mathbf {z}}=(0,0,1)^T$.

While the Eq. (28) is multiplied by ${{{\mathbf {A}}}_{{\mathbf {i}}}}{{{\mathbf {D}}}_{{\mathbf {i}}}}$, we have

$$\begin{aligned}&{{{\mathbf {A}}}_{{\mathbf {i}}}}{{{\mathbf {D}}}_{{\mathbf {i}}}}^T {\mathbf {v}}+((l_{i1}\cos (\gamma )+{{l}_{i3}})z/{{( l_{i2}^{2}-{{z}^{2}})}^{0.5}})\dot{z} +({{{\mathbf {u }}}_{{\mathbf {i}}}}\times {{{\mathbf {A}}}_{{\mathbf {i}}}}{{{\mathbf {D}}}_{{\mathbf {i}}}} )^T {\mathbf {w}}\nonumber \\&\quad =-sgn(i)({{{\mathbf {B}}}_{{\mathbf {i}}}}{{{\mathbf {D}}}_{{\mathbf {i}}}} \times {{{\mathbf {A}}}_{{\mathbf {i}}}} {{{\mathbf {D}}}_{{\mathbf {i}}}})^T{{\dot{{\mathbf {\gamma }}}}_{{\mathbf {i}}}}. \end{aligned}$$

(31)

The velocity Eq. (31) can be expressed in the following matrix form

$$\begin{aligned} K^{\#}\dot{{\mathbf {X}}}=T^{\#}\dot{\varvec{\Gamma }} \end{aligned}$$

(32)

where

$$\begin{aligned} K^{\#}= & {} \left[ \begin{array}{ll} {{{\mathbf {A}}}_{{\mathbf {1}}}}{{{\mathbf {D}}}_{{\mathbf {1}}}}^T+K_1{{{\mathbf {z}}}^{T}} & ( {\mathbf {u_1 }}\times {{{\mathbf {A}}}_{{\mathbf {1}}}}{{{\mathbf {D}}}_{{\mathbf {1}}}} )^T{\mathbf {z}}\\ {{{\mathbf {A}}}_{{\mathbf {2}}}}{{{\mathbf {D}}}_{{\mathbf {2}}}}^T+K_2{{{\mathbf {z}}}^{T}} & ( {\mathbf {u_2}}\times {{{\mathbf {A}}}_{{\mathbf {2}}}}{{{\mathbf {D}}}_{{\mathbf {2}}}} )^T{\mathbf {z}}\\ {{{\mathbf {A}}}_{{\mathbf {3}}}}{{{\mathbf {D}}}_{{\mathbf {3}}}}^T+K_3{{{\mathbf {z}}}^{T}} & ( {\mathbf {u_3 }}\times {{{\mathbf {A}}}_{{\mathbf {3}}}}{{{\mathbf {D}}}_{{\mathbf {3}}}} )^T{\mathbf {z}}\\ \end{array} \right] ,\\ T^{\#}= & {} \left[ \begin{array}{llll} T_{1} &{} 0 &{} 0 &{} 0 \\ 0 &{} T_{2} &{} 0 &{} 0 \\ 0 &{} 0 &{} T_{3} &{} 0 \\ \end{array} \right] ,\\ K_i= & {} {(l_{i1}\cos (\gamma )+{{l}_{i3}})z}/{{{\left( l_{i2}^{2}-{{z}^{2}} \right) }^{0.5}}}, \\ T_i= & {} -sgn(i)({{{\mathbf {B}}}_{{\mathbf {i}}}}{{{\mathbf {D}}}_{{\mathbf {i}}}}\times {{{\mathbf {A}}}_{{\mathbf {i}}}}{{{\mathbf {D}}}_{{\mathbf {i}}}})^T{\mathbf {z}}, i=1,2,3, \end{aligned}$$

and $\dot{\varvec{\Gamma }}=(\dot{\gamma _1}, \dot{\gamma _2},\dot{\gamma _3},\dot{\gamma _4})^T$ is the velocity vector of the passive joint variables in the joint space.

For the lifting subchain, according to the geometry we have

$$\begin{aligned} \left\| {{{\mathbf {B}}}_{{\mathbf {4}}}}{{{\mathbf {D}}}_{{\mathbf {4}}}} \right\| ^2=l_{42}^2-(R_4-l_{41} \cos {\theta _4}-l_{43})^2+(R_4-l_{41}\cos {\theta _4})^2. \end{aligned}$$

Again, differentiating the equation results in the lifting subchain velocity relationship.

$$\begin{aligned} ({{{\mathbf {V}}}_{{{{\mathbf {D}}}_{{\mathbf {4}}}}}} -{{{\mathbf {V}}}_{{{{\mathbf {B}}}_{{\mathbf {4}}}}}})^T \cdot {{{\mathbf {B}}}_{{\mathbf {4}}}}{{{\mathbf {D}}}_{{\mathbf {4}}}}= & {} M(x_4\dot{x}+y_4\dot{y}+(b_1-b_2) (y_4\cos {\phi }-x_4\sin {\phi })\dot{\phi })\nonumber \\&\quad +l_{41}l_{43}\sin {\theta _4}\dot{\theta _4} \end{aligned}$$

(33)

where $M=l_{43}/R_4$. Since ${{{\mathbf {V}}}_{{{{\mathbf {D}}}_{{\mathbf {4}}}}}}= {{{\mathbf {V}}}_{{{{\mathbf {D}}}_{{\mathbf {3}}}}}}$, it can be further deduced as

$$\begin{aligned}&{{{\mathbf {B}}}_{{\mathbf {4}}}}{{{\mathbf {D}}}_{{\mathbf {4}}}}^T {\mathbf {v}}-M(x_4\dot{x}+y_4\dot{y}) +({{\mathbf {u }}_{{\mathbf {3}}}}\times {{{\mathbf {B}}}_{{\mathbf {4}}}}{{{\mathbf {D}}}_{{\mathbf {4}}}} )^T {\mathbf {w}}\nonumber \\&\quad -M((b_1-b_2)(y_4\cos {\phi }-x_4\sin {\phi })\dot{\phi })\nonumber \\&\quad =({{{\mathbf {A}}}_{{\mathbf {4}}}}{{{\mathbf {B}}}_{{\mathbf {4}}}}\times {{{\mathbf {B}}}_{{\mathbf {4}}}} {{{\mathbf {D}}}_{{\mathbf {4}}}})^T{{\dot{{\mathbf {\theta }}}}_{{\mathbf {4}}}} +l_{41}l_{43}\sin {\theta _4}\dot{\theta _4}. \end{aligned}$$

(34)

The velocity Eq. (34) also can be expressed in a matrix form:

$$\begin{aligned} J_x^*\dot{{\mathbf {X}}}=J_{\theta }^*\dot{\varvec{\Theta }} \end{aligned}$$

(35)

where

$$\begin{aligned} J_{x}^{*}&=\left[ {\mathbf {{{B}}_{4}}{{D}_{4}}}^T-{\mathbf {C_4D_4}}^T \quad ( {\mathbf {{{u }}_{3}}}\times {\mathbf {{{B}}_{4}}{{D}_{4}}})^T {\mathbf {z}}+b \right] , \\ J_{\theta }^{*}&=\left[ 0 \quad 0 \quad 0 \quad( {\mathbf {{{A}}_{4}}{{B}_{4}}}\times {\mathbf {{{B}}_{4}}{{D}_{4}}} )^T(y_4{\mathbf {x}}-x_4{\mathbf {y}})/R_4+c \right] , \end{aligned}$$

and ${\mathbf {C_4D_4}}=M( {{x}_{4}},{{y}_{4}},0 )^T, b=-M({{b}_{1}}-{{b}_{2}} )( {{y}_{4}}\cos \phi -{{x}_{4}}\sin \phi ), c={{l}_{41}}{{l}_{43}}\sin {{\theta }_{4}}, {\mathbf {x}}=(1,0,0)^T, {\mathbf {y}}=(0,1,0)^T$.

Use the geometric relationship of $R_4$ and the z coordinate of the point $D_4$,

$$\begin{aligned} R_4\,=\,& {} l_{41}\cos \theta _4+l_{42}\cos (\theta _4-\gamma _4)+l_{43};\nonumber \\ z_4\,=\,& {} h_1+l_{41}\sin \theta _4+l_{42}\sin (\theta _4-\gamma _4). \end{aligned}$$

Differentiating these equations leads to the velocity relationship as follows,

$$\begin{aligned}&{({{x}_{4}}\dot{x}+{{y}_{4}}\dot{y}+( {{b}_{1}}-{{b}_{2}} )( {{y}_{4}}\cos \phi -{{x}_{4}}\sin \phi )\dot{\phi })}/{{{R}_{4}}}=\\&\quad -( {{l}_{41}}\sin {{\theta }_{4}}+{{l}_{42}}\sin ( {{\theta }_{4}}-{{\gamma }_{4}} ) ){{{\dot{\theta }}}_{4}}+{{l}_{42}}\sin ( {{\theta }_{4}}-{{\gamma }_{4}} ){{{\dot{\gamma }}}_{4}};\\&\quad \dot{z}=({{l}_{41}}\cos {{\theta }_{4}}+{{l}_{42}}\cos ({{\theta }_{4}}-{{\gamma }_{4}})){{\dot{\theta }}_{4}}-{{l}_{42}}\cos ({{\theta }_{4}}-{{\gamma }_{4}}){{\dot{\gamma }}_{4}}. \end{aligned}$$

Using equations above to eliminate ${{\dot{\theta }}_{4}}$, the velocity relationship between the end-effector and passive joint can be expressed in a matrix form:

$$\begin{aligned} K^*\dot{{\mathbf {X}}}=T^*\dot{\varvec{\Gamma }} \end{aligned}$$

(36)

where

$$\begin{aligned} K^{*}&=\left[ \begin{array}{ll} d{\mathbf {C}}_{\mathbf {4}} {\mathbf {D}}_{\mathbf {4}}^T-e{\mathbf {z}}^T& -b/l_{43} \\ \end{array} \right] , \\ T^{*}&=\left[ 0 \quad 0 \quad 0 \quad -l_{41}l_{42}\sin \gamma _4 \right] ,\end{aligned}$$

and $d=(l_{41}\cos \theta _4+l_{42}\cos (\theta _4-\gamma _4))/l_{43}, e=l_{41}\sin \theta _4+l_{42}\sin (\theta _4-\gamma _4)$.

Finally, the total manipulator velocity equation can be described as follows.

$$\begin{aligned} J_x\dot{{\mathbf {X}}}=J_{\theta }\dot{\varvec{\Theta }}\ \ \ \ \ \ \ \ \ \ K\dot{{\mathbf {X}}}=T\dot{\varvec{\Gamma }} \end{aligned}$$

(37)

where

$$\begin{aligned} {{J}_{x}}= & {} \left[ \begin{matrix} J_{x}^{\#} \\ J_{x}^{*} \\ \end{matrix} \right] , {{J}_{\theta }}=\left[ \begin{matrix} J_{\theta }^{\#} \\ J_{\theta }^{*} \\ \end{matrix} \right] ,\\ {K}= & {} \left[ \begin{matrix} K^{\#} \\ K^{*} \\ \end{matrix} \right] , {T}=\left[ \begin{matrix} T^{\#} \\ T^{*} \\ \end{matrix} \right] . \end{aligned}$$

The forward instantaneous kinematic problem (FIKP) is solvable for a given configuration if there exist $J_F$ and $P_F$, satisfying $\dot{{\mathbf {X}}}={J}_{F}\dot{\varvec{\Theta }}$ and $\dot{\varvec{\Gamma }}={{P}_{F}}\dot{\varvec{\Theta }}$, where $J_F=J_x^{-1}J_\theta , P_F=T^{-1}KJ_x^{-1}J_\theta$. The inverse instantaneous kinematic problem (IIKP) is solvable for a given configuration if there exist $J_I$ and $P_I$, satisfying $\dot{\varvec{\Theta }}={J}_{I}\dot{{\mathbf {X}}}$ and $\dot{\varvec{\Gamma }}={{P}_{I}}\dot{{\mathbf {X}}}$, where $J_I=J_\theta ^{-1}J_x$ and $P_I=T^{-1}K$. Based on these four matrices $J_F, P_F, J_I$ and $P_I$, there are six types of singularities to be discussed [18].

5.1 Redundant input type singularity

This kind of singularity occurs when the matrix $J_I$ does not exist. It implies det$(J_\theta )=0$. In such a configuration, there exist a non-zero input, $\dot{\varvec{\Theta }}\ne {\mathbf {0}}$, and a vector of passive joint velocities, $\dot{\varvec{\Gamma }}$, which satisfy the velocity equation for a zero-output, $\dot{{\mathbf {X}}}={\mathbf {0}}$. It always happens when one of the subchains reaches the boundary of its workspace. Its condition is equivalent to that at least one of the diagonal elements in $J_\theta$ is zero. For $J_\theta ^{\#}$ due to ${{\mathcal {RRP}}}_{a}{{\mathcal {R}}}$ subchains, if ${\mathbf {A_iB_i}}\text {//}{\mathbf {B_iD_i}}, i=1, 2$ or 3, the matrix will be rank deficient. This case only appears at $z=0$, i.e., the parallelograms are in the shape of rectangles. When the planar parallelograms are not rectangular, as long as ${\mathbf {A_iB_i}}$ and ${\mathbf {B_iD_i}}$ are coplanar vertically, the singularity will also occur (Fig. 9a). The singularity condition for the lifting subchain is not only ${\mathbf {A_4B_4}}\text {//}{\mathbf {B_4D_4}}$, but also $\sin \theta _4=0$. Figure 9b shows a configuration of the lifting subchain where points $A_4, B_4, {D_4}$ are colinear. In this case, when $\theta =0$ or $180^\circ$, a redundant input type singularity occurs at the lifting subchain.

Fig. 9

a A ${{\mathcal {RRP}}}_{a}{{\mathcal {R}}}$ subchain in singular configuration; b A configuration of the lifting subchain: $A_4, B_4, {D_4}$ are colinear

5.2 Redundant output type singularity

When the determinant of $J_x$ vanishes, the matrix $J_F$ does not exist. It means this configuration is a singularity of redundant output type. In such a configuration, there exists a non-zero output, $\dot{{\mathbf {X}}}\ne {\mathbf {0}}$, and a vector of passive joint velocities, $\dot{\varvec{\Gamma }}$, even for a zero-input, $\dot{\varvec{\Theta }}={\mathbf {0}}$.

From the matrix $J_x^{\#}$, the singularities may occur with full $360^{\circ }$ rotation of the end-effector. By observing $J_{x}^{\#}$, when ${\mathbf {u_i}}$ and ${\mathbf {B_iD_i}}$ are coplanar vertically (parallel to the z axis), the fourth element of the ith row is zero. The first three elements make up a vector, which is ${\mathbf {B_iD_i}}$ plus a z-direction vector, renamed vector ${\mathbf {B_iD_i^{'}}}$. If ${\mathbf {H_i}}{\mathbf {H_j}}$ and ${\mathbf {B_3D_3}}$ are vertically coplanar, and ${\mathbf {B_1D_1^{'}}}\text {//}{\mathbf {B_3D_3^{'}}}$ (or ${\mathbf {H_i}}{\mathbf {H_j}}$ and ${\mathbf {B_2D_2}}$ are vertically coplanar, and ${{\mathbf {B}}_{{\mathbf {2}}}{{\mathbf {D}}_{\mathbf {2}}}}^{'} \text {//}{\mathbf {B_3D_3^{'}}}$), this type of singularity occurs. A particular case is ${\mathbf {B_1D_1^{'}}}\text {//} {{\mathbf {B}}_{{\mathbf {2}}}{{\mathbf {D}}_{\mathbf {2}}}}^{'}\text {//}{\mathbf {B_3D_3^{'}}}$.

For $J_x^*$, the first three elements make up the vector ${\mathbf {B_4C_4}}$. It will be parallel to ${\mathbf {B_iD_i}}$ when the $ith\,{{\mathcal {RRP}}}_{a}{{\mathcal {R}}}$ subchain reaches the boundary of its workspace. The fourth element will be zero when ${\mathbf {u_i}}$ and ${\mathbf {B_4D_4}}$ are vertically coplanar. Mathematically, when ${\mathbf {u_i}}$ and ${\mathbf {B_4D_4}}$ are vertically coplanar and ${\mathbf {B_iD_i}}\text {//}{\mathbf {B_4C_4}}\text {//}{\mathbf {z}}$, the configuration is at the redundant output type singularity.

5.3 Impossible input type singularity

A configuration is a singularity of impossible input type if there exists a vector $\dot{\varvec{\Theta }}$ for which the velocity equation cannot be satisfied for any combination of $\dot{{\mathbf {X}}}$ and $\dot{\varvec{\Gamma }}$. It means neither of the matrices $J_I$ and $P_I$ exists. Both $J_\theta$ and T are rank deficient. Similarly, when ${\mathbf {B_iD_i}}$ and ${\mathbf {A_iD_i}}, i=1, 2$ or 3, are colinear or vertically coplanar, or ${\mathbf {A_4B_4}}$ and ${\mathbf {B_4C_4}}$ are colinear, $\det \left( T \right) =0$, there is a redundant input type singularity, which is also an impossible input type singularity.

5.4 Impossible output type singularity

A configuration is a singularity of impossible output type if there exists a vector $\dot{{\mathbf {X}}}$ for which the velocity equation cannot be satisfied for any combination of $\dot{\varvec{\Theta }}$ and $\dot{\varvec{\Gamma }}$. When both $J_x$ and T are rank deficient, the matrices $J_I$ and $P_I$ do not exist. one example of such singularity is when ${\mathbf {A_4B_4}}$ and ${\mathbf {B_4C_4}}$ are colinear, and ${\mathbf {B_1D_1^{'}}}\text {//}{{\mathbf {B}}_{{\mathbf {2}}}{{\mathbf {D}}_{\mathbf {2}}}}^{'}$ $\text {//}{\mathbf {B_3D_3^{'}}}$.

5.5 Increased instantaneous mobility type singularity

The increased instantaneous mobility type singularity occurs when both $J_x$ and $J_\theta$ are rank deficient. This type of singularity is a combination of the two aforementioned types (Sects. 5.1 and 5.2) of singularity. It depends not only on configurations but also on the geometric parameters such as link length and size of base and end-effector. An example of this kind singularity occurs when ${\mathbf {A_1B_1}}\text {//}{\mathbf {B_1D_1}} \text {//}{\mathbf {B_3D_3}}\text {//}{\mathbf {u_3}}$.

5.6 Redundant passive motion type singularity

A configuration is a singularity of redundant passive passive motion type if there exists a non-zero passive joint velocity vector, $\dot{\varvec{\Gamma }}\ne {\mathbf {0}}$, which satisfies the velocity equation for a zero input and a zero output. Such a configuration is singular, since both the FIKP and the IIKP are insolvable, when neither of the matrices $P_F$ and $P_I$ exists. Its condition is also that both $J_x$ and T are rank deficient. So, these singularities of this new parallel manipulator is the same as the impossible output type singularities.

6 Conclusion

In this paper, a novel 4-DoF Schönflies motion parallel manipulator, the T4 robot, is proposed. It is a 4-DoF version of the V3 robot, a planar parallel manipulator. It retains large workspace and unlimited rotation capability of the end-effector. Due to the introduction of the lifting subchain, a ${\mathcal {RRRRR}}$ serial chain, the T4 robot becomes a fully parallel manipulator able of translation along the common axis, which is more suitable for general pick-and-place operations. Further, it is shown in the paper that the kinematics of this manipulator have closed-form solutions. The workspace can be computed analytically by an algebraic derivation.