1 Introduction

Currently after a century of struggling to enhance industrial heat transfer by fluid mechanics, the limited ability of conventional fluids such as water, oil, and ethylene-glycol (EG) for transferring heat has been one of the major challenges in heat transfer science. One of the ways to overcome this problem is to replace these conventional fluids with advanced fluids with higher thermal conductivity. These so-called advanced fluids were supposed to be merely theoretical fluids for a long time before the rapid development of nanotechnology. Nanotechnology brought back the hope for developing an efficient heat exchanger for introducing a new branch of fluids called nanofluids. Nanofluids are produced by dispersing small quantities of metal or semi-metal particles with dimensions of up to 100 nm into a typical base fluid such as water, oil, or EG. The main idea goes back to Maxwell’s [1] study. He showed the possibility of increasing thermal conductivity of a fluid-solid mixture by having a greater volume fraction of solid particles. Particles with dimensions of micrometers or even millimeters were used. Those particles caused several problems such as abrasion, clogging, and pressure losses. Choi et al. [2] quantitatively analyzed some potential benefits of nanofluids on heat transfer enhancement, on reducing size, weight, and cost of thermal equipment, while incurring little or no penalty in the form of a pressure drop. Researchers have demonstrated that oxide ceramic nanofluids consisting of CuO or Al2O3 nanoparticles on water or EG exhibit enhanced thermal conductivity (Lee et al. [3]). On the other hand, larger particles with an average diameter of 40 nm led to an increase of less than 10 % (Lee et al. [3]). Furthermore, the effective thermal conductivity of a metallic nanofluid increased by up to 40 % for a nanofluid consisting of EG containing approximately 3 % vol. of a Cu nanoparticle of a mean diameter of less than 10 nm (Choi et al. [2]). Different concepts have been proposed to explain this enhancement in heat transfer and also to predict the effective thermal conductivity of the nanofluids.

The effective thermal conductivity increment may also depend on the shape of nanoparticles as discussed by [4–6]. They proposed a differential effective medium theory based on Bruggeman’s model (Keblinski et al. [7]) to approximate the effective thermal conductivity of nano-dispersion with non-spherical solid nanoparticles with consideration of the interfacial thermal resistance across the solid particles and the host fluids. They found that a high enhancement of effective thermal conductivity can be gained if the shape of nanoparticles deviates greatly from spherical. Many of the researchers suggested altogether new mechanisms for the transport of thermal energy (Keblinski et al. [7]). The subsequent simulation work from the same group of investigators concludes that these mechanisms do not contribute considerably to heat transfer. Koo and Kleinstreuer [8] found that the role of Brownian motion is much more significant than the thermophoretic and osmophoretic motions. In conclusion, some investigators believe that nanoparticle aggregation plays an important role in thermal transport due to their chain shape but some others believe that the time-dependent thermal conductivity in the nanofluids proves the reduction of thermal conductivity by passing time due to clustering of nanoparticles with time (Karthikeyan et al. [9]).

Vadász [10] showed that heat transfer enhancement may be caused by a transient heat conduction process in nanofluids. Experiments demonstrate that a nanofluid thermal conductivity depends on a great number of parameters, such as the chemical composition of the solid particle and the base fluid, surfactants, particle shape, size, concentration, polydispersity, etc., though the exact variation trend of the conductivity with these factors has not yet been found. Additionally, the temperature influences the thermal conductivity of a nanofluid as shown in several studies that have been carried out to see that effect on CuO, Al2O3, TiO2, ZnO dispersed nanofluids by Yu et al. [11] and Karthikeyan et al. [9]

Eastman et al. [12] conducted a comprehensive review on thermal transport in nanofluids to conclude that a satisfactory explanation for the abnormal enhancement in thermal conductivity and viscosity of nanofluids needs further studies. Buongiorno [13] conducted a comprehensive study to account for the unusual behavior of nanofluids based on inertia, Brownian diffusion, thermophoresis, diffusiophoresis, Magnus effects, fluid drainage and gravity settling, and proposed a model incorporating the effects of Brownian diffusion and the thermophoresis. With the help of these equations, studies were conducted by Kim et al. [14] and more recently by Nield and Kuznetsov [15].

Poromechanics is the study of porous materials whose mechanical behavior is significantly influenced by the pore fluid. Poromechanics is relevant to disciplines as varied as geophysics, biomechanics, physical chemistry, agricultural engineering or materials science. It the porous materials and the fields concerned are many, their unity lies in the fact that they are all subject to same coupled processes: hydro-diffusion and subsidence, hydration and swelling, drying and shrinkage, heating and build-up of pore pressure, freezing, and spalling, capillary and cracking. Coussy [16] gave a unified and systemic continuum approach to poromechanics. Following the approach of Biot [17], Coussy developed two concepts of continuum mechanics of solids to poromechanics. The first concept is to consider the porous medium as the superposition of several continua that move with distinct kinematics, while mechanically interacting and exchanging energy and matter. Since the formulation of the constitutive equations of any solid requires its deformation to be referred to an initial configuration, the second concept is to transport the equations governing the physics of the superposed fluid and solid continua from their common current configuration to an initial reference configuration related to the solid skeleton. Following concepts of Coussy [16], Sciarra and Coussy [18], Sciarra et al. [19] and Madeo et al. [20] developed the theory of second gradient poromechanics.

The problem under study deals with the linear and nonlinear stability for the onset of convection in a horizontal layer of a porous medium saturated by a nanofluid. In the formulation of the problem, the Brownian motion and thermophoresis are ignored. However the effect of the variation of thermal conductivity and viscosity with nanofluid particle fraction using the theory of mixtures with cross diffusion is examined, following the approach of Tiwari and Das [21]. It is assumed that the nanofluid is diluted so that the nanofluid volume fraction is small compared with unity. Then the basic solution is such that this fraction is a linear function of the vertical coordinate. Thus, to a first approximation, the thermal conductivity and the viscosity can be taken as weak functions of the vertical coordinate. This means that we can treat the problem as one involving a weakly heterogeneous porous medium using an approach developed by the authors (see the papers surveyed by Nield [22]) to obtain an approximate analytical solution.

2 Analysis

2.1 Conservation equations

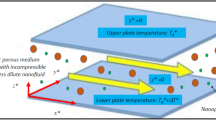
We select a coordinate frame in which the z-axis is aligned vertically upwards. We consider a horizontal layer of fluid confined between the planes z ∗=0 and z ∗=H. Asterisks are used to denote dimensional variables. Each boundary wall is assumed to be perfectly thermally conducting. The temperatures at the lower and upper boundary are taken to be \(T_{0}^{*} + \varDelta T^{*}\) and T ∗. The Oberbeck Boussinesq approximation is employed. In the linear stability theory being applied here, the temperature change in the fluid is assumed to be small in comparison with \(T_{0}^{*}\). The conservation equations for the total mass, momentum, thermal energy and nanoparticles takes the form as

$$\begin{aligned} &{\nabla^{*}.\mathbf{v}_{D}^{*} = 0 } \end{aligned}$$
(1)
$$\begin{aligned} &{\frac{\rho}{\varepsilon} \frac{\partial\mathbf{v}_{D}^{*}}{ \partial t^{*}} = - \nabla^{ *} p^{ *} - \frac{\mu_{eff}}{K}\mathbf{v}_{D}^{*} + \rho g } \end{aligned}$$
(2)
$$\begin{aligned} &{ \begin{aligned}[b] &( \rho c )_{m} \frac{\partial T^{ *}}{ \partial t^{ *}} + ( \rho c )_{f} \mathbf{v}_{D}^{*}. \nabla^{*}T^{ *} \\ &\quad = k_{m} \nabla^{*2}T^{ *} + \varepsilon ( \rho c )_{p} \\ &\qquad{}\times \biggl[ D_{B} \nabla^{*} \phi^{*}.\nabla T^{*} + D_{T} \frac{\nabla T^{*}.\nabla T^{*}}{T^{*}} \biggr]\end{aligned} } \end{aligned}$$
(3)
$$\begin{aligned} &{\frac{\partial\phi^{*}}{\partial t^{*}} + \frac{1}{\varepsilon} \mathbf{v}_{D}^{*}. \nabla^{*}\phi^{*} = D_{B} \nabla^{*2} \phi^{*} + \frac{D_{T}}{ T_{C}^{*}}\nabla^{*2}T^{*} } \end{aligned}$$
(4)

Here, \(\mathbf{v}_{D}^{*} = ( u^{*}, v^{*}, w^{*})\) is the nanofluid Darcy velocity, ρ is the overall density of the nanofluid, which we now assume to be given by \(\rho= \phi^{*} \rho_{p} + (1 - \phi^{*} )\rho_{0} [1 - \beta_{T} ( T^{*} - T_{0}^{*} ) ]\), where ρ p is the particle density, ρ 0 is a reference density for the fluid, and β T is the thermal volumetric expansion. c is the fluid specific heat (at constant pressure), k m is the overall thermal conductivity of the porous medium saturated by the nanofluid, and c p is the nanoparticle specific heat of the material constituting the nanoparticles. k m =εk eff +(1−ε)k s where ε is the porosity, k eff is the effective conductivity of the nanofluid (fluid plus nanoparticles), and k s is the conductivity of the solid material forming the matrix of the porous medium. ϕ ∗ is the nanoparticle volume fraction, T ∗ is the temperature, D B is the Brownian diffusion coefficient, and D T is the thermophoretic diffusion coefficient.

We now introduce the viscosity and the conductivity dependence on nanoparticle fraction. Following Tiwari and Das [21], we adopt the formulas, based on a theory of mixtures,

$$\begin{aligned} &{\frac{\mu_{eff}}{\mu_{f}} = \frac{1}{(1 - \phi^{*})^{2.5}} } \end{aligned}$$
(5)
$$\begin{aligned} &{\frac{k_{eff}}{k_{f}} = \frac{(k_{p} + 2k_{f}) - 2\phi^{*}(k_{f} - k_{p})}{(k_{p} + 2k_{f}) + \phi^{*}(k_{f} - k_{p})} } \end{aligned}$$
(6)

Here k f and k p are the thermal conductivities of the fluid and the nanoparticles, respectively.

Equation (5) was obtained by Brinkman [23], and Eq. (6) is the Maxwell-Garnett formula for a suspension of spherical particles that dates back to Maxwell [24].

In the case where ϕ ∗ is small compared with unity, we can approximate these formulas by

$$\begin{aligned} \begin{aligned} &\frac{\mu_{eff}}{\mu_{f}} = 1 + 2.5\phi^{*}, \\ &\frac{k_{eff}}{k_{f}} = \frac{(k_{p} + 2k_{f}) - 2\phi^{*}(k_{f} - k_{p})}{(k_{p} + 2k_{f}) + \phi^{*}(k_{f} - k_{p})} \\ &\qquad = 1 + 3\phi^{*}\frac{(k_{p} - k_{f})}{(k_{p} + 2k_{f})} \end{aligned} \end{aligned}$$
(7)

We assume that the temperature and the volumetric fraction of the nanoparticles are constant on the boundaries. Thus the boundary conditions are

$$\begin{aligned} &{w^{*} = 0,\qquad T^{*} = T_{0}^{*} + \varDelta T^{*}, } \\ &{\phi^{*} = \phi_{0}^{*} \quad\mathrm{at} \ z^{*} = 0, \qquad w^{*} = 0,\qquad T^{*} = T_{0}^{*}, } \\ &{\phi^{*} = \phi_{1}^{*} \quad\mathrm{at} \ z^{*} = H } \end{aligned}$$
(8)

We introduce dimensionless variables as follows. We define

$$ \begin{aligned} &(x,y,z) = \bigl(x^{*},y^{*},z^{*} \bigr)/H,\qquad t = t^{*}\alpha_{m}/\sigma H^{2}, \\ &(u,v,w) = \bigl(u^{*},v^{*},w^{*}\bigr)H/ \alpha_{m}, \\ &p =p^{*}K/\mu_{f}\alpha_{m}, \\ &\phi= \frac{\phi^{*} - \phi_{0}^{*}}{\phi_{1}^{*} - \phi_{0}^{*}},\qquad T = \frac{T^{*} - T_{0}^{*}}{\varDelta T^{*}} \end{aligned} $$
(9)

where

$$\alpha_{m} = \frac{k_{m}}{(\rho c_{p})_{f}},\qquad \sigma= \frac{(\rho c_{p})_{m}}{(\rho c_{p})_{f}} $$

We also define

$$ \begin{aligned} &\tilde{\mu} = \frac{\mu_{eff}}{\mu_{f}},\qquad \tilde{k}_{p} = \frac{k_{p}}{k_{f}},\qquad\tilde{k}_{s} = \frac{k_{s}}{k_{f}}, \\ &\tilde{k} = \frac{k_{m}}{k_{f}} \end{aligned} $$
(10)

From Eqs. (7), and (10), we have

$$\begin{aligned} \begin{aligned} &\tilde{\mu} = 1 + 2.5 \bigl[ \phi_{0}^{*} + \phi \bigl( \phi_{1}^{*} - \phi_{0}^{*} \bigr) \bigr], \\ &\tilde{k} = \varepsilon \biggl\{ 1 + 3 \bigl[\phi _{0}^{*} + \phi \bigl(\phi_{1}^{*} - \phi_{0}^{*} \bigr) \bigr]\frac{\tilde{k}_{p} - 1}{\tilde{k}_{p} + 2} \biggr\} + (1 - \varepsilon)\tilde{k}_{s} \end{aligned} \end{aligned}$$
(11)

Then Eqs. (1)–(4), and (8) takes the form:

$$\begin{aligned} &{\nabla.\mathbf{v} = 0 } \end{aligned}$$
(12)
$$\begin{aligned} &{ \begin{aligned}[b] & \biggl( \gamma_{a} \frac{\partial\mathbf{v}}{\partial t} + \nabla p + \mathit{Rm} \hat{e}_{z} - \mathit{Ra}_{T}T \hat{e}_{z} + \mathit{Rn} \phi \hat{e}_{z} \biggr) + \tilde{\mu} \mathbf{v} \\ &\quad = 0\end{aligned} } \end{aligned}$$
(13)
$$\begin{aligned} &{ \begin{aligned}[b] \frac{\partial T}{\partial t} + \mathbf{v}.\nabla T &= \tilde{k}\nabla^{2}T + \frac{N_{B}}{\mathit{Ln}}\nabla\phi.\nabla T \\ &\quad{} + \frac{N_{A}N_{B}}{\mathit{Ln}}\nabla T.\nabla T\end{aligned} } \end{aligned}$$
(14)
$$\begin{aligned} &{\frac{1}{\sigma} \frac{\partial\phi}{\partial t} + \frac{1}{\varepsilon} \mathbf{v}. \nabla \phi= \frac{1}{\mathit{Ln}}\nabla^{2}\phi+ \frac{N_{A}}{\mathit{Ln}} \nabla^{2}T } \end{aligned}$$
(15)
$$\begin{aligned} &{ \begin{aligned} &w = 0,\qquad T = 1,\qquad \phi= 0\quad \mathrm{at}\ z = 0, \\ &w = 0,\qquad T = 0,\qquad \phi= 1\quad \mathrm{at}\ z = 1\end{aligned} } \end{aligned}$$
(16)

Here

$$\begin{aligned} &{\gamma_{a} = \frac{\varepsilon}{\sigma \mathit{Va}},\qquad \mathit{Ln} = \frac{\alpha_{m}}{D_{B}},\qquad \mathit{Va} =\frac{\varepsilon^{2}\Pr}{\mathit{Da}},} \\ &{\Pr= \frac{\mu_{f}}{\rho\alpha_{m}}, \qquad \mathit{Da} = \frac{K}{H^{2}},} \\ &{\mathit{Ra}_{T} = \frac{\rho_{0}gK ( 1 - \phi_{0}^{*} )\beta_{T}H\varDelta T^{*}}{\mu_{f}\alpha_{m}},} \\ &{\mathit{Rm} = \frac{ [ \rho_{p}\phi _{0}^{ *} + \rho_{0}(1 - \phi_{0}^{ *} ) ]gKH}{\mu_{f}\alpha_{m}},} \\ &{\mathit{Rn} = \frac{(\rho_{p} - \rho_{0})(\phi_{1}^{*} - \phi_{0}^{*})gKH}{\mu_{f}\alpha_{m}},} \\ &{N_{A} = \frac{D_{T}\varDelta T^{*}}{D_{B}T_{c}^{*}(\phi_{1}^{ *} - \phi_{0}^{*})},} \\ &{N_{B} = \frac{(\rho c)_{p} (\phi_{1}^{ *} - \phi_{0}^{*})}{(\rho c)_{f}}.} \end{aligned}$$

The parameter γ a is the non-dimensional acceleration coefficient, Ln is a Lewis number, Va is a Vadász number, Pr is the Prandtl number, Da is the Darcy number and Ra T is the familiar thermal Rayleigh–Darcy number. The new parameters Rm and Rn may be regarded as a basic-density Rayleigh number and a concentration Rayleigh number, respectively. The parameter N A is a modified diffusivity ratio and is some what similar to the Soret parameter that arises in cross-diffusion phenomena in solutions, while N B is a modified particle-density increment.

Equation (13) has been linearized by neglecting a term proportional to the product of ϕ and T. This assumption is likely to be valid in the case of small temperature gradients in a dilute suspension of nanoparticles.

2.2 Basic solution

We seek a time-independent quiescent solution of Eqs. (12)–(16) with temperature and nanoparticle volume fraction varying in the z-direction as we assume the nanofluid to be rest at the basic state, that is a solution of the form

$$ \begin{aligned} &\mathbf{v} = 0,\qquad p = p_{b}(z),\qquad T=T_{b} (z),\\ &\phi= \phi_{b}(z) \end{aligned} $$
(17)

Equations (13)–(15) reduces to

$$\begin{aligned} &{0 = - \frac{dp_{b}}{dz} - \mathit{Rm} + \mathit{Ra}_{T}T_{b} - \mathit{Rn} \phi_{b} } \end{aligned}$$
(18)
$$\begin{aligned} &{\tilde{k}\frac{d^{2}T_{b}}{dz^{2}} + \frac{N_{B}}{\mathit{Ln}}\frac{d\phi_{b}}{dz} \frac{dT_{b}}{dz} + \frac{N_{A}N_{B}}{\mathit{Ln}} \biggl( \frac{dT_{b}}{dz} \biggr)^{2} = 0 } \end{aligned}$$
(19)
$$\begin{aligned} &{\frac{d^{2}\phi_{b}}{dz^{2}} + N_{A}\frac{d^{2}T_{b}}{dz^{2}} = 0 } \end{aligned}$$
(20)

According to Buongiorno [13], for most nanofluids investigated so far \(\mathit{Ln}/(\phi_{1}^{ *} - \phi_{0}^{ *})\) is large, of order 105–106, and since the nanoparticle fraction decrement is typically no smaller than 103 this means that Ln is large, of order 102–103, while N A is no greater than about 10. Using this approximation, the basic solution is found to be

$$ T_{b} = 1 - z\quad \mbox{and so}\quad \phi_{b} = z $$
(21)

2.3 Perturbation solution

We now superimpose perturbations on the basic solution. We write

$$ \begin{aligned} &\mathbf{v} = \mathbf{v}',\qquad p = p_{b} + p', \qquad T = T_{b} + T', \\ &\phi= \phi_{b} + \phi'\end{aligned} $$
(22)

Substitute in Eqs. (10)–(15), and linearize by neglecting products of primed quantities. The following equations are obtained when Eq. (21) is used.

$$\begin{aligned} &{\nabla.\mathbf{v}' = 0 } \end{aligned}$$
(23)
$$\begin{aligned} &{ \begin{aligned}[b] & \biggl( \nabla p' + \gamma_{a}\frac{\partial\mathbf{v}'}{\partial t} - \mathit{Ra}_{T} T'\hat{e}_{z} + \mathit{Rn} \phi' \hat{e}_{z} \biggr) + \tilde{\mu} \mathbf{v}' \\ &\quad = 0,\end{aligned} } \end{aligned}$$
(24)
$$\begin{aligned} &{ \begin{aligned}[b] \frac{\partial T'}{\partial t} - w' &= \tilde{k} \nabla^{2}T' + \frac{N_{B}}{\mathit{Ln}} \biggl( \frac{\partial T'}{\partial z} - \frac{\partial \phi'}{\partial z} \biggr) \\ &\quad{} - \frac{2N_{A} N_{B}}{\mathit{Ln}}\frac{\partial T'}{\partial z}\end{aligned} } \end{aligned}$$
(25)
$$\begin{aligned} &{\frac{1}{\sigma} \frac{\partial\phi'}{\partial t} + \frac{1}{\varepsilon} w' = \frac{1}{\mathit{Ln}}\nabla^{2}\phi' + \frac{N_{A}}{\mathit{Ln}} \nabla^{2}T' } \end{aligned}$$
(26)
$$\begin{aligned} &{ \begin{aligned}[b] &w' = 0,\qquad T' = 0,\qquad \phi' = 0\quad \mathrm{at}\ z = 0 \\ &\quad \mathrm{and\ at}\ z = 1\end{aligned} } \end{aligned}$$
(27)

where now we can approximate the viscosity and conductivity distributions by substituting the basic solution expression for ϕ, namely that given by Eq. (21), into Eq. (11), we obtain

$$\begin{aligned} \tilde{\mu} (z) =& 1 + 2.5 \bigl[ \phi_{0}^{*} + \bigl( \phi_{1}^{*} - \phi_{0}^{*} \bigr) z \bigr], \\ \tilde{k}(z) =& \varepsilon \biggl\{ 1 + 3 \bigl[ \phi_{0}^{*} + \phi \bigl( \phi_{1}^{*} - \phi_{0}^{*} \bigr) z \bigr] \frac{\tilde{k}_{p} - 1}{\tilde{k}_{p} + 2} \biggr\} \\ &{} + (1 - \varepsilon) \tilde{k}_{s} \end{aligned}$$
(28)

It will be noted that the parameter Rm is just a measure of the basic static pressure gradient and is not involved in these and subsequent equations.

We now recognize that we have a situation where properties are heterogeneous. These are now the viscosity and conductivity (rather that the more usual ones, namely permeability and conductivity) and we can now proceed as in a number of papers by the authors that are surveyed by Nield [22]. We assume that the heterogeneity is weak in the sense that the maximum variation of a property over the domain considered is small compared with the mean value of that property.

The six unknowns u′, v′, w′, p′, T′, ϕ′ can be reduced to three by operating on Eq. (24) with \(\hat{e}_{z}\) curl curl and using the identity curl \(\mathit{curl} \equiv \mathrm{grad\,div} - \nabla^{2}\) together with Eq. (23) and the weak heterogeneity approximation. The result (after using Eq. (28)) is

$$ \bigl( s \gamma_{a} + \tilde{\mu} (z) \bigr)\nabla^{2}w' = \mathit{Ra}_{T}\nabla_{H}^{2}T' - \mathit{Rn} \nabla_{H}^{2}\phi' $$
(29)

Here \(\nabla_{H}^{2}\) is the two-dimensional Laplacian operator on the horizontal plane.

The differential Eqs. (24), (25), (29) and the boundary conditions (27) constitute a linear boundary-value problem that can be solved using the method of normal modes.

We write

$$ \bigl( w', T',\phi' \bigr) = \bigl[ W(z), \varTheta(z),\varPhi(z) \bigr] \exp ( st + ilx + imy ) $$
(30)

and substitute into the differential equations to obtain

$$\begin{aligned} &{ \begin{aligned}[b] & \bigl( \tilde{\mu} (z) + \gamma_{a} s \bigr) \bigl( D^{2} - \alpha^{2} \bigr)W + \mathit{Ra}_{T} \alpha^{2}\varTheta- \mathit{Rn} \alpha^{2} \varPhi \\ &\quad = 0\end{aligned} } \end{aligned}$$
(31)
$$\begin{aligned} &{ \begin{aligned}[b] &W + \biggl( \tilde{k}(z) \bigl( D^{2} - \alpha^{2} \bigr) + \frac{N_{B}}{\mathit{Ln}}D - \frac{2N_{A}N_{B}}{\mathit{Ln}}D - s \biggr)\varTheta \\ &\quad{} - \frac{N_{B}}{\mathit{Ln}}D\varPhi= 0 \end{aligned} } \end{aligned}$$
(32)
$$\begin{aligned} &{ \begin{aligned}[b] &\frac{1}{\varepsilon} W - \frac{N_{A}}{\mathit{Ln}} \bigl( D^{2} - \alpha^{2} \bigr)\varTheta- \biggl( \frac{1}{\mathit{Ln}} \bigl( D^{2} - \alpha^{2} \bigr) - \frac{1}{\sigma} s \biggr) \varPhi \\ &\quad = 0\end{aligned} } \end{aligned}$$
(33)
$$\begin{aligned} &{W = 0, \qquad \varTheta= 0, \qquad \varPhi= 0\quad \mathrm{at}\ z = 0 \ \mbox{and}\ z = 1 } \end{aligned}$$
(34)

where

$$ D\equiv \frac{d}{dz}\quad \mbox{and}\quad \alpha= \bigl(l^{2} + m^{2} \bigr)^{1/2} $$
(35)

Thus α is a dimensionless horizontal wave number.

For neutral stability the real part of s is zero. Hence we now write s=iω, where ω is real and is a dimensionless frequency.

We now employ a Galerkin-type weighted residuals method to obtain an approximate solution to the system of Eqs. (31)–(34). We choose as trial functions (satisfying the boundary conditions) W p ,Θ p ,Φ p ; p=1,2,3,… and write

$$ \begin{aligned} &W=\sum_{p = 1}^{N} A_{p} W_{p},\qquad\varTheta= \sum _{p = 1}^{N} B{}_{p}\varTheta_{P}, \\ &\varPhi= \sum_{p = 1}^{N} C{}_{p}\varPhi_{P} \end{aligned} $$
(36)

Substitute into Eqs. (31)–(34), and make the expressions on the left-hand sides of those equations (the residuals) orthogonal to the trial functions, thereby obtaining a system of 3N linear algebraic equations in the 3N unknowns A p ,B p ,C p , p=1,2,…,N. The vanishing of the determinant of coefficients produces the eigenvalue equation for the system. One can regard Ra T as the eigenvalue. This enables us to find Ra T in terms of the other parameters.

Trial functions satisfying the boundary condition (34) can be chosen as

$$ W_{p} = \varTheta_{p} = \varPhi_{p} = \sin p \pi z;\quad p = 1, 2, 3, \ldots $$
(37)

The eigenvalue equation is

$$ \det M = 0 $$
(38)

where,

$$ M = \left [ \begin{array}{c@{\quad }c@{\quad }c} M_{11}& M_{12}& M_{13} \\ M_{21}& M_{22}& M_{23} \\ M_{31}& M_{32}& M_{33} \end{array} \right ] $$
(39)

and, for i, j=1,2,…,N,

$$\begin{aligned} &{ \begin{aligned} ( M_{11} )_{ij} &= - \bigl\langle \bigl( \tilde{\mu} ( z ) + \gamma_{a}s \bigr)W_{j}D^{2}W_{i} \bigr\rangle \\ &\quad{} + \alpha^{2} \bigl\langle \bigl( \tilde{\mu} ( z )+ \gamma_{a}s \bigr)W_{j}W_{i} \bigr\rangle \end{aligned}} \\ &{( M_{12} )_{ij} = - \mathit{Ra}_{T} \alpha^{2} \langle W_{j}\varTheta_{i} \rangle} \\ &{( M_{13} )_{ij} = \mathit{Rn}\alpha^{2} \langle W_{j}\varPhi_{i} \rangle} \\ &{( M_{21} )_{ij} = - \langle\varTheta_{j}W_{i} \rangle} \\ &{ \begin{aligned}[b] ( M_{22} )_{ij} &= - \bigl\langle \tilde{k} ( z ) \varTheta_{j}D^{2} \varTheta_{i} \bigr\rangle + \alpha^{2} \bigl\langle \tilde{k} ( z )\varTheta_{j} \varTheta_{i} \bigr\rangle \\ &\quad{} + s \langle \varTheta_{j} \varTheta_{i} \rangle + \biggl( \frac{2N_{A}N_{B}}{\mathit{Ln}} - \frac{N_{B}}{\mathit{Ln}} \biggr) \langle \varTheta_{j}D\varTheta_{i} \rangle\end{aligned}} \\ &{( M_{23} )_{ij} = - \frac{N_{B}}{\mathit{Ln}} \langle \varTheta_{j}D\varPhi_{i} \rangle} \\ &{( M_{31} )_{ij} = - \frac{1}{\varepsilon} \langle \varTheta_{j}W \rangle_{i}} \\ &{( M_{32} )_{ij} = \frac{N_{A}}{\mathit{Ln}} \bigl( - \bigl\langle \varPhi_{j}D^{2}\varTheta_{i} \bigr\rangle + \alpha^{2} \langle \varPhi_{j}\varTheta_{i} \rangle \bigr)} \\ &{( M_{33} )_{ij} = \frac{1}{\mathit{Ln}} \bigl( - \bigl\langle \varPhi_{j}D^{2}\varPhi_{i} \bigr\rangle + \alpha^{2} \langle \varPhi_{j}\varPhi_{i} \rangle \bigr) + \frac{s}{\sigma} \langle \varPhi_{j}\varPhi_{i} \rangle} \end{aligned}$$

Here

$$ \bigl\langle f ( z ) \bigr\rangle \equiv\int_{0}^{1} f ( z )dz. $$
(40)

In the present case, where viscosity and conductivity variations are incorporated, the critical wave number is unchanged and the stability boundary becomes

$$\begin{aligned} \mathit{Ra}_{T} =& \frac{1}{ ( \frac{J}{\mathit{Ln}} + \frac{s}{\sigma} )\alpha^{2}} \biggl[ ( \nu+ s \boldsymbol{\gamma}_{a} )J \biggl( \frac{J}{\mathit{Ln}} + \frac{s}{\sigma} \biggr) ( J \eta+ s ) \\ &{} - \frac{\mathit{Rn} \alpha^{2}}{\varepsilon} ( J \eta+ s ) - \frac{\mathit{Rn} \alpha^{2} N_{A}}{\mathit{Ln}} J \biggr] \end{aligned}$$
(41)

where

$$ \begin{aligned} &J = \bigl(\pi^{2} + \alpha^{2} \bigr), \\ &\nu= 1 + 1.25 \bigl( \phi_{1}^{*} + \phi_{0}^{*} \bigr), \\ &\eta= \varepsilon+ (1 - \varepsilon) \tilde{k}_{s} + \frac{3 ( \phi_{1}^{*} + \phi_{0}^{*} )\varepsilon}{2} \biggl( \frac{\tilde{k}_{p} - 1}{\tilde{k}_{p} + 2} \biggr)\end{aligned} $$
(42)

We observe that when there is no conductivity variation (that is η=1, as when \(\tilde{k}_{s} = 1\) and \(\tilde{k}_{p} = 1\)) the effect of viscosity variation is to increase the critical Rayleigh number by a factor ν. The additional effect of conductivity variation η is expressed by Eq. (42). When \(\tilde{k}_{s} = 1\), the maximum value of η is \(2.5 ( \phi_{1}^{*} + \phi_{0}^{*} )\) attained when ε=1 and \(\tilde{k}_{p} \to\infty\).

It is worth noting that the factor ν comes from the mean value of \(\tilde{\mu}(z)\) over the range [0, 1] and the factor η is the mean value of \(\tilde{k} ( z )\) over the same range. That means that when evaluating the critical Rayleigh number it is a good approximation to base that number on the mean values of the viscosity and conductivity based in turn on the basic solution for the nanofluid fraction.

3 Linear stability analysis

3.1 Stationary mode

For the validity of principle of exchange of stabilities (i.e., steady case), we have s=0 (i.e., s=s r +is i =s r =s i =0) at the margin of stability. For a first approximation we take N=1. Then the Rayleigh number at which marginally stable steady mode exists becomes,

$$ \mathit{Ra}_{T}^{St} = \frac{ ( \pi^{2} + \alpha^{2} )^{2}\nu\eta}{ \alpha^{2}} - \mathit{Rn} \biggl( N_{A} + \frac{\mathit{Ln} \eta}{\varepsilon} \biggr) $$
(43)

Finding the minimum as α varies results in

$$ \mathit{Ra}_{T}^{St} = 4\pi^{2} \nu\eta- \mathit{Rn} \biggl( N_{A} + \frac{\mathit{Ln} \eta}{ \varepsilon} \biggr) $$
(44)

with the minimum being attained at α=π. We recognize that in the absence of nanoparticles we recover the well-known result that the critical Rayleigh number is equal to 4π 2. Usually when one employs a single-term Galerkin approximation in this context one gets an overestimate by about 3 % (e.g. 1750 instead of 1708 in the case of the standard Bénard problem) but in this case the approximation happens to give the exact result.

3.2 Oscillatory mode

We now set s=iω, where \(\omega= \operatorname{Im} (\omega)\) (ω r =0) in Eq. (41) and clear the complex quantities from the denominator, to obtain

$$ \mathit{Ra}_{T} = \varDelta _{1} + i \omega \varDelta _{2} $$
(45)

For oscillatory onset Δ 2=0 (ω i ≠0) and this gives a dispersion relation of the form (on dropping the subscript i)

$$ b_{1} \bigl( \omega^{2} \bigr)^{2} + b_{2} \bigl( \omega^{2} \bigr) + b_{3} = 0 $$
(46)

Now Eq. (45) with Δ 2=0 gives

$$ \mathit{Ra}_{T}^{\mathit{Osc}} = a_{0} \bigl( a_{1} + \omega^{2}a_{2} \bigr) $$
(47)

where b 1,b 2 and b 3 and a 0,a 1 and a 2 and Δ 1 and Δ 2 are not presented here for brevity.

We find the oscillatory neutral solutions from Eq. (47). It proceeds as follows: First determine the number of positive solutions of Eq. (46). If there are none, then no oscillatory instability is possible. If there are two, then the minimum (over a 2) of Eq. (47) with ω 2 given by (46) gives the oscillatory neutral Rayleigh number. Since Eq. (46) is quadratic in ω 2, it can give rise to more than one positive value of ω 2 for fixed values of the parameters Rn, Ln, N A , σ, γ a , ν, η. However, our numerical solution of Eq. (46) for the range of parameters considered here gives only one positive value of ω 2 indicating that there exists only one oscillatory neutral solution. The analytical expression for oscillatory Rayleigh number given by Eq. (47) is minimized with respect to the wavenumber numerically, after substituting for ω 2 (>0) from Eq. (46), for various values of physical parameters in order to know their effects on the onset of oscillatory convection.

4 Non-linear stability analysis

In order to explore how the cross diffusion co-efficient terms affects the nonlinear development of onset of convection in porous layer saturated with nanofluid, it is necessary to solve the full nonlinear Eqs. (12)–(15). However, we will in the first place consider the early stages of nonlinear convection, when the basic structure of the convective rolls is still determined by the behavior of the linearized solution. In the neighborhood of the stability boundary, we develop the nonlinear analysis in which the amplitudes are no longer small but finite. For simplicity, we consider the case of two dimensional rolls, assuming all physical quantities to be independent of y. Eliminating the pressure and introducing the stream function we obtain:

$$\begin{aligned} &{( \nu+ s \gamma_{a} ) \nabla^{2}\varPsi+ \mathit{Ra}_{T} \frac{\partial T}{\partial x} - \mathit{Rn}\frac{\partial S}{\partial x} = 0 } \end{aligned}$$
(48)
$$\begin{aligned} &{\frac{\partial T}{\partial t} + \frac{\partial\varPsi}{\partial x} = \eta \nabla^{2}T + \frac{\partial ( \varPsi,T )}{\partial ( x,z )} } \end{aligned}$$
(49)
$$\begin{aligned} &{\frac{1}{\sigma} \frac{\partial S}{\partial T} + \frac{1}{\varepsilon} \frac{\partial\varPsi}{\partial x} = \frac{1}{\mathit{Ln}}\nabla^{2}S + \frac{N_{A}}{\mathit{Ln}} \nabla^{2}T + \frac{1}{\varepsilon} \frac{\partial (\varPsi,S)}{\partial(x,z)} } \end{aligned}$$
(50)

We solve Eqs. (48)–(50) subjecting them to stress-free, isothermal, iso-nanoconcentration boundary conditions:

$$ \psi= \frac{\partial^{2}\psi}{\partial z^{2}} = T = S = 0\quad \mathrm{at}\ z = 0, 1 $$
(51)

To perform a local non-linear stability analysis, we take the following Fourier expressions:

$$\begin{aligned} &{\psi= \sum_{n = 1}^{\infty} \sum _{m = 1}^{\infty} A_{_{m n}} ( t ) \sin ( m \alpha x ) \sin ( n\pi z ) } \\ &{T = \sum_{n = 1}^{\infty} \sum _{m = 1}^{\infty} B_{_{m n}} (t)\cos ( m \alpha x ) \sin ( n\pi z ) } \\ &{S = \sum_{n = 1}^{\infty} \sum _{m = 1}^{\infty} C_{_{m n}}(t) \cos(m \alpha x) \sin (n\pi z) } \end{aligned}$$
(52)

Further, we take the modes (1,1) for stream function, and (0,2) and (1,1) for temperature, and nanoparticle concentration, to get

$$\begin{aligned} &{\psi= A_{11}(t) \sin(\alpha x) \sin(\pi z) } \\ &{T = B_{11}(t)\cos(\alpha x) \sin (\pi z) + B_{02}(t) s\in (2 \pi z) } \\ &{S = C_{11}(t)\cos(\alpha x) \sin (\pi z) + C_{02}(t) \sin (2 \pi z) } \end{aligned}$$
(53)

where the amplitudes A 11(t), B 11(t), B 02(t), C 11(t) and C 02(t) are functions of time and are to be determined. Taking the orthogonality condition with the eigenfunctions associated with the considered minimal model, we get

$$ \begin{aligned} & \begin{aligned}[b] \frac{dA_{11}(t)}{dt} &= \frac{1}{\gamma_{a}\delta^{2}} \bigl[ \alpha \mathit{Rn} C_{11}(t) - \alpha \mathit{Ra} B_{11}(t) \\ &\quad{} - \nu\delta^{2}A_{11}(t) \bigr]\end{aligned} \\ &\frac{dB_{11}}{dt} = - \bigl[ \alpha A_{11}(t) + \eta\delta ^{2}B_{11}(t) + \alpha\pi A_{11}(t)B_{02}(t) \bigr] \\ & \frac{dB_{02}}{dt} = - \eta 4\pi^{2}B_{02}(t) + \frac{\alpha\pi}{2}A_{11}(t)B_{11}(t) \\ & \begin{aligned}[b] \frac{dC_{11}}{dt} &= - \sigma \biggl[ \frac{1}{\varepsilon} \alpha A_{11}(t) + \delta^{2} \biggl( \frac{C_{11}(t)}{\mathit{Ln}} + \frac{N_{A}}{\mathit{Ln}}B_{11}(t) \biggr) \\ &\quad{} + \frac{1}{\varepsilon} \alpha A_{11}(t)C_{02}(t) \biggr]\end{aligned} \\ & \begin{aligned}[b] \frac{dC_{02}}{dt} &= - \sigma \biggl[ \frac{1}{\mathit{Ln}}4\pi^{2}C_{02}(t) + 4\pi^{2}B_{03}(t) \frac{N_{A}}{\mathit{Ln}} \\ &\quad{} - \frac{a\pi}{2\varepsilon} A_{11}(t)C_{11}(t) \biggr] \end{aligned} \end{aligned} $$
(54)

In case of steady motion \(\frac{d ( )}{dt} = D_{i} = 0\), (i=1,2,…,5) and write all D i ’s in terms of A 11. Thus we get

$$\begin{aligned} \begin{aligned} D_{1} &= \frac{1}{\gamma_{a}\delta^{2}} \bigl[ \alpha \mathit{Rn} C_{11}(t) - \alpha \mathit{Ra} B_{11}(t) - \nu\delta^{2}A_{11}(t) \bigr] \\ D_{2} &= - \bigl[\alpha A_{11}(t) + \eta \delta^{2}B_{11}(t) + \alpha\pi A_{11}(t)B_{02}(t) \bigr] \\ D_{3} &= - \eta4\pi^{2}B_{02}(t) + \frac{\alpha\pi}{ 2}A_{11}(t)B_{11}(t) \\ D_{4} &= - \sigma \biggl[ \frac{1}{\varepsilon} \alpha A_{11}(t) + \delta^{2} \biggl[ \frac{C_{11}(t)}{\mathit{Ln}} + \frac{N_{A}}{\mathit{Ln}}B_{11}(t) \biggr] \\ &\quad {} + \frac{1}{\varepsilon} \alpha A_{11}(t) C_{02}(t) \biggr] \\ D_{5} &= - \sigma \biggl[ \frac{1}{\mathit{Ln}}4\pi^{2}C_{02}(t) + 4\pi^{2}B_{02}(t)\frac{N_{A}}{\mathit{Ln}} \\ &\quad {} - \frac{1}{\varepsilon} \frac{a\pi}{ 2}A_{11}(t)C_{11}(t) \biggr]\quad \mbox{and} \\ D_{1} &= D_{2} = D_{3} = D_{4} = D_{5} = 0 \end{aligned} \end{aligned}$$
(55)

The above system of simultaneous autonomous ordinary differential equations is solved numerically using Runge–Kutta–Gill method. One may also conclude that the trajectories of the above equations will be confined to the finiteness of the ellipsoid. Thus, the effect of the parameters Rn, Ln, N A on the trajectories is to attract them to a set of measure zero, or to a fixed point to say.

5 Heat and nanoparticle concentration transport

The thermal Nusselt number, Nu is defined as

$$\begin{aligned} \mathit{Nu}(t) =& \frac{\mathrm{Heat}\ \mathrm{transport}\ \mathrm{by}\ (\mbox{conduction $+$ convection})}{\mbox{Heat transport by conduction}} \\ =& 1 + \biggl[ \frac{\int_{0}^{2\pi} \frac{\partial T}{\partial z} dx}{\int_{0}^{2\pi/a} \frac{\partial T_{B}}{\partial z} dx} \biggr]_{z = 0} \end{aligned}$$

Substituting expressions (21) and (53) in above equation we get

$$\mathit{Nu}(t) = 1 - 2\pi B_{02}(t) $$

The Sherwood number (nanoparticle concentration Nusselt number), Sh is defined similar to the thermal Nusselt number. Following the procedure adopted for arriving at Nu(t), one can obtain the expression for Sh(t) in the form:

$$\mathit{Sh}(t) = \bigl( 1 - 2\pi C_{02}(t) \bigr) + N_{A} \bigl(1 - 2 \pi B_{02}(t) \bigr) $$

6 Results and discussions

The expressions of thermal Rayleigh number for stationary and oscillatory convections are given by Eqs. (43) and (47) respectively. Figures 1a–1d show the effect of various parameters on the neutral stability curves for stationary convection for Rn=−0.1, Ln=200, N A =−5, σ=10, ε=0.9, ν=1, η=1 with variation in one of these parameters. The effect of nanoparticle concentration Rayleigh number Rn is shown in Fig. 1a. It is shown that the thermal Rayleigh number decreases with increase in nanoparticle concentration Rayleigh number Rn, which means that nanoparticle concentration Rayleigh number Rn destabilizes the system. It should be noted that the negative value of Rn indicates a bottom-heavy case, while a positive value indicates a top-heavy case. The effect of Lewis number Ln on the thermal Rayleigh number is shown in Fig. 1b. One can see that the thermal Rayleigh number increases with increase in Lewis number, indicating that the Lewis number stabilizes the system. The effect of viscosity ratio ν and conductivity ratio η on the thermal Rayleigh number is depicted in Figs. 1c and 1d respectively, these figures show that as ν and η increases, Ra T increases which indicates that ν and η will stabilize the system. The effect of concentration Rayleigh number Rn and Lewis number Ln on thermal Rayleigh number Ra T for stationary convection show the similar results obtained by Long Sheu [25].

Fig. 1
figure 1

Neutral curves on stationary convection for different values of (a) nanoparticle concentration Rayleigh number Rn, (b) Lewis number Ln, (c) viscosity ratio ν, (d) conductivity ratio η

Full size image

Figures 2a–2h display the variation of thermal Rayleigh number for oscillatory convection with respect to various parameters. In Fig. 2a it is seen that for negative values of Rn (bottom-heavy case) the thermal Rayleigh number decreases as Rn increases which will advance the onset of convection. As the Lewis number Ln increases the thermal Rayleigh number Ra T decreases as seen in Fig. 2b which imply that Lewis number Ln destabilizes the system. The modified diffusivity ratio N A do not show any affect on the oscillatory convection (Fig. 2c). From Fig. 2d, one can reveal that the porosity ε destabilizes the system for oscillatory convection, that is, an increase in ε decreases the thermal Rayleigh number. As the thermal capacity ratio σ increases, the thermal Rayleigh number also increases as can be observed in Fig. 2e, which implies that σ has a stabilizing effect on the system for oscillatory convection. The effect of viscosity ratio ν and conductivity ratio η on thermal Rayleigh number is depicted in Figs. 2f and 2g respectively. From these figures one can conclude that both ν and η increases the thermal Rayleigh number for oscillatory convection thus delaying the onset of convection. The effect of Vadász number Va on thermal Rayleigh number is depicted in Fig. 2h. From this figure one can see that as Va increases the thermal Rayleigh number decreases thus Va destabilizes the system. The effect of concentration Rayleigh number Rn, Lewis number Ln and thermal capacity ratio σ on thermal Rayleigh number Ra T for oscillatory convection show the similar results obtained by Long Sheu [25].

Fig. 2
figure 2figure 2

Neutral curves on oscillatory convection for different values of (a) nanoparticle concentration Rayleigh number Rn, (b) Lewis number Ln, (c) modified diffusivity ratio N A , (d) porosity ε, (e) thermal capacity ratio σ, (f) viscosity ratio ν, (g) conductivity ratio η, (h) Vadász number Va

Full size image

The nonlinear analysis provides not only the onset threshold of finite amplitude motion but also the information of heat and mass transports in terms of Nusselt Nu and Sherwood Sh numbers. The Nu and Sh are computed as the functions of Ra T , and the variations of these non-dimensional numbers with Ra T for different parameter values are depicted in Figs. 3a–3d and 4a–4e respectively. In Figs. 3a–3d and 4a–4e it is observed that in each case, Sherwood number is always greater than Nusselt number and both Nusselt number and Sherwood number start with the conduction state value 1 at the point of onset of steady finite amplitude convection. When Ra T is increased beyond \(\mathit{Ra}_{T_{c}}\), there is a sharp increase in the values of both Nu and Sh. However further increase in Ra T will not change Nu and Sh significantly. It is to be noted that the upper bound of Nu is 3 (similar results were obtained by Malashetty et al. [26]). It should also be noted that the upper bound of Sh is not 3 (similar results were obtained by Bhadauria and Agarwal [27]). The upper bound of Nu remains 3 only for both clear and nanofluid. Whereas, the upper bound for Sh for clear fluid is 3 but for nanofluid it is not fixed.

Fig. 3
figure 3

Variation of Nusselt number Nu with critical Rayleigh Number for different values of (a) nanoparticle concentration Rayleigh number Rn, (b) Lewis number Ln, (c) viscosity ratio ν, (d) conductivity ratio η

Full size image
Fig. 4
figure 4

Variation of Sherwood number Sh with critical Rayleigh Number for different values of (a) nanoparticle concentration Rayleigh number Rn, (b) Lewis number Ln, (c) modified diffusivity ratio N A , (d) viscosity ratio ν, (e) conductivity ratio η

Full size image

In Figs. 3a and 4a we observe that as the concentration Rayleigh number Rn increases, the value of Nu and Sh decreases, thus showing a decrease in the rate of heat and mass transport. Figures 3b and 4b shows that as Lewis number increases both Nu and Sh decreases, which imply that increasing the Lewis number suppresses the heat and mass transport. We observe that on increasing modified diffusivity ratio N A , there is no effect on the Nusselt number, whereas in Fig. 4c we observe that on increasing modified diffusivity ratio N A it increases the Sherwood number (which is similar result observed by Bhadauria and Agarwal, [27]). As the viscosity ratio ν (Figs. 3c and 4d) and conductivity ratio η (Figs. 3d and 4e) increases, both the Nu and Sh decreases implying that ν and η suppresses the heat and mass transports.

The linear solutions exhibit a considerable variety of behavior of the system, and the transition from linear to non-linear convection can be quite complicated, but interesting to deal with. A time dependent results needs to be studied to analyze the same. The transition can be well understood by the analysis of Eq. (54) whose solution gives a detailed description of the two dimensional problem. The autonomous system of unsteady finite amplitude equations is solved numerically using the Runge-Kutta method. The Nusselt and Sherwood numbers are evaluated as the functions of time t, the unsteady transient behavior of Nu and Sh is shown graphically in Figs. 5a–5f and 6a–6f respectively.

Fig. 5
figure 5

Transient Nusselt number Nu with time for different values of (a) nanoparticle concentration Rayleigh number Rn, (b) Lewis number Ln, (c) modified diffusivity ratio N A , (d) viscosity ratio ν, (e) conductivity ratio η, (f) Vadász number Va

Full size image
Fig. 6
figure 6

Transient Sherwood number Sh with time for different values of (a) nanoparticle concentration Rayleigh number Rn, (b) Lewis number Ln, (c) modified diffusivity ratio N A , (d) viscosity ratio ν, (e) conductivity ratio η, (f) Vadász number Va

Full size image

These figures indicate that initially when time is small, there occur large scale oscillations in the values of Nu and Sh indicating an unsteady rate of heat and mass transport in the fluid. As time passes by, these values approaches to their steady state values corresponding to a near convection stage.

Figure 5a depicts the transient nature of Nusselt number on nanoparticle concentration Rayleigh number Rn. It is observed that as Rn increases Nu decreases, thus showing a decrease in the heat transport, which is the similar result observed by Agarwal et al. [28]. From Figs. 5b, 5d, 5e and 5f we observe that as Lewis number, viscosity ratio, conductivity ratio and Vadász number increases the Nu decreases indicating that there is retardation on heat transport. The modified diffusivity ratio enhances the heat transport as seen in Fig. 5c.

It is seen from Figs. 6a, 6d, 6e and 6f that as nanoparticle concentration Rayleigh number Rn, viscosity ratio ν, conductivity ratio η and Vadász number Va increases the Sherwood number (concentration Nusselt number) decreases, which implies the suppress of mass transport. The mass transport is enhanced for Lewis number Ln and modified diffusivity ratio N A as seen in Fig. 6b and 6c respectively.

7 Conclusions

We considered linear and non-linear stability analysis in a horizontal porous medium saturated by a nanofluid, heated from below and cooled from above, using Darcy model which incorporates the effect of Brownian motion along with thermophoresis. Further the viscosity and conductivity dependence on nanoparticle fraction was also adopted following Tiwari and Das [21]. Linear analysis has been made using normal mode technique. However for weakly nonlinear analysis truncated Fourier series representation having only two terms is considered. We draw the following conclusions

  1. 1.

    For stationary convection Lewis number, viscosity ratio and conductivity ratio has a stabilizing effect while nanoparticle concentration Rayleigh number destabilize the system.

  2. 2.

    For oscillatory convection thermal capacity ratio, viscosity ratio and conductivity ratio stabilizes the system whereas nanoparticle concentration Rayleigh number, Lewis number, porosity, and Vadász number destabilizes the system.

  3. 3.

    For steady finite amplitude motions, the heat and mass transport decreases with increase in the values of nanoparticle concentration Rayleigh number, Lewis number, viscosity ratio and conductivity ratio. The mass transport increases with increase in modified diffusivity ratio and Vadász number.

  4. 4.

    The transient Nusselt number and Sherwood number increases with increase in Lewis number and modified diffusivity ratio and decreases with nanoparticle concentration Rayleigh number, viscosity ratio and conductivity ratio.

  5. 5.

    The effect of time on transient Nusselt number and Sherwood number is found to be oscillatory when time is small. However, when time becomes very large both the transient Nusselt and Sherwood value approaches to their steady state values.