1 Introduction

The analysis of cold extrusion for shaped sections has been performed in the previous works utilizing analytical, numerical and physical techniques. Investigation of the material flow is one of the main purposes considered by the researchers.

Chitkara and Abrinia [1] established a generalized method using upper bound to analyze extrusion and derived an admissible velocity field for shaped sections. Gordon et al. [2] presented six flexible velocity fields for axisymmetric extrusion through dies. Three base velocity fields were derived, assuming proportional angles, areas or distances from the centerline within the deformation region. Kar et al. [3] utilized the modified Spatial Elementary Rigid Region (SERR) technique for the upper bound analysis of extrusion of T-section bars from square billets through square dies. The SERR technique was applied by Sahoo et al. [4] to obtain minimal forming stress for the round-to-angle section extrusion. Abrinia and Ghorbani [5] presented a new generalized formulation for the nonsymmetric sections based on the new division of deforming region. By developing a theoretical solution, Ponalagusamy et al. [6] observed that the streamlined die designed based on Bezier curve was superior to the polynomial equation based die. Ketabchi and Seyedrezai [7] investigated extrusion of L-section and showed that the process efficiency improved in streamlined die with intermediate section. In another work, Kloppenborg et al. [8] published their work on topology optimizations in extrusion dies. The method improved dead zones for streamlined die geometries in the application of a flat and a porthole die on two-dimensional models. Haghighat and Moradmand [9] investigated extrusion process of thick wall tubes through rotating curved dies by the method of upper bound. In another work, upper bound method and finite element method were used to study the backward extrusion process through arbitrarily curved punches [10]. Ajiboye and Adeyemi [11] evaluated the effects of die land on the extrusion pressures by the upper bound method for square, rectangular, I, and T-shaped sections. Khalili Meybodi et al. [12] developed a general methodology to design the proper bearing in order to eliminate the curvature of the final extruded product and validated the design using physical modeling. The appropriate applicability of Plasticine for the physical modeling of extrusion was shown by Sofuoglu and Gedikli [13]. The development of two new definitions of shape complexity incorporating all significant geometrical features of an extrusion die profile was proposed by Qamar et al. [14]. Flitta and Sheppard [15] utilized a finite element model analysis to comprehend the material flow and the DMZ formation. Qamar [16] explored the effect of shape complexity on metal flow for cold extrusion. He concluded that factors such as die profile symmetry and extrusion ratio may have significant roles in the formation of DMZ. Eivani and Karimi Taheri [17] investigated the effects of die angle and friction on the geometry of DMZ using an upper bound model during equal channel angular extrusion.

As mentioned above, the problem of extrusion process has been tackled by various methods. However, these studies ignored the variation of DMZ at different sector angles. The previous analytical works were mostly performed using unrealistic simplified assumptions which limit the definition of deforming region as well as the DMZ. This deficiency is intensified for the extrusion of profiled sections with no axis of symmetry in which the geometry of deforming region is more complicated. On the other hand, employing numerical tools for the metal forming analysis in the extrusion process requires considerable time and expertise. In this article, a newly developed formulation for the forward extrusion is presented accommodating the variation of the dead zone geometry at different sector angles and the extrusion of square, rectangular and L-shaped sections has been dealt with as the examples. In the proposed method the velocity field incorporates curved surfaces of entry to and exit from the deforming region. In order to verify the analysis, physical modelling experiments and finite element simulation have also been used.

2 Theory

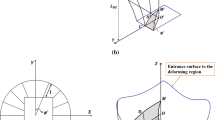
The flat entry and exit velocity discontinuity surfaces are the common assumptions used in a large number of the published literature in order to define the deforming region of the extrusion process. In the present work a more realistic definition of the DMZ, as compared to previous works, was considered in the theoretical solution. In addition, the proposed method embraces other modifications such as the homogeneous internal flow pattern to eliminate internal discontinuities and the Hermite streamlines to eliminate the velocity discontinuities at the entry and exit surfaces. The DMZ length varies at different sector angles of the deforming region for non-axisymmetric sections. Consider Fig. 1(a) which demonstrates a simple circle-to-square extrusion. As it is clear from the figure, the nest area of the material differs at different angles and consequently influences the shape of flow lines. The amount of the nest at different angles from the geometrical center of the exit section has been utilized to propose a new definition of DMZ. The deforming region for producing a square profile as a non-axisymmetric case is shown in Fig. 1(b). For the sake of clarity, a quarter of the deforming region is shown in detail.

Fig. 1
figure 1

(a) Variation of l at different angles and (b) The geometry of deforming region

Full size image

A general particle of material enters the deforming region at point D touching the velocity discontinuity surface and it leaves the deforming region at point D′. The particle flows on a general streamline DD′ where the velocity variations occur. The entry and exit surfaces of the deforming zone are:

$$ \begin{aligned} &Z_{1} = Z_{1}(OE,\varphi ) \\ &Z_{2} = Z_{2}\bigl(O'E', \varphi'\bigr) \end{aligned} $$
(1)

where Z 1 is the entry surface (t=0) and Z 2 is the exit surface (t=1) of the deforming region. The position vector of the material particle on a general streamline is:

$$ \vec{r}(u,q,t) = f(u,q,t)\vec{i} + g(u,q,t)\vec{j} + h(u,q,t)\vec{k} $$
(2)

where parameters u, q and t are dimensionless variables changing between 0 and 1 and functions f, g and h define the X, Y and Z coordinates of any point in the deforming region. The parameters u and q are:

$$ u = \frac{OE}{R}\quad \mbox{and}\quad q = \frac{\varphi}{2\pi} $$
(3)

where R is the billet radius. By changing these parameters from 0 to 1 the radial and angular positions of any point in the deforming region could be defined.

3 Defining the entry surface of deforming region (Z 1)

In this study the entry surface of deformation zone has been defined based on considering the DMZ length at different sector angles. To apply this, a new function for the DMZ length has been introduced which modifies the geometry of deforming region at the entry:

$$ L_{DZ}\bigl(\varphi '\bigr) = L_{c}\biggl(1 + \frac{l(\varphi ')}{R}\biggr) $$
(4)

where L DZ is the dead zone length, l is the material land at angle φ′ and L c is the optimization parameter for the upper bound. This function employs the material land at different sector angles to provide a realistic definition of the DMZ length. To obtain the DMZ length, the minimum upper bound value was also considered. Utilizing the dimensionless term l(φ′)/R in the function deals with the dimensional variations and demonstrates the generality of the formulation.

Using this function, the entry surface position at u=1 could be determined. For example in Fig. 1, the corresponding DMZ length in point A is smaller than C, because point A has smaller l-value than point C. This is in accordance with the physical modeling observations. In the present study a fourth-degree polynomial equation has been used to define the entry surface as follows:

$$\begin{aligned} Z_{1} &= p_{00} + p_{10}X_{0} + p_{01}Y_{0} + p_{20}X_{0}^{2} + p_{11}X_{0}Y_{0} \\ &\quad + p_{02}Y_{0}^{2} + p_{22}X_{0}^{2}Y_{0}^{2} + p_{30}X_{0}^{3} + p_{03}Y_{0}^{3} \end{aligned}$$
(5)

where:

$$ \begin{aligned} &X_{0} = uR\mathrm{sin}(2\pi q) \\ &Y_{0} = uR\mathrm{cos}(2\pi q) \end{aligned} $$
(6)

where X 0 and Y 0 are the X and Y coordinates of any point on the entry surface of deforming region and p 00, p 10, p 01, p 20, p 11, p 02, p 22, p 30 and p 03 are the coefficients in the equation. To obtain Z 1, surface fitting technique has been employed using a number of points around the entry surface of deforming region, with their Z-components being equal to their corresponding DMZ length, including point M as the center point. In fact, surface Z 1 is fitted to the followings:

$$ \begin{aligned} &\mathrm{Point}\ 1{:}\\ & P_{1} = \bigl[ R\mathrm{cos}(2\pi / n) \quad R\mathrm{sin}(2\pi / n) \quad L_{DZ}(2\pi / n) \bigr] \\ &\ldots \\ &\mathrm{Point}\ i{:}\\ & P_{i} = \bigl[ R\mathrm{cos}(2\pi i / n) \quad R \mathrm{sin}(2\pi i / n) \quad L_{DZ}(2\pi i / n) \bigr] \\ &\ldots \\ &\mathrm{Point}\ n{:}\\ & P_{n} = \bigl[ R\mathrm{cos}(2\pi ) \quad R \mathrm{sin}(2\pi ) \quad L_{DZ}(2\pi ) \bigr]\quad \mbox{and} \\ & \mathrm{Point}\ M = \bigl[ 0 \quad 0 \quad O'M \bigr] \end{aligned} $$
(7)

where n is the number of points around the entry surface with the same angular distances. In this paper, n is equal to 16 and 24 for the rectangular and L-shaped sections respectively. Matlab Surface Fitting Tool was used for fitting the surface through the extracted points from Eq. (7).

Consequently, the position vector of the entry surface of deformation zone could be expressed by:

$$ \vec{r}_{1} = uR\mathrm{sin} ( 2\pi q )\vec{i} + uR\mathrm{cos} ( 2\pi q )\vec{j} + Z_{1}(u,q)\vec{k} $$
(8)

3.1 Defining the exit surface of deforming region (Z 2)

The exit surface of deforming region is defined by choosing a cubic parametric Bezier function in terms of parameter u. Unlike the entry surface which has different Z-values at different angular positions for u=1, the exit surface has equal Z-values. Therefore, the Bezier function provides a more accurate definition of the exit surface than a polynomial function. It is defined by four control points two of which are the starting and the ending points on the curve and the remaining two points control the curvature and tangents to the curve as follows:

$$ \begin{aligned}[b] Z_{2}(u)& = (1 - u)^{3}P_{0z} + 3u(1 - u)^{2}P_{1z}\\ &\quad + 3u^{2}(1 - u)P_{2z} + u^{3}P_{3z} \end{aligned} $$
(9)

where P 0 and P 3 are the first and final points on the curve respectively. The slope of the curve at the first control point is along the line towards the second control point, so P 0 and P 1 must have equal z components to obtain a logical tangent vector:

$$ \begin{aligned} &P_{0z} = d \\ &P_{1z} = d \\ &P_{2z} = 3d / 4 \\ &P_{3z} = 0 \end{aligned} $$
(10)

where d is the parameter equal to O′M′. Hence, for the exit surface:

$$ Z_{2}(u) = \biggl(1 - \frac{3u^{2}}{4} - \frac{u^{3}}{4}\biggr)d $$
(11)

In this research d is equal to 0.4L c . Rotating the base function around Z-axis will cover all points on the exit surface. To determine the position of a general point like E′ on line O′E′ at exit surface the following expression is proposed:

$$ O'E' = u^{k}O'C' $$
(12)

where k is the parameter which takes special values in different positions on the exit section. This function increases the homogeneity of the cross sectional flow pattern by minimization of internal discontinuities. Hence the position vector of the exit surface of deformation zone is:

$$ \vec{r}_{2} = u^{k}\bigl(O'C' \mathrm{sin}\varphi '\vec{i} + O'C' \mathrm{cos}\varphi '\vec{j}\bigr) + Z_{2}(u,q)\vec{k} $$
(13)

3.2 Streamlines

A cubic parametric Hermite function is assumed to define the material flow path in the deforming region. Geometry of the streamlines has been proposed in a way that eliminates the velocity discontinuities at the entry and exit of deforming region by equating to zero the X- and Y-components of the starting and ending tangent vectors \(\vec{r}'_{1}\) and \(\vec{r'}_{2}\). Therefore, the position vector of any general point is:

$$\begin{aligned} \begin{aligned}[b] \vec{r} &= \vec{r}_{1}\bigl(1 - 3t^{2} + 2t^{3}\bigr) + \vec{r}_{2}\bigl(3t^{2} - 2t^{3}\bigr) \\ &\quad + \vec{r}'_{1}\bigl(t - 2t^{2} + t^{3}\bigr) + \vec{r}'_{2} \bigl( - t^{2} + t^{3}\bigr) \\ &= \left [ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l} 1 - 3t^{2} + 2t^{3} & 3t^{2} - 2t^{3} & t - 2t^{2} + t^{3} & - t^{2} + t^{3} \end{array} \right ] \\ &\quad \times \left [ \begin{array}{l@{\quad }l@{\quad }l} uR\mathrm{sin} ( 2\pi q ) & uR\mathrm{cos} ( 2\pi q ) & Z_{1} \\ u^{k}O'C'\mathrm{sin}\varphi ' & u^{k}O'C'\mathrm{cos}\varphi ' & Z_{2} \\ 0 & 0 & C_{1}L_{c} + uL_{c} \\ 0 & 0 & - C_{1}L_{c} - uL_{c} \end{array} \right ]\\ &\quad \times \left [ \begin{array}{c} \vec{i} \\ \vec{j} \\ \vec{k} \end{array} \right ] \end{aligned} \end{aligned}$$
(14)

All the points in the deforming region are defined by assigning values between 0 and 1 to parameters u, q, and t.

3.3 Velocity field

The velocity vector of any particle in the deformation zone is:

$$ \vec{V} = V_{x}\vec{i} + V_{y}\vec{j} + V_{z} \vec{k} $$
(15)

where V x , V y and V z are the velocity components in the X, Y and Z directions and given by:

$$ V_{y} = \frac{g_{t}}{h_{t}}V_{z},\quad V_{x} = \frac{f_{t}}{h_{t}}V_{z},\quad V_{z} = M(u,q,t) $$
(16)

where f t , g t and h t are the derivatives of f, g and h with respect to t and M is a general function in terms of u, q and t which is obtained from the incompressibility conditions:

$$ \frac{\partial V_{x}}{\partial X} + \frac{\partial V_{y}}{\partial Y} + \frac{\partial V_{z}}{\partial Z} = 0 $$
(17)

Substituting from Eq. (16) into Eq. (17): (See [5])

$$\begin{aligned} M &= C(u,q)/\bigl((f_{u}g_{q} - f_{q}g_{u}) \\ &\quad + h_{q}/h_{t}(f_{t}g_{u} - f_{u}g_{t}) + h_{u}/h_{t}(f_{q}g_{t} - f_{t}g_{q})\bigr) \end{aligned}$$
(18)

C is determined from the specific boundary conditions:

$$\begin{aligned} C(u,q) &= \bigl[ (f_{u}g_{q} - f_{q}g_{u}) + h_{q}/h_{t}(f_{t}g_{u} - f_{u}g_{t}) \\ &\quad + h_{u}/h_{t}(f_{q}g_{t} - f_{t}g_{q}) \bigr]_{_{t = 0}} \end{aligned}$$
(19)

3.4 The upper bound solution

The total power consumption for the extrusion process is:

$$ J^{*} = \dot{W}_{i} + \dot{W}_{e} + \dot{W}_{x} + \dot{W}_{f} $$
(20)

\(\dot{W}_{i}\), the power due to internal deformation, is given by:

$$ \begin{aligned}[b] \dot{W}_{i} &= \sigma_{m}\int _{V} \dot{\varepsilon}\, dV \\ & = \frac{2\sigma_{m}}{\sqrt{3}} \int_{0}^{1} \int _{0}^{1} \int_{0}^{1} \biggl( \biggl(\frac{\dot{\varepsilon}_{xx}^{2} + \dot{\varepsilon}_{yy}^{2} + \dot{\varepsilon}_{zz}^{2}}{2}\biggr) \\ &\quad + \dot{\varepsilon}_{xy}^{2} + \dot{\varepsilon}_{yz}^{2} + \dot{\varepsilon}_{zx}^{2} \biggr)^{\frac{1}{2}}\det J\partial u\partial q\partial t \end{aligned} $$
(21)

and \(\dot{W}_{f}\), the power due to friction between workpiece and die surface, is:

$$\begin{aligned} \dot{W}_{f} &= m\frac{\sigma_{m}}{\sqrt{3}} \iint_{s} \Delta V_{f}dS_{f} \\ &= m\frac{\sigma_{m}}{\sqrt{3}} \iint \sqrt {v_{x}^{2} + v_{y}^{2} + v_{z}^{2}} \Big\vert _{u = 1}dS_{f} \end{aligned}$$
(22)

where m is the friction factor, ΔV f and S f are the velocity discontinuity and the surface of velocity discontinuity due to material-tool interface respectively. The power due to velocity discontinuities at the entry, \(\dot{W}_{e}\), and the exit, \(\dot{W}_{x}\), can be calculated by the following relationship:

$$\begin{aligned} \dot{W}_{e} &= \frac{\sigma_{m}}{\sqrt{3}} \iint_{S_{e}} \Delta V_{e}dS_{e} \\ &= \frac{\sigma_{m}}{\sqrt{3}} \int_{0}^{1} \int _{0}^{1} \bigl[ V_{x}^{2} + V_{y}^{2} + (V_{z} - V_{0})^{2} \bigr]_{{t = 0}}^{{\frac{1}{2}}} \\ &\quad \times\frac{\partial (x,y)}{\partial (u,q)_{t = 0}} \end{aligned}$$
(23)
$$\begin{aligned} \dot{W}_{x} &= \frac{\sigma_{m}}{\sqrt{3}} \iint_{S_{x}} \Delta V_{e}dS_{e} \\ &= \frac{\sigma_{m}}{\sqrt{3}} \int_{0}^{1}\!\! \int _{0}^{1} \bigl[ V_{x}^{2} + V_{y}^{2} + \bigl(V_{z} - V_{0}(S_{e}/S_{x}) \bigr)^{2} \bigr]_{{t = 1}}^{{\frac{1}{2}}} \\ &\quad \times\frac{\partial (x,y)}{\partial (u,q)_{t = 1}} \end{aligned}$$
(24)

The present formulation for streamlines produces no velocity discontinuities at the velocity boundaries. Therefore, the components \(\dot{W}_{e}\) and \(\dot{W}_{x}\) are 0. The average extrusion pressure is:

$$ P_{ave} = \frac{J^{*}}{\pi R^{2}v_{0}} $$
(25)

where v 0 is the initial velocity of the billet material.

4 Physical modelling

The present study employs physical modeling experiments with Plasticine so as to verify the analytical results based on the new DMZ definition. The experiments were performed for extrusion of a square, rectangular and L-shaped section from a round billet using flat-face dies. The billets were prepared with two contrasting colors of Plasticine to generate the DMZ distinguishable from flowing material after deformation. The diameter and height of the billets were 40 and 45 millimeters respectively. In all cases, 60 % reduction of area has been applied to the billet. The Physical Modelling tooling, which was manufactured from Plexiglas, and a deformed sample (as an example) after the test are illustrated in Figs. 2(a) and (b) respectively (the sample is an extruded rectangular profile which has been cut from two directions). The dimensions of the sections for which the tests were performed are shown in Fig. 2(c). Many tests were carried out and the lengths of the DMZ at different angles were measured.

Fig. 2
figure 2

(a) The tooling, (b) a deformed sample and (c) dimensions of the sections used for the tests

Full size image

5 Finite element simulation

In addition to Physical Modelling experiments, finite element simulation was also carried out. The finite element program DEFORMTM 3D was used to simulate the process of cold extrusion using the same conditions as in the analytical method. The parts were modeled using SOLIDWORKS and then they were imported into DEFORMTM 3D software (Fig. 3). Modeling of the parts was carried out for the dies, punch and the billets. The die and the punch were taken as rigid bodies and the billet as a deformable solid. Tetrahedral elements were used for the workpiece. The frictional conditions used in the simulation were the same as in the analytical study for the sake of comparison (m=1).

Fig. 3
figure 3

The deformed finite element model

Full size image

6 Results and discussion

A deeper understanding of the DMZ formation which is under influence of inhomogeneity of material flow is presented here. As mentioned earlier, the present analytical solution takes account of the variation of DMZ length at different angular positions. The geometry of DMZ for the three introduced sections, analyzed by the present method, is observed in Fig. 4. For the sake of clarity, the DMZ for just a half of each section is plotted. All process conditions such as percentage of reduction and friction factor are the same for these cases. It is seen from the figure that higher shape complexity has given rise to larger DMZ. This has been discussed in more details below.

Fig. 4
figure 4

Geometry of DMZ: (a) square section (b) rectangular section (c) L-shaped section

Full size image

Variation of relative extrusion pressure for different values of L c /R for the extrusion of square, rectangular and L-shaped section is demonstrated in Fig. 5(a). Also, the effect of the reduction of area on the optimum value of L c /R is shown in Fig. 5(b). For each case the optimum value of L c which predicts the geometry of the deforming region along the Z-axis increases at higher reductions. It can also be observed that the optimum value of L c /R is highly affected by shape complexity. More complex sections have higher optimum L c , contributing to more inhomogeneous metal flow.

Fig. 5
figure 5

(a) Effect of L c /R on the relative extrusion pressure and (b) Effect of reduction of area on optimum L c /R, with changing shape complexity

Full size image

For a better comprehension of the variation of dead zone size, the data from the theory and physical modelling experiments have been compared in Table 1. The dead zone length at different angular directions has been obtained for all sections. The analytical results are in good agreement with those given by the physical modelling experiments in terms of magnitude and the trend.

Table 1 Variation of Dead Zone length at different angular directions
Full size table

Apart from giving a more realistic deforming region and DMZ size and reducing upper bound value, the proposed formulation embraces some other improvements as well. To get a clearer picture of the capability of the method, the effect of profile complexity and the reduction of area on the relative extrusion pressure have been investigated in Figs. 6 and 7. The frictional conditions used in the simulation were the same as in the analytical study for the sake of comparison. As depicted in Figs. 6(a) and (b), the extrusion pressure increases at higher levels of complexity; and for each level, the authors’ method gives lower upper bounds and also closer agreements with FEM results. However, for more complex sections the capability of the method is more apparent. This is because variation of l-value intensifies for the complicated profiles and this strongly affects the geometry of DMZ and the deforming region. Hence, the solution based on flat entry surface of deforming region predicts upper bound values for the complex sections which are more inaccurate. It can be observed from Figs. 7(a) and (b) that similar results have been obtained varying the area reduction. In fact, the current method has an advantage at lower reductions at which the variation of l-value noticeably increases.

Fig. 6
figure 6

Effect of complexity level on the relative extrusion pressure (m=1) for: (a) rectangular section and (b) symmetrical L-shaped section

Full size image
Fig. 7
figure 7

Effect of area reduction on the relative extrusion pressure (m=1) for: (a) rectangular section and (b) symmetrical L-shaped section

Full size image

7 Conclusions

A new upper bound solution has been developed for three-dimensional extrusion of shaped sections from a circular billet. It was shown that the DMZ size is under the influence of the shape complexity. A more realistic definition of the deforming region was proposed based on the variation of DMZ length. The effect of profile complexity and the reduction of area on the relative extrusion pressure were investigated and the capability of the method was shown for the cases with considerable variation of DMZ. It is concluded that the current analytical method can predict the process behavior with various levels of complexity.