1 Introduction

Coating flows are fluid flows that generate thin liquid films on surfaces as a result of external forces such as inertia, viscosity, gravity, and surface tension [1]. These coating flows are useful for covering a large surface area with one or more thin, uniform liquid layers [2].

The behavior of thin film flows has been studied experimentally [3, 4], analytically [5–18], and numerically [19–43]. Sun et al. [34] presented a detailed implementation of an adaptive finite element method, and demonstrated its performance on the thin-film problem with a moving contact line. Lee et al. [32, 36] solved a thin film flow over a plane containing well-defined single and grouped topographic features using a full approximation storage multigrid algorithm and employing automatic mesh adaptivity.

In this paper, we develop an adaptive finite difference method for a nonlinear time-dependent gravity-driven thin liquid film equation.

The rest of the paper is organized as follows. In Sect. 2, we briefly describe the governing equation for gravity-driven thin liquid film flow with a lubrication model. In Sect. 3, the fully discrete and nonlinear multigrid scheme and adaptive mesh refinement (AMR) method for the governing equation are given. In Sect. 4, we present numerical results. Conclusions are given in Sect. 5.

2 Governing equation

We consider the dynamics of a thin liquid layer on an inclined surface driven by gravity [24].

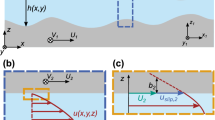
Figures 1(a) and 1(b) show a schematic illustration and real experimental result for s gravity-driven thin film [24], respectively. The coordinate x increases in the flow direction, y measures distance in the transverse direction, and z is the elevation perpendicular to the substrate. Let z=h(x,y,t) be the thickness of the thin liquid layer. The motion of the fluid is governed by the time-dependent lubrication equation [24]:

$$\begin{aligned} &{\frac{\partial{h}}{\partial t}=\frac{-1}{3\eta}\nabla \cdot \bigl[ \tau h^3 \nabla\Delta h\,{+}\,\rho g h^3 (\sin\alpha{\bf{e}}_x \,{-}\, \cos \alpha\nabla h) \bigr],} \\ \end{aligned}$$
(1)

where η is viscosity, τ is surface tension, ρ is density, g is the gravitational constant, α is the angle of inclination of the substrate from the horizontal, and e x =(1,0).

Fig. 1
figure 1

(a) A schematic diagram of the thin film flow. (b) A photo of fluid flowing down an inclined plane: Figure reprinted with permission from L. Kondic, SIAM Review, 45, 95–115 (2003) [24]. Copyright (2012) SIAM. Note that a similar physical experiment was also performed by H.E. Huppert [6]

Full size image

To non-dimensionalize Eq. (1), we employ non-dimensional variables (denoted by hats) by defining the characteristic variables in terms of balancing terms.

$$\begin{aligned} h = H \hat{h}, \qquad x= L \hat{x}, \qquad y = L \hat{y}, \quad \mbox{and} \quad t = T \hat {t}. \\ \end{aligned}$$
(2)

Here H is the thickness of the flat upstream part of the film. L and T are then given by

$$\begin{aligned} L = { \biggl( \frac{\tau H}{ \rho g \sin\alpha} \biggr)}^{1/3} \quad \mbox{and} \quad T = \frac{3\eta L}{\rho g H^2 \sin\alpha}. \end{aligned}$$
(3)

After substituting Eqs. (2) and (3) into Eq. (1) and dropping the ‘ \(\hat{}\) ’, we obtain the dimensionless thin film equation as

$$\begin{aligned} h_t + \bigl(h^3\bigr)_x = \nabla\cdot \bigl({ h^3 \nabla(Dh-\Delta h)} \bigr), \end{aligned}$$
(4)

where \(D = ( \frac{H^{2} \rho g \sin\alpha}{\tau} )^{1/3} \cot \alpha\) measures the size of the normal component of gravity.

3 Numerical method

First, we split the fourth order Eq. (4) into a system of second order equations as follows.

$$\begin{aligned} h_t + f_x(h) = \nabla\cdot\bigl(f(h) \nabla\mu \bigr), \quad h=h(x,y,t), \end{aligned}$$
(5)
$$\begin{aligned} &{\mu= Dh- \Delta h, \quad \mbox{for}\ (x,y)\in\varOmega=(0,L_x)\times (0,L_y),} \\ \end{aligned}$$
(6)

where f(h)=h 3. Boundary conditions are given by

$$\begin{aligned} &{h(0,y,t)=h_\infty, \qquad h(L_x,y,t)=b,} \\ &{h(x,0,t)=h(x,L_y,t),} \\ &{\mu_x(0,y,t)=\mu_x(L_x,y,t)=0,} \\ &{\mu(x,0,t)=\mu(x,L_y,t),} \end{aligned}$$

where h ∞ is a constant upstream height and b is a precursor film thickness.

3.1 Discretization of the proposed scheme

We now present fully discrete schemes for Eqs. (5) and (6) in the two-dimensional domain Ω=(0,L x )×(0,L y ). Let N x and N y be positive even integers, Δx=L x /N x =L y /N y be the uniform mesh size, and Ω Δx ={(x i ,y j ):x i =(i−0.5)Δx,y j =(j−0.5)Δx,1≤i≤N x ,1≤j≤N y } be the set of cell-centers. Let \(h_{ij}^{n}\) and \(\mu_{ij}^{n}\) be approximations of h(x i ,y j ,nΔt) and μ(x i ,y j ,nΔt), respectively. Here, Δt=T/N t is the time step, T is the final time, and N t is the total number of time steps. Then, a semi-implicit time and centered difference space discretization of Eqs. (5) and (6) is

$$\begin{aligned} \frac{h_{ij}^{n+1}-h_{ij}^n}{\Delta t} =& \nabla_d \cdot \bigl( f(h)_{ij}^{n+1} \nabla_d {\mu}_{ij}^{n+1} \bigr) - \frac {f_x(h_{ij}^{n+1})}{2} \\ &{} -\frac{f_x(h_{ij}^{n})}{2}, \end{aligned}$$
(7)
$$\begin{aligned} {\mu}_{ij}^{n+1} =& Dh_{ij}^{n+1}- \Delta_d h_{ij}^{n+1}, \end{aligned}$$
(8)

where the superscripts denote discrete time steps. Here, we use five points to discretize the terms \(\Delta_{d}h_{ij}^{n+1}\) and \(\nabla_{d} \cdot ( f(h)_{ij}^{n+1} \nabla_{d} {\mu}_{ij}^{n+1})\) as

$$\begin{aligned} &{\Delta_{d}h_{ij}^{n+1}} \\ &{\quad =\frac{h^{n+1}_{i,j+1}+h^{n+1}_{i,j-1} +h^{n+1}_{i+1,j}+h^{n+1}_{i-1,j}-4h^{n+1}_{ij} }{h^2},} \end{aligned}$$
$$\begin{aligned} &{\nabla_d \cdot \bigl( f(h)_{ij}^{n+1} \nabla_d {\mu}_{ij}^{n+1} \bigr)} \\ &{\quad =\mbox{$\displaystyle \frac{f_{i+\frac{1}{2},j}^{n+1}({\mu}_{i+1,j}^{n+1}-{\mu}_{ij}^{n+1}) -f_{i-\frac{1}{2},j}^{n+1}({\mu}_{ij}^{n+1}-{\mu}_{i-1,j}^{n+1})}{h^2}$}} \\ &{\qquad {}+ \frac{f_{i,j+\frac{1}{2}}^{n+1}({\mu}_{i,j+1}^{n+1}-{\mu}_{ij}^{n+1}) -f_{i,j-\frac{1}{2}}^{n+1}({\mu}_{ij}^{n+1}-{\mu}_{i,j-1}^{n+1})}{h^2},} \end{aligned}$$

where \(f_{i+\frac{1}{2},j}^{n+1}=f((h_{ij}^{n+1}+h_{i+1,j}^{n+1})/2)\), and the other terms are similarly defined. \(f_{x}(h_{ij}^{n})\) and \(f_{x}(h_{ij}^{n+1})\) are treated using an explicit and a semi-implicit essentially non-oscillatory (ENO) type scheme [44], respectively.

$$\begin{aligned} f_x\bigl(h_{ij}^{n}\bigr) = f' \bigl(h_{ij}^{n}\bigr) \biggl( \frac{ \bar{h}_{i+\frac{1}{2},j}^{n} - \bar{h}_{i-\frac {1}{2},j}^{n}}{\Delta x} \biggr). \end{aligned}$$

The values \(\bar{h}_{i+\frac{1}{2},j}^{n}\) are calculated as follows:

$$k = \left \{ \begin{array}{{l@{\quad}l}} i &{\mbox{if $f'(h_{ij})\geq0$}} \\ i+1 &{\mbox{otherwise.}} \end{array} \right . $$
$$a = \frac{{h_{kj}^{n} - h_{k-1,j}^{n}}}{{\Delta x}}, \qquad c = \frac{{h_{k+1,j}^{n} - h_{kj}^{n}}}{{\Delta x}}, $$
$$d_{kj} = \left \{ { \begin{array}{l@{\quad}l} a &{\mbox{if }\vert a \vert \le \vert c \vert } \\ c &{\mbox{otherwise.}} \end{array} } \right . $$
$$\bar{h}_{i+\frac{1}{2},j}^{n}=h_{kj}^n+ \frac{\Delta x}{2}d_{kj}\bigl(1-2(k-i)\bigr). $$

As f′(h)=3h 2>0, then with k=i we can define

$$\begin{aligned} &{f_x\bigl(h_{ij}^{n}\bigr) := f'\bigl(h_{ij}^{n}\bigr) \biggl( \frac{ h_{ij}^{n} - h_{i-1,j}^{n}}{\Delta x} \biggr)+\Im\bigl(h_{ij}^{n}\bigr),} \\ &{f_x\bigl(h_{ij}^{n+1}\bigr) := f'\bigl(h_{ij}^{n+1}\bigr) \biggl( \frac{ h_{ij}^{n+1} - h_{i-1,j}^{n+1}}{\Delta x} \biggr)+\Im\bigl(h_{ij}^{n}\bigr),} \end{aligned}$$

where \(\Im(h_{ij}^{n})=0.5(d_{ij}-d_{i-1,j})f'(h_{ij}^{n})\). We define the boundary condition as

$$\begin{aligned} &{h_{0j}=2h_{\infty}-h_{1j}, \qquad h_{N_x+1,j}=2b-h_{N_xj},} \\ &{ h_{i0}=h_{iN_y},} \\ &{h_{i,N_y+1}=h_{i1}, \qquad \mu_{0j}=\mu_{1j}, \qquad \mu_{N_x+1,j}=\mu_{N_xj},} \\ &{\mu_{i0}=\mu_{iN_y}, \qquad \mu_{i,N_y+1}=\mu_{i1}.} \end{aligned}$$

In this paper, we use AMR [45] to solve the nonlinear discrete system (7) and (8) at the implicit time level. Figure 2 shows a schematic diagram of block-structured local refinement with a four level AMR method. A pointwise Gauss–Seidel relaxation scheme is used as the smoother in the multigrid method. The next section gives further details of the AMR algorithm.

Fig. 2
figure 2

Block-structured local refinement with four levels

Full size image

3.2 Dynamic adaptive mesh refinement algorithms

In the AMR algorithms, we consider a hierarchy of increasingly finer grids, \(\varOmega_{l+1}, \ldots, \varOmega_{l+l^{*}}\), which are restricted to smaller and smaller subdomains, while the last hierarchy of global grids is Ω 0,Ω 1,…,Ω l . That is, we consider a hierarchy of grids, \(\varOmega_{0}, \varOmega_{1}, \ldots, \varOmega_{l+0}, \varOmega_{l+1}, \ldots, \varOmega_{l+l^{*}}\). Here, we denote Ω l+0 as level zero, Ω l+1 as level one, and so on. Construction of the multilevel mesh begins at the zero-level grid. Finer resolution grids are added at level one to cover those grid points on the zero grid where refinement is flagged. This process continues in the same fashion until level l ∗ is reached. Moreover, the grid spacing Δx k on level k is related to that of the next level (k+1) as Δx k =2Δx k+1. Figure 2 shows a schematic illustration of the set of finer grids with four levels (l ∗=3). The AMR is performed by uniformly subdividing each mother cell into four daughter cells.

3.3 Creation of the grid hierarchy

There are many possible criteria for deciding where refinement is necessary. In many physical problems, physical quantities such as sharp density gradients or large charge distributions may provide indicators for refinement. In the current implementation, the grid is adapted dynamically based on the undivided gradient |∇ u h|k, which is defined as

$$\begin{aligned} | \nabla_u h|_{ij}^k=\sqrt{ \bigl(h_{i+1,j}^k-h_{i-1,j}^k \bigr)^2+\bigl(h_{i,j+1}^k-h_{i,j-1}^k \bigr)^2}, \end{aligned}$$

where \(h_{ij}^{k}\) are cell center values defined with respect to the level-k grids on the domain Ω l+k . We then tag cells containing the front, i.e., those in which the undivided gradient of the film height is greater than a critical value tol, i.e., |∇ u h|k>tol. Throughout this paper, we use tol=0.01. Once we have decided which cells are to be refined, we use this information to create a hierarchy of levels. We use the algorithm of Berger and Rigoutsos [46], in which tagged points are clustered into efficient boxes. The efficiency of a grid is defined as the number of cells in the grid that were tagged for refinement divided by the total number of cells in the grid. The grid generator takes a list of tagged points and draws the smallest box around them. For efficiency, the boxes are not allowed to become too small. This procedure performs the following steps:

  1. 1.

    Fit a box to enclose the tagged cells.

  2. 2.

    Recursively sub-divide the box. Split the box in the longest direction at a position based on the histogram formed from the sum of the number of tagged cells per row or column.

  3. 3.

    After splitting the box, fit new bounding boxes to each half and repeat the process. Continue until the size of every box is not smaller than a given value and every box consists of a minimum number of non-tagged cells.

  4. 4.

    Compute the fill ratio, which is defined as the number of tagged cells divided by the size of the box. For example, the fill ratio in Fig. 3(c) is 135/182. If this grid does not satisfy an efficiency criterion (in the current implementation, fill ratio ≥0.75), the grid generator will look for the best way to subdivide the tagged points in order to create more efficient boxes, as shown in Fig. 3(d).

    Fig. 3
    figure 3

    Three steps in the regridding algorithm: (a) tag cells and enclose them in a box, (b) split the box into two boxes using a histogram of the column or row sums of tagged cells, (c) fit new boxes to each split box and repeat if the ratio of tagged to untagged cells is too small, and (d) the most efficient rectangles

    Full size image

A schematic illustration of our proposed adaptive meshes with different views is shown in Fig. 4. Note that our method is not based on triangular adaptive mesh refinement, we simply illustrate these with a triangular mesh plot using MATLAB 2012a [47].

Fig. 4
figure 4

Schematic illustration of our proposed adaptive meshes with different views

Full size image

3.4 Coarse-fine boundary interpolation

In order to discretize the Laplacian on a generic level grid, we use the standard nearest neighbor stencils in the definitions of the discrete derivatives to fill the ghost-layer values by interpolation.

The grid-to-ghost-layer exchange process is illustrated in Fig. 5(a). The main idea is to use quadratic interpolation through coarse cells (open circles) to get intermediate values (solid circles), then use intermediate values with fine cells (×’s) to get ghost cell values (open triangles) for computing the coarse-fine fluxes (arrows).

Fig. 5
figure 5

Interpolation on the coarse-fine boundary: Use quadratic interpolation through coarse cells (open circles) to get intermediate values (solid circles), then use intermediate value with fine cells (×’s) to get ghost cell values (open triangles) for computing coarse-fine fluxes (arrows)

Full size image

To obtain the value \(h^{c}_{i,j+\frac{1}{4}}\) (solid circle), we use three points \(h^{c}_{i,j-1}\), \(h^{c}_{i,j}\), and \(h^{c}_{i,j+1}\) with the quadratic polynomial approximation as shown in Fig. 5(b). Let the quadratic polynomial approximation be \(h^{c}_{i}(t)=\alpha t^{2}+\beta t+\gamma\). And assume \(h^{c}_{i}(-\Delta_{x}^{c})=h^{c}_{i,j-1}\), \(h^{c}_{i}(0)=h^{c}_{ij}\), and \(h^{c}_{i}(\Delta_{x}^{c})=h^{c}_{i,j+1}\). The parameters α, β, and γ can be calculated by the following equations.

$$\begin{aligned} \left ( { \begin{array}{c} \alpha\\ \beta\\ \gamma \end{array} } \right ) =& \left ( { \begin{array}{c@{\quad}c@{\quad}c} (\Delta_x^c)^2 & -\Delta_x^c & 1 \\ 0 & 0 & 1 \\ (\Delta_x^c)^2 & \Delta_x^c & 1 \end{array} } \right )^{-1} \left ( { \begin{array}{c} h^c_{i,j-1} \\ h^c_{ij} \\ h^c_{i,j+1} \end{array} } \right ). \end{aligned}$$

Using α, β, and γ, we get \(h_{i,j+\frac {1}{4}}^{c}=h_{i}^{c}(\Delta_{x}^{c}/4)\). To obtain \(h^{f}_{2i,2j}\), we implement another quadratic interpolation with the values \(h^{c}_{i,j+\frac{1}{4}}\), \(h^{f}_{2i+1,2j}\), and \(h^{f}_{2i+2,2j}\) in a similar fashion.

3.5 Numerical solution—adaptive nonlinear multigrid method

In this subsection, we will only describe the adaptive full approximation storage cycle to solve the nonlinear discrete system of Eqs. (7) and (8). The algorithm of the V-cycle multigrid method for solving the discrete system is as follows. First, let us rewrite Eqs. (7) and (8) as N(h n+1,μ n+1)=(ϕ n,ψ n), where \(N(h^{n+1},\mu^{n+1}) = (\frac{h_{ij}^{n+1}}{\Delta t} -\nabla_{d} \cdot ({f(h)_{ij}^{n+1}} \nabla_{d} \mu_{ij}^{n+1} )+\frac{f'(h_{ij}^{n+1})}{2} (\frac{ h_{ij}^{n+1} - h_{i-1,j}^{n+1}}{\Delta x} ), \mu_{ij}^{n+1} -Dh_{ij}^{n+1}+ \Delta_{d} h_{ij}^{n+1} )\) and the source term is \((\phi^{n}, \psi^{n}) = (\frac{h_{ij}^{n}}{\Delta t}- \frac {f'(h_{ij}^{n})}{2} ( \frac{ h_{ij}^{n} - h_{i-1,j}^{n}}{\Delta x} )-\Im(h_{ij}^{n}), 0 )\).

Using the above notation on all levels k=0,1,…,l,l+1,…,l+l ∗, an adaptive multigrid cycle is formally written as follows [48]:

Adaptive cycle

First we calculate \(\phi^{n}_{k},\psi^{n}_{k}\) on all levels and set the previous time solution as the initial guess, i.e., \((h_{k}^{0},\mu_{k}^{0}) = (h_{k}^{n},\mu_{k}^{n})\).

$$\begin{aligned} &{\bigl(h_k^{m+1}, \mu_k^{m+1}\bigr)} \\ &{\quad = \mathit{ADAPTIVEcycle}\bigl(k, h_k^m, h_{k-1}^m, \mu_k^m,mu_{k-1}^m,N_k,} \\ &{ \hphantom{\quad = \mathit{ADAPTIVEcycle}\bigl(}\ \phi^n_k,\psi^n_k,\nu\bigr).} \end{aligned}$$

(1) Presmoothing

• Compute \((\bar{h}_{k}^{m},~\bar{\mu}_{k}^{m}) \) by applying ν smoothing steps to \((h_{k}^{m},~\mu_{k}^{m}) \) on Ω k .

$$\begin{aligned} \bigl(\bar{h}_k^m , \bar{\mu}_k^m \bigr) = \mathit{SMOOTH}^{\nu}\bigl(h_k^m, \mu_k^m,N_k,\phi ^n_k, \psi^n_k\bigr), \end{aligned}$$

where one SMOOTH relaxation operator step consists of solving Eqs. (11) and (12) given below by 2×2 matrix inversion for each i and j. Note that a pointwise Gauss–Seidel relaxation scheme is used as the smoother in the multigrid method. Rewriting Eqs. (7) and (8), we get

$$\begin{aligned} &{\biggl(\frac{1}{\Delta t}+\frac{f'(h_{ij}^{n+1})}{2\Delta x} \biggr)h_{ij}^{n+1}} \\ &{\qquad {} + \frac{f_{i+\frac{1}{2},j}^{n+1} + f_{i-\frac{1}{2},j}^{n+1} +f_{i,j+\frac{1}{2}}^{n+1} + f_{i,j-\frac{1}{2}}^{n+1}}{\Delta x^2} \mu_{ij}^{n+1}} \\ &{\quad = \phi_{ij}^n + \frac{ f_{i+\frac{1}{2},j}^{n+1} \mu_{i+1,j}^{n+1} + f_{i-\frac {1}{2},j}^{n+1} \mu_{i-1,j}^{n+1}}{\Delta x^2}} \\ &{\qquad {}+ \frac{f_{i,j+\frac{1}{2}}^{n+1} \mu_{i,j+1}^{n+1}+ f_{i,j-\frac {1}{2}}^{n+1} \mu_{i,j-1}^{n+1}}{\Delta x^2}} \\ &{\qquad {} +\frac{f'(h_{ij}^{n+1})h_{i-1,j}^{n+1}}{2\Delta x},} \end{aligned}$$
(9)
$$\begin{aligned} &{ - \biggl(D+\frac{4}{\Delta x^2} \biggr) h_{ij}^{n+1}+ { \mu}_{ij}^{n+1} } \\ &{\quad =\psi_{ij}^n - \frac{h_{i+1,j}^{n+1} +h_{i-1,j}^{n+1}+h_{i,j+1}^{n+1} +h_{i,j-1}^{n+1}}{\Delta x^2}.} \end{aligned}$$
(10)

Next, we replace \(h_{kl}^{n+1} \mbox{ and } \mu_{kl}^{n+1}\) in Eqs. (9) and (10) with \({\bar{h}}_{kl}^{m} \mbox{ and } {\bar{\mu}}_{kl}^{m}\) if k≤i and l≤j; otherwise we replace them with \(h_{kl}^{m} \mbox{ and } \mu_{kl}^{m}\), i.e.,

$$\begin{aligned} &{\biggl(\frac{1}{\Delta t}+\frac{f'(h_{ij}^{m})}{2\Delta x} \biggr){{\bar{h}}_{ij}^m}} \\ &{\qquad {} +\frac{f_{i+\frac{1}{2},j}^m + f_{i-\frac{1}{2},j}^m +f_{i,j+\frac{1}{2}}^m+f_{i,j-\frac{1}{2}}^m}{\Delta x^2} {\bar{\mu}}_{ij}^m} \\ &{\quad = \phi_{ij}^n + \frac{f_{i+\frac{1}{2},j}^m \mu_{i+1,j}^m+ f_{i-\frac{1}{2},j}^m {\bar{\mu}}_{i-1,j}^m}{\Delta x^2}} \\ &{\qquad {}+ \frac{f_{i,j+\frac{1}{2}}^m \mu_{i,j+1}^m+ f_{i,j-\frac{1}{2}}^m {\bar{\mu}}_{i,j-1}^m}{\Delta x^2}} \\ &{\qquad {} +\frac{f'(h_{ij}^{m})\bar{h}_{i-1,j}^{ m}}{2\Delta x},} \end{aligned}$$
(11)
$$\begin{aligned} &{ - \biggl( D + \frac{4}{\Delta x^2} \biggr) {\bar{h}}_{ij}^m + {\bar{\mu}}_{ij}^m} \\ &{\quad =\psi_{ij}^n -\frac{h_{i+1,j}^m +{\bar{h}}_{i-1,j}^m+h_{i,j+1}^m + {\bar{h}}_{i,j-1}^m}{\Delta x^2},} \end{aligned}$$
(12)

(2) Coarse-grid correction

$$\begin{aligned} &{\bigl(\bar{h}_{k-1}^m, \bar{\mu}_{k-1}^m \bigr) = \left \{ \begin{array}{l@{\quad}l} I_k^{k-1} ( \bar{h}_k^m , \bar{\mu}_k^m) & \mbox{on } \varOmega_{k-1} \cap \varOmega_k\\ (h_{k-1}^m,\mu_{k-1}^m) & \mbox{on } \varOmega_{k-1} - \varOmega_k. \end{array} \right .} \\ &{\bigl(\phi^n_{k-1},\psi^n_{k-1}\bigr) = \left \{ \begin{array}{l} I_k^{k-1} \{ (\phi^n_k,\psi^n_k)-N_k (\bar{h}_k^m, \bar{\mu}_k^m) \} \\ \quad {} + N_{k-1}I_k^{k-1} ({\bar{h}}_k^m, \bar{\mu}_k^m) \\ \quad \mbox{on } \varOmega _{k-1} \cap\varOmega_k \\ (\phi^n_{k-1},\psi^n_{k-1}) \quad \mbox{on } \varOmega_{k-1} - \varOmega_k. \end{array} \right .} \end{aligned}$$

• Compute an approximate solution \((\hat{h}_{k-1}^{m}, \hat{\mu}_{k-1}^{m}) \) of the coarse grid equation on Ω k−1, i.e.,

$$\begin{aligned} N_{k-1}\bigl(h_{k-1}^m, \mu_{k-1}^m \bigr) = \bigl(\phi^n_{k-1},\psi^n_{k-1} \bigr). \end{aligned}$$
(13)

If k=1, we explicitly invert a 2×2 matrix to obtain the solution. If k>1, we solve Eq. (13) using \((\bar{h}_{k-1}^{m}, \bar{\mu}_{k-1}^{m} )\) as an initial approximation to perform an adaptive multigrid k-grid cycle:

$$\begin{aligned} & \bigl(\hat{h}_{k-1}^m,\hat{\mu}_{k-1}^m \bigr) \\ &\quad = \mathit{ADAPTIVEcycle}\bigl(k-1,\bar{h}_{k-1}^m,\bar{\mu}_{k-1}^m, h_{k-2}^m, \\ &\quad \hphantom{= \mathit{ADAPTIVEcycle}\bigl(}\mu_{k-2}^m, N_{k-1}, \phi^n_{k-1},\psi^n_{k-1},\nu\bigr). \end{aligned} $$

• Compute the correction at Ω k−1∩Ω k .

$$\bigl({\hat{u}}_{k-1}^m, {\hat{v}}_{k-1}^m \bigr)= \bigl(\hat{h}_{k-1}^m, \hat{\mu}_{k-1}^m \bigr)- \bigl(\bar{h}_{k-1}^m, \bar{\mu}_{k-1}^m \bigr). $$

• Set the solution at the other points of Ω k−1−Ω k .

$$\bigl(h_{k-1}^{m+1}, \mu_{k-1}^{m+1} \bigr)= \bigl(\hat{h}_{k-1}^m, \hat{\mu}_{k-1}^m \bigr). $$

• Interpolate the correction to Ω k ,

$$\bigl({\hat{u}}_k^m, {\hat{v}}_k^m \bigr)= I_{k-1}^k \bigl({\hat{u}}_{k-1}^m, {\hat{v}}_{k-1}^m\bigr). $$

• Compute the corrected approximation on Ω k .

$$\bigl(h_k^{m,\mathrm{after}\,CGC}, \mu_k^{m, \mathrm{after}\, CGC} \bigr) = \bigl(\bar{h}_k^m + \hat{u}_k^m, \bar{\mu}_k^m + \hat{v}_k^m\bigr). $$

(3) Postsmoothing

$$\begin{aligned} &\bigl(h_k^{m+1},\mu_k^{m+1} \bigr) \\ &\quad = \mathit{SMOOTH}^{\nu} \bigl(h_k^{m,\mathrm{after}\,CGC},\mu_k^{m, \mathrm{after}\, CGC}, \\ & \quad \hphantom{=\mathit{SMOOTH}^{\nu} \bigl(} N_k,\phi^n_k, \psi^n_k\bigr). \end{aligned} $$

This completes the nonlinear ADAPTIVE cycle.

4 Numerical experiments

In this section, we perform numerical experiments to determine the evolution of a thin film with AMR, compare the uniform and adaptive mesh methods, study the effect of parameter values, compare the experimental and numerical data, and numerically simulate multiple thin films. Unless otherwise specified, we use h ∞=1 and b=0.01 in this paper.

4.1 Evolution of thin film with adaptive mesh refinement

We start with a numerical simulation for the temporal evolution of a thin film using AMR with the initial condition h(x,y,0)=0.5[h ∞+b−(h ∞−b)tanh(3(x−10)+rand(x,y))], where rand(x,y) is a random value between −1 and 1. In this numerical simulation, D=0.1, l ∗=3 levels, and the level zero domain Ω l+0=64×32 are used on the computational domain Ω=(0,200)×(0,100). The maximum mesh size is Δx max=3.13 and the finer mesh sizes are 64×32, 128×64, 256×128, and 512×256. The calculation is run until time T=150 with a time step Δt=0.2. Figure 6 shows the evolution of the contour (h=0.5) of the thin film at times t=0,75, and 150. It can be observed from the figures that gravity-driven fingers develop and become longer as time evolves. At the same time, the grid hierarchy structure dynamically adjusts itself to capture the developing finger feature.

Fig. 6
figure 6

Time evolution of the fluid front with the adaptive mesh method. The dimensionless times are shown below each figure. l ∗=3 levels and level zero domain, Ω l+0=64×32 are used on the computational domain Ω=(0,200)×(0,100)

Full size image

4.2 Comparison between uniform and adaptive mesh

In this numerical simulation, we compare a sequence of results with different mesh sizes for a thin film simulation. We compare the numerical solutions obtained on uniform and adaptively refined meshes. The initial condition is h(x,y,0)=0.5[h ∞+b−(h ∞−b)tanh(3(x−10)+cos(πy/25))] on the computational domain Ω=(0,200)×(0,100). We use a set of increasingly finer meshes 26+n×25+n in the uniform test and l ∗=n levels in the adaptive mesh method for n=3,4, and 5. The maximum grid spacing is Δx max=3.13 and D=0.1. With time step Δt=0.2, the calculations are run until T=150. Figure 7 compares the simulation results obtained on uniform and adaptively refined meshes. This indicates that they are in good agreement.

Fig. 7
figure 7

Comparison between uniform mesh (solid line) and adaptive mesh method (circle) at t=150. Here, contours of fluid are at h=0.1,0.4,0.7,0.9, and 1.2

Full size image

To show the efficiency of our proposed AMR method, the CPU time required for the two methods is listed in Table 1. On a 2048×1024 grid, the uniform mesh method requires more than 37.4 hours. However, the adaptive mesh needs only 1056, which is about 128 times faster than the uniform mesh. The adaptive method uses 10240 nodes at t=0 and 40960 nodes at t=150, which is small compared to the 2048×1024 nodes in the uniform mesh.

Table 1 Comparison of CPU time for uniform and adaptively refined meshes
Full size table

4.3 Effect of parameter D

The non-dimensional parameter D plays an important role in the thin film equation. By changing the film thickness (H) and inclination angle (α), we can adjust \(D = (\frac{H^{2} \rho g \sin\alpha }{\tau})^{1/3} \cot\alpha\) in the experiment. In general, we have \(\frac {H^{2} \rho g \sin\alpha }{\tau}\ll1\) (see Refs. [49, 50]), therefore |D|<|cotα|.

To see the effect of D on the evolution of the thin liquid film, we take two different values, D=0 (α=π/2) and D=0.5 (0<α<π/2). The initial condition is h(x,y,0)=0.5[h ∞+b−(h ∞−b)tanh(3(x−10)+cos(πy/25))]. l ∗=3 and Ω l+0=64×32 are used on the computational domain Ω=(0,200)×(0,100) with a time step Δt=0.2. Figure 8 shows snapshots of the contact line profiles for the flow down a vertical plane D=0 and an inclined plane D=0.5 at t=160. The results suggest that, as the value of the parameter D becomes smaller, the growth of the fingering patterns becomes faster.

Fig. 8
figure 8

Snapshots of the contact line profiles for the flow down a vertical plane D=0 and an inclined plane D=0.5

Full size image

4.4 Dynamic contact angle

When a liquid is brought into contact with a solid surface, the adhesion of the solid with the liquid and the cohesion of the liquid become interacting forces. The contact angle represents the balance between the cohesion forces of the liquid and the adhesion forces between the liquid and the solid [59]. The contact angle of a thin film can be defined as the angle between the tangent vector of the interface and the solid (see Fig. 9).

Fig. 9
figure 9

Contact angle, defined as the angle between the solid and a tangent line to the interface of the thin film

Full size image

The dynamic contact angle of thin-film flows has been extensively studied [18, 33, 56, 60, 61], where the authors considered the surface forces to study the wetting phenomena of a spreading liquid drop in contact with a solid surface. We will investigate the effect of b on the dynamic contact angle with two different models. One is a precursor film model, and the other is a slipping model. The difference between these two approaches is that the velocity at the bottom boundary is zero in the precursor model and nonzero in the slipping model. A schematic illustration of the two models is shown in Fig. 10. A detailed comparison of the two models is given in [18, 56, 61]. The different boundary condition leads to a modification to f(h)=h 3+Ch in Eq. (5). Here, C is a small positive parameter. Note that in the slipping model, b has no physical meaning, but is chosen to numerically preserve non-negativity of solutions. We use b=10−6 in the slipping model.

Fig. 10
figure 10

Schematic illustration of (a) precursor film model and (b) slipping model

Full size image

To calculate the dynamic contact angle, we use a method based on the quadratic polynomial approximation. Let X m =(x m ,y m ) for m=1,…,M be uniformly distributed Lagrangian points such that h(X m )=0.5 (see ‘+’ symbol in Fig. 11(a)). For each X m , we consider the normal coordinate s with origin at X m . Along the normal direction (solid line in Fig. 11(a)), we define a function \(\bar{h}_{m}(s)\) by interp2, which is a 2D interpolation program in MATLAB 2012a [47]. Let k be an integer that satisfies \(\bar{h}_{m}(k \Delta x) \geq2b\) and \(\bar{h}_{m} ((k+1) \Delta x)\leq2b\). We define the quadratic polynomial, ϕ m (s), passing three points \(((k-2) \Delta x, \bar{h}_{m}((k-2) \Delta x))\), \(((k-1) \Delta x, \bar{h}_{m}((k-1) \Delta x))\), and \((k \Delta x, \bar{h}_{m}(k \Delta x))\). Let s ∗ be the point that satisfies ϕ m (s ∗)=b and s ∗≥kΔx (see Fig. 11(b)). The dynamic contact angle at X m is then defined as \(\theta_{m}=- {\tan^{-1} \frac{d\phi _{m}(s_{*})}{ds}}\). The average dynamics contact angle is given as \(\theta=\sum_{m=1}^{M} \theta_{m} /M\). We perform a numerical experiment with two initial conditions, h(x,y,0)=0.5[h ∞+b−(h ∞−b)tanh(3(x−5)+cos(πy/25))] and h(x,y,0)=0.5[h ∞+b−(h ∞−b)tanh(3(x−5))]. Ω l+0=64×32 and l ∗=3 are used on Ω=(0,100)×(0,50). We choose Δt=0.2, and D=0. In the precursor model, we use a set of different precursor film heights b=0.1, 0.01, 0.001, and 0.0001. The slipping model uses C=0.1, 0.01, 0.001, and 0.0001 with a fixed b=10−6. In Figs. 12(a) and 12(b), we show the evolution of the average dynamic contact angle obtained by the two models with and without initial perturbation, respectively. As the values of b and C decrease, the dynamic contact angle increases. In Figs. 13(a) and 13(b), we compare the profiles (contour at h=0.5) given by each model at T=80 with and without initial perturbation, respectively. As can be seen, smaller values of b or C give a faster evolution of the thin-film front. We can also observe that the two methods generate more developed finger shapes when larger values b or C are used.

Fig. 11
figure 11

Schematic illustration of dynamic contact angle computation. (a) The solid line is the normal direction at the front which is the contour at h=0.5. (b) Computation of dynamic contact angle

Full size image
Fig. 12
figure 12

Evolution of average dynamic contact angle with precursor film model and slipping model. (a) The initial profile is h(x,y,0)=0.5[h ∞+b−(h ∞−b)tanh(3(x−5)+cos(πy/25))]. (b) The initial profile is h(x,y,0)=0.5[h ∞+b−(h ∞−b)tanh(3(x−5))]

Full size image
Fig. 13
figure 13

Comparison of profiles (contour at h=0.5) at T=80 with precursor film model and slipping model. (a) The initial profile is h(x,y,0)=0.5[h ∞+b−(h ∞−b)tanh(3(x−5)+cos(πy/25))]. (b) The initial profile is h(x,y,0)=0.5[h ∞+b−(h ∞−b)tanh(3(x−5))]

Full size image

4.5 Comparison between simulation and experiment of gravity-driven fingering

We compare our numerical simulation results with the experimental data in [24], where silicon oil (surface tension: τ=21 dyn/cm and density: ρ=0.96 g/cm3) was used. Since the film thickness H is 0.5–1 mm [24] and the precursor film is thinner than 10−3 mm [56]. We use b=10−4 to fit the experimental condition. The computational results were in good agreement with the experimental data for wetting drops using b≤10−4 [57, 58]. D=(H 2 ρgsinα/τ)1/3cotα=0.265 with α=π/3, g=9.8 m/s2, and H=0.5 mm.

To define the initial configuration, we take a part of the experimental photo data from [24] (see top of Fig. 14(a)). Next, we detect the fluid front by an image segmentation technique [51–55]. The goal is to partition a given image into several regions, each of which has homogeneous intensity. For a given image f 0(x) on the image domain Ω, we find the level-set function \(\phi({\bf{x}})\) that satisfies

$$\begin{aligned} \phi({\bf{x}}) \left \{ \begin{array}{l@{\quad}l} >0 & \mbox{if } \textbf{x} \in\mbox{inside } \varGamma, \\ =0 & \mbox{if } \textbf{x} \in\varGamma, \\ <0 & \mbox{if } \textbf{x} \in\mbox{outside } \varGamma, \end{array} \right . \end{aligned}$$

where Γ is the segmenting curve. The geometric active contour model based on the mean curvature motion is given by the following evolution equation:

$$\begin{aligned} \phi_t =g(f_0) \biggl(-\frac{ F'(\phi)}{\epsilon^2} + \Delta\phi \biggr)+\lambda g(f_0)F(\phi), \end{aligned}$$
(14)

where g(f 0) is an edge stopping function, F(ϕ)=0.25(1−ϕ 2)2, and λ is a parameter. For more details, please refer to [53].

Fig. 14
figure 14

Comparison between numerical simulation and experimental data: (a) and (b) show comparisons at t=0 and t=65, respectively. From top to bottom, they are experimental data, numerical simulation (filled contours in h=b, h ∞, 0.8h max, and h max), and a superposition of the experimental data and numerical simulation result. Experimental figures are reprinted with permission from L. Kondic, SIAM Review, 45, 95–115 (2003)

Full size image

With the image segmentation technique, we can divide the whole domain into four regions, as shown in the middle of Fig. 14(a). As the initial condition, we set h(x,y,0)=h ∞ in the black region, 0.8h max in the gray domain, h max in the nail part of the fingers, and b in the precursor region. Here, h max is the maximum thickness of the thin film. To obtain h max, we perform a typical simulation with the initial condition h(x,y,0)=0.5[h ∞+b−(h ∞−b)tanh(3(x−10)+rand(x,y))]. Here, h ∞=1, b=10−4, and D=0.265 are chosen. l ∗=4 levels and the level zero domain Ω l+0=64×32 are used on the computational domain Ω=(0,420)×(0,210). The calculation is run until T=300 with a time step Δt=0.1. We obtain a value of h max=1.61 and use this to define the initial condition shown in the middle of Fig. 14(a). Figures 14(a) and 14(b) compare the results at t=0 and t=65, respectively. From top to bottom, they show the experimental data, numerical simulation (filled contours in h=b, h ∞, 0.8h max, and h max), and a superposition of the experimental data and numerical simulation result. Figure 14(b) indicates that the numerical result gives a qualitatively good agreement with the experimental data.

4.6 Multiple thin film simulation

We consider the temporal evolution of multiple thin films. The initial condition is h(x,y,0)=0.5[h ∞+b+(h ∞−b)tanh(3(x−10)+3cos(πy/25))] if x<10+l 1+ . Otherwise, h(x,y,0)=0.5[h ∞+b−(h ∞−b)tanh(3(x−10−l 1−l 2)+3cos(πy/25))] on the computational domain Ω=(0,800)×(0,100). Here, l 1 is the length between two initial bumps and l 2 is the size of the preceding bump. Ω l+0=128×16, l ∗=4, Δt=0.1, and D=0 are used.

Figures 15(a)–15(d) are the evolution of multiple thin-film for (l 1,l 2)=(100,150), (100,300), (200,150), and (200,150), respectively. From left to right, each column is a snapshot at t=0, 300, 360, 420, and 540. The filled contours are at the levels h=0.1, 0.5, 1, and 1.6. In Fig. 15(a), the evolution of the preceding part becomes slower due to the limited volume of fluid. On the other hand, for the behind bump, fluid is kept supplied through the Dirichlet boundary condition. The front velocity is dependent on a jump of fluid film height across the front, i.e., (f(h +)−f(h −))/(h +−h −), where h + and h − are behind and ahead fluid heights of the front, respectively [62, 63]. These lead the following fluid to catch and merge with the preceding fluid front.

Fig. 15
figure 15

(a)–(d) are the evolution of multiple thin-film for (l 1,l 2)=(100,150), (100,300), (200,150), and (200,150), respectively. The filled contours are at the levels h=0.1, 0.5, 1, and 1.6. The times are shown below each column

Full size image

To see the effect of the volume of the preceding fluid, we consider a larger l 2, as shown in Fig. 15(b). At time t=300, the finger profile of the following fluid is similar to the previous reference case (a). In this case, it takes more time to catch the preceding fluid front. After the two fronts merge, the fingering profile is similar to the reference case, except for slightly smaller finger sizes. Next, we consider the effect of l 1 on the fingering dynamics (see Fig. 15(c)). At t=300, the fingering pattern of the preceding fluid front is similar to the reference case. However, the finger of the following fluid is more developed compared to the reference case. This phenomenon continues until it merges to the preceding front. After merging, the finger size of the behind front is reduced. The final numerical experiment is a phase shifted initial condition (Fig. 15(d)). That is, for the preceding fluid, h(x,y,0)=0.5[h ∞+b−(h ∞−b)tanh(3(x−10−l 1−l 2)+3sin(πy/25))] for x>10+l 1. Until t=480, the fingering pattern is similar to the case in Fig. 15(c). However, during the merging process, the fronts disrupt each other, which leads to a smaller finger pattern.

5 Conclusions

In this paper, we presented a robust and accurate finite difference method for simulating a gravity-driven thin film through numerical investigations with an implicit essentially non-oscillatory scheme. The associated time-dependent governing equation was solved using a nonlinear full approximation storage multigrid algorithm by employing AMR. A set of representative numerical experiments were presented. By comparing the AMR results with those from a uniform mesh method, it was shown that the adaptive multigrid offers increased flexibility together with a significant reduction in memory requirement. A further comparison of our numerical solution with experimental data demonstrated the efficiency of our method.