1 Introduction

Functionally graded materials (FGMs) belong to a new generation of advanced composite materials and they were first introduced for fabricating thermal barrier systems [1]. The function of thermal barriers is achieved by tailoring the material properties in a special manner such that the macroscopic properties, i.e. heat conductivity, elastic modulus, mass density, etc. vary continuously and smoothly in the domain. More details about FGMs can be referred to references [2, 3]. Owing to the superior properties against the conventional composite laminates, FGMs have found increasing applications in modern engineering designs, such as aircraft fuselage, rocking-motor casing, packaging materials in microelectronic industry, human implants, and so on. At the same time, mechanical models and mathematical methods for predicting the mechanical and thermal behavior of unidirectional FGMs have experienced a parallel development during the past decades [4–7]. However, as demonstrated by Steinberg [8], the fuselage of a spacecraft undergoes an extremely high temperature environment with extreme temperature gradient along both its surface and thickness directions when the plane is cruising at a transonic speed leaving and entering the atmosphere. In such circumstances, the conventional thickness-wise unidirectional FGMs most probably fail to resist multi-directional severe variations in temperature. Hence, the practical demand is undoubtedly great to tailor novel FGMs with macro-properties graded in two directions (2-D FGMs) or even in three directions (3-D FGMs) to withstand more complex temperature field.

Plates resting on elastic foundations have found considerable applications in structural engineering problems. Reinforced-concrete pavements of highways, airport runways, foundation of storage tanks, swimming pools, and deep walls together with foundation slabs of buildings are well-known direct applications of these kinds of plates. The underlying layers are modeled by a Winkler-type elastic foundation. The most serious deficiency of the Winkler foundation model is to have no interaction between the springs. In other words, the springs in this model are assumed to be independent and unconnected.

The Winkler foundation model is fairly improved by adopting the Pasternak foundation model, a two-parameter model, in which the shear stiffness of the foundation is considered.

A closed-form solution for the vibration frequencies of simply supported Mindlin plates on Pasternak foundations and subjected to biaxial initial stresses was presented by Xiang et al. [9]. The buckling load of Mindlin plates on Pasternak foundations was obtained in terms of the thin plate solution. Based on first-order shear deformation plate theory, the buckling and vibration analysis of moderately thick laminates on Pasternak foundations were presented by Xiang et al. [10]. The effects of foundation parameters, transverse shear deformation, and rotary inertia and the number of layers on the buckling and vibration of cross-ply laminates were examined. Wang et al. [11] presented relationships between the buckling loads of simply supported plates on a Pasternak foundation determined by classical Kirchhoff plate theory, Reissner–Mindlin plate theory, and Reddy plate theory. The vibration of polar orthotropic circular plates on an elastic foundation has been investigated by Gupta et al. [12]. The Mindlin shear deformable plate theory was employed and the Chebyshev collocation method was applied to obtain the frequency parameters for the circular plates. Ju et al. [13] developed a finite element model to study the vibration of Mindlin plates with multiple stepped variations in thickness and resting on non-homogeneous elastic foundations. Gupta et al. [14, 15] studied the effect of elastic foundation on axisymmetric vibrations of polar orthotropic circular plates of variable thickness by taking approximating polynomials in Rayleigh–Ritz method. Laura and Gutierrez [16] analyzed the free vibration of a solid circular plate of linearly varying thickness attached to Winkler foundation using the Ritz method. Matsunaga [17] analyzed the natural frequencies and buckling stresses of FG plates using a higher order shear deformation theory which are based on the series expansion of the displacement components. Zhou et al. [18] used Ritz method to analyze the free-vibration characteristics of rectangular thick plates resting on elastic foundations. Matsunaga [19] investigated a two-dimensional, higher-order theory for analyzing the thick simply supported rectangular plates resting on elastic foundations. Yas and Sobhani [20] studied free vibration characteristics of rectangular continuous grading fiber reinforced (CGFR) plates resting on elastic foundations using DQM. Yas and Tahouneh [21] investigated the free vibration analysis of thick FG annular plates on elastic foundations via differential quadrature method based on the three-dimensional elasticity theory and Tahouneh and Yas [22] investigated the free vibration analysis of thick FG annular sector plates on Pasternak elastic foundations using DQM. Recently, Tahouneh et al. [23] studied free vibration characteristics of annular continuous grading fiber reinforced (CGFR) plates resting on elastic foundations using DQM and More recently, Tahouneh and Yas [24] used DQM to study 3-D free vibration of multi-directional functionally graded annular sector plates under various boundary conditions. Liew et al. [25] employed the differential quadrature method for studying the Mindlin’s plate on Winkler foundation. Moreover, Zhou et al. [26] described an excellent investigation of the 3-D free vibration of thick circular plates resting on Pasternak foundation by using the Chebyshev–Ritz method. Yang and Shen [27] used the classical plate theory to study free and forced vibration of functionally graded rectangular thin plates subjected to initial in plane stresses and rested on elastic foundations. Cheng and Kitipornchai [28] proposed a membrane analogy to derive an exact explicit eigenvalues for vibration and buckling of simply supported FG plates resting on elastic foundations using the first-order shear deformation theory (FSDT). Batra and Jin [29] used the FSDT coupled with the finite element method (FEM) to study free vibrations of a functionally graded (FG) anisotropic rectangular plate. Cheng and Batra [30] used Reddy’s third-order plate theory to study steady state vibrations and buckling of a simply supported functionally gradient isotropic polygonal plate resting on a Pasternak elastic foundation and subjected to uniform in-plane hydrostatic loads. Malekzadeh [31] studied free vibration analyses of functionally graded plates on elastic foundations based on the three-dimensional elasticity.

In the above-mentioned papers, the material properties are assumed having a smooth variation usually in one direction. A conventional FGM may also not be so effective in some design problems since all outer surfaces of the body will have the same composition distribution. So, it is necessary to develop appropriate methods to investigate the mechanical responses of multi-directional functionally graded structures.

In structural mechanics, one of the most popular semi-analytical methods is differential quadrature method (DQM) [32], remarkable success of which has been demonstrated by many researchers in vibration analysis of plates, shells, and beams. The differential quadrature method (DQM) is found to be a simple and efficient numerical technique for structural analysis [33, 34]. Better convergence behavior is observed by DQM compared with its peer numerical competent techniques viz. the finite element method, the finite difference method, the boundary element method and the meshless technique. The mathematical fundamental and recent developments of differential quadrature method as well as its major applications in engineering are discussed in detail in book by Shu [35].

This paper is motivated by the lack of studies in the technical literature concerning to the three-dimensional vibration analysis of bi-directional FG rectangular plates resting on elastic foundations. To the authors’ best knowledge, research on the vibration of thick bi-directional FG rectangular plates on a two-parameter elastic foundation based on the three-dimensional theory of elasticity has not been seen until now. In this study, for the first time a graded rectangular plate resting on an elastic foundation with 2-D power-law distribution of the volume fraction of the constituents along the thickness and in the in-plane directions is considered. The Mori–Tanaka scheme as an accurate micromechanics model is used for estimating the homogenized material properties. In the present paper, the differential quadrature method is employed to develop a semi-analytical solution for free vibration analyses of two-directional functionally graded rectangular plates. Simultaneous variations of the material properties through the thickness and in the in-plane directions are described by a general function. A sensitivity analysis is performed, and the natural frequencies are calculated for different sets of boundary conditions and different combinations of the geometric, material, and foundation parameters. Therefore, very complex combinations of the material properties, boundary conditions, and foundation stiffness are considered in the present semi-analytical solution approach.

2 Problem formulation

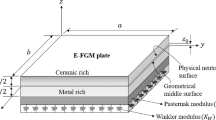
Consider a 2-D FGM rectangular plate with length a, width b, and thickness h which is made from a mixture of ceramics and metals as depicted in Fig. 1. The plate is supported by an elastic foundation with Winkler’s (normal) and Pasternak’s (shear) coefficients. The deformations defined with reference to a Cartesian coordinate system (x,y,z) are u, v and w in the x, y and z directions, respectively.

Fig. 1
figure 1

The sketch of a rectangular plate functionally graded in both thickness-wise and in-plane domains resting on a two-parameter elastic foundation and setup of the coordinate system

Full size image

2.1 Two-directional six-parameter power-law distribution

In this work, it is proposed that the volume fraction of the ceramic phase follows a 2-D six-parameter power-law distribution:

$$\begin{aligned} V_{c} =& \biggl[\biggl(\biggl(\frac{1}{2} - \frac{z}{h} \biggr) + \alpha_{z}\biggl(\frac{1}{2} + \frac {z}{h} \biggr)^{\beta_{z}}\biggr)^{\gamma _{z}}(V_{b} - V_{a}) \\ &{} + V_{a}\biggr]\biggl(\alpha_{y}\biggl(\frac{1}{2} + \frac {y}{b}\biggr)^{\beta_{y}} + 1 - \biggl(\frac{1}{2} + \frac{y}{b}\biggr)\biggr)^{\gamma_{y}} \end{aligned}$$
(1)

where γ y and γ z are the volume fractions index along y- and z-axes, respectively. The parameters α y , β y and α z , β z govern the material variation profile along the y- and z-axes, respectively. The volume fractions V a and V b , which have values that range from 0 to 1, denote the ceramic volume fractions of the two different isotropic materials. For example, with assumption V b =1 and V a =0.3, some material profiles along the y−(μ y =y/b) and z−(μ z =z/h) directions are illustrated in Figs. 2–4. As can be seen from Fig. 2, the classical volume fraction profile along the thickness and width of the plate is presented as a special case of the 2-D power-law distribution (1) by setting γ y =γ z =4, and α y =α z =0. With another choice of the parameters α y , β y , α z and β z , it is possible to obtain volume fraction profiles along the thickness and width of the plate as shown in Fig. 3. This figure shows a classical profile versus μ z and a symmetric profile versus μ y . Figure 4 illustrates symmetric profiles along the thickness and width of the plate obtained by setting α y =α z =1 and β y =β z =2. The effective material properties of the isotropic 2-D FGMs are determined in terms of the local volume fractions and material properties of the two isotropic phases by the Mori–Tanaka scheme. The Mori–Tanaka scheme [36, 37] for estimating the effective moduli is applicable to regions of the graded microstructure that have a well-defined continuous matrix and a discontinuous particulate phase. It takes into account the interaction of the elastic fields among neighboring inclusions. It is assumed that the matrix phase, denoted by the subscript m, is reinforced by spherical particles of a particulate phase, denoted by the subscript c. In this notation, K m and G m are the bulk modulus and the shear modulus, respectively, and V m is the volume fraction of the matrix phase. K c , G c , and V c are the corresponding material properties and the volume fraction of the particulate phase. Note that V m +V c =1, that the Lamé constant λ is related to the bulk and the shear moduli by λ=K−2G/3, and that the stress–temperature modulus is related to the coefficient of thermal expansion by β=(3λ+2G)α=3Kα. The following estimates for the effective local bulk modulusKand shear modulus G are useful for a random distribution of isotropic particles in an isotropic matrix:

$$\begin{aligned} &{\frac{K - K_{m}}{K_{c} - K_{m}}} \\ &{\quad = \frac{V_{c}}{1 + (1 - V_{c})(K_{c} - K_{m}) / (K_{m} + (4 / 3)K_{m})}} \end{aligned}$$
(2)
$$\begin{aligned} &{\frac{G - G_{m}}{G_{c} - G_{m}} = \frac{V_{c}}{1 + (1 - V_{c})(G_{c} - G_{m}) / (G_{m} + f_{m})}} \end{aligned}$$
(3)

where f m =G m (9K m +8G m )/6(K m +2G m ). The effective values of Young’s modulus, E, and Poisson’s ratio, υ, are found from:

$$ E = \frac{9KG}{3K + G},\qquad\upsilon= \frac{3K - 2G}{2(3K + G)} $$
(4)

we choose a metal/ceramic rectangular plate with the metal (Al) taken as the matrix phase and the ceramic (SiC) taken as the particulate phase. The material properties of aluminum and silicon carbide are listed in Table 1 [38, 39].

Fig. 2
figure 2

Variations of the classical volume fraction profile along the y- and z-axes of the rectangular plate (γ y =γ z =4, α y =α z =0)

Full size image
Fig. 3
figure 3

Variations of the volume fraction profile along the y- and z-axes of the rectangular plate (γ y =γ z =3, β y =2, α y =1, α z =0)

Full size image
Fig. 4
figure 4

Variations of the symmetric volume fraction profiles along the y- and z-axes of the rectangular plate (γ y =γ z =3, β y =β z =2, α y =α z =1)

Full size image
Table 1 Material properties of aluminum and silicon carbide
Full size table

2.2 Governing equations

Using the three-dimensional constitutive relations and the strain-displacement relations, the equations of motion in terms of displacement components for a linear elastic 2-D FG plate with infinitesimal deformations can be written as

$$\begin{aligned} &{c_{11}\frac{\partial^{2}u}{\partial x^{2}} + c_{12}\frac{\partial^{2}v}{\partial x\partial y} + c_{13}\frac{\partial^{2}w}{\partial x\partial z} + \frac {\partial c_{66}}{\partial y}\biggl(\frac{\partial v}{\partial x} + \frac{\partial u}{\partial y}\biggr)} \\ &{\qquad {} + c_{66}\biggl(\frac{\partial ^{2}v}{\partial y\partial x} + \frac{\partial^{2}u}{\partial y^{2}}\biggr) + \frac{\partial c_{55}}{\partial z}\biggl(\frac{\partial w}{\partial x} + \frac{\partial u}{\partial z}\biggr)} \\ &{\qquad {} + c_{55}\biggl(\frac{\partial^{2}w}{\partial z\partial x} + \frac{\partial ^{2}u}{\partial z^{2}}\biggr) = \rho \frac{\partial^{2}u}{\partial t^{2}}} \end{aligned}$$
(5)
$$\begin{aligned} &{c_{66}\biggl(\frac{\partial^{2}v}{\partial x^{2}} + \frac {\partial^{2}u}{\partial x\partial y}\biggr) + \frac{\partial c_{12}}{\partial y}\frac{\partial u}{\partial x} + c_{12}\frac{\partial^{2}u}{\partial y\partial x}} \\ &{\qquad {} + \frac{\partial c_{22}}{\partial y}\frac{\partial v}{\partial y} + c_{22}\frac{\partial^{2}v}{\partial y^{2}} + \frac{\partial c_{23}}{\partial y}\frac{\partial w}{\partial z} + c_{23}\frac{\partial ^{2}w}{\partial y\partial z}} \\ &{\qquad {} + \frac{\partial c_{44}}{\partial z}\biggl(\frac{\partial v}{\partial z} + \frac {\partial w}{\partial y}\biggr) + c_{44}\biggl(\frac{\partial^{2}v}{\partial z^{2}} + \frac{\partial ^{2}w}{\partial z\partial y}\biggr)} \\ &{\quad = \rho \frac{\partial^{2}v}{\partial t^{2}}} \end{aligned}$$
(6)
$$\begin{aligned} &{c_{55}\biggl(\frac{\partial^{2}w}{\partial x^{2}} + \frac {\partial^{2}u}{\partial x\partial z}\biggr) + \frac{\partial c_{44}}{\partial y}\biggl(\frac{\partial v}{\partial z} + \frac{\partial w}{\partial y}\biggr)} \\ &{\quad {} + c_{44}\biggl(\frac{\partial^{2}v}{\partial y\partial z} + \frac{\partial ^{2}w}{\partial y^{2}}\biggr) + \frac{\partial c_{13}}{\partial z}\frac {\partial u}{\partial x} + c_{13}\frac{\partial^{2}u}{\partial z\partial x}} \\ &{\quad {} + \frac{\partial c_{23}}{\partial z}\frac{\partial v}{\partial y} + c_{23}\frac{\partial^{2}v}{\partial z\partial y} + \frac{\partial c_{33}}{\partial z}\frac{\partial w}{\partial z} + c_{33}\frac{\partial^{2}w}{\partial z^{2}}} \\ &{\quad = \rho \frac{\partial ^{2}w}{\partial t^{2}}} \end{aligned}$$
(7)

Equations (5) and (6) represent the in-plane equations of motion along the x- and y-axes, respectively; and Eq. (7) is the transverse or out-of-plane equation of motion. The related boundary conditions at z=−h/2 and h/2 are as follows: at z=−h/2:

$$ \begin{array}{l} \sigma_{zx} = 0, \\ \sigma_{zy} = 0,\sigma_{zz} = K_{w}w - K_{g}\biggl(\displaystyle\frac{\partial ^{2}w}{\partial x^{2}} + \frac{\partial^{2}w}{\partial y^{2}}\biggr) \end{array} $$
(8)

at z=h/2:

$$ \begin{array}{l} \sigma_{zx} = 0, \\ \sigma_{zy} = 0, \\ \sigma_{zz}= 0 \end{array} $$
(9)

where σ ij are the components of stress tensor; K w and K g are Winkler and shearing layer elastic coefficients of the foundation. The stress components are related to the displacement components using the three-dimensional constitutive relations as

$$ \begin{array}{l} \sigma_{xx} = c_{11}\displaystyle\frac{\partial u}{\partial x} + c_{12}\frac{\partial v}{\partial y} + c_{13}\frac{\partial w}{\partial z},\\ \sigma_{yz} = c_{44}\biggl(\displaystyle\frac{\partial w}{\partial y} + \frac{\partial v}{\partial z}\biggr) \\ \sigma_{yy} = c_{12}\displaystyle\frac{\partial u}{\partial x} + c_{22}\frac{\partial v}{\partial y} + c_{23}\frac{\partial w}{\partial z},\\ \sigma_{xz} = c_{55}\biggl(\displaystyle\frac{\partial u}{\partial z} + \frac{\partial w}{\partial x}\biggr) \\ \sigma_{zz} = c_{13}\displaystyle\frac{\partial u}{\partial x} + c_{23}\frac{\partial v}{\partial y} + c_{33}\frac{\partial w}{\partial z},\\ \sigma_{xy} = c_{66}\biggl(\displaystyle\frac{\partial v}{\partial x} + \frac{\partial u}{\partial y}\biggr) \end{array} $$
(10)

different types of classical boundary conditions at edges y=−b/2 and b/2 of the plate can be stated as

  • Simply supported (S):

    $$ \sigma_{yy} = 0,\qquad w = 0, \qquad u = 0; $$
    (11)

  • Clamped (C):

    $$ u = 0,\qquad v = 0,\qquad w = 0; $$
    (12)

  • Free (F):

    $$ \sigma_{yy} = 0,\qquad\sigma_{xy} = 0,\qquad\sigma_{yz} = 0 $$
    (13)

3 Solution procedure

Here, plates with two opposite edges x=−a/2 and a/2 simply supported and arbitrary conditions at edges y=−b/2 and b/2 are considered. For free vibration analysis, by adopting the following form for the displacement components the boundary conditions at edges x=−a/2 and a/2 are satisfied,

$$\begin{aligned} &{\begin{array}{l} u(x,y,z,t) = U_{m}(y,z,t)\cos\bigl(m\pi(x + a / 2) / a\bigr)e^{i\omega t}, \\ v(x,y,z,t) = V_{m}(y,z,t)\sin\bigl(m\pi(x + a / 2) / a\bigr)e^{i\omega t}, \\ w(x,y,z,t) = W_{m}(y,z,t)\sin\bigl(m\pi(x + a / 2) / a\bigr)e^{i\omega t}\end{array}} \end{aligned}$$
(14)

where m is the wave number along the x-direction, ω is the natural frequency and \(i (=\sqrt{ - 1})\) is the imaginary number. Substituting for displacement components from Eq. (14) into Eqs. (5)–(7), one gets Eq. (5):

$$\begin{aligned} &{- c_{11}\biggl(\frac{m\pi}{a}\biggr)^{2}U_{m} + c_{12}\biggl(\frac{m\pi}{a} \biggr)\frac{\partial V_{m}}{\partial y}} \\ &{\qquad {} + c_{13}\biggl(\frac{m\pi}{a}\biggr)\frac{\partial W_{m}}{\partial z} + \frac{\partial c_{66}}{\partial y}\biggl(\frac{m\pi}{a}V_{m}+ \frac{\partial U_{m}}{\partial y} \biggr)} \\ &{\qquad {} + c_{66}\biggl(\frac{m\pi}{a} \frac{\partial V_{m}}{\partial y} + \frac{\partial ^{2}U_{m}}{\partial y^{2}}\biggr) + \frac{\partial c_{55}}{\partial z}\biggl( \frac{m\pi}{a}W_{m}} \\ &{\qquad {} + \frac {\partial U_{m}}{\partial z}\biggr) + c_{55} \biggl(\frac{m\pi}{a}\frac{\partial W_{m}}{\partial z} + \frac{\partial ^{2}U_{m}}{\partial z^{2}}\biggr)} \\ &{\quad = - \rho \omega^{2}U_{m}} \end{aligned}$$
(15)

Equation (6):

$$\begin{aligned} &{c_{66}\biggl( - \biggl(\frac{m\pi}{a} \biggr)^{2}V_{m} - \biggl(\frac{m\pi}{a} \biggr) \frac{\partial U_{m}}{\partial y}\biggr)} \\ &{\quad {}+ \frac{\partial c_{12}}{\partial y}\biggl( - \frac{m\pi}{a} \biggr)U_{m} + c_{12}\biggl(\frac{ - m\pi}{a}\biggr) \frac{\partial U_{m}}{\partial y}} \\ &{\quad{} + \frac{\partial c_{22}}{\partial y}\frac{\partial V_{m}}{\partial y} + c_{22} \frac{\partial^{2}V_{m}}{\partial y^{2}} + \frac{\partial c_{23}}{\partial y}\frac{\partial W_{m}}{\partial z}} \\ &{\quad{} + c_{23} \frac {\partial^{2}W_{m}}{\partial y\partial z} + \frac{\partial c_{44}}{\partial z}\biggl(\frac{\partial V_{m}}{\partial z} + \frac{\partial W_{m}}{\partial y}\biggr)} \\ &{\quad{} {} + c_{44}\biggl(\frac{\partial^{2}V_{m}}{\partial z^{2}} + \frac{\partial ^{2}W_{m}}{\partial z\partial y}\biggr) = - \rho\omega^{2}V_{m}} \end{aligned}$$
(16)

Equation (7):

$$\begin{aligned} &{c_{55}\biggl( - \biggl(\frac{m\pi}{a} \biggr)^{2}W_{m} - \biggl(\frac{m\pi}{a} \biggr) \frac{\partial U_{m}}{\partial z}\biggr) + \frac{\partial c_{44}}{\partial y}\biggl(\frac{\partial V_{m}}{\partial z}} \\ &{\quad {} + \frac{\partial W_{m}}{\partial y}\biggr) + c_{44}\biggl(\frac{\partial ^{2}V_{m}}{\partial y\partial z} + \frac{\partial^{2}W_{m}}{\partial y^{2}}\biggr)} \\ &{\quad {} {} + \frac{\partial c_{13}}{\partial z}\biggl( - \frac{m\pi}{a} U_{m}\biggr) + c_{13}\biggl( - \frac{m\pi}{a} \frac{\partial U_{m}}{\partial z}\biggr)} \\ &{\quad {} {} + \frac{\partial c_{23}}{\partial z}\frac{\partial V_{m}}{\partial y} + c_{23} \frac {\partial^{2}V_{m}}{\partial z\partial y} + \frac{\partial c_{33}}{\partial z}\frac{\partial W_{m}}{\partial z}} \\ &{\quad {}+ c_{33} \frac{\partial^{2}W_{m}}{\partial z^{2}} = - \rho\omega ^{2}W_{m}} \end{aligned}$$
(17)

The geometrical and natural boundary conditions stated in Eqs. (8) and (9) can also be simplified, however, for brevity purpose they are not shown here. It is necessary to develop appropriate methods to investigate the mechanical responses of 2-D FGM structures. But, due to the complexity of the problem caused by the two-directional inhomogeneity, it is difficult to obtain the exact solution. In this paper, the differential quadrature method (DQM) approach is used to solve the governing equations of 2-D FGM rectangular plates. One can compare DQM solution procedure with the other two widely used traditional methods for plate analysis, i.e., Rayleigh-Ritz method and FEM. The main difference between the DQM and the other methods is how the governing equations are discretized. In DQM the governing equations and boundary conditions are directly discretized, and thus elements of stiffness and mass matrices are evaluated directly. But in Rayleigh-Ritz and FEMs, the weak form of the governing equations should be developed and the boundary conditions are satisfied in the weak form. Generally by doing so larger number of integrals with increasing amount of differentiation should be done to arrive at the element matrices. Also, the number of degrees of freedom will be increased for an acceptable accuracy. The basic idea of the DQM is the derivative of a function, with respect to a space variable at a given sampling point, is approximated as a weighted linear sum of the sampling points in the domain of that variable. In order to illustrate the DQ approximation, consider a functionf(ξ,η)defined on a rectangular domain 0≤ξ≤a and 0≤η≤b. Let in the given domain, the function values be known or desired on a grid of sampling points. According to DQM method, the rth derivative of the function f(ξ,η) can be approximated as

$$ \begin{aligned} &\frac{\partial^{r}f(\xi,\eta)}{\partial\xi^{r}}\bigg| (\xi ,\eta) = (\xi_{i},\eta_{j}) = \sum_{m = 1}^{N_{\xi}} A_{im}^{\xi(r)}f(\xi_{m},\eta_{j}) \\ &\quad = \sum _{m = 1}^{N_{\xi}} A_{im}^{\xi (r)}f_{mj} \\ &\quad \mbox{for}\ i=1,2,\dots,N_{\xi}\ \mbox{and}\ r=1,2,\dots,N_{\xi} - 1 \end{aligned} $$
(18)

where N ξ represents the total number of nodes along the ξ-direction. From this Equation one can deduce that the important components of DQM approximations are the weighting coefficients (\(A_{ij}^{\xi(r)}\)) and the choice of sampling points. In order to determine the weighting coefficients a set of test functions should be used in Eq. (18). The weighting coefficients for the first-order derivatives in ξ-direction are thus determined as [33]

$$ \begin{aligned} \hphantom{}& {A_{ij}^{\xi} = \left\{ \begin{array}{l@{\quad}l} \frac{1}{a}\frac{M(\xi_{i})}{(\xi_{i} - \xi_{j})M(\xi _{j})} & \mbox{for}\ i \ne j \\ - \sum_{{\scriptstyle j = 1 \atop\scriptstyle i \ne j}}^{N_{\xi}} A_{ij}^{\xi} & \mbox{for}\ i = j \end{array} \right.;} \\ &{\quad i,j = 1,2,\ldots,N_{\xi}} \end{aligned} $$
(19)

where

$$ M(\xi_{i}) = \prod_{j = 1,i \ne j}^{N_{\xi}} (\xi_{i} - \xi_{j}) $$
(20)

The weighting coefficients of the second-order derivative can be obtained in the matrix form [33]:

$$ \bigl[ B_{ij}^{\xi} \bigr] = \bigl[ A_{ij}^{\xi} \bigr] \bigl[ A_{ij}^{\xi} \bigr] = \bigl[ A_{ij}^{\xi} \bigr]^{2} $$
(21)

In a similar manner, the weighting coefficients for the η-direction can be obtained.

The natural and simplest choice of the grid points is equally spaced points in the direction of the coordinate axes of computational domain. It was demonstrated that non-uniform grid points gives a better result with the same number of equally spaced grid points [33]. It is shown [40] that one of the best options for obtaining grid points is Chebyshev–Gauss–Lobatto quadrature points:

$$\begin{aligned} &{\frac{\xi_{i}}{a} = \frac{1}{2} \biggl\{ 1 - \cos \biggl[ \frac{(i - 1)\pi }{(N_{\xi} - 1)} \biggr] \biggr\},} \\ &{\frac{\eta_{j}}{b} = \frac{1}{2} \biggl\{ 1 - \cos \biggl[ \frac {(j - 1)\pi}{(N_{\eta} - 1)} \biggr] \biggr\}} \\ &{\quad \mbox{for}\ i = 1,2,\dots,N_{\xi};\ j = 1,2,\dots,N_{\eta}} \end{aligned}$$
(22)

where N ξ and N η are the total number of nodes along the ξ- and η-directions, respectively.

At this stage, the DQ method can be applied to discretize the equations of motion (15)–(17) and the boundary conditions. As a result, at each domain grid point (y j ,z k ) with j=2,…,N y −1 and k=2,…,N z −1, the discretized equations take the following forms

Equation (15):

$$\begin{aligned} &{- (c_{11})_{jk}\biggl(\frac{m\pi}{a}\biggr)^{2}U_{mjk} + (c_{12})_{jk}\biggl(\frac{m\pi}{a}\biggr)\sum _{n = 1}^{N_{y}} A_{jn}^{y} V_{mnk}} \\ &{\qquad {} + (c_{13})_{jk}\biggl(\frac{m\pi}{a} \biggr)\sum_{n = 1}^{N_{z}} A_{kn}^{z} W_{mjn} + \biggl(\frac{\partial c_{66}}{\partial y}\biggr)_{jk}} \\ &{\qquad{}\times \Biggl( \frac{m\pi}{ a}V_{mjk} + \sum_{n = 1}^{N_{y}} A_{jn}^{y} U_{mnk}\Biggr)} \\ &{\qquad {} + (c_{66})_{jk} \Biggl(\frac{m\pi}{a}\sum_{n = 1}^{N_{y}} A_{jn}^{y} V_{mnk} + \sum_{n = 1}^{N_{y}} B_{jn}^{y}U_{mnk} \Biggr)} \\ &{\qquad {} + \biggl(\frac{\partial c_{55}}{\partial z}\biggr)_{jk}\Biggl( \frac{m\pi}{a}W_{mjk} + \sum_{n = 1}^{N_{z}} A_{kn}^{z} U_{mjn}\Biggr)} \\ &{\qquad {} {} + (c_{55})_{jk} \Biggl(\frac{m\pi}{a}\sum_{n = 1}^{N_{z}} A_{kn}^{z} W_{mjn} + \sum _{n = 1}^{N_{z}} B_{kn}^{z} U_{mjn}\Biggr)} \\ &{\quad = - \rho_{jk}\omega ^{2}U_{mjk}} \end{aligned}$$
(23)

Equation (16):

$$\begin{aligned} &{(c_{66})_{jk}\Biggl( - \biggl(\frac{m\pi}{a} \biggr)^{2}V_{mjk} + \biggl(\frac{ - m\pi}{a}\biggr)\sum _{n = 1}^{N_{y}} A_{jn}^{y} U_{mnk}\Biggr)} \\ &{\qquad {} + \biggl(\frac{\partial c_{12}}{\partial y}\biggr)_{jk} \biggl( \frac{ - m\pi}{a} \biggr)U_{mjk}} \\ &{\qquad {} + (c_{12})_{jk}\Biggl( \biggl(\frac{ - m\pi}{a}\biggr)\sum_{n = 1}^{N_{y}} A_{jn}^{y} U_{mnk}\Biggr)} \\ &{\qquad {} + \biggl(\frac{\partial c_{22}}{\partial y} \biggr)_{jk} \Biggl(\sum_{n = 1}^{N_{y}} A_{jn}^{y} V_{mnk}\Biggr)} \\ &{\qquad {} + (c_{22})_{jk} \sum_{n = 1}^{N_{y}} B_{jn}^{y} V_{mnk}} \\ &{\qquad {} + \biggl(\frac{\partial c_{23}}{\partial y}\biggr)_{jk}\Biggl(\sum _{n = 1}^{N_{z}} A_{kn}^{z} W_{mjn}\Biggr)} \\ &{\qquad {} + (c_{23})_{jk}\Biggl(\sum _{n = 1}^{N_{y}} \sum_{r = 1}^{N_{z}} A_{kr}^{z} A_{jn}^{y}W_{mnr} \Biggr)} \\ &{\qquad {} + \biggl(\frac{\partial c_{44}}{\partial z}\biggr)_{jk}\Biggl(\sum _{n = 1}^{N_{z}} A_{kn}^{z} V_{mjn} + \sum_{n = 1}^{N_{y}} A_{jn}^{y} W_{mnk}\Biggr)} \\ &{\qquad {} + (c_{44})_{jk} \Biggl(\sum_{n = 1}^{N_{z}} B_{kn}^{z}V_{mjn}} \\ &{\qquad{} + \sum_{n = 1}^{N_{y}} \sum _{r = 1}^{N_{z}} A_{kr}^{z}A_{jn}^{y} W_{mnr}\Biggr)} \\ &{\quad = - \rho _{jk}\omega^{2}V_{mjk}} \end{aligned}$$
(24)

Equation (17):

$$\begin{aligned} &{(c_{55})_{jk}\Biggl( - \biggl(\frac{m\pi}{a} \biggr)^{2}W_{mjk} - \frac {m\pi}{a}\sum _{n = 1}^{N_{z}} A_{kn}^{z} U_{mjn}\Biggr)} \\ &{\qquad {} + \biggl(\frac{\partial c_{44}}{\partial y}\biggr)_{jk} \Biggl(\sum_{n = 1}^{N_{z}} A_{kn}^{z} V_{mjn} + \sum_{n = 1}^{N_{y}} A_{jn}^{y} W_{mnk}\Biggr)} \\ &{\qquad{} + (c_{44})_{jk} \Biggl(\sum_{n = 1}^{N_{y}} \sum _{r = 1}^{N_{z}} A_{kr}^{z} A_{jn}^{y}V_{mnr}} \\ &{\qquad{} + \sum _{n = 1}^{N_{y}} B_{jn}^{y} W_{mnk}\Biggr) + \biggl(\frac{\partial c_{13}}{\partial z}\biggr)_{jk}\biggl( - \frac{m\pi}{a}U_{mjk}\biggr)} \\ &{\qquad{} + (c_{13})_{jk}\Biggl( - \frac{m\pi}{a} \sum_{n = 1}^{N_{z}} A_{kn}^{z} U_{mjn}\Biggr)} \\ &{\qquad{} + \biggl(\frac{\partial c_{23}}{\partial z}\biggr)_{jk}\sum _{n = 1}^{N_{y}} A_{jn}^{y} V_{mnk}} \\ &{\qquad{} + (c_{23})_{jk}\sum _{n = 1}^{N_{y}} \sum_{r = 1}^{N_{z}} A_{kr}^{z}A_{jn}^{y} V_{mnr}} \\ &{\qquad{} + \biggl(\frac{\partial c_{33}}{\partial z}\biggr)_{jk}\sum_{n = 1}^{N_{z}} A_{kn}^{z} W_{mjn}} \\ &{\qquad{} + (c_{33})_{jk} \sum_{n = 1}^{N_{z}} B_{kn}^{z} W_{mjn}} \\ &{\quad = - \rho_{jk}\omega ^{2}W_{mjk}} \end{aligned}$$
(25)

where \(A_{ij}^{y}\), \(A_{ij}^{z}\) and \(B_{ij}^{y}\), \(B_{ij}^{z}\) are the first and second order DQ weighting coefficients in the y- and z-directions, respectively. In a similar manner the boundary conditions can be discretized. For this purpose, using Eq. (14) and the DQ discretization rules for spatial derivatives, the boundary conditions at z=−h/2 and h/2 become, at z=−h/2

$$\begin{aligned} &{\biggl(\frac{m\pi}{a}\biggr)W_{mjk} + \sum _{n = 1}^{N_{z}} A_{kn}^{z} U_{mjn} = 0,} \\ &{\sum_{n = 1}^{N_{y}} A_{jn}^{y} W_{mnk} + \sum _{n = 1}^{N_{z}} A_{kn}^{z} V_{mjn} = 0,} \\ &{(c_{13})_{jk}\biggl( \frac{ - m\pi}{a}\biggr)U_{mjk} + (c_{23})_{jk}\sum _{n = 1}^{N_{y}} A_{jn}^{y} V_{mnk}} \\ &{\qquad {} + (c_{33})_{jk}\sum _{n = 1}^{N_{z}} A_{kn}^{z} W_{mjn}} \\ &{- k_{w}W_{mjk} + k_{g}\Biggl( - W_{mjk} \biggl(\frac {m\pi}{a}\biggr)^{2} + \sum_{n = 1}^{N_{y}} B_{jn}^{y}W_{mnk} \Biggr)} \\ &{\quad = 0} \end{aligned}$$
(26)

at z=h/2

$$\begin{aligned} &{\biggl(\frac{m\pi}{a}\biggr)W_{mjk} + \sum _{n = 1}^{N_{z}} A_{kn}^{z} U_{mjn} = 0,} \\ &{\sum_{n = 1}^{N_{y}} A_{jn}^{y} W_{mnk} + \sum_{n = 1}^{N_{z}} A_{kn}^{z} V_{mjn} = 0,} \\ &{(c_{13})_{jk}\biggl(\frac{ - m\pi}{a} \biggr)U_{mjk} + (c_{23})_{jk}\sum _{n = 1}^{N_{y}} A_{jn}^{y} V_{mnk}} \\ &{\quad{} + (c_{33})_{jk}\sum _{n = 1}^{N_{z}} A_{kn}^{z} W_{mjn} = 0} \end{aligned}$$
(27)

where k=1 at z=−h/2 and k=N z at z=h/2, and j=1,2,…,N y .

The boundary conditions at y=−b/2 and b/2 become,

  • Simply supported (S):

    $$ \begin{array}{l} U_{mjk} = 0,\qquad W_{mjk} = 0, \\ - (c_{12})_{jk}\biggl(\displaystyle\frac{m\pi}{a}\biggr)U_{mjk} + (c_{22})_{jk}\sum_{n = 1}^{N_{y}} A_{jn}^{y} V_{mnk}\\ \quad {} + (c_{23})_{jk}\displaystyle\sum _{n = 1}^{N_{z}} A_{kn}^{z} W_{mjn} = 0 \end{array} $$
    (28)

  • Clamped (C):

    $$ U_{mjk} = 0,\qquad V_{mjk} = 0,\qquad W_{mjk} = 0 $$
    (29)

  • Free (F):

    $$ \begin{array}{l} (c_{12})_{jk}\biggl(\displaystyle\frac{ - m\pi}{a}\biggr)U_{mjk} + (c_{22})_{jk}\sum_{n = 1}^{N_{y}} A_{jn}^{y} V_{mnk}\\ {}+ (c_{23})_{jk}\displaystyle\sum_{n = 1}^{N_{z}} A_{kn}^{z} W_{mjn} = 0, \\ \biggl(\displaystyle\frac{m\pi}{a}\biggr)V_{mjk} + \sum_{n = 1}^{N_{y}} A_{jn}^{y} U_{mnk} = 0,\\ \displaystyle\sum_{n = 1}^{N_{z}} A_{kn}^{z} V_{mjn} + \sum_{n = 1}^{N_{y}} A_{jn}^{y} W_{mnk} = 0 \end{array} $$
    (30)

In the above equations k=2,…,N z −1; also j=1 at y=−b/2 and j=N y at y=b/2.

In order to carry out the eigenvalue analysis, the domain and boundary nodal displacements should be separated. In vector forms, they are denoted as {d} and {b}, respectively. Based on this definition, the discretized form of the equations of motion and the related boundary conditions can be represented in the matrix form as:

Equations of motion (23)–(25):

$$ \bigl[ [ K_{db} ] [ K_{dd} ] \bigr]\left \{ \begin{array} {l} \{ b \} \\ \{ d \} \end{array} \right \} - \omega^{2} [ M ] \{ d \} = \{ 0 \} $$
(31)

Boundary conditions (26), (27) and (28)–(30):

$$ [ K_{bd} ] \{ d \} + [ K_{bb} ] \{ b \} = \{ 0 \} $$
(32)

Eliminating the boundary degrees of freedom in Eq. (31) using Eq. (32), this equation becomes,

$$ [ K ] - \omega^{2} [ M ] \{ d \} = \{ 0 \} $$
(33)

where [K]=[K dd ]−[K db ][K bb ]−1[K bd ]. The above eigenvalue system of equations can be solved to find the natural frequencies and mode shapes of the plate.

4 Numerical results and discussion

Due to lack of appropriate results for free vibration of 2-D FG rectangular plates for direct comparison, validation of the presented formulation is conducted in two ways. Firstly, the results are compared with those of 1-D conventional functionally graded rectangular plates, and then, the results of the presented formulations are given in the form of convergence studies with respect to N z and N y , the number of discrete points distributed along the thickness and width of the plate, respectively. The boundary conditions of the plate are specified by the letter symbols, for example, S-C-S-F denotes a plate with edges x=−a/2 and a/2 simply supported (S), edge y=−b/2 clamped (C) and edge y=b/2 free (F).

As a first example, the properties of the plate are assumed to vary through the thickness of the plate with a desired variation of the volume fractions of the two materials in between the two surfaces. The modulus of elasticity E and mass density ρ are assumed to be in terms of a simple power law distribution and Poisson’s ratio υ is assumed to be constant as follows:

$$ \begin{array}{l} E(z) = E_{M} + E_{CM}V_{f},\qquad \upsilon(z) = \upsilon _{0},\\ \rho(z) = \rho_{M} + \rho _{CM}V_{f}, \\ E_{CM} = E_{C} - E_{M},\qquad\rho_{CM} = \rho_{C} - \rho _{M},\\ V_{f} = (0.5 + z / h)^{p} \end{array} $$
(34)

where −h/2≤z≤h/2 and p is the power law index which takes values greater than or equal to zero. Subscripts M and C refer to the metal and ceramic constituents which denote the material properties of the bottom and top surface of the plate, respectively. The mechanical properties are as follows:

  • Metal (Aluminum, Al):

    $$\begin{array}{l} E_{M} = 70*10^{9}~\mathrm{N}\mbox{/}\mathrm{m}^{2},\quad\upsilon= 0.3,\\ \rho_{M} = 2702~\mathrm{kg}\mbox{/}\mathrm{m}^{3}. \end{array} $$

  • Ceramic (Alumina, Al2O3):

    $$\begin{array}{l} E_{C} = 380*10^{9}~\mathrm{N}\mbox{/}\mathrm{m}^{2},\quad \upsilon= 0.3,\\ \rho_{C} = 3800~\mathrm{kg}\mbox{/}\mathrm{m}^{3}. \end{array} $$

In Table 2, the first seven non-dimensional natural frequency parameters of simply supported thick FG plate are compared with those of Matsunaga [17] and Yas and Sobhani [20].

Table 2 Convergence behavior and accuracy of the first seven non-dimensional natural frequencies (\(\varpi= \omega h\sqrt{\rho_{C} / E_{C}}\)) of a simply supported FG plate against the number of DQ grid points (b/h=2)
Full size table

As the second example, in order to validate the results for plates on an elastic foundation, the results for the first three natural frequency parameters of isotropic thick plate with two different values of thickness-to-length ratios and different values of Winkler elastic coefficient are presented in Table 3. They are compared with those of Zhou et al. [18], Matsunaga [19] and Yas and Sobhani [20]. In this example the non-dimensional natural frequency, Winkler and shearing layer elastic coefficients are as follows:

$$ \begin{aligned}[b] &\lambda= \omega\displaystyle\frac{b^{2}}{\pi^{2}}\sqrt{\rho _{C}h / D_{C}},\quad D_{C} = E_{C}h^{3} / 12\bigl(1 - \upsilon_{C}^{2}\bigr), \\ &k_{g} = K_{g}b^{2} / D_{C},\quad k_{w} = K_{w}b^{4} / D_{C} \end{aligned} $$
(35)

According to the data presented in the above-mentioned tables, excellent solution agreements can be observed between the present method and those of the other methods.

Table 3 Comparison of the first three non-dimensional natural frequency parameters of a simply supported square isotropic plate on the elastic foundation (k g =10)
Full size table

Based on the above studies, a numerical value of N z =N y =13 is used for the next studies.

After demonstrating the convergence and accuracy of the method, parametric studies for 3-D vibration analysis of bi-directional FG rectangular plates for different types of ceramic volume fraction profiles and various length to width ratio (a/b) and different combinations of free, simply supported and clamped boundary conditions at the edges, are computed. It should be noted that, the 2-D FG rectangular plates considered in this work are assumed to be composed of aluminum and silicon carbide as shown in Table 1. In the following, we have compared several different ceramic volume fraction profiles of conventional 1-D and 2-D FGMs with appropriate choice of the thickness and width of the plate parameters of the 2-D six-parameter power-law distribution, as shown in Table 4. It should be noted that, for example, the notation Classical–Symmetric indicates that the 2-D FG rectangular plate has classical and symmetric volume fraction profiles through the thickness and width of the plate directions, respectively. Similarly, the other notations Classical–Classical, Symmetric–Symmetric, etc. have been used. Remember also Figs. 2, 3 and 4 obtained by Eq. (1).

Table 4 Various ceramic volume fraction profiles, different parameters, and volume fraction indices of 2-D power-law distributions
Full size table

The non-dimensional natural frequency, Winkler and shearing layer elastic coefficients are as follows:

$$ \begin{aligned}[b] &\Omega= \omega\displaystyle\frac{b^{2}}{\pi^{2}}\sqrt{\rho _{Al}h / D_{Al}},\quad D_{Al} = E_{Al}h^{3} / 12\bigl(1 - \upsilon_{Al}^{2}\bigr), \\ &k_{g} = K_{g}b^{2} / D_{AL},\quad k_{w} = K_{w}b^{4} / D_{AL} \end{aligned} $$
(36)

where ρ Al , E Al and υ Al are mechanical properties of aluminum.

The effect of the Winkler elastic coefficient on the fundamental frequency parameters for different boundary conditions is shown in Figs. 5, 6 and 7 and Tables 5, 6 and 7. It is observed that the fundamental frequency parameters converge with increasing Winkler elastic coefficient of the foundation. According to this figures, the lowest frequency parameter is obtained by using Classical-Classical volume fraction profile. On the contrary, the 1-D FG rectangular plate with symmetric volume fraction profile has the maximum value of the frequency parameter.

Fig. 5
figure 5

Variations of fundamental frequency parameters of a S-C-S-C bi-directional FG rectangular plate resting on a two-parameter elastic foundation with Winkler elastic coefficient for different volume fraction profiles (k g =100, h/b=0.5, a/b=1, γ z =2)

Full size image
Fig. 6
figure 6

Variations of fundamental frequency parameters of a S-C-S-S bi-directional FG rectangular plate resting on a two-parameter elastic foundation with Winkler elastic coefficient for different volume fraction profiles (k g =100, h/b=0.5, a/b=1, γ z =2)

Full size image
Fig. 7
figure 7

Variations of fundamental frequency parameters of a S-F-S-F bi-directional FG rectangular plate resting on a two-parameter elastic foundation with Winkler elastic coefficient for different volume fraction profiles (k g =100, h/b=0.5, a/b=1, γ z =2)

Full size image
Table 5 The first non-dimensional natural frequency parameter of S-C-S-C square bi-directional FG rectangular plates resting on elastic foundations (k g =100, h/b=0.5, γ z =2)
Full size table
Table 6 The first non-dimensional natural frequency parameter of S-C-S-S square bi-directional FG rectangular plates resting on elastic foundations (k g =100, h/b=0.5, γ z =2)
Full size table
Table 7 The first non-dimensional natural frequency parameter of S-F-S-F square bi-directional FG rectangular plates resting on elastic foundations (k g =100, h/b=0.5, γ z =2)
Full size table

The variations of fundamental frequency parameters of 2-D FG rectangular plates resting on an elastic foundation with length to width ratio (a/b) for different types of volume fraction profiles are depicted in Figs. 8, 9 and 10 and Tables 8, 9 and 10. It can also be inferred from these figures that the frequency is greatly influenced in that fundamental frequency parameter decreases steadily as length to width ratio (a/b) becomes larger and remains almost unaltered for the large values of length to width ratio. As can be seen from Figs. 8, 9 and 10, for the all length to width ratio, Classical-Classical volume fraction profile has the lowest frequencies followed by Classical-Symmetric, Classical, Symmetric-Symmetric and Symmetric profiles.

Fig. 8
figure 8

The effect of length to width ratio (a/b) of a S-C-S-C bi-directional FG rectangular plate on the non-dimensional natural frequency (k w =k g =100, h/b=0.5, γ z =2)

Full size image
Fig. 9
figure 9

The effect of length to width ratio (a/b) of a S-C-S-S bi-directional FG rectangular plate on the non-dimensional natural frequency (k w =k g =100, h/b=0.5, γ z =2)

Full size image
Fig. 10
figure 10

The effect of length to width ratio (a/b) of a S-F-S-F bi-directional FG rectangular plate on the non-dimensional natural frequency (k w =k g =100, h/b=0.5, γ z =2)

Full size image
Table 8 The effect of length to width ratio (a/b) of a S-C-S-C bi-directional FG rectangular plate on the first non-dimensional natural frequency (k w =k g =100, h/b=0.5, γ z =2)
Full size table
Table 9 The effect of length to width ratio (a/b) of a S-C-S-S bi-directional FG rectangular plate on the first non-dimensional natural frequency (k w =k g =100, h/b=0.5, γ z =2)
Full size table
Table 10 The effect of length to width ratio (a/b) of a S-F-S-F bi-directional FG rectangular plate on the first non-dimensional natural frequency (k w =k g =100, h/b=0.5, γ z =2)
Full size table

The effect of different types of ceramic volume fraction profiles on the frequency parameters of S-C-S-C bi-directional rectangular plates for different values of circumferential wave number (m) is shown in Fig. 11 and Table 11, According to this figure and table, the lowest frequency parameter is obtained by using Classical-Classical volume fractions profile. On the contrary, the 1-D FG rectangular plate with symmetric volume fraction profiles has the maximum value of the frequency parameter. Therefore, a graded ceramic volume fraction in two directions has high capabilities to reduce the frequency parameter than conventional 1-D FGM. Moreover, in Fig. 11, the interesting results show that, with increasing values of the circumferential wave number (m), frequency parameter of the Classical FG rectangular plate is close to that of a Symmetric-Symmetric. Therefore, it can be concluded that using 2-D six-parameter power-law distribution leads to a more flexible design so that maximum or minimum value of natural frequency can be obtained to a required manner.

Fig. 11
figure 11

Variation of the frequency parameters versus circumferential wave numbers (m) with different volume fraction profiles for a S-C-S-C bi-directional FG rectangular plates resting on a two-parameter elastic foundation (k w =k g =100, h/b=0.5, a/b=1, γ z =2)

Full size image
Table 11 The variations of the frequency parameters (Ω m1) versus circumferential wave numbers (m) with different volume fraction profiles for a S-C-S-C bi-directional FG rectangular plate resting on a two-parameter elastic foundation (k w =k g =100, h/b=0.5, a/b=1, γ z =2)
Full size table

The variations of fundamental frequency parameters of 2-D FG rectangular plates with length to width ratio (a/b), and the volume fraction index through the thickness of the plates for S-C-S-C boundary conditions are shown in Fig. 12 and Table 12, by considering (k w =k g =100, h/b=0.5, a/b=1, α y =α z =0, γ y =2) for Classical-Classical 2-D FG plates. Confirming the effect of length to width ratio (a/b) on the natural frequency already shown in the Figs. 8–10, it is found that the frequency parameter decreases by increasing the thickness volume fraction index. This behavior is also observed for other boundary conditions, not shown here for brevity.

Fig. 12
figure 12

Variation of fundamental frequency parameters of a S-C-S-C bi-directional FG rectangular plate resting on a two-parameter elastic foundation with a/b ratio and the volume fraction index through thickness of the plates (k w =k g =100, h/b=0.5, α y =α z =0, γ y =2)

Full size image
Table 12 The frequency parameters (Ω 11) of a S-C-S-C bi-directional FG rectangular plate resting on a two-parameter elastic foundation with a/b ratio and the volume fraction index through thickness of the plates (k w =k g =100, h/b=0.5, α y =α z =0, γ y =2)
Full size table

Now we study the influence of various types of the ceramic volume fraction profile on fundamental natural frequency at various volume fraction indices through the thickness direction (γ z ) of the rectangular plates (Fig. 13 and Table 13). The results show that, for the all boundary conditions the frequency parameter decreases by increasing the thickness volume fraction index, due to the fact that the silicon carbide fraction decreases, and as we know silicon carbide has a much higher Young’s modulus than aluminum. It is also seen, that the thickness volume fraction index has less effect on the frequency parameter for the Classical–Classical volume fraction profile.

Fig. 13
figure 13

Frequency variation against volume fraction index (γ z ) for a bi-directional FG rectangular plate resting on a two-parameter elastic foundation. (k w =k g =100, h/b=0.5, a/b=1, α y =α z =0, γ y =2)

Full size image
Table 13 The frequency parameters (Ω 11) of bi-directional FG rectangular plates resting on a two-parameter elastic foundation for different boundary conditions (k w =k g =100, h/b=0.5, a/b=1, α y =α z =0, γ y =2)
Full size table

5 Conclusion

In this research work, differential quadrature method was employed to obtain a highly accurate semi-analytical solution for free vibration of bi-directional rectangular plates resting on a two-parameter elastic foundation under various boundary conditions. The study was carried out based on the three-dimensional, linear and small strain elasticity theory. Material properties were assumed to vary not only through the thickness but also in the in-plane directions following a novel 2-D six-parameter power-law distribution. The effective material properties at a point were determined in terms of the local volume fractions and material properties by the Mori-Tanaka scheme. The effects of different boundary conditions, various geometrical parameters, different ceramic volume fraction profiles along the thickness and in-plane directions and elastic coefficients of foundation of bi-directional rectangular plates resting on a two-parameter elastic foundation were investigated. Moreover, vibration behavior of 2-D FG plates was compared with one-dimensional conventional FG plates. From this study, some conclusions can be made:

  • The non-dimensional natural frequency parameters converge with increasing Winkler elastic coefficient of the foundation.

  • The interesting results show that the lowest magnitude frequency parameter is obtained by using a Classical–Classical volume fraction profile. It can be concluded that a graded ceramic volume fraction in two directions has higher capabilities to reduce the natural frequency than a conventional 1-D FGM.

  • The results show that with increasing values of the circumferential wave number (m), frequency parameter of the Classical FG rectangular plate is close to that of a Symmetric-Symmetric.

  • The results show that the fundamental natural frequency decreases by increasing a/b ratio and then approaches a constant value.

  • It is also seen, that the thickness volume fraction index exerts an insignificant influence on the frequency parameter for the Classical–Classical volume fraction profile.

Based on the achieved results, using 2-D six-parameter power-law distribution leads to a more flexible design so that maximum or minimum value of natural frequency can be obtained to a required manner.