A complementarity-based rolling friction model for rigid contacts

Abstract

In this work (also, preprint ANL/MCS-P3020-0812, Argonne National Laboratory) we introduce a complementarity-based rolling friction model to characterize dissipative phenomena at the interface between moving parts. Since the formulation is based on differential inclusions, the model fits well in the context of nonsmooth dynamics, and it does not require short integration timesteps. The method encompasses a rolling resistance limit for static cases, similar to what happens for sliding friction; this is a simple yet efficient approach to problems involving transitions from rolling to resting, and vice-versa. We propose a convex relaxation of the formulation in order to achieve algorithmic robustness and stability; moreover, we show the side effects of the convexification. A natural application of the model is the dynamics of granular materials, because of the high computational efficiency and the need for only a small set of parameters. In particular, when used as a micromechanical model for rolling resistance between granular particles, the model can provide an alternative way to capture the effect of irregular shapes. Other applications can be related to real-time simulations of rolling parts in bearing and guideways, as shown in examples.

1 Introduction

Rolling resistance has attracted the interest of researchers since the early ages of applied mechanics [8, 26, 37]. During the past two centuries many models have been proposed, depending on the required level of detail and on the type of phenomena that cause the rolling resistance; usually the number of parameters increases with the complexity of the model. At one end of the spectrum, for instance, there is case of the rolling tire, which often requires sophisticated models with a large number of parameters [24]. In this work, on the other hand, we are interested in a model that has a small number of parameters but is easily applicable to problems with large number of parts, or with requirements of high computational efficiency in general. Superior performance stems from the adoption of a set-valued formulation that finds the solution in terms of a complementarity problem.

The advantages of a complementarity-based rolling friction model are multiple: it encompasses both the moving and the static cases, it does not require regularization and stiff force fields, it is an intuitive extension of the classic Coulomb-Amontons sliding friction model to the rolling case, and it requires few parameters. A literature search reveals only a few contributions on this topic; among these we cite the relevant work of [20].

A complementarity-based model can be particularly useful in simulations that require algorithmic robustness and efficiency, such as in real-time simulators, robotics, and virtual and augmented reality. To this end we present an application of the method to the efficient simulation of a linear guideway with recirculating ball bearings.

Another motivation, also discussed in this paper, is the simulation of rolling resistance among a large number of parts. This happens, for example, when studying granular materials, such as in the interaction between machines and soils (tracked vehicles on sand, tires on deformable ground, etc.) In the context of granular material dynamics, rolling friction between microscopic spherical particles has the side effect of approaching, on a macroscopic scale, the same global behavior of the granular assembly if it were modeled with many faceted irregular shapes: there exists a relation between the degree of irregularity of the surfaces and the rolling friction coefficient [9].

In the literature, typical approaches to the simulation of contacts are based on the regularization of contact forces; such forces, which are discontinuous in nature, are approximated by smooth functions. Smoothness allows the problem to be dealt as system of ordinary differential equations (ODEs), the drawback being that the resulting ODEs, while tractable, are stiff, thereby requiring short timesteps and leading to high computational times [12]. The adoption of implicit integrators might alleviate, but not eliminate, the issue of stiffness. For instance, since the seminal work of [7], most implementations of the discrete element method (DEM) for the simulation of granular materials are based on regularization of contact forces and stiff ODEs. For very large systems, regardless of the fact that one can exploit powerful hardware, the computational time can be so high that some problems become untractable.

For this reason in [32] we proposed an approach based on differential variational inequalities (DVIs), as an alternative to the classical regularization-based approaches. The DVI approach, whose capabilities are not necessarily confined to granular problems, is a recent general way of dealing with nonsmooth mechanical problems; the approach encompasses ODEs as subcases as well as complementarity-based methods. In DVIs one can describe forces by means of set-valued functions (multifunctions) that capture the nonsmooth nature of models such as the Signorini contact law or the Coulomb friction; no stiff regularizations of discontinuities are needed because discontinuities are presented directly as complementarity constraints. Large timesteps are allowed, but at the cost of solving a variational inequality problem (a complementarity problem, in the simplest case) for each timestep [25].

A generic variational inequality (VI) is a problem of the type

$$ \mathbf {u} \in \mathbb{K}{:}\quad \bigl\langle F(\mathbf {u}),\mathbf {y}-\mathbf {u} \bigr\rangle \geq 0 \quad \forall \mathbf {y} \in \mathbb{K} $$

(1)

given a closed and convex $\mathbb{K} \in \mathbb{R}^{n}$ set, and given a continuous $F(\mathbf {u}): \mathbb{K} \rightarrow \mathbb{R}^{n}$. We call $\mathsf{SOL}(\mathbb{K},F)$ the solution of problem (1). Variational inequalities are powerful mathematical tools that have recently been used also in game theory, continuum mechanics and other scientific fields; a good reference is [18].

Assuming that the state of the system is defined by x, one can define a DVI as the problem of finding the function x on [0,T],

(2)

(3)

along with boundary conditions Γ(x(0),x(T))=0. For the class of mechanical problems that we are interested in, for example, the state can be x={q ^T,v ^T}^T, with positions q and velocities v, and with u as the set of reaction forces, that must satisfy a VI. References about DVIs can be found in [28, 29]; details about their practical implementations in terms of timestepping schemes can be found, for instance, in [3, 11, 16, 25, 30, 31].

In the following we show that the introduction of set-valued rolling friction does not affect overly the complexity of the original DVI problem; the computational requirements are simply doubled with respect to the case of just sliding friction. Also, spinning friction (also known as drilling friction) can be added easily in a similar way.

2 Set-valued rolling friction

In this paper we use set-valued functions to model rolling contact forces between rigid parts. Such model has mathematical similarities with the model for sliding friction in the Amontons-Coulomb theory; similar to the Amontons-Coulomb friction model, the proposed approach requires a small number of parameters to describe the rolling resistance effect.

2.1 Rolling friction phenomena

Although the nonsmooth nature of the sliding friction is evident in nature, because the friction force is abruptly clamped to a maximum value as soon as the objects start sliding, the same sharpness is not evident in the experimental observation of the rolling friction, because rolling friction effect increases smoothly as the rolling speeds increases. In fact, resistance to the rolling motion usually takes place because in the contact area there may be inelastic deformations of elasto-plastic materials [24]: the final outcome of this hysteric deformation is that the resultant of all pressures is always placed a bit ahead of the position that it would take if the parts were not rolling.

Many classical textbooks about applied mechanics [8, 26, 37] describe a simplified model for this effect, considering a rolling wheel of radius R and expressing the displacement of the contact force by a single friction parameter ρ, which has the dimension of length, or by a dimensionless coefficient of rolling friction f _ρ =ρ/R. The latter is also meant to allow an easy comparison with sliding friction: Given a normal force N acting on a rolling disc, the horizontal force that is needed to keep it rolling at constant speed is T=f _ρ N (see Fig. 1), similar to the Coloumb sliding friction case, T=f _s N, with f _s the coefficient of dry sliding friction. Equivalently, the effect of T on the disc can be replaced with a tractive torque M=TR, that is, M=f _ρ NR or

(4)

Fig. 1

Rolling friction. Two examples in the two-dimensional case

This model is highly nonlinear because it states that the displacement, whose amount is ρ regardless of the speed, has to change direction when the rolling speed changes sign and must go to zero if there is no rolling speed. This tristate model cannot be used practically within a general-purpose numerical simulation framework because scenarios often occur where a sphere or a disc should come to rest over a horizontal surface: since numerical roundoff considerations make impossible that the speed will be exactly null, the speed may actually oscillate around the null value, but even small oscillations will change the sign of the rolling speed and, consequently, also the displacement of the contact force will oscillate over the endpoints of the −ρ,+ρ interval. The final result will be numerically unstable.

For this reason, we express the rolling friction model (4) as the following constraint with inequality

$$ \begin{array}{lll} \|M\|\leq\rho \|N\|, \cr\noalign{\vspace{3pt}} \|\omega_r\|(\rho N - M)=0, \quad M \omega_r \leq 0, \end{array} $$

(5)

where ω _r is the rolling angular velocity, which must be opposite to the rolling resistant moment M. The third condition of Eq. (5) can also be written as 〈M,ω _r 〉=−∥M∥∥ω _r ∥.

Note that for whatever positive or negative rolling speed, this model corresponds to the classical rolling-friction model (4), but for the transition from steady state to moving state it changes the displacement in the [−ρ,ρ] limit. With this improvement, the model can be seen as the counterpart of the Amontons-Coulomb friction model, because both can consider the static case.

2.2 Three dimensional rolling friction model

For extending the two-dimensional rolling friction model to the generic case of contact between shapes in three-dimensional space, we introduce the following assumption.

Assumption A1

The resisting torque is opposite to the relative (rolling) angular velocity of the two bodies, if any.

Although Assumption A1 is always verified for 2D problems, in some three-dimensional problems the resisting torque can be misaligned with respect to the relative angular velocity. See Appendix A for a derivation of the relative angular velocity.

In cases with plane symmetry in the surroundings of the contact (for instance if the area of contact between two rolling bodies is an ellipse aligned to the rolling direction and the material properties are anisothropic), the speed of deformation of the material is symmetric with respect to the plane of rotation, thus resulting in a symmetric pressure distribution at the area of contact, regardless of the type of viscous constitutive law of the material. In this case, Assumption A1 is always verified. This happens, for example, in case of spheres that are in contact, each with anisothropic material, or in spheres that are rolling on flat surfaces.

Another special case that has much relevance in engineering applications is the contact between two surfaces that can be locally approximated as two cylinders with parallel axes. This happens, for instance, in cam followers and in rollers over flat surfaces. In these cases, the torque is aligned to the rolling angular velocity.

In other situations, such as in the case of two generic ellipsoids, the pressure distribution in the area of contact (that is elliptical and not necessarily with one of its main axes aligned to the direction of rolling) generates a normal reaction whose offset with respect to the plane of contact might be not aligned to the direction of rolling, thus resulting in a resisting moment that is not exactly aligned to the vector of the angular velocity.

Given the ith contact, among two bodies A and B, let n ⁱ be the normal at the contact point, directed toward the exterior of the A body. Let u ⁱ and w ⁱ be two vectors in the contact plane such that n ⁱ,u ⁱ,w ⁱ∈ℝ³ are mutually orthogonal vectors.

The signed gap function Φ ⁱ represents the contact distance. For each contact that is active (that is Φ ⁱ(⋅)=0 because bodies are touching), we introduce the contact forces, while inactive contacts (Φ ⁱ(⋅)>0) do not enforce any reaction.

The normal contact force is $\mathbf {F}_{N}^{i}={{} \hat {\gamma }_{n}^{i}} \mathbf {n}^{i}$, where ${{} \hat {\gamma }_{n}^{i}} \geq 0$ is the multiplier that represents the modulus of the reaction. Friction force, if any, is represented by the multipliers ${{} \hat {\gamma }_{u}^{i}}$, and ${{} \hat {\gamma }_{w}^{i}}$ which lead to the tangential component of the reaction $\mathbf {F}_{T}^{i}={{} \hat {\gamma }_{u}^{i}} \mathbf {u}^{i}+{{} \hat {\gamma }_{w}^{i}} \mathbf {w}^{i}$.

Because of the inequality ${{} \hat {\gamma }_{n}^{i}} \geq 0$, the mathematical description of this unilateral model involves the Signorini complementarity problem [30]:

(6)

We introduce the rolling friction torque using the multipliers ${{}\hat {\tau }_{n}^{i}}$, ${{} \hat {\tau }_{u}^{i}}$, and ${{} \hat {\tau }_{w}^{i}}$, which correspond to a normal component of the torque $\mathbf {M}_{N}^{i}={{} \hat {\tau }_{n}^{i}} \mathbf {n}^{i}$ and two tangential components of the torque $\mathbf {M}_{T}^{i}={{} \hat {\tau }_{u}^{i}} \mathbf {u}^{i}+{{} \hat {\tau }_{w}^{i}} \mathbf {w}^{i}$.

The normal component of the torque $\mathbf {M}_{N}^{i}$ is responsible for friction that reacts to spinning around the vertical axis, while the tangential component $\mathbf {M}_{T}^{i}={{}\hat {\tau }_{u}^{i}} \mathbf {u}^{i}+{{} \hat {\tau }_{w}^{i}} \mathbf {w}^{i}$ is the effect of the classical rolling friction. The model (5) is extended to the three-dimensional case, the following inequality holds for nonzero rolling velocity.

This corresponds to the inequality $\rho^{i} {{} \hat {\gamma }_{n}^{i}}\, {\geq}\, \sqrt{{{{} \hat {\tau }_{u}^{i}}}^{2}+{{} \hat {\tau }_{w}^{i}}^{2}}$.

The rolling velocity vector $\mathbf {\omega}_{T}^{i}$ is the part of the relative angular velocity vector $\mathbf {\omega}_{r}^{i}$ that lies on the contact plane, that is, $\mathbf {\omega}_{T}^{i}=\mathbf {\omega}_{r}^{i} - \mathbf {n}^{i} \langle \mathbf {\omega}_{r}^{i}, \mathbf {n}^{i} \rangle$; the condition that requires $\mathbf {\omega}_{T}^{i}$ to be aligned and opposite to $\mathbf {M}_{T}^{i}$ can be expressed as

Therefore, the full rolling friction model for a contact with rolling friction parameter ρ ⁱ is mathematically equivalent to the following constraints:

(7)

Additionally, one can introduce the spinning friction, represented by a parameter σ _i , giving

(8)

Rolling contacts can be either sliding or not sliding. In the former case there could be also tangential forces caused by dynamical friction; in the latter case there could be forces caused by sticking, the consequence of static friction. Therefore we must introduce the Amontons-Coulomb friction model to take care of the tangential forces, either sliding or static.

Within the classic theory of dry friction, the friction coefficient μ ⁱ limits the ratio between the normal and the tangential force, and the tangential force must have a direction that is opposite to $\mathbf {v}_{T}^{i}$, the tangential component of the relative velocity $\mathbf {v}_{r}^{i}$ , if any, thus requiring

(9)

3 The complete DVI model

The system state is defined by the vector of generalized coordinates $\mathbf {q} \in \mathbb{R}^{m_{q}}$ and the vector of generalized speeds $\mathbf {v} \in \mathbb{R}^{m_{v}}$. It might happen that m _q >m _v because rotations of rigid bodies in three-dimensional space are represented with unimodular quaternions ϵ∈ℍ₁ to avoid singularities in the parametrization of SO(ℝ,3); anyway it is straightforward to define a (linear) map $\dot{\mathbf {q}}=\varGamma(\mathbf {q}) \mathbf {v}$ if $\dot{\mathbf {q}}$ is needed.

We also introduce generalized force fields f _e (q,v,t) and gyroscopic forces f _c (q,v) giving a total force field $\mathbf {f}_{t}(\mathbf {q},\mathbf {v},t) \in \mathbb {R}^{m_{v}}$.

The inertial properties of the system are represented by the mass matrix ${M}(\mathbf {q}) \in \mathbb{R}^{m_{v} \times m_{v}}$, assumed positive definite, usually block-diagonal in the case of rigid bodies only.

Bilateral constraints are introduced through a set of scalar constraint equations, assumed differentiable everywhere:

(10)

We introduce ∇ _q Ψ ⁱ=[∂Ψ ⁱ/∂ q]^T and $\nabla \varPsi^{i^{T}} = \nabla_{q} \varPsi^{i^{T}} \varGamma(\mathbf {q})$, to express the constraint (10) at the velocity level after differentiation:

(11)

Frictional unilateral contacts define a set . For each contact , we introduce the tangent space generators $\mathbf {D}_{\gamma_{u}}^{i}$, $\mathbf {D}_{\gamma_{w}}^{i}$, $\mathbf {D}_{\tau_{u}}^{i}$, $\mathbf {D}_{\tau_{w}}^{i}$, $\mathbf {D}_{\tau_{n}}^{i} \in \mathbb{R}^{m_{v}}$; for details about their formulation, see Appendix B.

Another way to write (7), (8), and (9) is to use the maximum dissipation principle, thus leading respectively to the following constraints on the dynamic equilibrium

(12)

(13)

(14)

Here, , , and, respectively, , are the rolling, spinning, and respectively, friction cone sections. Alternatively, for the case where the tangential rolling torques is not zero, we derive the Fritz John optimality conditions for the nonlinear program (12),

(15)

(16)

When the tangential rolling torques are zero, the functions defining , are not differentiable so the above derivation does not hold. However, for purposes of exposing our formulation we will assume the opposite the case, and in later developments (40) we remove this assumptions by using cone polar formalisms.

The same derivation can be performed for (12) and (13); hence the complete model, including inertial effects, force fields, bilateral constraints, unilateral contacts with friction, rolling friction, and spinning friction, is the following differential variational inequality

(17)

The former DVI can be discretized in time. Using a time step h, posing $\gamma=h \hat {\gamma}$, and adopting the exponential map Λ(⋅) described in [33] to allow direct integration on the Lie group, we have the following problem.

(18)

This is a mixed nonlinear complementarity problem, whose solution is not guaranteed to exist. Indeed, most existence results require monotonicity of the mapping defining the complementarity problem. In turn, this implies convexity of the solution set of the nonlinear complementarity problem [10]. Unfortunately, not even the weaker condition of the convexity of the solution set can be guaranteed. Indeed, it has been already shown that, for the subcase of a linear complementarity problem (LCP) corresponding to a simple pyramidal frictional model, the solution set may be nonconvex [1]. This situation can occur only if the mapping of the LCP is nonmonotone, which in the linear case implies that its matrix is not positive semi-definite.

4 Casting to a convex solvable problem

In the following we show that, under mild conditions, the original problem can be relaxed as a monotone cone complementarity problem (CCP) that guarantees existence of the solution and convexity of the solution set. The problem is equivalent to a convex optimization problem, a feasible quadratic programming problem (QP) with conical constraints. We note that while one cannot guarantee uniqueness of the solution of the CCP (indeed, lack of uniqueness of the forces is known to appear even in frictionless cases that are linear and convex problems), one can guarantee under some mild assumptions uniqueness of the velocity solution [2]. The latter condition is sufficient for a predictive time-stepping scheme to exist.

Assume that for each contact we define the vector of wrench reactions

and the corresponding twist of local linear and angular velocities in the contact point, plus the stabilization term $\frac{1}{h} \varPhi(\mathbf {q})$, that is,

In the rest of this section we omit the i indexes for compactness.

We differentiate the Fritz John optimality conditions (15) obtaining, for the rolling friction part,

(19)

(20)

Then,

(21)

Note that for the sliding friction one gets similar results, $\mathbf {v}^{T} \mathbf {D}_{\gamma_{u}} = \lambda_{v} \gamma_{u} 1/\sqrt{\gamma _{u}^{2} + \gamma_{w}^{2}}$ and $\mathbf {v}^{T} \mathbf {D}_{\gamma_{w}} = \lambda_{v} \gamma_{w} 1/\sqrt{\gamma _{u}^{2} + \gamma_{w}^{2}}$, with $\lambda_{v} = \sqrt{(\mathbf {D}_{\gamma_{u}}^{T} \mathbf {v})^{2} + (\mathbf {D}_{\gamma_{w}}^{T} \mathbf {v})^{2}}$; whereas for the spinning friction $\mathbf {v}^{T} \mathbf {D}_{\tau_{n}} = \lambda_{\tau} \tau_{n} / |\tau_{n}|$, with $\lambda_{\tau} = \mathbf {D}_{\tau_{n}}^{T} \mathbf {v} |\tau_{n}| / \tau_{n}$.

Now, the inner product for the complementarity in the optimality condition requires that

(22)

Similarly one can derive, for sliding and spinning,

(23)

(24)

If we assume the orthogonality of and , we have

(25)

By adding a relaxation term A _r for the normal velocity, the orthogonality condition for unilateral contact in the discretized DVI (18) becomes

Since complementarity implies nullity of inner product, we then have

(26)

By exploiting (26), (19), (20), and so forth, recalling that x ²/|x|=|x|, with simple algebraic manipulation, we rewrite (25) as

(27)

By substituting (22), (23), and (24) in (27), and by simplifying γ _n , we have that the relaxation term that allows orthogonality of γ’s and u’s is, for the ith contact ,

(28)

The introduction of the $A_{r}^{i}$ term has the drawback of modifying the contact constraint; from a practical point of view there is the side effect that the gap between objects increase with the sliding speed instead of remaining equal to zero; this effect has been discussed in [33] for the simple case of sliding friction. Now, introducing also rolling and spinning friction, one can see from Eq. (28) that rotational motion increases the gap (the $\sqrt{ (\mathbf {D}_{\tau _{u}}^{i} \mathbf {v})^{2} + (\mathbf {D}_{\tau_{w}}^{i} \mathbf {v})^{2} }$ term is also the norm of $\mathbf {\omega}_{T}^{i}$), and that the increase is always directed outward. This is the price for having convexified the original problem. In many situations this can be acceptable, indeed one can demonstrate that at steady state, i.e. when ∇Φ ^{i T} v=0 in (26), the separation gap Φ ⁱ decreases with low speeds, low μ, ρ, σ, and small timesteps.

We note that if we plan to use rolling friction to simulate granular material, the above mentioned side effect of the relaxation leads to a dilatancy effect that really happens in physical world.

Aiming at a generic compact notation, we now introduce , and we build the following aggregate vectors , , :

(29)

For each contact we can define a matrix with six columns,

(30)

and a six-dimensional cone that defines the set of admissible reactions in the sliding, rolling, spinning friction contact:

(31)

Similarly, for bilateral constraints, we have , and :

(32)

The complete aggregate vectors and matrices of the entire system are

(33)

(34)

Moreover we define the product of all the sliding and rolling friction cones and the possible values of reactions in bilateral constraints as

(35)

and its polar (note that ℝ^∘={0}):

(36)

Now we proceed with a simplification by introducing

(37)

From the relaxed version of (18) one can see that , where

(38)

(39)

The entire system is described by the following CCP:

(40)

The CCP (40) is also equivalent to a variational inequality as expressed in the VI of Eq. (1), namely

(41)

Several theoretical results for (41) can be obtained by noting that it is related to the following optimization problem.

(42)

Theorem 1

Consider the variational inequality (41) and the optimization problem (42). Then the following statements hold:

• (i) If (42) has a solution, then that solution satisfies the variational inequality (41). Conversely, any solution of (41) is a solution of (42).

• (ii) Either (42) has a solution, or there exists such that .

• (iii) If (42) has two solutions and , then they must satisfy .

Proof

If (42) has a solution, then since the constraints ϒ are convex, they must satisfy the Kuhn-Tucker conditions, which are simply the statement of (41). Conversely, because of the convexity of the cone ϒ and of the objective function, any Kuhn-Tucker solution is a global solution, which proves Part (i).

For Part (ii), if the objective function of (42) is bounded below over the convex set ϒ, it follows that the problem (42) must have a solution. Assume that this is not the case, that is, that there exists a sequence , n=0,1,2,… such that . Because of the continuity of the objective function, such a sequence must satisfy (otherwise the objective function would stay bounded). In particular, this implies that

(43)

for some integer n ₀. Define the scaled vector . Since the scaled vector sequence is in the unit ball, which is compact, it must have a limit point, which we denote by . We assume, without loss of generality, that the entire sequence converges to this point. Dividing (43) by and taking the limit, we have that the second term goes to 0, and we obtain

Using the expression for N, (38), and the fact that the mass matrix is positive definite, this implies that , which in turn proves Part (ii) of the theorem.

For Part (iii), assume that there are two solutions of the optimization problem (42), and . Then, by the fact that the objective function is convex and that the constraints are convex, for any t∈[0,1], we have that is also a solution of (42). That is, the objective function value

is constant in t. This function is a quadratic, and this can occur only if the coefficient in t ² is 0, that is,

Again using the expression for N, (38), and the fact that the mass matrix is positive definite, this implies that , which in turn proves Part (iii) of the theorem. The proof of the theorem is complete. □

After the dual variables have been obtained from the VI (41), one can easily compute also the primal variables with the affine mapping:

(44)

In what sense the problem has a unique solution now revolves around the results of Theorem 1. The key assumption that we make is that the friction cone of our problem is pointed, that is,

(45)

Note that ϒ is only a set of multipliers (that is, the contact constraint forces in the coordinates attached to the contact, not the bodies) that is mapped into friction forces (and the friction cone, that is, in general coordinate) by means of the mapping , and thus (45) is a statement about friction forces. Moreover, we use here an algebraic definition of pointedness, although it does have a geometrical interpretation in the all-contact case: the friction cone does not contain a nontrivial linear space, and thus its origin is “pointed”. The reason we use the algebraic formulation is that it applies for cases where joint constraints are also included and where the constraint set is algebraically pointed, but not geometrically. More importantly the algebraic definition is also intuitive from a mechanics perspective: there are no contact forces that are valid from a constraint perspective but that produce a zero total force. In other words, the multibody system cannot get stuck through its internal forces, a configuration known to lead to virtually unpredictable behavior. For one contact, this condition immediately holds when we have rolling, sliding, and spinning friction; for more contacts, whether this holds depends on the configuration.

With this definition we have the following result, which elucidates the existence and uniqueness of a solution.

Theorem 2

Assume that the friction cone attached to the CCP (or VI) (41) is pointed in the sense of definition (45). Then

• (i) The VI (41) has a solution.

• (ii) Any two solutions of the VI result in the same velocity vector (44).

Proof

If the friction cone is pointed, then, by Theorem 1(ii), the optimization problem (42) must have a solution. Then, by Theorem 1, that solution is also a solution of the variational inequality (41), which proves the claim (i). For the second part, assume that the VI (41) has two solutions, , and . From Theorem 1(i), these are also solutions of the optimization problem (42). From Theorem 1(ii), these solutions satisfy

Looking at (44) and how the velocity solutions are computed from the solutions of (42), one can see that this relationship implies that the velocities computed from either are the same. The proof of (ii) and the theorem is complete. □

With this theorem, it follows that under the condition of pointedness of the friction cone, the VI (41) is well posed and its solution is unique in velocities. The latter condition is sufficient to result in a predictive simulation, since it results in uniqueness of the trajectory. We also point out that in the case of friction it is unreasonable to expect that the forces are unique, as can be immediately contemplated from the example of a block resting on a table with friction, which has multiple frictional solutions.

5 Numerical solution scheme

Obtaining the unknown dual variables from the VI of Eq. (41) is the most complex and time-consuming task in the simulation process. In fact, the solution of large VIs is currently a debated and actively researched topic in applied mathematics, and there exist no unique “best” algorithms to approach their solution.

As a comparison, the much easier linear problems that often arise in the simulation of classical ODEs and DAEs belong to the so-called polynomial P-class because they can be solved in polynomial time O(n ^c), if n represents the size of the problem in our case, the number of constraints on the system. On the other hand, VIs (as well as QPs, LCPs, and CCPs as special cases) are highly nonlinear problems, whose general complexity class is said to be nondeterministic-polynomial NP-hard, which often means an intractable growth of computational time for even moderate sizes of the domain [4]. Only special subcases of VIs can exploit the more friendly and tractable P class, such as the monotone VIs that we are dealing with. Exact methods for their solution, although running with polynomial time O(n ^c), might experience high c; thus the solution is still difficult, and often it is necessary to accept truncation to approximate solutions [22].

In [33] we presented a fixed-point iteration that can solve the CCP problem with Amontons-Coulomb friction only. Adding the set-valued rolling and spinning friction model presented in this paper, one can develop a new flavor of that iterative scheme, with minor modifications. Omitting the details, we note that the method iterates the following function, which is convergent for a proper choice of ω∈ℝ⁺, λ∈(0,1] and K:

(46)

The Π _ϒ operator is a projection onto ϒ, so that Π _ϒ (γ)=argmin _ζ∈ϒ ∥γ−ζ∥. Given the separable cone structure of Π _ϒ as defined in Eq. (35), the computation of Π _ϒ (γ) can be split into projections and into identities (no projections are required for the bilateral constraints). The original projection discussed in [33] operates only on the three values of the reactions that must obey the Amontons-Coulomb friction. In the advanced case, however, that includes also rolling friction and spinning friction one must map the six-dimensional wrench onto the six-dimensional cone defined in Eq. (31), so . See Appendix C for details about this projection.

Given the requirement of solving a VI for each timestep, the DVI approach appears to be less competitive than the classic DEM concept of regularizing nonsmooth phenomena via smooth but stiff force fields, because DEMs lead to uncoupled equations of motion of ODE type with basic linear O(n _b ) complexity for each timestep. However, our DVI setting permits large timesteps because it does not suffer from the stability issues implied by stiff forces in DEMs, so the increased workload for each timestep is paid back by fewer timesteps being required [32].

We remark that a parallel version of this rolling and spinning friction model can be easily implemented on parallel hardware of GPU type, as described in [34], and on hybrid high-performance computers [21].

6 Examples

6.1 Comparison against analytical solution

A simple validation against the analytical solution for a rolling disk is presented here. We consider a rolling disk with radius R=1 m, mass M=10 kg, moment of inertia $J=4~\mathrm{kg\,m^{2}}$, initial position x| _t=0=0 m initial horizontal speed on x axis $v_{x}|_{t=0}=1~\mathrm{m/s}$, initial angular velocity $\omega|_{t=0}=-1~\mathrm{rad/s}$. We use a rolling friction parameter ρ=0.02 m and a sliding/static friction coefficient μ=0.9. The gravity acceleration is $g_{y}= -9.8~\mathrm{m/s^{2}}$.

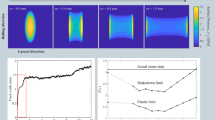
Figure 2 plots the motion of the disk which rolls until it comes to a rest because of the deceleration caused by the rolling friction. Figure 3 shows that the deceleration is constant (linear speed) in analytical theory, which uses the constant resistant torque T _r =M⋅g _y ⋅ρ; a similar behavior can be seen in the results of the DVI model.

Fig. 2

Motion of the rolling disk: comparison with classic theory

Fig. 3

Velocity of the rolling disk: comparison with classic theory

6.2 Simulation of a linear guideway

Linear guideways based on recirculating ball bearings represent an advanced technology for constraining linear motion. They avoid the problem of sliding friction between the translating parts by interposing rows of rolling spheres that can recirculate back in enclosed channels, like tracks in a tank. In this section we present the simulation of the linear system depicted in Fig. 4, as an example of a device that involves many contacts with rolling friction. The model is based on a 35 mm wide rail, with four rows of recirculating balls, each steel ball having a diameter of 2R _b =6.4 mm. Nine balls, on average, provide the contact in each row, and the four rows define four contact directions with 45^∘ orientation, as shown in Fig. 5.

Fig. 4

The simulated linear guideway, with the scheme of the recirculating balls

Fig. 5

Section of the linear guideway, showing the contact between balls and grooves

Although this type of guideway avoids sliding friction, a small resistance remains, caused by rolling friction, as shown in the scheme of Fig. 6. This effect can be easily simulated by using the proposed complementarity-based approach to rolling friction: we modeled the guideway in a 3D CAD software, we saved the parts using a custom translation software, we imported the file in our software, and we simulated it.

Fig. 6

Schematic representation of the forces acting on the rolling balls

We assumed that the contact between the spheres and the raceways is always aligned to the 45^∘ direction, so we introduced eight stretched boxes as collision shapes, as shown in Fig. 7; in this way the collision algorithm of our software can automatically compute the contact points between the balls and the raceways. In other types of guideways, the raceways are shaped like Gothic arcs: these can be modeled as well, but such nodeling would not add much to the discussion.

Fig. 7

Collision primitives used in the simulation

No significant side contact occurs between rolling balls (in some models plastic spacers exclude this possibility), and we did not consider static preload, although it could be simulated as well.

Since the system has many more contact constraints than needed, the indeterminacy is solved by introducing a Tikhonov regularization: from a numerical point of view this means adding a nonzero diagonal C to the N matrix of Eq. (38), that is, N _Tyk=N+C. From a mechanical point of view, the Tikhonov regularization means that we introduce compliance in contacts; in detail, we generate C from the inverses of the stiffness values in contact points, as computed by the Hertz-Mindlin theory.

The manufacturer of the guideway provides the following formula for estimating the resistance to horizontal sliding at low speeds: F _x =−sign(v _x )(ζF _y +S), where F _y is the normal load, ζ is typically about 0.005, and S is the force caused by the sliding friction of seals and scrapers, in our case S=5.3 N. Such friction is introduced in our model by using a convex box-constraint of the type $-S \leq \hat{\gamma}_{S} \leq S$, whose effect on the DVI is similar to the already discussed, and more complex, contact constraints. The effect of the ζF _y term comes from the simulation of the many rolling contacts, each with a rolling friction parameter ρ=ζR _b . Results from the simulations show precise agreement with the above formula, as shown in Fig. 8. For zero speed, the model is able to describe also the sticking effect that, although modest, can be measured on this class of devices.

Fig. 8

Resisting force F _x for different values of rolling friction parameter ρ, with and without the effect of seal friction (case of load F _y =490 N)

6.3 Application to the simulation of granular materials

The mechanics of granular matter has became a fertile research topic only recently, because of the vast computational resources that are required. One of the fields that would benefit from advances in this area is pharmaceutical engineering, where multibody dynamics could be used to study processes that involve powders: milling, blending, granulation, compression, and coating [17].

In the popular discrete element method (DEM), the bulk material is discretized in many particles with unilateral frictional contacts [7]. Various micromechanical contact models are available in the DEM field in order to define the interaction between the particles; in most cases, the nonsmooth nature of contact means that those models always produce stiff contact forces, and hence, that short integration timesteps are needed.

The need of rolling friction in granular simulations is motivated by experimental evidence; for example [23] shows that rolling resistance can have marked influence on the mechanics of particle assemblies at microscales; in some cases, its effect can be more relevant than interparticle sliding friction [36]. Rolling friction has been shown to affect only marginally the elastic properties of granular assemblies, but other collective phenomena such as shear resistance and dilatancy are significantly affected [5].

In some cases the simple inhibition of particle rotations in DEM algorithms can improve the solution with respect to the case of free frictionless rotation [6]. During the past few years, more sophisticated models of rolling friction have been proposed for interparticle contacts, for example in [14]. Given the difficulty of tuning the parameters of complex models, approaches based on few parameters such as the approach of [15] are welcome.

To some extent, the macroscopic effect of rolling friction in granular media is similar to the effect of dealing with nonspherical particles [19].

The collective behavior of particles with irregular and faceted shapes is different from the behavior of spherical particles, even if granular assemblies share the same granulometry and friction; in general, oddly shaped particles tend to generate less deformable assemblies when compared with spherical particles of equal size [35]. Of course, a straightforward approach could take into account the simulation of all the detailed shapes, but this would lead to high simulation times, both because there will be multiple contacts between pairs of particles and because the collision detection phase would require more RAM and CPU time to process those contacts.

The rolling friction model discussed above can be used for simulating the granular materials such as in the example of Fig. 9. If one tries to simulate the pile of gravel with plain rigid spheres, the angle of repose of the cone will be small when compared with the real case, because the lack of irregularities on the simulated spheres lead to a loose, granular flow. Yet, by introducing increasing values of rolling and spinning friction in a model with simple spheres, the stacking is less loose and we can obtain the same results that one can achieve by introducing particles with odd shapes (which would require much larger computational resources).

Fig. 9

A typical pile of gravel and a conveyor, in a plant for separating raw materials

We simulated the free stacking of 10,000 particles, each with a diameter D _s =45 mm, falling from an height of 1 m into a 2 m × 2 m flat container. The density of the particles is δ=2 028 kg/m²; the sliding friction coefficient is μ=0.6, also used as static friction coefficient. The flow is about 800 particles/s, and gravity is g=−9.81 m/s². We simulated this system for increasing values of rolling and spinning friction. Specifically, we tested values of rolling friction parameter in the 0–0.01 m range; for simplicity we made the spinning friction parameter equal to the rolling one in all tests. The timestep was h=0.005 s, and the simulated time 15 s. As shown in Fig. 10, the case without rolling friction produces an almost flat stack, whereas Fig. 11 shows that the proposed rolling friction model is able to produce a steep cone typical of particles of irregular shapes yet featuring the benefit of using simple spheres (see also Figs. 12 and 13).

Fig. 10

Simulated pile of gravel, without rolling friction. Case with ρ=0 m, σ=0 m, after 13 s of simulation

Fig. 11

Simulated pile of gravel, with rolling friction ρ=0.01 m and spinning friction σ=0.01 m

Fig. 12

Angle of repose for different values of rolling friction

Fig. 13

Angle of repose ψ with same μ=0.6, for increasing values of ρ

7 Conclusion

We presented a rolling friction model that fits in the context of DVIs, and we discussed theoretical issues about the existence and uniqueness of the solution. Details about an implementation in the form of a convex cone-complementarity problem are given, showing that the approach features a relatively simple algorithmic complexity yet provides stable, fast, and robust solutions. These features, coupled with the ease of use, make the method a good candidate for enriching the capabilities of DVI simulations of rigid contacts, especially when fast, real-time performance is required or when a large number of parts is involved, such as in granular flows.

Appendices

Appendix A: Kinematics of rolling in three-dimensional space

Let $\mathbf {\omega}_{A,W}^{(W)}$ and $\mathbf {\omega}_{B,W}^{(W)}$ denote the angular velocities of two bodies A and B, relative to the absolute reference frame W and expressed in the basis of the frame (W). We assume A and B to be rigid or with negligible deformations. Introducing the rotation matrix R _A,W ∈SO(ℝ,3) that represents the rotation of A respect to W, we have $\mathbf {\omega}_{A,W}^{(W)} = {R}_{A,W} \mathbf {\omega}_{A,W}^{(A)}$ and $\mathbf {\omega}_{B,W}^{(W)} = {R}_{B,W} \mathbf {\omega}_{B,W}^{(A)}$.

Let the unimodular quaternion $\mathbf {\varepsilon }_{A,W} \in \mathbb{H}_{1}$ represent the rotation of the frame A respect to absolute frame W. We recall that, for unimodular quaternions, the inverse $\mathbf {\varepsilon }^{-1}$ is also the conjugate $\mathbf {\varepsilon }^{*}$. We also recall that it is possible to compute R from $\mathbf {\varepsilon }$ and vice versa.

Thanks to a property of quaternion algebra [13] the relative rotation of two references is

By performing differentiation respect to time, we get

From the result in [27], the quaternion derivative can be transformed in angular velocity, using pure quaternions:

(47)

(48)

Since $( \mathbf {\varepsilon }_{1}^{*} \mathbf {\varepsilon }_{2})^{*} = \mathbf {\varepsilon }_{2}^{*} \mathbf {\varepsilon }_{1}$, and remembering that $\mathbf {\varepsilon } \mathbf {\varepsilon }^{*} =1$, we can develop Eq. (48) into

(49)

The product $\dot{ \mathbf {\varepsilon }}_{B,W} \mathbf {\varepsilon }_{B,W}^{*}$ in the second term of the summation can be replaced with the pure quaternion $\frac{1}{2}[0, \mathbf {\omega}_{B,W}^{(W)}]$ using Eq. (47). Also, the first term can be premultiplied by $\mathbf {\varepsilon }_{A,W}^{*} \mathbf {\varepsilon }_{A,W} =1$, becoming $2 \mathbf {\varepsilon }_{A,W}^{*} \mathbf {\varepsilon }_{A,W} \dot{ \mathbf {\varepsilon }}_{A,W}^{*} \mathbf {\varepsilon }_{A,W}$; here the product between the second and third quaternion can be replaced with the pure quaternion $\frac{1}{2}[0, \mathbf {\omega}_{A,W}^{(W)}]^{*}$, again using Eq. (47). Thus we have

(50)

A rotation in 3D space of the vector part of a pure quaternion can be obtained with unitary quaternions, that is, $[0,\mathbf {v}^{(W)}]= \mathbf {\varepsilon }_{A,W} [0,\mathbf {v}^{(A)}] \mathbf {\varepsilon }_{A,W}^{*}$.

Hence, recalling that $[0, \mathbf {\omega}_{A,W}^{(W)}]^{*}= -[0, \mathbf {\omega}_{A,W}^{(W)}]$ by the property of conjugate quaternions, we can rewrite Eq. (50) and obtain the expected result for relative angular velocity $\mathbf {\omega}_{r}$:

$$ \everymath{\displaystyle }\begin{array}{@{}rll} \bigl[0,\mathbf {\omega}_{BA}^{(A)}\bigr] &=& - \bigl[0, \mathbf { \omega}_{A,W}^{(A)}\bigr] + \bigl[0, \mathbf { \omega}_{B,W}^{(A)}\bigr] \cr\noalign{\vspace{3pt}} \mathbf {\omega}_{BA}^{(A)} &=& \mathbf {\omega}_{B,W}^{(A)} - \mathbf {\omega}_{A,W}^{(A)}. \end{array} $$

(51)

Appendix B: Formulation of D vectors

We assume that the vector of generalized velocities v contains the speeds of the centers of mass of the bodies $\dot{\mathbf {x}}^{(W)}$, expressed in absolute coordinates (W) and the angular velocities $\mathbf {\omega}^{(i)}$ expressed in the local coordinates of the ith body, as $\mathbf {v}= [ \dot{\mathbf {x}}^{(W)}_{1}, \mathbf {\omega}^{(1)}_{1}, \dot{\mathbf {x}}^{(W)}_{2}, \mathbf {\omega}^{(2)}_{2}, \ldots ]^{T}$.

Given a contact between a pair of two rigid bodies A and B, we define the positions of the two contact points with respect to the centers of mass, expressed in the coordinate systems of the two bodies, as $\mathbf {s}_{A}^{(A)}$ and $\mathbf {s}_{B}^{(B)}$. The absolute rotations of the coordinate systems of the bodies are ${R}_{A}^{(W)}, {R}_{B}^{(W)} \in \mathsf{SO}(\mathbb{R},3)$ and the absolute rotation of the contact plane is ${R}_{P}^{(W)} \in \mathsf{SO}(\mathbb{R},3) = [ \mathbf {n}, \mathbf {u}, \mathbf {w} ]$. Thus, the vectors $\mathbf {D}_{\gamma_{n}}$, $\mathbf {D}_{\gamma_{u}}$, $\mathbf {D}_{\gamma_{w}}$ can be computed as ${D}_{\gamma}= [ \mathbf {D}_{\gamma_{n}}, \mathbf {D}_{\gamma_{u}}, \mathbf {D}_{\gamma_{w}} ] \in \mathbb{R}^{3 \times m_{v}}$,

(52)

where ${ \tilde {s}}$ is the skew symmetric matrix such that ${ \tilde {s}}\mathbf {x} = \mathbf {s} \wedge \mathbf {x}$.

Similarly, recalling the result in Eq. (51), one can compute the vectors $\mathbf {D}_{\tau_{n}}$, $\mathbf {D}_{\tau_{u}}$, $\mathbf {D}_{\tau_{w}}$ as ${D}_{\tau}= [ \mathbf {D}_{\tau_{n}}, \mathbf {D}_{\tau_{u}}, \mathbf {D}_{\tau_{w}} ] \in \mathbb{R}^{3 \times m_{v}}$:

(53)

We remark that, because of the extreme sparsity of (52) and (53), only the following four 3×6 matrices need to be stored per each contact

(54)

(55)

(56)

(57)

Here we considered B as the reference body: otherwise, if A were the reference for contact coordinates, signs should be swapped in all terms in Eqs. (52)–(57).

Appendix C: Computing projections on intersections of cones

We describe the procedure to compute the Euclidean projection of a point x on an intersection of circular cones that have one common component (in the case studied here, that component is the normal force). We assume that a generic point x is structured as follows:

(58)

and that the m circular cones are second-order cones defined by

where μ _i >0, i=1,2,…,m. We are interested in computing the projection of a vector x on ⋂K _i , that is,

For example, in the case treated in this work, we are interested in simultaneous modeling of sliding, rolling, and spinning friction in three dimensional configurations. That is, we have three cones, m=3 and x is a six-dimensional vector, x=(γ _n ,γ _u ,γ _w ,τ _u ,τ _w ,τ _n ). The mapping (58) is the following: x ₀=γ _n , l ₁=(γ _u ,γ _w ), l ₂=(τ _u ,τ _w ), l ₃=τ _n . The friction coefficients are μ ₁=μ, μ ₂=ρ, μ ₃=σ.

The crucial observation that simplifies the computation of the projection is that the component $\tilde{l}_{i}$ of the projection $\tilde{x}$ must be collinear with l _i . Indeed, if this is not the case, then rotating $\tilde{l}_{i}$ over l _i will preserve feasibility but will necessarily reduce $\| x-\tilde{x} \|$, a contradiction. Therefore, there exists t _i such that $\tilde{l}_{i}=t_{i} l_{i}$. The optimization that defines the projection then becomes

We have normalized the component of y in terms of y ₀ to allow for the range of t _i to be the same. For a given y ₀, the optimal t _i , which we denote by t _i (y ₀), is easy to compute. Indeed we obtain the following

Substituting t _i for the optimal values t _i (y ₀) in the optimization problem, we obtain that the problem is equivalent to

Here I is the indicator function of a set. It is immediately apparent that this function is piecewise quadratic and that it is convex. Indeed, convexity follows from the fact that each term function is convex, the first term as a quadratic, and the other terms as their graphs are the union of a parabola with a flat line.

To find its optimum, we can do the following.

• 1. Define and order the breakpoints 0, and $\frac{\| l_{i} \|}{\mu_{i}}$, with i=1,2,…,m. Successive breakpoints define a piece.

• 2. On each piece find the minimum of the quadratic function.

• 3. Compute the overall minimum, which is the lowest value of all such minima.

Once $\tilde{x}_{0}=y_{0}$ is determined, t _i (y ₀) is computed, and the other components of the projection are computed as $\tilde{l}_{i}=t_{i}(\tilde{x}_{0})\frac{\mu_{i} \tilde{x}_{0}}{\| l_{i} \|}$.

For a large number of breakpoints we can exploit convexity of ψ, by noting that we can evaluate the function at the breakpoints, and find the minimum value. Then, by convexity, the overall minimum must occur in a segment that neighbors the breakpoint with the minimum value. Hence, one minimizes the quadratic only in those intervals.

To summarize:

• 1. Define and order the breakpoints 0, and $\frac{\| l_{i} \|}{\mu_{i}}$, with i=1,2,…,m. Successive breakpoints define a piece. We assume without loss of generality that the labels have been permuted so that the natural order has the breakpoints in increasing order, that is, i<j⇒ $\frac{\| l_{i} \|}{\mu_{i}} < \frac{\| l_{j} \|}{\mu_{j}}$. If two breakpoints have the same value, we delete their index.

• 2. Enumerate the objective function ψ at the breakpoints, and find the i for which $\psi(\frac{\| l_{i} \|}{\mu_{i}}) \leq \psi(\frac{\| l_{j} \|}{\mu_{j}})$, ∀j. If there is one such i, the overall minimum is on a neighboring segment; if there are two, it is on the segment in between (there cannot be three different indices, since the function is not piecewise constant).

• 3. Minimize the piecewise quadratic on either the one or two segments identified, and report the result.

For a small number of breakpoints (i.e., the number of cones m is small), it is not likely that this reduced method would practically be much faster than comprehensive enumeration.