1 Introduction

The motion of a fluid in a rotating or translating cylinder is of interest to both theoretical and practical domains. The flow through rotating cylinders, started from rest, has applications in the food industry and is one of the most important and most interesting problems of motion near rotating bodies. It has been intensively studied since G.I. Taylor (1923) reported the results of his famous investigations [1]. For Newtonian fluids, the velocity distribution for a fluid contained in a circular cylinder can be found in [2], while the case of a fluid contained in an annular region between two cylinders, with a common axis, is given by [3]. Waters and King [4] studied the start-up Poiseuille flow of an Oldroyd-B fluid in a straight circular tube. The exact solution was obtained using the Laplace transform method. Since an integral form of the constitutive equation is used, only one initial condition is required for this unsteady problem. During recent years quite a number of papers on this type of flow have been published. Unsteady, pressure-driven flow of a classical Maxwell fluid in a pipe was studied by Rahaman and Ramkissoon [5]. Exact solutions were obtained as infinite Fourier-Bessel series. Wood [6] has considered the general case of helical flow of an Oldroyd-B fluid, due to the combined action of rotating cylinders (with constant angular velocities) and a constant axial pressure gradient. Hayat et al. [7] obtained the velocity fields for some simple flows of Oldroyd-B fluids using Fourier transform. Recently, Fetecau [8] has established exact solutions for some unidirectional flows of the same fluids in unbounded domains which geometrically are axi-symmetric pipelike.

It is very important to study the mechanism of viscoelastic fluids flow in many industry fields, such as oil exploitation, chemical and food industry and bio-engineering. The first exact solutions for flows of non-Newtonian fluids in such a domain seem to be those of Ting [9] corresponding to Second grade fluids and Srivastava [10] for Maxwell fluids. During recent years quite many papers of this type have been published. The most general solutions corresponding to the helical flow of a Second grade fluid seem to be those of Fetecau and Corina Fetecau [11], in which the cylinder is rotating around its axis and sliding along the same axis with time-dependent velocities. Other interesting solutions for different flows of the same fluids have been also obtained by Hayat et al. [12]. Exact solutions for the helical flows of Oldroyd-B fluid in cylindrical domains have been obtained Fetecau et al. [13]. In the meantime a lot of papers regarding such motions have been published [14, 15].

Nowadays, fractional calculus has encountered much success in the description of viscoelasticity [16–20]. The starting point of the fractional derivative model of a non-Newtonian fluid is usually a classical differential equation which is modified by replacing the time derivative of an integer order by the fractional calculus operators. This generalization allows one to define precisely non-integer order integrals or derivatives. Tan et al. [18] and Xu and Tan [21] examined the velocity field, stress field and vortex sheet of a generalized Second-order fluid with fractional anomalous diffusion. Song and Jiang [22] achieved satisfactory result to apply the constitutive equation with fractional derivative to the experimental data of viscoelasticity. Tan et al. [23] and Tan and Xu [24] applied fractional derivative to the constitutive relationship models of Maxwell viscoelastic fluid and Second grade fluid, and studied some unsteady flows.

The main idea of this work is to establish exact solutions for the velocity field, and the adequate shear stress corresponding to the unsteady rotational flow of an incompressible Oldroyd-B fluid with fractional derivatives through an infinite circular cylinder induced by a time-dependent shear. The motion of the fluid is produced by the cylinder, which after time t=0+, begins to rotate about its axis with a time-dependent angular velocity. The solutions that have been obtained, presented under series form in terms of the generalized G-functions, are established by means of the finite Hankel and Laplace transforms. The similar solutions for the Maxwell and Second grade fluids with fractional derivatives and for ordinary fluids (Oldroyd-B, Maxwell, Second grade and Newtonian fluids) performing the same motion, are obtained as limiting cases of general solutions.

2 Governing equations

The flows to be here considered have the velocity v and the extra-stress S of the form [25]

(1)

where e θ is the unit vector in the θ-direction of the cylindrical coordinates system r, θ and z. For such flows, the constraint of incompressibility is automatically satisfied.

Furthermore, if initially the fluid is at rest, then

(2)

The governing equations, corresponding to such motions of Oldroyd-B fluid, are given by [25]

(3)
(4)

where μ is the dynamic viscosity, ν=μ/ρ is the kinematic viscosity, ρ being the constant density of the fluid, λ is the relaxation time, λ r is the retardation time, and τ(r,t)=S rθ (r,t) is the non-trivial shear stress.

The governing equations corresponding to an incompressible Oldroyd-B fluid with fractional derivatives (OBFFD), performing the same motion, are obtained by replacing the inner time derivatives with respect to t from Eqs. (3) and (4), by the fractional differential operator [17, 26]

(5)

where Γ(⋅) is the Gamma function.

Consequently, the governing equations to be used here are

(6)
(7)

When β,γ→1, Eqs. (6) and (7) reduce to Eqs. (3) and (4), because \(D^{1}_{t}f=\frac{df}{dt} \). Furthermore, the new material constants λ and λ r (although, for the simplicity, we keep the same notation) reduce to the previous ones for β,γ→1.

3 Starting flow through an infinite circular cylinder

Suppose that an incompressible OBFFD is situated at rest in an infinite circular cylinder of radius R (>0). After time t=0+, the cylinder suddenly begins to rotate about its axis with an angular velocity Ωt p. Owing to the shear the inner fluid is gradually moved, its velocity being of the form (1)1. The governing equations are given by Eqs. (6) and (7), while the appropriate initial and boundary conditions are

(8)
(9)

where Ω is a constant and \(\emph{N}\) is the set of natural numbers.

Equations (6) and (7) containing fractional derivatives along with initial and boundary conditions can be solved in principle by several methods, i.e. Homotopy Perturbation Method (HPM), Variational Iteration Method (VIM), Homotopy Analysis Method (HAM), and Adomian Decomposition Method (ADM). Of these methods the integral transform technique is systematic, efficient and powerful tool. In the following, we shall use the Laplace transform to eliminate the time variable, and the finite Hankel transform for the removal of spatial variable. However, in order to avoid the burdensome calculations of residues and contour integrals, we shall apply the discrete inverse Laplace transform method.

3.1 Calculation of the velocity field

Applying the Laplace transform to Eqs. (7) and (9), we get

(10)
(11)

where \(\overline{w}(r,q)\) and \(\overline{w}(R,q)\) are the Laplace transforms of the functions w(r,t) and w(R,t), respectively.

We shall denote by [27]

$$ \overline{w}_{{}_H}(r_{{n}},q)=\int_0^Rr \overline{w}(r,q)J_1(rr_{{n}})\,dr , $$
(12)

the finite Hankel transform of the function \(\overline{w}(r,q)\), and the inverse Hankel transform of \(\overline{w}_{H}(r_{{n}},q)\) is given by [27]

r n being the positive roots of the equation J 1(Rr)=0, and J p (.) is the Bessel function of the first kind of order p. Multiplying now both sides of Eq. (10) by rJ 1(rr n ), then integrating with respect to r from 0 to R, and taking into account Eqs. (11) and (12), and the result which we can easily prove

(13)

we find that

(14)

It can be also written in the suitable form

(15)

where

(16a)
(16b)

Applying the inverse Hankel transform to Eqs. (16a) and (16b), and using the known formula

we get

(17a)
(17b)

Using the identity

(18)

Eq. (17b) can be written as

(19)

After taking the inverse Hankel transform of Eq. (15), it leads to

(20)

Now taking the inverse Laplace transform of Eq. (20), the velocity field w(r,t) is given by

(21)

where the generalized function G a,b,c (⋅,⋅) is defined by [28, Eqs. (97) and (101)]

(22)

3.2 Calculation of the shear stress

Applying the Laplace transform to Eq. (6), we find that

(23)

where \(\overline{w}(r,q)=\overline{w}_{1}(r,q)+\overline{w}_{2}(r,q)\).

Using Eqs. (17a) and (17b), we can calculate

(24)

and by using Eqs. (23) and (24), we have

(25)

In view of the identity (18), Eq. (25) can be equivalently written as

(26)

Now taking the inverse Laplace transform of both sides of Eq. (26) and using Eq. (22), we find that

(27)

4 The special cases

4.1 Ordinary Oldroyd-B fluid

Making β,γ→1 into Eqs. (21) and (27), we obtain the similar solutions for the velocity field

(28)

and for the shear stress

(29)

for an ordinary Oldroyd-B fluid performing the same motion.

4.2 Maxwell fluid with fractional derivatives

Making λ r →0 into Eqs. (21) and (27), we obtain the velocity field

(30)

and the associated shear stress

(31)

corresponding to Maxwell fluid with fractional derivatives performing the same motion are recovered [29, Eqs. (21) and (26)].

4.3 Ordinary Maxwell fluid

Making β→1 in Eqs. (30) and (31), we get the expressions for velocity field

(32)

and the associated shear stress

(33)

corresponding to an ordinary Maxwell fluid.

4.4 Second grade fluid with fractional derivatives

Making λ→0, taking νλ r =α and α 1=αρ (the material constants for Second grade fluid) into Eqs. (21) and (27), and using (A.1) and (A.2), the expressions for the velocity field

(34)

and the associated shear stress

(35)

corresponding to Second grade fluid with fractional derivatives performing the same motion are recovered [30, Eqs. (21) and (26)].

4.5 Ordinary Second grade fluid

Making γ→1 into Eqs. (34) and (35), we obtain the velocity field

(36)

and the associated shear stress

(37)

corresponding to an ordinary Second grade fluid performing the same motion.

These solutions can also simplified to give (see also Eqs. (A.3)–(A.4) from Appendix)

(38)
(39)

Equation (39) doesn’t hold for p=1, for linear case Ωt, we put p=1 in Eqs. (36) and (37), and using Eqs. (A.3) (for p=1) and (A.5) from Appendix, we get the following expression

(40)
(41)

which are the similar solutions for flows induced by a circular cylinder subject to a constant angular acceleration Ω that have been recently obtained in [13].

4.6 Newtonian fluid

Now, making λ r →0 in Eqs. (38) and (39), we get the velocity field w(r,t) as

(42)

and the associated shear stress

(43)

corresponding to a Newtonian fluid performing the same motion for p>1.

Now, making λ r →0 into Eqs. (40) and (41), we obtain the velocity field

(44)

and the associated shear stress

(45)

corresponding to a Newtonian fluid subject to flow induced by a circular cylinder which is subject to a constant angular acceleration Ω.

5 Numerical results and discussion

In the previous sections, exact analytical solutions for the velocity field and the adequate shear stress corresponding to the unsteady flow of an incompressible OBFFD through an infinite circular cylinder are obtained. In order to reveal some relevant physical aspects of the obtained results, the diagrams of the velocity as well as those of the shear stress are depicted against r for different values of time t and of the pertinent parameters.

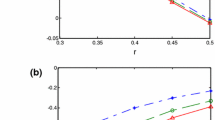
Figures 1a and 1b clearly show that both the velocity and the shear stress are increasing functions of t. They are also increasing functions of r, excepting τ(r,t) on a small interval near the boundary. Figure 2 shows the influence of the parameter p on the fluid motion, it shows that the velocity and the shear stress are also increasing functions of p. The influence of the kinematic viscosity ν on the fluid motion is shown in Figs. 3a and 3b, velocity w(r,t) is an increasing function of ν, while shear stress τ(r,t) is a decreasing function of ν.

Fig. 1
figure 1

Profiles of the velocity w(r,t) and shear stress τ(r,t) given by Eqs. (21) and (27) for R=0.2, V=1, p=2, λ=6, λ r =3, ν=0.0035, μ=2.96, β=0.7, γ=0.8 and different values of t

Full size image
Fig. 2
figure 2

Profiles of the velocity w(r,t) and shear stress τ(r,t) given by Eqs. (21) and (27) for t=4, R=0.2, V=1, λ=6, λ r =3, ν=0.0035, μ=2.96, β=0.7, γ=0.8 and different values of p

Full size image
Fig. 3
figure 3

Profiles of the velocity w(r,t) and shear stress τ(r,t) given by Eqs. (21) and (27) for t=5, p=2, R=0.2, V=1, λ=7, λ r =4, μ=2.96, β=0.6, γ=0.9 and different values of ν

Full size image

The influences of relaxation time λ and retardation time λ r on the velocity and shear stress are shown in Figs. 4 and 5. The two parameters, as expected, have opposite effects on the fluid motion. More exactly the velocity and the shear stress are decreasing functions with respect to λ and increasing ones with regards to λ r . The influences of the fractional parameters β and γ on the fluid motion are presented in Figs. 6 and 7. Their effects are also opposite, but they are qualitatively the same as those of λ r and λ, respectively. More exactly the velocity w(r,t) and the shear stress τ(r,t) are increasing functions with regards to β and decreasing ones with regards to γ.

Fig. 4
figure 4

Profiles of the velocity w(r,t) and shear stress τ(r,t) given by Eqs. (21) and (27) for t=6, R=0.2, p=2, V=2, λ r =5, ν=0.0025, μ=2.96, β=0.8, γ=0.9 and different values of λ

Full size image
Fig. 5
figure 5

Profiles of the velocity w(r,t) and shear stress τ(r,t) given by Eqs. (21) and (27) for t=6, R=0.2, p=2, V=1, λ=7, ν=0.003, μ=2.96, β=0.7, γ=0.8 and different values of λ r

Full size image
Fig. 6
figure 6

Profiles of the velocity w(r,t) and shear stress τ(r,t) given by Eqs. (21) and (27) for t=7, R=0.2, p=2, V=1, λ=6, λ r =3, ν=0.003, μ=2.96, γ=0.9 and different values of β

Full size image
Fig. 7
figure 7

Profiles of the velocity w(r,t) and shear stress τ(r,t) given by Eqs. (21) and (27) for t=7, R=0.2, p=2, V=1, λ=10, λ r =4, ν=0.003, μ=2.96, β=0.2 and different values of γ

Full size image

Finally, for comparison, the profiles of w(r,t) and τ(r,t) corresponding to the flow of Oldroyd-B, Maxwell and Second grade fluids with fractional derivatives and ordinary fluids (Oldroyd-B, Maxwell, Second grade and Newtonian) are together depicted in Fig. 8 for the same values of t and of the common material parameters. The Maxwell fluid with fractional derivatives, as it results from these figures, is the slowest and the Second grade fluid with fractional derivatives is the swiftest on the whole flow domain. The units of the material constants are SI units within all figures, and the roots r n have been approximated by (4n+1)π/(4R).

Fig. 8
figure 8

Profiles of the velocity w(r,t) and shear stress τ(r,t) corresponding to the Oldroyd-B, Maxwell and Second grade fluids with fractional derivatives and ordinary fluids (Oldroyd-B, Maxwell, Second grade and Newtonian), for t=6, R=0.2, p=2, V=1, λ=3, λ r =1, ν=0.003, μ=2, β=0.1 and γ=0.1

Full size image

6 Concluding remarks

The purpose of this paper was to establish exact analytical solutions for the velocity field and the adequate shear stress corresponding to the unsteady flow of an incompressible OBFFD through an infinite circular cylinder. The motion of the fluid is produced by the cylinder, which after time t=0+, begins to rotate about its axis with a time-dependent angular velocity. The solutions that have been obtained by means of the finite Hankel and Laplace transforms, are presented under series form in terms of the generalized G and Bessel functions satisfy all initial and boundary conditions. The similar solutions for the Maxwell and Second grade fluids with fractional derivatives and ordinary fluids (Oldroyd-B, Maxwell, Second grade and Newtonian fluids) performing the same motion, are obtained as limiting cases of general solutions. Furthermore, the solutions (30) and (31) corresponding to Maxwell fluid with fractional derivatives, solutions (34) and (35) corresponding to Second grade fluid with fractional derivatives and solutions (40) and (41) corresponding to Second grade fluid are equivalent to those obtained in [11, 29, 30] by a different technique. The results categorically indicate the following findings:

  • The solutions obtained for Maxwell and Second grade fluids with fractional derivatives and ordinary Second grade fluid by two different methods are equivalent.

  • It is noted that the velocity of the fluid is an increasing function with respect to t and r on the whole flow domain.

  • The velocity of the fluid increases for increasing ν while the shear stress has opposite property.

  • It is observed that rheological parameters λ and λ r have a strong influence on the fluid motion, but their effects are opposite.

  • The fractional parameters β and γ have a opposite effects on the fluid motion.

  • The rheological parameters λ and fractional parameters γ qualitatively have the same effects on the fluid motion. It is also observed that rheological parameters λ r and fractional parameters β qualitatively have same effects on the fluid motion, but opposite to λ and γ.

  • The Maxwell and Oldroyd-B fluids with fractional derivatives are slower than the ordinary Maxwell and Oldroyd-B fluids while Second grade fluid with fractional derivatives is faster than ordinary Second grade fluid.