1 Introduction

Nanofluids are multiphase colloidal suspensions which are comprised of nanometer sized metallic or non metallic particles suspended in abase liquid [1]. These liquids show a considerable increase in thermal conductivity for very small volume fraction of solid particles. Therefore, research is underway to apply nanofluids in environments where higher heat flux is en-countered and the conventional fluid is not capable of achieving the desired heat transfer. Kuznetsov and Nield [2] discussed natural convection boundary-layer flow of a nanofluid past a vertical plate. The Cheng–Minkowycz problem for natural convective boundary-layer flow in a porous medium saturated by a nanofluid was studied by Nield and Kuznetsov [3]. In this article they used a model incorporates the effects of Brownian motion and thermophoresis as well as the Darcy model for the porous medium. Kuznetsov and Nield [4] developed a theory of double-diffusive nanofluid convection in porous media and applied it to investigating the onset of nanofluid convection in a horizontal layer of a porous medium saturated by a nanofluid for the case when the base fluid of the nanofluid is itself a binary fluid such as salty water. Thermal instability in a porous medium layer saturated by a nanofluid was reported by Nield and Kuznetsov [5]. They found that the critical thermal Rayleigh number can be reduced or increased by a substantial amount, depending on whether the basic nanoparticle distribution is top-heavy or bottom-heavy, by the presence of the nanoparticles. A literature survey shows that the comprehensive review of these problems was made by the authors [6–11].

In recent years, the local thermal non-equilibrium model has been given considerable attention and has been utilized in various fields [12] due to its pertinence in applications. For example, Lee and Vafai [13] employed the thermal non-equilibrium model to investigate the forced convection flow through a channel filled with a porous medium. They obtained analytical solutions for the fluid- and solid-phase temperature distributions. Mansour et al. [14] used the non-equilibrium model to study natural convection a porous cavity under the influence of thermal radiation. Chamkha et al. [15] studied the flow and heat transfer of a micropolar fluid a long a elliptic cylinder in porous media using thermal non-equilibrium model. For nanofluids, Kuznetsov and Nield [16] reported on effect of local thermal non-equilibrium on the onset of convection in a porous medium layer.

On the other hand, the study of heat transfer near irregular surfaces is of fundamental importance because it is often found in many industrial applications. The presence of irregular surface not only alters the flow field but also alters the heat transfer characteristics. Hady et al. [17] discussed the problem of MHD free convection flow along a vertical wavy surface with heat generation or absorption effect. Kumar and Shalini [18] studied the non- Darcy free convection induced by a vertical wavy surface in a thermally stratified porous medium. Molla et al. [19] examined the natural convection flow along a vertical wavy surface with uniform surface temperature in the presence of heat generation or absorption. Hossain and Rees [20] studied the heat and mass transfer in natural convection flow along a vertical wavy surface with constant wall temperature and concentration in Newtonian fluids. Cheng [21] presented the solutions of the heat and mass transfer in natural convection flow along a vertical wavy surface in porous medium saturated with Newtonian fluids. Mahdy [22] investigated the effect of Soret and Dufour numbers on MHD non-Darcian free convection from a vertical wavy surface. Jang and Yan [23] studied the transient problem of natural convection heat and mass transfer along a wavy surface.

Motivated by the investigations mentioned above, the purpose of the present work is to consider the problem of boundary-layer free convection along a vertical wavy surface in a porous medium saturated by a nanofluid using thermal non-equilibrium model.

2 Formulation and analysis

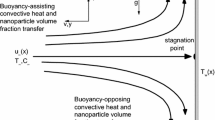
Consider unsteady, two-dimensional flow of a nanofluid consisting of a base fluid and small nanoparticles over a vertical wavy surface. Figure 1 shows the schematic of the problem under consideration and coordinate system. In the present problem, the following assumptions have been made:

  1. (a)

    The wavy surface is described by \(y = \bar{\sigma} (x) = \bar{a} \cdot\sin(2\pi x/L)\).

  2. (b)

    The fluid porous medium properties are assumed to be homogeneous.

  3. (c)

    The effect of Brownian motion is considered.

  4. (d)

    The local thermal non-equilibrium model among the particles, fluid, and solid-matrix phases is applied.

  5. (e)

    The Oberbeck–Boussinesq approximation is employed.

  6. (f)

    Initially, i.e. t<0, the fluid, wavy surface, particle temperatures and nanoparticles volume fraction have constant values T ∞ and ϕ ∞, respectively.

  7. (g)

    At time t=0, the temperatures of fluid, wavy surface, particles and nanoparticles volume fraction changed to new values T w and ϕ w , respectively.

Fig. 1
figure 1

Physical model and coordinates

Full size image

With the above assumptions, the governing equations for fluid flow are given as (see [2], [16] and [23]).

Continuity equation

$$ \nabla\cdot V = 0. $$
(1)

Momentum equation

(2)

Temperature equation for fluid phase

(3)

Temperature equation for particle phase

(4)

Temperature equation for solid phase

(5)

Nanoparticle volume fraction equation

$$ \frac{\partial\phi}{\partial t} + \frac{1}{\varepsilon} V \cdot\nabla\phi= D_{B}\bigl(\nabla^{2}\phi\bigr) + \biggl[ \frac{D_{T}}{T_{\infty}} \nabla^{2}T_{f} \biggr] $$
(6)

where, V=(u,v) is the velocity vector with u and v being the x- and y-components of velocity and all the parameters appearing in the above equations are given in the nomenclatures.

Introducing the following dimensionless quantities

$$ \begin{array}{l} \displaystyle\bar{x} = \frac{x}{L},\qquad\bar{y} = \frac{y - \bar{\sigma}}{L}\mathit{Ra}^{1/4},\qquad\tau= \frac{\alpha_{f}t}{L^{2}}\mathit{Ra}^{1/2},\\[7pt] \displaystyle\sigma=\frac{\bar{\sigma}}{L},\qquad \bar{u} = \frac{Lu}{\alpha_{f}}\mathit{Ra}^{ - 1/2},\\[7pt] \displaystyle\bar{v} = \frac{L}{\alpha_{f}}\mathit{Ra}^{ - 1/4} ( v - \sigma'u ),\qquad \bar{p} = \frac{L^{2}}{\rho\alpha_{f}^{2}}\mathit{Ra}^{ - 1}p,\\[7pt] \displaystyle\theta= \frac{T - T_{\infty}}{T_{w} - T_{\infty}} ,\qquad\varPhi= \frac{\phi- \phi_{\infty}}{\phi_{w} - \phi_{\infty}} . \end{array} $$
(7)

By using Eq. (7) and ignoring the small order terms in Ra (after allowing Ra→∞), Eqs. (1)–(6) are converted to

(8)
(9)
(10)
(11)
(12)
(13)
(14)

where,

(15)
(16)
(17)
(18)
(19)
(20)
(21)
(22)
(23)
(24)
(25)
(26)
(27)

In the current problem, the pressure gradient \(\frac{\partial \bar{p}}{\partial\bar{x}}\) is zero [23]. Therefore, Eqs. (9) and (10) can be reduced to the following equation:

(28)

It is noticeable that σ′ and σ″ indicate the first and second differentiations of σ with respect to \(\bar{x}\). In addition, the singularity at the leading edge can be removed by introducing the following transformation.

$$ \begin{array}{l} \displaystyle X = \bar{x},\qquad Y = \frac{\bar{y}}{(4\bar{x})^{1/4}}, \\[7pt] \displaystyle U = \frac{\bar{u}}{(4\bar{x})^{1/2}},\qquad V = (4\bar{x})^{1/4}\bar{v}. \end{array} $$
(29)

Equations (8), (11), (12), (13), (14) and (28) become:

(30)
(31)
(32)
(33)
(34)
(35)

The dimensionless forms of the boundary are

(36)

The local Nusselt number for fluid, particle and solid phases are defined, respectively, as:

(37)
(38)
(39)

The local Sherwood number is defined by:

(40)

The local skin friction coefficient C fx is defined as:

$$ C_{fx} = \frac{2\tau_{w}}{\rho\tilde{U}^{2}} $$
(41)

where \(\tilde{U} = \frac{L}{\alpha_{f}\mathit{Ra}^{1/2}}\) is characteristic velocity and the shearing stress on the wavy surface is

$$ \tau_{w} = \biggl[ \mu \biggl( \frac{\partial v}{\partial x} + \frac{\partial u}{\partial y} \biggr) \biggr]_{y = 0}. $$
(42)

Substituting Eq. (42) into Eq. (41) yields:

(43)

3 Results and discussion

In order to solve these unsteady, non-linear coupled Eqs. (32) to (35) under the conditions (36), an implicit finite difference scheme of Crank-Nicolson type has been employed. This method has been extensively developed in recent years and remains one of the most reliable procedures for solving partial differential equation systems. The details of this method can be found in recent article reported by Chamkha et al. [24]. The steady-state criteria for the relative deviations of the variables U, V, θ f , θ p , θ s and Φ between two time intervals is less than 10−5. Figure 2 shows an accuracy tests using the finite difference method using three sets of grids: 30×30, 40×40, 60×60. A 40×40 uniform grid is found to meet the requirements of both the grid independence study and the computational time limits. The numerical method was implemented in a FORTRAN software. The obtained results are plotted in 2D and 3D graphs by using ORIGIN6 software and MATLAB software, respectively. The results of the present problem are presented in Figs. 3–16. In all the results to be reported below, the values of N t , N b , N r , Pr and Le are taken to be 0.5, 0.5, 0.5, 10 and 10 respectively, as Kuznetsov and Nield [2]. Also, values of ε, ε p , ε s , γ p , γ s and Da are fixed at 0.4, 1, 1, 1, 1 and 1, respectively (Mansour et al. [14] and Chamkha et al. [15]).

Fig. 2
figure 2

Grid independence results at (A=0.1, Da=1, Le=10, Pr=10, N b =0.5, N r =0.5, N t =0.5, N Hp =1, N Hs =10)

Full size image
Fig. 3
figure 3

Effects of dimensionless time parameter τ on the local skin friction coefficient at (A=0.1, Da=1, Pr=10, Le=10, N b =0.5, N r =0.5, N t =0.5, N Hp =1, N Hs =1)

Full size image
Fig. 4
figure 4

Effects of dimensionless time parameter τ on the local Sherwood number at (A=0.1, Da=1, Pr=10, Le=10, N b =0.5, N r =0.5, N t =0.5, N Hp =1, N Hs =1)

Full size image
Fig. 5
figure 5

Effects of dimensionless time parameter τ on the local Nusselt for fluid phase at (A=0.1, Da=1, Pr=10, Le=10, N b =0.5, N r =0.5, N t =0.5, N Hp =1, N Hs =1)

Full size image
Fig. 6
figure 6

Effects of dimensionless time parameter τ on the local Nusselt number for particle phase at (A=0.1, Da=1, Pr=10, Le=10, N b =0.5, N r =0.5, N t =0.5, N Hp =1, N Hs =1)

Full size image

Figures 3–7 show the effects of dimensionless time parameter τ on the local skin friction coefficient, local Sherwood number, local Nusselt for fluid phase, local Nusselt number for particle phase and local Nusselt number for solid phase, respectively. It is found that, at the initial transients, the hydrodynamic boundary layer thickness and the wall shear stress take small values. The reason for that is the buoyancy-induced flow velocity is relatively low at the initial transients. As the time parameter τ increases the hydrodynamic boundary layer thickness and the wall shear stress increase, which in turn, the skin-friction coefficient increases as well. Also, the maximum values of skin-friction coefficient arises beside the wall but these values decreases as X increases (far way from the wall). Regarding the local Sherwood number, local Nusselt for fluid phase, local Nusselt number for particle phase and local Nusselt number for solid phase, it decrease with increase the dimensionless time parameter. In addition, at the initial transients the maximum values of the local Sherwood number, local Nusselt for fluid phase, local Nusselt number for particle phase and local Nusselt number for solid phase remain the same. But, as the time proceeds, these values decrease as X increases. All these behaviors are plotted in Figs. 3–7 with referenced case A=0.1, Da=1, Pr=10, Le=10, N b =0.5, N r =0.5, N t =0.5, N Hp =1, N Hs =1.

Fig. 7
figure 7

Effects of dimensionless time parameter τ on the local Nusselt number for solid phase at (A=0.1, Da=1, Pr=10, Le=10, N b =0.5, N r =0.5, N t =0.5, N Hp =1, N Hs =1)

Full size image

The effects of thermal nonequilibrium between the fluid and particle represented by the variations of Nield number for the fluid/particle interface N Hp on the steady profiles of local skin-friction coefficient and local Sherwood number are plotted in Fig. 8. The results show that, increasing in the Nield number for the fluid/particle interface N Hp leads to a decreasing the intensity of buoyancy and hence the flow intensity, which in turn, the skin-friction coefficient decreases as well. The same behavior is observed for the local Sherwood number. In addition, the variations of N Hp have a significant effects on the local Nusselt number for fluid, particle and sold-matrix phases. This clearly can be found in Fig. 9. The Nusselt number for fluid and solid-matrix phases increase as N Hp increases whereas, the Nusselt number for particle phase takes the inverse behaviors.

Fig. 8
figure 8

Effects of Nield number for the fluid/particle interface N Hp on the steady profiles of local skin-friction coefficient and local Sherwood number at (A=0.1, Da=1, Pr=10, Le=10, N b =0.5, N r =0.5, N t =0.5, N Hs =1)

Full size image
Fig. 9
figure 9

Effects of Nield number for the fluid/particle interface N Hp on the steady profiles of local Nusselt numbers for fluid, particle and solid phases at (A=0.1, Da=1, Pr=10, Le=10, N b =0.5, N r =0.5, N t =0.5, N Hs =1)

Full size image

With the help of Figs. 10 and 11, the effects of thermal nonequilibrium between the fluid and solid phases at the steady state can be observed. The variations of Nield number for the fluid/solid interface N Hs represent this influence. The referenced case for these figures is A=0.1, Da=1, Pr=10, Le=10, N b =0.5, N r =0.5, N t =0.5, N Hp =1. The results show that, increasing in N Hs results in an increase in the thermal nonequilibrium state between the fluid and solid phases. This can be found clearly in the profiles of skin-friction coefficient and local Nusselt number for solid matrix. These profiles have significant influences with variations of N Hs beside the wall but far away from the wall these influences is little observed. This can be attributed to the difference between the fluid temperature and solid-matrix temperature which decrease as X increases (far away from the wall). In addition, increasing in N Hs leads to increase both of skin-friction, local Nusselt number for fluid phase and local Nusselt number for solid phase, however, it decrease local Sherwood number and local Nusselt number for particle phase.

Fig. 10
figure 10

Effects of Nield number for the fluid/solid interface N Hs on the steady profiles of local skin-friction coefficient and local Sherwood number at (A=0.1, Da=1, Pr=10, Le=10, N b =0.5, N r =0.5, N t =0.5, N Hp =1)

Full size image
Fig. 11
figure 11

Effects of Nield number for the fluid/solid interface N Hs on the steady profiles of local Nusselt numbers for fluid, particle and solid phases at (A=0.1, Da=1, Pr=10, Le=10, N b =0.5, N r =0.5, N t =0.5, N Hp =1)

Full size image

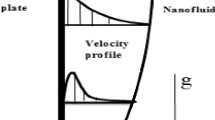
Figures 12–16 display the axial velocity component U, nanoparticle volume fraction Φ, fluid temperature θ f , particle temperature θ p and solid-matrix temperature θ s as a function of the axial and transverse coordinates at the steady-state case. It is clear that, the effect of sinusoidal variation of the wavy surface is significant through the profiles of the velocity, nanoparticle volume fraction, fluid temperature, particle temperature and solid matrix temperature. Also, the amplitude of the velocity component takes its maximum beside the wall and it decreases as X increases. However, the amplitudes of nanoparticle volume fraction, fluid temperature, particle temperature and solid matrix temperature remain the same. These profiles can be found in Figs. 12–16 with referenced case A=0.1, Da=1, Pr=10, Le=10, N b =0.5, N r =0.5, N t =0.5, N Hp =1, N Hs =1.

Fig. 12
figure 12

Axial velocity profiles at (A=0.1, Da=1, Pr=10, Le=10, N b =0.5, N r =0.5, N t =0.5, N Hp =1, N Hs =1)

Full size image
Fig. 13
figure 13

Profiles of nanoparticle volume fraction Φ at (A=0.1, Da=1, Pr=10, Le=10, N b =0.5, N r =0.5, N t =0.5, N Hp =1, N Hs =1)

Full size image
Fig. 14
figure 14

Fluid temperature profiles θ f at (A=0.1, Da=1, Pr=10, Le=10, N b =0.5, N r =0.5, N t =0.5, N Hp =1, N Hs =1)

Full size image
Fig. 15
figure 15

Particle temperature profiles θ p at (A=0.1, Da=1, Pr=10, Le=10, N b =0.5, N r =0.5, N t =0.5, N Hp =1, N Hs =1)

Full size image
Fig. 16
figure 16

Solid-matrix temperature profiles θ s at (A=0.1, Da=1, Pr=10, Le=10, N b =0.5, N r =0.5, N t =0.5, N Hp =1, N Hs =1)

Full size image

4 Conclusions

In the present paper, heat transfer by natural convection of a nanofluid over a wavy surface using thermal nonequilibrium model was studied. The nonequilibrium state was taken among fluid, particle and solid phases. A numerical solution of the problem was obtained using finite-difference method with Crank-Nicolson type. A parametric study was performed to examine the effects of dimensionless time parameter, Nield number for the fluid/particle interface and Nield number for the fluid/solid interface on the flow and heat transfer characteristics. From this investigation, we can draw the following conclusions:

  • The local skin-friction coefficient increases monotonically as the dimensionless time parameter increases, whereas, the local Sherwood number, local Nusselt numbers for fluid, particle and solid phases decreases as the dimensionless time parameter increases.

  • Increasing in the Nield number for the fluid/particle interface leads to increase the difference between the fluid and particle temperatures which increase the nonequilibrium state between the fluid and particle.

  • Both of Nusselt numbers for fluid and solid phases increase as Nield number for the fluid/particle interface increases whereas, the skin-friction coefficient, Sherwood number and Nusselt number for particle phase take the inverse behaviors.

  • Increasing in the Nield number for the fluid/solid interface leads to increase skin-friction coefficient, Nusselt number for fluid phase and Nusselt number for solid phase, whereas, the Sherwood number and Nusselt number for particle phase take the opposite behaviors.